西电随机信号分析大作业

数字信号处理MATLAB上机作业M 2.21.题目The square wave and the sawtooth wave are two periodic sequences as sketched in figure ing the function stem. The input data specified by the user are: desired length L of the sequence, peak value A, and the period N. For the square wave sequence an additional user-specified parameter is the duty cycle, which is the percent of the period for which the signal is positive. Using this program generate the first 100 samples of each of the above sequences with a sampling rate of 20 kHz ,a peak value of 7, a period of 13 ,and a duty cycle of 60% for the square wave.2.程序% 用户定义各项参数参数A = input('The peak value =');L = input('Length of sequence =');N = input('The period of sequence =');FT = input('The desired sampling frequency =');DC = input('The square wave duty cycle = ');% 产生所需要的信号t = 0:L-1;T = 1/FT;x = A*sawtooth(2*pi*t/N);y = A*square(2*pi*(t/N),DC);% Plotsubplot(2,1,1)stem(t,x);ylabel('幅度');xlabel('n');subplot(2,1,2)stem(t,y);ylabel('幅度');xlabel('n');3.结果4.结果分析M 2.41.题目(a)Write a matlab program to generate a sinusoidal sequence x[n]= Acos(ω0 n+Ф) and plot thesequence using the stem function. The input data specified by the user are the desired length L, amplitude A, the angular frequency ω0 , and the phase Фwhere 0<ω0 <pi and 0<=Ф<=2pi. Using this program generate the sinusoidal sequences shown in figure 2.15. (b)Generate sinusoidal sequences with the angular frequencies given in Problem 2.22.Determine the period of each sequence from the plot and verify the result theoretically. 2.程序%用户定义的参数L = input('Desired length = ');A = input('Amplitude = ');omega = input('Angular frequency = ');phi = input('Phase = ');%信号产生n = 0:L-1;x = A*cos(omega*n + phi);stem(n,x);xlabel('n');ylabel('幅度');title(['\omega_{o} = ',num2str(omega)]);3.结果(a)ω0=0ω0=0.1πω0=0.8πω0=1.2π(b)ω0=0.14πω0=0.24πω0=0.34πω0=0.68πω0=0.75π4.结果分析M 2.51.题目Generate the sequences of problem 2.21(b) to 2.21(e) using matlab.2.程序(b)n = 0 : 99;x=sin(0.6*pi*n+0.6*pi);stem(n,x);xlabel('n');ylabel('幅度');(c)n = 0 : 99;x=2*cos(1.1*pi*n-0.5*pi)+2*sin(0.7*pi*n);stem(n,x);xlabel('n');ylabel('幅度');(d)n = 0 : 99;x=3*sin(1.3*pi*n-4*cos(0.3*pi*n+0.45*pi));stem(n,x);xlabel('n');ylabel('幅度');(e)n = 0 : 99;x=5*sin(1.2*pi*n+0.65*pi)+4*sin(0.8*pi*n)-cos(0.8*pi*n);stem(n,x);xlabel('n');ylabel('幅度');(f)n = 0 : 99;x=mod(n,6);stem(n,x);xlabel('n');ylabel('幅度');3.结果(b)(c)(d)(e)(f)4.结果分析M 2.61.题目Write a matlab program to plot a continuous-time sinusoidal signal and its sampled version and verify figure 2.19. You need to use the hold function to keep both plots.2.程序%用户定义的参数fo = input('Frequency of sinusoid in Hz = ');FT = input('Samplig frequency in Hz = ');%产生信号t = 0:0.001:1;g1 = cos(2*pi*fo*t);plot(t,g1,'-')xlabel('时间t');ylabel('幅度')holdn = 0:1:FT;gs = cos(2*pi*fo*n/FT);plot(n/FT,gs,'o');hold off3.结果4.结果分析M 3.11.题目Using program 3_1 determine and plot the real and imaginary parts and the magnitude and phase spectra of the following DTFT for various values of r and θ:G(e jω)=1, 0<r<1.1−2r(cosθ)e−jω+r2e−2jω2.程序%program 3_1%discrete-time fourier transform computatition%k=input('Number of frequency points = ');num=input('Numerator coefficients= ');den=input('Denominator coefficients= ');%computer the frequency responsew=0:pi/k:pi;h=freqz(num,den,w);%plot the frequency responsesubplot(221)plot(w/pi,real(h));gridtitle('real part')xlabel('\omega/\pi');ylabel('Amplitude') subplot(222)plot(w/pi,imag(h));gridtitle('imaginary part')xlabel('\omega/\pi');ylabel('Amplitude') subplot(223)plot(w/pi,abs(h));gridtitle('magnitude spectrum')xlabel('\omega/\pi');ylabel('magnitude') subplot(224)plot(w/pi,angle(h));gridtitle('phase spectrum')xlabel('\omega/\pi');ylabel('phase,radians')3.结果(a)r=0.8 θ=π/6(b)r=0.6 θ=π/34.结果分析M 3.41.题目Using matlab verify the following general properties of the DTFT as listed in Table 3.2:(a) Linearity, (b) time-shifting, (c) frequency-shifting, (d) differentiation-in-frequency, (e) convolution, (f) modulation, and (g) Parseval’s relation. Since all data in matlab have to be finite-length vectors, the sequences to be used to verify the properties are thus restricted to be of finite length.2.程序%先定义两个信号N = input('The length of the sequence = ');k = 0:N-1;%g为正弦信号g = 2*sin(2*pi*k/(N/2));%h为余弦信号h = 3*cos(2*pi*k/(N/2));[G,w] = freqz(g,1);[H,w] = freqz(h,1);%*************************************************************************%% 线性性质alpha = 0.5;beta = 0.25;y = alpha*g+beta*h;[Y,w] = freqz(y,1);figure(1);subplot(211),plot(w/pi,abs(Y));xlabel('\omega/\pi');ylabel('|Y(e^j^\omega)|');title('线性叠加后的频率特性');grid;% 画出Y 的频率特性subplot(212),plot(w/pi,alpha*abs(G)+beta*abs(H));xlabel('\omega/\pi');ylabel('\alpha|G(e^j^\omega)|+\beta|H(e^j^\omega)|');title('线性叠加前的频率特性');grid;% 画出alpha*G+beta*H 的频率特性%*************************************************************************% % 时移性质n0 = 10;%时移10个的单位y2 = [zeros([1,n0]) g];[Y2,w] = freqz(y2,1);G0 = exp(-j*w*n0).*G;figure(2);subplot(211),plot(w/pi,abs(G0));xlabel('\omega/\pi');ylabel('|G0(e^j^\omega)|');title('G0的频率特性');grid;% 画出G0的频率特性subplot(212),plot(w/pi,abs(Y2));xlabel('\omega/\pi');ylabel('|Y2(e^j^\omega)|');title('Y2的频率特性');grid;% 画出Y2 的频率特性%*************************************************************************% % 频移特性w0 = pi/2; % 频移pi/2r=256; %the value of w0 in terms of number of samplesk = 0:N-1;y3 = g.*exp(j*w0*k);[Y3,w] = freqz(y3,1);% 对采样的512个点分别进行减少pi/2,从而生成G(exp(w-w0))k = 0:511;w = -w0+pi*k/512;G1 = freqz(g,1,w);figure(3);subplot(211),plot(w/pi,abs(Y3));xlabel('\omega/\pi');ylabel('|Y3(e^j^\omega)|');title('Y3的频率特性');grid;% 画出Y3的频率特性subplot(212),plot(w/pi,abs(G1));xlabel('\omega/\pi');ylabel('|G1(e^j^\omega)|');title('G1的频率特性');grid;% 画出G1 的频率特性%*************************************************************************% % 频域微分k = 0:N-1;y4 = k.*g;[Y4,w] = freqz(y4,1);%在频域进行微分y0 = ((-1).^k).*g;G2 = [G(2:512)' sum(y0)]';delG = (G2-G)*512/pi;figure(4);subplot(211),plot(w/pi,abs(Y4));xlabel('\omega/\pi');ylabel('|Y4(e^j^\omega)|');title('Y4的频率特性');grid;% 画出Y4的频率特性subplot(212),plot(w/pi,abs(delG));xlabel('\omega/\pi');ylabel('|delG(e^j^\omega)|');title('delG的频率特性');grid;% 画出delG的频率特性%*************************************************************************% % 相乘性质y5 = conv(g,h);%时域卷积[Y5,w] = freqz(y5,1);figure(5);subplot(211),plot(w/pi,abs(Y5));xlabel('\omega/\pi');ylabel('|Y5(e^j^\omega)|');title('Y5的频率特性');grid;% 画出Y5的频率特性subplot(212),plot(w/pi,abs(G.*H));%频域乘积xlabel('\omega/\pi');ylabel('|G.*H(e^j^\omega)|');title('G.*H的频率特性');grid;% 画出G.*H的频率特性%*************************************************************************% % 帕斯瓦尔定理y6 = g.*h;%对于freqz函数，在0到2pi直接取样[Y6,w] = freqz(y6,1,512,'whole');[G0,w] = freqz(g,1,512,'whole');[H0,w] = freqz(h,1,512,'whole');% Evaluate the sample value at w = pi/2% and verify with Y6 at pi/2H1 = [fliplr(H0(1:129)') fliplr(H0(130:512)')]';val = 1/(512)*sum(G0.*H1);% Compare val with Y6(129) i.e sample at pi/2 % Can extend this to other points similarly% Parsevals theoremval1 = sum(g.*conj(h));val2 = sum(G0.*conj(H0))/512;% Comapre val1 with val23.结果(a)(b)(c)(d)(e)4.结果分析M 3.81.题目Using matlab compute the N-point DFTs of the length-N sequences of Problem 3.12 for N=3, 5, 7, and 10. Compare your results with that obtained by evaluating the DTFTs computed in Problem 3.12 at ω= 2pik/N, k=0, 1,……N-1.2.程序%用户定义N的长度N = input('The value of N = ');k = -N:N;y1 = ones([1,2*N+1]);w = 0:2*pi/255:2*pi;Y1 = freqz(y1, 1, w);%对y1做傅里叶变换Y1dft = fft(y1);k = 0:1:2*N;plot(w/pi,abs(Y1),k*2/(2*N+1),abs(Y1dft),'o');grid;xlabel('归一化频率');ylabel('幅度');(a)clf;N = input('The value of N = ');k = -N:N;y1 = ones([1,2*N+1]);w = 0:2*pi/255:2*pi;Y1 = freqz(y1, 1, w);Y1dft = fft(y1);k = 0:1:2*N;plot(w/pi,abs(Y1),k*2/(2*N+1),abs(Y1dft),'o');xlabel('Normalized frequency');ylabel('Amplitude');(b)%用户定义N的长度N = input('The value of N = ');k = -N:N;y1 = ones([1,2*N+1]);y2 = y1 - abs(k)/N;w = 0:2*pi/255:2*pi;Y2 = freqz(y2, 1, w);%对y1做傅里叶变换Y2dft = fft(y2);k = 0:1:2*N;plot(w/pi,abs(Y2),k*2/(2*N+1),abs(Y2dft),'o');grid;xlabel('归一化频率');ylabel('幅度');(c)%用户定义N的长度N = input('The value of N = ');k = -N:N;y3 =cos(pi*k/(2*N));w = 0:2*pi/255:2*pi;Y3 = freqz(y3, 1, w);%对y1做傅里叶变换Y3dft = fft(y3);k = 0:1:2*N;plot(w/pi,abs(Y3),k*2/(2*N+1),abs(Y3dft),'o');grid;xlabel('归一化频率');ylabel('幅度');3.结果(a)N=3N=5 N=7N=10 (b)N=3N=5 N=7N=10 (c)N=3N=5 N=7N=104.结果分析M 3.191.题目Using Program 3_10 determine the z-transform as a ratio of two polynomials in z-1 from each of the partial-fraction expansions listed below:(a)X1(z)=−2+104+z−1−82+z−1,|z|>0.5,(b)X2(z)=3.5−21−0.5z−1−3+z−11−0.25z−2,|z|>0.5,(c)X3(z)=5(3+2z−1)2−43+2z−1+31+0.81z−2,|z|>0.9,(d)X4(z)=4+105+2z−1+z−16+5z−1+z−2,|z|>0.5.2.程序% Program 3_10% Partical-Fraction Expansion to rational z-Transform %r = input('Type in the residues = ');p = input('Type in the poles = ');k = input('Type in the constants = ');[num, den] = residuez(r,p,k);disp('Numberator polynominal coefficients');disp(num) disp('Denominator polynomial coefficients'); disp(den)4.结果分析M 4.61.题目Plot the magnitude and phase responses of the causal IIR digital transfer functionH(z)=0.0534(1+z−1)(1−1.0166z−1+z−2) (1−0.683z−1)(1−1.4461z−1+0.7957z−2).What type of filter does this transfer function represent? Determine the difference equation representation of the above transfer function.2.程序b=[0.0534 -0.00088644 -0.00088644 0.0534];a=[1 -2.1291 1.7833863 -0.5434631];figure(1)freqz(b,a);figure(2)[H,w]=freqz(b,a);plot(w/pi,abs(H)),grid;xlabel('Normalized Frequency (\times\pi rad/sample)'),ylabel('Magnitude');幅度化成真值之后：4.结果分析H(z)=0.0534−0.00088644z−1−0.00088644z−2+0.0534z−31−2.1291z−1+1.7833863z−2−0.5434631z−3M 4.71.题目Plot the magnitude and phase responses of the causal IIR digital transfer functionH(z)=(1−z−1)4(1−1.499z−1+0.8482z−2)(1−1.5548z−1+0.6493z−2).2.程序b=[1 -4 6 -4 1];a=[1 -3.0538 3.8227 -2.2837 0.5472]; figure(1)freqz(b,a);figure(2)[H,w]=freqz(b,a);plot(w/pi,abs(H)),grid;xlabel('Normalized Frequency (\times\pi rad/sample)'), ylabel('Magnitude');3.结果4.结果分析。

数字信号处理大作业班级：021231学号：姓名：指导老师：吕雁一写出奈奎斯特采样率和和信号稀疏采样的学习报告和体会1、采样定理在进行A/D信号的转换过程中，当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max>2fmax)，采样之后的数字信号完整地保留了原始信号中的信息，一般实际应用中保证采样频率为信号最高频率的5～10倍；采样定理又称奈奎斯特定理。

(1)在时域频带为F的连续信号 f(t)可用一系列离散的采样值f(t1),f(t1±Δt)，f(t1±2Δt)，...来表示,只要这些采样点的时间间隔Δt≤1/2F，便可根据各采样值完全恢复原始信号。

(2)在频域当时间信号函数f(t)的最高频率分量为fmax时,f(t)的值可由一系列采样间隔小于或等于1/2fo的采样值来确定,即采样点的重复频率fs ≥2fmax。

2、奈奎斯特采样频率(1)概述奈奎斯特采样定理：要使连续信号采样后能够不失真还原，采样频率必须大于信号最高频率的两倍（即奈奎斯特频率）。

奈奎斯特频率（Nyquist frequency）是离散信号系统采样频率的一半，因哈里·奈奎斯特（Harry Nyquist）或奈奎斯特－香农采样定理得名。

采样定理指出，只要离散系统的奈奎斯特频率高于被采样信号的最高频率或带宽，就可以真实的还原被测信号。

反之，会因为频谱混叠而不能真实还原被测信号。

采样定理指出，只要离散系统的奈奎斯特频率高于采样信号的最高频率或带宽，就可以避免混叠现象。

从理论上说，即使奈奎斯特频率恰好大于信号带宽，也足以通过信号的采样重建原信号。

但是，重建信号的过程需要以一个低通滤波器或者带通滤波器将在奈奎斯特频率之上的高频分量全部滤除，同时还要保证原信号中频率在奈奎斯特频率以下的分量不发生畸变，而这是不可能实现的。

在实际应用中，为了保证抗混叠滤波器的性能，接近奈奎斯特频率的分量在采样和信号重建的过程中可能会发生畸变。

随机信号分析习题一1. 设函数⎩⎨⎧≤>-=-0 ,0 ,1)(x x e x F x ，试证明)(x F 是某个随机变量ξ的分布函数.并求下列概率：)1(<ξP ，)21(≤≤ξP 。

2. 设),(Y X 的联合密度函数为(), 0, 0(,)0 , otherx y XY e x y f x y -+⎧≥≥=⎨⎩, 求{}10,10<<<<Y X P 。

3. 设二维随机变量),(Y X 的联合密度函数为⎥⎦⎤⎢⎣⎡++-=)52(21exp 1),(22y xy x y x f XY π 求:（1）边沿密度)(x f X ,)(y f Y（2)条件概率密度|(|)Y X f y x ，|(|)X Y f x y4. 设离散型随机变量X 的可能取值为{}2,1,0,1-，取每个值的概率都为4/1，又设随机变量3()Y g X X X ==-。

(1）求Y 的可能取值 （2）确定Y 的分布. （3）求][Y E 。

5. 设两个离散随机变量X ，Y 的联合概率密度为:)()(31)1()3(31)1()2(31),(A y A x y x y x y x f XY --+--+--=δδδδδδ试求：（1)X 与Y 不相关时的所有A 值。

（2）X 与Y 统计独立时所有A 值。

6. 二维随机变量（X ，Y )满足:ϕϕsin cos ==Y Xϕ为在[0，2π]上均匀分布的随机变量，讨论X ,Y 的独立性与相关性。

7. 已知随机变量X 的概率密度为)(x f ,求2bX Y =的概率密度)(y f .8. 两个随机变量1X ，2X ,已知其联合概率密度为12(,)f x x ,求12X X +的概率密度？9. 设X 是零均值，单位方差的高斯随机变量，()y g x =如图，求()y g x =的概率密度()Y f y\10. 设随机变量W 和Z 是另两个随机变量X 和Y 的函数222W X Y Z X⎧=+⎨=⎩ 设X ，Y 是相互独立的高斯变量。

随机信号分析大作业2016.12.6希尔伯特变换及其应用一、背景及意义在通信系统中，经常需要对一个信号进行正交分解，即分解为同相分量和正交分量。

由于希尔伯特变换可以提供90度的相位变化而不影响频谱分量的幅度，即对信号进行希尔伯特变换就相当于对该信号进行正交移相，使它成为自身的正交对。

因此，希尔伯特在通信领域获得了广泛应用。

对HHT采样频率、终止准则、曲线拟合、边界处理以及模态混叠等问题进行了分析，并基于HHT的时间特征尺度概念，提出了一种新的边界处理方法：边界局部特征尺度延拓法，较好地改善了边界效应对EMD分解的影响。

将HHT用于电力系统的信号处理，并根据HHT的信号突变检测性能，提出了一种超高压输电线路的EMD故障测距方法。

仿真实验表明，该方法能很好地实现故障定位及测距。

物理意义：希尔伯特可看成一种滤波，其本质上是对所有输入信号的90度相移器；对于稳定的实因果信号，其傅立叶变换的实部和虚部满足希尔伯特变换关系，同时其对数幅度谱和相位谱之间也满足此关系，前提是该信号为最小相位信号。

工程意义：对于自由度为一维的条信号，比如PAM，其等效基带信号是实的，这意味着对应的基带频谱是共轭对称的，即一半的频谱是冗余的，那么就可以将频谱滤除一半再进行传输，这就形成了所谓的单边带调制(SSB)。

而理论上，一个信号和其Hilbert 变化后的值相加，就可以得到所谓解析信号，该信号只保留原信号的正频谱。

而单边带调制虽然节省传输频率，但为了进行边带滤波，必须进行复杂的频谱成形，发送和接收的复杂度都比较高，相干载波的相位误差所造成的影响大。

所以，选择PAM信号进行频谱滤除的滤波器具有一定的滚降，即保留部分PAM信号中的冗余频谱，这样就成为VSB调制。

二、希尔伯特变换的发展现状近年来，随着现代信号的向前发展，人们从不同的研究领域和应用角度出发，提出了拓展经典Hilbert变换，提出了分数阶Hilbert变换，拓展了它的应用范围。

大连民族学院《随机信号分析》大作业9.3.2随机变量及其数字特征运算的MATLAB实现班级:学号:姓名:指导老师:二零一五年一月《随机信号分析》大作业摘要编制一通用程序，实现产生两个任意指定区间[a,b]和[c,d]上的均匀分布的随机变量。

分别计算这两个随机变量的均值和方差以及两个随机变量的协方差和相关系数，并根据计算结果分析这两个随机变量的相关性（两个随机数的长度要相等）。

关键词：均值；方差；协方差；相关系数目录摘要 (II)第1章要求 (1)1.1预习内容 (1)1.2任务 (1)1.3思考题 (1)第2章随机变量及其数字特征运算 (2)2.1连续型随机变量的数学期望（均值） (2)2.1.1连续型随机变量的数学期望 (2)2.1.2数学期望的性质 (2)2.2随机变量的方差 (2)2.2.1定义 (2)2.2.2性质 (3)2.3协方差和相关系数 (3)2.3.1定义 (3)2.3.2协方差的性质 (3)2.3.3相关系数的性质 (3)第3章程序实现及代码 (4)3.1任务 (4)3.1.1 代码 (4)3.1.2 结果 (5)3.1.3 结果分析 (6)3.2思考题 (7)3.2.1 代码 (7)3.2.2 结果 (8)参考文献 (11)B 卷 (12)第1章要求1.1 预习内容计算随机变量数字特性的部分MATLAB函数见表9.2，这些函数的调用方法及使用举例参见9.1节的相关内容。

1.2 任务编制一通用程序，实现产生两个任意指定区间[a,b]和[c,d]上的均匀分布的随机变量。

分别计算这两个随机变量的均值和方差以及两个随机变量的协方差和相关系数，并根据计算结果分析这两个随机变量的相关性（两个随机数的长度要相等）。

1.3 思考题利用MATLAB的在线帮助功能，自学与指数分布有关的MATLAB函数的使用方法。

编制一通用程序，实现产生任意指定参数λ1和λ2的两个指数分布随机变量（随机元素为30个）。

数字信号处理大作业班级：021231学号：姓名：指导老师：吕雁一写出奈奎斯特采样率和和信号稀疏采样的学习报告和体会1、采样定理在进行A/D信号的转换过程中，当采样频率fs.max大于信号中最高频率fmax的2倍时(fs.max>2fmax)，采样之后的数字信号完整地保留了原始信号中的信息，一般实际应用中保证采样频率为信号最高频率的5～10倍；采样定理又称奈奎斯特定理。

(1)在时域频带为F的连续信号 f(t)可用一系列离散的采样值f(t1),f(t1±Δt)，f(t1±2Δt)，...来表示,只要这些采样点的时间间隔Δt≤1/2F，便可根据各采样值完全恢复原始信号。

(2)在频域当时间信号函数f(t)的最高频率分量为fmax时,f(t)的值可由一系列采样间隔小于或等于1/2fo的采样值来确定,即采样点的重复频率fs ≥2fmax。

2、奈奎斯特采样频率(1)概述奈奎斯特采样定理：要使连续信号采样后能够不失真还原，采样频率必须大于信号最高频率的两倍（即奈奎斯特频率）。

奈奎斯特频率（Nyquist frequency）是离散信号系统采样频率的一半，因哈里·奈奎斯特（Harry Nyquist）或奈奎斯特－香农采样定理得名。

采样定理指出，只要离散系统的奈奎斯特频率高于被采样信号的最高频率或带宽，就可以真实的还原被测信号。

反之，会因为频谱混叠而不能真实还原被测信号。

采样定理指出，只要离散系统的奈奎斯特频率高于采样信号的最高频率或带宽，就可以避免混叠现象。

从理论上说，即使奈奎斯特频率恰好大于信号带宽，也足以通过信号的采样重建原信号。

但是，重建信号的过程需要以一个低通滤波器或者带通滤波器将在奈奎斯特频率之上的高频分量全部滤除，同时还要保证原信号中频率在奈奎斯特频率以下的分量不发生畸变，而这是不可能实现的。

在实际应用中，为了保证抗混叠滤波器的性能，接近奈奎斯特频率的分量在采样和信号重建的过程中可能会发生畸变。

DSP实验课程序设计报告学院：电子工程学院学号：1202121013姓名：赵海霞指导教师：苏涛DSP实验课大作业设计一实验目的在DSP上实现线性调频信号的脉冲压缩、动目标显示（MTI）和动目标检测(MTD)，并将结果与MATLAB上的结果进行误差仿真。

二实验内容2.1 MATLAB仿真设定带宽、脉宽、采样率、脉冲重复频率，用MATLAB产生16个脉冲的LFM，每个脉冲有4个目标（静止，低速，高速），依次做2.1.1 脉压2.1.2 相邻2脉冲做MTI，产生15个脉冲2.1.3 16个脉冲到齐后，做MTD，输出16个多普勒通道2.2 DSP实现将MATLAB产生的信号，在visual dsp中做脉压，MTI、MTD，并将结果与MATLAB作比较。

三实验原理3.1 线性调频线性调频脉冲压缩体制的发射信号其载频在脉冲宽度内按线性规律变化即用对载频进行调制(线性调频)的方法展宽发射信号的频谱，在大时宽的前提下扩展了信号的带宽。

若线性调频信号中心频率为f，脉宽为τ，带宽为B，幅度为A，μ为调频斜率，则其表达式如下：]212cos[)()(20t t f t rect A t x μπτ+••=；)(为矩形函数rect 在相参雷达中，线性调频信号可以用复数形式表示，即)]212(exp[)()(20t t f j t rect A t x μπτ+••= 在脉冲宽度内，信号的角频率由220μτπ-f 变化到220μτπ+f 。

3.2 脉冲压缩原理脉冲雷达信号发射时，脉冲宽度τ决定着雷达的发射能量，发射能量越大， 作用距离越远；在传统的脉冲雷达信号中，脉冲宽度同时还决定着信号的频率宽度B ，即带宽与时宽是一种近似倒数的关系。

脉冲越宽，频域带宽越窄，距离分辨率越低。

脉冲压缩的主要目的是为了解决信号的作用距离和信号的距离分辨率之间的矛盾。

为了提高信号的作用距离，我们就需要提高信号的发射功率，因此，必须提高发射信号的脉冲宽度，而为了提高信号的距离分辨率，又要求降低信号的脉冲宽度。

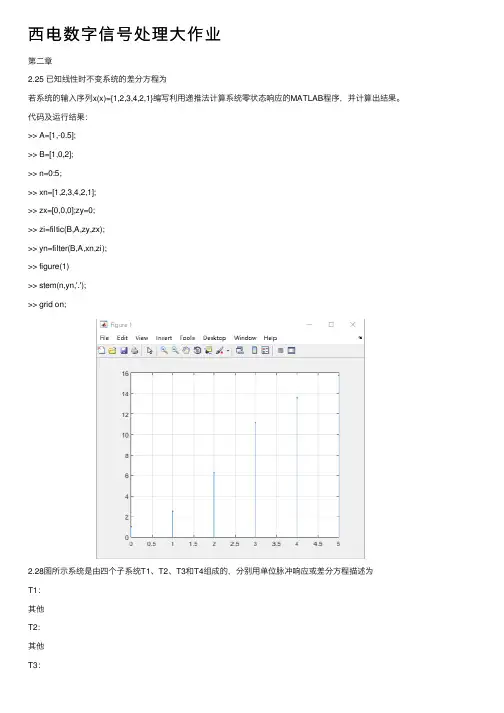
西电数字信号处理⼤作业第⼆章2.25 已知线性时不变系统的差分⽅程为若系统的输⼊序列x(x)={1,2,3,4,2,1}编写利⽤递推法计算系统零状态响应的MATLAB程序，并计算出结果。

代码及运⾏结果：>> A=[1,-0.5];>> B=[1,0,2];>> n=0:5;>> xn=[1,2,3,4,2,1];>> zx=[0,0,0];zy=0;>> zi=filtic(B,A,zy,zx);>> yn=filter(B,A,xn,zi);>> figure(1)>> stem(n,yn,'.');>> grid on;2.28图所⽰系统是由四个⼦系统T1、T2、T3和T4组成的，分别⽤单位脉冲响应或差分⽅程描述为T1：其他T2:其他T3：T4:编写计算整个系统的单位脉冲响应h(n)，0≤n≤99的MATLAB程序，并计算结果。

代码及结果如下：>> a=0.25;b=0.5;c=0.25;>> ys=0;>> xn=[1,zeros(1,99)];>> B=[a,b,c];>> A=1;>> xi=filtic(B,A,ys);>> yn1=filter(B,A,xn,xi);>> h1=[1,1/2,1/4,1/8,1/16,1/32]; >> h2=[1,1,1,1,1,1];>> h3=conv(h1,h2);>> h31=[h3,zeros(1,89)]; >> yn2=yn1+h31;>> D=[1,1];C=[1,-0.9,0.81]; >> xi2=filtic(D,C,yn2,xi); >> xi2=filtic(D,C,ys);>> yn=filter(D,C,yn2,xi); >> n=0:99;>> figure(1)>> stem(n,yn,'.');>> title('单位脉冲响应'); >> xlabel('n');ylabel('yn');2.30 利⽤MATLAB画出受⾼斯噪声⼲扰的正弦信号的波形，表⽰为其中v(n)是均值为零、⽅差为1的⾼斯噪声。

随机信号分析之简答题
1. 什么是随机过程非线性变换的变换法?
利用傅里叶变换或者拉普拉斯变换 ,将非线性函数变换成转移函数 ,将概率密度转换成特征函数 , 改变积分形式后再进行运算的方法就是变换法。

非线性变换的厄密特多项式法适用于何种随机过程?为什么?
适用于输入为正态随机过程。

因为输入随机过程为正态分布, 则可将用麦克劳林级数展开, 变成厄密特多项式, 由于分项积分容易计算, 正交性
重积分简化为一重积分。

此方法运算简便,因而广被引用。

普赖斯法适用的条件是什么?
普赖斯法适用于输入为平稳正态过程 , 且非线性函数经 k
缓变包络法适用的条件是什么?
缓变包络法适用于
2.
一维分布为瑞利分布 ,相位服从均匀分布
输出电压服从指数分布
N 次再积累输出,其输出随机变量服从何种分
加法器的输出电压服从 2N ,输出电压的均值为 2N ,方差为 4N 3. R (t 的一维概率分布服从何种分布?
服从
SNR<<1时, R (t 的一维概率分布近似为何种分布?
当信噪比时, R (t 的一维概率分布近似为何种分布? 近似为正态分布
By Elwin 2012年 11月 12日。

浅谈奈奎斯特频率采样和压缩感知信息技术的飞速发展使得人们对信息的需求量剧增。

现实世界的模拟化和信号处理工具的数字化决定了信号采样是从模拟信源获取数字信息的必经之路。

在信号和图像处理领域，凡是涉及到计算机作为处理工具的场合，所面临的首要问题就是模拟信号的数字化问题，然后再对得到的离散的样本进行各种处理。

连续信号转化为离散的数字化信号的过程称为采样。

对模拟信号采样所得的离散数字信号能否代表并恢复成原来的连续模拟信号呢？如能恢复应具备什么样的条件呢？这个问题直接关系到是否可以用数字处理工具和数字化的方法处理模拟信号。

一奈奎斯特频率采样奈奎斯特采样定理给我们提供了如何采样的重要理论基础。

它指出，如果信号是带限的，采样速率必须达到信号带宽的两倍以上才能精确重构信号。

事实上，在音频和可视电子设备、医学图像设备、无线接收设备等设备中的所有信号采样协议都隐含了这样的限制。

奈奎斯特采样定理至出现以来一直是数字信号和图像处理领域的重要理论基础，它支撑着几乎所有的信号和图像处理过程，包括信号和图像的获取、存储、处理、传输等。

采样定理，又称香农采样定理，奈奎斯特采样定理，是信息论，特别是通讯与信号处理学科中的一个重要基本结论.E.T.Whittaker (1915年发表的统计理论),克劳德·香农与Harry Nyquist都对它作出了重要贡献。

另外,V. A. Kotelnikov 也对这个定理做了重要贡献。

采样是将一个信号（即时间或空间上的连续函数）转换成一个数值序列（即时间或空间上的离散函数）。

采样定理指出，如果信号是带限的，并且采样频率高于信号带宽的一倍，那么，原来的连续信号可以从采样样本中完全重建出来。

带限信号变换的快慢受到它的最高频率分量的限制，也就是说它的离散时刻采样表现信号细节的能力是有限的。

采样定理是指，如果信号带宽小于奈奎斯特频率（即采样频率的二分之一），那么此时这些离散的采样点能够完全表示原信号。

《随机信号分析》试题1.考试形式：闭卷；2.考试日期：2011年11月23日；3.本试卷共8大题，满分100分。

一．填空与简答题（共30分，每小题3分）1．设()X t 为平稳过程，其自相关函数是以T 为周期的函数，即()()ττ+=X X R T R ，则有2{[()()]}-+=E X t X t T 。

2．已知{} ,2,1,=n X n 为仅取0或1的齐次马氏链，且{}6.0011===-N N X X P ，{}3.0111===-N N X X P ，则{}100N N P X X -=== ，{}=====00,1,11432X X X X P 。

3．设随机过程()X t 的数学期望为2[()]35E X t t =+，则随机过程2()()dX t Y t t t dt =+的数学期望为 。

4．某电话交换台在时间[0,]t 上受理的呼叫次数()X t 是泊松过程，其平均呼叫次数2λ=次/分钟，则在5分钟内电话呼叫次数为3次的概率为 ；泊松增量过程()()()X t t X t Y t t+∆-=∆的均值为 。

5．若输入信号()X t 是正态的，具有零均值的随机过程，其自相关函数为)(τX R ，经过某系统后，输出信号为2()()Y t bX t a =+，其中a 、b 为常数，则输出随机过程()Y t 的自相关函数()Y R τ= 。

6．线性系统输入为高斯过程，输出也是高斯过程。

若输入为非高斯过程，在什么条件下，系统的输出近似为高斯过程？7．一个均值具有遍历性的随机过程()X t 通过RC 低通滤波器的输出信号为()Y t ，问()Y t 的均值是否具有遍历性，并说明理由。

8．说明齐次马氏链平稳性的物理意义。

试问平稳的马氏链一定是遍历的吗？9．判断图1中的两条函数曲线是否为平稳过程的正确的自相关函数曲线，并说明理由。

()a ()b图110．简述随机过程的定义。

用什么来完整描述随机过程的统计特性？二．计算题（共70分，第1小题10分，其余五个小题各12分）1．已知随机过程()2sin X t V t =，其中V 是均值为3，方差为1的随机变量，求随机过程201()()Y t X d t πλλ=⎰的均值、相关函数、协方差函数和方差。

一、用matlab语言产生一个随机白噪声序列的样本序列X(n)，要求
3.用遍历性估计X(n)的自相关序列R X(m)，画出R X(m)的图像。

二、将一中产生的序列通过一个线性系统，其单位脉冲响应为h(n)=0.9n，n=0，
1，…，100
三、比较X(n)与Y(n)的幅度分布直方图，发生了什么变化。

分析其变化的原
因。

随机信号经过线性系统后，不会增加新的频率分量，但是输出的幅度和相位会发生变化。

白噪声X(n)的幅度基本相同，而Y(n)的幅度基本呈正态分布。

因为均匀白噪声是一种宽带非正态过程，所以通过一有限带宽线性系统后，输出Y(n)近似呈正态分布。

——via 1402011 赵春昊。

数字信号处理上机大作业实验一：信号、系统及系统响应(1) 简述实验目的及实验原理。

1.实验目的●熟悉连续信号经理想采样前后的频谱变化关系，加深对时域采样定理的理解。

●熟悉时域离散系统的时域特性。

●利用卷积方法观察分析系统的时域特性。

●掌握序列傅里叶变换的计算机实现方法，利用序列的傅里叶变换对连续信号、离散信号及系统响应进行频域分析。

2.实验原理与方法●时域采样。

● LTI系统的输入输出关系。

(2)按实验步骤附上实验过程中的信号序列、系统单位脉冲响应及系统响应序列的时域和幅频特性曲线，并对所得结果进行分析和解释。

Matlab源程序如下：A=1;T1=1/1000;T2=1/300;T3=1/200;a=25*pi;w0=30*pi;n=0:99;x1=A*exp(-a*n*T1).*sin(w0*n*T1);x2=A*exp(-a*n*T2).*sin(w0*n*T2);x3=A*exp(-a*n*T3).*sin(w0*n*T3);m=linspace(-pi,pi,10000);X1=x1*exp(-j*n'*m);%n'与m构造矩阵，xi向量与矩阵每一列相乘对应元素相加，构成DTFT后的矩阵X2=x2*exp(-j*n'*m);X3=x3*exp(-j*n'*m);figure(1);subplot(3,2,1)plot(m/pi,abs(X1));xlabel('\omega/π');ylabel('|H(e^j^\omega)|');title('采样频率为1000Hz时的幅度谱');subplot(3,2,3)plot(m/pi,abs(X2));xlabel('\omega/π');ylabel('|H(e^j^\omega)|');title('采样频率为300Hz时的幅度谱');subplot(3,2,5)plot(m/pi,abs(X3));xlabel('\omega/π');ylabel('|H(e^j^\omega)|');title('采样频率为200Hz时的幅度谱');subplot(3,2,2)plot(n,abs(x1));xlabel('n');ylabel('x1(t)');title('采样频率为1000Hz时的时域波形');subplot(3,2,4)plot(n,abs(x2));xlabel('n');ylabel('x2(t)');title('采样频率为300Hz时的时域波形');subplot(3,2,6)plot(n,abs(x3));xlabel('n');ylabel('x3(t)');title('采样频率为200Hz时的时域波形');波形图如下：-1-0.8-0.6-0.4-0.200.20.40.60.81ω/π|H (e j ω)|采样频率为1000Hz 时的幅度谱ω/π|H (e j ω)|采样频率为300Hz 时的幅度谱ω/π|H (e j ω)|采样频率为200Hz 时的幅度谱102030405060708090100nx 1(t )采样频率为1000Hz 时的时域波形nx 2(t )采样频率为300Hz 时的时域波形nx 3(t )采样频率为200Hz 时的时域波形② 时域离散信号、 系统和系统响应分析。

实验一、信号的采样clc,clear;dt=0.001;tf=6;t=0:dt:tf;xa=sqrt(t)+cos(t);T=0.5;n=0:tf/T;x=sqrt(n*T)+cos(n*T);figure(1)subplot(2,1,1)plot(t,xa),grid on ;title('original image')subplot(2,1,2)stem(n*T,x),grid on ,title('digital image')实验二、信号与系统的时域分析差分方程为)()2()1()(21n bx n y a n y a n y +----=，其中8.01-=a ，64.02=a ，866.0=b 。

系统单位脉冲响应)(n ha1=-0.8;a2=0.64;b=0.866;ys=0;xn=[1,zeros(1,49)];B=1;A=[1,a1,a2];xi=filtic(B,A,ys);yn=filter(B,A,xn,xi);n=0:length(yn)-1;subplot(1,1,1);stem(n,yn,'.')title('(a)');xlabel('n');ylabel('y(n)')输入x(n)=cos(n)T=0.1;z=cos(n*T);zn=conv(yn,z); figure(2);n1=1:99;stem(n1,zn,'.')实验三、系统的频域和Z域分析程序代码（画出dtft的幅度和频率谱）clc,clear;n=0:1:7;x=(0.9*exp(j*pi/3)).^n;w=0:pi/200:pi;X=x*exp(-j).^(n'*w);realX=real(X);imagX=imag(X);angX=angle(X);magX=abs(X);subplot(2,2,1);plot(w/pi,magX);grid xlabel('frequency in pi unit');title('magnitude part');subplot(2,2,2);plot(w/pi,realX);grid xlabel('frequency in pi unit');title('real part');subplot(2,2,3);plot(w/pi,imagX);grid xlabel('frequency in pi unit');title('imaginary part');subplot(2,2,4);plot(w/pi,angX);grid xlabel('frequency in pi unit');title('angel part');clc,clear;a=[1,-0.5,0.06];b=[1,1,0];m=0:length(b)-1;l=0:length(a)-1;w=0:pi/500:pi;num=b*exp(-j*m'*w);den=a*exp(-j*l'*w);H=num./den;magH=abs(H);angH=angle(H);H1=freqz(b,a,w);magH1=abs(H1);angH1=angle(H1);subplot(2,2,2);plot(w/pi,angH);grid;xlabel('w(frequency in pi units)');ylabel('Ïàλrad/w');subplot(2,2,1);plot(w/pi,magH);grid;xlabel('w(frequency in pi units)');ylabel('·ù¶È|H|');subplot(2,2,3);plot(w/pi,magH1);grid;xlabel('w(frequency in pi units)');ylabel('·ù¶È|H1|');subplot(2,2,4);plot(w/pi,angH);grid;xlabel('w(frequency in pi units)');ylabel('Ïàλrad/w');axis([0,1,-0.8,0]); figure(2);zplane(b,a);实验四、信号的频谱分析程序代码clc,clear;n=0:7;k=0:7;N=8;w=n*(2*pi)/8;x=(0.9*exp(j*pi/3)).^n;X1=[x zeros(1,8)];X2=[X1 zeros(1,16)];XK=x*exp(-j*k'*w);k1=0:15;n1=0:15;w1=n1*(2*pi)/16;XK1=X1*exp(-j*k1'*w1);k2=0:31;n2=0:31;w2=n2*(2*pi)/16;XK2=X2*exp(-j*k2'*w2);w3=0:pi/200:2*pi;X=x*exp(-j*n'*w3);magX=abs(X);angX=angle(X);magXK=abs(XK);angXK=angle(XK);magXK1=abs(XK1);angXK1=angle(XK1);magXK2=abs(XK2);angXK2=angle(XK2);subplot(4,2,1);plot(w3/pi,magX);xlabel('w/pi');ylabel('·ù¶È|X|');grid on;subplot(4,2,2);plot(w3/pi,angX);xlabel('w/pi');ylabel('Ïàλrad/pi'); subplot(4,2,3);stem(n,magXK);xlabel('K');ylabel('·ù¶È|XK|');subplot(4,2,4);stem(n,magXK);xlabel('K');ylabel('Ïàλrad/pi'); subplot(4,2,5);stem(n1,magXK1);xlabel('K1');ylabel('·ù¶È|XK1|'); subplot(4,2,6);stem(n1,magXK1);xlabel('K1');ylabel('Ïàλrad/pi'); subplot(4,2,7);stem(n2,magXK2);xlabel('K2');ylabel('·ù¶È|XK2|'); subplot(4,2,8);stem(n2,magXK2);xlabel('K2');ylabel('Ïàλrad/pi');实验五、IIR数字滤波器设计IIR汉宁窗低通高通低通巴特沃斯通带截止频率wp=0.2pi 通带最大衰减R=1dB阻带截止频率wp=0.35pi 阻带最大衰减R=10dBclc,clear;Wp=0.2;Ws=0.35;Rp=1;Rs=100;[N,Wc]=buttord(Wp,Ws,Rp,Rs);[Bz,Az]=butter(N,Wc)w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);;ang=angle(H);H=20*log10(abs(H))subplot(4,2,1); plot(w/pi,H) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('µÍͨÂ˲¨Æ÷')subplot(4,2,2);plot(w/pi,ang);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')[Bz1,Az1]=butter(N,Wc,'high')w=0:0.1:pi;[H1,w2]=freqz(Bz1,Az1,w);ang1=angle(H1);H1=20*log10(abs(H1))subplot(4,2,3); plot(w/pi,H1) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('¸ßͨÂ˲¨Æ÷')subplot(4,2,4);plot(w/pi,ang1);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')Wp1=[0.2 0.8];Ws1=[0.35 0.65];[N2,Wc1]=buttord(Wp1,Ws1,Rp,Rs);[Bz2,Az2]=butter(N2,Wc1,'stop')w=0:0.1:pi;[H2,w3]=freqz(Bz2,Az2,w);ang2=angle(H2);H2=20*log10(abs(H2))subplot(4,2,5); plot(w/pi,H2) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('´ø×èÂ˲¨Æ÷')subplot(4,2,6);plot(w/pi,ang2);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')Wp1=[0.2 0.8];Ws1=[0.35 0.65];[N2,Wc1]=buttord(Wp1,Ws1,Rp,Rs);[Bz3,Az3]=butter(N2,Wc1)w=0:0.1:pi;[H3,w4]=freqz(Bz3,Az3,w);ang3=angle(H3);H3=20*log10(abs(H3))subplot(4,2,7); plot(w/pi,H3) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('´øͨÂ˲¨Æ÷')subplot(4,2,8);plot(w/pi,ang3);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')切比雪夫1型通带截止频率wp=0.7pi 通带最大衰减R=1dB阻带截止频率wp=0.5pi 阻带最大衰减R=40dBclc,clear;Wp=0.7;Ws=0.5;Rp=1;Rs=40;[N,Wpo]=cheb1ord(Wp,Ws,Rp,Rs);[Bz,Az]=cheby1(N,Rp,Wpo)w=0:0.1:pi;[H,w1]=freqz(Bz,Az,w);ang=angle(H);H=20*log10(abs(H))subplot(4,2,1); plot(w/pi,H) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('µÍͨÂ˲¨Æ÷')subplot(4,2,2);plot(w/pi,ang);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')[Bz1,Az1]=cheby1(N,Rp,Wpo,'high');w=0:0.1:pi;[H1,w2]=freqz(Bz1,Az1,w);ang1=angle(H1);H1=20*log10(abs(H1))subplot(4,2,3); plot(w/pi,H1) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('¸ßͨÂ˲¨Æ÷')subplot(4,2,4);plot(w/pi,ang1);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')Wp1=[0.2 0.8];Ws1=[0.35 0.65];[N2,Wpo1]=cheb1ord(Wp1,Ws1,Rp,Rs);[Bz2,Az2]=cheby1(N2,Rp,Wpo1,'stop')w=0:0.1:pi;[H2,w3]=freqz(Bz2,Az2,w);ang2=angle(H2);H2=20*log10(abs(H2))subplot(4,2,5); plot(w/pi,H2) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('´ø×èÂ˲¨Æ÷')subplot(4,2,6);plot(w/pi,ang2);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')Wp1=[0.2 0.8];Ws1=[0.35 0.65];[N2,Wpo1]=cheb1ord(Wp1,Ws1,Rp,Rs);[Bz3,Az3]=cheby1(N2,Rp,Wpo1)w=0:0.1:pi;[H3,w4]=freqz(Bz3,Az3,w);ang3=angle(H3);H3=20*log10(abs(H3))subplot(4,2,7); plot(w/pi,H3) ;gridon ;xlabel('\omega/\pi');ylabel('|H(e^j^\omega)|/dB');title('´øͨÂ˲¨Æ÷')subplot(4,2,8);plot(w/pi,ang3);gridon ;xlabel('\omega/\pi');ylabel('Phase/dB')实验六、FIR数字滤波器设计FIR汉宁窗低通高通低通% 采用Hamming窗设计一个带阻FIR滤波器阻带：0~0.5pi，阻带最小衰减Rs=40dB；通带：0.5~pi，通带最大衰减：Rp=1dB。