机械原理作业答案 叶仲和 蓝兆辉版

8-3 推证渐开线齿轮法向齿距n p 、基圆齿距b p 和分度圆齿距p 之间的关系为式为απαcos cos m p p p b n ===。

证明：根据渐开线的性质：即渐开线的发生线沿基圆滚过的长度，等于基圆上被滚过的圆弧长度有b n p p =设齿轮的齿数为z ，模数为m ，基圆半径为b r ，分度圆半径为r ，压力角为α因为 b b r zp π2=，r zp π2= 又因为 αcos r r b = 所以 αcos p p b = 因为 m p π=所以 απαcos cos m p p p b n === 证毕。

8-4 用范成法加工渐开线直齿圆柱齿轮，刀具为标准齿条型刀具，其基本参数为：mm m 2=， 20=α，正常齿制。

（1）齿坯的角速度s rad5.221=ω时，欲切制齿数90=z 的标准齿轮，确定齿坯中心与刀具分度线之间的距离a 和刀具移动的线速度v ； （2）在保持上面的a 和v 不变的情况下，将齿坯的角速度改为s rad231=ω。

这样所切制出来的齿轮的齿数z 和变位系数x 各是多少？齿轮是正变位齿轮还是负变位齿轮？（3）同样，保持a 和v 不变的情况下，将齿坯的角速度改为s rad1.221=ω，所切制出来的齿轮的齿数z 和变位系数x 各是多少？最后加工的结果如何？ 解：（1）、由于是加工标准齿轮，齿坯中心与刀具分度线之间的距离为mm mz a 9029022=⨯==刀具移动的线速度为O解题8-3图s mm mz v 45.22129022=⋅⨯=⋅=ω （2）、齿轮的齿数z 为922312422=⨯⨯==ωm v z变位系数x 为122922902-=⨯-=-=m mz a x 因为变位系数小于零，所以齿轮是负变位齿轮。

（3）、齿轮的齿数z 为4.881.2212422=⨯⨯==ωm v z 变位系数x 为8.0224.882902=⨯-=-=m mz a x 因为变位系数为正，所以齿轮是正变位齿轮。

机械原理习题及答案修订版IBMT standardization office【IBMT5AB-IBMT08-IBMT2C-ZZT18】第二章 平面机构的结构分析2-1 绘制图示机构的运动简图。

2-3 计算图示机构的自由度，并指出复合铰链、局部自由度和虚约束。

解：(a) C 处为复合铰链。

7,n =p h =0，p l =10。

自由度 323721001W l h F n p p =--=⨯-⨯-=。

(b) B 处为局部自由度，应消除。

3n =， p h =2，p l =2自由度 323323121W l h F n p p =--=⨯-⨯-⨯=。

(c) B 、D 处为局部自由度，应消除。

3n =， p h =2，p l =2。

自由度 323323121W l h F n p p =--=⨯-⨯-⨯=。

(d) CH 或DG 、J 处为虚约束，B 处为局部自由度，应消除。

6n =，p h =1，p l =8。

自由度 32362811W l h F n p p =--=⨯-⨯-=。

(e) 由于采用对称结构，其中一边的双联齿轮构成虚约束，在连接的轴颈处，外壳与支架处的连接构成一个虚约束转动副,双联齿轮与外壳一边构成虚约束。

其中的一边为复合铰链。

其中4n =，p h =2，p l =4。

自由度 32342422W l h F n p p =--=⨯-⨯-=。

(f) 其中，8n =，p h =0，p l =11。

自由度 323821102W l h F n p p =--=⨯-⨯-=。

(g) ① 当未刹车时，6n =，p h =0，p l =8，刹车机构自由度为② 当闸瓦之一刹紧车轮时，5n =，p h =0，p l =7，刹车机构自由度为③ 当两个闸瓦同时刹紧车轮时，4n =，p h =0，p l =6，刹车机构自由度为2-3 判断图示机构是否有确定的运动，若否，提出修改方案。

分析 (a) 要分析其运动是否实现设计意图，就要计算机构自由度，不难求出该机构自由度为零，即机构不能动。

机械原理课后习题答案（顺序有点乱，不过不影响）第2章2-1 何谓构件?何谓运动副及运动副元素?运动副是如何进行分类的?答：参考教材5~7页。

2-2 机构运动简图有何用处?它能表示出原机构哪些方面的特征?答：机构运动简图可以表示机构的组成和运动传递情况，可进行运动分析，而且也可用来进行动力分析。

2-3 机构具有确定运动的条件是什么?当机构的原动件数少于或多于机构的自由度时，机构的运动将发生什么情况?答：参考教材12~13页。

2-4 何谓最小阻力定律?试举出在机械工程中应用最小阻力定律的1、2个实例。

2-5 在计算平面机构的自由度时，应注意哪些事项?答：参考教材15~17页。

2-6 在图2-20所示的机构中，在铰链C、B、D处，被连接的两构件上连接点的轨迹都是重合的，那么能说该机构有三个虚约束吗?为什么?答：不能，因为在铰链C、B、D中任何一处，被连接的两构件上连接点的轨迹重合是由于其他两处的作用，所以只能算一处。

2-7 何谓机构的组成原理?何谓基本杆组?它具有什么特性?如何确定基本杆组的级别及机构的级别?答：参考教材18~19页。

2-8 为何要对平面高副机构进行“高副低代"?“高副低代”应满足的条件是什么?答：参考教材20~21页。

2-9 任选三个你身边已有的或能观察到的下列常用装置(或其他装置)，试画出其机构运动简图，并计算其自由度。

1)折叠桌或折叠椅；2)酒瓶软木塞开盖器；3)衣柜上的弹簧合页；4)可调臂台灯机构；5)剥线钳；6)磁带式录放音机功能键操纵机构；7)洗衣机定时器机构；8)轿车挡风玻璃雨刷机构；9)公共汽车自动开闭门机构；10)挖掘机机械臂机构；…。

2-10 请说出你自己身上腿部的髋关节、膝关节和踝关节分别可视为何种运动副?试画出仿腿部机构的机构运动简图，并计算其自由度。

2-11图示为一简易冲床的初拟设计方案。

设计者的思路是：动力由齿轮j输入，使轴A连续回转；而固装在轴^上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动，以达到冲压的目的。

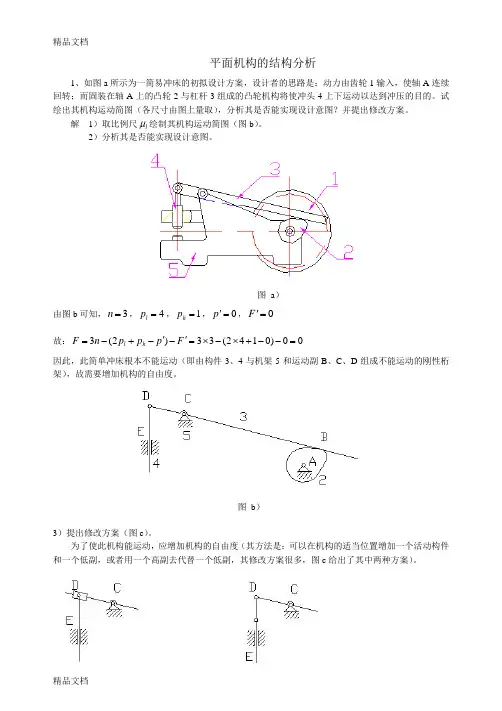
平面机构的结构分析1、如图a 所示为一简易冲床的初拟设计方案，设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。

试绘出其机构运动简图（各尺寸由图上量取），分析其是否能实现设计意图？并提出修改方案。

解 1）取比例尺l μ绘制其机构运动简图（图b ）。

2）分析其是否能实现设计意图。

图 a ） 由图b 可知，3=n ，4=l p ，1=h p ，0='p ，0='F 故：00)0142(33)2(3=--+⨯-⨯='-'-+-=F p p p n F h l因此，此简单冲床根本不能运动（即由构件3、4与机架5和运动副B 、C 、D 组成不能运动的刚性桁架），故需要增加机构的自由度。

图 b ）3）提出修改方案（图c ）。

为了使此机构能运动，应增加机构的自由度（其方法是：可以在机构的适当位置增加一个活动构件和一个低副，或者用一个高副去代替一个低副，其修改方案很多，图c 给出了其中两种方案）。

图 c1） 图 c2）2、试画出图示平面机构的运动简图，并计算其自由度。

图a ）解：3=n ，4=l p ，0=h p ，123=--=h l p p n F图 b ）解：4=n ，5=l p ，1=h p ，123=--=h l p p n F3、计算图示平面机构的自由度。

将其中的高副化为低副。

机构中的原动件用圆弧箭头表示。

3－1解3－1：7=n ，10=l p ，0=h p ，123=--=h l p p n F ，C 、E 复合铰链。

3－2解3－2：8=n ，11=l p ，1=h p ，123=--=h l p p n F ，局部自由度3－3 解3－3：9=n ，12=l p ，2=h p ，123=--=h l p p n F4、试计算图示精压机的自由度解：10=n ，15=l p ，0=h p 解：11=n ，17=l p ，0=h p13305232=⨯-+⨯='-'+'='n p p p h l 26310232=⨯-⨯='-'+'='n p p p h l0='F 0='FF p p p n F h l '-'-+-=)2(3 F p p p n F h l '-'-+-=)2(310)10152(103=--+⨯-⨯= 10)20172(113=--+⨯-⨯=（其中E 、D 及H 均为复合铰链） （其中C 、F 、K 均为复合铰链）5、图示为一内燃机的机构简图，试计算其自由度，并分析组成此机构的基本杆组。

机械原理课后全部习题答案目录第1章绪论 (1)第2章平面机构的结构分析 (3)第3章平面连杆机构 (8)第4章凸轮机构及其设计 (15)第5章齿轮机构 (19)第6章轮系及其设计 (26)第8章机械运动力学方程 (32)第9章平面机构的平衡 (39)第一章绪论一、补充题1、复习思考题1)、机器应具有什么特征？机器通常由哪三部分组成？各部分的功能是什么？2）、机器与机构有什么异同点？3）、什么叫构件？什么叫零件？什么叫通用零件和专用零件？试各举二个实例。

4）、设计机器时应满足哪些基本要求？试选取一台机器，分析设计时应满足的基本要求。

2、填空题1)、机器或机构，都是由组合而成的。

2）、机器或机构的之间，具有确定的相对运动。

3）、机器可以用来人的劳动，完成有用的。

4）、组成机构、并且相互间能作的物体，叫做构件。

5）、从运动的角度看，机构的主要功用在于运动或运动的形式。

6）、构件是机器的单元。

零件是机器的单元。

7）、机器的工作部分须完成机器的动作，且处于整个传动的。

8）、机器的传动部分是把原动部分的运动和功率传递给工作部分的。

9）、构件之间具有的相对运动，并能完成的机械功或实现能量转换的的组合，叫机器。

3、判断题1)、构件都是可动的。

（）2）、机器的传动部分都是机构。

（）3）、互相之间能作相对运动的物件是构件。

（）4）、只从运动方面讲，机构是具有确定相对运动构件的组合。

（）5）、机构的作用，只是传递或转换运动的形式。

（）6）、机器是构件之间具有确定的相对运动，并能完成有用的机械功或实现能量转换的构件的组合。

（）7）、机构中的主动件和被动件，都是构件。

（）2 填空题答案1）、构件2）、构件3）、代替机械功4）、相对运动5）、传递转换6）、运动制造7）、预定终端8）、中间环节9）、确定有用构件3判断题答案1）、√2）、√3）、√4）、√5）、×6）、√7）、√第二章 机构的结构分析2-7 是试指出图2-26中直接接触的构件所构成的运动副的名称。

机械原理课后习题答案（顺序有点乱，不过不影响）第2章2-1 何谓构件?何谓运动副及运动副元素?运动副是如何进行分类的?答：参考教材5~7页。

2-2 机构运动简图有何用处?它能表示出原机构哪些方面的特征?答：机构运动简图可以表示机构的组成和运动传递情况，可进行运动分析，而且也可用来进行动力分析。

2-3 机构具有确定运动的条件是什么?当机构的原动件数少于或多于机构的自由度时，机构的运动将发生什么情况?答：参考教材12~13页。

2-4 何谓最小阻力定律?试举出在机械工程中应用最小阻力定律的1、2个实例。

2-5 在计算平面机构的自由度时，应注意哪些事项?答：参考教材15~17页。

2-6 在图2-20所示的机构中，在铰链C、B、D处，被连接的两构件上连接点的轨迹都是重合的，那么能说该机构有三个虚约束吗?为什么?答：不能，因为在铰链C、B、D中任何一处，被连接的两构件上连接点的轨迹重合是由于其他两处的作用，所以只能算一处。

2-7 何谓机构的组成原理?何谓基本杆组?它具有什么特性?如何确定基本杆组的级别及机构的级别?答：参考教材18~19页。

2-8 为何要对平面高副机构进行“高副低代"?“高副低代”应满足的条件是什么?答：参考教材20~21页。

2-9 任选三个你身边已有的或能观察到的下列常用装置(或其他装置)，试画出其机构运动简图，并计算其自由度。

1)折叠桌或折叠椅；2)酒瓶软木塞开盖器；3)衣柜上的弹簧合页；4)可调臂台灯机构；5)剥线钳；6)磁带式录放音机功能键操纵机构；7)洗衣机定时器机构；8)轿车挡风玻璃雨刷机构；9)公共汽车自动开闭门机构；10)挖掘机机械臂机构；…。

2-10 请说出你自己身上腿部的髋关节、膝关节和踝关节分别可视为何种运动副?试画出仿腿部机构的机构运动简图，并计算其自由度。

2-11图示为一简易冲床的初拟设计方案。

设计者的思路是：动力由齿轮j输入，使轴A连续回转；而固装在轴^上的凸轮2与杠杆3组成的凸轮机构使冲头4上下运动，以达到冲压的目的。

2-8解：（1）取μ= m/mml作机构位置图如（a)图（2）求v、ω、列矢量方程式取μ,作速度（b)图v（3）求a、α列矢量方程式作加速度（c)图题5-8解αa1=arccos(rb/ra1)=arccos[(z1cosα)/(z1+2ha*)] =31°46′O1 α PN2B2N1αa2=26°14′10″B1P=B1N1-N1PB1 PbⅠ=mz1/2·cosα(tgαa1- tgα′)=11.39mm B2P=12.72mm B1B2=24.11mm 作用弧CD=B1B2cosα′=25.66mm 作用角 ϕ 1 =CD/r1′=25.66/47.5=30°58 ′αⅡO2εα=B1B2/Pb=1.63题5-12解N 1 N 2 = 2 N 1 P = 2r sin α N 1 N 2 2r sin α ∴ tgα a = = = 2tgα = 0.7279 O1 N 1 r cos α 3′ α a = 36° 9″ rb r cos α z cos α 又 cos α a = = = * ra r + ha z + 2ha* 2ha cos α ∴z = = 12.323 cos α − cos α aO1 α ra rb (B2) αa P rb ra αa α O2 N1(B1) N2∴不根切，z最少为13题5-13解h m − xm = MN* aMN = PN sinα = OPsin2 α mz 2 = sin α 2* az 2 x = h − sin α 2x=1-35/2 sin 20° =-1.0471 or x=(17-35)/17=-1.05882题5-15解解题思路： 1.设计题，主要确定尺寸 r 、ra、r f 、rb 2.变位齿轮传动设计步骤：由 a 、 a ′、 α → α ′ → x Σ → x 1、 x 2 ← x min ← 据 z = 12 z Σ、 α 、 α ′ → y 、 x Σ → ∆ y 计算： r 、 ra、 r f 、 rb 3 .验证 s a < 0 .2 m 、 ε α ≥ 1题5-15解1.选择传动类型 2. 求 α ′和 x Σα ′ = arccos(m a = ( z1 + z 2 ) = 120mm < a ′ 2a cos α ) = 29 ° 5 0 ′ 2 8 ′′ a′x∑( z 1 + z 2 )( inv α ′ − inv α ) = = 1 . 2505 2 tg α17 − 12 z1 = z2 = 12 < 17,∴ x1.2 > = 0.2941 17 ∴ x1 = x2 = x∑ / 2 = 1.2505/ 2 = 0.62533.分配 x 1 和 x 24.求y和∆y y = (a ′ − a ) / m = (130 − 120) / 10 = 1; ∆y = x ∑ − y = 0.2505 mz 1.2 = 60mm 5.r1.2 = 2 * ra 1.2 = r1.2 + ( ha + x1.2 − ∆y )m = 73.75mm* r f 1.2 = r1.2 − ( ha + c * − x1.2 )m = 53.75mmmz 1.2 rb1.2 = cos α = 56.38mm 2 6.验算sa 和ε α ′23 s = (π / 2 + 2 x1.2 tgα )m = 20.26mm ;α a 1.2 = arccos(rb1.2 / ra 1.2 ) = 40°8 ″ sa 1.2 = s ra 1.2 − 2ra 1.2 ( invα a 1.2 − invα ) r1.2 73.75 − 2 × 73.75(0.142715 − 0.014904) = 6.05mm > 0.2m 60= 20.26 ×题5-15解1 [ z1 ( tgα a 1 − tgα ′ ) + z 2 ( tgα a 2 − tgα ′ )] εα = 2π 1 = z1 ( tgα a 1 − tgα ′ ) = 1.03π题5-16解 用等变位修复，小正变位；大负变位* * ∆d a 2 = d 2 + 2( ha + x 2 )m − ( d 2 + 2ha m ) = 2 x 2 m则 x 2 = ∆d a 2 / 2m = −1 而 x1 = − x 2 = 1d 1 = 96mm ; d 2 = 384mm ; d a 1 = 112mm ; d a 2 = 384mm ; d f 1 = 94mm ; d f 2 = 366mm ; d b1 = 90.21mm ; d b 2 = 360.84mm ; a ′ = a = 240mm .验算sa 和ε α d b1 α a 1 = arccos( ) = 36°21′; d a1α a 2 = 20° sa 1 = πm / 2 • d a 1 / d 1 − d a 1 ( invα a 1 − invα )= 1.02mm > 0.2m sa 2 ↑ 不验算 1 εα = [ z1 ( tgα a 1 − tgα ) + z 2 ( tgα a 2 − tgα )] 2π = 1.42mn (1 ) a ′ = a 12 = ( z3 + z4 ) 34 2 cos β ∴ cos β = 0 . 79412 , β = 37 ° 25 ′ 41 ″ m n z3 ( 2 )d 3 = m t z 3 = = 45 .33 mm ; d 4 = m t z 4 = 90 .67 mm ; cos β* d f 3 = d 3 − 2 ( han + c * ) m = 40 .33 mm ; d f 4 = 85 .67 mm ; * d a 3 = d 3 + 2 han m = 49 .33 mm ; d a 4 = 94 .67 mm tg α t = tg α n / cos β = 0 .4583 ; α t′ = α t = 24 ° 37 ′ 25 ″题5-20解d b 3 = d 3 cos α t = 41 .21 mm ; d b 4 = 82 . 42 mmα at 3 = arccos( d b 3 / d a 3 ) = 33 ° 20 ′ 35 ″; α at 4 = 29 ° 28 ′ 16 ″ εγ = εα + ε β= 3 . 118 1 = [ z 3 ( tg α at 3 − tg α t ) + z 4 ( tg α at 4 − tg α t )] 2π。

习题参考答案第二章 机构的结构分析2-2 图2-38所示为一简易冲床的初拟设计方案。

设计者的思路是：动力由齿轮1输入，使轴A 连续回转；而固装在轴A 上的凸轮2与杠杆3组成的凸轮机构将使冲头4上下运动以达到冲压的目的。

43512解答：原机构自由度F=3⨯3- 2 ⨯4-1 = 0，不合理 ，2-3 图2-39所示为一小型压力机，其中，1为滚子；2为摆杆；3为滑块；4为滑杆；5为齿轮及凸轮；6为连杆；7为齿轮及偏心轮；8为机架；9为压头。

试绘制其机构运动简图，并计算其自由度。

O齿轮及偏心轮ωA齿轮及凸轮BEFDC压头机架连杆滑杆滑块摆杆滚子解答：n=7; P l =9; P h =2，F=3⨯7-2 ⨯9-2 = 12-6 试计算图2-42所示凸轮—连杆组合机构的自由度。

解答：a) n=7; P l =9; P h =2，F=3⨯7-2 ⨯9-2 =1 L 处存在局部自由度，D 处存在虚约束 b) n=5; P l =6; P h =2，F=3⨯5-2 ⨯6-2 =1 E 、B 处存在局部自由度，F 、C 处存在虚约束b)a)A EMDFELKJIFBCCDBA2-7 试计算图2-43所示齿轮—连杆组合机构的自由度。

BDCA(a)CDBA(b)解答：a) n=4; P l =5; P h =1，F=3⨯4-2 ⨯5-1=1 A 处存在复合铰链b) n=6; P l =7; P h =3，F=3⨯6-2 ⨯7-3=1 B 、C 、D 处存在复合铰链2-8 试计算图2-44所示刹车机构的自由度。

并就刹车过程说明此机构自由度的变化情况。

解答：① 当未刹车时，F=3⨯6-2 ⨯8=2② 在刹车瞬时，F=3⨯5-2⨯7=1，此时构件EFG 和车轮接触成为一体，位置保持不变，可看作为机架。

③ 完全刹死以后，F=3⨯4-2⨯6=0，此时构件EFG 、HIJ 和车轮接触成为一体，位置保持不变，可看I F EHJOGCAB D作为机架。

6-1 A pair of standard involute spur gears have a module of 5mm, pressure angle α=20︒ , center distance a =350mm, transmission ratio i 12 =9/5. Calculate the numbers of teeth (Z 1 and Z 2), reference diameters (d 1 and d 2), addendum diameters (d a1 and d a2), base diameters (d b1 and d b2), tooth thickness s, spacewidth e, pressure angles on the addendum circles (αa1 and αa2), the radii of curvatures of tooth profile on the reference circles (ρ1 and ρ2), and the radii of curvatures of tooth profile on the addendum circles (ρa1 and ρa2).. 解：593502'1'212'2'1===+=d d i mmd da mmd mmd 450250'2'1=='11'221122*111*2221122250450250505450905222502*1*5260224502*1*5460cos 250*cos 20234.92cos 450*cos 20422.86522a a a a a a o b o b d d mmd d mmd z mm m d z mmm d d h d h m mm d d h d h m mmd d mm d d mm p m se ααππ===========+=+=+==+=+=+=======*====7.8542mm=6-2 How many teeth would an external standard involute spur gear has when its dedendum circle and its base circle coincide? Which one is bigger as the number of teeth increases ? 解：****2cos cos cos 21cos 22*133.161cos 1cos 2034If Z increases, then da is bigger.a ba a a a a od d d h d z h z z h z h zh z z ααααα=-=-=-=-====--≥6-3 In Fig6-1 there are a pair of involute profiles C1 and C2with the common normal n-n passing through the contact point K.1)Draw the two base circles and two pitch bel the theoretical line ofaction N1N2 and actual line of action bel the working pressure angle α’ and pressure angle αK at the point bel the actual working section DG of the profile C2.5)Find out point M2on the profile C2that will engage with point M1on the6-4 In Fig6-2 there are a pair of involute pinion and rack with their pitch circle and pitch line. Determine graphically the actual line of action B1B2, the actual working section EF on the tooth profile of the pinion and the actual working6-5 In a pair of external spur gears Z 1=10, Z 2=27, m=10mm, α=20︒, ha*=1, c*=0.25, working center distance a’=185mm. Neither gear has cutter interference.(1) What type of corrected gear pair does it belong to? Why?(2) Calculate the ranges of modification coefficients x 1 and x 2, respectively. (3) When x 1=0.5, calculate r a2, r b2, S 2, αa2, and ρa2 for gear 2. 解：（1）()()()12012121210102718522cos cos 202tan 0m z z a mma a x x inv inv z z x x αααααα+⨯+===''='=+'=+++=为等变位齿轮（2）220*112sin 10sin 2010.42220.42az x h x α⨯≥-=-=≤- （3）()()()12****11111*21002220220.50.521010(10.25)*100.5*1042.5218542.50.25101401027cos cos 20cos 20126.86222tan 20.5tan 2022f a a a f b x x mz r r h c m x m h c m x m mm r a r c m mm mz r r mm s x m αππα==-=-++=-++⨯=-++='=--=--⨯=⨯====⎛⎫⎛=+=+⨯- ⎪ ⎝⎭⎝1012.07mm⎫⨯=⎪⎭002222126.86arccos arccos 25.0225012014059.22b a a a r r mmαρ'''=======6-6 In a pair of external spur gears ,Z 1=20, Z 2=40, m=2mm, (ha*=1, c*=0.25,) α=20︒, d f1=37.0mm, S 2=2.413652185mm.(1) Calculate the modification coefficients x 1 and x 2(2) What type of corrected gear pair does it belong to? Why? (3) Calculate r b1, r a1, αa1, ρa1, S 1, and ρ1 of gear 1. 解：（1）()()****11111122237.018.5220.52tan 2.41365218520.5f a a mz r r h c m x m h c m x m x s x m mmx πα=-++=-++===⎛⎫=+= ⎪⎝⎭=-（2）120x x +=∴为等变位齿轮（3）()()()11011****2222212*12111202cos 20cos 2018.792240(10.25)20.5236.526026036.50.2522318.79arccosarccos 23b f a a a f b a a mzr mmr r mmmz r r h c m x m h c m x m mm ma a z z mm r a r c m mmr r αα====⨯==-++=-++⨯=-+⨯-⨯='∴==+='=--=--⨯====这一对齿轮为等变位齿轮001011135.2235130713.262tan 20.5tan 202 3.8722 6.85a mm S x m mmmm ρππαρ'''====⎛⎫⎛⎫=+=+⨯⨯= ⎪ ⎪⎝⎭⎝⎭===6-7 There are a pair of external standard spur gears in a shaping machine with Z1=17, Z2=118, m=5mm, α=20︒, h a*=1, c*=0.25. The pinion is worn out and the gear is worn to such an extent that the tooth thickness is decreased by 0.75mm. The gear is to be repaired by addendum modification and a new pinion is to be manufactured to mesh with the repaired gear.(1)What is the minimum modification coefficient of the new pinion if the originalframe is still used?(2)When x1=0.3, calculate r a1, r f1, S1, αa1, ρa1, and εα.解：（1）（2）2222max121min2tan0.75220.210.2100.21s x m mx xa ax x xππα⎛⎫=+=-⎪⎝⎭=-⇒=-'=∴+=⇒=此对齿轮为等变位齿轮()()()1211221122**111****222220.30.342.522952cos42.5cos2039.94cos295cos20277.2142.5(10.25)50.3537.7525118(10.25)2bbf af a ax xmzr mmmzr mmr r mmr r mmr r h c m x m mmmzr r h c m x m h c m x mαα=⇒=-======⨯===⨯==-++=-+⨯+⨯==-++=-++⨯=-+()12*12*2150.35287.25337.52337.5287.250.25549337.537.750.255298.5a fa fmmma a z z mmr a r c m mmr a r c m mm⨯-⨯='∴==+='=--=--⨯='=--=--⨯=这一对齿轮为等变位齿轮00111002221111139.94arccos arccos35.4035240949277.21arccos arccos21.77214614298.528.392tan20.3tan2058.95 221tan tan2baabaaaarrrrmmS x m mmzαααρππαεαπ''' ====''' =======⎛⎫⎛⎫=+=+⨯⨯=⎪ ⎪⎝⎭⎝⎭=-()()()()220000tan tan117tan35.40tan20118tan21.77tan2021.60azαααπ''+-⎡⎤⎣⎦⎡⎤=⨯-+⨯-⎣⎦=6-8 In the gear train shown in Fig6-3, both gear pairs must have the same working center distance. Z 1=27, Z 2=60, Z 2’=63, Z 3=25, (ha*=1, c*=0.25,)m =5mm. The gear pair 2’ and 3 is a corrected gear pair with reference center distance . The modification coefficient x 2 of the gear 2 is zero.(1) What type of corrected gear pair should the gear pair 1 and 2 be? Give the briefreason.(2) Is the gear 2 a standard gear? Why? (3) Calculate x 1, S 1, r b1, r f1, αa1, and ρa1. 解: （1）（2）齿轮2不是标准齿轮。