万有引力定律单元复习

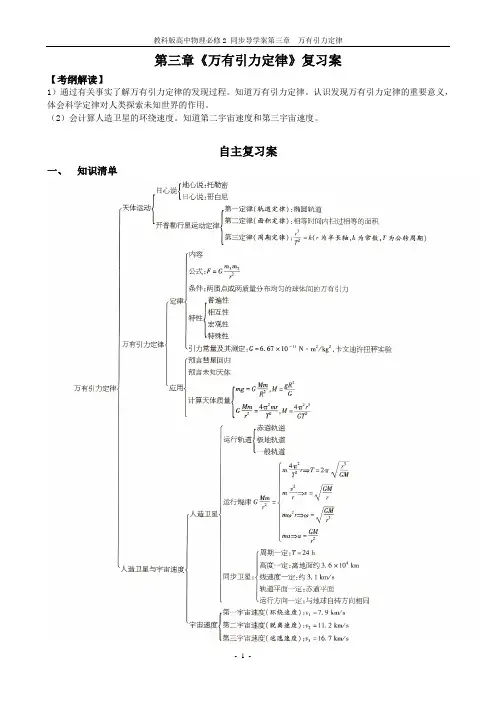
第三章《万有引力定律》复习案【考纲解读】1）通过有关事实了解万有引力定律的发现过程。

知道万有引力定律。

认识发现万有引力定律的重要意义，体会科学定律对人类探索未知世界的作用。

（2）会计算人造卫星的环绕速度。

知道第二宇宙速度和第三宇宙速度。

自主复习案一、知识清单【我的疑问】课中探究案【问题探究】1.(2011重庆理综第21题).某行星和地球绕太阳公转的轨道均可视为圆。

每过N 年，该行星会运行到日地连线的延长线上，如题21图所示。

该 行星与地球的公转半径比为 A ．231()N N + B. 23()1N N -C ．321()N N+ D. 32()1NN -2．（2012·重庆理综）冥王星与其附近的另一星体卡戎可视为双星系统，质量比约为7∶1，同时绕它们连线上某点O 做匀速圆周运动，由此可知，冥王星绕O 点运动的 A ．轨道半径约为卡戎的17B ．角速度大小约为卡戎的17C ．线速度大小约为卡戎的7倍D ．向心力大小约为卡戎的7倍3.（2011四川理综卷第17题）据报道，天文学家近日发现了一颗距地球40光年的“超级地球”，名为“55 Cancri e ”，该行星绕母星（中心天体）运行的周期约为地球绕太阳运行周期的1480，母星的体积约为太阳的60倍。

假设母星与太阳密度相同，“55 Cancri e ”与地球均做匀速圆周运动，则“55 Cancri e ”与地球的A.C.4. （2012·新课标理综）假设地球是一半径为R 、质量分布均匀的球体。

一矿井深度为d 。

已知质量分布均匀的球壳对壳内物体的引力为零。

矿井底部和地面处的重力加速度大小之比为 A.Rd -1 B. Rd +1 C. 2)(Rd R - D. 2)(dR R -一、课堂探究１．总结应用万有引力定律的两条基本思路。

２．求天体质量、密度有哪些方法？３．根据本章所学知识，总结卫星的运动规律。

二、课堂检测1．甲、乙两个质点间的万有引力大小为F，若甲物体的质量不变，乙物体的质量增加到原来的2倍，同时，它们之间的距离减为原来的1/2，则甲、乙两物体间的万有引力大小将变为( )A．F B．F/2C．8F D．4F2.第一宇宙速度是物体在地球表面附近环绕地球做匀速圆周运动的速度,则有（）A.被发射的物体质量越大,第一宇宙速度越大B.被发射的物体质量越小,第一宇宙速度越大C.第一宇宙速度与被发射物体的质量无关D.第一宇宙速度与地球的质量有关3．由于通信和广播等方面的需要，许多国家发射了地球同步轨道卫星，这些卫星的() A．质量可以不同B．轨道半径可以不同C．轨道平面可以不同D．速率可以不同4．质量为m的探月航天器在接近月球表面的轨道上飞行，其运动视为匀速圆周运动．已知月球质量为M，月球半径为R，月球表面重力加速度为g，引力常量为G，不考虑月球自转的影响，则航天器的( )A．线速度v＝GMRB．角速度ω＝gRC．运行周期T＝2πRgD．向心加速度a＝GmR25.一宇宙飞船绕地心做半径为r的匀速圆周运动，飞船舱内有一质量为m的人站在可称体重的台秤上.用R 表示地球的半径，g表示地球表面处的重力加速度，g′表示宇宙飞船所在处的地球引力加速度，F N表示人对台秤的压力，这些说法中，正确的是( )A.g′=0B.22Rg gr'= C.F N=0 D.NRF m gr=6.我国于1986年2月1日成功发射了一颗实验地球同步卫星,于1999年11月20日又成功地发射了“神舟”号实验飞船,飞船在太空中飞行了21 h,环绕地球运转了14圈,又顺利地返回地面,那么此卫星与飞船两者相比较（）A.卫星运转周期比飞船大B.卫星运转速率比飞船大C.卫星运转加速度比飞船大D.卫星离地高度比飞船大7.如图所示，A是地球的同步卫星，另一卫星B的圆轨道位于赤道平面内，离地面高度为h.已知地球半径为R，地球自转角速度为ω0，地球表面的重力加速度为g，O为地球中心．(1)求卫星B的运行周期；(2)如卫星B绕行方向与地球自转方向相同，某时刻A、B两卫星相距最近(O、B、A在同一直线上)，则至少经过多长时间，它们再一次相距最近？。

万有引⼒定律复习资料万有引⼒定律⼀、开普勒三定律：开普勒第⼀定律：所有的⾏星分别在⼤⼩不同的椭圆轨道上围绕太阳运动，太阳是在这些椭圆的⼀个焦点上。

开普勒第⼆定律：对每个⾏星来说，太阳和⾏星的连线在相等的时间内扫过相等的⾯积。

开普勒第三定律：所有⾏星的椭圆轨道的长半轴的三次⽅跟公转周期的平⽅的⽐值都相等。

即 R TK 32=常数（）⼆、万有引⼒定律：1、内容：任何两个物体都是互相吸引的，引⼒的⼤⼩跟两个物体的质量的乘积成正⽐，跟它们的距离的平⽅成反⽐。

这就是万有引⼒定律。

2、公式F Gm m R =122应注意：（1）公式中G 称作万有引⼒恒量，经测定G N m Kg =?-667101122./·。

（2）公式中的R 为质点间的距离。

对于质量分布均匀的球体，可把它看做是质量集中在球⼼的⼀个点上。

（3）从G N m Kg =?-667101122./·可以看出，万有引⼒是⾮常⼩的，平时很难觉察，所以它的发现经历了对天体（质量特别⼤）运动的研究过程。

⼩结：1、万有引⼒定律的公式：F Gm m r=122只适⽤于质点间的相互作⽤。

这⾥的“质点”要求是质量分布均匀的球体，或是物体间的距离r 远远⼤于物体的⼤⼩d r d ()>>，这两种情况。

2、运⽤万有引⼒定律解决具体问题时，要特别注意指数运算。

3、在计算过程中，如果要求精度不⾼，可取G N m Kg =?-203101122·/来运算，这样可使计算简化。

三、公式的转换1、根据环绕天体绕中⼼天体表⾯转动时2、根据环绕天体绕中⼼天体在以某⾼度转动时3、已知中⼼天体的半径和表⾯重⼒加速度时4、⾓速度，线速度，周期的关系可得：结论：线速度、⾓速度、周期都与卫星的质量⽆关，仅由轨道半径决定。

当卫星环绕地球表⾯运⾏时，轨道半径最⼩为地球半径（r=R ），此时线速度最⼤，⾓速度最⼤，周期最⼩。

1．⽕星的质量和半径分别约为地球的101和21，地球表⾯的重⼒加速度为g ，则⽕星表⾯的重⼒加速度约为（）A ．0.2gB ．0.4gC ．2.5gD ．5g2、据报道．我国数据中继卫星“天链⼀号01 星”于2008 年4 ⽉25 ⽇在西昌卫星发射中⼼发射升空，经过4 次变轨控制后，于5⽉l ⽇成功定点在东经77°⾚道上空的同步轨道。

《认识万有引力定律》知识清单一、什么是万有引力定律万有引力定律是指任何两个物体之间都存在相互吸引的力，这个力的大小与这两个物体的质量成正比，与它们之间距离的平方成反比。

用公式表示就是：F ＝ G （m1 m2) ／ r²，其中 F 表示两个物体之间的引力，G 是万有引力常量，约为 667×10⁻¹¹ N·m²/kg²，m1 和 m2 分别表示两个物体的质量，r 是两个物体质心之间的距离。

二、万有引力定律的发现者万有引力定律是由英国科学家艾萨克·牛顿发现的。

据说，牛顿是在看到苹果从树上落下时，开始思考物体下落的原因，并最终发现了万有引力定律。

这个故事虽然简单，但却生动地展示了牛顿敏锐的观察力和深刻的思考能力。

三、万有引力定律的意义1、解释天体运动万有引力定律成功地解释了天体的运动规律，包括行星绕太阳的运动、卫星绕行星的运动等。

它使得人们能够准确地预测天体的位置和运动轨迹，为天文学的发展奠定了坚实的基础。

2、统一了地上和天上的力学在牛顿之前，人们认为天上和地上的物体遵循不同的力学规律。

万有引力定律的发现表明，无论是地球上的物体还是天体，都受到相同的引力作用，从而统一了地上和天上的力学。

3、推动科学技术的发展万有引力定律在航天技术、卫星通信、导航等领域有着广泛的应用。

例如，在计算卫星的轨道、发射火箭时，都需要用到万有引力定律。

四、万有引力定律的适用范围1、宏观物体万有引力定律适用于宏观物体，对于微观粒子，由于量子力学效应的影响，万有引力定律不再适用。

2、弱引力场在强引力场中，如黑洞附近，万有引力定律需要进行修正，需要用到广义相对论。

五、万有引力常量的测量1、卡文迪许扭秤实验英国科学家亨利·卡文迪许通过巧妙的扭秤实验，成功地测量出了万有引力常量 G 的值。

他的实验设计非常精巧，利用了微小的引力作用产生的扭转力矩来测量引力的大小。

高考物理专题复习：万有引力定律一、单选题1．已知某空间站在距地面高度为h 的圆轨道上运行，经过时间t ，通过的弧长为s 。

已知引力常量为G ，地球半径为R 。

下列说法正确的是（ ） A ．空间站运行的速度大于第一宇宙速度 B ．空间站的角速度为stC ．空间站的周期为2)R h tsπ+（ D ．地球平均密度为. 22234()s G t R h π+2．假设某星球可视为质量均匀分布的球体，已知该星球表面的重力加速度在两极的大小为g 1，在赤道的大小为g 2，星球自转的周期为T ，引力常量为G ，则该星球的密度为（ ） A ．23GT πB ．1223g GT g π⋅ C ．12123g GT g g π⋅- D ．12213g g GT g π-⋅ 3．某探测器在半径为R 的土星上空离土星表面高h 的圆形轨道上绕土星飞行，环绕n 周飞行时间为t ，已知引力常量为G ，关于土星质量M 和平均密度ρ的表达式正确的是（ ） A ．2324()R h M Gt π+=，3233()R h G Rπρ+= B ．2224()R h M Gtπ+=，2233()R h Gt R πρ+= C ．2324()R h M Gt π+=，3233()R h Gn R πρ+=D ．22324()n R h M Gt π+=，23233()n R h Gt R πρ+=4．某探测器在距火星表面高度为h 的轨道上绕火星做周期为T 的匀速圆周运动，再经多次变轨后成功着陆，着陆后测得火星表面的重力加速度为g ，已知火星的半径为R ，万有引力常量为G ，忽略火星自转及其他星球对探测器的影响，以下说法正确的是（ ） A ．火星的质量为2324πR GTB ．火星的质量为()3224πR h gT +C ．火星的密度为23πGT D ．火星的密度为34πgG R5．宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统，通常可忽略其他星体对它们的引力作用．设四星系统中每个星体的质量均为m ，半径均为R ，四颗星稳定分布在边长为a 的正方形的四个顶点上．已知引力常量为G .关于宇宙四星系统，下列说法错误的是（ ）A ．四颗星围绕正方形对角线的交点做匀速圆周运动B ．四颗星的轨道半径均为2aC ．四颗星表面的重力加速度均为2GmR D．四颗星的周期均为2π6．质量为m 的着陆器在着陆火星前，会在火星表面附近经历一个时长为0t 、速度由0v 减速到零的过程。

万有引力定律复习知识总结一、开普勒第一、第二、第三定律的内容1．关于开普勒行星运动的公式23TR ＝k ，以下理解正确的是（ ）A ．k 是一个与行星无关的常量B ．若地球绕太阳运转轨道的半长轴为R 地，周期为T 地；月球绕地球运转轨道的长半轴为R 月，周期为T 月，则2323月月地地T R T RC ．T 表示行星运动的自转周期D ．T 表示行星运动的公转周期2．从天文望远镜中观察到银河系中有两颗行星绕某恒星运行，两行星的轨道均为椭圆，观察测量到它们的运行周期之比为8∶1，则它们椭圆轨道的半长轴之比为 （ ） A ．2∶1 B ．4∶1 C ．8∶1 D ．1∶4二、.三种宇宙速度（1）第一宇宙速度（环绕速度）：v 1=7.9 km/s ，是人造地球卫星的最小发射速度，也是人造地球卫星绕地球做圆周运动的最大速度. （2）第二宇宙速度（脱离速度）：v 2=11.2 km/s ，是使物体挣脱地球引力束缚的最小发射速度.（3）第三宇宙速度（逃逸速度）：v 3=16.7 km/s ，是使物体挣脱太阳引力束缚的最小发射速度.三、万有引力定律万有引力定律的公式F=Gm 1m 2/r 2，只适用于质点之间的相互作用，但下列两种情况下定律也适用。

1、当两个物体间的距离远大于物体本身的大小时，物体可视为质点。

2、均匀的球体可视为质点，但r 是两球心间的距离。

3、万有引力和重力的关系因地球自转，地球赤道上的物体也会随着一起绕地轴做圆周运动，这时物体受地球对物体的万有引力和地面的支持力作用，物体做圆周运动的向心力是由这两个力的合力提供，受力分析如图所示．实际上，物体受到的万有引力产生了两个效果，一个效果是维持物体做圆周运动，另一个效果是对地面产生了压力的作用，所以可以将万有引力分解为两个分力：一个分力就是物体做圆周运动的向心力，另一个分力就是重力，如图所示．这个重力与地面对物体的支持力是一对平衡力．在赤道上时这些力在一条直线上．在赤道上的物体随地球自转做圆周运动时，由万有引力定律和牛顿第二定律可得其动力学关系为22224TmR ma mR N R Mm G πω===-向，式中R 、M 、ω、T 分别为地球的半径、质量、自转角速度以及自转周期。

万有引力定律的复习一、万有引力定律1.内容：自然界任何两个物体之间都存在着相互作用的引力，两物体间的引力的大小，跟它们的质量的乘积成正比，跟它们的距离的平方成反比.表达式：F ＝Ｇ221rm m 其中G ＝６．６７×１０－１１ Ｎ·ｍ２／ｋｇ２，叫万有引力常量，卡文迪许在实验室用扭秤装置，测出了引力常量.2.适用条件：公式适用于质点间的相互作用，当两个物体间的距离远大于物体本身的大小时，物体可视为质点.均匀球体可视为质点，r 为两球心间的距离.3.万有引力遵守牛顿第三定律，即它们之间的引力总是大小相等、方向相反.4、万有引力与重力：万有引力可以分为两个分力：重力和跟随地球自转所需的向心力。

重力的方向在赤道和两极处指向地心，在其它方向并不指向地心。

二、用万有引力定律分析天体的运动1.基本方法：把天体运动近似看作圆周运动，它所需要的向心力由万有引力提供，即 Ｇr v m r Mm 22=＝ｍω２ｒ＝ｍr T224π 2.估算天体的质量和密度由G 2rMm ＝ｍr T 224π得：Ｍ＝2324Gt r π．即只要测出环绕星体M 运转的一颗卫星运转的半径和周期，就可以计算出中心天体的质量.由ρ＝V M ，Ｖ＝34πＲ３得：ρ＝3233RGT r π．R 为中心天体的星体半径 当ｒ＝Ｒ时，即卫星绕天体M 表面运行时，ρ＝23GT π，由此可以测量天体的密度. 3.卫星的绕行速度、角速度、周期与半径的关系(1)由Ｇr v m rMm 22=得:ｖ＝r GM ． 即轨道半径越大，绕行速度越小 (2)由Ｇ2rMm ＝ｍω２ｒ得：ω＝3r GM 即轨道半径越大，绕行角度越小 (3)由G 3r Mm ＝４π２2T mR 得：Ｔ＝２πGMR 3即轨道半径越大，绕行周期越大. 问题：一颗卫星受微薄气体的阻力作用，它的轨道半径怎么变化？线速度怎么变化？4.宇宙速度(1)第一宇宙速度——环绕速度7.9km/s 。

第五章万有引力定律高考要求：内容要求说明万有引力定律Ⅱ万有引力定律的应用、人造地球卫星的运动( 限于圆轨道 ) Ⅱ宇宙速度Ⅰ本章特色：牛顿运动定律与天体运动的的联合在近几年高考取还是热门，因为它切合科技发展的认识需要，万有引力定律的考点有三个（见上表），波及并用于议论天体运动的知识点是高考的重点内容，近几年高考取出现率达100% ，可能会是一道选择题，也可能是一道中等难度的计算题，近几年高考对万有引力定律的观察主要表此刻两个方面：一是重申基础的同时加大与其余部分的综合，如在其余星球上做自由落体、平抛、竖直上抛、单摆，近似地球上的实验，与g 有关的知识，与天体有关的地理知识等；二是应用万有引力定律解决实质问题，固然考点不多，但需要利用这个定律解决的习题题型多，综合性强，波及到的题型以天体运动为中心，如估量天体质量或均匀密度问题，变轨问题，能量问题，中心是：（ 1 ）行星绕恒星的圆周运动，二者之间的万有引力供应向心力；（ 2 ）星球表面重力在忽视星球自转的状况低等于万有引力，即可推出常用的黄金代换：2 GMgR近几年高考取出题的特色是以近几年中国及世界上空间技术的飞快发展为背景的天体问题，一方面能够使学生认识近几年这方面的大事，如：火星、土星探测，“神五”“神六”发射与回收，“金星快车”的发射，人类撞击彗星等，另一方面还能够观察学生从资料信息中获得“有效信息”的能力，第一单元万有引力定律知识重点一、万有引力定律1 ．内容 : 宇宙间全部物体都是互相吸引的，两个物体间的引力大小，跟它们的质量的乘积成正比，跟它们的距离的平方成反比．2．公式： F G m1 m2其G = 6.67 ×10-11222N·m /kg r3．合用条件：公式只合用于质点间的互相作用．当两个物体间的距离远远大于物体自己大小时公式也近似合用，但此时它们间距离r 应为两物体质心间距离．均匀的球体可视为质点，r 是两球心间的距离．4 ．注意：公式中 F 是两物体间的引力， F 与两物体质量乘积成正比与两物体间距离的平方成反比，不要理解成 F 与两物体质量分别成正比、与距离成反比．二、划分万有引力和重力1．因为地球的吸引而使物体遇到的力称为重力，但重力不是万有引力，不过万有引力的一个分力，另一个分力是物体随处球自转而绕地轴做匀速圆周运动所需要的向心力 f , 如下图，因为纬度的变化，物体做圆周运动的向心力 f 不停变化, 所以地球表面物体的重力随纬度的变化而变化，即重力加快度g 随纬度变化而变化，从赤道到两极渐渐增大。

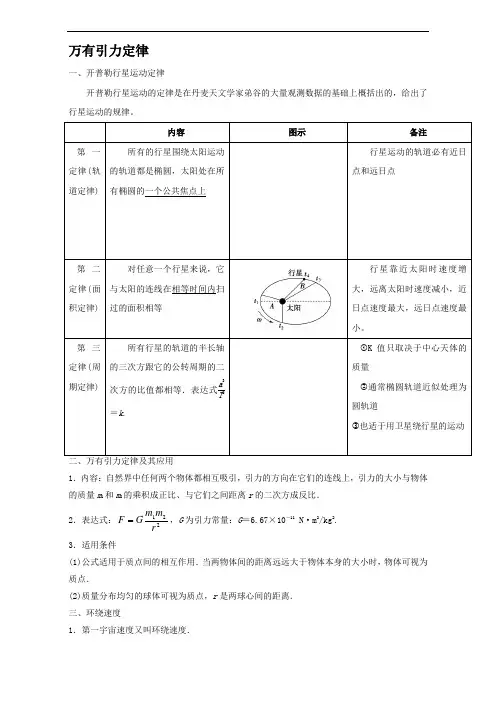
万有引力定律一、开普勒行星运动定律开普勒行星运动的定律是在丹麦天文学家弟谷的大量观测数据的基础上概括出的，给出了行星运动的规律。

内容图示备注第一定律(轨道定律) 所有的行星围绕太阳运动的轨道都是椭圆，太阳处在所有椭圆的一个公共焦点上行星运动的轨道必有近日点和远日点第二定律(面积定律) 对任意一个行星来说，它与太阳的连线在相等时间内扫过的面积相等行星靠近太阳时速度增大，远离太阳时速度减小，近日点速度最大，远日点速度最小。

第三定律(周期定律) 所有行星的轨道的半长轴的三次方跟它的公转周期的二次方的比值都相等．表达式a 3T2＝k .①K 值只取决于中心天体的质量②通常椭圆轨道近似处理为圆轨道③也适于用卫星绕行星的运动1．内容：自然界中任何两个物体都相互吸引，引力的方向在它们的连线上，引力的大小与物体的质量m 1和m 2的乘积成正比、与它们之间距离r 的二次方成反比． 2．表达式：221rm m G F ，G 为引力常量：G ＝6.67×10－11 N·m 2/kg 2. 3．适用条件(1)公式适用于质点间的相互作用．当两物体间的距离远远大于物体本身的大小时，物体可视为质点．(2)质量分布均匀的球体可视为质点，r 是两球心间的距离． 三、环绕速度1．第一宇宙速度又叫环绕速度．r mv rMm G mg 212== 得：gR rGMv ==1＝7.9 km/s. 第一宇宙速度是人造卫星的最大环绕速度，也是人造地球卫星的最小发射速度． 第二宇宙速度(脱离速度)：v 2＝11.2 km/s ，使物体挣脱地球引力束缚的最小发射速度． 第三宇宙速度(逃逸速度)：v 3＝16.7 km/s ，使物体挣脱太阳引力束缚的最小发射速度． 特别提醒:(1) 两种周期——自转周期和公转周期的不同(2)两种速度——环绕速度与发射速度的不同，最大环绕速度等于最小发射速度 (3)两个半径——天体半径R 和卫星轨道半径r 的不同 四、近地卫星、赤道上物体及同步卫星的运行问题 1．近地卫星、同步卫星、赤道上的物体的比较比较内容赤道表面的物体 近地卫星 同步卫星向心力来源 万有引力的分力 万有引力向心力方向指向地心重力与万有引力的关系 重力略小于万有引力重力等于万有引力线速度v1＝ω1Rv2＝GM Rv3＝ω3(R ＋h)＝GMR ＋hv 1＜v 3＜v 2(v 2为第一宇宙速度)角速度ω1＝ω自ω2＝GM R3ω3＝ω自＝GMR ＋h 3ω1＝ω3＜ω2向心加速度a 1＝ω21Ra 2＝ω2R ＝GM R2a 3＝ω23(R ＋h) ＝GMR ＋h 2a 1＜a 3＜a 2五、天体的追及相遇问题两颗卫星在同一轨道平面内同向绕地球做匀速圆周运动，a 卫星的角速度为ωa ，b 卫星的角速度为ωb ，若某时刻两卫星正好同时通过地面同一点正上方，相距最近(如图甲所示)。

《万有引力定律》1. 开普勒行星运动定律开普勒第一定律（轨道定律） 所有行星绕太阳运动的轨道都是________，太阳处在________的一个焦点上。

开普勒第二定律（面积定律） 对任意一个行星来说，它与太阳的连线在相等的时间内扫过相等的________。

说明行星在运转过程中离太阳越近速率________，离太阳越远速率________。

也就是说，行星在近日点的速率最大，在远日点的速率最小。

开普勒第三定律（周期定律） 所有行星的轨道的半长轴的________跟它的公转周期的________的比值都相等。

k Ta 23比值k 是一个与行星无关的常量，仅与中心天体——太阳的质量有关。

典型例题：木星绕太阳运动的周期为地球绕太阳运动周期的12倍。

那么，木星绕太阳运动轨道的半长轴是地球绕太阳运动轨道半长轴的多少倍？2. 万有引力定律自然界中任何两个物体都相互吸引，引力的大小与物体的________________的乘积成正比，与它们____________的二次方成反比，即________________。

（1） 对万有引力定律的进一步说明① 万有引力是宇宙间的一种基本的相互作用力，它适用于宇宙中的一切物体。

② 万有引力公式只适用于两质点间的引力的计算。

④ 万有引力公式中G 的是比例系数，叫做引力常量，是自然界中少数几个最重要的物理常量之一，通常取G=________________N·m 2/kg 2。

1. 对万有引力定律的理解（1）万有引力定律：自然界中任何两个物体都是相互吸引的，引力的大小跟这两个物体的质量的乘积成正比，跟它们的距离的平方成反比，两物体间引力的方向沿着二者的连线。

（2）公式表示：F=221rm Gm 。

（3）引力常量G ：①适用于任何两物体。

②意义：它在数值上等于两个质量都是1kg 的物体（可看成质点）相距1m 时的相互作用力。

③G 的通常取值为G=6。

67×10-11Nm 2/kg 2。

高三物理万有引力定律及应用专题复习一、单选题(共10小题,每小题5.0分,共50分)1.火星表面特征非常接近地球，可能适合人类居住。

2010年，我国志愿者王跃参与了在俄罗斯进行的“模拟登火星”实验活动。

已知火星半径是地球半径的，质量是地球质量的，自转周期也基本相同。

地球表面重力加速度是g，若王跃在地面上能向上跳起的最大高度是h，在忽略自转影响的条件下，下述分析正确的是( )A．王跃在火星表面所受火星引力是他在地球表面所受地球引力的倍B．火星表面的重力加速度是C．火星的第一宇宙速度是地球第一宇宙速度的倍D．王跃在火星上向上跳起的最大高度是2.“嫦娥三号”的环月轨道可近似看成是圆轨道。

观察“嫦娥三号”在环月轨道上的运动，发现每经过时间t通过的弧长为l，该弧长对应的圆心角为θ弧度，如图所示。

已知万有引力常量为G，由此可计算出月球的质量为( )A．B．C．D．3.若有一颗“宜居”行星，其质量为地球的p倍，半径为地球的q倍，则该行星卫星的环绕速度是地球卫星环绕速度的（）A．倍B．倍C．倍D．倍4.我国2013年6月发射的“神州十号”飞船绕地球飞行的周期约为90分钟，取地球半径为6400km，地表重力加速度为g。

设飞船绕地球做匀速圆周运动，则由以上数据无法估测（）A．飞船线速度的大小B．飞船的质量C．飞船轨道离地面的高度D．飞船的向心加速度大小5.已成为我国首个人造太阳系小行星的嫦娥二号卫星，2014年2月再次刷新我国深空探测最远距离纪录，超过7000万公里。

嫦娥二号是我国探月工程二期的先导星，它先在距月球表面高度为h的轨道上做匀速圆周运动，运行周期为T；然后从月球轨道出发飞赴日地拉格朗日L2点进行科学探测。

若以R表示月球的半径，引力常量为G，则( )A．嫦娥二号卫星绕月运行时的线速度为B．月球的质量为C．物体在月球表面自由下落的加速度为D．嫦娥二号卫星在月球轨道经过减速才能飞赴拉格朗日L2点6.宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统，通常可忽略其他星体对它们的引力作用．设四星系统中每个星体的质量均为m，半径均为R，四颗星稳定分布在边长为的正方形的四个顶点上．已知引力常量为G．关于四星系统，下列说法错误的是 ( )A．四颗星围绕正方形对角线的交点做匀速圆周运动B．四颗星的轨道半径均为C．四颗星表面的重力加速度均为D．四颗星的周期均为7.“嫦娥二号”环月飞行的高度为100km，所探测到的有关月球的数据将比环月飞行高度为200km的“嫦娥一号”更加详实。