一模分类四边形

一、平行四边形真题与模拟题分类汇编（难题易错题）1．如图，在平行四边形ABCD中，AD⊥DB，垂足为点D，将平行四边形ABCD折叠，使点B落在点D的位置，点C落在点G的位置，折痕为EF，EF交对角线BD于点P．（1）连结CG，请判断四边形DBCG的形状，并说明理由；（2）若AE＝BD，求∠EDF的度数．【答案】（1）四边形BCGD是矩形，理由详见解析；（2）∠EDF＝120°．【解析】【分析】（1）根据平行四边形的性质和折叠性质以及矩形的判定解答即可；（2）根据折叠的性质以及直角三角形的性质和等边三角形的判定与性质解答即可．【详解】解：（1）四边形BCGD是矩形，理由如下，∵四边形ABCD是平行四边形，∴BC∥AD，即BC∥DG，由折叠可知，BC＝DG，∴四边形BCGD是平行四边形，∵AD⊥BD，∴∠CBD＝90°，∴四边形BCGD是矩形；（2）由折叠可知：EF垂直平分BD，∴BD⊥EF，DP＝BP，∵AD⊥BD，∴EF∥AD∥BC，∴AE PD1==BE BP∴AE＝BE，∴DE是Rt△ADB斜边上的中线，∴DE＝AE＝BE，∵AE＝BD，∴DE＝BD＝BE，∴△DBE是等边三角形，∴∠EDB＝∠DBE＝60°，∵AB∥DC，∴∠DBC＝∠DBE＝60°，∴∠EDF＝120°．【点睛】本题考查了平行四边形的性质，折叠性质，等边三角形的性质和判定，主要考查学生运用定理进行推理和计算的能力，题目综合性比较强，有一定的难度2．如图1，在△ABC中，AB＝AC，AD⊥BC于D，分别延长AC至E，BC至F，且CE＝EF，延长FE交AD的延长线于G．（1）求证：AE＝EG；（2）如图2，分别连接BG，BE，若BG＝BF，求证：BE＝EG；（3）如图3，取GF的中点M，若AB＝5，求EM的长．【答案】（1）证明见解析（2）证明见解析（3）5 2【解析】【分析】（1）根据平行线的性质和等腰三角形的三线合一的性质得：∠CAD＝∠G，可得AE＝EG；（2）作辅助线，证明△BEF≌△GEC（SAS），可得结论；（3）如图3，作辅助线，构建平行线，证明四边形DMEN是平行四边形，得EM＝DN＝12AC，计算可得结论．【详解】证明：（1）如图1，过E作EH⊥CF于H，∵AD⊥BC，∴EH∥AD，∴∠CEH＝∠CAD，∠HEF＝∠G，∵CE＝EF，∴∠CEH＝∠HEF，∴∠CAD＝∠G，∴AE＝EG；（2）如图2，连接GC，∵AC＝BC，AD⊥BC，∴BD＝CD，∴AG是BC的垂直平分线，∴GC＝GB，∴∠GBF＝∠BCG，∵BG＝BF，∴GC＝BE，∵CE＝EF，∴∠CEF＝180°﹣2∠F，∵BG＝BF，∴∠GBF＝180°﹣2∠F，∴∠GBF＝∠CEF，∴∠CEF＝∠BCG，∵∠BCE＝∠CEF+∠F，∠BCE＝∠BCG+∠GCE，∴∠GCE＝∠F，在△BEF 和△GCE 中，CE GCE F CG BF EF =⎧⎪∠=∠⎨⎪=⎩，∴△BEF ≌△GEC （SAS ），∴BE ＝EG ；（3）如图3，连接DM ，取AC 的中点N ，连接DN ，由（1）得AE ＝EG ，∴∠GAE ＝∠AGE ，在Rt △ACD 中，N 为AC 的中点，∴DN ＝12AC ＝AN ，∠DAN ＝∠ADN ， ∴∠ADN ＝∠AGE ，∴DN ∥GF ，在Rt △GDF 中，M 是FG 的中点， ∴DM ＝12FG ＝GM ，∠GDM ＝∠AGE ， ∴∠GDM ＝∠DAN ，∴DM ∥AE ，∴四边形DMEN 是平行四边形， ∴EM ＝DN ＝12AC ， ∵AC ＝AB ＝5， ∴EM ＝52． 【点睛】 本题是三角形的综合题，主要考查了全等三角形的判定与性质，直角三角形斜边中线的性质，等腰三角形的性质和判定，平行四边形的性质和判定等知识，解题的关键是作辅助线，并熟练掌握全等三角形的判定方法，特别是第三问，辅助线的作法是关键．3．定义：我们把三角形被一边中线分成的两个三角形叫做“友好三角形”．性质：如果两个三角形是“友好三角形”，那么这两个三角形的面积相等．理解：如图①，在△ABC中，CD是AB边上的中线，那么△ACD和△BCD是“友好三角形”，并且S△ACD=S△BCD．应用：如图②，在矩形ABCD中，AB=4，BC=6，点E在AD上，点F在BC上，AE=BF，AF 与BE交于点O．（1）求证：△AOB和△AOE是“友好三角形”；（2）连接OD，若△AOE和△DOE是“友好三角形”，求四边形CDOF的面积．探究：在△ABC中，∠A=30°，AB=4，点D在线段AB上，连接CD，△ACD和△BCD是“友好三角形”，将△ACD沿CD所在直线翻折，得到△A′CD，若△A′CD与△ABC重合部分的面积等于△ABC面积的，请直接写出△ABC的面积．【答案】（1）见解析；（2）12；探究：2或2．【解析】试题分析：（1）利用一组对边平行且相等的四边形是平行四边形，得到四边形ABFE是平行四边形，然后根据平行四边形的性质证得OE=OB，即可证得△AOE和△AOB是友好三角形；（2）△AOE和△DOE是“友好三角形”，即可得到E是AD的中点，则可以求得△ABE、△ABF的面积，根据S四边形CDOF=S矩形ABCD-2S△ABF即可求解．探究：画出符合条件的两种情况：①求出四边形A′DCB是平行四边形，求出BC和A′D推出∠ACB=90°，根据三角形面积公式求出即可；②求出高CQ，求出△A′DC的面积．即可求出△ABC的面积．试题解析：（1）∵四边形ABCD是矩形，∴AD∥BC，∵AE=BF，∴四边形ABFE是平行四边形，∴OE=OB，∴△AOE和△AOB是友好三角形．（2）∵△AOE和△DOE是友好三角形，∴S△AOE=S△DOE，AE=ED=AD=3，∵△AOB与△AOE是友好三角形，∴S△AOB=S△AOE，∵△AOE≌△FOB，∴S△AOE=S△FOB，∴S△AOD=S△ABF，∴S四边形CDOF=S矩形ABCD-2S△ABF=4×6-2××4×3=12．探究：解：分为两种情况：①如图1，∵S△ACD=S△BCD．∴AD=BD=AB，∵沿CD折叠A和A′重合，∴AD=A′D=AB=×4=2，∵△A′CD与△ABC重合部分的面积等于△ABC面积的，∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC，∴DO=OB，A′O=CO，∴四边形A′DCB是平行四边形，∴BC=A′D=2，过B作BM⊥AC于M，∵AB=4，∠BAC=30°，∴BM=AB=2=BC，即C和M重合，∴∠ACB=90°，由勾股定理得：AC=，∴△ABC的面积是×BC×AC=×2×2=2；②如图2，∵S△ACD=S△BCD．∴AD=BD=AB，∵沿CD折叠A和A′重合，∴AD=A′D=AB=×4=2，∵△A′CD与△ABC重合部分的面积等于△ABC面积的，∴S△DOC=S△ABC=S△BDC=S△ADC=S△A′DC，∴DO=OA′，BO=CO，∴四边形A′BDC是平行四边形，∴A′C=BD=2，过C作CQ⊥A′D于Q，∵A′C=2，∠DA′C=∠BAC=30°，∴CQ=A′C=1，∴S△ABC=2S△ADC=2S△A′DC=2××A′D×CQ=2××2×1=2；即△ABC的面积是2或2．考点：四边形综合题．4．如图，已知矩形ABCD中，E是AD上一点，F是AB上的一点，EF⊥EC，且EF＝EC．（1）求证：△AEF≌△DCE．（2）若DE＝4cm，矩形ABCD的周长为32cm，求AE的长．【答案】（1）证明见解析；（2）6cm.【解析】分析：（1）根据EF⊥CE，求证∠AEF=∠ECD．再利用AAS即可求证△AEF≌△DCE．（2）利用全等三角形的性质，对应边相等，再根据矩形ABCD的周长为32cm，即可求得AE的长.详解：（1）证明：∵EF⊥CE，∴∠FEC=90°，∴∠AEF+∠DEC=90°，而∠ECD+∠DEC=90°，∴∠AEF=∠ECD．在Rt△AEF和Rt△DEC中，∠FAE=∠EDC=90°，∠AEF=∠ECD，EF=EC．∴△AEF≌△DCE．（2）解：∵△AEF≌△DCE．AE=CD．AD=AE+4．∵矩形ABCD的周长为32cm，∴2（AE+AE+4）=32．解得，AE=6（cm）．答：AE的长为6cm．点睛：此题主要考查学生对全等三角形的判定与性质和矩形的性质等知识点的理解和掌握，难易程度适中，是一道很典型的题目．5．点P是矩形ABCD对角线AC所在直线上的一个动点（点P不与点A，C重合），分别过点A，C向直线BP作垂线，垂足分别为点E，F，点O为AC的中点．（1）如图1，当点P与点O重合时，请你判断OE与OF的数量关系；（2）当点P运动到如图2所示位置时，请你在图2中补全图形并通过证明判断（1）中的结论是否仍然成立；（3）若点P在射线OA上运动，恰好使得∠OEF＝30°时，猜想此时线段CF，AE，OE之间有怎样的数量关系，直接写出结论不必证明．【答案】（1）OE ＝OF ．理由见解析；（2）补全图形如图所示见解析，OE ＝OF 仍然成立；（3）CF ＝OE+AE 或CF ＝OE ﹣AE ．【解析】【分析】（1）根据矩形的性质以及垂线，即可判定()AOE COF AAS ∆≅∆，得出OE =OF ； （2）先延长EO 交CF 于点G ，通过判定()AOE COG ASA ∆≅∆，得出OG =OE ，再根据Rt EFG ∆中，12OF EG =，即可得到OE =OF ； （3）根据点P 在射线OA 上运动，需要分两种情况进行讨论：当点P 在线段OA 上时，当点P 在线段OA 延长线上时，分别根据全等三角形的性质以及线段的和差关系进行推导计算即可．【详解】（1）OE =OF ．理由如下：如图1．∵四边形ABCD 是矩形，∴ OA =OC ．∵AE BP ⊥，CF BP ⊥，∴90AEO CFO ∠=∠=︒．∵在AOE ∆和COF ∆中，AEO CFO AOE COF OA OC ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴()AOE COF AAS ∆≅∆，∴ OE =OF ；（2）补全图形如图2，OE =OF 仍然成立．证明如下：延长EO 交CF 于点G ．∵AE BP ⊥，CF BP ⊥，∴ AE //CF ，∴EAO GCO ∠=∠．又∵点O 为AC 的中点，∴ AO =CO ．在AOE ∆和COG ∆中，EAO GCO AO CO AOE COG ∠=∠⎧⎪=⎨⎪∠=⎩，∴()AOE COG ASA ∆≅∆，∴ OG =OE ，∴Rt EFG ∆中，12OF EG =，∴ OE =OF ； （3）CF =OE +AE 或CF =OE -AE ． 证明如下：①如图2，当点P 在线段OA 上时．∵30OEF ∠=︒，90EFG ∠=︒，∴60OGF ∠=︒，由（2）可得：OF =OG ，∴OGF ∆是等边三角形，∴ FG =OF =OE ，由（2）可得：AOE COG ∆≅∆，∴ CG =AE ．又∵ CF =GF +CG ，∴ CF =OE +AE ；②如图3，当点P 在线段OA 延长线上时．∵30OEF ∠=︒，90EFG ∠=︒，∴60OGF ∠=︒，同理可得：OGF ∆是等边三角形，∴ FG =OF =OE ，同理可得：AOE COG ∆≅∆，∴ CG =AE ．又∵ CF =GF -CG ，∴ CF =OE -AE ．【点睛】本题属于四边形综合题，主要考查了矩形的性质、全等三角形的性质和判定以及等边三角形的性质和判定，解决问题的关键是构建全等三角形和证明三角形全等，利用矩形的对角线互相平分得全等的边相等的条件，根据线段的和差关系使问题得以解决．6．猜想与证明：如图1，摆放矩形纸片ABCD与矩形纸片ECGF，使B、C、G三点在一条直线上，CE在边CD上，连接AF，若M为AF的中点，连接DM、ME，试猜想DM与ME的关系，并证明你的结论．拓展与延伸：（1）若将”猜想与证明“中的纸片换成正方形纸片ABCD与正方形纸片ECGF，其他条件不变，则DM和ME的关系为．（2）如图2摆放正方形纸片ABCD与正方形纸片ECGF，使点F在边CD上，点M仍为AF 的中点，试证明（1）中的结论仍然成立．【答案】猜想：DM=ME，证明见解析；（2）成立，证明见解析.【解析】试题分析：延长EM交AD于点H，根据ABCD和CEFG为矩形得到AD∥EF，得到△FME和△AMH全等，得到HM=EM，根据Rt△HDE得到HM=DE，则可以得到答案；（1）、延长EM交AD于点H，根据ABCD和CEFG为矩形得到AD∥EF，得到△FME和△AMH全等，得到HM=EM，根据Rt△HDE得到HM=DE，则可以得到答案；（2）、连接AE，根据正方形的性质得出∠FCE=45°，∠FCA=45°，根据RT△ADF中AM=MF得出DM=AM=MF，根据RT△AEF中AM=MF得出AM=MF=ME，从而说明DM=ME.试题解析：如图1，延长EM交AD于点H，∵四边形ABCD和CEFG是矩形，∴AD∥EF，∴∠EFM=∠HAM，又∵∠FME=∠AMH，FM=AM，在△FME和△AMH中，∴△FME≌△AMH（ASA）∴HM=EM，在RT△HDE中，HM=DE，∴DM=HM=ME，∴DM=ME．（1）、如图1，延长EM交AD于点H，∵四边形ABCD和CEFG是矩形，∴AD∥EF，∴∠EFM=∠HAM，又∵∠FME=∠AMH，FM=AM，在△FME和△AMH中，∴△FME≌△AMH（ASA）∴HM=EM，在RT△HDE中，HM=EM∴DM=HM=ME，∴DM=ME，（2）、如图2，连接AE，∵四边形ABCD和ECGF是正方形，∴∠FCE=45°，∠FCA=45°，∴AE和EC在同一条直线上，在RT△ADF中，AM=MF，∴DM=AM=MF，在RT△AEF中，AM=MF，∴AM=MF=ME，∴DM=ME．考点：（1）、三角形全等的性质；（2）、矩形的性质.7．如图，在正方形ABCD中，点G在对角线BD上（不与点B，D重合），GE⊥DC于点E，GF⊥BC于点F，连结AG．（1）写出线段AG，GE，GF长度之间的数量关系，并说明理由；（2）若正方形ABCD的边长为1，∠AGF=105°，求线段BG的长．【答案】（1）AG2=GE2+GF2（2）【解析】试题分析：（1）结论：AG2=GE2+GF2．只要证明GA=GC，四边形EGFC是矩形，推出GE=CF，在Rt△GFC中，利用勾股定理即可证明；（2）作BN⊥AG于N，在BN上截取一点M，使得AM=BM．设AN=x．易证AM=BM=2x，MN=x，在Rt△ABN中，根据AB2=AN2+BN2，可得1=x2+（2x+x）2，解得x=，推出BN=，再根据BG=BN÷cos30°即可解决问题.试题解析：（1）结论：AG2=GE2+GF2．理由：连接CG．∵四边形ABCD是正方形，∴A、C关于对角线BD对称，∵点G在BD上，∴GA=GC，∵GE⊥DC于点E，GF⊥BC于点F，∴∠GEC=∠ECF=∠CFG=90°，∴四边形EGFC是矩形，∴CF=GE，在Rt△GFC中，∵CG2=GF2+CF2，∴AG2=GF2+GE2．（2）作BN⊥AG于N，在BN上截取一点M，使得AM=BM．设AN=x．∵∠AGF=105°，∠FBG=∠FGB=∠ABG=45°，∴∠AGB=60°，∠GBN=30°，∠ABM=∠MAB=15°，∴∠AMN=30°，∴AM=BM=2x，MN=x，在Rt△ABN中，∵AB2=AN2+BN2，∴1=x2+（2x+x）2，解得x=，∴BN=，∴BG=BN÷cos30°=．考点：1、正方形的性质，2、矩形的判定和性质，3、勾股定理，4、直角三角形30度的性质8．如图1所示，（1）在正三角形ABC中，M是BC边（不含端点B、C）上任意一点，P 是BC延长线上一点，N是∠ACP的平分线上一点，若∠AMN=60°，求证：AM=MN．（2）若将（1）中“正三角形ABC”改为“正方形ABCD”，N是∠DCP的平分线上一点，若∠AMN=90°，则AM=MN是否成立？若成立，请证明；若不成立，说明理由．（3）若将（2）中的“正方形ABCD”改为“正n边形A1A2…A n“，其它条件不变，请你猜想：当∠A n﹣2MN=_____°时，结论A n﹣2M=MN仍然成立．（不要求证明）【答案】0 (2)180 nn【解析】分析：（1）要证明AM=MN，可证AM与MN所在的三角形全等，为此，可在AB上取一点E，使AE=CM，连接ME，利用ASA即可证明△AEM≌△MCN，然后根据全等三角形的对应边成比例得出AM=MN．（2）同（1），要证明AM=MN，可证AM与MN所在的三角形全等，为此，可在AB上取一点E，使AE=CM，连接ME，利用ASA即可证明△AEM≌△MCN，然后根据全等三角形的对应边成比例得出AM=MN．详（1）证明：在边AB上截取AE=MC，连接ME．在正△ABC中，∠B=∠BCA=60°，AB=BC．∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAE，BE=AB-AE=BC-MC=BM，∴∠BEM=60°，∴∠AEM=120°．∵N是∠ACP的平分线上一点，∴∠ACN=60°，∴∠MCN=120°．在△AEM与△MCN中，∠MAE=∠NMC，AE=MC，∠AEM=∠MCN，∴△AEM≌△MCN（ASA），∴AM=MN．（2）解：结论成立；理由：在边AB上截取AE=MC，连接ME．∵正方形ABCD中，∠B=∠BCD=90°，AB=BC．∴∠NMC=180°-∠AMN-∠AMB=180°-∠B-∠AMB=∠MAB=∠MAE，BE=AB-AE=BC-MC=BM，∴∠BEM=45°，∴∠AEM=135°．∵N是∠DCP的平分线上一点，∴∠NCP=45°，∴∠MCN=135°．在△AEM与△MCN中，∠MAE=∠NMC，AE=MC，∠AEM=∠MCN，∴△AEM≌△MCN（ASA），∴AM=MN．（3）由（1）（2）可知当∠A n-2MN等于n边形的内角时，结论A n-2M=MN仍然成立；即∠A n-2MN=()02180nn-时，结论A n-2M=MN仍然成立；故答案为[()02180nn-]．点睛：本题综合考查了正方形、等边三角形的性质及全等三角形的判定，同时考查了学生的归纳能力及分析、解决问题的能力．难度较大．9．如图1，在菱形ABCD中，ABC=60°，若点E在AB的延长线上，EF∥AD，EF=BE，点P 是DE的中点，连接FP并延长交AD于点G．（1）过D作DH AB,垂足为H，若DH=，BE=AB,求DG的长；（2）连接CP，求证：CP FP；（3）如图2，在菱形ABCD中，ABC=60°，若点E在CB的延长线上运动，点F在AB的延长线上运动，且BE=BF，连接DE,点P为DE的中点，连接FP、CP，那么第（2）问的结论成立吗？若成立，求出的值；若不成立，请说明理由．【答案】（1）1；（2）见解析；（3）．【解析】试题分析：（1）根据菱形得出DA∥BC，CD=CB，∠CDG=∠CBA=60°，则∠DAH=∠ABC=60°，根据DH⊥AB得出∠DHA=90°，根据Rt△ADH的正弦值得出AD的长度，然后得出BE的长度，然后证明△PDG≌△PEF，得出DG=EF，根据EF∥AD，AD∥BC 得出EF∥BC，则说明△BEF为正三角形，从而得出DG的长度；（2）连接CG、CF，根据△PDG≌△PEF得出PG=PF，然后证明△CDG≌△CBF，从而得到CG=CF，根据PG=PF得出垂直；（3）过D作EF的平行线，交FP延长于点G，连接CG、CF证△PEF≌△PDG，然后证明△CDG≌△CBF，从而得出∠GCE=120°，根据Rt△CPF求出比值．试题解析：（1）解：∵四边形ABCD为菱形∴DA∥BC CD="CB" ∠CDG=∠CBA=60°∴∠DAH=∠ABC=60°∵DH⊥AB ∴∠DHA=90°在Rt△ADH中 sin∠DAH=∴AD=∴BE=AB=×4=1 ∵EF∥AD ∴∠PDG=∠PEB ∵P为DE的中点∴PD=PE∵∠DPG=∠EPF ∴△PDG≌△PEF ∴DG=EF ∵EF∥AD AD∥BC ∴EF∥BC∴∠FEB=∠CBA=60°∵BE=EF ∴△BEF为正三角形∴EF=BE=1 ∴DG=EF=1、证明：连接CG、CF由（1）知△PDG≌△PEF ∴PG=PF在△CDG与△CBF中易证：∠CDG=∠CBF=60° CD=CB BF=EF=DG ∴△CDG≌△CBF∴CG=CF ∵PG=PF ∴CP⊥GF（3）如图：CP⊥GF仍成立理由如下：过D作EF的平行线，交FP延长于点G连接CG、CF证△PEF≌△PDG ∴DG=EF=BF ∵DG∥EF ∴∠GDP=∠EFP ∵DA∥BC∴∠ADP=∠PEC∴∠GDP－∠ADP=∠EFP－∠PEC ∴∠GDA=∠BEF=60°∴∠CDG=∠ADC+∠GDA=120°∵∠CBF=180°－∠EBF=120°∴∠CBF=∠CDG ∵CD=BC DG=BF ∴△CDG≌△CBF∴CG=CF ∠DCG=∠FCE ∵PG=PF ∴CP⊥PF ∠GCP=∠FCP∵∠DCP=180－∠ABC=120°∴∠DCG+∠GCE=120°∴∠FCE+∠GCE=120°即∠GCE=120°∴∠FCP=∠GCE=60°在Rt△CPF中 tan∠FCP=tan60°==考点：三角形全等的证明与性质．10．（本题满分10分）如图1，已知矩形纸片ABCD中，AB＝6cm，若将该纸片沿着过点B的直线折叠（折痕为BM），点A恰好落在CD边的中点P处．（1）求矩形ABCD的边AD的长．（2）若P为CD边上的一个动点，折叠纸片，使得A与P重合，折痕为MN，其中M在边AD上，N在边BC上，如图2所示．设DP＝x cm，DM＝y cm，试求y与x的函数关系式，并指出自变量x的取值范围．（3）①当折痕MN的端点N在AB上时，求当△PCN为等腰三角形时x的值；②当折痕MN的端点M在CD上时，设折叠后重叠部分的面积为S，试求S与x之间的函数关系式【答案】（1）AD＝3；（2）y=－其中，0＜x＜3；（3）x=；（4）S=.【解析】试题分析：（1）根据折叠图形的性质和勾股定理求出AD的长度；（2）根据折叠图形的性质以及Rt△MPD的勾股定理求出函数关系式；（3）过点N作NQ⊥CD，根据Rt△NPQ 的勾股定理进行求解；（4）根据Rt△ADM的勾股定理求出MP与x的函数关系式，然后得出函数关系式.试题解析：（1）根据折叠可得BP=AB=6cm CP=3cm 根据Rt△PBC的勾股定理可得：AD＝3．（2）由折叠可知AM＝MP，在Rt△MPD中，∴∴y=－其中，0＜x＜3.（3）当点N在AB上，x≥3，∴PC≤3，而PN≥3，NC≥3.∴△PCN为等腰三角形，只可能NC＝NP．过N点作NQ⊥CD，垂足为Q，在Rt△NPQ中，∴解得x=．（4）当点M在CD上时，N在AB上，可得四边形ANPM为菱形．设MP＝y，在Rt△ADM中，，即∴ y=．∴ S=考点：函数的性质、勾股定理.。

类型2：平四与特殊平四的性质与判定（1）选填 1、（广东中考10）如图，已知正方形ABCD ，点E 是BC 边的中点，DE 与AC 相交于点F ，连接BF ，下列结论：①；②；③；④,其中正确的是( )A .①③B .②③C .①④D .②④ 2、（朝阳一模8）如图，广场中心的菱形花坛ABCD 的周长是40米，∠A =60°，则A ，C 两点之间的距离为（ ）A .5米B .53米C .10米D .103米3、（通州一模8）如图，将一张矩形的纸对折，旋转90°后再对折，然后沿着右图中的虚线剪下，则剪下的纸片打开后的形状一定为（ ） A ．三角形 B ．菱形 C ．矩形 D ．正方形4、（海淀二模4）如图，ABCD 中，AD =5，AB =3，∠BAD 的平分线AE 交BC 于E 点，则EC 的长为（ ）A ．4B ．3C ．2D ．1 5、（平谷一模2）把一个边长为1的正方形如图所示放在数轴上，以正方形的对角线为半径画弧交数轴于点A ，则点A对应的数是（ ） A ．1B ．2C ．3D ．26、（河南中考9）我们知道：四边形具有不稳定性．如图，在平面直角坐标系中，边长为2的正方形ABCD 的边AB 在x 轴上，AB 的中点是坐标原点O ，固定点A ，B ，把正方形沿箭头方向推，使点D 落在y 轴正半轴上点D ′处，则点C 的对应点C ′的坐标为（ ）A ．（√3，1）B ．（2，1）C ．（1，√3）D ．（2，√3）7、（青岛中考7）如图，平行四边形ABCD 的对角线AC与BD 相交于点O ，AE ⊥BC ，垂足为E ，3=AB ，AC ＝2，BD ＝4，则AE 的长为（ ） A ．23 B ．23C ．721 D ．7212ABF ADF S S =△△4CDF CBF S S =△△2ADF CEF S S =△△2ADF CDF S S =△△A -13210B E CA D8、（德州中考11）如图放置的两个正方形，大正方形ABCD 边长为a ，小正方形CEFG 边长为b （a ＞b ），M 在BC 边上，且BM =b ，连接AM ，MF ，MF 交CG 于点P ，将△ABM 绕点A 旋转至△ADN ，将△MEF 绕点F 旋转至△NGF ．给出以下五个结论：①∠AND =∠MPC ；②CP =；③△ABM≌△NGF ；④S 四边形AMFN =a 2+b 2；⑤A ，M ，P ，D 四点共圆．其中正确的个数是（ ）A ．2B ．3C ． 4D ．59、（苏州中考10）如图，在菱形CD AB 中，60∠A =，D 8A =，F 是AB 的中点．过点F 作F DE ⊥A ，垂足为E ．将F ∆AE 沿点A 到点B 的方向平移，得到F '''∆A E ．设P 、'P 分别是F E 、F ''E 的中点，当点'A 与点B 重合时，四边形CD 'PP 的面积为（ ）A ．283B ．243C .323D ．3238-10、（顺义二模15）如图，在正方形ABCD 和正方形AEFG 中，顶点E 在边AD 上，连接DG 交EF 于点H ，若FH ＝1，EH ＝2，则DG 的长为 ． 11、（西城二模13）如图，正方形ABCD ，AC 为对角线，点E 在AC 上，且AE =AB ，则∠BED 的度数为 °．12、（怀柔一模13）如图，在ABCD 中，ED =2，BC =5，∠ABC的平分线交AD 于点E ，则AB 的长为_______________． 13、（通州一模15）如图，Rt △ABC ≌Rt △DCB ，两斜边交于点O ，如果AC =3，那么OD 的长为_____________．14、（苏州中考18）如图，在矩形CD AB 中，将C ∠AB 绕点A 按逆时针方向旋转一定角度后，C B 的对应边C ''B 交CD 边于点G ．连接'BB 、CC '，若D 7A =，CG 4=，G ''AB =B ，则CC '='BB _______________（结果保留根号）．2b b a-E DCB AOABCDH GF EDCB A D GC B AFEM NP15、（北京中考20） 数学家吴文俊院士非常重视古代数学家贾宪提出的“从长方形对角线上任一点作两条分别平行于两邻边的直线，则所容两长方形面积相等（如图所示）”这一推论，他从这一推论出发，利用“出入相补”原理复原了《海岛算经》九题古证. （以上材料源于《古证复原的原理》、《吴文俊与中国数学》和《古代世界数学泰斗刘徽》） 请根据上图完成这个推论的证明过程．证明：()ADC ANF FGC NFGD S S S S ∆∆∆=-+矩形，ABC EBMF S S ∆=-矩形（____________+____________）． 易知，ADC ABC S S ∆∆=，_____________=______________，______________=_____________． 可得NFGD EBMF S S =矩形矩形．（2）解答题（基础、中等） 16、（顺义一模19）如图，□ABCD 中，BE ⊥CD 于E ，CE =DE ．求证：∠A =∠ABD ．17、（通州一模19）如图，在矩形ABCD 中，连接对角线AC ，BD ，延长BC 至点E ，使BC =CE ，连接DE . 求证：DE =AC .18、（燕山一模19）在△ABC 中, AD =BF ,点D ,E ,F 分别是AC ,BC ,BA 延长线上的点,四边形ADEF 为平行四边形. 求证: AB =ACAB C D EEDBA C FE DAB C19、（杭州中考21）如图，在正方形ABCD 中，点G 在对角线BD 上（不与点B ，D 重合），GE ⊥DC 于点E ，GF ⊥BC 于点F ，连结AG 。

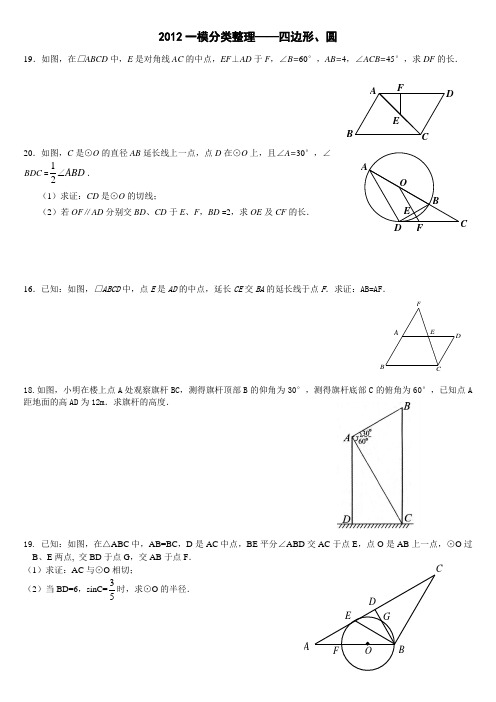
2012一模分类整理——四边形、圆19．如图，在□ABCD 中，E 是对角线AC 的中点，EF ⊥AD 于F ，∠B=60°，AB=4，∠ACB=45°，求DF 的长．20．如图，C 是⊙O 的直径AB 延长线上一点，点D 在⊙O 上，且∠A=30°，∠BDC =12A B D ．（1）求证：CD 是⊙O 的切线；（2）若OF ∥AD 分别交BD 、CD 于E 、F ，BD =2，求OE 及CF 的长．16．已知：如图，□ABCD 中，点E 是AD 的中点，延长CE 交BA 的延长线于点F ．求证：AB=AF ．18.如图，小明在楼上点A 处观察旗杆BC ，测得旗杆顶部B 的仰角为30°，测得旗杆底部C 的俯角为60°，已知点A 距地面的高AD 为12m ．求旗杆的高度．19. 已知：如图，在△ABC 中，AB=BC ，D 是AC 中点，BE 平分∠ABD 交AC 于点E ，点O 是AB 上一点，⊙O 过B 、E 两点, 交BD 于点G ，交AB 于点F ． （1）求证：AC 与⊙O 相切； （2）当BD=6，sinC=53时，求⊙O 的半径．FE DCO B AF EDCBAEBCDAFC19．如图，直角梯形纸片A B C D 中，A D B C ∥，90A ∠=°，30C ∠=°．折叠纸片使B C 经过点D ，点C 落在点E 处，B F 是折痕，且8B FC F ==．（1）求BD F ∠的度数； （2）求A B 的长．20．如图，O ⊙的直径A B 与弦C D （不是直径）相交于点E ，且CE DE =，过点B 作C D 的平行线交A D 延长线于点F ． （1）求证：B F 是O ⊙的切线；（2）连结B C ，若O ⊙的半径为4，3sin 4B C D ∠=，求C D 的长．18．如图，在四边形ABCD 中，A D DC ⊥，对角线A C C B ⊥，若AD ＝2，AC ＝3cos 5B =．试求四边形ABCD的周长．19．已知：如图，在△ABC 中，∠A ＝∠B ＝30º， D 是AB 边上一点，以AD 为直径作⊙O 恰过点C ． （1）求证：BC 所在直线是⊙O 的切线； （2）若AD ＝AC 的长．18．如图，在□ABCD 中，AB ＝5，AD ＝10，cos B ＝35，过BC 的中点E 作EF ⊥AB ，垂足为点F ，连结DF ，求DF 的长．19．如图，已知直线PA 交⊙O 于A 、B 两点，AE 是⊙O 的直径，C 为⊙O 上一点，且AC 平分∠PAE ，过点C 作CD ⊥PA 于D ．（1） 求证：CD 是⊙O 的切线；（2） 若AD ：DC =1：3，AB =8，求⊙O 的半径．19. 已知：如图，在△ABC 中，∠ACB =90°，点E 为AB 的中点，过点E 作ED ⊥BC 于D ，F 在DE 的延长线上，且AF =CE ，若AB =6，AC =2，求四边形ACEF 的面积.20.如图，在△ABC 中，AB =AC ，以AB 为直径的⊙O 分别交BC 、AC 于D 、E 两点，过点D 作DF ⊥AC ，垂足为F .（1）求证：DF 是⊙O 的切线；（2）若AE = DE ，DF =2，求⊙O 的半径.F DCBA FEDCB A19．如图，在 ABCD 中，过点B 作BE ∥AC ，在BG 上取点E ，联结DE 交AC 的延长线于点F ． （1）求证：DF =EF ；（2）如果AD =2，∠ADC =60°，AC ⊥DC 于点C ，AC =2CF ，求BE 的长．（丰台）20．如图，四边形ABCD 内接于O ，BD 是O 的直径，A E C D ⊥于 点E ，DA 平分BD E ∠． （1）求证：AE 是O 的切线；（2）如果AB =4，AE =2，求O 的半径．19．如图，在四边形ABCD 中，∠ABC =90︒，∠CAB =30︒, DE ⊥AC 于E ，且AE=CE ，若DE=5，EB=12，求四边形ABCD 的周长．20．如图，△ABC 内接于⊙O , AD 是⊙O 直径, E 是CB 延长线上一点, 且∠BAE =∠C . （1）求证：直线AE 是⊙O 的切线； （2）若EB =AB , 54cos =E , AE =24，求EB 的长及⊙O 的半径．20．如图，梯形ABCD 中，AD ∥BC ，90A ∠=︒，BC=2，15ABD ∠=︒，60C ∠=︒．(1) 求∠BDC 的度数； (2) 求AB 的长．FD CBA EGED C B A21．如图，AC为⊙O的直径，AC=4，B、D分别在AC两侧的圆上，∠BAD=60°，BD与AC的交点为E．(1) 求点O到BD的距离及∠OBD的度数；(2) 若DE=2BE，求cos O ED的值和CD的长．19. 如图，梯形ABCD中，AB∥CD，AD⊥AB，AB=2，BC=CD=4，求∠B的度数和AC的长．21. 已知：如图，M是AB的中点，以AM为直径的⊙O与BP相切于点N，OP∥MN.（1）求证：直线PA与⊙O相切；（2）求tan∠AMN的值.PA BD。

2022年上海市15区中考数学一模考点分类汇编专题07 阅读理解题型1.(2022崇明一模17) 定义：有一组对边相等而另一组对边不相等的凸四边形叫做“对等四边形”，如图，在Rt PBC △中，90PCB ∠=︒，点A 在边BP 上，点D 在边CP 上，如果11BC =，12tan 5PBC ∠=，13AB =，四边形ABCD 为“对等四边形”，那么CD 的长为_____________．2、（2022杨浦一模17）新定义：已知三条平行直线，相邻两条平行线间的距离相等，我们把三个顶点分别在这样的三条平行线上的三角形称为格线三角形．如图，已知等腰Rt △ABC 为“格线三角形”，且∠BAC ＝90°，那么直线BC 与直线c 的夹角α的余切值为 ．3.（2022长宁一模17）定义: 在 △ABC 中, 点 D 和点 E 分别在 AB 边、 AC 边上, 且DE //BC ，点 D 、点 E 之间距离与直线 DE 与直线 BC 间的距离之比称为 DE 关于 BC 的横纵比. 已知, 在 △ABC 中, 4,BC BC = 上的高长为 3,DE 关于 BC 的横纵比为 2:3, 则 DE =_______．4.（2022松江一模17）我们知道：四个角对应相等，四条边对应成比例的两个四边形是相似四边形．如图，已知梯形ABCD 中，AD ∥BC ，AD ＝1，BC ＝2，E 、F 分别是边AB 、CD 上的点，且EF ∥BC ，如果四边AEFD 与四边形EBCF 相似，那么AEEB的值是_____．5.（2022虹口一模17）在网格中，每个小正方形的顶点称为格点，以格点为顶点的三角形称为“格点三角形”．如图，在4×4的网格中，△ABC 是一个格点三角形，如果△DEF 也是该网格中的一个格点三角形，它与△ABC 相似且面积最大，那么△DEF 与△ABC 相似比的值是 ．6.（2022青浦一模18）如图，一次函数y ＝ax +b （a ＜0，b ＞0）的图象与x 轴，y 轴分别相交于点A ，点B ，将它绕点O 逆时针旋转90°后，与x 轴相交于点C ，我们将图象过点A ，B ，C 的二次函数叫做与这个一次函数关联的二次函数．如果一次函数y ＝﹣kx +k （k ＞0）的关联二次函数是y ＝mx 2+2mx +c （m ≠0），那么这个一次函数的解析式为 ．7.（2022黄埔一模18）若抛物线2111y ax b x c =++的顶点为A ，抛物线2222y ax b x c =-++的顶点为B ，且满足顶点A 在抛物线2y 上，顶点B 在抛物线1y 上，则称抛物线1y 与抛物线2y 互为“关联抛物线”，已知顶点为M 的抛物线()223y x =-+与顶点为N 的抛物线互为“关联抛物线”，直线MN 与x 轴正半轴交于点D ，如果3tan 4MDO ∠=，那么顶点为N 的抛物线的表达式为_________8. 如果一条抛物线()20y ax bx c a =++≠与x 轴有两个交点，那么以该抛物线的顶点和这两个交点为顶点的三角形称为这条拋物线的“特征三角形”．已知()2>0y x bx b =+的“特征三角形”是等腰直角三角形，那么b 的值为_________．9.（2022长宁一模15）我国古代数学著作 《九章算术》中记载：“今有邑方不知大小, 各中开门. 出北门三十步有木, 出 西门七百五十步有木. 问邑方几何? ”示意图如图, 正方形ABCD 中, F G 、 分别是 AD 和 AB 的 中点, 若,30,,750EF AD EF GH AB GH ⊥=⊥=, 且 EH 过点 A , 那么正方形 ABCD 的边长为______．10.（2022奉贤一模17）《九章算术》是我国古代的数学名著，书中有这样一个问题：“今有邑方不知大小，各中开门，出北门一百步立一表，出西门二百二十五步适可见之，问邑方几何？”它的意思是：如图，M 、N 分别是正方形ABCD 的边AD ，AB 的中点，ME ⊥AD ，NF ⊥AB ，EF 过点A ，且ME ＝100步，NF ＝225步，那么该正方形城邑边长AD 约为 步．11.（2022静安一模22）据说, 在距今2500 多年前, 古希腊数学家就已经较准确地测出了埃及金字塔的高度, 操作过程大致如下：如图所示，设AB是金字塔的高。

初三专题复习------尺规作图的理论依据班级___________姓名___________ 成绩___________ 几何作图题同一般画图题不同，它规定只准用直尺和圆规为工具，而且每一步作图都必须有根有据，不能随便画．比较复杂的作图题，要经过严格的分析，才能找到作图的根据和作法．1．阅读下面材料：在数学课上，老师提出如下问题：尺规作图：作一条线段的垂直平分线．已知：线段AB ．小芸的作法如下：如图，（1）分别以点A 和点B 为圆心，大于12AB 的长为半径作弧，两弧相交于C 、D 两点；（2）作直线CD .所以直线CD 就是所求作的垂直平分线.老师说：“小芸的作法正确．”请回答：小芸的作图依据是________________________________________________．2已知：直线l 和l 外一点P . 求作：直线l 的垂线，使它经过点P .作法：如图．(1)在直线l 上任取两点A ，B ；(2)分别以点A ，B 为圆心，AP ，BP 长为半径作弧，两弧相交于点(3)作直线PQ .所以直线PQ 就是所求的垂线．请回答：该作图的依据是______________________________________________________________________.3．阅读下面材料：在数学课上，老师提出如下问题：尺规作图：过直线外一点作已知直线的平行线．已知：直线l 及其外一点A .求作：l 的平行线，使它经过点A .小云的作法如下：(1)在直线l 上任取一点B ，以点B 为圆心，AB 长为半径作弧，交直线l 于点C ；(2)分别以A ，C 为圆心，以AB(3)作直线AD .所以直线AD 即为所求．老师说：“小云的作法正确．”请回答：小云的作图依据是____________________________________________．4．阅读下面材料：数学课上，老师提出如下问题：尺规作图：经过已知直线上一点作这条直线的垂线．已知：直线AB 和AB 上一点C .求作：AB 的垂线，使它经过点C .小艾的作法如下：如图，(1)在直线AB 上取一点D ，使点D 与点C 不重合，以点C 为圆心，CD 长为半径作弧，交AB 于D ，E 两点；(2)分别以点D 和点E 为圆心，大于12DE 长为半径作弧，两弧相交于点F ； (3)作直线CF .所以直线CF 就是所求作的垂线．老师表扬了小艾的作法是对的．请回答：小艾这样作图的依据是．5．阅读下面材料：在数学课上，老师提出如下问题：如图，已知△ABC ，AB <BC ，用尺规作图的方法在BC 上取一点P ，使得P A ＋PC ＝BC . 甲、乙、丙、丁四位同学的主要作法如下：甲同学的作法：如图甲：以点B 为圆心，BA 长为半径画弧，交BC 于点P ，则点P 就是所求的点．乙同学的作法：如图乙：作线段AC 的垂直平分线交BC 于点P ，则点P 就是所求的点． 丙同学的作法：如图丙：以点C 为圆心，CA 长为半径画弧，交BC 于点P ，则点P 就是所求的点．丁同学的作法：如图丁：作线段AB 的垂直平分线交BC 于点P ，则点P 就是所求的点．请你判断哪位同学的作法正确________；这位同学作图的依据是________________________________________________________________________．6． 如图，已知∠AOB .小明按如下步骤作图：①以点O 为圆心，任意长为半径画弧，交OA 于点D ，交OB 于点E .②分别以D ，E 为圆心，大于12DE 长为半径画弧，在∠C . ③画射线OC .所以射线OC 为所求∠AOB 的平分线．根据上述作图步骤，回答下列问题：(1)写出一个正确的结论：___________________________________________.(2)如果在OC 上任取一点M ，那么点M 到OA ，OB 的距离相等．依据是：________________________________________________________________________.7．阅读下面材料：数学课上，老师提出如下问题：尺规作图：作一角等于已知角．已知：∠AOB .求作：∠FBE ，使得∠FBE ＝∠AOB .小明的解答如图所示：老师说：“小明的作法正确．”请回答：(1)小明的作图依据是________________________________________________________________________；(2)他所画的痕迹弧MN 是以点________为圆心，________为半径的弧．8．阅读下面材料：在数学课上，老师提出如下问题：尺规作图，作一个角的平分线．已知：∠AOB .求作：射线OC ，使它平分∠AOB .小米的作法如下：如图，(1)以点O 为圆心，任意长为半径作弧，交OA 于点D ，交OB 于点E ；(2)分别以点D ，E 为圆心，大于12DE 的长为半径作弧，两弧交于点C ； (3)作射线OC .所以射线OC 就是所求作的射线．老师说：“小米的作法正确．”请回答：小米的作图依据是________________________________________________________________________．9．数学课上，同学们兴致勃勃地尝试着利用不同画图工具画一个角的平分线． 小明用直尺画角平分线的方法如下：(1)用直尺的一边贴在∠AOB 的OA 边上，沿着直尺的另一条边画直线m ；(2)再用直尺的一边贴在∠AOB 的OB 边上，沿着直尺的另一条边画直线n ，直线m 与直线n 交于点P ；(3)作射线OP .射线OP 是∠AOB 的平分线．请回答：小明的画图依据是．10．阅读下面材料：在数学课上，老师提出如下问题：已知：Rt △ABC ，∠ABC ＝90°.求作：矩形ABCD.小敏的作法如下：①作线段AC的垂直平分线交AC于点O；②连接BO并延长，在延长线上截取OD＝BO；③连接DA，DC.则四边形ABCD即为所求．老师说：“小敏的作法正确．”请回答：小敏的作图依据是11．阅读下面材料：实际生活中，有时会遇到一些“不能接近的角”，如图中的∠P，我们可以采用下面的方法作一条直线平分∠P(1)作直线l与∠P的两边分别交于点A，B，分别作∠P AB分线相交于点M；(2)作直线k与∠P的两边分别交于点C，D，分别作∠PCD和∠PDC的平分线，两条角平分线相交于点N；(3)作直线MN.所以，直线MN平分∠P.请回答：上面作图方法的依据是12．在数学课上，老师提出如下问题：已知：如图，线段AB，BC，求作：平行四边形ABCD.小明的作法如下：如图：(1)以点C为圆心，AB长为半径作弧；(2)以点A为圆心，BC长为半径作弧；(3)两弧在BC上方交于点D，连接AD，CD，四边形ABCD为所求作的平行四边形．老师说：“小明的作法正确．”请回答：小明的作图依据是________________________________________________________________________．13．在数学课上，老师提出如下问题：已知：如图，线段AB，BC，∠ABC＝90°求作：矩形ABCD.小明的作图过程如下：(1)连接AC，作线段AC的垂直平分线，交AC于M；(2)连接BM并延长，在延长线上取一点D，使MD＝MB，连接AD，CD.∴四边形ABCD即为所求．老师说：“小明的作法正确．”请回答：小明这样作图的依据是________________________________________________________________________．。

2021年上海市16区中考数学一模汇编专题04 四边形一、单选题1．（2021·上海宝山区·九年级一模）如图，//AB DE ，//BC DF ，已知::AF FB m n =，BC a =，那么CE 等于（ ）．A ．amnB ．an mC ．amm n+ D ．anm n+ 2．（2021·上海九年级一模）如图，在ABC 中，点D 在边AB 上，DE BC //，DF AC //，联结BE ，BE 与DF 相交于点G ，则下列结论一定正确的是（ ）A ．AD DEDB BC= B ．AE BFAC BC= C ．BD BFAD DE= D ．DG BFGF FC= 3．（2021·上海奉贤区·九年级一模）如图，在梯形ABCD 中，//,3AD BC BC AD =，对角线AC BD 、交于点,O EF 是梯形ABCD 的中位线，EF 与BD AC 、分别交于点G H 、，如果OGH ∆的面积为1，那么梯形ABCD 的面积为（ ）A ．12B ．14C ．16D ．18二、填空题4．（2021·上海杨浦区·九年级一模）如图，已知在ABC 中，90C ∠=︒，10AB =，1cot 2B =，正方形DEFG 的顶点G 、F 分别在边AC 、BC 上，点D 、E 在斜边AB 上，那么正方形DEFG 的边长为_____．5．（2021·上海黄浦区·九年级一模）已知一个直角三角形的两条直角边长分别为3和6．则该三角形的重心到其直角顶点的距离是________．6．（2021·上海浦东新区·九年级一模）如图，矩形DEFG 的边EF 在ABC 的边BC 上，顶点D 、G 分别在边AB 、AC 上，已知ABC 的边BC 长60厘米，高AH 为40厘米，如果DE=2DG ，那么DG=______厘米．7．（2021·上海嘉定区·九年级一模）正方形的边长与其对角线长的比为________.8．（2021·上海徐汇区·九年级一模）如图，已知ABC 是边长为2的等边三角形，正方形DEFG 的顶点,D E 分别在边,AC AB 上，点,F G 在边BC 上，那么AD 的长是_____．9．（2021·上海长宁区·九年级一模）如图，矩形ABCD 沿对角线BD 翻折后，点C 落在点E 处．联结CE 交边AD 于点F ．如果DF ＝1，BC ＝4，那么AE 的长等于_________．10．（2021·上海九年级一模）如果四边形边上的点，它与对边两个端点的连线将这个四边形分成的三个三角形都相似，我们就把这个点叫做该四边形的“强相似点”．如图1，在四边形ABCD 中，点Q 在边AD 上，如果QAB 、QBC 和QDC 都相似，那么点Q 就是四边形ABCD 的“强相似点”；如图2，在四边形ABCD 中，AD BC //，2AB DC ==，8BC =，60B ∠=︒，如果点Q 是边AD 上的“强相似点”，那么AQ =___．11．（2021·上海九年级一模）直角三角形的重心到斜边中点的距离为2，那么该直角三角形的斜边长为____________．12．（2021·上海杨浦区·九年级一模）如图，已知在平行四边形ABCD 中，点E 在边AB 上，12AE EB =，联结DE 交对角线AC 于点O ，那么AOOC的值为_____．13．（2021·上海静安区·九年级一模）在△ABC 中，点G 是重心，△BGC =90°，BC =8，那么AG 的长为____． 14．（2021·上海宝山区·九年级一模）在一块直角三角形铁皮上截一块正方形铁皮，如图，已有的铁皮是Rt ABC △，90C ∠=︒，要截得的正方形EFGD 的边FG 在AB 上，顶点E 、D 分别在边CA 、CB 上，如果4AF =，9GB =，那么正方形铁皮的边长为______．15．（2021·上海宝山区·九年级一模）已知等腰梯形上底为5，高为4，底角的余弦值为35，那么其周长为______．三、解答题16．（2021·上海青浦区·九年级一模）如图，在平行四边形ABCD 中，8BC =，点E 、F 是对角线BD 上的两点，且BE EF FD ==，AE 的延长线交BC 于点G ，GF 的延长线交AD 于点H ．（1）求HD 的长；（2）设BGE △的面积为a ，求四边形AEFH 的面积．（用含a 的代数式表示） 2021年上海市16区中考数学一模汇编专题04 四边形一、单选题1．（2021·上海宝山区·九年级一模）如图，//AB DE ，//BC DF ，已知::AF FB m n =，BC a =，那么CE 等于（ ）．A ．amnB ．an mC ．amm n+ D ．anm n+ 【答案】D【分析】先证明：四边形DEBF 是平行四边形，可得DF BE =，利用::AF FB m n =，再求解AF mAB m n=+，再证明ADF ACB ∽，利用相似三角形的性质求解BE ，再利用线段的和差可得答案． 【详解】解：//AB DE ，//BC DF ，∴ 四边形DEBF 是平行四边形，DF BE ∴=，::AF FB m n =，AF mAB m n∴=+，//DF BC ，ADF ACB ∴∽ ，AF DF ADAB BC AC ∴==, //AB DE ，BE AD mBC AC m n ∴==+，BC a =，ma BE m n ∴=+，.ma na CE a m n m n∴=-=++ 故选：.D【点睛】本题考查的是平行四边形的判定与性质，比例的基本性质，相似三角形的判定与性质，掌握以上知识是解题的关键．2．（2021·上海九年级一模）如图，在ABC 中，点D 在边AB 上，DE BC //，DF AC //，联结BE ，BE 与DF 相交于点G ，则下列结论一定正确的是（ ）A ．AD DEDB BC= B ．AE BFAC BC= C ．BD BFAD DE= D ．DG BFGF FC= 【答案】C【分析】根据相似三角形的判定和平行线分线段成比例进行判断即可． 【详解】解：△DE△BC ，DF△AC ，△四边形DFCE 是平行四边形，△DE=CF ，DF=CE ，△DE△BC ，DF△AC ，△△ADE△△ABC ，△BFD△△BAC ，△AD DEAB BC=，故A 错误； AE AD AC AB BC CF==，即AE CF AC BC=，故B 错误； △DF△AC ，△BD BF BFAD CF DE==，故C 正确； △DE△BC ，△DG DE CFGF BF BF==，故D 错误，故选：C ． 【点睛】本题考查了相似三角形的判定与性质、平行线分线段成比例、平行四边形的判定与性质，熟练掌握相似三角形的性质和平行线分线段成比例是解答的关键．3．（2021·上海奉贤区·九年级一模）如图，在梯形ABCD 中，//,3AD BC BC AD =，对角线AC BD 、交于点,O EF 是梯形ABCD 的中位线，EF 与BD AC 、分别交于点G H 、，如果OGH ∆的面积为1，那么梯形ABCD 的面积为（ ）A ．12B ．14C ．16D ．18【答案】C【分析】设AD=2x ，BC=6x ，根据EF 是梯形ABCD 的中位线，求得EG=FH=12AD =x ，GF=12BC =3x ，证得GH=AD ，由此得到1OGH AOD S S ∆∆==，39BOC OGH S S ∆∆==，033A B DOC AOD S S S ∆∆∆===，即可求出答案． 【详解】设AD=2x ，BC=6x ，△EF 是梯形ABCD 的中位线， △点E 、F 、G 、H 分别为AB 、CD 、BD 、AC 的中点，EF△AD△BC ，△EF=1()24AD BC +=x ， △EG=FH=12AD =x ，GF=12BC =3x ，△GH=2x ，△GH=AD ， △GH△AD,△△OAD△△OHG,△1OD ADOG GH==，△OG=OD ，1OGH AOD S S ∆∆==， △GH△BC,△△OGH△△OBC ，△2163GH x BC x ==，△99BOC OGH S S ∆∆==， △O 是DG 的中点，G 是BD 的中点，△033A B DOC AOD S S S ∆∆∆===，133916ABCD S ∴=+++=， 故选：C ．．【点睛】此题考查梯形中位线的性质定理，三角形中位线的性质定理，同底或同高三角形面积的关系，相似三角形的性质，这是一道与中位线相关的综合题． 二、填空题4．（2021·上海杨浦区·九年级一模）如图，已知在ABC 中，90C ∠=︒，10AB =，1cot 2B =，正方形DEFG 的顶点G 、F 分别在边AC 、BC 上，点D 、E 在斜边AB 上，那么正方形DEFG 的边长为_____．【答案】207【分析】作CM△AB 于M ，交GF 于N ，由勾股定理可得出AB ，由面积法求出CM ，证明△CGF△△CAB ，再根据对应边成比例，即可得出答案．【详解】作CM△AB 于M ，交GF 于N ，如图所示： △Rt△ABC 中，△C ＝90°，AB ＝10，1cot B 2=，△设BC ＝k ，则AC ＝2k ，AB 2＝AC 2＋BC 2，即：102＝（2k ）2＋k 2，解得：k ＝△BC ＝AC ＝△CM ＝AC BC AB ⋅＝10＝4，△正方形DEFG 内接于△ABC ，△GF ＝EF ＝MN ，GF△AB ，△△CGF△△CAB ， △CN GF =CM AB ，即4EF EF 410-=，解得：EF ＝207；故答案为：207．【点睛】本题考查的是相似三角形的判定和性质、正方形的性质、勾股定理等知识；正确作出辅助线、灵活运用相似三角形的判定定理和性质定理是解题的关键．5．（2021·上海黄浦区·九年级一模）已知一个直角三角形的两条直角边长分别为3和6．则该三角形的重心到其直角顶点的距离是________．【分析】根据题意，画出图形，如解图所示，连接CO 并延长交AB 于点D ，利用勾股定理求出AB ，根据直角三角形斜边上的中线等于斜边的一半即可求出CD ，再利用三角形重心的性质即可求出结论．【详解】解：Rt△ABC 中，△ACB=90°，AC=6，BC=3，点O 为三角形的重心，连接CO 并延长交AB 于点D ，，CD 为△ABC 的中线，△CD=12AB =2△O 为△ABC 的重心，△该三角形的重心到其直角顶点的距离CO=23【点睛】此题考查的是直角三角形的性质和重心的定义及性质，掌握勾股定理、直角三角形斜边上的中线等于斜边的一半和重心的定义及性质是解题关键．6．（2021·上海浦东新区·九年级一模）如图，矩形DEFG 的边EF 在ABC 的边BC 上，顶点D 、G 分别在边AB 、AC 上，已知ABC 的边BC 长60厘米，高AH 为40厘米，如果DE=2DG ，那么DG=______厘米．【答案】15【分析】如图，记,AH DG 的交点为M ， 设,DG x = 2,402,DE x AM x ==-再证明：,ADG ABC ∽利用相似三角形的性质可得：,DG AMBC AH=再列方程，解方程可得答案． 【详解】解：如图，记,AH DG 的交点为M ，设,DG x = 2DE DG =， 2,DE x ∴= ,AH BC ⊥ 四边形DEFG 为矩形，40AH =，2,402,MH DE x AM x ∴===- ,AH DG ⊥ //,DG EF ,ADG ABC ∴∽ ,DG AMBC AH∴= 60BC =，402,6040x x -∴= 402400120,x x ∴=- 1602400,x ∴= 15,x ∴= 15.DG ∴=故答案为：15.【点睛】本题考查的是矩形的性质，相似三角形的判定与性质，掌握以上知识是解题的关键．7．（2021·上海嘉定区·九年级一模）正方形的边长与其对角线长的比为________.【答案】1【分析】设正方形的边长为1，计算即得结果.【详解】解：设正方形的边长为1，所以正方形的边长与其对角线长的比为1【点睛】此题主要考查对正方形的性质和线段比的定义的理解及运用．难度不大，属于基础题型． 8．（2021·上海徐汇区·九年级一模）如图，已知ABC 是边长为2的等边三角形，正方形DEFG 的顶点,D E 分别在边,AC AB 上，点,F G 在边BC 上，那么AD 的长是_____．【答案】6【分析】根据等边三角形以及正方形的性质，在Rt△CDG 中运用正弦的定义建立方程求解即可．【详解】根据题可知，△ADE 为等边三角形，即：AD=DE ，根据正方形的性质可知DE=DG ，DG△BC ，△C=60°， 设AD=x ，则DG=x ，DC=AC -AD=2-x ，△在Rt△CDG 中，DG sinC CD=，即：602DG x sinC sin CD x =︒===-6=x ，经检验6=x 是上述分式方程的解，故答案为：6．【点睛】本题考查正方形和等边三角形的性质，以及利用锐角三角函数解直角三角形，灵活根据题意找准合适的直角三角形是解题关键．9．（2021·上海长宁区·九年级一模）如图，矩形ABCD 沿对角线BD 翻折后，点C 落在点E 处．联结CE 交边AD 于点F ．如果DF ＝1，BC ＝4，那么AE 的长等于_________．【分析】由折叠的性质可得Rt BCD Rt BED ∆≅∆，由矩形的性质可证明Rt DAB Rt BCD ∆≅∆，故可得Rt DAB Rt BED ∆=∆，再证明Rt BCD Rt CDF ∆∆求得CD=2，在Rt AEF ∆中由勾股定理可得解．【详解】解：△四边形ABCD 是矩形，△BED 是由△BCD 翻折得到，△Rt BCD Rt BED ∆≅∆，CE BD ⊥，△4AD BC ==，AB CD ED ==，△四边形ABCD 是矩形，△AD=BC ，AB=CD ，又BD=DB△Rt DAB Rt BCD ∆≅∆△Rt DAB Rt BED ∆≅∆△AB ED =，ABD EDB ∠=∠△四边形ABDE 是等腰梯形，△CE BD ⊥，//AE BD △CE AE ⊥，△EAD ADB DBC =∠=∠△△90,90DBC FCB FBC FCD ︒︒+∠=∠+∠=△△DBC FCD =∠△Rt BCD Rt CDF ∆∆△FD CD CD BC =，即14CD CD =△2CD =或-2（舍去） 在Rt DCB ∆中，21tan 42CD DBC BC ∠===，△△EAD DBC =∠△1tan 2EAD ∠= 在Rt AEF ∆中，12EF AE =由勾股定理得，222AE AF EF =- 即2221()()2AE AD FD AE =--△2221(41)4AE AE =--解得：AE =．故答案为：5．【点睛】本题考查了矩形的性质、解直角三角形，勾股定理的运用以及折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．10．（2021·上海九年级一模）如果四边形边上的点，它与对边两个端点的连线将这个四边形分成的三个三角形都相似，我们就把这个点叫做该四边形的“强相似点”．如图1，在四边形ABCD 中，点Q 在边AD 上，如果QAB 、QBC 和QDC 都相似，那么点Q 就是四边形ABCD 的“强相似点”；如图2，在四边形ABCD 中，AD BC //，2AB DC ==，8BC =，60B ∠=︒，如果点Q 是边AD 上的“强相似点”，那么AQ =___．【答案】3+3【分析】过点A 作AE△CD ，交BC 于点E ，可证四边形ADCE 是平行四边形，由平行四边形的性质可得AD 的长，利用“强相似点”的定义可得△ABQ△△DQC ，则由相似三角形的性质可得AQ DC AB DQ=，再根据线段之间的数量关系建立关于AQ 的方程，求解后即可求出AQ 的长．【详解】解：如图，过点A 作AE△CD ，交BC 于点E ，△在四边形ABCD 中，AD BC //，2AB DC ==，△四边形ADCE 是平行四边形，△AE ＝CD ＝AB ＝2，AD ＝CE ．△60B ∠=︒，△△ABE 是等边三角形．△BE＝AE＝AB＝2．△AD＝BC－BE＝6．△点Q是边AD上的“强相似点”，△△ABQ△△DQC．△AQ DC AB DQ=．设AQ＝x，则DQ＝6－x，即226xx=-．解得135x，235x．故答案为：3+3【点睛】本题考查了相似三角形的性质、平行四边形的判定与性质等知识，掌握平行四边形的判定与性质及相似三角形的性质并能灵活应用所学知识是解题的关键．11．（2021·上海九年级一模）直角三角形的重心到斜边中点的距离为2，那么该直角三角形的斜边长为____________．【答案】12【分析】先根据三角形重心的性质求出斜边中线的长，再根据三角形斜边上的中线等于斜边的一半即可求得斜边的长．【详解】解：由题意得，GD=2，△点G是△ABC的重心，△CD=3GD=6，CD是△ABC的中线，在Rt△ACB中，△ACB=90°，CD是△ABC的中线，△AB=2CD=12，故答案为：12．【点睛】本题考查了直角三角形斜边上的中线的性质和重心的性质，熟练掌握在直角三角形中，斜边上的中线等于斜边的一半以及重心到顶点的距离与重心到对边中点的距离之比为2：1是解决问题的关键．12．（2021·上海杨浦区·九年级一模）如图，已知在平行四边形ABCD中，点E在边AB上，12AEEB=，联结DE交对角线AC于点O，那么AOOC的值为_____．【答案】1 3【分析】由题意可以得到△AOE△△COD，再根据三角形相似的性质和已知条件可以求得AO：OC的值．【详解】解：△四边形ABCD是平行四边形，△△OAE=△DCO，△OEA=△ODC，△△AOE△△COD，△AO AE AEOC CD AB==，△122AEEB AEEB=∴=，，△133AE AE AEAB AE EB AE===+，△13AOOC=，故答案为13．【点睛】本题考查平行四边形与相似三角形的综合运用，熟练掌握平行四边形的性质、三角形相似的判定和性质是解题关键．13．（2021·上海静安区·九年级一模）在△ABC中，点G是重心，△BGC=90°，BC=8，那么AG的长为____．【答案】8【分析】延长AG交BC于D，根据重心的定义，点D为BC的中点，先由直角三角形斜边上的中线等于斜边的一半求得DG的长，再由重心的性质：三角形的重心到一顶点的距离等于到对边中点距离的2倍进行求解即可．【详解】解：延长AG交BC于D，△点G是重心，△点D为BC的中点，且AG=2DG，△△BGC=90°，BC=8，△DG=12BC=4，△AG=2DG=8，故答案为：8．【点睛】本题考查了三角形的重心、直角三角形斜边上的中线性质，熟练掌握三角形的重心定义和性质是解答的关键．14．（2021·上海宝山区·九年级一模）在一块直角三角形铁皮上截一块正方形铁皮，如图，已有的铁皮是Rt ABC △，90C ∠=︒，要截得的正方形EFGD 的边FG 在AB 上，顶点E 、D 分别在边CA 、CB 上，如果4AF =，9GB =，那么正方形铁皮的边长为______．【答案】6【分析】设正方形铁皮的边长为x ，证明△AEF△△DBG ，得到EF AF BG DG =，49x x=，求解即可． 【详解】设正方形铁皮的边长为x ，△90C ∠=︒，△△A+△B=90︒，在正方形EFGD 中，EF=DG=FG=x ，△EFG=△DGF=90︒,△△AFE=△BGD=90︒，△△A+△AEF=90︒,△△AEF=△B ，△△AEF△△DBG ，△EF AF BG DG =，△49x x =，解得x=6（负值舍去）， 故答案为：6．【点睛】此题考查正方形的性质，相似三角形的判定及性质，根据已知条件证明△AEF△△DBG 是解题的关键． 15．（2021·上海宝山区·九年级一模）已知等腰梯形上底为5，高为4，底角的余弦值为35，那么其周长为______． 【答案】26【分析】作DF△BC 于F ，AE△BC 于E ，根据等腰梯形的性质就可以得出△AEB△△DFC 就可以求出FC=BE ，然后根据底角的余弦值为35，求得BE ，AB ，从而求出周长． 【详解】解：如图示，作DF△BC 于F ，AE△BC 于E ，△四边形ABCD 是等腰梯形，△△B=△C ，AB=CD ，AD△BC ，△△ADF=△DFC=90°，△△AEF=△DFE=△ADF=90°，△四边形AEFD 是矩形，5EF AD ，在△AEB 和△DFC 中，△△AEB△△DFC （AAS ），△BE=CF ；△35cos E ABB B ， 设3BE x =，则5AB x =，根据勾股定理，有：2222534AEAB BE x x ， 解之得：1x =（取正值），△3BE =，5AB =，△3FCBE ，5DC AB ==，△周长AB BE EF FC CD AD 53535526，故答案是：26．【点睛】本题考查了等腰梯形的性质的运用，三角函数，矩形的判定及性质的运用，等腰三角形的性质的运用，全等三角形的判定及性质的运用，能熟练应用相关性质是解题的关键．三、解答题16．（2021·上海青浦区·九年级一模）如图，在平行四边形ABCD 中，8BC =，点E 、F 是对角线BD 上的两点，且BE EF FD ==，AE 的延长线交BC 于点G ，GF 的延长线交AD 于点H ．（1）求HD 的长；（2）设BGE △的面积为a ，求四边形AEFH 的面积．（用含a 的代数式表示）【答案】（1）2HD =；（2）7=2四边形AEFH a S 【分析】（1）由△ADE△△GBE ，可求出BG 的长，再由△HDF△△GBF ，即可求出HD 的长；（2）由△ADE△△GBE ，可求出S △ADE =4S △BGE =4a ，再由△HDF△△GBF ，即可求出S △DHF =14S △BGF ，由三角形的面积公式可求出S △DHF =14S △BGF ，进而可求四边形AEFH 的面积． 【详解】解：（1）△四边形ABCD 是平行四边形，△AD//BC ，AD=BC=8，△△ADE△△GBE ，△AD DE BG BE =． △BE EF FD ==，△BG=12AD=4．△AD//BC ，△△HDF△△GBF ，△HD DF BG BF=． △BE EF FD ==，△HD=12BG=2； （2）△△ADE△△GBE ， BE EF FD ==，△S △ADE =4S △BGE =4a ．△△HDF△△GBF ，△S △DHF =14S △BGF ．△BE EF =，△S △BGF =2S △BGE ， △S △DHF =12S △BGE =12a ，△17=4-=22AEFH a S a a 四边形． 【点睛】本题考查了平行四边形的性质，相似三角形的判定与性质，熟练掌握相似三角形的判定与性质是解答本题的关键．。

2021上海初三数学一模试题分类整理（几何综合题）1．（长宁）已知，在矩形ABCD 中，点M 是边AB 上的一个点（与点A B 、不重合），联结CM ，作90CMF ︒∠=，且MF 分别交边AD 于点E 、交边CD 的延长线于点F ，点G 为线段MF 的中点，联结DG .（1）如图1，如果4AD AM ==，当点E 与点G 重合时，求MFC ∆的面积；（2）如图2，如果2AM =，4BM =，当点G 在矩形ABCD 内部时，设AD x =，2DG y =，求y 关于x 的函数解析式，并写出定义域；（3）如果6AM =，8CD =，F EDG ∠=∠，求线段AD 的长．（直接写出计算结果）ABCDEF(G )M图1ABCDEFGM图2第25题图2．（杨浦）如图，已知在Rt△ABC 中，∠ACB =90°，AC =BC =4，点D 为边BC 上一动点（与点B 、C 不重合），点E 为边AB 上一点，∠EDB =∠ADC ，过点E 作EF ⊥AD ，垂足为点G ，交射线AC 于点F .（1）如果点D 为边BC 的中点，求∠DAB 的正切值；（2）当点F 在边AC 上时，设CD =x ，CF =y ，求y 关于x 的函数解析式及定义域；（3）联结DF ，如果△CDF 与△AGE 相似，求线段CD 的长.备用图ABC第25题图ABCEDG F3．（徐汇）如图，在ABC Rt ∆中，︒=∠90ACB ，12=AC ，5=BC ，点D 是边AC 上的动点，以CD 为边在ABC ∆外作正方形CDEF ，分别联结AE 、BE ，BE 与AC 交于点G ．（1）当BE AE ⊥时，求正方形CDEF 的面积；（2）延长ED 交AB 于点H ，如果BEH ∆和ABG ∆相似，求ABE ∠sin 的值；（3）当AE AG =时，求CD 的长．（备用图）BAC（第25题图）GFED BAC4．（松江）如图，已知在等腰△ABC中，AB=AC=，tan∠ABC=2，BF⊥AC，垂足为F，点D是边AB上一点（不与A，B重合）.（1）求边BC的长；（2）如图2，延长DF交BC的延长线于点G，如果CG=4，求线段AD的长；（3）过点D作DE⊥BC，垂足为E，DE交BF于点Q，联结DF，如果△DQF和△ABC相似，求线段BD的长.D·B AFC（图1）DBAFC（图2）G BAFC（备用图）5．（普陀）如图，矩形ABCD 中，1AB =，3BC =，点E 是边BC 上一个动点（不与点B 、C 重合），AE 的垂线AF 交CD 的延长线于点F ．点G 在线段EF 上，满足:1:2FG GE =．设BE x =．（1）求证：AD DFAB BE=；（2）当点G 在△ADF 的内部时，用x 的代数式表示ADG ∠的余切；（3）当∠FGD =∠AFE 时，求线段BE 的长．F图14CB A DE G备用图CBAD6．（浦东）四边形ABCD 是菱形，∠B ≤90°，点E 为边BC 上一点，联结AE ，过点E 作EF ⊥AE ，EF 与边CD 交于点F ，且EC =3CF ．（1）如图1，当∠B =90°时，求ABE S △与ECF S △的比值；（2）如图2，当点E 是边BC 的中点时，求cos B 的值；（3）如图3，联结AF ，当∠AFE =∠B 且CF =2时，求菱形的边长．（第25题图3）（第25题图2）（第25题图1）7．（闵行）如图，在矩形ABCD 中，2AB =，1AD =，点E 在边AB 上（点E 与端点A 、B 不重合），联结DE ，过点D 作DF ⊥DE ，交BC 的延长线于点F ，联结EF ，与对角线AC 、边CD 分别交于点G 、H ．设AE x =，DH y =．（1）求证：△ADE ∽△CDF ，并求EFD ∠的正切值；（2）求y 关于x 的函数解析式，并写出该函数的定义域；（3）联结BG ．当△BGE 与△DEH 相似时，求x 的值．（第25题图）B A CF ED GH（备用图）B A CFEDGH8．（静安）已知∠MAN 是锐角，点B 、C 在边AM 上，点D 在边AN 上，∠EBD =∠MAN ，且CE //BD ，sin∠MAN=35，AB =5，AC =9．（1）如图1，当CE 与边AN 相交于点F 时，求证：DF ·CE=BC ·BE ；（2）当点E 在边AN 上时，求AD 的长；（3）当点E 在∠MAN 外部时，设AD =x ，△BCE 的面积为y ，求y 与x 之间的函数解析式，写出定义域．（第25题图）（备用图）（图1）FAB DCE NM9.（嘉定）在矩形ABCD 中，6AB =，8AD =，点E 在CD 边上，1tan 2DAE ∠=.点F 是线段AE 上一点，联结BF ，CF.（1）如图11，如果3tan 4CBF ∠=，求线段AF 的长；（2）如图12，如果12CF BC =，①求证：∠CFE =∠DAE ；②求线段EF 的长.图11图12备用图10．（黄浦）如图10，四边形ABCD 中，AB =AD =4，CB =CD =3，∠ABC =∠ADC =90°，点M 、N 是边AB 、AD 上的动点，且∠MCN =12∠BCD ，CM 、CN 与对角线BD 分别交于点P 、Q .（1）求sin∠MCN 的值；（2）当DN =DC 时，求∠CNM 的度数；（3）试问：在点M 、N 的运动过程中，线段比PQMN的值是否发生变化？如不变，请求出这个值；如变化，请至少给出两个可能的值，并说明点N 相应的位置.P NM DC BAQ（图10）11．（虹口）如图12，在△ABC 中，∠ABC =90°，AB =3，BC =4，过点A 作射线AM //BC ，点D、E 是射线AM 上的两点（点D 不与点A 重合，点E 在点D 右侧），联结BD 、BE 分别交边AC 于点F 、G ，∠DBE =∠C ．（1）当AD =1时，求FB 的长；（2）设AD =x ，FG =y ，求y 关于x 的函数关系式，并写出x 的取值范围；（3）联结DG 并延长交边BC 于点H ，如果△DBH 是等腰三角形，请直接写出AD 的长．C FGE D A B 图12C A B 备用图MM12.（奉贤）已知⊙O 的直径AB =4，点P 为弧AB 上一点，联结PA 、PO ，点C 为劣弧AP 上一点（点C 不与点A 、P 重合），联结BC 交PA 、PO 于点D 、E .（1）如图10，当cos∠CBO =87时，求BC 的长；（2）当点C 为劣弧AP 的中点，且△EDP 与△AOP 相似时，求∠ABC 的度数；（3）当AD =2DP ，且△BEO 为直角三角形时，求四边形AOED 的面积.备用图备用图A B图10PA BC D EO A B13．（崇明）如图，Rt△ABC 中，90ACB ∠=︒，6AC =，8BC =．点D 为斜边AB 的中点，ED ⊥AB ，交边BC 于点E ．点P 为射线AC 上的动点，点Q 为边BC 上的动点，且运动过程中始终保持PD QD ⊥．（1）求证：△ADP ∽△EDQ ；（2）设AP x =，BQ y =．求y 关于x 的函数解析式，并写出该函数的定义域；（3）联结PQ ，交线段ED 于点F ．当△PDF 为等腰三角形时，求线段AP 的长．A D BCPEQ 第25题图A D B C P E Q 第25题备用图F14.（宝山）如图3，已知Rt△ABC 中，∠ACB =90°，AC =BC ，点D、E 在边AB 上，∠DCE =45°，过点A 作AB 的垂线交CE 的延长线于点M ，联结MD.（1）求证：DE BE CE ⋅=2；（2）当AC =3，AD =2BD 时，求DE 的长；（3）过点M 作射线CD 的垂线，垂足为点F .设x BCBD =，y FMD =∠tan ，求y 关于x 的函数关系式，并写出定义域.EM DCAB （图3）15．（青浦）在△ABC 中，∠C=90°，AC =2，BC =23，点D 为边AC 的中点（如图），点P 、Q 分别是射线BC 、BA 上的动点，且BQ =32BP ，联结PQ 、QD 、DP ．（1）求证：PQ ⊥AB ；（2）如果点P 在线段BC 上，当△PQD 是直角三角形时，求BP 的长；（3）将△PQD 沿直线QP 翻折，点D 的对应点为点'D ，如果点'D 位于△ABC 内，请直接写出BP 的取值范围．（第25题图）（备用图）A C O 第25题备用图16.（金山）定理：一条弧所对的圆周角等于这条弧所对的圆心角的一半.如图1中，O A ∠=∠21.已知：如图2，AC 是⊙O 的一条弦，点D 在⊙O 上（与A 、C 不重合），联结DC 交射线AO 于点E ，联结OD ，⊙O 的半径为5，43tan =∠OAC .(1)求弦AC 的长.(2)当点E 在线段OA 上时，若DOE ∆与AEC ∆相似，求DCA ∠的正切值.(3)当1=OE 时，求点A 与点D 之间的距离（直接写出答案）.AB CO第25题图1第25题图2E D C A O。

2019-2020年广东省中考数学各地区模拟试题分类（东莞专版）——四边形一．选择题1．（2020•东莞市一模）能判定四边形ABCD为平行四边形的题设是（）A．AB∥CD，AD＝BC B．∠A＝∠B，∠C＝∠DC．AB＝CD，AD＝BC D．AB＝AD，CB＝CD2．（2020•东莞市二模）从一个多边形的任何一个顶点出发都只有5条对角线，则它的边数是（）A．6 B．7 C．8 D．9 3．（2020•东莞市一模）一个多边形每个外角都等于30°，这个多边形是（）A．六边形B．正八边形C．正十边形D．正十二边形4．（2020•东莞市一模）若一个多边形的每个外角都等于45°，则它的边数是（）A．11 B．10 C．9 D．8 5．（2019•东莞市模拟）正方形面积为36，则对角线的长为（）A．6 B．C．9 D．6．（2020•东莞市一模）在四边形ABCD中，AC与BD相交于点O，且AD∥BC，给出下列条件：①AB∥CD；②AB＝CD；③∠DAB＝∠DCB；④AD＝BC；⑤∠OAD＝∠ODA．从中选1个作为条件，能使四边形ABCD为平行四边形的选法有（）A．2种B．3种C．4种D．5种7．（2020•东莞市校级二模）如图，正方形ABCD中，点E是AD边的中点，BD，CE交于点H，BE、AH交于点G，则下列结论：①∠ABE＝∠DCE；②AG⊥BE；③S△BHE ＝S△CHD；④∠AHB＝∠EHD．其中正确的是（）A ．①③B ．①②③④C ．①②③D ．①③④二．填空题 8．（2020•东莞市校级模拟）若正多边形的一个内角的度数等于它外角度数的5倍，则这个正多边形的边数为 ．9．（2020•东莞市校级模拟）一个菱形的两条对角线的长分别为5和8，那么这个菱形的面积是 ．10．（2020•东莞市一模）已知正多边形的一个外角为40°，则这个正多边形的内角和为 ．11．（2020•东莞市校级二模）若一个正n 边形的一个外角为36°，则n 等于 ．12．（2020•东莞市一模）如图，在菱形ABCD 中，∠BAD ＝60°，AC 与BD 交于点O ，E 为CD延长线上的一点，且CD ＝DE ，连接BE 分别交AC 、AD 于点F 、G ，连接OG ，则下列结论中一定成立的是 ．（把所有正确结论的序号都填在横线上）①OG ＝AB ；②与△EGD 全等的三角形共有5个；③S 四边形ODGF ＞S △ABF ；④由点A 、B 、D 、E 构成的四边形是菱形．三．解答题13．（2020•东莞市校级模拟）如图，动点E 从矩形ABCD 的点B 沿线段BC 向点C 运动，连接AE ，DE ，以AE 为边作矩形AEFG ，使FG 过点D ．（1）求证：矩形ABCD 与矩形AEFG 的面积相等；（2）若AB ＝2，BC ＝6，直接写出BE 为何值时，△AED 为等腰三角形．14．（2020•东莞市一模）如图，在平面直角坐标系中，四边形OABC为菱形，点C的坐标为（8，0），∠AOC＝60°，垂直于x轴的直线l从y轴出发，沿x轴正方向以每秒1个单位长度的速度运动，设直线l与菱形OABC的两边分别交于点M、N（点M在点N的上方）．（1）求A、B两点的坐标；（2）设△OMN的面积为S，直线l运动时间为t秒（0≤t≤12），求S与t的函数表达式；（3）在（2）的条件下，t为何值时，S最大？并求出S的最大值．15．（2019•东莞市模拟）（1）【问题发现】如图①，正方形AEFG的两边分别在正方形ABCD的边AB和AD上，连接CF．填空：①线段CF与DG的数量关系为；②直线CF与DG所夹锐角的度数为．（2）【拓展探究】如图②，将正方形AEFG绕点A逆时针旋转，在旋转的过程中，（1）中的结论是否仍然成立，请利用图②进行说明．（3【解决问题】如图③，△ABC和△ADE都是等腰直角三角形，∠BAC＝∠DAE＝90°，AB＝AC＝4，O为AC的中点．若点D在直线BC上运动，连接OE，则在点D的运动过程中，线段OE长的最小值为（直接写出结果）．参考答案一．选择题1．解：如图所示，根据平行四边形的判定定理知，只有C符合条件．故选：C．2．解：设这个多边形是n边形．依题意，得n﹣3＝5，解得n＝8．故这个多边形的边数是8．故选：C．3．解：∵多边形的外角和为360°，360°÷30°＝12，∴这个多边形是正十二边形，故选：D．4．解：∵多边形的外角和是360°，每个外角都等于45°，∴360÷45＝8，∴正多边形的边数为8．故选：D．5．解：设对角线长是x．则有x2＝36，解得：x＝6．故选：B．6．解：已知AD∥BC，加上①AB∥CD可根据两组对边分别平行的四边形是平行四边形进行判定；加上②AB＝CD不能判定是平行四边形；加上③∠DAB＝∠DCB可证明AB∥CD，可根据两组对边平行的四边形是平行四边形进行判定；加上④AD＝BC可根据一组对边平行且相等的四边形是平行四边形进行判定；加上⑤∠OAD ＝∠ODA 不能判定是平行四边形；故选：B ．7．解：∵四边形ABCD 是正方形，E 是AD 边上的中点，∴AE ＝DE ，AB ＝CD ，∠BAD ＝∠CDA ＝90°，∴△BAE ≌△CDE （SAS ），∴∠ABE ＝∠DCE ，故①正确；∵四边形ABCD 是正方形，∴AD ＝DC ，∠ADB ＝∠CDB ＝45°，DH ＝DH ，∴△ADH ≌△CDH （SAS ），∴∠HAD ＝∠HCD ，∵∠ABE ＝∠DCE∴∠ABE ＝∠HAD ，∵∠BAD ＝∠BAH +∠DAH ＝90°，∴∠ABE +∠BAH ＝90°，∴∠AGB ＝180°﹣90°＝90°，∴AG ⊥BE ，故②正确；∵AD ∥BC ，∴S △BDE ＝S △CDE ，∴S △BDE ﹣S △DEH ＝S △CDE ﹣S △DEH ，即；S △BHE ＝S △CHD ，故③正确；∵△ADH ≌△CDH ，∴∠AHD ＝∠CHD ，∴∠AHB ＝∠CHB ，∵∠BHC ＝∠DHE ，∴∠AHB＝∠EHD，故④正确；故选：B．二．填空题（共5小题）8．解：设这个正多边的外角为x°，由题意得：x+5x＝180，解得：x＝30，360°÷30°＝12．故答案为：十二．9．解：∵菱形的两条对角线的长分别为5和8，∴这个菱形的面积是×5×8＝20；故答案为：20．10．解：正多边形的每个外角相等，且其和为360°，据此可得，解得n＝9．（9﹣2）×180°＝1260°，即这个正多边形的内角和为1260°．故答案为：1260°．11．解：n＝360°÷36°＝10．故答案为10．12．解：∵四边形ABCD是菱形，∴AB＝BC＝CD＝DA，AB∥CD，OA＝OC，OB＝OD，AC⊥BD，∴∠BAG＝∠EDG，△ABO≌△BCO≌△CDO≌△AOD，∵CD＝DE，∴AB＝DE，在△ABG 和△DEG 中，，∴△ABG ≌△DEG （AAS ），∴AG ＝DG ，∴OG 是△ACD 的中位线，∴OG ＝CD ＝AB ，①正确；∵AB ∥CE ，AB ＝DE ，∴四边形ABDE 是平行四边形，∵∠BCD ＝∠BAD ＝60°，∴△ABD 、△BCD 是等边三角形，∴AB ＝BD ＝AD ，∠ODC ＝60°， ∴OD ＝AG ，四边形ABDE 是菱形，④正确；∴AD ⊥BE ，由菱形的性质得：△ABG ≌△BDG ≌△DEG ，在△ABG 和△DCO 中，，∴△ABG ≌△DCO （SAS ），∴△ABO ≌△BCO ≌△CDO ≌△AOD ≌△ABG ≌△BDG ≌△DEG ，②不正确；∵OB ＝OD ，AG ＝DG ，∴OG 是△ABD 的中位线， ∴OG ∥AB ，OG ＝AB ，∴△GOD ∽△ABD ，△ABF ∽△OGF ，∴△GOD 的面积＝△ABD 的面积，△ABF 的面积＝△OGF 的面积的4倍，AF ：OF ＝2：1， ∴△AFG 的面积＝△OGF 的面积的2倍，又∵△GOD 的面积＝△AOG 的面积＝△BOG 的面积，∴S 四边形ODGF ＝S △ABF ；不正确；正确的是①④．故答案为：①④．三．解答题（共3小题）13．（1）法一：证明：∵四边形ABCD 和四边形AEFG 是矩形，∴∠B ＝∠G ＝∠BAD ＝∠EAG ＝90°，又∵∠BAE +∠EAD ＝∠EAD +∠DAG ＝90°，∴∠BAE ＝∠DAG ，∴△ABE ∽△AGD ，∴，∴AB •AD ＝AG •AE ，∴矩形AEFG 与矩形ABCD 的面积相等． 法二：连接ED ，∵S 矩形AEFG ＝2S △ADE ，S 矩形ABCD ＝2S △ADE ，∴S 矩形AEFG ＝S 矩形ABCD ．（2）当AE ＝AD 时，如图2，BE ＝＝；当DE ＝AD 时，如图3，CE＝，∴BE＝BC﹣CE＝6﹣2；当AE＝DE时，如图4，过E作EM⊥AD于点M，则BE＝AM，∵AE＝DE，∴AM＝＝3，∴BE＝3．综上，当BE为2或3或3﹣2时，△AED为等腰三角形．14．解：（1）过点A作AD⊥OC于D，∵四边形OABC为菱形，点C的坐标为（8，0），∴OA＝AB＝BC＝CO＝8．∵∠AOC＝60°，∴OD＝4，AD＝4．∴A（4，4），B（12，4）；（2）直线l从y轴出发，沿x轴正方向运动与菱形OABC的两边相交有三种情况：①0≤t≤4时，直线l与OA、OC两边相交，（如图①）．∵MN⊥OC，∴ON＝t．∴MN＝ON tan60°＝t．∴S＝ON•MN＝t2；②当4＜t≤8时，直线l与AB、OC两边相交，（如图②）．S＝ON•MN＝×t×4＝2t；③当8＜t≤12时，直线l与AB、BC两边相交，（如图③）．设直线l与x轴交于点H．∵MN＝4﹣（t﹣8）＝12﹣t，∴S＝OH•MN＝×t×（12﹣t）＝﹣t2+6t；＝×42＝8，（3）由（2）知，当0≤t≤4时，S最大＝16，当4＜t≤8时，S最大当8＜t≤12时，S＝﹣t2+6t＝﹣（t﹣6）2+18∴当8＜t≤12时，S＜16＝16．综上所述，当t＝8时，S最大15．解：（1）【问题发现】如图①中，①线段CF与DG的数量关系为CF＝DG；②直线CF与DG所夹锐角的度数为45°．理由：如图①中，连接AF．易证A，F，C三点共线．∵AF＝AG．AC＝AD，∴CF＝AC﹣AF＝（AD﹣AG）＝DG．故答案为CF＝DG，45°．（2）【拓展探究】结论不变．理由：连接AC，AF，延长CF交DG的延长线于点K，AG交FK于点O．∵∠CAD＝∠FAG＝45°，∴∠CAF＝∠DAG，∵AC＝AD，AF＝AG，∴＝＝，∴△CAF∽△DAG，∴＝＝，∠AFC＝∠AGD，∴CF＝DG，∠AFO＝∠OGK，∵∠AOF＝∠GOK，∴∠K＝∠FAO＝45°．（3）【解决问题】如图3中，连接EC．∵AB＝AC，AD＝AE，∠BAC＝∠DAE＝90°，∴∠BAD＝∠CAE，∠B＝∠ACB＝45°，∴△BAD≌△CAE（SAS），∴∠ACE＝∠ABC＝45°，∴∠BCE＝90°，∴点E的运动轨迹是在射线CE上，当OE⊥CE时，OE的长最短，易知OE的最小值为，故答案为，。

初中数学杜老师-----136********1、14东城一模19. 如图，将一张矩形纸片ABCD 沿直线MN 折叠，使点C 落在点A 处，点D 落在点E 处，直线MN 交BC 于点M ，交AD 于点N ． （1）求证：CM =CN ； （2）若△CMN 的面积与△CDN 的面积比为3：1，且CD =4，求线段MN 的长．19.（本小题满分5分）（1）证明：由折叠的性质可得：∠ANM =∠CNM . ∵ 四边形ABCD 是矩形，∴ AD ∥BC . ∴ ∠ANM =∠CMN . ∴ ∠CMN =∠CNM . ∴ CM =CN . ………2分 （2）解：过点N 作NH ⊥BC 于点H ，则四边形NHCD 是矩形. ∴ HC =DN ，NH =DC . ∵ △CM N 的面积与△CDN 的面积比为3：1， ∴ MC =3ND =3HC .∴ MH =2HC .设DN =x ，则HC =x ，MH =2x ， ∴CM =3x =CN ， 在Rt △CDN 中，DC =2x =4，∴x =∴ HM =2.在Rt △MNH 中，MN=2、14西城一模19．如图，在△ABC 中，AB =AC ，AD 平分∠BAC ，CE ∥AD 且CE=AD ． （1）求证：四边形ADCE 是矩形；（2）若△ABC 是边长为4的等边三角形，对角线AC ，DE 相交于点O ，在CE 上截取CF=CO ，连接OF ，求FC 的长及四边形AOFE 的面积．19．解：（1）∵CE ∥AD 且CE=AD ，∴四边形ADCE 是平行四边形． ··························································· 1分又在△ABC 中，AB =AC ，AD 平分∠BAC ， ∴AD ⊥BC ． ∴∠ADC =90°．.∴四边形ADCE 是矩形． ····································································· 2分 （2）作 OH ⊥CE 于点H ，∵△ABC 是边长为4的等边三角形， ∴∠ACB =60°, 1302DAC BAC ∠=∠=︒,122CD BC ==．由（1）知四边形ADCE 是矩形， ∴AC 与DE 互相平分，AO =OC 122AC ==． ∴FC =OC =2． ······································ 3分 ∵在矩形ADCE 中．∠AED =∠DCE =90°． ∴∠ACE =∠DCA =30°．在Rt △COH 中， 112OH OC ==. ························································ 4分∴CH EH ==∴11122ACE FOC AOFE S S S AE CE CF OH ∆∆=-=⋅-⋅=四边形． ········ 5分 3、14年海淀一模19． 如图，在△ABC 中，∠ACB =90º，∠ABC =30º，BC=AC 为边在△ABC 的外部作等边△ACD ，连接BD ．（1）求四边形ABCD 的面积； （2）求BD 的长．19． 解：（1）∵在△ABC 中，∠ACB =90º，∠ABC =30º，BD =∴1cos ,2BC ABC AC AB AB ∠==,90903060BAC ABC ∠=-∠=-=.∴14,42cos 2BC AB AC ABC ====⨯=∠. …………………………1分∵△ACD 为等边三角形，∴2AD CD AC ===,60DAC ∠=. 过点D 作DE AC ⊥于E ， 则sin 2sin603DE AD DAC =∠=⨯=∴ABC ACD ABCD S S S =+△△四边形1122AC BC AC DE=⋅+⋅112222=⨯⨯⨯=. ………………………………………3分 （2）过点D 作DF AB ⊥于F .∵180180606060DAF BAC DAC ∠=-∠-∠=--=, ∴sin 2sin603DF AD DAF =⋅∠==A CDcos 2cos601AF AD DAF =⋅∠==. ………………………………………4分∴415BF AB AF =+=+=． ∵DF AB ⊥，∴在Rt BDF△中，22222528BD DF BF =+=+=.∴BD = …………………………………………………………………5分4、14年朝阳19．如图，△ABC 中，BC >AC ，点D 在BC 上，且CA =CD ，∠ACB 的平分线交AD 于点F ，E 是AB 的中点． （1）求证：EF ∥BD ； （2）若∠ACB =60°，AC =8，BC =12，求四边形BDFE 的面积．19．（1）证明：∵ CA =CD ，CF 平分∠ACB ，∴ CF 是AD 边的中线． …………………………………………………1分 ∵ E 是AB 的中点，∴ EF 是△ABD 的中位线．∴ EF ∥BD ； ………………………………………………………………2分（2）解：∵ ∠ACB =60°，CA =CD ，∴ △CAD 是等边三角形．∴ ∠ADC =60°，AD =DC =AC =8．∴ BD =BC -CD =4．过点A 作AM ⊥BC ，垂足为M ．∴ sin AM AD ADC=⋅∠=．12ABD S BD AM ∆=⋅= …………………………………………………… 3分∵ EF ∥BD ，∴ △AEF ∽△ABD ，且12EF BD =．∴14AEF ABD S S ∆∆=．∴AEF S ∆= …………………………………………… 4分 四边形BDFE的面积=ABD AEF S S ∆∆-= ………………………………… 5分5、１４年石景山一模19．如图，在四边形ABCD 中，2AB =,︒=∠=∠60C A ,DB AB⊥于点B ， 45DBC ∠=︒，求BC 的长.GFEDCBA19. 解：过点D 作BC DE ⊥于点E . ……………………1分︒=∠=⊥60 2,A AB AB DB ，，∴3260tan =︒⨯=AB BD . ………………2分 45DBC ∠=︒，BC DE ⊥，∴645sin =︒⨯==BD DE BE …………3分︒=∠︒=∠=∠9060DEC A C ， 260tan =︒=∴DECE . ……………………4分62+=∴BC .………………………………5分６、１４门头沟一模19.如图7，菱形ABCD 的对角线交于O 点，DE ∥AC ，CE ∥BD ， （1）求证：四边形OCED 是矩形;（2）若AD =5，BD =8，计算sin DCE ∠的值. 19．（1） ∵DE ∥AC ，CE ∥BD∴四边形OCED 是平行四边形 ……………………………..1 ∵四边形ABCD 是菱形∴ AC BD ⊥ (2)90DOC ∠=o∴四边形OCED 是矩形 …………………………….3 （2）∵四边形ABCD 是菱形，BD =8 ∴12OD BD ==4，OC=OA ，AD=CD ∵AD =5，由勾股定理得OC =3 ……………………………4 ∵四边形OCED 是矩形∴DE=OC=3，在Rt △DEC 中，sin DCE ∠=35DE DC = ……………………………5 ７、１４年丰台一模19. 如图，在ABCD 中，E F 、分别为边AB CD 、的中点，BD 是对角线，过A 点作AG DB ∥交CB 的延长线于点.G （1）求证：四边形DEBF 是平行四边形；（2）如果90G ∠=°，60C ∠=°，=2BC ，求四边形DEBF 的面积．图7GFEDCBA19. 解：（1）在ABCD 中，∴AB CD AB CD =∥， ……………………1分 E F 、分别为边AB CD 、的中点1122DF DC BE AB ∴==，DF BE DF BE ∴=∥， …………………………2分 ∴四边形DEBF 为平行四边形…………………………3分（2）作BH ⊥CD 于点HAG BD ∥90G DBC ∴∠=∠=° DBC ∴△为直角三角形又∵ 60C ∠=°，且BC=2∴CD=4，∴BH =又F 为边CD 的中点∴DF=2……………………………………………………4分∴DEBFS =………………………………………5分８、19．解：过点E 作AC EF ⊥于点F ， ∵四边形ABCD 是正方形，∴AC D BAD ,90︒=∠=∠平分BAD ∠， DC AD =．∴︒=∠45CAD ，AD AC 2=．∵E 是AD 中点，∴AD DE AE 21==． …………………………1分设x DE AE ==，则x DC AD 2==，x AC 22=，x CE 5=．在Rt △AEF 中，x CAD AE EF 22sin =∠⋅=，x EF AF 22==．……2分∴x x x AF AC CF 2232222=-=-=． ………………………………3分HABCDEFGBCDEF∴101035223cos ===∠xxCECF ACE ，…………………………………………4分 3122322t a n ===∠xx CFEF ACE ． …………………………………………5分9、14年昌平一模19. 已知：BD 是四边形ABCD 的对角线，AB ⊥BC ，∠C =60°，AB =1，BC=3+CD=（1）求tan ∠ABD 的值；（2）求AD 的长.19. 解：(1) 作DE BC ⊥于点E .∵在Rt △CDE 中，∠C =60°，CD=，∴ 3.CE DE ==………………………………………………… 1分 ∵BC=3+∴3 3.BE BC CE =-=∴ 3.DE BE == ………………………………………………… 2分 ∴在Rt △BDE 中，∠EDB = ∠EBD =45º.∵AB ⊥BC ，∠ABC =90º，∴∠ABD =∠ABC -∠EBD =45º.∴tan∠ABD =1. ………………………………………………………………………………3分 (2) 作AF BD ⊥于点F .在Rt △ABF 中，∠ABF =45º, AB =1，2BF AF ∴==……………………………………………………………………… 4分 ∵在Rt △BDE 中，3DE BE ==，∴BD =DCEDC BA∴22DF BD BF =-== ∴在Rt△AFD中，AD == ……………………………………… 5分10、14年顺义一摸19．如图，在四边形ABCD 中，∠B=∠D=90°，∠C=60°，BC=4，CD=3，求AB 的长．19．解：延长BA 、CD 交于点E ．∵∠B=90°，∠C=60°，BC=4，∴∠E=30°，CE =8，BE= 2分 ∵CD=3， ∴DE =5．……………………………………… 3分∴5cos cos30DE AE E ===︒ 4分∴AB BE AE =-== 5分 11、14年房山一模19．已知：如图，在△ABC 中，点D 是BC 中点，点E 是AC 中点，且AD ⊥BC ，BE ⊥AC ， BE,AD 相交于点G ，过点B 作BF ∥AC 交AD 的延长线于点F ， DF=6. (1) 求AE 的长； (2) 求AEG FBGSS的值.19. 证明：（1）∵点D 是BC 中点，点E 是AC 中点，AD ⊥BC ， BE ⊥AC ，AC AB CB ∴==∴△ABC 是等边三角形 ..................................2分60C ∴∠= 30F ∴∠=∵6DF =12BD BC ∴==又∵BD DC EC AE ===AE ∴=..................................3分（2）由（1）DF =6，∠ F =30°，∠ BDF =90° ∴BF= ∴12AE BF = ..................................4分 ∵AE ∥BF ∴△AEG ∽△FBG∴221124AEG FBG S AE S BF ∆∆⎛⎫⎛⎫=== ⎪ ⎪⎝⎭⎝⎭ ..................................5分 12、14年燕山一模19. 如图，在四边形ABCD 中，BC AD //，25=AB ，4=BC ，连接BD ，BAD ∠的平分线交BD 于点E ，且CD AE //． （1）求AD 的长；（2）若︒=∠30C ，求四边形ABCD 的周长．19.解：（1）延长AE 交BC 于点F .∵AE 平分BAD ∠，∴DAF BAF ∠=∠. ∵BC AD //， ∴DAF AFB ∠=∠， ∴AFB BAF ∠=∠， ………1分∴25==AB BF . ∵4=BC ， ∴23254=-=FC . ……………2分 ∵BC AD DC AF //,//，∴四边形AFCD 是平行四边形，∴23==FC AD .………3分 （2）过B 作AF 的垂线BG ，垂足为G . ∵DC AF //，︒=∠=∠30C AFB ，ED CBAGF ED CBA在BGF Rt ∆中，435232530cos =⨯=︒⋅=BF GF ， ∴23543522=⨯===GF AF DC . ………………4分 ∴四边形ABCD 的周长.235823235425+=+++=+++=DA CD BC AB………………5分19．∵四边形ABCD 是平行四边形，∴AB ∥DC ，AB=CD ，……………………………….1分 ∵AE ∥BD ， ∴四边形ABDE 是平行四边形，…………….. 2分 ∴AB=DE=CD ，…………………………………….. 3分 即D 为CE 中点， ∵EF ⊥BC ， ∴∠EFC=90°， ∵AB ∥CD ， ∴∠DCF=∠ABC=60°，…………………………4分 ∴∠CEF=30°， ∵EF=， ∴CE=2，∴AB=1，………………………………………………5分14、14年通州一模20．如图：在矩形ABCD 中，AB =2，BC =5，E 、P 分别在AD 、BC 上，且DE =BP =1．求证：四边形EFPH 为矩形.PADC B H F EACEFD20．解： 在矩形ABCD 中 ∴,DC AB =AD//BCED ＝BP∴四边形DEBP 是平行四边形 ∴BE//DPAD=BC ，AD//BC ，DE=BP ∴AE=CP∴四边形AECP 是平行四边形∴AP//CE∴四边形EFPH 是平行四边形 在矩形ABCD 中∴∠ADC=∠ABP=90º,AD=BC=5,AB=CD=2 ∴CE=5,同理BE =2 ∴ 222BC CE BE =+ ∴∠BEC=90º∴四边形EFPH 是矩形15、14年一模平谷19．如图，在△ABC 中，D 为AB 边上一点、F 为AC 的中点，过点C 作CE //AB 交DF 的延长线于点E ，连结AE ．（1）求证：四边形ADCE 为平行四边形．（2）若EF =22，︒=∠︒=∠4530AED FCD ，，求DC 的长．19．(本小题满分5分)（1）证明：∵CE //AB ，∴∠DAF =∠ECF ． ∵F 为AC 的中点，∴AF =CF ． 在△DAF 和△ECF 中⎪⎩⎪⎨⎧∠=∠=∠=∠，，，CFE AFD CF AF ECF DAF ∴ △DAF ≌△ECF ．∴ AD =CE ． ------------------------------------------------------------------------------------2分H ACEFD∵CE //AB ，∴ 四边形ADCE 为平行四边形． --------------------------------------------------------------------3分（2）作FH ⊥DC 于点H ．∵ 四边形ADCE 为平行四边形．∴ AE //DC ，DF = EF =22， ∴∠FDC =∠AED =45°．在Rt △DFH 中，∠DHF=90°，DF =22，∠FDC=45°， ∴ sin ∠FDC=22=DF FH ，得FH =2，tan ∠FDC=1=HDHF ，得DH =2． ----------------------------------------------------------------------4分 在Rt △CFH 中，∠FHC=90°，FH =2，∠FCD=30°，∴ FC =4． 由勾股定理，得HC =32．∴ DC=DH+HC=2+32． ------------------------------------------------------------------------5分 16、14年怀柔一模19．如图，在平行四边形ABCD 中，∠ABC=45°，E 、F 分别在CD 和BC的延长线上，AE∥BD，∠EFC=30°， AB=2. 求CF 的长．19．解：∵四边形ABCD 是平行四边形，∴AB∥DC，AB=DC ，∵AE∥BD， ∴四边形ABDE 是平行四边形，∴AB=DE=CD，……………………………………………2分 即D 为CE 中点， ∵AB=2，∴CE=4，…………………………………………3分 又∵AB∥CD，∴∠E CF=∠ABC=45°， 过点E 作EH ⊥BF 于点H ，∵CE=4，∠ECF=45°，∴EH=CH=22，………………………………………………4分 ∵∠EFC=30°，∴ FH=26，∴ CF=22+26．…………………………………5分 17、14年延庆一模20. 如图，在Rt △ABC 中，∠C =90°，AB 的垂直平分线与AC ，AB 的交点分别为D ，E ． （1）若AD =15，4cos 5BDC ∠=， 求AC 的长和tan A 的值；（2）设BDC α∠=，计算tan2α的值．（用sin α和cos α的式子表示）20.解：（1）∵ DE 垂直平分AB ，∴ 15BD AD ==． ………………………………1分H FE D C B A （第20题）BACED（第20题）BACED在Rt △ACD 中，90C ∠=︒，AD =15，4cos 5BDC ∠=， ∴ 4cos 15125CD AD BDC =⋅∠=⨯=． 3sin 1595BC AD BDC =⋅∠=⨯=．∴ 27AC CD AD =+=． ……………………………2分 在Rt △ABC 中，90C ∠=︒， ∴ 91tan 273BC A AC ===． …………………………3分 （2）在Rt △ACD 中，90C ∠=︒，∴ cos CD AD BDC =⋅∠．sin BC AD BDC =⋅∠．∴ cos AC CD AD AD BDC =+=⋅∠． ……………………………4分 在Rt △ABC 中，90C ∠=︒， ∴ sin sin tan cos 1cos BC AD BDC BDCA AC AD AD BDC BDC∠∠===+∠+∠． ……………5分。