一元二次不等式解法-恒成立问题

一元二次不等式恒成立与能成立问题5大题型不等式是高考数学的重要内容。

其中，“含参不等式恒成立与能成立问题”把不等式、函数、三角、几何等内容有机地结合起来，其以覆盖知识点多、综合性强、解法灵活等特点备受高考命题者的青睐。

另一方面，在解决这类数学问题的过程中涉及的“函数与方程”、“化归与转化”、“数形结合”、“分类讨论”等数学思想对锻炼学生的综合解题能力，培养其思维灵活性、创造性都有这独到的作用。

一元二次不等式应用广泛，考察灵活，高考复习过程要注重知识与方法的灵活运用。

一、一元二次不等式在实数集上的恒成立1、不等式对任意实数恒成立⇔00==⎧⎨>⎩a b c 或0Δ<0>⎧⎨⎩a 2、不等式对任意实数恒成立⇔00==⎧⎨<⎩a b c 或0Δ<0<⎧⎨⎩a 【注意】对于二次不等式恒成立问题，恒大于0就是相应的二次函数的图像在给定的区间上全部在x 轴上方；恒小于0就是相应的二次函数的图像在给定的区间上全部在x 轴下方．二、一元二次不等式在给定区间上的恒成立问题求解方法方法一：若在集合中恒成立，即集合是不等式的解集的子集，可以先求解集，再由子集的含义求解参数的值(或范围)；方法二：转化为函数值域问题，即已知函数的值域为，则恒成立⇒，即；恒成立⇒，即.三、给定参数范围的一元二次不等式恒成立问题解决恒成立问题一定要清楚选谁为主元，谁是参数；一般情况下，知道谁的范围，就选谁当主元，求谁的范围，谁就是参数.即把变元与参数交换位置，构造以参数为变量的函数，根据原变量的取值范围列式求解。

四、常见不等式恒成立及有解问题的函数处理方法不等式恒成立问题常常转化为函数的最值来处理，具体如下：1、对任意的，恒成立⇒；若存在，有解⇒；若对任意，无解⇒.2、对任意的，恒成立⇒；若存在，有解⇒；若对任意，无解⇒.【题型1一元二次不等式在实数集上的恒成立问题】【例1】（2022·重庆沙坪坝·重庆八中校考模拟预测）使得不等式210x ax -+>对R x ∀∈恒成立的一个充分不必要条件是（）A ．02a <<B ．02a <≤C ．2a <D ．2a >-【变式1-1】（2022秋·山东·高三山东省实验中学校考阶段练习）已知命题“x ∃∈R ，使()24110x a x +-+≤”是假命题，则实数a 的取值范围是（）A ．(,3)-∞-B ．()5,3-C ．(5,)+∞D ．(3,5)-【变式1-2】（2023·全国·高三专题练习）若命题“关于x 的不等式22410mx mx m ++-<对一切实数x 恒成立”是假命题，则实数m 的取值范围是____________．【变式1-3】（2022秋·广西钦州·高三校考阶段练习）已知关于x 的不等式0k x->恒成立，则实数k 的取值范围是_____________．【变式1-4】（2022秋·山东聊城·高三山东聊城一中校考期末）关于x 的不等式()2216(4)10ax a x ----≥的解集为∅，则实数a 的取值范围为_________．【题型2一元二次不等式在某区间上的恒成立问题】【例2】（2022秋·辽宁沈阳·高三沈阳市第三十一中学校考开学考试）已知不等式220x bx c -++>的解集{}13x x -<<，若对任意10x -≤≤，不等式224x bx c t -+++≤恒成立．则t 的取值范围是__________．【变式2-1】（2022秋·山东青岛·高三统考期中）已知关于x 的不等式2(13)20ax a x +-+≥的解集为A ，设{1,1}B =-，B A ⊆，则实数a 的取值范围为（）A ．3124a -≤≤B ．1342a -≤≤C ．14a -≤D ．32a ≥【变式2-2】（2022秋·河南·高三期末）已知0a >，b ∈R ，若0x >时，关于x 的不等式()()2250ax x bx -+-≥恒成立，则4b a+的最小值为（）A ．2B ．25C ．43D ．32【变式2-3】（2022秋·广西钦州·高三校考阶段练习）已知函数()2f x ax x a =++，不等式()5f x <的解集为3—12⎛⎫⎪⎝⎭，．（1）求a 的值；（2）若()f x mx >在(]0,5x ∈上恒成立，求m 的取值范围．【变式2-4】（2021秋·陕西西安·高三校考阶段练习）已知二次函数()f x 满足()21f =-，()11f -=-，且()f x 的最大值是8.（1）试确定该二次函数的解析式；（2）()2f x x k >+在区间[]3,1-上恒成立，试求k 的取值范围.【题型3给定参数范围的一元二次不等式恒成立问题】【例3】（2021·吉林松原·校考三模）若不等式21634x ax x a -≥--对任意[]2,4a ∈-成立，则x 的取值范围为（）A ．(][),83,-∞-⋃+∞B ．()[),01,-∞+∞C ．[]8,6-D ．(]0,3【变式3-1】（2022秋·湖北襄阳·高三校考阶段练习）若命题“[]()21,3,2130a ax a x a ∃∈---+-<”为假命题，则实数x 的取值范围为（）A ．[]1,4-B ．50,3⎡⎤⎢⎥⎣⎦C ．[]51,0,43⎡⎤⎢⎥⎣-⎦D ．[)51,0,43⎛⎤- ⎥⎝⎦【变式3-2】（2022秋·广东深圳·高三深圳中学校考阶段练习）已知当11a -≤≤时，()24420x a x a +-+->恒成立，则实数x 的取值范围是（）A ．(),3-∞B ．][(),13,∞∞-⋃+C ．(),1-∞D ．()(),13,-∞⋃+∞【变式3-3】（2023·全国·高三专题练习）当[]2,3a ∈时，不等式210ax x a -+-≤恒成立，求x 的取值范围．【变式3-4】（2021·辽宁沈阳·高三沈阳二中校考开学考试）设函数()21f x mx mx =--．（1）若对于[]2,2x ∈-，()5f x m <-+恒成立，求m 的取值范围；（2）若对于[]2,2m ∈-，()5f x m <-+恒成立，求x 的取值范围．【题型4一元二次不等式在实数集上的有解问题】【例4】（2023·全国·高三专题练习）若存在实数x ，使得()220mx m x m --+<成立，则实数m 的取值范围为（）A ．(),2-∞B ．(]13,0,32∞⎛⎫-⋃ ⎪⎝⎭C ．2,3⎛⎫-∞ ⎪⎝⎭D ．(),1-∞【变式4-1】（2022秋·广西钦州·高三校考阶段练习）若关于x 的不等式()()224210ax a x -++-≥的解集不为空集，则实数a 的取值范围为（）A ．62,5⎛⎤- ⎥⎝⎦B ．62,5⎡⎤-⎢⎥⎣⎦C ．6(,2)[,)5-∞-⋃+∞D ．6(,2],5⎡⎫-∞-⋃+∞⎪⎢⎣⎭【变式4-2】（2023·全国·高三专题练习）若关于x 的不等式29(2)04ax a x -++<有解，则实数a 的取值范围是____．【变式4-3】（2022·全国·高三专题练习）若关于x 的不等式2210ax x ++<有实数解，则a 的取值范围是_____【题型5一元二次不等式在某区间上的有解问题】【例5】（2022·甘肃张掖·高台县第一中学校考模拟预测）若关于x 的不等式2620x x a -+->在区间[]0,5内有解，则实数a 的取值范围是（）．A ．()2,+∞B ．(),5-∞C ．(),3-∞-D ．(),2-∞【变式5-1】（2023·全国·高三专题练习）已知关于x 的不等式2630mx x m -+<在(]02，上有解，则实数m 的取值范围是（）A ．(3-∞，B ．127⎛⎫-∞ ⎪⎝⎭，C ．)3+∞，D ．127⎛⎫+∞ ⎪⎝⎭，【变式5-2】（2022·全国·高三专题练习）命题:{|19}p x x x ∃∈≤≤，2360x ax -+≤，若p 是真命题，则实数a 的取值范围为（）A ．37a ≥B ．13a ≥C ．12a ≥D ．13a ≤【变式5-3】（2022秋·北京·高三统考阶段练习）若存在[0,1]x ∈，有2(1)30x a x a +-+->成立，则实数a 的取值范围是__________.【变式5-4】（2023·全国·高三专题练习）已知命题“[1,1]x ∃∈-，20030-++>x x a ”为真命题，则实数a 的取值范围是______．【变式5-5】（2022·全国·高三专题练习）设()f x 为奇函数，()g x 为偶函数，对于任意x R ∈均有()()24f x g x mx +=-.若()()220f x x g x -+≥在()0,x ∈+∞上有解，则实数m 的取值范围是______.（建议用时：60分钟）1．（2022·甘肃张掖·高台县第一中学校考模拟预测）已知命题p ：x ∀∈R ，220x x m -+>，则满足命题p 为真命题的一个充分条件是（）A ．m>2B ．0m <C ．1m <D ．m 1≥2．（2022秋·北京大兴·高三统考期中）若命题“2,20x x x m ∃∈++≤R ”是真命题，则实数m 的取值范围是（）A ．1m <B ．1m £C ．1m >D ．1m ≥3．（2022秋·全国·高三校联考阶段练习）设m ∈R ，则“34m >-”是“不等式210x x m -++≥在R 上恒成立”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件4．（2022秋·宁夏银川·高三校考期中）已知命题p ：R x ∀∈，20x x a -+>，若p ⌝是假命题，则实数a 的取值范围是（）A ．1,4⎛⎤-∞ ⎥⎝⎦B ．11,42⎛⎫ ⎪⎝⎭C ．1,4⎛⎫+∞ ⎪⎝⎭D ．1,2⎡⎫+∞⎪⎢⎣⎭5．（2022秋·河南·高三校联考阶段练习）设函数()22f x ax ax =-，命题“[]0,1x ∃∈，()3f x a ≤-+”是假命题，则实数a 的取值范围为（）A ．(),3-∞B ．()3,+∞C ．24,7⎛⎫+∞ ⎪⎝⎭D ．3,2⎛⎫+∞ ⎪⎝⎭6．（2023·全国·高三专题练习）若对任意的2[1,0],2420x x x m ∈--+++≥恒成立，则m 的取值范围是（）A ．[4,)+∞B ．[2,)+∞C ．(,4]-∞D ．(,2]-∞7．（2021秋·河南南阳·高三南阳中学校考阶段练习）设函数()21f x mx mx =--，若对于任意的{|13}x x x ∈≤≤，()4f x m <-+恒成立，则实数m 的取值范围为（）A ．57m <B ．507m ≤<C ．0m <或507m <<D ．0m ≤8．（2022秋·湖南邵阳·高三统考期中）设函数22()223f x x ax a a =++-+，若对于任意的x R ∈，不等式()()0f f x ≥恒成立，则实数a 的取值范围是（）A ．32a ≥B ．2a ≤C ．322a <≤D ．32a ≤9．（2022秋·辽宁鞍山·高三校联考期中）设R a ∈，若关于x 的不等式210x ax -+≥在12x ≤≤上有解，则（）A ．2a ≤B ．2a ≥C ．52a ≤D ．52a ≥10．（2023·全国·高三专题练习）已知命题“0x ∃∈R ，()20014204x a x +-+≤”是真命题，则实数a 的取值范围（）A ．(],0-∞B ．[]0,4C ．[4,+∞）D ．(],0-∞[)4⋃+∞,11．（2022·全国·高三专题练习）已知关于x 的不等式2243x x a a -+≥-在R 上有解，则实数a 的取值范围是（）A ．{}14a a -≤≤B ．{}14a a -<<C ．{4a a ≥或}1a ≤-D ．{}41a a -≤≤12．（2022·全国·高三专题练习）若关于x 的不等式220x ax +->在区间[]1,5上有解，则实数a 的取值范围为（）A ．23,5⎛⎫-+∞ ⎪⎝⎭B ．23,15⎡⎤-⎢⎥⎣⎦C ．()1,+∞D ．23,5⎛⎫-∞-⎪⎝⎭13．（2021秋·江苏徐州·高三统考阶段练习）若存在实数x ，使得关于x 的不等式2430ax x a -+-<成立，则实数a 的取值范围是______.14．（2021·全国·高三专题练习）已知函数2,0()20x x x f x x x ⎧-≤⎪=⎨>⎪⎩.若存在x ∈R 使得关于x 的不等式()1f x ax ≤-成立，则实数a 的取值范围是________.15．（2020·上海杨浦·复旦附中校考模拟预测）若命题：“存在整数x 使不等式()24(4)0kx kx ---<成立”是假命题，则实数k 的取值范围是____________.16．（2022秋·江苏连云港·高三校考开学考试）2210,0ax x x -+≥∀>恒成立，则实数a 的取值范围是_________.17．（2021·全国·高三专题练习）若不等式22x mx ->对满足1m ≤的一切实数m 都成立，则x 的取值范围是___________18．（2023·全国·高三专题练习）若不等式22210x t at -+-+≥对任意[1,1]x ∈-及[1,1]a ∈-恒成立，则实数t 的取值范围是__________．参考答案【题型1一元二次不等式在实数集上的恒成立问题】【例1】（2022·重庆沙坪坝·重庆八中校考模拟预测）使得不等式210x ax -+>对R x ∀∈恒成立的一个充分不必要条件是（）A ．02a <<B ．02a <≤C ．2a <D ．2a >-【答案】A【解析】由不等式210x ax -+>对R x ∀∈恒成立，得Δ0<，即()240a --<，解得22a -<<，从选项可知02a <<是22a -<<的充分不必要条件，故选：A.【变式1-1】（2022秋·山东·高三山东省实验中学校考阶段练习）已知命题“x ∃∈R ，使()24110x a x +-+≤”是假命题，则实数a 的取值范围是（）A ．(,3)-∞-B ．()5,3-C ．(5,)+∞D ．(3,5)-【答案】D【解析】因为命题“R x ∃∈，使()24110x a x +-+≤”是假命题，所以，命题“R x ∀∈，()24110x a x +-+>”是真命题，所以，2Δ(1)160a =--<，解得35a -<<，故实数a 的取值范围是(3,5)-．故选：D.【变式1-2】（2023·全国·高三专题练习）若命题“关于x 的不等式22410mx mx m ++-<对一切实数x 恒成立”是假命题，则实数m 的取值范围是____________．【答案】1m ≤-或0m >【解析】若命题是真命题：当0m =时，22410mx mx m ++-<，可化为10-<，成立；当0m ≠时，()20Δ16810m m m m <⎧⎨=--<⎩，解得10m -<<综合得当10m -<≤时，关于x 的不等式22410mx mx m ++-<对一切实数x 恒成立是真命题，若命题“关于x 的不等式22410mx mx m ++-<对一切实数x 恒成立”是假命题则1m ≤-或0m >【变式1-3】（2022秋·广西钦州·高三校考阶段练习）已知关于x 的不等式0x kk x->恒成立，则实数k 的取值范围是_____________．【答案】[0,4)0k x->，即0(0)x x k x -+>>，令0t x =>，则20(0)t kt k t -+>>恒成立．所以202000kk k ⎧≤⎪⎨⎪-⨯+≥⎩或()202Δ40k k k ⎧>⎪⎨⎪=--<⎩,解得04k ≤<，故实数k 的取值范围是[0,4)．【变式1-4】（2022秋·山东聊城·高三山东聊城一中校考期末）关于x 的不等式()2216(4)10ax a x ----≥的解集为∅，则实数a 的取值范围为_________．【答案】1245a a ⎧⎫-<≤⎨⎬⎩⎭∣【解析】当4a =时，不等式可化为10-≥，无解，满足题意；当4a =-时，不等式化为810x -≥，解得18x ≥，不符合题意，舍去；当4a ≠±时，要使得不等式()2216(4)10a x a x ----≥的解集为∅，则()()222160,44160,a a a ⎧-<⎪⎨∆=-+-<⎪⎩解得1245a -<<．综上，实数a 的取值范围是1245a a ⎧⎫-<≤⎨⎬⎩⎭∣．【题型2一元二次不等式在某区间上的恒成立问题】【例2】（2022秋·辽宁沈阳·高三沈阳市第三十一中学校考开学考试）已知不等式220x bx c -++>的解集{}13x x -<<，若对任意10x -≤≤，不等式224x bx c t -+++≤恒成立．则t 的取值范围是__________．【答案】2t ≤-【解析】由题设，22b =且32c -=-，可得4,6b c ==，所以22420x x t -+++≤在10x -≤≤上恒成立，而222)4(f x x x t +=-++在(,1)-∞上递增，故只需2(0)0f t +≤=即可，所以2t ≤-.【变式2-1】（2022秋·山东青岛·高三统考期中）已知关于x 的不等式2(13)20ax a x +-+≥的解集为A ，设{1,1}B =-，B A ⊆，则实数a 的取值范围为（）A ．3124a -≤≤B ．1342a -≤≤C ．14a -≤D ．32a ≥【答案】B【解析】由题意，23)(20x a x x ++≥-在{1,1}B =-上恒成立，所以410320a a +≥⎧⎨-≥⎩，可得1342a -≤≤.故选：B【变式2-2】（2022秋·河南·高三期末）已知0a >，b ∈R ，若0x >时，关于x 的不等式()()2250ax x bx -+-≥恒成立，则4b a+的最小值为（）A ．2B ．25C ．43D ．32【答案】B【解析】设2y ax =-（0x >），25y x bx =+-（0x >），因为0a >，所以当20x a<<时，20y ax =-<；当2x a=时，20y ax =-=；当2x a >时，20y ax =->；由不等式()2(2)50ax x bx -+-≥恒成立，得：22050ax x bx -≤⎧⎨+-≤⎩或22050ax x bx -≥⎧⎨+-≥⎩，即当20x a<≤时，250x bx +-≤恒成立，当2x a≥时，250x bx +-≥恒成立，所以当2x a =时，250y x bx =+-=，则20425b a a +-=，即225a b a =-，则当0a >时，4524555222222a a a b a a a a a+=-+=+≥⨯=当且仅当522a a =，即55a =时等号成立，所以4b a+的最小值为25故选：B.【变式2-3】（2022秋·广西钦州·高三校考阶段练习）已知函数()2f x ax x a =++，不等式()5f x <的解集为3—12⎛⎫⎪⎝⎭，．（1）求a 的值；（2）若()f x mx >在(]0,5x ∈上恒成立，求m 的取值范围．【答案】（1）2a =；（2）{|5}m m <．【解析】（1）()25f x ax x a =++<的解集为312⎛⎫-⎪⎝⎭，即250ax x a ++-<的解集为312，⎛⎫-⎪⎝⎭，031123512a a a a >⎧⎪⎪-+=-∴⎨⎪-⎪-⨯=⎩，解得2a =；（2）由(Ⅰ)可得()222f x x x =++，()f x mx > 在(]05x ∈，上恒成立，即()22120x m x +-+>恒成立，令()()2212h x x m x =+-+，则()0h x >在(]05，上恒成立，有()104020m h -⎧≤⎪⎨⎪=>⎩或()2105412240m m -⎧<≤⎪⎨⎪--⨯⨯<⎩或()()154552510m h m -⎧>⎪⎨⎪=+->⎩，解得1m £或15m <<或m ∈∅，综上可得m 的范围为{|5}m m <．【变式2-4】（2021秋·陕西西安·高三校考阶段练习）已知二次函数()f x 满足()21f =-，()11f -=-，且()f x 的最大值是8.（1）试确定该二次函数的解析式；（2）()2f x x k >+在区间[]3,1-上恒成立，试求k 的取值范围.【答案】（1）()2447f x x x =-++；（2）k 的取值范围为(),35∞--.【解析】（1）由(2)(1)f f =-，得21122x -==为二次函数的对称轴，因函数()f x 的最大值为8，所以可设()2182f x a x ⎛⎫=-+ ⎪⎝⎭，又因9(2)814f a =+=-，所以4a =-，因此()2447f x x x =-++.（2）由(1)不等式()2f x x k >+，可化为24472x x x k -++>+，所以2427k x x <-++，因为()2f x x k >+在区间[]3,1-上恒成立，所以2427k x x <-++在区间[]3,1-上恒成立，故()2min 427k x x <-++，其中[]3,1x ∈-，又函数22129427444y x x x ⎛⎫=-++=--+ ⎪⎝⎭，又当3x =-时，35y =-，当1x =时，5y =，所以函数2427y x x =-++在[]3,1-上的最小值为-35，所以35k <-，所以k 的取值范围为(),35∞--.【题型3给定参数范围的一元二次不等式恒成立问题】【例3】（2021·吉林松原·校考三模）若不等式21634x ax x a -≥--对任意[]2,4a ∈-成立，则x 的取值范围为（）A ．(][),83,-∞-⋃+∞B ．()[),01,-∞+∞ C ．[]8,6-D ．(]0,3【答案】A【解析】由题得不等式2(4)3160x a x x ---+≤对任意[]2,4a ∈-成立，所以22(4)(2)3160(4)43160x x x x x x ⎧----+≤⎨---+≤⎩，即2252400x x x x ⎧--+≤⎨-+≤⎩，解之得3x ≥或8x ≤-.故选：A【变式3-1】（2022秋·湖北襄阳·高三校考阶段练习）若命题“[]()21,3,2130a ax a x a ∃∈---+-<”为假命题，则实数x 的取值范围为（）A ．[]1,4-B ．50,3⎡⎤⎢⎥⎣⎦C ．[]51,0,43⎡⎤⎢⎥⎣-⎦D ．[)51,0,43⎛⎤- ⎥⎝⎦【答案】C【解析】命题“[]()21,3,2130a ax a x a ∃∈---+-<”为假命题，其否定为真命题，即“[]()21,3,2130a ax a x a ∀∈---+-≥”为真命题．令22()23(21)30g a ax ax x a x x a x =-++-=--++≥，则(1)0(3)0g g -≥⎧⎨≥⎩，即22340350x x x x ⎧-++≥⎨-≥⎩，解得14503x x x -≤≤⎧⎪⎨≥≤⎪⎩或，所以实数x 的取值范围为[]51,0,43⎡⎤⎢⎥⎣-⎦.故选：C【变式3-2】（2022秋·广东深圳·高三深圳中学校考阶段练习）已知当11a -≤≤时，()24420x a x a +-+->恒成立，则实数x 的取值范围是（）A ．(),3-∞B ．][(),13,∞∞-⋃+C ．(),1-∞D ．()(),13,-∞⋃+∞【答案】D【解析】()24420x a x a +-+->恒成立，即()22440x a x x -+-+>，对任意得[]1,1a ∈-恒成立，令()()2244f a x a x x =-+-+，[]1,1a ∈-，当2x =时，()0f a =，不符题意，故2x ≠，当2x >时，函数()f a 在[]1,1a ∈-上递增，则()()2min 12440f a f x x x =-=-++-+>，解得3x >或2x <（舍去），当2x <时，函数()f a 在[]1,1a ∈-上递减，则()()2min 12440f a f x x x ==-+-+>，解得1x <或2x >（舍去），综上所述，实数x 的取值范围是()(),13,-∞⋃+∞.故选：D.【变式3-3】（2023·全国·高三专题练习）当[]2,3a ∈时，不等式210ax x a -+-≤恒成立，求x 的取值范围．【答案】1,12⎡⎤-⎢⎥⎣⎦．【解析】由题意不等式210ax x a -+-≤对[]2,3a ∈恒成立，可设2()(1)(1)f a x a x =-+-+，[]2,3a ∈，则()f a 是关于a 的一次函数，要使题意成立只需(2)0(3)0f f ≤⎧⎨≤⎩，即22210320x x x x ⎧--≤⎨--≤⎩，解2210x x --≤，即()()2110x x +-≤得112x -≤≤，解2320x x --≤，即()()3210x x +-≤得213x -≤≤，所以原不等式的解集为1,12⎡⎤-⎢⎥⎣⎦，所以x 的取值范围是1,12⎡⎤-⎢⎥⎣⎦．【变式3-4】（2021·辽宁沈阳·高三沈阳二中校考开学考试）设函数()21f x mx mx =--．（1）若对于[]2,2x ∈-，()5f x m <-+恒成立，求m 的取值范围；（2）若对于[]2,2m ∈-，()5f x m <-+恒成立，求x 的取值范围．【答案】（1）6,7⎛⎫-∞ ⎪⎝⎭；（2）()1,2-【解析】（1）若对于[]2,2x ∈-，()5f x m <-+恒成立，即260mx mx m -+-<对于[]2,2x ∈-恒成立，即261m x x <-+对于[]2,2x ∈-恒成立．令()226611324h x x x x ==-+⎛⎫-+⎪⎝⎭，[]2,2x ∈-，则()min 66(2)253744h x h =-==+，故67m <，所以m 的取值范围为6,7⎛⎫-∞ ⎪⎝⎭．（2）对于[]2,2m ∈-，()5f x m <-+恒成立，即215mx mx m --<-+恒成立，故()2160m x x -+-<恒成立，令()()216g m m x x =+--，则()()()()222216022160g x x g x x ⎧-=--+-<⎪⎨=-+-<⎪⎩，解得12x -<<，所以x 的取值范围为()1,2-．【题型4一元二次不等式在实数集上的有解问题】【例4】（2023·全国·高三专题练习）若存在实数x ，使得()220mx m x m --+<成立，则实数m 的取值范围为（）A ．(),2-∞B ．(]13,0,32∞⎛⎫-⋃ ⎪⎝⎭C ．2,3⎛⎫-∞ ⎪⎝⎭D ．(),1-∞【答案】C【解析】①当0m =时，不等式化为20x <，解得：0x <，符合题意；②当0m >时，()22y mx m x m =--+为开口方向向上的二次函数，只需()222243440m m m m ∆=--=--+>，即203m <<；③当0m <时，()22y mx m x m =--+为开口方向向下的二次函数，则必存在实数x ，使得()220mx m x m --+<成立；综上所述：实数m 的取值范围为2,3⎛⎫-∞ ⎪⎝⎭.故选：C.【变式4-1】（2022秋·广西钦州·高三校考阶段练习）若关于x 的不等式()()224210ax a x -++-≥的解集不为空集，则实数a 的取值范围为（）A ．62,5⎛⎤- ⎥⎝⎦B ．62,5⎡⎤-⎢⎥⎣⎦C ．6(,2)[,)5-∞-⋃+∞D ．6(,2],5⎡⎫-∞-⋃+∞⎪⎢⎣⎭【答案】C【解析】根据题意，分两种情况讨论：①当240a -=时，即2a =±，若2a =时，原不等式为410x -≥，解可得：14x ≥，则不等式的解集为1|4x x ⎧⎫≥⎨⎬⎩⎭，不是空集；若2a =-时，原不等式为10-≥，无解，不符合题意；②当240a -≠时，即2a ≠±，若22(4)(2)10a x a x -++-≥的解集是空集，则有22240Δ(2)4(4)0a a a ⎧-<⎨=++-<⎩，解得625a -<<，则当不等式22(4)(2)10a x a x -++-≥的解集不为空集时，有2a <-或65a ≥且2a ≠，综合可得：实数a 的取值范围为6(,2)[,)5-∞-⋃+∞；故选：C ．【变式4-2】（2023·全国·高三专题练习）若关于x 的不等式29(2)04ax a x -++<有解，则实数a 的取值范围是____．【答案】(,1)(4,)-∞+∞ 【解答】当0a =时，不等式为9204x -+<有解，故0a =，满足题意；当0a >时，若不等式29(2)04ax a x -++<有解，则满足29(2)404a a ∆=+-⋅>，解得1a <或4a >；当a<0时，此时对应的函数的图象开口向下，此时不等式29(2)04ax a x -++<总是有解，所以a<0，综上可得，实数a 的取值范围是(,1)(4,)-∞+∞ .【变式4-3】（2022·全国·高三专题练习）若关于x 的不等式2210ax x ++<有实数解，则a 的取值范围是_____．【答案】(),1∞-【解析】当0a =时，不等式为210x +<有实数解，所以0a =符合题意；当a<0时，不等式对应的二次函数开口向下，所以不等式2210ax x ++<有实数解，符合题意；当0a >时，要使不等式2210ax x ++<有实数解，则需满足440∆=->a ，可得1a <，所以01a <<，综上所述：a 的取值范围是(),1∞-，【题型5一元二次不等式在某区间上的有解问题】【例5】（2022·甘肃张掖·高台县第一中学校考模拟预测）若关于x 的不等式2620x x a -+->在区间[]0,5内有解，则实数a 的取值范围是（）．A ．()2,+∞B ．(),5-∞C ．(),3-∞-D ．(),2-∞【答案】D【解析】不等式2620x x a -+->在区间[]0,5内有解，仅需2max (62)x x a -+>即可，令2()62f x x x =-+，因为()f x 的对称轴为6321x -=-=⨯，(0)2f =，(5)3f =-，所以由一元二次函数的图像和性质的得2max (62)2x x -+=，所以2a <，故选：D【变式5-1】（2023·全国·高三专题练习）已知关于x 的不等式2630mx x m -+<在(]02，上有解，则实数m 的取值范围是（）A ．(3-∞，B ．127⎛⎫-∞ ⎪⎝⎭，C ．)3+∞，D ．127⎛⎫+∞⎪⎝⎭，【答案】A【解析】由题意得，2630mx x m -+<，(]02x ∈，，即263xm x <+，故问题转化为263xm x <+在(]02，上有解，设26()3x g x x =+，则266()33x g x x x x ==++，(]02x ∈，，对于323x x+，当且仅当3(0,2]x =时取等号，则max ()323g x =3m ，故选：A【变式5-2】（2022·全国·高三专题练习）命题:{|19}p x x x ∃∈≤≤，2360x ax -+≤，若p 是真命题，则实数a 的取值范围为（）A ．37a ≥B ．13a ≥C ．12a ≥D ．13a ≤【答案】C【解析】 命题:{|19}p x x x ∃∈≤≤，使2360x ax -+≤为真命题，即{|19}x x x ∃∈≤≤，使2360x ax -+≤成立，即36a x x≥+能成立设36()f x x x=+，则3636()212f x x x x x=+≥⋅=，当且仅当36x x=，即6x =时，取等号，即min ()12f x =，12a ∴≥，故a 的取值范围是12a ≥．故选：C ．【变式5-3】（2022秋·北京·高三统考阶段练习）若存在[0,1]x ∈，有2(1)30x a x a +-+->成立，则实数a 的取值范围是__________.【答案】(),3∞-【解析】将原不等式参数分离可得231x x a x ++<+，设()231x x f x x ++=+，已知存在[0,1]x ∈，有2(1)30x a x a +-+->成立，则()max a f x <，令1t x =+，则()()22113133t t t f x t t t tt -+-+==+-+=-，[]1,2t ∈，由对勾函数知()f x 在3⎡⎣上单调递减，在3,2⎤⎦上单调递增，()311131f =+-=，()3522122f =+-=，所以()()max 13f x f ==，即3a <.【变式5-4】（2023·全国·高三专题练习）已知命题“[1,1]x ∃∈-，20030-++>x x a ”为真命题，则实数a 的取值范围是______．【答案】()2,-+∞【解析】因为命题“[1,1]x ∃∈-，20030-++>x x a ”为真命题则[1,1]x ∃∈-，23>-a x x 有解，设2()3f x x x =-，则2239324()⎛⎫-=-- ⎝⎭=⎪f x x x x ，当[1,1]x ∈-时，()f x 单调递减，所以2()4f x -≤≤，所以2a >-.【变式5-5】（2022·全国·高三专题练习）设()f x 为奇函数，()g x 为偶函数，对于任意x R ∈均有()()24f x g x mx +=-.若()()220f x x g x -+≥在()0,x ∈+∞上有解，则实数m 的取值范围是______.【答案】4m ≥【解析】由题设，()()22240f x x g x mx x -+=--≥，即240x mx -+≤在()0,x ∈+∞上有解，对于24y x mx =-+，开口向上且对称轴为2mx =，216m ∆=-，0|4x y ==，∴002m ∆≥⎧⎪⎨>⎪⎩，可得4m ≥.（建议用时：60分钟）1．（2022·甘肃张掖·高台县第一中学校考模拟预测）已知命题p ：x ∀∈R ，220x x m -+>，则满足命题p 为真命题的一个充分条件是（）A ．m>2B ．0m <C ．1m <D ．m 1≥【答案】A【解析】∵命题p 为真命题，∴不等式220x x m -+>在R 上恒成立，∴Δ440m =-<，解得1m >，对于A ，m>2⇒1m >，∴m>2是1m >的充分条件，∴m>2是命题p 为真命题的充分条件，选项A 正确；对于B ，0m <¿1m >，∴0m <不是1m >的充分条件，∴0m <不是命题p 为真命题的充分条件，选项B 不正确；对于C ，1m <¿1m >，∴1m <不是1m >的充分条件，∴1m <不是命题p 为真命题的充分条件，选项C 不正确对于D ，m 1≥¿1m >，∴m 1≥不是1m >的充分条件，∴m 1≥不是命题p 为真命题的充分条件，选项D 不正确.故选：A.2．（2022秋·北京大兴·高三统考期中）若命题“2,20x x x m ∃∈++≤R ”是真命题，则实数m 的取值范围是（）A ．1m <B ．1m £C ．1m >D ．1m ≥【答案】B【解析】由题可知，不等式220x x m ++≤在实数范围内有解，等价于方程220x x m ++=有实数解，即440m ∆=-≥，解得1m ≤.故选：B.3．（2022秋·全国·高三校联考阶段练习）设m ∈R ，则“34m >-”是“不等式210x x m -++≥在R 上恒成立”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A【解析】由不等式210x x m -++≥在R 上恒成立，得()()2Δ1410m =--+≤，解得34m ≥-．所以“34m >-”是“不等式210x x m -++≥在R 上恒成立”的充分不必要条件．故选：A4．（2022秋·宁夏银川·高三校考期中）已知命题p ：R x ∀∈，20x x a -+>，若p ⌝是假命题，则实数a 的取值范围是（）A ．1,4⎛⎤-∞ ⎥⎝⎦B ．11,42⎛⎫ ⎪⎝⎭C ．1,4⎛⎫+∞ ⎪⎝⎭D ．1,2⎡⎫+∞⎪⎢⎣⎭【答案】C【解析】已知命题:R p x ∀∈，20x x a -+>，若p ⌝是假命题，则不等式20x x a -+>在R 上恒成立，140a ∴∆=-<，解得14a >.因此，实数a 的取值范围是1,4⎛⎫+∞ ⎪⎝⎭.故选：C.5．（2022秋·河南·高三校联考阶段练习）设函数()22f x ax ax =-，命题“[]0,1x ∃∈，()3f x a ≤-+”是假命题，则实数a 的取值范围为（）A ．(),3-∞B ．()3,+∞C ．24,7⎛⎫+∞ ⎪⎝⎭D ．3,2⎛⎫+∞ ⎪⎝⎭【答案】C【解析】因为命题“[]()0,1,3x f x a ∃∈≤-+”是假命题，所以[]()0,1,3x f x a ∀∈>-+是真命题，又()3f x a >-+可化为223ax ax a ->-+，即()2213a x x -+>，当[]0,1x ∈时，272128x x ⎡⎤+∈⎢⎣-⎥⎦，所以2321m x x >-+在[]0,1x ∈上恒成立，所以2max321m x x ⎛⎫->⎪+⎝⎭其中,[]0,1x ∈，当14x =时221x x -+有最小值为78，此时2321x x -+有最大值为247，所以247m >，故实数m 的取值范围是24,7⎛⎫+∞ ⎪⎝⎭，故选：C6．（2023·全国·高三专题练习）若对任意的2[1,0],2420x x x m ∈--+++≥恒成立，则m 的取值范围是（）A ．[4,)+∞B ．[2,)+∞C ．(,4]-∞D ．(,2]-∞【答案】A【解析】因为对任意的2[1,0],2420x x x m ∈--+++≥恒成立，所以对任意的2[1,0],242x m x x ≥-∈--恒成立，因为当[1,0]x ∈-，()[]22142,4y x =--∈-，所以()2max 2424m x x --≥=，[1,0]x ∈-，即m 的取值范围是[4,)+∞，故选：A7．（2021秋·河南南阳·高三南阳中学校考阶段练习）设函数()21f x mx mx =--，若对于任意的{|13}x x x ∈≤≤，()4f x m <-+恒成立，则实数m 的取值范围为（）A ．57m <B ．507m ≤<C ．0m <或507m <<D ．0m ≤【答案】A【解析】若对于任意的13{|}x x x ∈≤≤，()4f x m <-+恒成立,即可知：250mx mx m -+-<在13{|}x x x ∈≤≤上恒成立,令()25g x mx mx m =-+-，对称轴为12x =.当0m =时，50-<恒成立，当0m <时，有()g x 开口向下且在[]1,3上单调递减，∴在[]1,3上()()max 150g x g m ==-<，得5m <，故有0m <.当0m >时，有()g x 开口向上且在[]1,3上单调递增∴在[]1,3上()()max 3750g x g m ==-<，∴507m <<综上，实数m 的取值范围为57m <，故选：A.8．（2022秋·湖南邵阳·高三统考期中）设函数22()223f x x ax a a =++-+，若对于任意的x R ∈，不等式()()0f f x ≥恒成立，则实数a 的取值范围是（）A ．32a ≥B ．2a ≤C ．322a <≤D ．32a ≤【答案】B【解析】∵222()223()23f x x ax a a x a a =++-+=+-+，即开口向上且[)()23,f x a ∈-++∞，由()()0f f x ≥恒成立，即()0f x ≥在[)23,a -++∞上恒成立，∴当230a -+≥时，即32a ≤，由二次函数的性质，()0f x ≥显然成立；当32a >时，()y f x =有两个零点，则只需满足23(23)0a a f a -≤-+⎧⎨-+≥⎩，解得2a ≤，故322a <≤；综上，a 的取值范围是2a ≤.故选：B9．（2022秋·辽宁鞍山·高三校联考期中）设R a ∈，若关于x 的不等式210x ax -+≥在12x ≤≤上有解，则（）A ．2a ≤B ．2a ≥C ．52a ≤D ．52a ≥【答案】C【解析】由210x ax -+≥在12x ≤≤上有解，得21x a x+≥在12x ≤≤上有解，则2max1x a x ⎛⎫+≤ ⎪⎝⎭，由于211x x x x +=+，而1+x x在12x ≤≤单调递增，故当2x =时，1+x x 取最大值为52，故52a ≤，故选：C10．（2023·全国·高三专题练习）已知命题“0x ∃∈R ，()20014204x a x +-+≤”是真命题，则实数a 的取值范围（）A ．(],0-∞B ．[]0,4C ．[4,+∞）D ．(],0-∞[)4⋃+∞,【答案】D【解析】由题意，命题“0x ∃∈R ，()20014204x a x +-+≤”是真命题故221(2)44404a a a ∆=--⨯⨯=-≥，解得4a ≥或0a ≤.则实数a 的取值范围是(],0-∞[)4⋃+∞,故选：D.11．（2022·全国·高三专题练习）已知关于x 的不等式2243x x a a -+≥-在R 上有解，则实数a 的取值范围是（）A ．{}14a a -≤≤B ．{}14a a -<<C ．{4a a ≥或}1a ≤-D ．{}41a a -≤≤【答案】A【解析】因为关于x 的不等式2243x x a a -+≥-在R 上有解，即22430x x a a -+-≤在R 上有解，只需2243y x x a a =-+-的图象与x 轴有公共点，所以()()224430a a ∆=--⨯-≥，即2340a a --≤，所以()()410a a -+≤，解得：14a -≤≤，所以实数a 的取值范围是{}14a a -≤≤，故选：A.12．（2022·全国·高三专题练习）若关于x 的不等式220x ax +->在区间[]1,5上有解，则实数a 的取值范围为（）A ．23,5⎛⎫-+∞ ⎪⎝⎭B ．23,15⎡⎤-⎢⎥⎣⎦C ．()1,+∞D ．23,5⎛⎫-∞-⎪⎝⎭【答案】A【解析】关于x 的不等式220x ax +->在区间[1，5]上有解，22ax x ∴>-在[1x ∈，5]上有解，即2a x x>-在[1x ∈，5]上成立；设函数2()f x x x=-，[1x ∈，5]，()f x ∴在[1x ∈，5]上是单调减函数，又()1211f =-=，()2235555f =-=-所以()f x 的值域为23[5-，1]，要2a x x>-在[1x ∈，5]上有解，则235a >-，即实数a 的取值范围为23,5⎛⎫-+∞ ⎪⎝⎭．故选：A ．13．（2021秋·江苏徐州·高三统考阶段练习）若存在实数x ，使得关于x 的不等式2430ax x a -+-<成立，则实数a 的取值范围是______.【答案】4a <【解析】3a <时，若0x =，则不等式为30a -<，不等式成立，满足题意，3a ≥时，在在x 使得不等式2430ax x a -+-<成立，则164(3)0a a ∆=-->，∴34a ≤<．综上，4a <．14．（2021·全国·高三专题练习）已知函数2,0()20x x x f x x x ⎧-≤⎪=⎨>⎪⎩.若存在x ∈R 使得关于x 的不等式()1f x ax ≤-成立，则实数a 的取值范围是________.【答案】(,3][1,)-∞-⋃-+∞【解析】由题意，当0x =时，不等式()1f x ax ≤-可化为01≤-显然不成立；当0x <时，不等式()1f x ax ≤-可化为21x x ax -+≤，所以11a x x≤+-，又当0x <时，11()2x x x x ⎡⎤⎛⎫+=--+-≤- ⎪⎢⎥⎝⎭⎣⎦，当且仅当1x x -=-，即=1x -时，等号成立；当0x >时，不等式()1f x ax ≤-可化为21x ax ≤，即21111a x x x ⎫≥=-≥-⎪⎭；因为存在x ∈R 使得关于x 的不等式()1f x ax ≤-成立，所以，只需213a ≤--=-或1a ≥-.15．（2020·上海杨浦·复旦附中校考模拟预测）若命题：“存在整数x 使不等式()24(4)0kx kx ---<成立”是假命题，则实数k 的取值范围是____________.【答案】[1,4]【解析】设不等式()24(4)0kx k x ---<的解集为A ，当0k =时，不等式()24(4)0kx k x ---<化为>4x ，存在整数x 使不等式成立，所以此时不满足题意，所以0k ≠；当0k >时，原不等式化为4[()](4)0x k x k-+-<，因为4424k k kk+≥⋅,当且仅当4,k k =即2k =时取等号，所以4{|4}A x x k k =<<+，要使命题：“存在整数x 使不等式()24(4)0kx k x ---<成立”是假命题，则需445k k ≤+≤，解得14k ≤≤；当0k <时，原不等式化为4[()](4)0x k x k-+->，而()44424k k k k k k ⎛⎫⎛⎫+=--+≤--⋅=- ⎪ ⎪--⎝⎭⎝⎭，当且仅当4,k k -=-即2k =-时取等号，所以()4,4,A k k ⎛⎫=-∞+⋃+∞ ⎪⎝⎭,所以存在整数x 使不等式()24(4)0kx kx ---<成立，所以0k <不合题意.综上可知，实数k 的取值范围是[1,4].16．（2022秋·江苏连云港·高三校考开学考试）2210,0ax x x -+≥∀>恒成立，则实数a 的取值范围是_________.【答案】[1)+∞，【解析】由2210,0axx x -+≥∀>恒成立，可得，221a x x ≥-对0x ∀>恒成立，令221y x x =-，则2111y x ⎛⎫=-- ⎪⎝⎭，10x ⎛⎫> ⎪⎝⎭，当11x=时，max 1y =，所以max 1a y ≥=.17．（2021·全国·高三专题练习）若不等式22x mx ->对满足1m ≤的一切实数m 都成立，则x 的取值范围是___________【答案】<2x -或2x >【解析】因为22x mx ->，所以220mx x -+<令()22f m mx x =-+，即()0f m <在1m ≤恒成立，即11m -≤≤时()0f m <恒成立，所以()()1010f f ⎧<⎪⎨-<⎪⎩，即222020x x x x ⎧-+<⎨--+<⎩，解220x x -+<得2x >或1x <-；解220x x --+<得1x >或<2x -，所以原不等式组的解集为()(),22,x ∈-∞-⋃+∞18．（2023·全国·高三专题练习）若不等式22210x t at -+-+≥对任意[1,1]x ∈-及[1,1]a ∈-恒成立，则实数t 的取值范围是__________．【答案】(,2]{0}[2,)-∞-+∞U U 【解析】由题意得2221t at x -+≥对任意[1,1]x ∈-及[1,1]a ∈-恒成立，所以2211t at -+≥对任意[1,1]a ∈-恒成立，即220t at -≥对[1,1]a ∈-恒成立，令22()22g a t at ta t =-=-+，则()g a 是关于a 的一次函数，所以只需(1)0(1)0g g ≥⎧⎨-≥⎩，即222020t t t t ⎧-≥⎨+≥⎩，解得2t ≥或2t ≤-或0=t ，所以实数t 的取值范围是(,2]{0}[2,)-∞-+∞U U ．。

含参一元二次不等式的解法与恒成立问题
一元二次不等式是几何、代数以及统计学等领域中使用最广泛的不等式之一，其解法和恒成立问题也是学习和研究的重要内容。

首先，要理解含参一元二次不等式的解法，我们需要对一元二次方程有所了解。

一元二次不等式也可以表示为一元二次方程形式，也可以将一元二次方程化为一元二次不等式形式。

一元二次方程有一般形式ax^2 + bx + c = 0,其中a,b,c均为实数，且a≠0，这个方程有两个实根，如果a,b,c满足一定条件，那么解得的方程式可以写作
x^2+px+q≥0,其中p为常数，q为常数。

在求解含参一元二次不等式的时候，要先化成一元二次方程的形式，然后根据首项系数是正还是负，分两种情况讨论，如果ax^2为正，那么此一元二次不等式在实数集上有解，只要保证满足一定条件即可；若ax^2为负，则含参一元二次不等式可以分离，而只要满足条件就必定存在解。

当求解不等式的恒成立问题时，一般的思路是先将不等式的非负部分和负部分分开，求解其左右两边的值，例如：若有ax^2+bx+c≥0，可先将其分解为ax^2+c≥0和bx≥0，然后求解其左右两边的值，根据不等式的性质，求解其两个值，确定其恒成立条件。

总之，一元二次不等式的解法及其恒成立问题是学习和研究中重要的内容，也是大家常用的不等式之一。

要正确求解，首先要正确分离不等式，然后根据不等式的性质确定相应的恒成立条件。

一元二次不等式恒成立问题一元二次不等式是指形如ax^2 + bx + c > 0的不等式，其中a, b, c是实数，且a ≠ 0。

要解决一元二次不等式恒成立的问题，需要先了解一元二次不等式的基本性质和解法。

接下来，我将介绍一元二次不等式的基本理论，以及如何判断一元二次不等式是否恒成立。

一、基本理论1.一元二次不等式的解集对于一元二次不等式ax^2 + bx + c > 0，我们要求找到满足不等式的x的取值范围。

这个取值范围称为一元二次不等式的解集。

2.一元二次函数的图像一元二次不等式的解集可以通过一元二次函数的图像来表示。

一元二次函数的图像为抛物线，可以分为开口向上和开口向下两种情况。

3.一元二次函数的顶点一元二次函数的顶点是抛物线的最高点（开口向下）或最低点（开口向上）。

顶点的横坐标为-b/2a。

二、判断一元二次不等式是否恒成立1.利用一元二次函数的图像可以通过一元二次函数的图像来判断一元二次不等式的解集。

如果一元二次函数的图像位于x轴上方，则一元二次不等式恒成立；反之，如果一元二次函数的图像位于x轴下方，则一元二次不等式不恒成立。

2.利用一元二次函数的顶点当一元二次函数开口向上时，只有当顶点在x轴上方时，一元二次不等式恒成立。

当一元二次函数开口向下时，只有当顶点在x轴下方时，一元二次不等式恒成立。

3.利用一元二次不等式的解集性质一元二次不等式的解集性质可以通过判别式Δ = b^2 - 4ac的正负来判断：-当Δ > 0时，一元二次不等式有两个不等的实根，解集为x < x1或x > x2。

-当Δ = 0时，一元二次不等式有一个重根，解集为x = x1。

-当Δ < 0时，一元二次不等式无实根，解集为空集。

三、案例分析现在我们通过一些具体的例子来说明如何判断一元二次不等式是否恒成立。

1.例子1：2x^2 - 5x + 3 > 0首先，计算判别式Δ = (-5)^2 - 4 * 2 * 3 = 25 - 24 = 1。

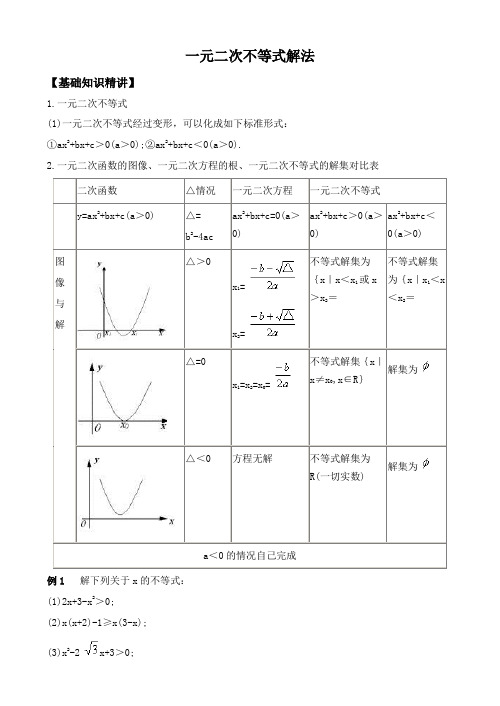
一元二次不等式解法【基础知识精讲】1.一元二次不等式(1)一元二次不等式经过变形，可以化成如下标准形式：①ax2+bx+c＞0(a＞0);②ax2+bx+c＜0(a＞0).2.一元二次函数的图像、一元二次方程的根、一元二次不等式的解集对比表二次函数△情况一元二次方程一元二次不等式y=ax2+bx+c(a＞0) △=b2-4ac ax2+bx+c=0(a＞0)ax2+bx+c＞0(a＞0)ax2+bx+c＜0(a＞0)图像与解△＞0x1=x2=不等式解集为｛x｜x＜x1或x＞x2＝不等式解集为｛x｜x1＜x＜x2＝△=0x1=x2=x0=不等式解集｛x｜x≠x0,x∈R｝解集为△＜0 方程无解不等式解集为R(一切实数)解集为a＜0的情况自己完成例1解下列关于x的不等式：(1)2x+3-x2＞0;(2)x(x+2)-1≥x(3-x);(3)x2-2x+3＞0;(4)x2+6(x+3)＞3;分析解一元二次不等式一般步骤是：①化为标准形式；②确定判别式△=b2-4ac的符号；③若△≥0，则求出该不等式对应的二次方程的根；若△＜0，则对应二次方程无根；④联系二次函数的图像得出不等式的解集.特别地，若一元二次不等式的左边的二次三项式能分解因式，则可立即写出不等式的解集(在两根之内或两根之外).解：(1)原不等式可化为x2-2x-3＜0,(x-3)(x+1)＜0.∴不等式的解集为｛x｜-1＜x＜3｝.(2)原不等式可化为2x2-x-2≥0,(2x+1)(x-1)≥0.∴不等式的解集为｛x｜x≤-，或x≥1｝.(3)原不等式可化为(x-)2＞0.∴不等式的解集为｛x｜x∈R且x≠｝.(4)原不等式可化为x2+6x+15＞0.∵△＜0，方程x2+6x+15=0无实根，∴不等式的解集为R.评析熟练掌握一元二次方程、二次函数、一元二次不等式三者之间的关系，再加上熟练地分解因式、配方技能，解一元二次不等式就能得心应手.例3已知f(x)=x2+2(a-2)x+4.(1)如果对一切x∈R，f(x)＞0恒成立，求实数a的取值范围.(2)如果对x∈〔-3，1〕，f(x)＞0成立，求实数a的取值范围.解：f(x)的图像开口向上.(1)对一切实数x，f(x)＞0，则△＜0，即(a-2)2-4＜0，∴0＜a ＜4；(2)当x∈〔-3，1〕时，f(x)＞0，对称轴2-a 可在区间内，也可在区间外，∴ 或或解得- ＜a ＜4评析 函数f(x)在给定区间上f(x)＞0(或f(x)＜0) f(x)在该区间上的最小(或最大)值大于(或小于)零.只有深刻理解了二次函数在给定区间上的最值意义，才能正确处理函数的局部性质与整体性质的关系.含参数的一元二次不等式的解法解含参数的一元二次不等式，通常情况下，均需分类讨论，那么如何讨论呢？对含参一元二次不等式常用的分类方法有三种： 一、按2x 项的系数a 的符号分类，即0,0,0<=>a a a ; 例1 解不等式：()0122>+++x a ax例2． 解不等式()00652≠>+-a a ax ax二、按判别式∆的符号分类，即0,0,0<∆=∆>∆； 例3 .解不等式042>++ax x例4 解不等式()()R m x x m ∈≥+-+014122三、按方程02=++c bx ax 的根21,x x 的大小来分类，即212121,,x x x x x x <=<；例5 解不等式)0( 01)1(2≠<++-a x aa x例6 解不等式06522>+-a ax x ，0≠a1、已知不等式[]22023x x a x -+>∈对任意实数，恒成立。

教师姓名韩贺凤单位名称巴州第一中学填写时间2020·8·15学科数学年级/册高一年级教材版本人教A版课题名称必修五第三章第二节3.2 解决一元二次不等式的恒成立问题难点名称根据实物，概括棱柱、棱椎、棱台的结构特征难点分析从知识角度分析为什么难对一元二次不等式恒成立的理解与一元二次不等式的解集二者之间的关联性。

从学生角度分析为什么难1、一元二次不等式的解法在教材中是利用二次函数的图像分析出来的，学生往往只重视结果，而忽视了它的形成过程。

2、一元二次不等式恒成立的理解不能与解法有机结合。

难点教学方法数形结合的思想方法教学环节教学过程导入从教材的一道例题的解法作为本节课的导入复习一元二次不等式的解法，教材例2：求不等式-x2+2x-3>0的解集知识讲解（难点突破）通过由简入难的螺旋思维形成过程，设计三道例题例1：已知关于x的不等式x2-x+a>0的解集是R，求a的取值范围。

分析：不等式的解集是R，意思是x取任何实数，都能使不等式成立，因此，二次函数y=x2-x+a的图像就要保证x为任何实数时，都要使y>0，所以，∆=1-4a<0,从而得到a>¼例2：已知关于x的不等式x2-ax+4≥0的解集是R，求a的取值范围分析：同样不等式的解集为R，意思是x取任何实数不等式都成立，因此，二次函数y=x2-ax+4的图像也就要保证x取任何实数都要使y≥0，所以，∆≤0，即：a2-16≤0,从而得到-4≤a≤4例3：已知关于x的不等式2ax2+ax-83<0对一切实数x都成立，求a的取值范围。

分析：不等式对一切实数x都成立，意思是不等式的解集为R，也就是实数x取任何值，不等式都成立，因此二次函数y=2ax2+ax- （a≠0)的图像就要保证x取任何实数都要使y<0，从而得到-3<a<0我们可以发现,题中并没有告诉a≠0，所以需检验a=0的情况，看是否也能保证题意成立。

一元二次不等式含参数的恒成立问题一元二次不等式，听起来有点高深，对吧？这玩意儿就是形如 ( ax^2 + bx + c > 0 ) 的式子，咱们今天就来聊聊这东西是咋回事，尤其是当里面有个参数的时候。

这可不是简单的数学问题，常常让人觉得像是在解谜。

不过别担心，咱们就当是在拆礼物，看看里面藏着什么。

什么叫“恒成立”呢？打个比方，恒成立就像是你家里的冰箱，不管你是夏天还是冬天，打开都是凉的。

就像这个不等式，无论参数怎么变，它的结果总是满足我们的条件。

想象一下，如果你是个做饭的高手，常常需要调整配方，但总能做出好吃的菜，那就是恒成立的感觉了。

可是，问题来了，怎么才能保证这个不等式在参数变动的情况下，依然能“保持冰箱的温度”呢？咱们先说说这个一元二次不等式的基本形态。

它的图像是个抛物线，像个微笑的脸，如果开口向上，那就是快乐的象征。

如果开口向下，那可得小心了，可能是要掉眼泪。

要是我们想要它“始终微笑”，就得确保它的判别式大于零，或者为零，这样才能让它的根要么没有，要么只有一个，不然它可会出现“烦恼”的地方。

说到这里，可能有人问，参数到底是什么鬼？想象一下，这就像是给冰淇淋添加不同的口味。

有时候是巧克力，有时候是草莓，这样你的冰淇淋总是新鲜的。

如果参数能控制不等式的根，那你就得仔细分析了。

比如说，如果 ( a > 0 )，那这条抛物线一定是向上的，对吧？而如果 ( a < 0 )，那就要小心咯，可能会“翻车”。

有个小技巧，咱们可以考虑它的顶点。

顶点的坐标就像是那颗糖果的心，甜得让人开心。

顶点的 ( x ) 坐标是 ( frac{b{2a )，然后代入这个 ( x ) 值，算出 ( y ) 的值，这样就能知道这条抛物线的最高或最低点。

如果这个点的值大于零，那就说明不等式是恒成立的。

这可真是个“万无一失”的法宝！再来聊聊这种不等式的解法。

有时会用到一些不等式性质，就像是教你怎么调味。

比如说，CauchySchwarz 不等式，听起来高大上，其实就是在告诉你，合理搭配就能获得最优结果。

一元二次不等式在给定区间上恒成立问题的解题方法一元二次不等式在给定区间上恒成立问题的解题方法一元二次不等式在给定区间上恒成立问题是高中数学中的一个重要知识点，它涉及到一元二次不等式的求解和区间的概念。

在解决这类问题时，我们需要灵活运用一元二次不等式的性质和求解方法，并结合区间的特性进行分析。

本文将从简单到复杂，由浅入深地探讨一元二次不等式在给定区间上恒成立问题的解题方法，帮助读者更深入地理解这一知识点。

1. 一元二次不等式的基本形式在开始讨论一元二次不等式在给定区间上恒成立问题的解题方法之前，我们先来回顾一下一元二次不等式的基本形式。

一元二次不等式通常可以写成以下形式：ax^2 + bx + c > 0其中，a、b、c为实数且a ≠ 0，x为变量。

在求解一元二次不等式时，我们通常需要先将不等式化为标准形式，再根据不等式的性质和判定条件进行求解。

2. 一元二次不等式的解题思路对于一元二次不等式在给定区间上恒成立问题，我们首先需要确定该区间，并根据不等式的特性进行分析。

在求解过程中，我们需要考虑以下几点：（1）对一元二次不等式进行因式分解，寻找合适的解题方法；（2）利用一元二次不等式的图象和判定条件，确定不等式在给定区间上的变化趋势；（3）结合区间的特性，分析不等式在给定区间上的取值范围；（4）判断一元二次不等式在给定区间上是否恒成立，给出相应的解法。

3. 求解方法举例接下来，我们通过一个具体的例子来演示一元二次不等式在给定区间上恒成立问题的解题方法。

例题：求解不等式x^2 - 4x + 3 > 0在区间(1, 3)上是否恒成立。

解：我们对不等式x^2 - 4x + 3 > 0进行因式分解，得到(x - 1)(x - 3) > 0。

我们可以利用一元二次不等式的图象和判定条件来分析不等式在区间(1, 3)上的变化趋势。

当x属于区间(1, 3)时，(x - 1)和(x - 3)的取值分别为正和负，或者为负和正。