流量系数的计算
- 格式:docx
- 大小:210.17 KB
- 文档页数:18

调节阀流量系数计算公式和选择数据调节阀是工业生产过程中常用的一种流量控制设备,通过改变阀门开度实现流量的调节和控制。
调节阀的流量特性是一个非线性曲线,通常通过流量系数来描述。
流量系数是指,在单位压差下,通过阀门所能流过的液体的流量与阀门的开度之间的关系。
调节阀流量系数计算公式通常包含两个主要参数:阀门的开度和压差。
常见的调节阀流量系数计算公式有两种:流量系数计算公式和修正流量系数计算公式。
1.流量系数计算公式流量系数计算公式通常为以下形式:Cv=Q/√ΔP其中,Cv是调节阀的流量系数,Q是通过调节阀的液体流量,ΔP是压差。
2.修正流量系数计算公式修正流量系数计算公式是对流量系数计算公式进行修正,考虑了液体的特性、密度、黏度等因素,通常为以下形式:Cv=Q/√(SG*ΔP)其中,Cv是修正流量系数,Q是通过调节阀的液体流量,ΔP是压差,SG是液体的相对密度。
选择数据通常包括以下几个方面:1.流量范围根据实际工艺要求和流体特性,确定调节阀的流量范围。
包括最小流量、额定流量和最大流量。
2.压差范围根据实际工艺情况和管路布局,确定调节阀的压差范围。
包括最小压差、额定压差和最大压差。
3.流体特性根据液体的物理、化学特性,选择适合的调节阀型号。
包括液体的温度、压力、粘度、相对密度等参数。
4.调节特性根据实际工艺要求,选择适合的调节阀调节特性。
常见的调节特性有线性、等百分比、快开、快关等。
5.阀门材质根据液体的化学性质,选择适合的阀门材质。
常见的阀门材质有铸钢、不锈钢、铸铁、黄铜等。

流量系数计算公式
水流量系数(C)是用来衡量水流量和流速之间关系的重要指标,其用于求解
水流切线和角度变化、水流波浪乘法和其他相关问题。
水流量系数等于水流量(Q)与水流的波浪速度(v)的比值,它的单位是1/s,表示水流量和速度的比值。
C也可以用于预示水流衰减系数和流量截面积方面的变化。
它的计算公式为C=Q/v,当Q的值和v的值相等时,C的值最大,指出了波浪
最浓密时的流量。
但是要注意,C值并不能完全反映水流本身的实际情况及特性,
只能作为参考。
此外,C值不仅与流量和速度有关,还应考虑水深和环境因素。
水深的变化会
影响整个水流流量,进而影响C值。
环境因素也会受到水流影响,例如温度、浊度和含盐量。
如果温度变化较大,则水流波浪也会发生变化,从而影响C值。
此外,C的值也受基础水流的影响,它会随着季节的变化而变化,因此在使用
C值进行计算时,应注意这种变化。
要获得准确的C值,应进行相关的实验,并综合考虑水深、温度、环境因素等,以达到更准确的C值。
总之,水流量系数C是一个重要概念,它衡量着水流量、流速及其变化之间的
关系,在水文学和水工工程中应用广泛,可以用于计算和预测水流系数和流量截面积的变化。
计算C值时,应注意水深的变化、环境因素的影响以及季节的变化,预示准确的C值,以使计算更精确。

1、流量系数计算公式表示调节阀流量系数的符号有C、Cv、Kv等,它们运算单位不同,定义也有不同。
C-工程单位制(MKS制)的流量系数,在国内长期使用。
其定义为:温度5-40℃的水,在1kgf/cm2(0.1MPa)压降下,1小时内流过调节阀的立方米数。
Cv-英制单位的流量系数,其定义为:温度60℃F (15.6℃)的水,在1b/in2(7kpa)压降下,每分钟流过调节阀的美加仑数。
Kv-国际单位制(SI制)的流量系数,其定义为:温度5-40℃的水,在10Pa(0.1MPa)压降下,1小时流过调节阀的立方米数。
注:C、Cv、Kv之间的关系为Cv=1.17Kv,Kv=1.01C 国内调流量系数将由C系列变为Kv系列。
(1)Kv值计算公式(选自《调节阀口径计算指南》)①不可压缩流体(液体)(表1-1)Kv值计算公式与判不式(液体)低雷诺数修正:流经调节阀流体雷诺数Rev小于104时,其流量系数Kv需要用雷诺数修正系数修正,修正后的流量系数为:在求得雷诺数Rev值后可查曲线图得FR值。
计算调节阀雷诺数Rev公式如下:关于只有一个流路的调节阀,如单座阀、套筒阀,球阀等:关于有五个平行流路调节阀,如双座阀、蝶阀、偏心施转阀等文字符号讲明:P1--阀入口取压点测得的绝对压力,MPa;P2--阀出口取压点测得的绝对压力,MPa;△P--阀入口和出口间的压差,即(P1-P2),MPa;Pv--阀入口温度饱和蒸汽压(绝压),MPa;Pc--热力学临界压力(绝压),MPa;F F--液体临界压力比系数,F R--雷诺数系数,依照ReV值可计算出;F L--液体压力恢复系数QL--液体体积流量,m3/h P L--液体密度,Kg/cm3ν--运动粘度,10-5m2/s W L--液体质量流量,kg/h,②可压缩流体(气体、蒸汽)(表1-2)Kv值计算公式与判不式(气体、蒸气)表1-2文字符号讲明:X-压差与入口绝对压力之比(△P/P1);X T-压差比系数;K-比热比;Qg-体积流量,Nm3/hWg-质量流量,Kg/h; P1-密度(P1,T1条件),Kg/m3T1-入口绝对温度,K;M-分子量;Z-压缩系数;Fg-压力恢复系数(气体);f(X,K)-压差比修正函数; P1-阀入口取压点测得的绝对压力,MPa;PN-标准状态密度(273K,1.0.13×102kPa),Kg/Nm3;③两相流(表1-3)Kv值计算公式(两相流)表1-3。

1 流量系数KV的来历调节阀同孔板一样,是一个局部阻力元件。
前者,由于节流面积可以由阀芯的移动来改变,因此是一个可变的节流元件;后者只不过孔径不能改变而已。
可是,我们把调节阀模拟成孔板节流形式,见图2-1。
对不可压流体,代入伯努利方程为:(1)解出命图2-1 调节阀节流模拟再根据连续方程Q= AV,与上面公式连解可得:(2)这就是调节阀的流量方程,推导中代号及单位为:V1 、V2 ——节流前后速度;V ——平均流速;P1 、P2 ——节流前后压力,100KPa;A ——节流面积,cm;Q ——流量,cm/S;ξ——阻力系数;r ——重度,Kgf/cm;g ——加速度,g = 981cm/s;如果将上述Q、P1、P2 、r采用工程单位,即:Q ——m3/ h;P1 、P2 ——100KPa;r——gf/cm3。
于是公式(2)变为:(3)再令流量Q的系数为Kv,即:Kv =或(4)这就是流量系数Kv的来历。
从流量系数K v的来历及含义中,我们可以推论出:(1)Kv值有两个表达式:Kv = 和(2)用Kv公式可求阀的阻力系数ξ = (5.04A/Kv)×(5.04A/Kv);(3),可见阀阻力越大Kv值越小;(4);所以,口径越大Kv越大。
2 流量系数定义在前面不可压流体的流量方程(3)中,令流量Q的系数为Kv,故Kv 称流量系数;另一方面,从公式(4)中知道:Kv∝Q ,即Kv 的大小反映调节阀流量Q 的大小。
流量系数Kv国内习惯称为流通能力,现新国际已改称为流量系数。
2.1 流量系数定义对不可压流体,Kv是Q、△P的函数。
不同△P、r时Kv值不同。
为反映不同调节阀结构,不同口径流量系数的大小,需要跟调节阀统一一个试验条件,在相同试验条件下,Kv的大小就反映了该调节阀的流量系数的大小。

阀门流量系数与流阻系数的计算公式1、流量系数标准公式:)1式()m ( 2---∆=pQ C ρ Q :体积流量,单位m 3/hρ:介质相对水的密度,单位为1△p :静压力损失,单位bar2、流量系数计算用公式: )2(式)m ( 1000002水---∆⨯⨯=p QC ρρ Q :体积流量,单位m 3/hρ:介质密度,单位kg/m3 ρ水:水的密度,单位kg/m 3△p :静压力损失,单位Pa3、流阻系数:)3(式(无量纲) 22---∆=v pK ρ△p :静压力损失,单位Paρ:介质密度,单位kg/m3 v :流体速度,单位m/s4、水头损失:)4(式---(m) g ph ρ∆=△p :静压力损失,Paρ:介质密度,kg/m3 g :重力加速度,g=9.80665m/s 25、阀门流量系数和流阻系数的关系式:)5(式---360002⨯=K A CC :流量系数A :阀门截面积,单位m 2K :流阻系数6、流阻系数与当量长度换算公式)6(式---DL K ⨯=λ K :流阻系数λ:沿程阻力系数L :阀门当量长度,单位mD :阀门直径,单位m7、沿程阻力系数 )7(式---22vL D h g ⨯⨯⨯⨯=λ λ:沿程阻力系数,无量纲g :重力加速度,g=9.80665m/s 2h :水头损失,单位mD :阀门直径,单位mL :阀门当量长度,单位mv :流体速度,单位m/s8、功率损失)8(式---106.36⨯⨯⨯⨯=Qg h P ρP :功率损失,单位KWh :水头损失,单位mρ:介质密度,kg/m3 g :重力加速度,g=9.80665m/s2 Q :体积流量,单位m 3/h欢迎您的下载,资料仅供参考!致力为企业和个人提供合同协议,策划案计划书,学习课件等等打造全网一站式需求。

喷头流量计算公式
喷头流量计算公式是根据液体或气体的流量、压力、密度、粘度等参数来计算的。
下面是常见的几种喷头流量计算公式:
1. 等压降法公式:
Q=K×C×A×√(2ΔP/ρ)
其中,Q为流量,K为喷嘴系数,C为修正系数,A为喷嘴截面积,ΔP为压降,ρ为介质密度。
2. 流量系数法公式:
Q=Cv×ΔP×G
其中,Q为流量,Cv为流量系数,ΔP为压降,G为介质质量流量。
3. 标准流量法公式:
Q=K×C×A
其中,Q为流量,K为喷嘴系数,C为修正系数,A为喷嘴截面积。
需要注意的是,不同的喷头类型和介质会有不同的喷嘴系数和修正系数,需要根据实际情况进行选择和计算。
同时,喷头流量计算还需要考虑介质的温度、压力、粘度等因素对流量的影响,以确保计算结果的准确性和可靠性。

水流量计算公式1.曼宁公式曼宁公式是最常用的水流量计算公式,适用于一般自由流条件下的河流和渠道。
公式的表达式为:Q=k×A×R^(2/3)×S^(1/2)其中Q为水流量,单位为立方米每秒;k为曼宁系数,为经验常数,对于河流通常取0.03-0.4,对于渠道通常取0.025-0.035;A为流域横截面积,单位为平方米;R为湿周与流域横截面积的比值,即湿周/流域横截面积;S为水流坡降,单位为米每米。
2.韦斯布鲁克公式韦斯布鲁克公式适用于小径流条件下的强流,公式的表达式为:Q=k'×A×(h-0.1)^(1/2)×(h+0.1)^(-1/2)其中Q为水流量,单位为立方米每秒;k'为经验系数,对于不同类型的地表可以取不同的值,一般为0.24-1.28;A为流域横截面积,单位为平方米;h为水深,单位为米。
3.纳瓦宁-斯托克斯公式纳瓦宁-斯托克斯公式适用于流速较慢的条件下,公式的表达式为:Q=(1.49/n)×A×R^(2/3)×S^(1/2)其中Q为水流量,单位为立方米每秒;n为克伦肖系数,取决于河床或渠道的粗糙程度,对于河流一般取0.02-0.05,对于渠道一般取0.03-0.08;A为流域横截面积,单位为平方米;R为湿周与流域横截面积的比值,即湿周/流域横截面积;S为水流坡降,单位为米每米。
需要注意的是,以上的计算公式仅为常见的一些公式,实际计算中可能会根据具体情况进行调整或使用其他的计算公式。
掌握合适的公式和准确的参数对于水流量的计算非常重要,可以通过实地观察和测量来获取所需的参数值。

关于流量计算方法一. 流量计算公式近几年CSD 使用了孔板,弯管,阿牛巴,威力巴等流量测量元件。
现将公式整理如下。
1. 孔板流量计算式:4m q d π=(1)q v =q m /ρ1 式中 q m ——质量流量,kg/s ; q v ——体积流量,m 3/s ; C ——流出系数;ε——可膨胀性系数; β——直径比,β=d/D ;d ——工作条件下节流件的孔径,m ; D ——工作条件下上游管道内径,m ; △p ——差压,Pa ;ρ1——上游流体密度,kg/m 3。
由上式可见,流量为C 、ε、d 、ρ、△p 、β(D )6个参数的函数,此6个参数可分为实测量(d 、ρ、△p 、β(D ))和统计量(C ,ε)两类。
实测量有的在制造安装时测定,如d 和β(D ),有的在仪表运行时测定,如△p 和ρ1统计量则是无法实测的量(指按标准文件制造安装,不经校准使用),在现场使用时由标准文件确定的C 及ε值与实际值是否符合,是由设计、制造、安装及使用一系列因素决定的,只有完全遵循标准文件(如GB/T2624-93)的规定,其实际值才会与标准值符合。
但是,一般现场是难以做到的,因此,检查偏离标准就成为现场使用的必要工作。
应该指出,与标准条件的偏离,有的可定量估算(可进行修正),有的只能定性估计(估计不确定的幅度与方向)。
在实际应用时,有时并非仅一个条件偏离,如果多个条件同时偏离,并没有很多试验根据,因此遇到多种条件同时偏离时应慎重对待。
2. 阿牛巴流量计算式:211vb vkp RD a M Y PB TB TF PV b g q N F F S F F F F F Z F D =⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅ (2)vb q ——体积流量 (Nm 3/h )vkp N ——单位换算系数 RD F ——雷诺数修正系数 a F ——材料热膨胀系数 M S (k )——流量系数 Y F ——气体膨胀系数PB F ——标准压力的校正系数 TB F ——标准温度的校正系数 TF F ——流动温度的校正系数 PV F ——超压缩因子b Z ——在标准温度和压力下,气体的压缩系数 g F ——气体的比重系数D ——管道内径(mm ) f p ——工体压力(kpa )p ∆——差压(kpa )前11项为测量系数,我们用C 表示(C 值由生产商提供) q vb =CD 2fPP ∆ (2)3. 威力巴流量计算式:()()[]5.0015.273/1000t p D C Q p +⨯⨯⋅= (3)注 公式(3)带压力和温度自动补偿的流量计算公式。

调节阀流量系数计算公式及数据选择调节阀的流量系数(Cv)是指在给定的压差下,调节阀能够通过的流体的体积流量。
它是衡量调节阀性能的重要参数之一、通常情况下,调节阀流量系数的计算公式为:Cv = Q / sqrt(ΔP)其中,Cv为流量系数,Q为流量,ΔP为压差。
在实际应用中,选择合适的流量系数对于调节阀的性能至关重要。
以下是一些常用的数据选择方法和公式。
1.流量系数计算公式:根据调节阀的使用场景和流体介质的特性,可以选择不同的流量系数计算公式。
常见的计算公式包括:- 标准流量系数公式:Cv = Q / sqrt(ΔP)- 输入流量系数公式:Cv = Q / sqrt(△h * g)- 出口流量系数公式:Cv = Q / sqrt(△z)2.流量系数选择方法:为了选择合适的流量系数,需要考虑以下因素:-流量需求:首先需要确定所需的流量范围,包括最小和最大流量。
-压差需求:根据流量要求和管道系统的特性,确定所需的压差范围。
-流体介质:不同的流体介质对调节阀的流量系数有不同的要求,例如气体和液体,不同的密度和黏度对流量系数具有影响。
-系统要求:根据系统的性能要求,选择合适的流量系数。
3.流量系数常用值:根据实际经验和行业标准,一些常用的流量系数值如下:-常规控制阀:Cv=0.01~10-高流量控制阀:Cv=10~50-小流量控制阀:Cv<0.01-紧急切断阀:Cv>504.其他因素的考虑:流量系数的选择还需要考虑其他因素,如调节阀的类型、阀座直径和开启程度等。
不同类型的调节阀可能需要不同的流量系数。
综上所述,在选择调节阀的流量系数时,需要根据流量需求、压差需求、流体介质和系统要求等因素进行评估。
在实际应用中,可以根据常见的流量系数计算公式和经验值来进行选择,并结合实验数据进行调整和优化。

压力与流量换算公式
压力与流量的换算公式可以根据流体的类型(液体或气体)以及具体情境有所不同。
对于液体来说,由于其被认为是不可压缩的,压力对其流速和管径没有影响,但会影响其密度。
一个常用的计算公式是:Q=CA√(ΔP/ρ),其中Q是流量,C是流量系数,A是管道截面积,ΔP是管道两端的压力差,ρ是流体密度。
对于气体来说,因其可压缩,压力对气体的密度和流速有较大影响,此时可以用气态方程式去换算P×V=RT。
在理想情况下,也可以利用公式Q = CA√(ΔP/ρ)进行计算,但需要注意的是这里的密度需要用气体的特定状态方程来计算。
此外,如果已知管道直径D、管道内压力P以及管道内流体的平均速度V,可以通过公式Q = (∏D^2)/ 4•v计算出流量。
然而,即便知道了这些参数,也不能精确地求出管道中流体的流速和流量。
总的来说,压力与流量之间的关系受多种因素影响,包括流体类型、密度、温度等。
实际应用时应根据具体情况选择适当的计算公式。
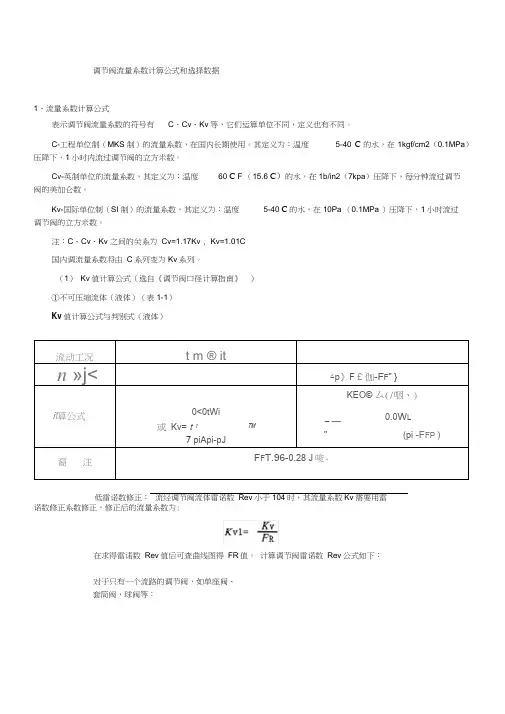
调节阀流量系数计算公式和选择数据1、流量系数计算公式表示调节阀流量系数的符号有C、Cv、Kv等,它们运算单位不同,定义也有不同。
C-工程单位制(MKS 制)的流量系数,在国内长期使用。
其定义为:温度5-40 C的水,在1kgf/cm2(0.1MPa)压降下,1小时内流过调节阀的立方米数。
Cv-英制单位的流量系数,其定义为:温度60 C F (15.6 C)的水,在1b/in2(7kpa)压降下,每分钟流过调节阀的美加仑数。
Kv-国际单位制(SI 制)的流量系数,其定义为:温度5-40 C的水,在10Pa (0.1MPa )压降下,1小时流过调节阀的立方米数。
注:C、Cv、Kv 之间的关系为Cv=1.17Kv , Kv=1.01C国内调流量系数将由C系列变为Kv系列。
(1)Kv值计算公式(选自《调节阀口径计算指南》)①不可压缩流体(液体)(表1-1)Kv值计算公式与判别式(液体)低雷诺数修正:流经调节阀流体雷诺数Rev小于104时,其流量系数Kv需要用雷诺数修正系数修正,修正后的流量系数为:在求得雷诺数Rev值后可查曲线图得FR值。
计算调节阀雷诺数Rev公式如下:对于只有一个流路的调节阀,如单座阀、套筒阀,球阀等:文字符号说明:对于有五个平行流路调节阀,如双座阀、 蝶阀、偏心施转阀等4949O (2L"—严兰二pv/pc坨7 丨『io m io :|$ io'RevP1--阀入口取压点测得的绝对压力, MPa ; P2--阀出口取压点测得的绝对压力,MPa ;△ P--阀入口和出口间的压差,即( P1-P2), MPa ; Pv--阀入口温度饱和蒸汽压(绝压) ,MPa ; Pc--热力学临界压力(绝压),MPa ; F F --液体临界压力比 系数,F R --雷诺数系数,根据 ReV 值可计算出;3QL--液体体积流量,m/h V -运动粘度,10-5m 2/s②可压缩流体(气体、蒸汽) (表1-2)Kv 值计算公式与判别式(气体、蒸气)PcF L --液体压力恢复系数3P L --液体密度,Kg/cm W L --液体质量流量,kg/h ,表1-2尸射局艸关弟曲线1.0吓幵 1 ]卩「「W f'文字符号说明:X-压差与入口绝对压力之比(△ P/P1);X T-压差比系数;K-比热比; 3Qg-体积流量,Nm /hP1-密度(P1, T1条件):Wg-质量流量,Kg/h ;Kg/m3T1-入口绝对温度,K ;M-分子量;Z-压缩系数;Fg-压力恢复系数(气体)P1-阀入口取压点测得的绝f(X,K)-压差比修正函数;对压力,MPa ;PN-标准状态密度(273K2 31.0.13 10 kPa) , Kg/Nm ;③两相流(表1-3)Kv值计算公式(两相流)表1-3注:本计鄆公式仅适用干气(汽).液均匀谁合栩流休.并冲单相谎体均未达到阻塞漁条件. 文字符号说明: pi-阀人口取压点测得的绝对压力. 以--阀岀II 取圧点、测得的绝对压力,--气体、蒸汽质kg/h ; pe--两相锻育效密度,®'nPPL ■气体、裁汽密tt (pi.ri 条件),kg/m$; px-气体、英汽标准状态密度(273K t 1.0l3Xl02kpah kg/Nm>; pL --液体密度,kjj/m* Fg--气体压力恢父系数;彳X,心一压差比修正系数.Fgftt 与於人卩计算式同町体i|•算式相同; T L■人口绝对温度.K : M —分予诫:Z-■压缩系数; F F —ffi 体临界压力比系敌.<2)cMiin 公式(选自«调节阀口径计算设计規定》CD5OA12-84) ①液体(表27) C 值计畀公式与判别式Oft 体)MPa: MPo;WL —液体质电流札kg/h :相密度条件).汲2-几一压力恢貝系数,怙哥调节阀压办恢复能力的系数;小一阀人□温度下液体介质的饱和蕉汽圧力(绝对压力)• kgf/cm 2rfllOOkPa;X ・・压基比,阀压降与阀人口压力之比.即*= 笊 尺■■液体临界压力比系数;“卅-■临界压差比,产土BQ 塞流时之X ; • ‘ 用-・比热比系数,空气介质为,1F 空气介质为△K--气沐绝热t&Sc ;Y-购胀系数,考虑气体(燕汽)密度在阀内发生变化的校正系故':14O L —液体体积aflltmVh :0•■气休休积流就■ E/h :(际准伏态-272K.1 OlhlO'PQ%—液体质址流如kg/h 必一蒸气质融流址kg/h ;Pi —液体密度仙6条件下).g/cm 5 屮一气体密度 kg/Nm s (标准状态一273K. 1.013X10呼3)pr ■慕汕密度(puT 僚件下Xkg/cm >门一阀入I 」处流体温取K (开尔文) Z--气体压缩系数■ : M —分子虽G —气体相对密度(空气为1).O )山武・雷尼威尔公司Cv 值计住公式(选门昊忠仪表厂c 产甜技术参数>)③气体•彼汽(丧2-Ctfi 计萍公式与判别式(气体.蒸汽)瀝动1:«别式气体计算公式非阻塞渡文字符号说明:pi —阀人口处流体绝对压力.kgf/cm?或10OkPa; 0 —阀出li 处流体绝对压力.kgr/cm^或lOOkPa; △p—阀两端任爰,0 hqi.".或LOOkPa; X< F K X T或匚■环①液体(表37)(Cv 工1.170Cv值计算公式与判别式(液体)表37文〒符号说明:Q一液体的股大流量.ni5/h; 0・*燉尢漩値时阀逬口压力,kgf/cm2ab$;p一-呆大流悵时阀出I」压力,kgf/em^bs; △/>--阀两瑞压并■ 3¥)-卩釘kfg/cm? G—液体的相廿密度(水•";He—计算流昴內的允许圧倉kfg/cnf刃一进口温度下液体的饱和蕪汽乐力.kgf/cm^abs; △r—iJ口压力下液体饱和滔烦与进M温度之差、匚⑦气体(丧3-2)文字符号说明:Q—标准状态(760mmHg,15g下气体的最大流ft. mVh;pi—fitA流尿时阀逬口压力.kgf/cm2abs; p2 —M大流.駅吋阀出口压力,kgf/cm2abs;△p—阀两端压差,Ap=pi-P2, kgf/cm2; G—气体的相对密度C空气巧);r-诡体温度,'C.③蒸汽(衣3・3)6值计算公女与判別式(蒸汽)表3-3(4)Fisher 公可CV 值计耳公式(选0FISHER 公诃《控制阀『砒 那:版}①液休(农4-1) 6值计耳公式与判别兀(液体)义字符号说明: W"水蒸汽、H 它張汽的故大渡St S ;P- — M 大熬開时的阀出I 」压力,kgC^m 2abs;K —K=E0.0013x 过热泪度,t ) w —岀11压力卜集汽比容.cmVg;P 一最大流址时的阀进L 】压力.kgf/cm 2abs;△p --泗两站压差,△p=i P 】-g kgf/cm 2; Vi —iff f ]压力卜蒸汽比务cm 3/£;C 仁Cg/Cv (C1由制造厂提供); Cg--气体流理系数; Cv--液体流量系数; △ P--压差,Psi ;P1--阀入,Psia ;G--气体相对密度(空气 =1.0);3T--气体入口的绝对温度,°R (兰金氏度);d1--人口蒸汽的密度,Ib/ft ;3Qscth--气体流量,scth (标准英尺寸 /小时);Qib/hr--蒸汽流量,lb/hr 。
各种流量计计算公式流量计的计算公式取决于所使用的流量计类型。
下面是一些常见的流量计类型及其计算公式:1.体积流量计:体积流量计用于测量液体或气体通过管道的体积流量。
其中最常见的类型是正置式容积流量计和回转翅片流量计。
-正置式容积流量计:体积流量(Q)=容积(V)/时间(t)-回转翅片流量计:体积流量(Q)=翅片个数(N)x翅片移动距离(D)x翅片容积(V)/时间(t)2.质量流量计:质量流量计用于测量液体或气体通过管道的质量流量。
其中最常见的类型是热式质量流量计和当量质量流量计。
-热式质量流量计:质量流量(Q)=功率(P)/热敏电阻的温差(ΔT)x热常数(K)-当量质量流量计:质量流量(Q)=压力差(ΔP)x流量系数(Cv)3.示值流量计:示值流量计用于以读数的形式显示液体或气体通过管道的流量。
其中最常见的类型是涡轮流量计和涡街流量计。
-涡轮流量计:体积流量(Q)=转速(N)x每转体积(V)x流量系数(K)-涡街流量计:体积流量(Q)=振动频率(f)x断面积(A)x英式系数(K)4.开孔流量计:开孔流量计是通过在管道上开设孔口进行测量的。
-压差式开孔流量计:流量(Q)= K x C x sqrt(2gH)在公式中,Q代表流量,V代表体积,t代表时间,N代表翅片个数或转速,D代表翅片移动距离,V代表翅片容积,P代表功率,ΔT代表热敏电阻的温差,K代表热常数,ΔP代表压力差,Cv代表流量系数,f代表振动频率,A代表断面积,K代表英式系数,K代表涡轮流量计的流量系数,C代表孔口系数,g代表重力加速度,H代表压差。
注意:每个流量计类型的计算公式可能有些变化,取决于具体的流量计设计和制造商。
因此,在实际应用中,应查看特定流量计的技术手册和使用手册,以获得准确的计算方法。
罐体流量计算公式
罐体流量的计算公式可以根据具体情况有所不同。
以下是两种常见的计算公式:
1.对于液体流量,可以使用以下公式:
流量= 流速× 管道截面积
其中,流速是液体在管道中的速度,管道截面积可以通过管道半径或直径计算得出。
对于圆形管道,管道截面积= π × (管道半径^2) 或π × (管道直径^2) ÷ 4。
2.对于气体流量,可以使用以下公式:
流量= 流量系数× 管道截面积× (压力差÷ 温度差) × 大气压力
其中,流量系数是一个无量纲数,与气体的流动状态和管道形状有关;管道截面积与液体流量计算中相同;压力差是管道进口和出口之间的压力差;温度差是管道进口和出口之间的温度差;大气压力是管道所在处的环境压力。
需要注意的是,以上公式仅为一般性的计算方法,实际应用中还需要考虑其他因素,如管道长度、弯头、阀门等的影响。
此外,对于不同类型的罐体(如软化罐、过滤罐等),其流量计算公式也可能有所不同。
因此,在实际应用中,需要根据具体情况选择合适的计算公式,并结合实际情况进行修正和调整。
流量Q=[( n /4)d A2 V(1+ 入L/d+ Z )] V(2gH)
式中:Q——流量,(mA3/s); n ------- 周率;d ——管内径(m),
L 管道长度(m); g 重力加速度(m/sA2); H 管道两端水头差(m)入管道的沿程阻力系数(无单位);Z --------------------------------------- 誉道
的局部阻力系数(无单位,有多个的要累加)。
使中部的截面积变为原来的一半,其他条件都不变,这就相当于增加
了一个局部阻力系数Z,流量变为:Q =[(n /4)dA2 V(1+入L/d+ Z +Z')]V (2gH>流量比原来小了。
流量减小的程度要看增加的Z与原来沿程阻力和局部阻力的相对大小。
当管很长(L很大),管径很小,原来管道局部阻力很大时,流量变化就小。
相反当管很短(L很小),管
径很大,原来管道局部阻力很小时,流量变化就大。
定量变化必须通过定量计算确定。
调节阀流量系数CV值的来历与计算方法液流:在此:Q =液流量(每分钟加仑数)△ P =通过的压降(psi)S =介质的具体重这个方程式适用于湍流和粘性接近于水的液体。
(Cv是指介质温度为60 o F的水,通过阀门产生1.0 psi压降时的每分钟流量。
)(这时水的具体重力是1。
)1915 年美国的FISHER GOVERNED司按设计条件积累了图表,按图表先定口径。
由于用这个方法调节阀的费用减少了,电动调节阀的寿命延长了,因此当时得到了好评。
但是按选定的口径比现在计算出来的还大些。
后来按选定法对液体,气体,蒸汽及各种形式的气动调节阀进行了进一步的算法研究。
直到1930年美国的FOXBORO公司ROLPHRJOKWEL和DR.@.E.MASON对以下的V 型(等百分比)球阀,最初使用CV值,并发表了CV计算公式。
1944年美国的MASON —NELLANREGULATO公司把ROKWELL和MAXON合并为MASON- NEILAN,发表了@ V 计算公式。
1945 年美国的SONALD EKMAN公司发表了和MASON—NELLAN差不多的公式,但对流通面积和流量系数相对关系展开研究工作。
1962 年美国的F@l (FLUID @ONTROLS INSTITUTE)发表了FCI 58-2 流量测定方法,并发表了调节阀口径计算。
迄今还在使用的CV计算式,但同FCI 62-1。
1960年西德的VDI/VDE也发表了KV计算式,但同FCI62-1 相同,仅仅是单位改为公制。
1966~1969年日本机械学会关于调节阀基础调查分会对定义瘩的口径计算,规格书,使用方法进行调查研究。
但到现在还未结束。
1977年美国的ISA (INSTRUMENT SOCIETY OF AMERICA)发表了标准S39。
1 “关于压缩流体的计算”公式。
1977~1978美国的ANSI/ISA 标准,S75.01 于1979年5月15日发表了NOW0046-79, 为工程服务的报告。
(完整版)流量系数的计算1 流量系数KV的来历调节阀同孔板⼀样,是⼀个局部阻⼒元件。
前者,由于节流⾯积可以由阀芯的移动来改变,因此是⼀个可变的节流元件;后者只不过孔径不能改变⽽已。
可是,我们把调节阀模拟成孔板节流形式,见图2-1。
对不可压流体,代⼊伯努利⽅程为:(1)解出命图2-1 调节阀节流模拟再根据连续⽅程Q= AV,与上⾯公式连解可得:(2)这就是调节阀的流量⽅程,推导中代号及单位为:V1 、V2 ——节流前后速度;V ——平均流速;P1 、P2 ——节流前后压⼒,100KPa;A ——节流⾯积,cm;Q ——流量,cm/S;ξ——阻⼒系数;r ——重度,Kgf/cm;g ——加速度,g = 981cm/s;如果将上述Q、P1、P2 、r采⽤⼯程单位,即:Q ——m3/ h;P1 、P2 ——100KPa;r——gf/cm3。
于是公式(2)变为:(3)再令流量Q的系数为Kv,即:Kv =或(4)这就是流量系数Kv的来历。
从流量系数Kv的来历及含义中,我们可以推论出:(1)Kv值有两个表达式:Kv = 和(2)⽤Kv公式可求阀的阻⼒系数ξ = (5.04A/Kv)×(5.04A/Kv);(3),可见阀阻⼒越⼤Kv值越⼩;(4);所以,⼝径越⼤Kv越⼤。
2 流量系数定义在前⾯不可压流体的流量⽅程(3)中,令流量Q的系数为Kv,故Kv 称流量系数;另⼀⽅⾯,从公式(4)中知道:Kv∝Q ,即Kv 的⼤⼩反映调节阀流量Q 的⼤⼩。
流量系数Kv国内习惯称为流通能⼒,现新国际已改称为流量系数。
2.1 流量系数定义对不可压流体,Kv是Q、△P的函数。
不同△P、r时Kv值不同。
为反映不同调节阀结构,不同⼝径流量系数的⼤⼩,需要跟调节阀统⼀⼀个试验条件,在相同试验条件下,Kv的⼤⼩就反映了该调节阀的流量系数的⼤⼩。
于是调节阀流量系数Kv的定义为:当调节阀全开,阀两端压差△P为100KPa,流体重度r为lgf/cm(即常温⽔)时,每⼩时流经调节阀的流量数(因为此时),以m/h 或t/h计。
管道的流量系数
管道的流量系数是指单位时间内流体流过管道横截面的体积与管道横截面积之比。
它反映了管道中流体的流动状态和流量的大小,是流体力学中一个重要的参数。
流量系数的计算公式为:流量系数 = 流速 / 管道横截面积。
在实际应用中,流量系数被广泛用于液体、气体等流体的流动计算和管道设计中。
它不仅可以用来评估流体在管道中的流动情况,还可以用来预测流量、压力损失等重要参数。
此外,不同的流动状态对应着不同的流量系数。
例如,当流量系数接近于0时,表示流体的流速很小,流动较为缓慢;当流量系数接近于1时,表示流体的流速很大,流动较为快速。
因此,流量系数是描述流体在管道中流动特性的重要参数,通过流速和管道横截面积的计算,可以得到流量系数的数值,进而评估流体的流动状态、预测流量和压力损失等。
1流量系数KV 的来历调节阀同孔板一样,是一个局部阻力元件。
前者,由于节流面积可以由阀芯的 移动来改变,因此是一个可变的节流元件;后者只不过孔径不能改变而已。
可是,我们 把调节阀模拟成孔板节流形式,见图2- 1。
对不可压流体,代入伯努利方程为:再根据连续方程 Q = AV ,与上面公式连解可得:这就是调节阀的流量方程,推导中代号及单位为:V1、V2 ――节流前后速度; V ――平均流速;P1、P2 ――节流前后压力,lOOKPa A ------ 节流面积,cm ; Q ――流量,cm / S; E ――阻力系数;r ------- 重度,Kgf / cm ; g------- 加速度,g = 981cm/s;3如果将上述 Q 、P1、P2、r 采用工程单位,即:Q ――m/ h ; P1、P2 —— lOOKPa ; r------- g f/cm 3。
于是公式(2)变为:c A L / lOOrLP 3600,心e __J 2.931x —.-^ = 5.04这就是流量系数Kv 的来历。
2gr 2g(1)2严解出r命(2)再令流量 Q 的系数为Kv ,即:Kv =(3)图2-1调节阀节流模拟从流量系数Kv 的来历及含义中,我们可以推论出:(2)用Kv 公式可求阀的阻力系数 E = (5.04A/KV )X( 5.04A/KV );,可见阀阻力越大 Kv 值越小;4;所以,口径越大Kv 越大2流量系数定义在前面不可压流体的流量方程 (3)中,令流量Q 的系数流量系数;另一方面,从公式(4)中知道:Kv *Q ,即Kv 的大小反映调节阀流量 Q 的大小。
流量系数 Kv 国内习惯称为流通能力,现新国际已改称为流量系数。
2.1流量系数定义对不可压流体,Kv 是Q >△ P 的函数。
不同△ P 、r 时Kv 值不同。
为反映不同调节阀 结构,不同口径流量系数的大小,需要跟调节阀统一一个试验条件,在相同试验条件下,Kv 的大小就反映了该调节阀的流量系数的大小。
于是调节阀流量系数 Kv 的定义为:当调节阀全开,阀两端压差△ P 为lOOKPa ,流体重度r 为lgf/cm (即常温水)时,每小时 流经调节阀的流量数(因为此时),以 m/h 或t /h 计。
例如:有一台Kv = 50的调节阀,则表示当阀两端压差为 lOOKPa 时,每小时的水量是 50m/h oKv = 0.1 ,阀两端压差为167—(— 83)= 2.50,气体重度约为1 .0X E (— 6),每小时流量大约为 158/h o= 43L/s=4.3/0.1sKv = 0.1,阀两端压差为1.6 7,气体重度约为12.2 Kv 与Cv 值的换算国外,流量系数常以 Cv 表示,其定义的条件与国内不同。
Cv 的定义为:当调 节阀全开,阀两端压差△ P 为1磅/英寸2,介质为60°F 清水时每分钟流经调节 阀的流量数,以加仑/分计。
由于Kv 与Cv 定义不同,试验所测得的数值不同,它们之间的换算关系:Cv =1.167Kv (5)(1) Kv 值有两个表达式:Kv =和为Kv ,故Kv 称2.3推论从定义中我们可以明确在应用中需要注意的两个问题:(1)流量系数Kv不完全表示为阀的流量,唯一在当介质为常温水,压差为lOOKPa时,Kv才为流量Q;同样Kv值下,「、△ P不同,通过阀的流量不同(2)Kv是流量系数,故没单位。
但是许多资料、说明书都错误地带上单位,值得改正。
3原流量系数Kv计算公式3.1不可压流体的流量系数公式公式(4)是以不可压流体来推导的,此公式即为不可压流体的流量系数公式。
3.2可压流体的流量系数公式可压流体由于考虑的角度不同,有不同的计算公式,主要采用的是压缩系数法和平均重度法两种。
压缩系数法是在不可压流体流量系数公式(4)基础上乘上一个压缩系数&而来,即卩并将r换算成标准状态(O C、760mmH)的气体重度:于是得出式中,& ――压缩系数,由试验确定为& = 1 —0.46 △ P/ P1,在再随AP的为:态),饱和状态时,△ P/ P1 = 0.5,此时流量不增加而增加,即产生了阻塞流(阻塞流的定义流体通过调节阀时,所达到的最大极限流量状见图2—2。
& = 1—0.46 X 0.5 = 0.76 ;t ――介质温度,C;N ——用于蒸气计算时,计算公式略有不同,见表23.3平均重度法平均重度法公式推导要复杂得多。
在推导中将调节阀相当长度为L、断面为A 的管道来代替,并假定介质为理想流体,当介质稳定地流过管道时,采用可压缩流体流乩(RS。
量方程式: (2-11 )= ”27 込式中,Lf ――摩擦功;g ――加速度。
在上式基础上,再引入三个辅助方程: 理想气体多变热力过程的变化规律方程由上述4个方程通过一系列纯数学推导(略),得到其流量方程为:为简化公式,把实际流动简化为等温度变化来处理,故取m ^ 1。
同时,把物理常数代入,即可整理心他I 卞(273+0 一 380 也P (召+ £)P1V1m = 常数状态方程P1V1 = RT1 连续方程VA / v =常数比容;m — -多变指数;R-- 气体常数;T -- -绝对温度;V —- 流速。
以上三式中:v得:⑺当△ P ^P1 > 0.5时,流量饱和,故以△ P = 0.5P1代入上式得:Kv =同样,蒸气的计算公式也是在公式( 综合上述,把原各种介质的 表2-1 流体原调节阀流量系数 压差条件(8)7)、( 8)基础上推导出来的。
Kv 值计算公式汇总在表 2- 1中。
Kv 值计算公式压缩系数法计算公式的二瞠或灼二G 重量流量(t / h )平均重度法 一般气体Kv _0^_用⑵川)■ 380 血丽 + £)马 <0.5^般气体G-—重量流量r=i+o,oi3x^4 KV 值计算新公式目前,调节阀计算技术国外发展很快, 就KV 值计算公式而言,早在20世纪70 年代初ISA(国际标准协会标准)就规定了新的计算公式,国际电工委员会IEC 也正在制定常用介质的计算公式。
下面介绍一种在平均重度法公式基础上加以修正的新公式。
4.1原公式推导中存在的问题在前节的KV 值计算公式推导中,我们可以看出原公式推导中存在如下问题:(1) 把调节阀模拟为简单形式来推导后,未考虑与不同阀结构实际流动之间 的修正问题。
(2) 在饱和状态下,阻塞流动(即流量不再随压差的增加)的差压条件为AP/P=0.5,同样未考虑不同阀结构对该临界点的影响问题。
(3) 未考虑低雷诺数和安装条件的影响。
4.2压力恢复系数FL由P1在原公式的推导中,认为调节阀节流处由P1直接下降到P2,见图2-3中虚线所示。
但实际上,压力变化曲线如图2-3中实线所示,存在差压力恢复的情况。
不同结构的阀,压力恢复的情况不同。
阻力越小的阀,恢复越厉害,越偏离原推导公式 的压力曲线,原公式计算的结果与实际误差越大。
因此,引入一个表示阀压力恢复程度的系数FL 来对原公式进行修正。
FL 称为压力恢复系数(Pressure reecvery factor ), 其表达式为:'■(9)式中,、表示产生闪蒸时的缩流处压差和阀前后压差。
关键是FL 的试验问题。
用透明阀体试验,将会发现当节流处产生闪蒸,即在 节流处产生气泡群时,Q 就基本上不随着AP的增加而增加。
这个试验说明:产生闪蒸 的临界压差就是产生阻塞流的临界压差,故 FL 又称临界流量系数(Critical flowfactor ),因此FL 既可表示不同阀结构造成的压力恢复,以修正不同阀结构造成的流Gs比=J____31.6V=330 R—H —蒸八、、 气图2-3阀内的压力恢复量系数计算误差,又可用于对正常流动,阻塞流动的差别,即FL 定义公式(9)中的压差厶Pc 就是该试验阀产生阻塞流动的临界压差。
这样,当△ P vA Pc 时为正常流动,当△ P >^ Pc 时为阻塞流动。
从(9)公式中我们即可解出液体介质的△ Pc 为:△ Pc = FL (P1-Pv )(10)由试验确定的各类阀的 FL 值见表2- 3。
4.3梅索尼兰公司的公式一一FL 修正法1)对流体计算公式的修正当厶P vA PC 时,为正常流动,仍采用原公式(4);当厶P >^P c 时,因AP 增加Q 基本不增加,故以△ Pc 值而不是AP 值代入公式(4)计算即可。
当△ Pv >0.5P1 时,意味差有较大的闪蒸,此时△ Pc 还应修正,由试验获得: 毗幷-(0 96』28国)氏_ 皿」 (11)式中:Pc 表示液体热力学临界点压力,见表2— 4。
2)对气体计算公式的修正原产生阻塞流的临界差压条件是△ Pc = 0.5P1,即固定在△ P / P1 = 0.5处,这 和实际情况出入较大。
实际上△ Pc 仍与FL 有关,由试验得临界压差条件为:△ Pc = 0.5 FL P1 (12)利用FL 概念推得的新公式有好几种,但以在原平均重度法公式基础上修正的 新公式最简单、方便,即平均重度修正法,它只需将原阻塞流动下的计算公式除上FL即可。
若要更精确些,则再除上一个系数( y — 0.14y ),其中 匚 。
蒸气计算公式的修正同上。
为了便于比较、应用,将采用FL 修正的新公式和原公式汇总于表2— 2中。
归纳起来,有两个不同:一是流动状态差别式不同;二是在阻塞流动的 情况下计算公式不同。
引入了3个新的参数:FL 、PC ( y — 0.148y )般流 动帆当-7 ' 1 时城誌(R-E )当斤八时流动 介质状态 原计算公式流动状态判别计算式新计算公式流动状态判断计算式阻 塞 流 动同原计算式一般流动△ P/P1 < 0.5|f^.2?3+O耳气体阻塞—>0§K -乞kP流动一 5同原计算式丄原计算式乘I或1冯U14沪)—H—蒸八、、一般流动饱和—H—蒸八、、气阻塞流动同气体同气体同气体心=鱼/13访同气体气一般流动过执八、、同气体G3 L+0.0013煉氏阳+时)同气体—H—蒸八、、气阻塞流动同气体p G5 1+0.0012^旳■------ -- -----------------13 $ £同气体同原计算式丄原计算式乘1或1恥-014诵同原计算式丄原计算式乘1或1兀3-014沪)Q:液体流量m /h表中代号及单位QN气体流量Nm^/hGS蒸气流量kgf/hr :液体重度g/cmrn :气体重度kg/NmP1:阀前压力lOOKPaP2:阀后压力lOOKPa探Pv :饱和蒸气压lOOKPaPc:临界点压力(见表2-4)FL:压力恢复系数(见表2-3 )t :摄氏温度°Ctsh :过热温度C△ Pc:临界压差100KPa(y-0.148/) y=其中% 可查GB2624-81或理化数据手册。