高考文科数学全国课标1卷考点清单
- 格式:doc
- 大小:58.00 KB
- 文档页数:2

2023年数学高考新课标1卷知识点分布一、概述数学是一门重要的学科,它在各个领域都有着广泛的应用。
高考数学作为考生升学的关键,对于教师和学生而言都是一项重要的考验。
了解高考数学试卷的知识点分布对于备战高考的学生和教师来说是至关重要的。
本文将对2023年数学高考新课标1卷的知识点分布进行详细的分析和解读。
二、基础知识1. 高中数学新课程标准2017年,我国出台了新的高中数学课程标准,对高中数学的教学目标、内容体系、教学方法等方面做出了全面的规定和要求。
新课标对于培养学生的创新精神、数学思维能力等方面提出了更高的要求,因此高考数学试卷的知识点分布也相应进行了调整。
2. 知识点分布的重要性了解高考数学试卷的知识点分布,有助于学生合理进行复习,抓住重点,针对性地提高自己的数学水平。
对于教师来说,通过了解知识点分布,可以更好地指导学生备战高考,使学生能够在考试中取得更好的成绩。
三、2023年数学高考新课标1卷的知识点分布根据最新的高考数学新课标1卷试卷分析,结合历年高考数学试卷的特点和趋势,对2023年数学高考新课标1卷的知识点分布进行如下分析:1. 几何部分几何部分一直是高考数学试卷中的难点和重点,2023年数学高考新课标1卷的几何部分主要包括平面几何和立体几何两个方面。
(1) 平面几何平面几何的知识点主要包括直线、角、三角形、四边形、圆等内容。
在2023年的高考数学新课标1卷中,平面几何部分依然占据了较大的比重,考查的知识点主要集中在角的性质、相似三角形、圆的性质等方面。
(2) 立体几何立体几何是高考数学试卷中的难点之一,它涉及到空间直线、平面、立体图形的性质和计算等内容。
2023年数学高考新课标1卷的立体几何部分主要考查了空间中的位置关系、多面体的表面积和体积计算等知识点。
2. 代数部分代数部分一直是高考数学试卷的重点之一,它包括了数列、函数、方程、不等式、概率等内容。
在2023年数学高考新课标1卷中,代数部分的知识点分布较为平均,主要考查了函数的性质、方程和不等式的解法、数列的性质和概率的计算等方面。

新高考全国i卷数学全解读一、整体评价(一)命题水平本套试题的命题水平很高,题目同时注重对基础概念的理解能力、灵活运用知识解决问题的能力、分析推理的逻辑能力和一定的解题经验。
本套试题没有出现“套路题型”,简单和适中的题目都可以使用基本的方法思路按部就班地解决,难题需要运用较强的综合分析能力,没有所谓背会几个“秒杀公式”“小窍门”就能轻松解决的问题。
总之,这是一套很好的试题,不论是简单的题目还是较难的题目,都可以用来作为做题训练的示范。
(二)题目难度本套试卷的难度整体偏难,但是算不上很难,没有“变态难”的题目。
选择填空的难度较以往偏难,解答题的难度较为适中。
本套试卷的计算量偏大,在近年来高考数学卷计算量加大的基础上又有增大。
特别是选择填空部分的计算量明显加大,解答题部分的计算量较以往持平。
整体难度偏难、计算量偏大、难度和计算量都主要体现在前面的选择填空部分,且大都集中在同一批选择填空题,很少有“思路难度大但计算量小”和“思路难度小但计算量大”的题目,导致解决题目的难度成几何级增大。
对于绝大部分习惯于按照顺序从头至尾依次答题的考生很不友好。
很容易在做选择填空题时花费过多时间,甚至自信心遭到很大打击,使得没有足够的时间和信心、耐心解决其实整体难度适中的解答题。
(三)综合影响本套试卷对考生产生的影响,不会主要在“优异”“普通”“薄弱”等不同水平的考生之间产生的区别,而是主要在心态良好、心态一般、心态较差的不同心态的考生之间产生差别,以及在“从前往后按顺序做”、“先挑会做的做”、“按顺序做的同时跳过不会”的不同答题顺序的考生之间产生差别。
高考的考察内容除了对知识的理解掌握之外,增加了更多心态和策略方面的影响。
二、逐题评价题目和题目的详细解答在最后,这里只对题目的难度、特点、方向等作简要分析,建议找套试题对照着一起看。
(一)单选题:第1题:考察集合的基本知识,非常简单,没有陷阱。
第2题:考察复数的运算,非常简单,没有陷阱。

2018年高考新课标全国卷Ⅰ文科数学考试范围与要求本部分包括必考内容和选考内容两部分.必考内容为《课程标准》的必修内容和选修系列1的内容;选考内容为《课程标准》的选修系列4的“坐标系与参数方程”、“不等式选讲”等2个专题。
必考内容(一)集合1.集合的含义与表示(1)了解集合的含义、元素与集合的属于关系.(2)能用自然语言、图形语言、集合语言(列举法或描述法)描述不同的具体问题.2.集合间的基本关系(1)理解集合之间包含与相等的含义,能识别给定集合的子集.(2)在具体情境中,了解全集与空集的含义.3.集合的基本运算(1)理解两个集合的并集与交集的含义,会求两个简单集合的并集与交集.(2)理解在给定集合中一个子集的补集的含义,会求给定子集的补集.(3)能使用韦恩(Venn)图表达集合的关系及运算.(二)函数概念与基本初等函数I(指数函数、对数函数、幂函数)1.函数(1)了解构成函数的要素,会求一些简单函数的定义域和值域;了解映射的概念.(2)在实际情境中,会根据不同的需要选择恰当的方法(如图象法、列表法、解析法)表示函数.(3)了解简单的分段函数,并能简单应用.(4)理解函数的单调性、最大值、最小值及其几何意义;结合具体函数,了解函数奇偶性的含义.(5)会运用函数图象理解和研究函数的性质.2.指数函数(1)了解指数函数模型的实际背景.(2)理解有理指数幂的含义,了解实数指数幂的意义,掌握幂的运算.(3)理解指数函数的概念,理解指数函数的单调性,掌握指数函数图象通过的特殊点.(4)知道指数函数是一类重要的函数模型.3.对数函数(1)理解对数的概念及其运算性质,知道用换底公式能将一般对数转化成自然对数或常用对数;了解对数在简化运算中的作用.(2)理解对数函数的概念,理解对数函数的单调性,掌握对数函数图象通过的特殊点.(3)知道对数函数是一类重要的函数模型.(44.幂函数(1)了解幂函数的概念.(25.函数与方程(1)结合二次函数的图象,了解函数的零点与方程根的联系,判断一元二次方程根的存在性及根的个数.(2)根据具体函数的图象,能够用二分法求相应方程的近似解.6.函数模型及其应用(1)了解指数函数、对数函数以及幂函数的增长特征,知道直线上升、指数增长、对数增长等不同函数类型增长的含义.(2)了解函数模型(如指数函数、对数函数、幂函数、分段函数等在社会生活中普遍使用的函数模型)的广泛应用.(三)立体几何初步1.空间几何体(1)认识柱、锥、台、球及其简单组合体的结构特征,并能运用这些特征描述现实生活中简单物体的结构.(2)能画出简单空间图形(长方体、球、圆柱、圆锥、棱柱等的简易组合)的三视图,能识别上述三视图所表示的立体模型,会用斜二侧法画出它们的直观图.(3)会用平行投影与中心投影两种方法画出简单空间图形的三视图与直观图,了解空间图形的不同表示形式.(4)会画某些建筑物的视图与直观图(在不影响图形特征的基础上,尺寸、线条等不做严格要求).(5)了解球、棱柱、棱锥、台的表面积和体积的计算公式.2.点、直线、平面之间的位置关系(1)理解空间直线、平面位置关系的定义,并了解如下可以作为推理依据的公理和定理.·公理1:如果一条直线上的两点在一个平面内,那么这条直线上所有的点都在此平面内.·公理2:过不在同一条直线上的三点,有且只有一个平面.·公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.·公理4:平行于同一条直线的两条直线互相平行.·定理:空间中如果一个角的两边与另一个角的两边分别平行,那么这两个角相等或互补.(2)以立体几何的上述定义、公理和定理为出发点,认识和理解空间中线面平行、垂直的有关性质与判定定理.理解以下判定定理:·如果平面外一条直线与此平面内的一条直线平行,那么该直线与此平面平行.·如果一个平面内的两条相交直线与另一个平面都平行,那么这两个平面平行.·如果一条直线与一个平面内的两条相交直线都垂直,那么该直线与此平面垂直.·如果一个平面经过另一个平面的垂线,那么这两个平面互相垂直.理解以下性质定理,并能够证明:·如果一条直线与一个平面平行,那么经过该直线的任一个平面与此平面的交线和该直线平行.·如果两个平行平面同时和第三个平面相交,那么它们的交线相互平行.·垂直于同一个平面的两条直线平行.·如果两个平面垂直,那么一个平面内垂直于它们交线的直线与另一个平面垂直.(3)能运用公理、定理和已获得的结论证明一些空间图形的位置关系的简单命题.(四)平面解析几何初步1.直线与方程(1)在平面直角坐标系中,结合具体图形,确定直线位置的几何要素.(2)理解直线的倾斜角和斜率的概念,掌握过两点的直线斜率的计算公式.(3)能根据两条直线的斜率判定这两条直线平行或垂直.(4)掌握确定直线位置的几何要素,掌握直线方程的几种形式(点斜式、两点式及一般式),了解斜截式与一次函数的关系.(5)能用解方程组的方法求两条相交直线的交点坐标.(6)掌握两点间的距离公式、点到直线的距离公式,会求两条平行直线间的距离.2.圆与方程(1)掌握确定圆的几何要素,掌握圆的标准方程与一般方程.(2)能根据给定直线、圆的方程判断直线与圆的位置关系;能根据给定两个圆的方程判断两圆的位置关系.(3)能用直线和圆的方程解决一些简单的问题.(4)初步了解用代数方法处理几何问题的思想.3.空间直角坐标系(1)了解空间直角坐标系,会用空间直角坐标表示点的位置.(2)会推导空间两点间的距离公式.(五)算法初步1.算法的含义、程序框图(1)了解算法的含义,了解算法的思想.(2)理解程序框图的三种基本逻辑结构:顺序、条件分支、循环.2.基本算法语句理解几种基本算法语句——输入语句、输出语句、赋值语句、条件语句、循环语句的含义.(六)统计1.随机抽样(1)理解随机抽样的必要性和重要性.(2)会用简单随机抽样方法从总体中抽取样本;了解分层抽样和系统抽样方法.2.用样本估计总体(1)了解分布的意义和作用,会列频率分布表,会画频率分布直方图、频率折线图、茎叶图,理解它们各自的特点.(2)理解样本数据标准差的意义和作用,会计算数据标准差.(3)能从样本数据中提取基本的数字特征(如平均数、标准差),并给出合理的解释.(4)会用样本的频率分布估计总体分布,会用样本的基本数字特征估计总体的基本数字特征,理解用样本估计总体的思想.(5)会用随机抽样的基本方法和样本估计总体的思想解决一些简单的实际问题.3.变量的相关性(1)会作两个有关联变量的数据的散点图,会利用散点图认识变量间的相关关系.(2)了解最小二乘法的思想,能根据给出的线性回归方程系数公式建立线性回归方程.(七)概率1.事件与概率(1)了解随机事件发生的不确定性和频率的稳定性,了解概率的意义,了解频率与概率的区别.(2)了解两个互斥事件的概率加法公式.2.古典概型(1)理解古典概型及其概率计算公式.(2)会用列举法计算一些随机事件所含的基本事件数及事件发生的概率.3.随机数与几何概型(1)了解随机数的意义,能运用模拟方法估计概率.(2)了解几何概型的意义.(八)基本初等函数Ⅱ(三角函数)1.任意角的概念、弧度制(1)了解任意角的概念.(2)了解弧度制的概念,能进行弧度与角度的互化.2.三角函数(1)理解任意角三角函数(正弦、余弦、正切)的定义.(2(3(4(5(6)了解三角函数是描述周期变化现象的重要函数模型,会用三角函数解决一些简单实际问题.(九)平面向量1.平面向量的实际背景及基本概念(1)了解向量的实际背景.(2)理解平面向量的概念,理解两个向量相等的含义.(3)理解向量的几何表示.2.向量的线性运算(1)掌握向量加法、减法的运算,并理解其几何意义.(2)掌握向量数乘的运算及其几何意义,理解两个向量共线的含义.(3)了解向量线性运算的性质及其几何意义.3.平面向量的基本定理及坐标表示(1)了解平面向量的基本定理及其意义.(2)掌握平面向量的正交分解及其坐标表示.(3)会用坐标表示平面向量的加法、减法与数乘运算.(4)理解用坐标表示的平面向量共线的条件.4.平面向量的数量积(1)理解平面向量数量积的含义及其物理意义.(2)了解平面向量的数量积与向量投影的关系.(3)掌握数量积的坐标表达式,会进行平面向量数量积的运算.(4)能运用数量积表示两个向量的夹角,会用数量积判断两个平面向量的垂直关系.5.向量的应用(1)会用向量方法解决某些简单的平面几何问题.(2)会用向量方法解决简单的力学问题与其他一些实际问题.(十)三角恒等变换1.和与差的三角函数公式(1)会用向量的数量积推导出两角差的余弦公式.(2)能利用两角差的余弦公式导出两角差的正弦、正切公式.(3)能利用两角差的余弦公式导出两角和的正弦、余弦、正切公式,导出二倍角的正弦、余弦、正切公式,了解它们的内在联系.2.简单的三角恒等变换能运用上述公式进行简单的恒等变换(包括导出积化和差、和差化积、半角公式,但对这三组公式不要求记忆).(十一)解三角形1.正弦定理和余弦定理掌握正弦定理、余弦定理,并能解决一些简单的三角形度量问题.2.应用能够运用正弦定理、余弦定理等知识和方法解决一些与测量和几何计算有关的实际问题.(十二)数列1.数列的概念和简单表示法(1)了解数列的概念和几种简单的表示方法(列表、图象、通项公式).(2)了解数列是自变量为正整数的一类函数.2.等差数列、等比数列(1)理解等差数列、等比数列的概念.(2(3)能在具体的问题情境中识别数列的等差关系或等比关系,并能用有关知识解决相应的问题.(4)了解等差数列与一次函数、等比数列与指数函数的关系.(十三)不等式1.不等关系了解现实世界和日常生活中的不等关系,了解不等式(组)的实际背景.2.一元二次不等式(1)会从实际情境中抽象出一元二次不等式模型.(2)通过函数图象了解一元二次不等式与相应的二次函数、一元二次方程的联系.(3)会解一元二次不等式,对给定的一元二次不等式,会设计求解的程序框图.3.二元一次不等式组与简单线性规划问题(1)会从实际情境中抽象出二元一次不等式组.(2)了解二元一次不等式的几何意义,能用平面区域表示二元一次不等式组.(3)会从实际情境中抽象出一些简单的二元线性规划问题,并能加以解决.4(1)了解基本不等式的证明过程.(2)会用基本不等式解决简单的最大(小)值问题.(十四)常用逻辑用语1.命题及其关系(1)理解命题的概念.(2的相互关系.(3)理解必要条件、充分条件与充要条件的意义.2.简单的逻辑联结词了解逻辑联结词“或”、“且”、“非”的含义.3.全称量词与存在量词(1)理解全称量词与存在量词的意义.(2)能正确地对含有一个量词的命题进行否定.(十五)圆锥曲线与方程(1)了解圆锥曲线的实际背景,了解圆锥曲线在刻画现实世界和解决实际问题中的作用.(2)掌握椭圆的定义、几何图形、标准方程及简单几何性质.(3)了解双曲线、抛物线的定义、几何图形和标准方程,知道它们的简单几何性质.(4)理解数形结合的思想.(5)了解圆锥曲线的简单应用.(十六)导数及其应用1.导数概念及其几何意义(1)了解导数概念的实际背景.(2)理解导数的几何意义.2.导数的运算(1(2)能利用下面给出的基本初等函数的导数公式和导数的四则运算法则求简单函数的导数.·常见基本初等函数的导数公式:) ;·常用的导数运算法则:法则1法则2法则33.导数在研究函数中的应用(1)了解函数单调性和导数的关系;能利用导数研究函数的单调性,会求函数的单调区间(其中多项式函数一般不超过三次).(2)了解函数在某点取得极值的必要条件和充分条件;会用导数求函数的极大值、极小值(其中多项式函数一般不超过三次);会求闭区间上函数的最大值、最小值(其中多项式函数一般不超过三次).4.生活中的优化问题.会利用导数解决某些实际问题.(十七)统计案例了解下列一些常见的统计方法,并能应用这些方法解决一些实际问题.1.独立性检验了解独立性检验(只要求2×2列联表)的基本思想、方法及其简单应用.2.回归分析了解回归分析的基本思想、方法及其简单应用.(十八)推理与证明1.合情推理与演绎推理(1)了解合情推理的含义,能利用归纳和类比等进行简单的推理,了解合情推理在数学发现中的作用.(2)了解演绎推理的重要性,掌握演绎推理的基本模式,并能运用它们进行一些简单推理.(3)了解合情推理和演绎推理之间的联系和差异.2.直接证明与间接证明(1)了解直接证明的两种基本方法——分析法和综合法;了解分析法和综合法的思考过程、特点.(2)了解间接证明的一种基本方法——反证法;了解反证法的思考过程、特点.(十九)数系的扩充与复数的引入1.复数的概念(1)理解复数的基本概念.(2)理解复数相等的充要条件.(3)了解复数的代数表示法及其几何意义.2.复数的四则运算(1)会进行复数代数形式的四则运算.(2)了解复数代数形式的加、减运算的几何意义.(二十)框图1.流程图(1)了解程序框图.(2)了解工序流程图(即统筹图).(3)能绘制简单实际问题的流程图,了解流程图在解决实际问题中的作用.2.结构图(1)了解结构图.(2)会运用结构图梳理已学过的知识,整理收集到的资料信息.选考内容(一)坐标系与参数方程1.坐标系(1)理解坐标系的作用.(2)了解在平面直角坐标系伸缩变换作用下平面图形的变化情况.(3)能在极坐标系中用极坐标表示点的位置,理解在极坐标系和平面直角坐标系中表示点的位置的区别,能进行极坐标和直角坐标的互化.(4)能在极坐标系中给出简单图形的方程.通过比较这些图形在极坐标系和平面直角坐标系中的方程,理解用方程表示平面图形时选择适当坐标系的意义.(5)了解柱坐标系、球坐标系中表示空间中点的位置的方法,并与空间直角坐标系中表示点的位置的方法相比较,了解它们的区别.2.参数方程(1)了解参数方程,了解参数的意义.(2)能选择适当的参数写出直线、圆和圆锥曲线的参数方程.(3)了解平摆线、渐开线的生成过程,并能推导出它们的参数方程.(4)了解其他摆线的生成过程,了解摆线在实际中的应用,了解摆线在表示行星运动轨道中的作用.(二)不等式选讲1.理解绝对值的几何意义,并能利用含绝对值不等式的几何意义证明以下不等式:(1(2(3)会利用绝对值的几何意义求解以下类型的不等式:2.了解下列柯西不等式的几种不同形式,理解它们的几何意义,并会证明.(1(2(3(此不等式通常称为平面三角不等式.)3.会用参数配方法讨论柯西不等式的一般情形:4.会用向量递归方法讨论排序不等式.5.了解数学归纳法的原理及其使用范围,会用数学归纳法证明一些简单问题.6.会用数学归纳法证明伯努利不等式:1的正整数).1的实数时伯努利不等式也成立.7.会用上述不等式证明一些简单问题.能够利用平均值不等式、柯西不等式求一些特定函数的极值.8.了解证明不等式的基本方法:比较法、综合法、分析法、反证法、放缩法.。

高三数学一卷知识点总结在高三这一年,数学作为一门核心科目,是同学们最为重视和关注的科目之一。
高三数学一卷的范围较广,内容较难,对于同学们来说是一个巨大的挑战。
本文将对高三数学一卷的主要知识点进行总结,以帮助同学们更好地备考。
一、函数与方程在数学一卷中,函数与方程是最基础、也是最常出现的知识点。
同学们需要熟练掌握一次函数、二次函数、指数与对数函数等各类函数的性质和图像变换规律。
同时,方程的求解也是必备的技能。
同学们要掌握解一元一次方程、一元二次方程、无理方程等各类方程的方法和步骤。
二、三角函数与解三角形三角函数是高中数学的重点知识之一。
同学们需要掌握正弦、余弦、正切等三角函数的定义和性质,能够灵活运用三角函数解决各类三角关系题和解三角形问题。
此外,同学们还要掌握三角函数的图像特征和变换规律。
三、初等数学的应用初等数学的应用是数学一卷的重点之一。
同学们需要通过综合运用已学的数学知识解决实际问题。
这其中包括解析几何、平面向量、概率论、统计学等内容。
同学们要能够灵活运用这些知识,能够分析和解决实际问题。
四、数列与数列的极限数列与数列的极限是高三数学一卷的难点,也是同学们备考时需要重点关注和突破的内容。
同学们需要掌握数列的定义、性质和常见类型,能够判断数列的收敛性,并能够计算数列的极限。
此外,同学们还需要掌握数列极限和函数极限的关系。
五、微积分的基础内容微积分是高中数学的重点领域之一,也是高三数学一卷的重要内容。
同学们需要熟练掌握函数的导数、不定积分和定积分的定义、性质和运算法则。
此外,同学们还需要熟练掌握微分方程、定积分的应用等相关内容。
总结起来,高三数学一卷的知识点较为广泛,需要同学们在复习备考时注重理解和掌握基本概念、性质和解题方法,并能够将所学的知识应用到实际问题中。
同学们要注重做题巩固知识点,多进行题型训练和模拟考试,及时总结和弥补知识漏洞。
同时,也要注重多思考、多思维训练,提高分析和解决问题的能力。


全国1卷高考知识点随着全国高考的到来,许许多多的学生为了能够取得好成绩而加紧复习备考。
而备考的基础就是掌握高考的知识点。
在全国1卷高考中,有许多重要的知识点需要掌握。
本文将介绍其中的一些重要知识点,并对其进行简单的解读。
数学是高考备考中绕不开的一门科目。
在全国1卷高考中,数学的知识点主要分为数与代数、函数、几何与概率统计等方面。
首先,数与代数是数学中的基础。
其中包括整数、有理数、实数、复数以及数的四则运算等。
掌握了这些知识,就能够轻松应对基础的数学题目。
其次,函数是数学中的重要概念。
在高考中,各种函数的性质与应用常常会出现在试卷中。
掌握了函数的定义、图像、性质与应用等知识点,能够解决与函数有关的各种数学问题。
最后,几何与概率统计也是高考中重要的知识点。
在几何方面,了解各种几何图形的性质、相关定理与解题技巧,有助于解决几何题目。
而在概率统计方面,理解概率的概念、计算方法以及统计与统计图表的应用,能够解决与概率统计相关的问题。
除了数学外,语文也是高考中的重要科目之一。
在全国1卷高考中,语文主要包括阅读理解、作文、写作等知识点。
首先,阅读理解是语文考试中的一大重点。
学生需要通过阅读各种文章,理解文章的内容、推理作者的意图,解答相关问题。
掌握阅读理解技巧,能够提高阅读理解的准确性与速度。
其次,作文是语文考试的一项重要内容。
学生需要通过作文来表达自己的观点与思考。
在写作过程中,逻辑性与条理性是重要的考察要点。
同时,语文考试也会对学生的语言表达能力进行考察。
除了数学和语文,英语也是高考的一项重要科目。
全国1卷高考中的英语知识点主要包括语法、阅读理解、听力与写作等。
首先,语法是英语学习的基础。
学生需要掌握词汇的用法、句子的结构与时态的运用等。
熟练掌握英语的语法知识,对解答选择题与完成填空题具有重要意义。
其次,阅读理解与听力是英语考试中重要的环节。
学生需要通过阅读文章和听力材料,提取关键信息,理解文章或对话的含义,并回答相关问题。


2013-2016全国Ⅰ卷高考数学(文科)知识点归类1.集合1.(2013年全国1卷第1题)已知集合},,,{4321A =,},|{A n n x x B 2∈==,则A∩B= ( )A.{1,4}B.{2,3}C.{9,16}D.{1,2}2.(2014年全国1卷第1题)已知集合{}{}|13,|21M x x N x x =-<<=-<<,则MN =( )A. )1,2(-B. )1,1(-C. )3,1(D. )3,2(-3.(2015年全国1卷第1题)已知集合{32,},{6,8,10,12,14}A x x n n N B ==+∈=,则集合A B 中的元素个数为( )A. 5B. 4C. 3D. 24. (2016年全国1卷第1题)设集合{1,3,5,7}A =,{|25}B x x =≤≤,则AB =( )A. {1,3}B. {3,5}C. {5,7}D. {1,7} 2.向量1.(2013年全国1卷第13题)已知两个单位向量b a ,的夹角为60°,b t a t c )1(-+=,若0=⋅c b ,则=t _________.2.(2014年全国1卷第6题)设F E D ,,分别为ABC ∆的三边AB CA BC ,,的中点,则=+FC EB ( )A.ADB.AD 21 C. BC 21D. BC 3.(2015年全国1卷第2题)已知点(0,1),(3,2)A B ,向量(4,3)AC =--,则向量BC =( )A. (7,4)--B. (7,4)C. (1,4)-D. (1,4)4.(2016年全国1卷第13题).设向量(,1)a x x =+,(1,2)b =,且a b ⊥,则x =_______ 3.复数1.(2013年全国1卷第2题)1+2i(1-i)2=( )A.-1-12iB.-1+12iC.1+12iD.1-12i2.(2014年全国1卷第3题)设i iz ++=11,则=||z ( ) A.21B. 22C. 23D. 23.(2015年全国1卷第3题)已知复数z 满足(1)1z i i -=+,则z =( )A. 2i --B. 2i -+C. 2i -D. 2i +4.(2016年全国1卷第2题)设(12)()i a i ++的实部与虚部相等,其中a 为实数,则a =( ) A. 3- B. 2- C. 2 D. 3 4.概率1.(2013年全国1卷第3题)从1,2,3,4中任取2个不同的数,则取出的2个数之差的绝对值为2的概率是( )A.12B.13C.14D.16 2.(2014年全国1卷第13题)将2本不同的数学书和1本语文书在书架上随机排成一行,则2本数学书相邻的概率为________.3.(2015年全国1卷第4题)如果3个正数可作为一个直角三角形三条边的边长,则称这3个数为一组勾股数,从1,2,3,4,5中任取3个不同的数,则这3个数构成一组勾股数的概率为( )A.310 B. 15 C. 110 D. 1204.(2016年全国1卷第3题)为美化环境,从红、黄、白、紫4种颜色的花中任选2种花种在一个花坛中,学优高考网余下的2种花种在另一个花坛中,则红色和紫色的花不在同一花坛的概率是( ) A.13 B.12 C.23 D.565.解析几何1.(2013年全国1卷第4题)已知双曲线)0,0(1:2222>>=-b a by a x C 的离心率为25,则C 渐近线方程为( ) A. x y 41±=B. x y 31±= C. x y 21±= D. x y ±= 2.(2013年全国1卷第8题)O 为坐标原点,F 为抛物线x y C 24:2=的焦点,P 为C 上一点,若24=PF ,则△POF 的面积为( )A. 2B.2 2C.2 3D.43.(2014年全国1卷第10题)已知抛物线C :x y =2的焦点为F ,00(,)A x y 是C 上一点,054AF x =,则0x ( )A. 1B. 2C. 4D. 84.(2014年全国1卷第4题)已知双曲线)0(13222>=-a y a x 的离心率为2,则=a ( ) A. 2 B.26 C. 25D. 1 5.(2015年全国1卷第5题)已知椭圆E 的中心为坐标原点,离心率为12,E 的右焦点与抛物线2:8C y x =的焦点重合,,A B 是C 的准线与E 的两个交点,则AB =( )A. 3B. 6C. 9D. 126.(2015年全国1卷第16题)已知P 是双曲线22:18y C x -=的右焦点,P 是C 左支上一点,(0,66A ,当APF ∆周长最小时,该三角形的面积为 .7.(2016年全国1卷第5题)直线l 经过椭圆的一个顶点和一个焦点,若椭圆中心到l 的距离为其短轴长的14,则该椭圆的离心率为( )A.13 B.12 C. 23 D.348.(2016年全国1卷第15题)设直线2y x a =+与圆22:220C x y ay +--=相交于A ,B 两点,若23AB =,则圆C 的面积为___________.6.立体几何1.(2013年全国1卷第11题)某几何函数的三视图如图所示,则该几何的体积为( ) A.π818+ B. π88+ C. π1616+ D. π168+2.(2013年全国1卷第15题)已知H 是球O 的直径AB 上一点,2:1:=HB AH ,AB ⊥平面α,H 为垂足,α截球O 所得截面的面积为π,则球O 的表面积为_______.3.(2014年全国1卷第8题)如图,网格纸的各小格都是正方形,粗实线画出的事一个几何体的三视图,则这个几何体是( )A.三棱锥B.三棱柱C.四棱锥D.四棱柱4.(2015年全国1卷第6题)如上右图,《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今 有委米依垣内角,下周八尺,高五尺,问”积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧长为8尺,米堆的高为5尺,米堆的体积和堆放的米各位多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放的米有( )A. 14斛B. 22斛C. 36斛D. 66斛5.(2015年全国1卷第11题)圆柱被一个平面截去一部分后与半球(半径为r )组成一个几何体,该几何体的三视图中的正视图和俯视图如图所示,若该几何体的表面积为1620π+,则r =( ) A. 1 B. 2 C. 4 D. 86. (2016年全国1卷第7题)如上右图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是28π3,则它的表面积是( )A. 17πB. 18πC. 20πD. 28π7.(2016年全国1卷第11题)平面α过正方体ABCD —A 1B 1C 1D 1的顶点A 11//CB D α平面,ABCD m α=平面,11ABB A n α=平面,则m ,n 所成角的正弦值为( )A.32 B.22C.33D.137.线性规划1.(2013年全国1卷第14题)设y x ,满足约束条件⎩⎨⎧≤-≤-≤≤0131y x x ,则y x z -=2的最大值为______.2.(2014年全国1卷第11题)设x ,y 满足约束条件,1,x y a x y +≥⎧⎨-≤-⎩且z x ay =+的最小值为7,则a =( )A.-5B.3C.-5或3D.5或-33. (2015年全国1卷第15题)若x ,y 满足约束条件20210220x y x y x y +-≤⎧⎪-+≤⎨⎪-+≥⎩,则z =3x +y 的最大值为 .4.(2016年全国1卷第16题)某高科技企业生产产品A 和产品B 需要甲、乙两种新型材料。

高考文科数学重要考点大全高考文科数学相对比理科数学而言会简单许多,想必很多人都想知道高考文科数学的核心知识点。
接下来是小编为大家整理的高考文科数学重要考点大全,希望大家喜欢!高考文科数学重要考点大全一考点一:集合与简易逻辑集合部分一般以选择题出现,属容易题。
重点考查集合间关系的理解和认识。
近年的试题加强了对集合计算化简能力的考查,并向无限集发展,考查抽象思维能力。
在解决这些问题时,要注意利用几何的直观性,并注重集合表示方法的转换与化简。
简易逻辑考查有两种形式:一是在选择题和填空题中直接考查命题及其关系、逻辑联结词、“充要关系”、命题真伪的判断、全称命题和特称命题的否定等,二是在解答题中深层次考查常用逻辑用语表达数学解题过程和逻辑推理。
考点二:函数与导数函数是高考的重点内容,以选择题和填空题的为载体针对性考查函数的定义域与值域、函数的性质、函数与方程、基本初等函数(一次和二次函数、指数、对数、幂函数)的应用等,分值约为10分,解答题与导数交汇在一起考查函数的性质。
导数部分一方面考查导数的运算与导数的几何意义,另一方面考查导数的简单应用,如求函数的单调区间、极值与最值等,通常以客观题的形式出现,属于容易题和中档题,三是导数的综合应用,主要是和函数、不等式、方程等联系在一起以解答题的形式出现,如一些不等式恒成立问题、参数的取值范围问题、方程根的个数问题、不等式的证明等问题。
考点三:三角函数与平面向量一般是2道小题,1道综合解答题。
小题一道考查平面向量有关概念及运算等,另一道对三角知识点的补充。
大题中如果没有涉及正弦定理、余弦定理的应用,可能就是一道和解答题相互补充的三角函数的图像、性质或三角恒等变换的题目,也可能是考查平面向量为主的试题,要注意数形结合思想在解题中的应用。
向量重点考查平面向量数量积的概念及应用,向量与直线、圆锥曲线、数列、不等式、三角函数等结合,解决角度、垂直、共线等问题是“新热点”题型.考点四:数列与不等式不等式主要考查一元二次不等式的解法、一元二次不等式组和简单线性规划问题、基本不等式的应用等,通常会在小题中设置1到2道题。
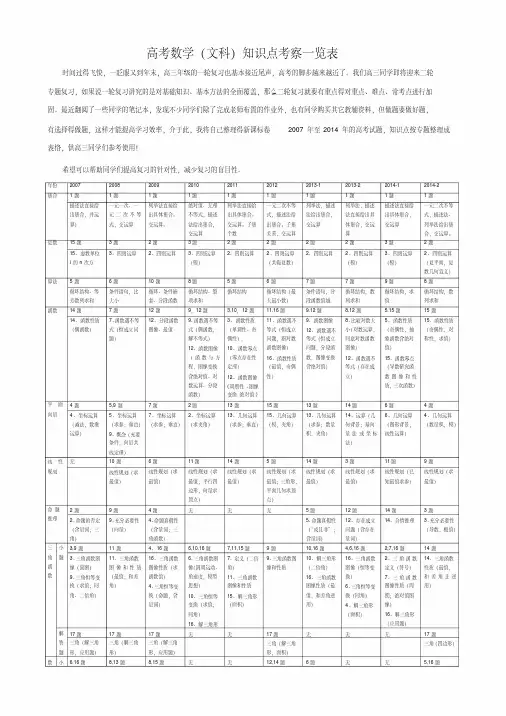
高考数学(文科)知识点考察一览表时间过得飞快,一眨眼又到年末,高三年级的一轮复习也基本接近尾声,高考的脚步越来越近了。
我们高三同学即将迎来二轮专题复习,如果说一轮复习讲究的是对基础知识、基本方法的全面覆盖,那么二轮复习就要有重点得对重点、难点、常考点进行加固。
最近翻阅了一些同学的笔记本,发现不少同学们除了完成老师布置的作业外,也有同学购买其它教辅资料,但做题要做好题,有选择得做题,这样才能提高学习效率,介于此,我将自己整理得新课标卷2007年至2014年的高考试题,知识点按专题整理成表格,供高三同学们参考使用!希望可以帮助同学们提高复习的针对性,减少复习的盲目性。
年份2007 2008 2009 2010 2011 2012 2013-1 2013-2 2014-1 2014-2集合1题1题1题1题1题1题1题1题1题1题描述法直接给出集合,并运算)一元一次、一元二次不等式,交运算列举法直接给出具体集合。
交运算。
绝对值、无理不等式,描述法给出集合,交运算列举法直接给出具体集合。
交运算。
子集个数一元二次不等式,描述法给出集合。
子集关系,交运算列举法,描述法给出集合,交运算列举法,描述法直接给出具体集合,交运算描述法直接给出具体集合,交运算一元二次不等式,描述法、列举法给出集合,交运算。
复数15题3题2题3题2题2题2题2题3题2题15、虚数单位i的n次方3、四则运算2、四则运算3、四则运算(模)2、四则运算2、四则运算(共轭复数)2、四则运算2、四则运算(模)3、四则运算(模)2、四则运算(复平面,复数几何意义)算法5题6题10题8题5题6题7题7题9题8题循环结构、等差数列求和条件语句,比大小循环、条件嵌套、分段函数循环结构、裂项求和循环结构循环结构(最大最小数)条件语句,分段函数值域循环结构,数列求和循环结构,求值循环结构,数列求和函数14题7题12题9,12题3,10,12题11,16题9,12题8,12题5,15题15题14、函数性质(偶函数)7、函数遇不等式(恒成立问题)12、分段函数图像、最值9、函数遇不等式(偶函数,解不等式)12、函数图像(函数与方程,图像变换含绝对值、对数运算、分段函数)3、函数性质(单调性、奇偶性);10、函数零点(零点存在性定理)12、函数图像(周期性,图像变换绝对值)11、函数遇不等式(恒成立问题,指对数函数图像)16、函数性质(最值,奇偶性)9、函数图像12、函数遇不等式(恒成立问题,分段函数,图像变换含绝对值)8、比较对数大小(对数运算,同底对数函数图像)12、函数遇不等式(存在成立)5、函数性质(奇偶性,抽象函数含绝对值)15、函数零点(导数研究函数图像和性质,三次函数)15、函数性质(奇偶性,对称性,求值)平面向量4题5,9题7题2题13题15题13题14题6题4题4、坐标运算(减法,数乘运算)5、坐标运算(求参;垂直)9、概念(充要条件,向量共线定理)7、坐标运算(求参;垂直)2、坐标运算(求夹角)13、几何运算(求参;垂直)15、几何运算(模,夹角)13、几何运算(求参;数量积,夹角)14、运算(几何背景;基向量法或坐标法)6、几何运算(图形背景,线性运算)4、几何运算(数量积,模)线性规划无10题6题11题14题5题14题3题11题9题线性规划(求最值)线性规划(求最值)线性规划(求最值;平行四边形,向量求顶点)线性规划(求最值)线性规划(求最值;三角形,平面几何求顶点)线性规划(求最值)线性规划(求最值)线性规划(已知最值求参)线性规划(求最值)命题推理2题9题4题无无无5题12题14题3题2、命题的否定(含量词;三角)9、充分必要性(向量)4、命题真假性(含量词;三角函数)5、命题真假性(“或且非”;含量词)12、存在成立问题(含存在量词)14、合情推理3、充分必要性(导数,极值)三角函数小题3,9题11题4、16题6,10,16题7,11,15题9题10,16题4,6,16题2,7,16题14题3、三角函数图像(简图)9、三角恒等变换(求值;同角、二倍角)11、三角函数图像和性质(最值;和差角)16、三角函数图像性质(求函数值)4、三角恒等变换(命题,含量词)6、三角函数图像(圆周运动、角速度,模型思想)10、三角恒等变换(求值;同角)16、解三角形7、定义(二倍角)11、三角函数图像和性质15、解三角形(面积)9、三角函数图像和性质10、解三角形(二倍角)16、三角函数图像性质(最值,和差角逆用)16、三角函数图像(恒等变换)6、三角恒等变换(同角)4、解三角形(面积)2、三角函数定义(符号)7、三角函数图像性质(周期;绝对值图像)16、解三角形(应用题)14、三角函数性质(最值,和差角正逆用)解答题17题17题17题无无17题无无无17题三角(解三角形,应用题)三角(解三角形)三角(解三角形,应用题)三角(解三角形,面积)三角(四边形)数小6,16题8,13题8,15题无无12,14题6题无无5,16题。

高考数学全国卷一知识点作为学生们追求的目标,高考是每个人生命中的重要关卡。
而数学作为高考的一门重要科目,广受学生的关注和重视。
下面,我们将详细介绍高考数学全国卷一的主要知识点。
第一章:数与代数数与代数是数学的基础,也是高中数学的核心内容。
这一章主要包括实数、多项式和一次函数三个主要知识点。
1. 实数:实数是指包括有理数和无理数在内的所有数。
在高考中,实数的性质是非常重要的。
比如,实数的大小关系、无理数的近似和无理数的运算等。
2. 多项式:多项式是指含有多个项的代数式,其中每个项由系数与次数的乘积构成。
在高考中,学生需要了解多项式的基本运算、多项式的整除与因式分解等。
3. 一次函数:一次函数是指函数的自变量的最高次数为1的函数。
在高考中,一次函数的性质是重要的考点。
包括线性方程与不等式的解法、函数的图像和性质等。
第二章:方程与不等式方程与不等式是高考数学中的重要内容,涉及到代数方程和不等式的解法。
1. 一元一次方程与一元一次不等式:在高考中,一元一次方程与一元一次不等式是最基本最简单的方程与不等式。
学生需要掌握解一元一次方程与不等式的基本方法,包括等式的变形与方程的解法等。
2. 二次函数与二次方程:二次函数与二次方程是高考中的重点内容。
学生需要掌握二次函数的图像和性质,二次方程的解法和关于二次方程的应用等。
第三章:函数与图像函数与图像是高考数学中的重要内容,涉及到函数的概念、性质和图像。
1. 函数的概念与性质:学生需要掌握函数的定义、定义域和值域、函数的奇偶性、周期性等性质。
此外,还需要掌握常见函数的特点,如一次函数、二次函数、指数函数和对数函数等。
2. 函数的图象:学生需要掌握函数的图像的绘制方法和特点。
特别是对于一次函数、二次函数、绝对值函数和分段函数等,需要掌握其图像的变化规律和性质。
第四章:几何与向量几何与向量是高考数学中的重要内容,涉及到平面几何与空间几何的知识点。
1. 平面几何:平面几何是指研究平面上几何图形性质的数学分支。
绝密★启用前2019年高考普通高等学校招生全国统一考试(全国1卷)文科数学注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。
如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上。
写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的。
1.(5分)设z=,则|z|=()A.2B.C.D.12.(5分)已知集合U={1,2,3,4,5,6,7},A={2,3,4,5},B={2,3,6,7},则B∩∁U A=()A.{1,6}B.{1,7}C.{6,7}D.{1,6,7} 3.(5分)已知a=log20.2,b=20.2,c=0.20.3,则()A.a<b<c B.a<c<b C.c<a<b D.b<c<a4.(5分)古希腊时期,人们认为最美人体的头顶至肚脐的长度与肚脐至足底的长度之比是(≈0.618,称为黄金分割比例),著名的“断臂维纳斯”便是如此.此外,最美人体的头顶至咽喉的长度与咽喉至肚脐的长度之比也是.若某人满足上述两个黄金分割比例,且腿长为105cm,头顶至脖子下端的长度为26cm,则其身高可能是()A.165cm B.175cm C.185cm D.190cm5.(5分)函数f(x)=在[﹣π,π]的图象大致为()A.B.C.D.6.(5分)某学校为了解1000名新生的身体素质,将这些学生编号1,2,…,1000,从这些新生中用系统抽样方法等距抽取100名学生进行体质测验.若46号学生被抽到,则下面4名学生中被抽到的是()A.8号学生B.200号学生C.616号学生D.815号学生7.(5分)tan255°=()A.﹣2﹣B.﹣2+C.2﹣D.2+8.(5分)已知非零向量,满足||=2||,且(﹣)⊥,则与的夹角为()A.B.C.D.9.(5分)如图是求的程序框图,图中空白框中应填入()A.A=B.A=2+C.A=D.A=1+10.(5分)双曲线C:﹣=1(a>0,b>0)的一条渐近线的倾斜角为130°,则C 的离心率为()A.2sin40°B.2cos40°C.D.11.(5分)△ABC的内角A,B,C的对边分别为a,b,c.已知a sin A﹣b sin B=4c sin C,cos A =﹣,则=()A.6B.5C.4D.312.(5分)已知椭圆C的焦点为F1(﹣1,0),F2(1,0),过F2的直线与C交于A,B两点.若|AF2|=2|F2B|,|AB|=|BF1|,则C的方程为()A.+y2=1B.+=1C.+=1D.+=1二、填空题:本题共4小题,每小题5分,共20分。
高考数学全国一卷知识点总结归纳在高中阶段,数学作为一门学科无疑是高考中最重要的科目之一。
尤其是全国一卷,作为数学试卷的代表,对考生的数学知识储备、理解能力和解题能力提出了非常高的要求。
为了帮助广大考生更好地备战高考数学一卷,本文将对其中的知识点进行总结和归纳。
一、代数与函数1. 一次函数与二次函数:通过对一次函数与二次函数的定义、性质以及相关的解题思路和方法进行梳理,帮助考生深入理解和掌握这两种常见的数学模型。
2. 不等式与绝对值:对于不等式与绝对值的基本概念、性质以及相关的解法进行详细讲解,帮助考生掌握不等式与绝对值的变换、组合和求解方法。
3. 多项式与初等函数:通过对多项式与初等函数的性质、运算法则以及相关的应用题进行分析,帮助考生理解多项式与初等函数的特点,并能够在解题过程中灵活运用相关知识。
4. 幂函数与对数函数:对幂函数与对数函数的定义、性质以及相关的变换和图像进行解析,帮助考生熟悉幂函数与对数函数的基本特征,并能够利用这些特征解决实际问题。
二、几何与三角1. 基础几何运算:对于平面几何中的基本概念,如点、直线、角等进行归纳和总结,帮助考生熟悉基础几何知识,并能够灵活运用到解题中。
2. 三角函数与三角恒等式:对三角函数的定义、性质以及相关的运算法则进行详细讲解,同时对常见的三角恒等式进行总结和归纳,帮助考生掌握三角函数的基本特点和运算规律,并能够灵活运用到解题中。
3. 三角形与平面向量:对于常见的三角形及其性质进行分类和总结,同时对平面向量的基本概念、性质以及相关的运算法则进行详细解析,帮助考生理解三角形和平面向量的基本特征,并能够灵活运用到解题中。
三、概率与统计1. 随机事件与概率:对随机事件和概率的基本概念进行详细解析,同时介绍常见的概率计算方法和相关的思维模式,帮助考生掌握概率计算的基本技巧,并能够在解题过程中熟练运用到实际问题中。
2. 抽样与统计指标:对随机抽样和统计指标的基本概念和计算方法进行梳理和总结,帮助考生理解统计学中的重要概念和方法,并能够运用到实际问题的分析与解决中。
高考文科数学题型汇总
选填考点
1、集合(必考)1
2、复数(必考) 1
3、向量(必考) 1
4、常用逻辑用语
5、程序框图(必考) 1
6、线性(非线性)规划及不等式(必考) 1
7、三角函数(必考)1-2道
8、数列(必考)1-2道
9、三视图
10、球的组合体、外接内切问题
11、直线与圆
12、圆锥曲线(必考)2道
13、函数与导数(必考)2-3道
14、立几(必考)2道
15、概率统计(高频) 1
16、逻语辑用(高频) 1
解答题
17、(1)三角:1、解三角。
2、三角函数
(2)数列
18概率统计(贴近生活、时事题型)
1、频率分步直方图
2、独立性检验
3、回归方程
4、茎叶图
19、立体几何
1、平行
2、垂直
3、体积、距离
20、圆锥曲线
21、函数与导数
选做填
23、极坐标与参数方程
1、直角坐标与极坐标互化
2、直角(普通)坐标方程、极坐标方程、参数方程互化
3、曲线与曲线的距离(最值问题)
4、弦长、线段和、线段差、线段积问题(涉及直线的标准参数方程)。
2024数学新高考一卷知识点
嘿,同学们!咱来聊聊2024 数学新高考一卷的知识点呀!比如说函数,这就像我们生活中的导航,能帮我们找到各种问题的答案呢!你看,当我们要计算一个物体的运动轨迹时,函数就派上大用场啦!就像你计划出门旅行,函数就是那张指引你怎么走的地图。
再说说几何,哇哦,那简直就是数学世界里的魔法城堡。
几何图形的各种奇妙特性,就像城堡里的秘密通道和宝藏,等着我们去探索发现。
比如说圆,它多圆润完美呀,在生活里也无处不在,像车轮子,那可多亏了圆的特性。
还有概率统计呢,这就像是一场有趣的猜测游戏。
想想看,我们预测明天下雨的可能性,不就是在运用概率知识嘛。
就好比扔骰子,每一面出现的机会都不一样,但又有着一定的规律可循。
在新高考一卷中,这些知识点可都是重要角色呀!它们相互配合,共同构建起了数学的奇妙世界。
我们可得把它们都牢牢掌握,这样才能在考场上游刃有余呀!。
高考文科数学题型汇总选填考点1、集合(必考)12、复数(必考) 13、向量(必考) 14、常用逻辑用语5、程序框图(必考) 16、线性(非线性)规划及不等式(必考) 17、三角函数(必考)1-2道8、数列(必考)1-2道9、三视图10、球的组合体、外接内切问题11、直线与圆12、圆锥曲线(必考)2道13、函数与导数(必考)2-3道14、立几(必考)2道15、概率统计(高频) 116、逻语辑用(高频) 1解答题17、(1)三角:1、解三角。
2、三角函数(2)数列18概率统计(贴近生活、时事题型)1、频率分步直方图2、独立性检验3、回归方程4、茎叶图19、立体几何1、平行2、垂直3、体积、距离20、圆锥曲线21、函数与导数选做填23、极坐标与参数方程1、直角坐标与极坐标互化2、直角(普通)坐标方程、极坐标方程、参数方程互化3、曲线与曲线的距离(最值问题)4、弦长、线段和、线段差、线段积问题(涉及直线的标准参数方程)以活活被整死;堂堂大元帅受辱骂;……这哪里还有什么尊重可言!3、用在设问句后。
如:(10)我们能让你计划实现吗?不会的。
4、用在选择问句中。
如:(11)我们是革命呢,还是要现大洋?(12)你到底是去,还是不去?●提示:在选择疑问句中,若该句为复句,一般只在句末用问号;若分句较长,或者为加强语气,各分句后也可用问号。
5、用在表疑问的独词句后。
如:(13)我?不可能吧。
●提示:若疑问句为倒装句,问号应放在句末。
如:(14)到底出了什么问题,你的车?(若说成:“到底出了什么问题?你的车。
”则错误。
)6、句子中对某词语有疑问或生卒年月不详时用问号,疑问句构成的标题后面也用问号。
如:(15)中国现今文坛(?)的状况,实在不佳……(16)曹邺(816--?),桂林人。
●特别提示:句号、问号均表示句末停顿。
句号用于陈述句末尾,问号用于疑问句末尾。
有些句中虽有疑问词,但全句并不是疑问句,句末只能用句号,不能用问号。
例如:(17)……最后应求出铜块的体积是多少?(18)面对千姿百态、纷繁芜杂的期刊世界,有哪位期刊编辑不想通过期刊版面设计为刊物分朱布白、添花增色呢?19)关于什么是智力?国内外争论多年也没有定论。
(17)()(19)三句都是非疑问句,(17)(18)句中问号均应改为句号,(19)句中的问号应改为逗号。
三、感叹号●特别提示:1、在表感叹或祈使语气的主谓倒装句中,感叹号要放在句末。
如:(20)多么雄伟壮观啊,万里长城!2、句前有叹词,后是感叹句,叹号放在句末。
如:(21)啊,这儿多么美丽!下面介绍句中点号的用法。
句中点号包括逗号、分号、顿号、和冒号四种。
一、逗号提示:复句内各分句之间的停顿,除了有时用分号外,都要用逗号。
二、顿号用于句中并列的词、词组之间较小的停顿。
如:(22)邓颖超的品德、人格、风范为中华民族树立了一座精神丰碑。
(23)从1918年起,鲁迅陆续发表了《狂人日记》、《药》、《祝福》等短篇小说。
●特别提示:以下九种情况不用顿号。
1、不定数的两个数字间不用顿号。
24)你的年龄大概是十六七岁。
(不能写成“十六、七岁”)●【注意】相邻的两个数字而非约数之间要用顿号。
如:(25)三年级四、五的学生。
(26)战斗在一、二的工人。
并列词语之间带有“啊”、“哇”、“啦”、“呀”等语气词时,并列成分之间用逗号,不用顿号。
2如:(26)他退休后生活很丰富,遛遛鸟呀,打打麻将呀,听听戏呀。
3标题中有并列词语时中间不用顿号,可在并列词语之间空一格。
4、并列的词组比较长、停顿较大的用逗号而不用顿号。
27)情况的了解,任务的确定,兵力的部署,军事和政治教育的实施,给养的筹划,武装的整理等等,都要包括在领导的工作之中。
5并列成分做补语且需要强调时用逗号而不用顿号。
如:(28)那种叫“水晶”的,〈长得长长的,绿绿的,晶莹剔透〉,真像是用水晶和玉石雕刻出来的。
6、并列成分做状语,并列成分是介宾短语,它们之间用逗号而不用顿号。
如:(29)他们[在朦胧的夜色中,在大青树下,在纺车旁边,用传统的诗一般的语言]倾吐着彼此的爱慕和理想。
●【注意】并列成分若都是单个词语或成语则用顿号。
30)我们应坚决、彻底、干净、全部消灭大国主义。
7、并列成分做谓语时,若并列成分是主谓短语,它们之间用逗号而不用顿号。
31)她衣服新潮,头发齐耳根长,走起路来风风火火,讲起话来大声大气。
●【注意】并列成分做谓语时,若共带一个宾语,并列词间用顿号如:(32)今年我公司研制、推出了两款新车。
8、并列的词或词组作复指成分时,并列成分之间用逗号,不用顿号。
33)老槐树下有两辈人:一个“老”字辈,一个“小”辈。
●【注意】如并列词或词组简单,它们之间则用顿号。
如:(34)抗战、团结、进步,这是共产党的三大方针。
9、并列结构内部又包含并列词语时,为分清层次在不同属类间用逗号。
35)过去、现在、未来,上下、左右,中国、外国,都是相互联系、相互影响、相互制约的。
三分号下列几种情况使用分号1、用在复句中表示并列分句间的停顿,非并列关系(转折、因果等)的多重复句,前后两部分之间也用分号。
如:(35)惨象,已使我目不忍视了;流言,犹使我耳不忍闻。
(36)她今年已经十八岁了,个子也长成了,按说该找个婆家;可是她母亲总是一个劲地说他还小。
2、分条说明一个完整的意思,在每一条里,不管是词、词组、单句,还是复句,都作为一个分句,各条末尾用分号,最后一条完了用句号。
如:(37)农民对一个好的村干部的要求是:一、办事公道,一碗水端平;二、自己不要吃得太饱;三、有经济头脑。
3、句子中有余指代词“等等”代表未说出的并列部分,在“等等”的前面也要用分号。
如:(38)阅读有许多好处:它能扩大你的知识面;能陶冶你的情操;能提高你的审美能力;等等。
●【提示:并列的几个分句,不论其结构是否一致,并列分句间均用分号,不能有的用分号有的用逗号】四冒号1、冒号用于提示下文或小结上文。
如:(39)我们的复习分为三个阶段:第一阶段为专项复习阶段;第二阶段为综合复习阶段;第三阶段……(40)她是秋天没丈夫的;他有一个小叔子,小她十岁;她靠打柴为生:我知道的就这些。
●【提示:用于提示下文的词语“注意”、“指出”、“宣称”、“证明”、“告诉”、“如下”、“例如”等后常用冒号。
】2、用于书信、讲话稿等称呼的后面。
3、用于需要说明的词语后。
如:(41)日期:10月20日地点:县剧院●【特别提醒】A、冒号提示的范围一般要管到句子末尾,不能只管到句子中间。
如:(42)参加国庆献礼的优秀影片:《风暴》、《青春之歌》、《林则徐》等,也将在各大城市上映。
(此句中的冒号应去掉)B部分引用别人的话,使之成为整个句子的一部分,引文前不用冒号。
如:(43)林则徐宣称:“若鸦片一日未绝,本大臣一日不回,誓与此事相始终,断无中止之理”,表示决心禁绝鸦片。
(应将冒号换成逗号)C、一个句子中不要出现两个冒号。
44)他在文中指出:我们要学习一些自己国家的历史,比如说:国家的政治史、文化史、经济史等。
(第二个冒号应删去。
)标号标号主要标明语句的性质和作用,包括引号、括号、破折号、省略号、着重号、书名号、间隔号、连接号和专名号九种。
一引号主要作用有:1 、表明引用的部分。
2、着重论述的对象或重要的特定的词语。
如:(45)股市有它的行话:如股票价格上涨叫“牛市”,因牛的眼睛总朝上看;反之叫“熊市”,因熊的眼睛总朝下看。
4、明是否定、反义或讽刺的词语。
如:(46)这样的“聪明”还是少来一点好。
(表否定)表明是简称。
如:(37)你的这种做法到底是姓“资”还是姓“社”。
5、表明是成语、熟语、术语。
如:(47)人们常常称技艺高超的工人为“能工巧匠”,赞精妙的艺术品为“巧夺天工”。
(48)我们有些同志喜欢写长文章,但是没有什么内容,真是“懒婆娘的裹脚,又臭又长”。
6表示特殊的日子,特殊的事件。
如:(49)“五四”运动(50)“一二·九”运动7、表明是象声词、音译词、绰号、专有名词。
如:(51)青蛙“呱呱”叫,惊醒了“豆腐西施”杨二嫂。
(52)一条“金利来”拴在脖子里,叫人不自在。
●【特别提醒】A、引文中有引文,要分双引和单引,单引中还有引文则用双引,总的原则是双中有单,单中有双。
B、引用的文字独立而又完整,则引文末尾的标点不能改动,并将其写在后引号的里面。
如:(53)爱因斯坦说:“想象力比知识更重要,因为知识是有限的,而想象力概括着世界上的一切,推动着进步,并且是知识进化的源泉。
”引文不独立,引用的话只作为作者自己话的一部分时,不管它是不是完整,后引号前都不能用点号(问号、叹号除外)。
如:(54)“满招损,谦受益”这句格言,流传到今天至少有两千年了。
55现代画家徐悲鸿笔下的马,正如有的评论家所说的那样,“形神兼备,充满生机”。
(56)在老张“同志们,走吧!”的招呼声中,我们这支队伍又出发了。
C、连续引用一篇文章的几个段落,只在每段开始使用前引号,该段末尾不用后引号,直到引文结束时才使用后引号。
二括号括号标明行文中的注释性的文字。
从注释的范围看,它有句内括号和句外括号之分。
只注释和补充说明句中一部分词语的叫句内括号。
57)猴子跳到一个十二三岁的孩子(他是船长的儿子)面前,把他的帽子摘下来。
补充和注释全句的叫句外括号。
它放在正文的句末点号之后。
如:(58)他培育了许多香花,繁殖和训练了许多小动物。
(他后来还曾照顾动物园里的一只没有妈妈的小虎,每天用牛奶喂它。
)●【特别提醒】句内括号内的文字末尾不能用句号;但可用问号或叹号。
句外括号里的注释如是一句话,句末可用点号。
如:(59)1861年以后,那拉氏(慈禧)曾搞所谓“垂帘听政”(这是那拉氏直接掌管政权的一种形式。
),指使刽子手……(句中括号里的句号应去掉)(60)她先是寄希望于刘女士的丈夫(那个美男子!),后又寄希望于Q男士。
三破折号破折号用来标明行文中解释说明的语句,或表示语义的转换、递进、中断、延长等。
破折号和括号用法不同:破折号引出的解释说明是正文的一部分,括号里的解释说明不是正文,只是注释。
其作用主要有:1、表示注释。
如:(61)迈进金黄色的大门,穿过宽阔的风门厅和衣帽厅,就到了大会堂建筑的枢纽部分——中央大厅。
2、表示意思的转折及转换。
如:(62)到山上打柴的记忆至今都是幸福而快乐的——尽管那是童年十分辛苦的一种劳作。
(54)“好香的菜,——听到风声了吗?”赵七爷站在七斤的后面说。
3表示意思的递进。
如:(63)自然是读着,读着,强记着——而且要背出来。
4、用于标明语句间的因果关系,破折号前是果,后是因。
如:(64)他首先指出早恋并不可耻——这是一种十分自然、正常的现象……早恋并不可爱——早结的果不甜,早开的花早谢。
’5表声音的延长、中断或停顿。