基于数据挖掘技术的葡萄酒评价体系研究

葡萄酒的评价摘要本文主要采用数学统计与分析方法，利用EXCEL,MATLAB等工具解决了有关葡萄酒质量评价的一系列问题。

关于问题一，分析判断两组评酒员评价结果有无显著性差异及哪组结果更可信。

首先我们采用t-检验法，根据T值判断差异的显著性，代入数据后求得P T t 双尾=0.00065<0.01，即两组评价结果差异性显著。

然后将第一组10位()评酒员对于酒样品所给评分的方差值与第二组10位评酒员对于酒样品所给评分的方差值做比较，得出第一组的方差较大，所以认为第一组评酒员打分较为严格，即更可信。

关于问题二，在不确定酿酒葡萄的理化指标和葡萄酒的质量之间的关系的情况下，运用主成分分析法粪别根据酿酒葡萄的理化指标和葡萄酒的质量对酿酒葡萄进行了分级，将红葡萄、白葡萄各分成了优质、较好、一般、劣质四个等级，结果详见表5.2.1至表5.2.4。

关于问题三，采用回归分析法，计算出酿酒葡萄与葡萄酒所共有的理化指标之间的相关系数，结果详见表5.3.1和表5.3.2，其相关系数的绝对值越大表示联系程度越紧密。

关于问题四，首先根据问题三的结果可知酿酒葡萄与葡萄酒的理化指标之间的联系，将分析过程简化为只考虑葡萄酒的理化指标对葡萄酒质量的影响。

然后查阅资料结合附表1，总结出口感和外观为葡萄酒质量的决定因素，而总酚、色泽、花色苷这三个理化指标为主要影响葡萄酒质量的因素。

最后结合附件3，发现芳香物质对葡萄酒质量也有影响，否定了用葡萄和葡萄酒的理化指标来评价葡萄酒的质量的可行性。

关键词：葡萄酒质量的评价EXCEL MATLAB、主成分分析相关系数T-检验1.问题重述确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。

每个评酒员在对葡萄酒进行品尝后对其分类指标打分，然后求和得到其总分，从而确定葡萄酒的质量。

酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系，葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量。

基于机器学习算法的红葡萄酒质量评价模型研究红葡萄酒是指采用红葡萄酿制而成的葡萄酒，其酿制过程中需要进行多个环节的控制，如选材、发酵、陈酿等，而其中一个非常重要的环节就是质量评价。

酒类行业一直以来都在探索如何通过科技手段来提高红葡萄酒的质量，机器学习算法作为其中的一个重要工具也开始受到了越来越多的关注。

本文将从机器学习算法的角度，探讨基于机器学习算法的红葡萄酒质量评价模型的研究。

一、机器学习算法简介机器学习是人工智能的一个分支，它的主要任务是通过训练数据集让机器能够自动学习并表现出某种行为或任务的能力。

机器学习算法可以分为监督学习、无监督学习、半监督学习、强化学习等几种，其中监督学习是应用最广泛的算法之一。

监督学习主要是基于已有的有标签数据集进行训练，让机器能够自动学习并对未知数据进行分类或预测等任务。

二、基于机器学习算法的红葡萄酒质量评价模型研究红葡萄酒质量评价是根据各种目标和指标来综合评价葡萄酒的质量，包括外观、香气、口感等各个方面。

传统的评价方法主要是依靠人工鉴定，但是这种方法有很多缺点，例如标准不统一、可靠性差、评价效率低等。

随着科技的发展，基于机器学习算法的红葡萄酒质量评价模型开始逐渐被应用于酒类行业中。

在基于机器学习算法的红葡萄酒质量评价模型中，主要是通过先给出一些红葡萄酒的质量数据集作为训练集，利用监督学习算法进行训练，然后通过训练出来的模型对新的红葡萄酒进行评价。

在数据集的选取上，一般需要考虑到数据的多样性、数量和质量等因素。

如何有效地选取数据集是机器学习中非常重要的一个环节。

在选择机器学习算法的时候，要根据任务的具体需求来进行选择。

例如，如果需要对红葡萄酒的外观进行评价，可以采用基于图像处理的机器学习算法，如卷积神经网络（CNN）等。

如果需要对红葡萄酒的香气进行评价，可以采用基于自然语言处理（NLP）的机器学习算法，如深度学习等。

三、机器学习算法在红葡萄酒质量评价中的应用案例随着机器学习算法的不断发展，它在红葡萄酒质量评价中的应用也越来越广泛。

葡萄酒的评价模型摘要近年来，我国掀起了一场葡萄酒热，对葡萄酒的需求与日俱增。

特别是随着食品科学技术的发展，人们不再满足传统感官评价葡萄酒的水平。

如何运用数据资料定量研究葡萄酒的品质，加快建立葡萄酒市场指标规则成为人们关注的焦点。

本文通过对感官评价分析，结合葡萄酒和酿酒葡萄的理化指标和芳香物质的大量数据，建立了客观可靠的葡萄酒质量综合评价模型。

针对问题一：本题需要检验两组品酒员的评价结果是否存在显著差异，并选出更可靠的一组。

我们将各种葡萄酒的10个二级指标得分，相加得到每种酒的总分。

在判断知每组品酒员的评价总分均服从正态分布后，用t检验分析两组品酒员对各葡萄酒评价的差异性，由此计算得到两组评价的显著性差异率为13.36%，即总体上两组品酒员的评价不存在显著差异。

但由于两组品酒员的评价仍存在部分差异，我们比较两组品酒员对55种葡萄酒评价的方差，发现第二组评分的方差普遍小于第一组，所以第二组的评价结果更可信。

针对问题二：为了对酿酒葡萄进行分级，我们将葡萄的理化指标作为媒介。

先根据国际指标制定适用于本题评分的分级标准，将葡萄酒进行分级，再根据理化指标经标准化之后的数值，利用欧氏距离对酿酒的55种酿酒葡萄进行Q型聚类分析。

聚类得到红白葡萄各六个分类后，再把各类酿酒葡萄对应至相应葡萄酒的等级，将酿酒红葡萄和酿酒白葡萄各分为五级。

针对问题三：由于各种酿酒葡萄的理化指标种类复杂，我们用主成分分析的方法，从酿酒红葡萄和酿酒白葡萄的27个有效指标中各提取出了8个和9个主要成分。

考虑到酿酒葡萄经化学反应酿造成葡萄酒的过程中各项理化指标一般存在线性关系，我们建立多元线性回归模型，得出酿酒葡萄和葡萄酒各项有效理化指标的正负相关关系。

关键词：显著性检验；聚类分析；主成分分析；多元回归。

一、问题的重述确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评。

每个评酒员在对葡萄酒进行品尝后对其分类指标打分，然后求和得到其总分，从而确定葡萄酒的质量。

红酒评级的科技与数据分析红酒作为一种具有浓厚文化底蕴和高端品质的酒类，一直以来都备受关注。

而对于红酒爱好者来说，了解不同品牌和产区的红酒评级成为了一种必备的技能。

而现代科技和数据分析的发展，为红酒评级带来了更为准确和便捷的方法。

在本文中，我们将探讨红酒评级的科技与数据分析的重要性和应用。

一、红酒评级科技的发展随着科技的进步和互联网的普及，红酒评级也逐渐与科技相结合，形成了一种新型的评级方式。

通过使用先进的科技手段，如人工智能、大数据分析和区块链技术等，收集和处理大量红酒相关的信息和数据，为红酒爱好者提供全面、准确的评级信息。

二、数据分析在红酒评级中的应用1. 评级指标的建立：数据分析帮助红酒评级建立起一套完整的评级指标体系。

通过分析红酒的各项数据，比如葡萄种植条件、酿造方法、口感特点等，确定不同参数对红酒品质的重要性，并建立起相应的评级体系。

2. 品鉴过程的辅助：传统的品鉴过程需要依赖专业品鉴师的经验和感觉，但这种主观性往往会带来评级的不准确性。

而借助数据分析技术，可以将一系列客观的指标纳入考量，例如颜色、香气、味道等，从而提高红酒评级的客观性和准确性。

3. 用户个性化推荐：通过分析红酒评级数据和用户的喜好，可以为用户提供个性化的红酒推荐。

根据用户的历史品鉴记录和对不同品牌、产区的评分，系统可以通过数据分析准确判断用户的口味偏好，进而为其推荐最符合其口味的红酒产品。

三、红酒评级科技的优势1. 提高评级准确性：传统的评级方式常常受到品鉴师主观意见的干扰，评级结果可能存在一定的主观性和不稳定性。

而采用科技手段进行红酒评级，可以从更多的客观数据中得出评级结果，避免主观因素的影响，提高评级的准确性和可靠性。

2. 提升评级效率：传统的红酒评级需要品鉴师花费大量时间和精力，而采用科技手段进行评级，可以减少人力成本和时间消耗，提升评级效率。

通过大数据分析和自动化技术，可以实现对大量红酒进行快速评级，为红酒爱好者提供更加及时准确的评级信息。

基于数据挖掘技术的红酒质量评价与等级划分研究红酒是一种受到广泛欢迎的酒类，在世界各地都有着众多的酒友和爱好者。

而红酒的品质和等级则成为了关注的重点之一，因为好的红酒能够为人们带来更美好的品尝体验。

然而，传统的红酒评价方式多为人工，时间和成本较高。

近年来，基于数据挖掘技术的红酒质量评价与等级划分研究越来越受到人们的关注。

一、数据挖掘技术与红酒质量评价数据挖掘技术是一种从大量数据中自动发现规律的方法，可以帮助人们快速准确地对红酒进行品质评价。

数据挖掘技术不仅包括了基础的数据统计和分析方法，还包括了人工智能、机器学习和深度学习等高级算法，可以更加准确地对红酒进行评价和分类。

在红酒质量评价中，数据挖掘技术主要通过构建模型实现。

模型的构建包括了特征提取、特征选择、模型训练和模型应用等多个过程。

其中，特征提取是数据挖掘技术的关键。

红酒的特征包括了多种成分和属性，如酒精度、酸度、甜度、色泽、气味等。

在特征提取中，需要选择合适的特征来对红酒进行描述和评价，同时，还需要对特征进行标准化和归一化等预处理操作。

二、基于数据挖掘技术的红酒品质等级划分方法基于数据挖掘技术的红酒品质等级划分方法主要包括了基于聚类的划分和基于分类的划分两种方法。

基于聚类的划分方法是将相似的红酒样本划分在一类中，不同的红酒样本则归为不同的类别。

在聚类过程中，需要选择合适的距离计算方法、聚类算法和聚类评价指标等。

在红酒品质等级划分中，可以选择基于距离的层次聚类或基于密度的DBSCAN聚类等算法来进行。

同时，也需要根据实际情况选择合适的聚类评价指标，如轮廓系数、DB指数等。

基于分类的划分方法是将红酒样本划分到已知的品质等级类别中。

在分类过程中，需要选择合适的分类算法和分类评价指标等。

在红酒品质等级划分中，可以选择k-NN、SVM、决策树等分类算法来进行。

同时，也需要根据实际情况选择合适的分类评价指标，如准确率、召回率、F1值等。

三、基于数据挖掘技术的红酒品质等级划分案例基于数据挖掘技术的红酒品质等级划分已经有一些实际应用案例。

全国大学生数学建模竞赛A题葡萄酒评价分析葡萄酒是一种古老而美妙的饮品，其种类繁多，风味各异。

如何对葡萄酒进行准确的评价和分析成为了葡萄酒爱好者和生产商们共同关注的问题。

在此次全国大学生数学建模竞赛A题中，我们将围绕葡萄酒的评价和分析展开讨论。

1. 引言葡萄酒是一种由葡萄经过发酵而成的酒类饮品。

葡萄酒的风味和品质受到许多因素的影响，如产地、葡萄品种、酿造工艺等。

为了准确评价葡萄酒的质量和特点，我们需要建立相应的评价指标和模型。

2. 数据分析为了进行葡萄酒评价，我们首先需要收集相关的数据。

通过对不同品牌、不同种类的葡萄酒进行采样和测试，我们可以获得葡萄酒的关键指标，如酒精含量、酸度、甜度、单宁含量等。

在数据分析中，我们可以运用统计学方法和数学建模技术，对数据进行整理和处理。

通过计算均值、方差、相关系数等指标，我们可以得到葡萄酒的基本特征和相互之间的关系。

3. 葡萄酒评价指标体系建立基于数据分析的结果，我们可以建立葡萄酒评价指标体系。

这一体系应该包含对葡萄酒各项指标的评价方法和权重。

常见的评价指标包括酒精含量、色泽、香气、口感等。

在指标体系中，我们可以采用层次分析法，通过对各个指标的重要性进行排序和评估。

同时，还可以利用数学模型，将各项指标综合起来，得到最终的评价结果。

4. 葡萄酒评价模型构建在对葡萄酒进行评价时，我们可以利用数学建模方法构建评价模型。

常用的模型包括多元回归模型、灰色关联度模型等。

多元回归模型可以用来分析葡萄酒各项指标之间的关系，进而预测葡萄酒的品质。

灰色关联度模型则可以用来度量葡萄酒各个指标对品质的影响程度。

通过不断地调整模型和参数，我们可以得到更准确的葡萄酒评价结果，并为葡萄酒生产商提供有针对性的改进建议。

5. 葡萄酒评价系统设计为了方便葡萄酒评价和分析的实施，我们可以设计一个葡萄酒评价系统。

该系统可以包括数据输入、数据处理、指标评价、模型计算等功能模块。

数据输入模块用于将葡萄酒相关数据录入系统。

基于机器学习的红酒质量检测研究随着世界科技的不断进步和发展，人工智能技术也逐渐走向成熟。

在各行各业中，人工智能技术已经开始发挥其独特的优势，掀起了一场马不停蹄的技术革命。

其中，基于机器学习的红酒质量检测研究已经成为了该领域中的一个热点话题。

红酒的质量往往是影响消费者购买的一大关键因素。

传统的红酒质量检测方式采用人工品尝鉴定，不仅耗时费力，而且还存在主观的偏差和误判，无法保证判定结果的准确性。

而基于机器学习的红酒质量检测则可以有效地解决上述问题，实现自动化、精确化、快速化检测。

首先，咱们来了解一下机器学习的基本概念。

机器学习是一门人工智能领域的重要分支，它通过计算机程序模拟人类学习的过程，从而使计算机能够进行自主学习和探索数据规律。

在红酒质量检测中，机器学习算法会自动从大量的历史数据中提取特征，建立相应的模型，并对新的红酒质量数据进行预测鉴定。

那么，机器学习如何应用在红酒质量检测中呢？首先，我们需要有一个足够的数据集进行训练。

这些数据集可能包括红酒的产地、葡萄品种、酒精度、pH值等多个方面的信息。

然后，我们需要选择适合的机器学习算法进行训练和预测。

常见的算法包括支持向量机（SVM）、决策树（Decision Tree）、随机森林（Random Forest）等。

这些算法具有不同的特点和适用范围，需要根据具体情况进行选择。

最后，我们需要对模型进行评估和优化，以保证其准确性和稳定性。

随着机器学习技术的不断发展和完善，基于机器学习的红酒质量检测已经取得了一定的研究成果。

例如，澳大利亚南澳大学的研究人员利用机器学习算法，成功分类了超过6000种来自54个国家的红酒。

同时，该研究还通过与人工品鉴比较，证明了机器学习的鉴定结果更为准确可靠。

然而，基于机器学习的红酒质量检测也存在一些挑战和限制。

首先，数据集的质量和数量会直接影响模型的准确性和可靠性。

如果数据集过小或者存在大量的噪声数据，那么模型很难学习到有效的信息，导致鉴定结果不准确。

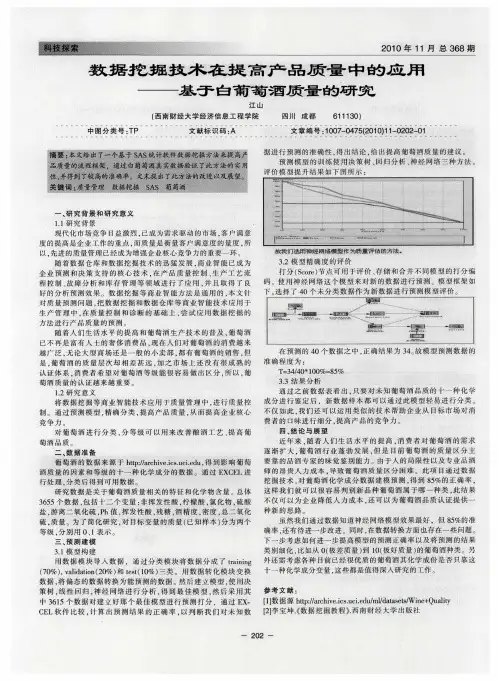
基于数据分析的葡萄酒评价模型摘要本文就葡萄酒的评价问题进行了分析研究，首先对所有评酒员的评分结果采用逐对比较法()1(2-≥=hn t hns hd ht hdα)和双样本t 假设检验法进行分析，然后对葡萄和葡萄酒的理化指标基本数据进行统计分析及无量纲化处理，再对其用主成分分析法(),,2,1,(),(p j i e x z p l ij i j i ij ===λ)、典型性相关分析法、多元线性规划分析法（[][]alpha X Y regress stats r b b ,,int,int,,=，int),(r r rcopht ）和TOPSIS 法（n j m i a a b mi ijijij ,,2,1,,,2,1,12===∑=）进行相关性分析，最后针对各个问题建立模型求解.针对问题一，我们首先利用EXCEL 对葡萄酒品尝评分表的分数数据进行处理，然后利用MATLAB 软件绘制出所有葡萄酒样品的分数曲线图，因为样本总体相同，i i y x -服从正态分布，采用逐对比较法得到两组红白葡萄酒综合评价的差值,确定出两组评分无显著性差异.再利用双样本t 假设检验方法判断最终得出第二组评酒员的评分结果更可信.针对问题二，我们首先利用EXCEL 及MATLAB 软件对附件二指标总表中的一、二级指标数据分别进行处理，然后利用主成份分析法，用贡献率（),,2,1(1p i pk ki=∑=λλ）对各主成分加权求和，得到样本总得分，由于我们在问题一中已得出第二组评酒员的评分结果更可信，故设样本总得分与第二组数据符合二八原理，计算得到一组综合分数，最终分析确定红葡萄可分为五个等级，白葡萄可分为六个等级.针对问题三，我们首先对酿酒葡萄和葡萄酒的理化指标数据进行预处理，提取两个有代表性的综合变量，再利用典型性相关分析处理得到两组指标之间的整体相关性联系，呈现出对应相关关系.针对问题四，由于在问题三中已得出酿酒葡萄和葡萄酒的理化指标之间存在着整体相关关系，我们首先对附件二指标总表中的数据进行无量纲化处理，然后采用多元线性回归分析得到酿酒葡萄和葡萄酒的理化指标与葡萄酒质量(分数)的线性相关关系，最后利用TOPSIS 法论证确定出不能用葡萄和葡萄酒的理化指标来评价葡萄酒的质量.关键字 t 假设检验 无量纲化 主成分分析 典型性相关分析 多元线性规划分析一问题提出1.1问题重述确定葡萄酒质量时一般是通过聘请一批有资质的评酒员进行品评.每个评酒员在对葡萄酒进行品尝后对其分类指标打分，然后求和得到其总分，从而确定葡萄酒的质量.酿酒葡萄的好坏与所酿葡萄酒的质量有直接的关系，葡萄酒和酿酒葡萄检测的理化指标会在一定程度上反映葡萄酒和葡萄的质量.附件1给出了某一年份一些葡萄酒的评价结果，附件2和附件3分别给出了该年份这些葡萄酒的和酿酒葡萄的成分数据.请尝试建立数学模型讨论下列问题：1. 分析附件1中两组评酒员的评价结果有无显著性差异，哪一组结果更可信？2. 根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分级.3. 分析酿酒葡萄与葡萄酒的理化指标之间的联系.4．分析酿酒葡萄和葡萄酒的理化指标对葡萄酒质量的影响，并论证能否用葡萄和葡萄酒的理化指标来评价葡萄酒的质量？1.2 问题分析问题要求我们通过研究葡萄酒和酿酒葡萄的理化指标以及葡萄酒的品尝评分，分析评价结果的差异性、可信度，以及酿酒葡萄对葡萄酒质量之间的影响，说明酿酒葡萄与葡萄酒的理化指标之间的关系，确定是否能用葡萄酒和葡萄的理化指标来评价葡萄酒的质量.问题一，根据附件一中两组品酒员对红白两种葡萄酒的评分，利用逐对比较法得出hd,bd,hs,bs,hd,bd,再得出btht,值，在利用双样本均值差t检验法得出两组评价结果有无显著性差异，再对所得数据进行双样本t假设检验方法判断哪组更可信.问题二，根据附件二中酿酒葡萄的理化指标，先对每种含量进行求和再平均，（见附录三表三、表四），然后利用主成分分析法，得出所有成分中的主成分、特征值特征向量以及主成分得分等，最后利用贡献率对主成分得分加权，得出一组得分，将总得分与附件一中二组的数据根据一定的比例进行加权计算，得到总得分，对总得分进行排序，就得到了酿酒葡萄的分级.问题三，针对本问题，先提取两组变量中具有代表性的数据，利用典型性分析，对这些数据建模求解，得到一个整体的相关性.反应酿酒葡萄与葡萄酒理化指标之间的联系.问题四，因为酿酒葡萄和葡萄酒的理化指标之间有联系，所以在考虑他们对葡萄酒质量影响时，可以把它们两个综合起来考虑对葡萄酒质量的影响，即希望能建立一种关系，所以用多元线性回归分析，这样便能得出它们对葡萄酒的质量有否影响.二模型假设1、假设题目所给数据真实可靠.2、假设每组评酒员品的是同一样酒.3、假设附件一中评酒员的评价结果反映了葡萄酒的质量.4、假设葡萄酒样品和葡萄酒一一对应，例如27号红葡萄酒是由27号红葡萄生产而来.5、假设二级指标影响很小，我们可以忽略它的影响.6、不考虑因个人口味、爱好不同对葡萄酒打分的影响，不考虑因环境等不同对葡萄酒和葡萄理化指标的影响.三符号说明x:第一组得分.y:第二组得分.hx:第一组每位品酒师对每个红酒样品各个方面评分的和，即综合评价.bx:第一组每位品酒师对每个白酒样品各个方面评分的和，即综合评价.hy:第二组每位品酒师对每个红酒样品各个方面评分的和，即综合评价.by:第二组每位品酒师对每个白酒样品各个方面评分的和，即综合评价.hd:两组红葡萄酒综合评价的差值.bd:两组白葡萄酒综合评价的差值.hs:hd的标准差.bs:bd的标准差.hd:hd的平均值.bd:bd的平均值.hn:红葡萄酒样品个数，即27.bn:白葡萄酒样品个数，即28.四模型建立与求解问题一1、数据处理利用附件一中的数据，求出每个评酒员对每个酒样评价的综合评分，用MATLAB 对这些数据进行处理，见附录三（表一，表二）.2、模型建立我们首先考虑对每个样品的十个综合评分求平均值，用MATLAB作图（见下图），结果不能判断有无显著性差异.然后采用逐对比较法，以红葡萄酒为例：红葡萄酒共有27对相互独立的观察结果：),(,),,(),,(27272211hy hx hy hx hy hx ，令272727222111,,,hy hx hd hy hx hd hy hx hd -=-=-= ，则2721,,,hd hd hd 相互独立，又由于2721,,,hd hd hd 是有统一因素所引起的，可认为他们服从同一分布.今假设i hd ～),(2hd hd N δμ，27,,2,1 =i .这就是说2721,,,hd hd hd 构成正态总体),(2hd hd N δμ的一个样本，其中2,hd hd δμ未知.我们需要基于这一样本检验假设： （1）;0:,0:10≠=hd hd H H μμ （2）;0:,0:10〉≤hd hd H H μμ (3) ;0:,0:10〈≥hd hd H H μμ分别记2721,,,hd hd hd 的样本均值和样本方差的观察值,hd 2hd s .检验问题（1），（2），（3）的拒绝域分别为（显著性水平为α）：)1(2-≥=hn t hns hd ht hdα，)1(-≥=hn t hns hd ht hdα， )1(--≤=hn t hns hd ht hd α.现在回过来讨论本例的检验问题.先做出同一试块分别由y x h h ,测得的结果之差.按题意需检验假设;0:,0:10≠=hd hd H H μμ现在4786.2)26()26(,27005.02===t t h n ε即知拒绝域为4786.2≥=hns hd ht hd.若4786.2〈ht ，则t 的值不落在拒绝域内，故接受0H ，认为两组对红葡萄酒的评分无显著性差异，反之则反. 3、 模型求解利用逐对比较法（程序见附录二附件一），求出ht 与bt （见图1），在α=0.01下进行t 分布的显著性分析，得出两组评酒员的评价结果无显著性差异，再对数据进行双样本均值差t 检验法（见图二），结果得出二组更可信.问题二1、 数据分析首先对附件二酿酒葡萄的理化指标进行数据处理（见附录三表三、表四） 2、 模型建立1）计算相关系数矩阵⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=pp p p p p r r r r r r r r r R 212222111211... （1） ij r （p j i ,...2,1,=）为原变量的i x 与j x 之间的相关系数，其计算公式为∑∑∑===----=nk nk j kj i kij j k nk i ik j i x x x xx x x xr 11221)()()()( （2）因为R 是是对称矩阵（即i j j i r r =），所以只需计算上三角元素或下三角元素即可. 2）计算特征值与特征向量首先解特征方程0=-R I λ,通常可用雅可比法（Jacobi ）求出特征值),,2,1(p i i =λ，并使其按顺序大小排列，即0...,321≥≥≥≥p λλλλ；然后分别求出对应于特征值i λ的特征向量),,2,1(p i e i =.这里要求,1=即∑==pj ij e 121，其中ij e 表示向量i e 的第j 个分量.3）计算主成分贡献率及累计贡献率 主成分i z 的贡献率i α为),,2,1(1p i pk ki=∑=λλ累计贡献率为),,2,1(11p i pk kik k=∑∑==λλ一般取累计贡献率达85-95%的特征值m λλλλ,,,,321 所对应的第一、第二、第)(p m m ≤个主成分. 4）计算主成分载荷量 其计算公式为),,2,1,(),(p j i e x z p l ij i j i ij ===λ （3）得到各主成分的载荷后，利用特征向量，得到各主成分的得分⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡=nm n n m m z z z z z z z z z Z 212222111211 （4）5）主成分分析用于系统评估利用主成分p z z z ,,,21 做线性组合，并以每一个主成分i z 的方差贡献率i α作为权数，构造一个综合评价函数p p z z z y ⋅++⋅+⋅=ααα 2211 （5） 也称y 为评估指数，依据对每个样品得出的y 值进行分级. 3、 模型求解利用MATLAB 编写程序，得出y 的值.(程序见附录二附件二) 得出的y 值越大说明酿酒葡萄的质量越高，葡萄酒质量的衡量用附件一中二组的数据（由题一知二组比一组更可靠），利用二八原理得出葡萄酒和酿酒葡萄的综合得分（见附录三表五），找出最大值max ，最小值min ，组距6min)(max -=d ，红葡萄酒得出5个小区间，划分为5个等级，白葡萄酒得出6个小区间，划分为6个等级，划分等1、 数据分析在两组变量中提取有代表性的两个综合变量，对综合变量进行标准化处理（见附录二附件三），利用这两个综合变量之间的相关关系来反映两组指标之间的整体相关性.2、 模型建立本模型对两组指标酿酒葡萄和葡萄酒的理化指标作典型相关分析.其中， 酿酒葡萄指标：211,,A A葡萄酒的理化指标：3022,,A A第一步，计算相关系数阵3030)(⨯=ij r R ，具体结果见附录表1A 2A … 29A 30A⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡--------0000.13113.02401.03680.03113.00000.13486.01073.02401.03486.00000.11097.03680.01073.01097.00000.1302921A A A A 第二步，典型相关系数及其检验，将酿酒葡萄指标和葡萄酒的理化指标数据经过整理利用 MATLAB 软件的canoncorr 函数进行处理，得出如表1所示结果：由表1可知，前6个典型相关系数均较高，表明相应典型变量之间密切相关.进行相关系数的2χ统计量检验确定典型变量相关性的显著程度，比较统计量2χ计算值从上表得知这9对典型变量均通过统计量检验，表明相应典型变量之间相关关系显著，酿酒葡萄与葡萄酒的理化指标之间有相关联系.第三步：典型相关模型由于原始变量的计量单位不同，不宜直接比较，本文采用标准化的典型系数，给出典型相关模型，如公式⑴～⑹所示⎪⎪⎪⎩⎪⎪⎪⎨⎧+++++=++++++++++++-=302928272625242322121201918171615141312111098765432110.1859A -0.1243A 0.8060A0.9033A - 0.1438A 0.7253A 1.1161A -0.5222A 0.9882A V0.2576A - 0.6898A 0.6145A 0.3881A 0.8054A -0.9221A -0.0797A 0.8424A 0.1035A-0.1112A 0.6588A 0.5552A - 0.6333A - 0.8875A 2.1858 -0.53080.07880.53010.0333- 0.14192666.0 A A A A A A A U ⑴ ⎪⎪⎪⎩⎪⎪⎪⎨⎧++++++=++++++++=302928272625242322221201918171615141312111098765432120.3811A 1.0582A 1.9635A0.7222A 0.6133A - 1.1626A -2.8979A 1.2812A - 0.5658A V0.2346A 0.2256A -0.1844A 0.1093A 0.0087A -1.4993A 0.1513A 0.7407A - 0.6954A-0.6504A - 0.3317A - 0.1804A - 0.0854A - 0.6617A -0.7315 0.2775 0.4173- 0.0114 0.0908- 0.8853-0.1777 A A A A A A A U ⑵ ⎪⎪⎪⎩⎪⎪⎪⎨⎧+-+++=+++++-+++++=302928272625242322321201918171615141312111098765432130.6108A 1.1652A -0.2270A0.2647A 0.5229A 0.4005A 1.3208A -0.3465A -0.0115A V0.7740A 0.0768A 0.1494A - 0.5894A 0.7736A 0.8003A 0.0571A 0.0390A -0.1631A - 0.1316A 0.3281A - 0.3523A - 0.5051A 0.7135A -1.9691 1.6219-0.6603 1.1176-0.4611- 0.0626 -0.1341A A A A A A A U ⑶ ⎪⎪⎪⎩⎪⎪⎪⎨⎧-++++=++++++++++++=302928272625242322421201918171615141312111098765432140.8632A - 0.6128A -2.1413A0.3405A 0.1296A 0.1725A 1.7119A -1.1137A 2.7421A - V0.4821A 0.2111A -0.0337A - -0.4764A 0.8511A - 3.8525A -0.4394A -0.8279A 0.7593A 1.6148A 1.4068A 0.0829A 0.4232A -1.5406A 2.0668 -0.90220.17060.2461-0.5411 0.1621-0.0964A A A A A A A U ⑷ ⎪⎪⎪⎩⎪⎪⎪⎨⎧-+++=+++++++++++=302928272625242322521201918171615141312111098765432150.9032A -0.5843A -1.5873A0.0911A - 0.1586A 0.1056A 1.3940A 1.8497A -1.4755A - VA 0.2073 0.0210A 0.6044A - 0.1196A - 0.8591A 0.2084A 0.2593A -0.1736A - 0.7033A - -0.3871A - 0.0474A 0.1275A - 0.3342A 0.0629A - 1.6602 -1.22400.1262 0.3456- 0.4287- 0.2810 -0.0774A A A A A A A U ⑸ ⎪⎪⎪⎩⎪⎪⎪⎨⎧-++=+++++++++++++=302928272625242322621201918171615141312111098765432160.0113A - 0.2930A -1.2336A 0.5983A 0.6340A 1.1863A -1.1943A -0.1001A -0.1006A V1.1199A 1.6234A -0.5710A - 0.4459A 1.2038A 1.1480A -1.0176A -0.2293A 0.1792A0.1712A 0.4702A 0.3912A 0.8888A 0.0378A - 1.1037 2.3197-0.59180.4889-0.2723 0.3094 0.3201- A A A A A A A U ⑹ 3、结果分析由公式⑴典型相关方程可知，酿酒葡萄的主要指标是7A ,8A ,14A ,16A ,17A ,说明酿酒葡萄中影响葡萄酒理化指标的主要因素是总酚(7A )、单宁(8A )、PH(14A )、干物质含量(16A )、果穗质量(17A )，葡萄酒的第一典型变量1V 与22A ,24A ,27A ,28A 呈高度相关；根据公式⑵典型相关方程，2A (花色苷)是酿酒葡萄的主要因素，葡萄酒的第二典型变量2V 与23A ,24A ,25A ,28A ,29A 呈高度相关；公式⑶中酿酒葡萄的主要指标是6A ,7A ,16A ,葡萄酒的第三典型变量3V 与24A ,29A 呈高度相关；公式⑷酿酒葡萄的主要指标是6A ,7A ,8A ,11A ,12A ,14A ,17A ,葡萄酒的第四典型变量4V 与22A ,23A ,24A ,28A 呈高度相关；公式⑸酿酒葡萄的主要指标是6A ,7A ,葡萄酒的第五典型变量5V 与22A ,23A ,24A ,28A 呈高度相关；公式⑹酿酒葡萄的主要指标是15A ,16A ,17A ,20A ,21A ，葡萄酒的第六典型变量6V 与24A ,25A ,28A 呈高度相关.由于第一组典型变量信息比重较大，所以总体上酿酒葡萄与葡萄酒主要理化高度相关的主要指标是7A ,6A ,16A ,17A ,8A ,14A ,2A ,11A ,12A ,14A ,15A ,20A ,21A ，反映葡萄酒的理化指标与酿酒葡萄高度相关的指标为22A ,23A ,24A ,25A ,27A ,28A ,29A .问题四1、模型建立[][]alpha X Y regress stats r b b ,,int,int,,= int),(r r rcophtn j m i aa b mi ijijij ,,2,1,,,2,1,12 ===∑=程序见附表二附件，残差图见附录一图三、图四. 2、结果分析 以红葡萄酒为例 2997.5;5148.7010==ββ y =70.5148+5.29971x ,9842.02=r ;(越接近于1，回归效果越显著) 05.00255.0≤=p ，回归模型成立.从残差图可以看出，除第8,11,20三个数据外,其余数据的残差离零点均较近，且残差的置信区间均包含零点，这说明回归模型y =70.5148+5.29971x ,能较好的符合原始数据，而这三个个数据可视为异常点. 同理，白葡萄的多元线性回归成立. 用TOPSIS 法，对能否用葡萄酒和葡萄酒的理化指标来评价葡萄酒的质量进行分析， （1）用向量规划化的方法求得规范决策矩阵。