第10章波动光学10.1-10.7

第7章气体动理论1.7 对气体状态的描述7.2 气体的压强和温度7.3 能量均分定理7.4 麦克斯韦速率分布律7.5 麦克斯韦 玻耳兹曼分布律7.6 麦克斯韦速率分布律的实验验证7.7 实际气体的状态方程7.8 碰撞及输运过程提要思考题习题第8章热力学基础8.1 热力学第一定律8.2 几个典型过程的分析8.3 循环过程8.4 热力学第二定律8.5 熵、熵增加原理提要思考题习题第9章振动与波动9.1 简谐振动9.2 两个简谐振动的合成9.3 阻尼振动受迫振动共振9.4 简谐波9.5 惠更斯原理9.6 波的叠加干涉驻波9.7 多普勒效应9.8 波动方程和波速提要思考题习题第10章波动光学10.1 光源发光机理和获得相干光的方法10.2 光的干涉10.3 双缝干涉10.4 半波损失的实验验证10.5 厚度均匀薄膜干涉——等倾干涉10.6 劈尖干涉——等厚干涉10.7 光的衍射10.8 夫琅禾费单缝衍射10.9 夫琅禾费圆孔衍射10.10 光栅和光栅衍射10.11 光的偏振10.12 偏振光的干涉提要思考题习题第11章狭义相对论基础11.1 狭义相对论的基本假设11.2 洛伦兹变换11.3 时间延缓和长度收缩11.4 相对论速度变换11.5 相对论动力学基础提要思考题习题第12章量子物理基础12.1 能量子假设12.2 光的粒子性12.3 粒子的波动性和波函数12.4 薛定谔方程粒子的波动性和波函数12.5氢原子理论。

大学物理波动光学-(带目录)大学物理波动光学摘要：波动光学是大学物理课程中重要的组成部分，主要研究光的波动性质及其在介质中的传播规律。

本文主要介绍了波动光学的基本概念、波动方程、干涉现象、衍射现象、偏振现象以及光学仪器等，旨在为读者提供系统的波动光学知识，为进一步学习和研究打下基础。

一、引言波动光学是研究光波在传播过程中所表现出的波动性质的科学。

光波是一种电磁波，具有波动性、粒子性和量子性。

波动光学主要关注光的波动性质，研究光波在介质中的传播、反射、折射、干涉、衍射、偏振等现象。

波动光学在科学技术、工程应用、日常生活等领域具有广泛的应用，如光纤通信、激光技术、光学仪器等。

二、波动方程波动方程是描述波动现象的基本方程。

光波在真空中的传播速度为c，介质中的传播速度为v。

波动方程可以表示为：∇^2E(1/c^2)∂^2E/∂t^2=0其中，E表示电场强度，∇^2表示拉普拉斯算子，t表示时间。

该方程描述了光波在空间和时间上的传播规律。

三、干涉现象1.极化干涉：当两束相干光波在空间某点相遇时，它们的电场矢量方向相同，相互加强，形成明条纹；当电场矢量方向相反，相互抵消，形成暗条纹。

2.非极化干涉：当两束相干光波在空间某点相遇时，它们的电场矢量方向垂直，相互叠加，形成干涉条纹。

四、衍射现象衍射现象是光波传播过程中遇到障碍物或通过狭缝时产生的现象。

衍射现象的本质是光波的传播方向发生改变，使得光波在空间中形成干涉图样。

衍射现象可以分为菲涅耳衍射和夫琅禾费衍射两种：1.菲涅耳衍射：当光波通过狭缝或障碍物时，光波在衍射角较小的情况下发生的衍射现象。

菲涅耳衍射的衍射图样与狭缝或障碍物的形状、大小以及光波的波长有关。

2.夫琅禾费衍射：当光波通过狭缝或障碍物时，光波在衍射角较大的情况下发生的衍射现象。

夫琅禾费衍射的衍射图样与狭缝或障碍物的形状、大小以及光波的波长有关。

五、偏振现象偏振现象是光波在传播过程中，电场矢量在空间某一方向上振动的现象。

《大学物理》课程标准课程代码：课程名称 : 大学物理英文名称： College Physics课程类型：专业必修课总学时： 144授课学时：108实践学时:36学分： 8适用对象：机械类及相近专业本科学生一、课程概述大学物理是高等院校非物理类理工科本科各专业学生一门重要的通识性必修基础课。

物理学是研究物质的基本结构、基本运动形式、相互作用的自然科学。

它的基本理论渗透在自然科学的各个领域，应用于生产技术的许多部门，是其他自然科学和工程技术的基础。

课程所教授的基本概念、基本理论和基本方法是构成学生科学素养的重要组成部分，是一个科学工作者和工程技术人员所必备的。

该课程在培养学生的探索精神和创新意识等方面，具有其他课程不能替代的重要作用。

二、课程目标通过本课程的学习，使学生逐步掌握物理学研究问题的思路和方法，在获取知识的同时，学生建立物理模型的能力，定性分析，估算与定量计算的能力，独立获取知识的能力，理论联系实际的能力获得同步提高与发展。

开阔思路，激发探索和创新精神，增强适应能力，提升其科学技术的整体素养。

同时，使学生掌握科学的学习方法和形成良好的学习习惯，养成辩证唯物主义的世界观和方法论。

三、课程的内容与要求（一）教学基本要求与内容第一部分力学.第1章运动学1.1 质点运动的描述1.2 加速度为恒矢量时的质点运动1.3 圆周运动1.4 相对运动基本要求：1.深入地理解质点、位移、速度和加速度等重要概念，深入理解质点的运动。

2.分析加速度为恒矢量时的质点运动方程。

3.明确圆周运动中角位移、角速度、切向加速度、法向加速度的关系。

重点与难点 :1.加速度为恒矢量时质点运动方程的描写。

2.质点圆周运动的分析。

第2章牛顿定律2.1 牛顿定律2.2 物理量的单位和量纲2.3 几种常见的力2.4 惯性参考系力学相对性原理基本要求：1.清晰的理解牛顿第一定律、牛顿第二定律和牛顿第三定律。

2.熟练掌握几种常见力。

3.掌握物理量的单位和量纲。

第十章第十章第十章第十章 波动光学波动光学波动光学波动光学思考题思考题思考题思考题10-1 普通光源中原子发光有何特征？答答答：答：：：因为普通光源是大量不同原子在不同时刻发的光，是自然光，因此不满足干涉条件，所以一 般普通光源观察不到干涉现象。

10-2 如何用实验检验一束光是线偏振光、部分偏振光还是自然光？答答答：答：：：拿一块偏振片迎着这束光，转动偏振片，观察透射光。

（1）视场中光强有变化且有消光现象 的为线偏振光；（2）光强有变化但无消光现象的为部分偏振光；（3）光强无变化的为自然光。

10-3 自然光可以用两个独立的、相互垂直的、振幅相等的光振动表示。

那么线偏振光是否也可以用两个相互垂直的光振动表示？如果可以，则这两个相互垂直的光振动之间关系如 何？10-4 如何用实验测定不透明媒质的折射率？答答答：答：：：光线入射到不透明的媒介上，改变入射角i ，并同时用偏振片测定反射光线的偏振化程度。

当反射光线为完全偏振光时，此时入射角i0 即为布儒斯特角，满足tan 可求得不透明介质的折射率n 。

10-5 如图(a)所示，一束自然光入射在方解石晶体的表面上，入射光线与光轴成一定角度；问将有几条光线从方解石透射 出来？如果把方解石切割成等厚的A 、B 两块，并平行地移 开很短一段距离，如图(b)所示，此时光线通过这两块方解石后有多少条光线射出来？如果把B 块沿沿沿沿光线转过一个角度， 此时将有几条光线从B 块射出来？为什么？i 0n ，测得 i0 即考思考思考思考题题题题10-5图图图图10-6 从普通光源获得两束相干光的一般方法是什么？在光的干涉中决定相遇点产生明纹或暗纹的因素是什么？答答答：答：：：分波阵面法和分振幅法。

波源的相位差和波源到相遇点的光程差决定相遇点产生明纹或暗纹。

10-7 如图所示，设光线a 、b 从周相相同的A 、B 点传至P 点，试讨论：（1）在图中的三种情况下，光线a 、b 在相遇处P 是 否存在光程差？为什么？（2）若a 、b 为相干光，那么在相遇处的干涉情况怎 样？考题思考题思考题思考题 10-7 图图图图10-8 在杨氏双缝实验中，当作如下调节时，屏幕上的干涉条纹将如何变化？（要说明理由）（1）使两缝之间的距离逐渐减小；（2）保持双缝的间距不变，使双缝与屏幕的距离逐渐减小；（3）如图所示，把双缝中的一条狭缝遮住，并在两缝的垂直平分线上放置一块平面反射镜。

第1章 刚体力学基础 物体的弹性1.1 （1）n=))(1(54013--⋅-s r e(2) )(10802160)1(54036026r e dt e dt N t --+=-==⎰⎰ω(3) )(27022--⋅==s r e dtdntβ 1.4 A 对物体：Mg-T=Ma 对滑轮：β221mR TR =βR a = 联立求解，得：MRmR Mg22+=βB 对滑轮：β221mR MgR =得：mRMg2=β 1.6 对物体：a m g m f T 22sin =--α αμsin 2g m f =对滑轮：β2121R m TR M z =- βR a =解得：[]Rm R m R u g m M m g m T Z 1222221)cos (sin )cos (sin ++-++=αααμα2122221)cos (sin R m R m Rg m M Z ++-=αμαβ由角量的运动方程：βθω22=[]2122221)cos (sin 2Rm R m R g m M Z ++-=αμαθω1.8 人和转盘组成的系统角动量守恒ωω)21(2122202t mu MR MR +=222022tmu MR MR +=ωω RutM m u R m M dt t mu MR MR dt tt 2arctan 220222020ωωωθ=+==⎰⎰1.12 解：（1）成人股骨断裂的压力)(1002.11061017547N S F ⨯=⨯⨯⨯=⋅=-σ（2）股骨断裂的线应变2107109.1109.01017-⨯=⨯⨯==E σε （3）长度的改变量)(105.95.0109.132m l l --⨯=⨯⨯=⋅=∆ε第2章 流体力学基础2.1 解：（1）主动脉血液流量)/(104.833.0)109(14.335231211s m V r V S Q --⨯=⨯⨯⨯=⋅==π (2)大动脉血液的平均流速)/(102.4222s m S QV -⨯==（3）毛细血管内血液的最大流速)/(1036.3433s m S QV -⨯==2.4 解：（1）)/(1s m S QV ==粗粗 （2）)/(4s m S QV ==细细 （3）2222112121v P v P 水水ρρ+=+=-=-2122212121v v P P 水水ρρgh 银ρ cm gv v h 5.5)212122=-=∴银水（ρρ2.8 解：（1）毛细血管两端血压降)10410214.3101100.3866.010214.381246-3326-4a P R l Q P （）（）（细⨯=⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯==∆-πη （2）毛细血管内血液的流量)/103.8312s m SV Q （细-⨯==（3）流阻)/(108.485234m Ns Rl⨯==πηβ 2.9根据伯努利方程，可得单位体积的油损耗的能量w=)(2121h h g p P -+-ρ 代入数值得：Jw 43310*29.45*8.9*10*9.010*2.1=+-=那么 35m 的油流过损失的能量为5*J 410*29.4J 510*145.2=第3章 振动与波 声波 超声和超声成像3.1解：矢量图略 画旋转矢量图可得1）)cos(πω+=t A x 2）)2/cos(πω+=t A x 3）)3/cos(πω+=t A x ； 4）)4/cos(πω+=t A x ；3.2 解：由图示可知 A v v m x ma ω-== T=0时， 6/,210πϕ==据此可以求得初相位m v v3.6解： )cos()cos(221πωω+==t A x t Ax ，该质点的合振动为)cos(2π+=wt Ax3.7 解：（1）因为p 1点振动方程为)2cos(1ϕπν+=t A y ，而p 2点落后p 1点的距离为L 1+ L 2， 所以p 2点的振动方程为])(2cos[212ϕλνπ++-=L L t A y（2）与p 1点相距λk ±的点与p 1点的振动状态相同。

波动光学第一节 光的干涉一、光波的相干叠加1、光波叠加原理：每一点的光矢量等于各列波单独传播时在该点的光矢量的矢量和。

2、光波与机械波相干性比较：（1)相同点：相干条件、光强分布。

（2)不同点：发光机制不同。

3、从普通光获得相干光的方法：(1)分波阵面法：将同一波面上不同部分作为相干光源。

(2)分振幅法：将透明薄膜两个面的反射（透射）光作为相干光源。

4、光程与光程差：（1）光程：即等效真空程：Δ=几何路程×介质折射率。

（2）光程差：即等效真空程之差。

5、光程差引起的相位差：Δφ=φ2-φ1+λ∆∏2，Δ为光程差，λ为真空中波长。

（1）Δφ=2k ∏时，为明纹。

（2）Δφ=（2k+1)∏时，为暗纹。

6、常见情况：（1）真空中加入厚d 的介质，增加（n-1)d 光程。

（2）光由光疏介质射到光密介质界面上反射时附加λ/2光程。

（3）薄透镜不引起附加光程。

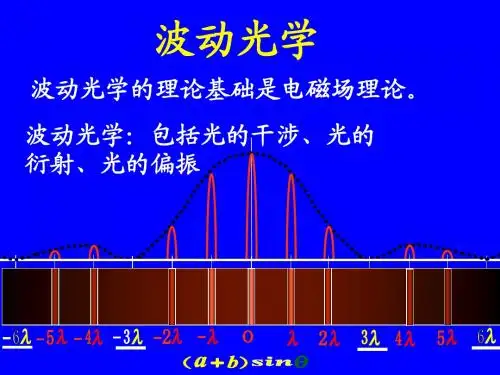
二、分波面两束光的干涉1、杨氏双缝实验：（1）Δ=±k λ时，（k=0,1,2,3……）为明纹。

Δ=±（2k-1)2λ时，（k=1,2,3……）为暗纹。

（2）x=λdD k ±时，为明纹。

x=2)12(λd D k -±时，为暗纹。

(k=0,1,2,……) （3）条纹形态：平行于缝的等亮度、等间距、明暗相间条纹。

（4）条纹亮度：Imax=4I1,Imin=0.（5）条纹宽度：λdD x =∆. 2、其他分波阵面干涉：菲涅耳双棱镜、菲涅耳双面镜。

三、分振幅干涉1、薄膜干涉：2sin 222122λ+-=i n n e Δ反（2λ项：涉及反射，考虑有无半波损失） 透Δi n n e 22122sin 2-=（无2λ项） 讨论：（1）反Δ/透Δ=k λ时，(k=1,2,3……）为明纹，（2k+1)2λ时，（k=0,1,2……）为暗纹。

（2）等倾干涉：e 一定，Δ随入射角i 变化。

（3）等厚干涉：i 一定，Δ随薄膜厚度e 变化。

第十章 波动光学第1课 电磁波 光的电磁本性教学目标：1.了解电磁场和电磁波的一般概念2.了解电磁波的性质及电磁波谱。

教学重点：光的电磁性 教学难点：物质发光的原理教学资源：网络视频、图片、多媒体设备 教学方法：讲授法、演示法、练习法 课 时：2 教学过程：引入课题：人们对光（这里主要指可见光）的规律和本性的认识经历了漫长的过程。

最早也是最容易观察到达规律是光的直线传播。

在机械观的基础上，人们认为光是一些微粒组成的，光线就是这些微粒的运动路径。

但人们已觉察到许多光现象可能需要用波动来解释，如牛顿环。

与牛顿同时代的惠更斯明确提出光是一种波动，直到进入19世纪，才由托马斯.杨和菲涅尔从实验和理论上建立起一套比较完整的光的波动理论。

19世纪中叶光的电磁理论的建立使人们对光波的认识更深入了一步，19世纪末麦克耳孙的实验及爱因斯坦的相对论更完善了光的波动理论。

本书关于光的波动规律基本上还是近200年前托马斯.杨和菲涅尔的理论。

但许多应用实例是现代化的。

正确的基本理论是不会过时的，而且它的应用将随时代的前进而不断翻新，现代的许多高新技术中的精密测量与控制就应用了光的干涉和衍射原理。

激光的发明也是40年前的事情。

人们对光的理论的认识也没有停止，20世纪初从理论和实验上证实了光具有粒子性，波动光学本身也在不断发展，光孤子就是一例。

本章主要光的波动理论及一些应用。

讲授新课： 一、电磁波的产生 1 无阻尼自由电磁振荡在电路中，电荷和电流以及与之相伴的电场和磁场的振动，称为电磁振荡。

LC 电磁振荡电路就是一种无阻尼的电磁振荡。

开关K 板向右边，使电源对电容器C 充电。

开关K 板向左边，使电容器C 和自感线圈L 相连接。

设某一时刻电路中的电流为i ，此时刻的自感电动势 由于 则令 则有 其解为无阻尼自由振荡中的电荷和电流随时间的变化KAB LCA B d d i qL V V t C ==-22d 1d q q t LC =-d d q i t=222d d q q o tω+=0cos()q Q ω t ϕ=+在LC 振荡电路中，电荷和电流都随时间作周期性变化，相应的电场和磁场能量也都作周期性的变化。