第四讲 共点力平衡

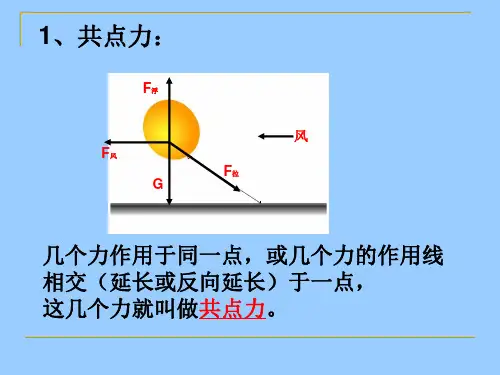
《共点力的平衡条件》讲义一、共点力的概念在物理学中，共点力是指几个力作用在物体上的同一点，或者它们的作用线相交于同一点。

例如，悬挂在天花板上的吊灯，受到竖直向下的重力和竖直向上的拉力，这两个力就是共点力。

要判断几个力是否为共点力，需要分析这些力的作用点和作用线。

如果力的作用点相同或者作用线能够相交于一点，那么这些力就是共点力；否则，就不是共点力。

二、共点力平衡的状态当物体受到几个共点力的作用时，如果物体保持静止或者做匀速直线运动，我们就说这个物体处于平衡状态。

静止状态比较容易理解，就是物体在空间中的位置不发生变化。

而匀速直线运动是指物体在直线上运动，并且速度的大小和方向都保持不变。

需要注意的是，平衡状态下物体的加速度为零。

如果物体具有加速度，那么它一定受到了非平衡力的作用，就不是处于平衡状态。

三、共点力的平衡条件共点力的平衡条件是：物体所受的合外力为零。

假设一个物体受到三个共点力 F1、F2 和 F3 的作用处于平衡状态，那么这三个力的合力必然为零，即 F1 ＋ F2 ＋ F3 ＝ 0。

可以将其进一步分解为在 x 轴和 y 轴方向上的分力之和也分别为零。

例如，在平面直角坐标系中，设 F1 在 x 轴和 y 轴上的分力分别为 F1x和 F1y，F2 的分力为 F2x 和 F2y，F3 的分力为 F3x 和 F3y。

那么有F1x ＋ F2x ＋ F3x ＝ 0 和 F1y ＋ F2y ＋ F3y ＝ 0 。

这个平衡条件是解决共点力平衡问题的关键。

四、共点力平衡条件的应用（一）求解未知力在很多实际问题中，我们常常需要根据已知力和物体的平衡状态来求解未知力。

例如，一个质量为 m 的物体放在水平地面上，受到重力 G、地面的支持力 N 和水平方向的摩擦力 f 的作用处于静止状态。

已知重力 G ＝mg，我们可以根据平衡条件得出 N ＝ G ＝ mg，f ＝ 0 。

再比如，一个悬挂着的物体，通过绳子与天花板相连，已知物体的重力和绳子与天花板的夹角，就可以通过共点力的平衡条件求出绳子的拉力。

第十二讲共点力平衡【知识梳理】一．共点力物体同时受几个力的作用，如果这几个力都作用于物体的同一点或者它们的作用线交于同一点，这几个力叫共点力．能简化成质点的物体受到的力可视为共点力。

二、平衡状态物体保持静止．．．．或匀速运动．．．．状态（或有固定转轴的物体匀速转动）．共点力的平衡：如果物体受到共点力的作用，且处于平衡状态，就叫做共点力的平衡。

共点力的平衡条件：为使物体保持平衡状态，作用在物体上的力必须满足的条件，叫做两种平衡状态：静态平衡v=0;a=0 动态平衡v≠0;a=0①瞬时速度为0时,不一定处于平衡状态. 如:竖直上抛最高点.只有能保持静止状态而加速度也为零才能认为平衡状态.②.物理学中的“缓慢移动”一般可理解为动态平衡。

推论：①非平行的三个力作用于物体而平衡，则这三个力一定共点。

②几个共点力作用于物体而平衡，其中任意几个力的合力与剩余几个力（一个力）的合力一定等值反向三力汇交原理：当物体受到三个非平行的共点力作用而平衡时，这三个力必交于一点；说明：①物体受到N个共点力作用而处于平衡状态时,取出其中的一个力,则这个力必与剩下的（N-1）个力的合力等大反向。

②若采用正交分解法求平衡问题，则其平衡条件为：F X合=0，F Y合=0；求解平衡问题的一般步骤：选对象，画受力图，建坐标，列方程。

例1、倾角为θ的斜面上有质量为m的木块，它们之间的动摩擦因数为μ.现用水平力F推动木块，如图所示，使木块恰好沿斜面向上做匀速运动.若斜面始终保持静止，求水平推力F的大小.练习1．下列关于质点处于平衡状态的论述`，正确的是（）A 质点一定不受力的作用B 质点一定没有加速度C 质点一定没有速度D 质点一定保持静止2．如图所示，重4N的物体与弹簧相连，静止在倾角为300的斜面上，若弹簧的弹力大小为4N，则物体受到的静摩擦力为（）A 方向必沿斜面向上B 方向可能沿斜面向下C 大小必为6ND 大小可能为6N3．如图所示，用轻绳将重球悬挂在竖直光滑墙上，当悬绳变长时，A 绳子拉力变小，墙对球的弹力变大B 绳子拉力变小，墙对球的弹力变小C 绳子拉力变大，墙对球的弹力变大D 绳子拉力变大，墙对球的弹力变小4．一个质点受到几个恒力的作用而处于平衡状态，若去掉其中一个大小为10N，方向水平向左的力，余下的力的合力是______N，方向______。

《共点力平衡条件的应用》讲义一、共点力平衡的概念当物体受到几个力的作用，如果这几个力都作用在物体的同一点，或者它们的作用线相交于一点，这几个力就叫做共点力。

当物体在共点力的作用下处于静止或者匀速直线运动状态时，我们就说物体处于共点力平衡状态。

二、共点力平衡条件共点力平衡的条件是合力为零。

也就是说，如果物体受到多个共点力的作用而处于平衡状态，那么这些力的合力必定为零。

可以用数学表达式表示为：＼（F_{合}＝0\）如果将力进行正交分解，分别在 x 轴和 y 轴上投影，则有：＼（F_{x合}＝0\）＼（F_{y合}＝0\）三、共点力平衡条件的应用1、静态平衡问题（1）物体在水平面上的平衡例如，一个静止在水平地面上的物体，受到重力＼（G\）、地面的支持力＼（N\）和水平方向可能存在的摩擦力＼（f\）。

由于物体处于静止状态，合力为零。

在竖直方向上，重力和支持力大小相等、方向相反，即＼（G ＝ N\）；在水平方向上，如果没有外力作用，摩擦力＼（f ＝ 0\）。

（2）物体在斜面上的平衡当一个物体静止在斜面上时，它受到重力＼（G\）、斜面的支持力＼（N\）和斜面的摩擦力＼（f\）。

将重力沿斜面和垂直斜面方向分解，分别为＼（G_{1}＼）和＼（G_{2}＼）。

在垂直斜面方向上，支持力＼（N\）与＼（G_{2}＼）大小相等、方向相反，即＼（N＝ G_{2}＼）；在沿斜面方向上，如果物体静止，摩擦力＼（f\）与＼（G_{1}＼）大小相等、方向相反，即＼（f ＝ G_{1}＼）。

2、动态平衡问题（1）缓慢移动问题在一些情况下，物体的位置在缓慢变化，但始终处于平衡状态。

比如，一个用绳子悬挂的物体，缓慢地从一个位置移动到另一个位置。

在这个过程中，因为移动缓慢，可以认为每个时刻物体都处于平衡状态，仍然满足合力为零的条件。

（2）多力动态平衡有些物体受到多个力的作用，且这些力的大小和方向在不断变化，但物体仍保持平衡。

例如，一个用三根绳子悬挂的重物，通过改变三根绳子的长度来改变拉力的大小和方向，使重物始终处于平衡状态。

力学专题04：共点力平衡七大题型解析
（原卷版）
共点力平衡问题是力学中经常遇到的一类问题，解析这类问题可以帮助我们深入理解平衡条件和力的合成分解。

本文将分析七大题型，帮助读者更好地掌握解决这类问题的方法。

1. 两力共线平衡问题：当两个力作用在同一直线上时，它们的合力为零，根据平衡条件可以解得未知力的大小和方向。

2. 三力共点平衡问题：当三个力作用在同一点上时，它们的合力为零，可以通过平衡条件解得未知力的大小和方向。

3. 四力共点平衡问题：当四个力作用在同一点上时，它们的合力为零，可以通过平衡条件解得未知力的大小和方向。

4. 三力共线平衡问题：当三个力作用在同一直线上时，它们的合力为零，可以通过平衡条件解得未知力的大小和方向。

5. 三力共面平衡问题：当三个力作用在同一平面上时，它们的
合力为零，可以通过平衡条件解得未知力的大小和方向。

6. 三力不共线平衡问题：当三个力作用在同一点上且不共线时，根据平衡条件可以解得未知力的大小和方向。

7. 多力平衡问题：当多个力作用在同一点上时，它们的合力为零，可以通过平衡条件解得未知力的大小和方向。

通过对以上七大题型的解析，我们可以掌握共点力平衡问题的
解题方法。

在解题过程中，我们应当注意使用合适的坐标系、合理
选择参考点，并利用力的平衡条件进行计算。

本文提供了对共点力平衡七大题型的解析，但并未引用无法确
认的内容。

读者可以根据自己的需要，参考本文的解题方法，独立
解决力学中的共点力平衡问题。

共点力的平衡【知识点的认识】1．共点力物体同时受几个力的作用，如果这几个力都作用于物体的同一点或者它们的作用线交于同一点，这几个力叫共点力。

能简化成质点的物体受到的力可视为共点力。

2．平衡状态物体保持静止或匀速运动状态（或有固定转轴的物体匀速转动）。

注意：这里的静止需要二个条件，一是物体受到的合外力为零，二是物体的速度为零，仅速度为零时物体不一定处于静止状态，如物体做竖直上抛运动达到最高点时刻，物体速度为零，但物体不是处于静止状态，因为物体受到的合外力不为零。

共点力的平衡：如果物体受到共点力的作用，且处于平衡状态，就叫做共点力的平衡。

共点力的平衡条件：为使物体保持平衡状态，作用在物体上的力必须满足的条件，叫做两种平衡状态：静态平衡v＝0；a＝0；动态平衡v≠0；a＝0；①瞬时速度为0时，不一定处于平衡状态。

如：竖直上抛最高点。

只有能保持静止状态而加速度也为零才能认为平衡状态。

②物理学中的“缓慢移动”一般可理解为动态平衡。

3．共点力作用下物体的平衡条件（1）物体受到的合外力为零。

即F合＝0；其正交分解式为F合x＝0；F合y＝0；（2）某力与余下其它力的合力平衡（即等值、反向）。

二力平衡：这两个力大小相等，方向相反，作用在同一直线上，并作用于同一物体。

（要注意与一对作用力与反作用力的区别）。

三力平衡：三个力的作用线（或者反向延长线）必交于一个点，且三个力共面。

称为汇交共面性。

其力大小符合组成三角形规律。

三个力平移后构成一个首尾相接、封闭的矢量形；任意两个力的合力与第三个力等大、反向（即是相互平衡）。

推论：①非平行的三个力作用于物体而平衡，则这三个力一定共点。

②几个共点力作用于物体而平衡，其中任意几个力的合力与剩余几个力（一个力）的合力一定等值反向。

三力汇交原理：当物体受到三个非平行的共点力作用而平衡时，这三个力必交于一点；说明：①物体受到N个共点力作用而处于平衡状态时，取出其中的一个力，则这个力必与剩下的（N﹣1）个力的合力等大反向。