下载文档原格式
托宾Q理论- 解释经济学家托宾于1969年提出了一个著名的系数，即“托宾Q”系数（也称托宾Q比率）。
该系数为企业股票市值对股票所代表的资产重置成本的比值，在西方国家，Q比率多在0.5和0.6之间波动。
因此，许多希望扩张生产能力的企业会发现，通过收购其他企业来获得额外生产能力的成本比自己从头做起的代价要低的多。
例如，如果平均Q比率在0.6左右，而超过市场价值的平均收购溢价是50%，最后的购买价格将是0.6乘以1.5，相当于公司重置成本的90%.因此，平均资产收购价格仍然比当时的重置成本低十个百分点。
托宾Q理论- 意义托宾q是指资本的市场价值与其重置成本之比。
这一比例兼有理论性和实践的可操作性，沟通了虚拟经济和实体经济,在货币政策、企业价值等方面有着重要的应用。
在货币政策中的应用主要表现在将资本市场与实业经济联系起来，揭示了货币经由资本市场而作用于投资的一种可能。
在未来,我国货币政策如果开始考虑股票市场的因素，则托宾q将会成为政策研究与政策制定的重要工具。
托宾q值常常被用来作为衡量公司业绩表现或公司成长性的重要指标。
尽管由于资本市场发展的不完善，托宾q理论在我国的应用还很有局限性，但它依然给我们提供了分析问题的一种思路。
托宾Q理论- 托宾的Q比率内容托宾的Q比率是公司市场价值对其资产重置成本的比率。
反映的是一个企业两种不同价值估计的比值。
分子上的价值是金融市场上所说的公司值多少钱，分母中的价值是企业的“基本价值”—重置成本。
公司的金融市场价值包括公司股票的市值和债务资本的市场价值。
重置成本是指今天要用多少钱才能买下所有上市公司的资产，也就是指如果我们不得不从零开始再来一遍，创建该公司需要花费多少钱。
其计算公式为：Q比率=公司的市场价值/资产重置成本当Q>1时,购买新生产的资本产品更有利,这会增加投资的需求；当Q<1时,购买现成的资本产品比新生成的资本产品更便宜,这样就会减少资本需求。
所以,只要企业的资产负债的市场价值相对于其重置成本来说有所提高,那么,已计划资本的形成就会有所增加。
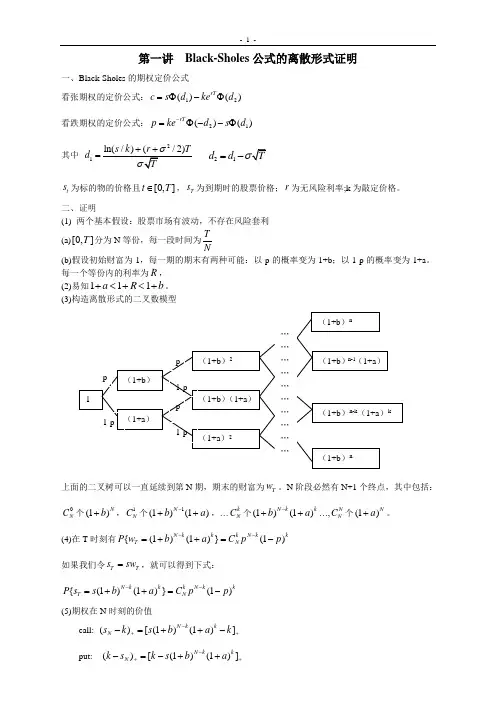
第一讲 Black-Sholes 公式的离散形式证明一、Black-Sholes 的期权定价公式看张期权的定价公式：12()()rT c s d ke d =Φ-Φ 看跌期权的定价公式：21()()rT p ke d s d -=Φ--Φ 其中21d =21d d σ=-t s 为标的物的价格且[0,]t T ∈，T s 为到期时的股票价格；r 为无风险利率;k 为敲定价格。
二、证明(1) 两个基本假设：股票市场有波动，不存在风险套利 (a)[0,]T 分为N 等份，每一段时间为T N(b)假设初始财富为1，每一期的期末有两种可能：以p 的概率变为1+b ；以1-p 的概率变为1+a 。
每一个等份内的利率为R ， (2)易知111a R b +<+<+。
(3)构造离散形式的二叉数模型上面的二叉树可以一直延续到第N 期，期末的财富为T w 。
N 阶段必然有N+1个终点，其中包括：N C 个(1)N b +，1N C 个1(1)(1)N b a -++，…k N C 个(1)(1)N kk b a -++…,N N C 个(1)Na +。
(4)在T 时刻有{(1)(1)}(1)N k k k N k kT N P w b a C p p --=++=- 如果我们令T T s sw =，就可以得到下式：{(1)(1)}(1)N kk k N kkT N P s s b a C pp --=++=-(5)期权在N 时刻的价值call: ()[(1)(1)]N k kN s k s b a k -++-=++- put: ()[(1)(1)]N k kN k s k s b a -++-=-++()01()(1)[(1)(1)](1)NN k N kk N kkN NNk cE s k Cpp s b a k R --++==-=-++-+∑()1()(1)[(1)(1)](1)NN k N kk N kkN NN k pE k s Cpp k s b a R --++==-=--+++∑(6)看张和看跌期权的平价关系由步骤（5）可知：(1)N N Nk c p s R -=-+(7)收益率的换算因为T rR N=，所以连续复利elim (1)lim (1)rTNNN N rT R N→∞→∞=+=+。
投资学分离定律的有效前沿为什么要进行多元化投资，进行资产组合管理，因为构建投资组合可以带来分散化的效用，从而带来免费的午餐，作为大多数非专业投资者，如果自己构建投资组合存在一定的难度，但这种好处确实又不容错过（毕竟在资本市场，长期来看免费的午餐并不多，分散化投资算是其中之一了），所以，本期主要谈谈如何合理构建最优投资组合（注意：区别于最优风险资产组合）。
最优投资组合的构建主要从两个层面展开，第一个层面是构建最优风险资产组合，请参阅从构建投资组合到超越指数化投资系列（六），第二个层面是构建最优投资组合（根据托宾提出的两基金分离定律，把最优风险资产组合和无风险资产进行再组合）。
话说在金融市场上，每一天每一刻，投资者们无不在绞尽脑汁思考两个问题：（1）有没有一个收益最大、风险最小的组合？（2）它在哪里？为了搞清楚这个问题，经济学家们简化了这个世界，在这个简化的世界中，马科维茨老爷爷率先找到了这个组合，即最优风险资产组合。
上文对构建最优风险资产组合权重怎么确定进行了介绍从构建投资组合到超越指数化投资系列（五），但马科维茨老爷爷也留给后人了一些问题，比如：在过往，我们需要为保守的投资者——比如跳广场舞的退休大妈——推荐风险较低的股票，凑成一个组合，然后为事业正在上升的年轻人——比如年轻有为的富二代——推荐高风险的股票，再重新构成一个新的组合。
这样操作还是比较麻烦的，毕竟每个人的风险偏好水平都各不相同，准确找到那些能为不同投资者带来最适合的风险水平的投资组合并不是一件容易的事情而且耗时耗力，而这会缩小管理资金的募集群体和范围，提高管理资金的成本费用率。
其实，留给后人的问题还挺多的，但都不是本期的重点，还比如，均值-方差模型体系隐含了收益率的正态分布假设（每次事后，我们都会反思黑天鹅，反思人性的贪婪与罪恶，但想要超越正态分布假设，跳出这一套体系，提出简单易行的收益-风险度量工具，目前还没有人能彻底摆脱）；再比如，假定当前市场价格、预期收益率、标准差和相关系数是外生变量，即金融资产价格是均衡价格，个人行为无法影响市场价格（在现实中，人的行为会影响价格，特别是大的金融机构投资者会影响到这些变量，这就是为什么行为金融学很喜欢分析异质性，也是为什么高频交易能挣钱的原因）。
新古典综合学派新古典综合派概述neo-classical synthesis二战后，在以萨缪尔森为代表的一批美国经济学家的努力下，逐渐形成了“新古典综合派”的宏观经济学。
一系列在凯恩斯基本理论基础上的最新研究成果被综合在一起，形成了所谓的”宏观经济学”。
而传统的经济学理论，包括价格理论，消费理论，生产理论，市场理论以及分配理论和一般均衡理论与福利经济学则被冠以”微观经济学”的名称。
新古典综合派是所谓的“凯恩斯革命”之后起初最有影响力的凯恩斯学派，又先后自称“后凯恩斯主流经济学（Post-Keynesian Mainstream）”和“现代主流经济学新综合”'。
反映这个学派理论观点的代表著作是萨缪尔森的《经济学》。
在经济政策上，主张运用财政政策和货币政策，调节总需求，以减少失业、消除危机。
在经济制度方面，主张混合经济论，即公私机构共同对经济施行控制。
新古典综合派产生的背景1929年爆发了一场震撼资本主义世界的经济大危机，1936年英国著名经济学家凯恩斯在其出版的《通论》一书中提出主张国家干预经济的政策。
第二次世界大战以后，凯恩斯的追随者纷纷根据经济现状发展凯恩斯主义，试图解决凯恩斯没有解决的问题。
在发展凯恩斯主义的热潮中，后凯恩斯主义经济学的内部大体上形成了两大主要支派：以美国萨缪尔森为首的新古典综合派和以英国琼罗宾逊为首的新剑桥学派。
新古典综合的经济理论以最完整的形式体现在萨缪尔森的《经济学》一书中。
上世纪五十年代以来，新古典综合派不但是西方资产阶级经济学界流行的主流经济学，而且他的政策主张也相继被主要资本主义国家作为基本经济政策付诸实施。
新古典综合派的政策主张1、所谓新古典综合，实质上是将马歇尔为代表的新古典经济学与凯恩斯主义经济理论综合在一起。
其核心思想是在采取凯恩斯主义的宏观财政政策和货币政策来调节资本主义的经济活动，使现代资本主义经济能避免过度的繁荣或萧条而趋于稳定的增长，实现充分就业的条件下，新古典经济学的主要理论将仍然是适用的。
俩基金分离定律
"俩基金分离定律"是投资学中的理论概念，也称为"马克维茨
定律"。
该定律是由诺贝尔经济学奖得主哈里·马克维茨于1952年提出的。
俩基金分离定律指出，投资者可以通过构建一个由无风险资产和风险资产（如股票、债券等）组成的组合来平衡风险和收益。
在该理论中，投资者可以将投资组合划分为两部分：一部分是具有确定收益但不带风险的无风险资产（如国债），另一部分是带有风险但可能带来更高收益的风险资产（如股票）。
根据俩基金分离定律，投资者可以根据自己的风险承受能力和收益目标，在无风险资产和风险资产之间进行合理的分配。
投资者可以选择适当的比例来平衡风险和收益，从而最大化其投资组合的效用。
总之，俩基金分离定律为投资者提供了一个方法，使他们能够根据自己的风险和收益偏好来构建投资组合，以实现最优化的投资目标。
分离定理名词解释金融
分离定理指在投资组合中可以以无风险利率自由借贷的情况下投资人选择投资组合时都会选择无风险资产和风险投资组合的得最优组合点，因为这一点相对于其他的投资组合在风险上或是报酬上都具有优势。
所以谁投资都会选择这一点。
投资人对风险的态度，只会影响投入的资金数量，而不会影响最优组合点。
此为分离定理。
不需要知道投资者对风险和回报的偏好，就能够确定其风险资产的最优组合。
分离定理也可以表述为最佳风险资产组合的确定独立于投资者的风险偏好。
它取决于各种可能风险组合的期望报酬率和标准差。
个人的投资行为可分为两个阶段：先确定最佳风险资产组合。
后考虑无风险资产和最佳风险资产组合的理想组合。
只有第二阶段受投资人风险反感程度的影响，只有在第二个阶段中投资人才决定是否融资，第一阶段也即确定最佳风险资产组合时不受投资者风险反感程度的影响。
关于投资与融资分离的决策理论被称作分离定理。
分离定理成立的原因在于：有效边界是线性的。
金融理论中的三个分离定理
(2009-09-02 01:19:35)
转载▼
标签：财经分类：经济学咖啡——先天下之忧
最近读文献，发现金融货币理论中有三个非常著名的分离定理（seperation theorem）,不应该混淆。
第一个是费雪的分离定理，意思是指在完全的金融市场中，生产技术的时间次序和个人的时间偏好无关。
这样，企业家可以独立的按照生产技术的时间约束来进行生产，而不用顾及消费问题，因为有完美的金融市场可以提供借贷。
第二个是托宾的分离定理，风险投资组合的选择与个人风险偏好无关。
这样基金经理就不用顾及客户的风险偏好特点，只选择最优的投资组合即可（风险既定下收益最大）。
第三个是，法玛的分离定理（两基金分离），风险投资组合的数量和构成与货币（无风险资产）无关。
这体现了法玛的“新货币经济学”思想——在经济体系中，货币是不重要的，物物交换的瓦尔拉斯世界可以在金融市场中实现。
这三个定理是非常重要的。
费雪定理告诉了人们金融市场是重要的；托宾分离告诉基金经理不要在乎客户的个人差异；法玛分离定理告诉人们货币对风险投资组合本身没有影响，并且任意投资组合都可以用一个无风险资产和风险资产组合的线性组合来表示。
▪表述：
▪在均方效率曲线上任意两点的线性组合，都是具有均方效率的有效组合。
▪或：有效组合边界上任意两个不同的点代表两个不同的有效投资组合，而其他任意点均可由该两点线性组合生成
▪
几何含义：过两点生成一条双曲线。
▪定理的前提：两基金（有效资产组合）的期望收益是不同的，即两基金分离。
▪金融含义：若有两家基金都投资于风险资产，且经营良好(即达到有效边界)，则按一定比例投资于该两基金，可达到投资于其他基金的同样结果。
这就方便了投资者的选择。
▪CAL、CML实际上是在有风险资产组合和无风险资产组合之间又进行了一次两基金分离。
此时投资者仅需确定一个有风险组合，即可达到各种风险收益水准的组合。
资本配置更加方便。
分离定理对组合选择的启示
❖若市场是有效的，由分离定理，资产组合选择问题可以分为两个独立的工作，即资本配置决策（Capital allocation decision）和资产选择决策（Asset allocation decision）。
❖资本配置决策：考虑资金在无风险资产和风险组合之间的分配。
❖资产选择决策：在众多的风险证券中选择适当的风险资产构成资产组合。
❖基金公司可以不必考虑投资者偏好的情况下，确定最优的风险组合。
❖两基金分离定理：在所有有风险资产组合的有效边界上，任意两个分离的点都代表两个分离的有效投资组合，而有效组合边界上任意其他的点所代表的有效投资组合，都可以由这两个分离的点所代表的有效投资组合的线性组合生成
❖作一点说明：
❖由前面情况2的介绍知，过任意两个分离的各自代表有风险资产的点可以生成一条双曲线。
❖有效组合边界上的两个分离的点可以看作两项有风险资产，它们也就可以生成一条双曲线。
•有效组合边界本身是一条双曲线。
任意两条不同的双曲线不可能在同一侧有两个分离的切点。
•而如果这两条双曲线在这两个点是相交的话，则由两个点生成的双曲线一定会有一部分落在有效组合边界所围区域的外面。
•由有效组合边界的定义知这是不可能的，所以这两条双曲线一定重合，亦即两基金分离定理成立。
•有一类专门从事分散化投资的金融中介机构叫做共同基金。
共同基金一方面发行小面额的受益凭证作为自己的负债，另一方面则把筹集到的大笔资金进行分散化投资，形成自己的投资组合。
•如果有两家不同的共同基金，它们都投资于有风险资产，而且都经营良好，经营良好意味着它们的收益／风险关系都能达到有效组合边界。
那么，两基金分离定理告
诉我们，任何别的投资于有风险资产的共同基金，如果经营良好(即能够达到有效组
合边界)的话，其投资组合一定与原来那两个共同基金的某一线性组合等同。
•只要找到这样两家不同的经营良好的共同基金，把自己的资金按一定的比例投资于这两家基金，就可以与投资于其他经营水平高的共同基金获得完全一样的效果。
•这一结论对投资策略的制定无疑有重要的意义。
