CFD基础讲座

格式：ppt
大小：1.61 MB
文档页数：8

下载文档原格式

第1课时 CFD基础教程

CFD基础教程
第一课时
1 什么是CFD？
CFD：即计算流体力学（Computational Fluid Dynamics），是近代流体力学，数值计算和计算机等结合产物。它以计算机为工具，应用各种离散化的数学方法，对流体力学的各类问题进行数值实验、计算机模拟和分析研究，以解决各种实际问题。
后处理
Tecplot、Origin、CFD-Post、ParaView、OpenDX…用
（3）海洋工程
2 CFD应用
（4）汽车工业
2 CFD应用
（4）能源工程
2 CFD应用
（5）化学工程
2 CFD应用
（5）生物工程
3 为什么需要CFD？
CFD优势：（1）不需要实验模型、风洞、仪器仪表等，周期短，可节省大量成本，（2）计算结果丰富，可提供详细流场结构。（3）可模拟难以进行实验的流动问题：超音速、高温高压（4）能实现虚拟设计与制造
CFD可以做什么？（1）复杂复杂流动问题：泵、风机、阀门等（2）化学组分混合、燃烧、反应过程：反应器、燃烧器、锅炉（3）传热、传质、相变过程：换热器、省煤器、过滤器、热水器（4）多相流动问题：气液、气固、气液固、油气水（5）流固耦合：应力分析
2 CFD应用
（1）航空航天
2 CFD应用
4 CFD发展
5 CFD模拟概述
6 CFD常用软件
前处理
CAD、Pro-E、SolidWorks、ICEM、Gambit、Delaundo、 Engrid、GMSH、gridgen、IA-FEMesh……
仿真计算
CFX、Fluent、CFX、Openfoam、COMSOL Multiphysics、FloEFD、PHOENICS、STAR-CD、STARCCM+、Polyflow、 Icepak、CFX-TASCflow……

CFD差分基础-2-1-1-李新亮老师课件

E u n u n x j j 移位算子：
（当移位为+1时可省略）
E t1u n E t u n u n1 j j j
1 2 2 x (Ex Ex ) 2
1 1
算术平均算子：
1 1 1 1 n n 2 x u ( u 1 u 1 ) ( E x 2 E x )u n j j j 2 2 2 2 n j
(后差) （中心差）
u ui 1, j ui 1, j o( x 2 ) x 2 x
（二阶导数中心差, 2 u ui 1, j 2ui , j ui 1, j 2 o( x ) 等网格步长） 2 2 x x
3u 3 x
3．差分算子 ●定义以下差分算子：
第二章有限差分法理论基础
★有限差分方法是计算流体力学中应用最多的离散化数值方法； ★作为计算技术它是历史最悠久，理论上相对成熟的数值方法。
§2.1 有限差分离散化方法 §2.2 差分格式的基本性质、基本定理 §2.3 差分格式的稳定性分析方法 §2.4 经典差分格式介绍
§2.1 有限差分离散化方法
. .
1 2 4 1 6 2 D 2 h 12 90
可导出二阶偏导数的紧致格式为：
1 2 D 2 h
1
2 4 o h 2
12

例4；紧致格式应用：
Dt 1 t oht ht

1
2 x
u 2u t x 2
若取消取极限过程，用 u( x0 x , y0 ) u( x0 , y0 ) x u |( x0 , y0 ) 就是一种差商近似。称为差分格式，，代替
x

CFD培训-1

講座内容1. 流體力学的基礎2. 流體解析的意義和概要3.熱流體守恒方程式的解法4.實施解析時必須的基礎知識1.流體力学的基礎什麼是流體?z固體的體積和形狀不易改變、液體的體積不易改變但形狀易改變、氣體的體積和形狀都易改變z流體（氣體, 液體）的流動是一種伴随着変形的運動z流體vs. 固體–流體受剪切應力的作用,會發生持續變形處於静止状態的流體則沒有剪切應力的發生–固體的変形則和剪切應力成正比（在彈性範圍內）(Hooke法則)τθ∝τθ∝&應力和應變成正比應力和應變速度正比流體的動量和粘性•流體的粘性:流體分子的動量轉移的結果•微觀地看、各個流體分子的運動是不規則的、無方向性的。

速度在一定範圍內分布的•宏觀地觀察靜止流體、雖然分子都在激烈運動、但整體上仍然處於靜止狀態•速度分布（如下図、2平板的上平板以一定速度的移動）、在ｙ方向上側的流体分子、在ｘ方向上的平均速度比下平板的分子速度大•ｙ断面上下両側有無数的不規則運動的分子通過該斷面-上→下：上面的分子支出動量、下面的分子的速度增加-下→上：下面的分子收穫動量、上面的分子的速度減小•最終的結果是由於動量交換、生成剪切應力流體力學的歷史1.Archimedes(B.C. 287-212)浮力定律2.Pascal (1623-1662)液壓原理3.Newton (1642-1727) 流体粘性的牛頓法則4.Bernoulli (1700-1783) 命名了流体力学(hydrodynamics)、和Bernoulli方程5.Euler (1707-1783) 導入流体壓力概念、和理想流体的運動方程式。

流体力学的始祖6.Navier(1785-1836), Stokes (1819-1903) 把牛頓粘性法則導入運動方程式、奠定了粘性流体力学的基礎7.Reynolds (1842-1912) 發現了層流/湍流的遷移、定義了Re数8.Prandtl(1875-1953) 邊界層理論(1904)、混合長理論(1925)9.Taylor的湍流統計理論(1935)10.Kolmogorov(1941) 3維湍流動能的能譜(Spectrum)、Kolmogorov scale.作為連續介質的流體•作為連續介質的流體,假設流場的尺寸遠大於流體分子的平均自由行程•在連續介質流體内各点的変量, 是各個微小體積内的平均値。

第2讲 CFD数学模型及物理意义汇编

• 基于局部
– 在一个有限的体积内 – 将体积划分为无限小，趋近于0 – 偏微分（控制）方程
x 0
基本控制方程
• 质量守恒
u v 0 x y
• 动量守恒定律 2u 2u u u 1 P x-mom: u v 2 2
x y
第一类边界条件：Dirichlet 问题第二类边界条件：Neumann问题
u f ( x, y)
u f ( x, y ) n源自第三类边界条件：Robin问题
u (k hu ) f ( x, y ) n
抛物型偏微分方程
u 2u a 2 t x
第一类边界条件第二类边界条件
• CFD未来发展的方向是什么？
引言
• 数值计算的出发点：数学模型 • 数学模型（Mathematical model) – 控制方程（Governing equations) • 基于基本原理与定律 • 偏微分方程组 – 定解条件（Boundary conditions） • 坐标系不同，控制方程的形式不尽相同 – 适当选取坐标系可以简化分析 • 必要的简化与化简
第二讲 CFD数学模型及物理意义
屠基元教授清华大学墨尔本皇家理工大学
CFD综述
计算流体力学非稳态无粘流粘性流
稳态
传热热传导热对流热辐射
可压缩流动
层流
湍流
可压缩流动内流
不可压缩流动外流
CFD - 问题（ I ）
• CFD问题中的物理流动过程有哪些？ • 流动的物理现象是如何在数学方程式中描述的？ • 流体流动和热传递的控制方程式是什么？ • 为什么边界条件非常重要？如何应用边界条件？

CFD讲座

口边界条件的位置选取
如果流动出口的边界太靠近固体障碍物，如果流动出口的边界太靠近固体障碍物，流动可能尚未达到充分发展的状态（在流动方向上梯度为零），这将未达到充分发展的状态（在流动方向上梯度为零），这将），导致相当大的误差。一般来讲，为了得到准确的结果，导致相当大的误差。一般来讲，为了得到准确的结果，出口边界必须位于最后一个障碍物后10 10倍于障碍高度或更远口边界必须位于最后一个障碍物后10倍于障碍高度或更远的位置。对于更高的精度要求，的位置。对于更高的精度要求，还要研究模拟结果对出口位于不同距离时的影响和敏感程度，位于不同距离时的影响和敏感程度，以保证内部模拟不受出口位置选取的影响。出口位置选取的影响。
中国电子学会
二、求解器
借助简单函数来近似待求的流动变量将该近似关系代入连续型的控制方程中，形成离散方将该近似关系代入连续型的控制方程中，程组求解代数方程组
中国电子学会
三、后处理器
计算域的几何模型及网格显示矢量图（如速度矢量线）矢量图（如速度矢量线）填充型的等值线图（云图）填充型的等值线图（云图）粒子轨迹图图像处理功能（平移、缩放、旋转等）图像处理功能（平移、缩放、旋转等）
有限体积法（有限体积法（Finite Volume Method, FVM）
有限体积法的关键是在导出离散方程的过程中，有限体积法的关键是在导出离散方程的过程中，需要对界面上的被求函数本身及其导数的分布作出某种形式的假定。FVM导出的离散方被求函数本身及其导数的分布作出某种形式的假定。FVM导出的离散方程可以保证具有守恒特性，且离散方程系数物理意义明确。程可以保证具有守恒特性，且离散方程系数物理意义明确。中国电子学会
中国电子学会

CFD基本知识培训

静压云图
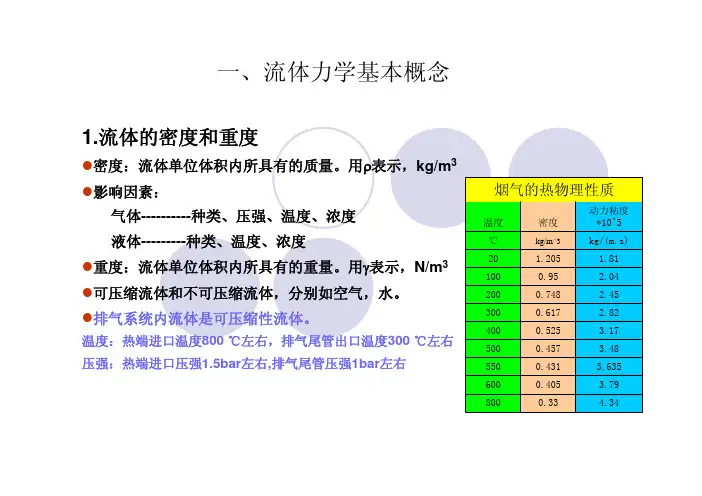
一、流体力学基本概念
8. 迹线和流线
z迹线：在一段时间内，流体质点在空间运动的轨迹线。

它给出一质点在不同时刻的速度方向。

S18_hotend气流迹线.avi
z流线：在同一时刻，不同流体质点组成的曲线。

它给出该时刻不同流体质点的速度方向。

计算流体动力学
壁面导热系数，对流传热系数，辐射换热系数
详细内容见分析报告）
结果分析（详细见分析报告）：
注：图中斜线（/）前的数值表示此处的体积流量L/s，斜线后的数值表示此处的体积流量占总体积流量的百分数。

图中红色箭头表示流动方向。

如表示此处的流体流量是62.6L/s，占总体积流量的100％。

CFD基础教程

CFD基础教程第1章 CFD 基础计算流体动⼒学(computational fluid dynamics ，CFD)是流体⼒学的⼀个分⽀，它通过计算机模拟获得某种流体在特定条件下的有关信息，实现了⽤计算机代替试验装置完成“计算试验”，为⼯程技术⼈员提供了实际⼯况模拟仿真的操作平台，已⼴泛应⽤于航空航天、热能动⼒、⼟⽊⽔利、汽车⼯程、铁道、船舶⼯业、化学⼯程、流体机械、环境⼯程等领域。

本章介绍CFD ⼀些重要的基础知识，帮助读者熟悉CFD 的基本理论和基本概念，为计算时设置边界条件、对计算结果进⾏分析与整理提供参考。

1.1 流体⼒学的基本概念1.1.1 流体的连续介质模型流体质点(fluid particle)：⼏何尺⼨同流动空间相⽐是极⼩量，⼜含有⼤量分⼦的微元体。

连续介质(continuum/continuous medium)：质点连续地充满所占空间的流体或固体。

连续介质模型(continuum/continuous medium model)：把流体视为没有间隙地充满它所占据的整个空间的⼀种连续介质，且其所有的物理量都是空间坐标和时间的连续函数的⼀种假设模型：u =u (t ,x ,y ,z )。

1.1.2 流体的性质1. 惯性惯性(fluid inertia)指流体不受外⼒作⽤时，保持其原有运动状态的属性。

惯性与质量有关，质量越⼤，惯性就越⼤。

单位体积流体的质量称为密度(density)，以r 表⽰，单位为kg/m 3。

对于均质流体，设其体积为V ，质量为m ，则其密度为mV(1-1)对于⾮均质流体，密度随点⽽异。

若取包含某点在内的体积V ，其中质量m ，则该点密度需要⽤极限⽅式表⽰，即0lim V mV(1-2)2. 压缩性作⽤在流体上的压⼒变化可引起流体的体积变化或密度变化，这⼀现象称为流体的可压缩性。

压缩性(compressibility)可⽤体积压缩率k 来量度Fluent ⾼级应⽤与实例分析2d /d /d d V V k p p(1-3) 式中：p 为外部压强。

汽车空调培训---CFD基础讲解

七.产品结构设计个人经验分享 1.根据边界布置我们的空调结构时尽量边界最大化； 2.通过给定的配件外形尺寸布置空间结构时不要出现太大的突变； 3.根据出模方向设计结构，尽量少镶块。 4.分风结构设计尽量对称，以整车中心为基准。
三.对网格划分中存在是错误进行分析优化并达到成功的划分网格。
对于网格划分失败无图片，按一下方法做修改直至网格划分成功： 1.去除空气体中的小圆角、小孔、小尖角、尖锐薄壁等； 2.在做差合空气体时，差合连接面需检查，这是容易出现薄壁的地方 (如风门、叶轮等);
四.对流体进行属性的定义、边界条件设Байду номын сангаас。
2.对速度-单元节点的查看分析
图片讲解
3.静压力-单元节点的查看分析
1.冷风吹面X轴Y轴静压力云图如下： X轴
Y轴
分析结果：（1）左右风管出风口出风截面大小差异较大。（2）左右风管路径上的对称截面大小有差异。
3.总压力-单元节点查看分析
总压力图片讲解
4.报告查看分析
1.对于报告的查看我们一般看出口的体积流量（如红圈），此时的体积单位为mm³ /s, 我们需将单位换算，可以通过UG中自带的换位换算器换算如图，也可以在办公软件里面换算。（例：6.36e+6=[6.36e+(6-9)]*3600=2.29e+1=22.9m³ /h） 2.根据报告的结果我们可以去分析在不同模式下风管的出风比例。
UG 软件流体分析基础讲解
1.对产品进行流体的提取及方法。 2.对流体进行网格的划分以及网格划分的方式。 3.对网格划分中存在是错误进行分析优化并达到成功的划分网格。
4.对流体进行属性的定义、边界条件设置。
5.对求解结果分析，并学习如何查看分析结果。 6.依据分析结果对产品进行结构的修改与优化。 7.产品结构设计个人经验分享。

CFD第一讲

2014-7-30
13
五、CFD的方法
• 现代科学研究的三大基本方法及其关系理论分析、实验研究、数值模拟
流体力学研究方法
数值分析
动力
实验研究
理论分析
条件
计算流体力学
2014-7-30
计算机技术飞速发展
14
（1）理论分析（Analytical）：所得结果具有普遍性，各种影响因素清晰可见，是指导实验研究和验证新的数值计算方法的理论基础。但它往往要求对计算对象进行抽象和简化，才有可能得出理论解。对于非线性情况，只有少数流动才能给出解析结果。
计算流体动力学
CFD
一、CFD基本概念
★计算流体力学（Computation Fluid Dynamics ，简称CFD）就是在电子计算机上数值求解流体与气体动力学基本方程的学科，通过计算机数值计算和图像显示，对包含有流体力学流动和热传导等到相关物理现象的系统所做的分析。
★控制方程：质量守恒方程、动量守恒方程、能量守恒方程、组分质量守恒方程
CFD控制方程
• 能量守恒方程(energy conservation equation)：微元体中能量的增加率等于进入微元体的净热流量加上体力与面力对微元体所做的功。
k ( T ) div( uT ) div grad T S T c t p
2014-7-30
11
四、CFD的基本原理
任何流体运动的规律都是以质量守恒定律、动量守恒定律和能量守恒定律为基础的。这些基本定律可由数学方程组来描述，计算流体力学可以看做是在流动基本方程，控制对流体的数值仿真模拟。
通过这些数值模拟，我们可以得到极其复杂问题的流场内各个位置上的基本物理量（如速度、压力、温度、浓度等）的分布，以及这些量随时间变化的情况，确定是否产生涡流，涡流分布特性及脱流区域等。

计算流体力学CFD基础课程PPT CFD2013-第4讲-差分方法2

(1 ei )
~ k eikx j x
于是： k~ 1 ei (1 cos) isin
kr 1 cos , ki sin
kx
例2： xu j (3u j 4u j1 u j2 ) /(2x) 2阶迎风
xu j
3u j
4u j1 u j2 2x
eikx j (3 4ei 2x
结论：要求分辨率相同的情况下，采用高阶格式可放宽空间网格步
长，从而减少计算量
重要方向：高分辨率差分格式
13
附录：部分差分格式
… j-2 j-1 j j+1 …
u a u 0 t x
✓迎风偏斜格式：上游的基架点更多些（或上游权重更大） ➢表中的迎风差分格式均针对 a>0 当a<0时，需把下标的“j+k” 换成 “j-k” （例如把j+2 换成j-2, 把j-1换成j+1); 并在表达式前加上“-”号。例：
9
➢如何计算修正波数？
方法1. 理论计算根据差分具体表达式及定义计算
定义： u(x j ) eikx j
~
xu j
k eikx j x
例1：
xu j
uj
u j1 x
1阶迎风
令
u j eikx j
则： xu j
uj
u j1 x
1 (eikx j x
eik ( x j x) )
eikx j x
uj (u j1 u j1) /(2x) u' j (3u j 4u j1 u j1) /(2x)
u' j (u j2 u j2 ) /(4x)
概念：群速度 —— 波包传播的速度

CFD讲义——北航

第一章理论基础知识：双曲型守恒律方程（组）例：一维 Eｕｌｅｒ方程
ρu ρ ∂ ∂ 2 ρ u + ρ u + p = 0, e = f ( p, ρ ) ∂t ∂x e u (e + p)
ρ 记 U = ρu = ，F e
Taylor 展开以后分别乘以系数 c0 c1 c2 之后用待定系数法
3 c = − c0 + c1 + c2 = 0 0 2 1 ⇒ c1 = 2 c1 + 2c2 = 1 1 c1 + 2c2 = c2 = − 0 2 2
f ′( x0 ) ≈
f ′( x0 ) =
1.6 通量 Jacobi 矩阵的特征值和特征向量 A 的特征值 λ １, 2λ , , λm ，相应的特征向量 r 1 , r2 , , rm ⇒ Ark = λk rk 构造矩阵 R = (r1 , r2 , , rm ) ，它是可逆的。

λ１ λ2 ＝RD 则 AR = ( Ar1 , Ar2 , , Arm ) ＝ (λ ＝ r , λ r , , λ r ) R １2 1 2 k m λk
*A 可以对角化＝A 存在 m 个线性无关的特征向量＝A 可以通过相似变换成对角矩阵，使得
R −1 AR = D
1.5 双曲型方程的不变性引入 v,使得 w=w(v)则有 Jacobi 矩阵
∂w =P ∂v
w1 (v1 , v2 , , vm ) w = w2 (v1 , v2 , , vm ) w (v , v , , v ) m m 1 2 ∂w =P ∂v ∂w ∂v ∂w ∂v ∂v ∂v ∂v ∂v ⇒ +A = 0) ⇒ + P −1 AP 0 ⇒ P + AP = 0(两边乘以＝ P −1 ∂v ∂t ∂v ∂x ∂t ∂x ∂t ∂x ∂v ∂v + A′ = 0 ⇒ ∂t ∂x

北航CFD讲义第20和21课

三．Godunov 格式（一）Godunov 格式的基本原理Godunov 格式的基本原理：在离散点的界面上求解Riemann 问题。

Godunov 认为从时间层t n t =∆的已知解n i U 求得下一时间层()1t n t =+∆的未知解1n i U +可以分成三步走：第1步：将已知解niU 在单元11,22i i ⎛⎫-+ ⎪⎝⎭内进行平均，即12121i n n ni i i i U U dx U x +-==∆⎰ （11-10）并得到相邻单元的平均值，11n n i i U U --=11n n i i U U ++=Ux2i U -1i U -iU 1i U +2i U +x∆2x ∆2x ∆()U x 2i -32i -1i -i1i +2i +12i -12i +32i +第2步：根据激波管原理，在相邻单元界面上，求得Riemann 解（即求解一维Euler 方程的解析解）：在12i -界面 ()()()10,,R R n n i i U U UU -= 在12i +界面 ()()()10,,R Rn n i iU U UU+=第3步：下一时间层()1t n t =+∆的未知解由Riemann 解在单元11,22i i ⎛⎫-+ ⎪⎝⎭内积分获得：()121211,,i R n iL R i x UU U U dx x t ++-⎛⎫= ⎪∆⎝⎭⎰ （11-12）由于界面12i -和界面12i +上的Riemann 解是不同的，需要分段积分，于是（11-12）式可写为()()22111011,,,,xx R R n n n n n i i i i i U U U U d U U U d x t x t ξξξξ∆∆+-+-⎛⎫⎛⎫=+ ⎪ ⎪∆∆∆∆⎝⎭⎝⎭⎰⎰ （11-13）在以上三步中，第1和第3步均为在单元内的积分，与方程的物理本质无关，而第2步则利用了激波管的物理特性，Godunov 求解控制方程的独特之处就是这第2步：将离散的数值求解化为求单元界面上的Riemann 问题。

CFD数值模拟(含Fluent)学习及培训课件

（4）
CFD 求解过程
为了进行CFD计算，用户可借助商用软件来完成所需要的任务，也可自己直接编写计算程序。具体工作过程如右图所示：
建立控制方程确定初始条件及边界条件
划分计算网格,生成计算节点
建立离散方程离散初始条件和边界条件
给定求解控制参数
求解离散方程
解收敛否?
N
Y
显示和输出计算结果
此外, 与CAD联合, 还可进行结构优化设计等。
CFD概述(续)
该方法与传统的实验测量方法、理论分析方法组成了研究流体流动问题的完整体系，如下图所示：
CFD克服了实验测量方法和理论分析方法存在的弊端，其更加形象、直观、高效、全面，被得到了广泛应用！
CFD的应用
随着计算机和CFD商业软件的发展，CFD以其强大的生命力，广泛应用于水利工程、土木工程、食品工程、航天航空、海洋结构工程、生物医学、工业制造、燃烧、电子技术和环境污染等各个领域。
CFD的求解过程(续)
❖ 离散初始条件和边界条件
在商用CFD软件中，往往在前处理阶段完成了网格划分后，直接在边界条件上指定初始条件和边界条件，然后由前处理软件自动将这些初始条件和边界条件按离散的方式分配到相应的节点上去。
❖ 给定求解控制参数
主要是给定流体的物理参数和湍流模型的经验系数，给定迭代计算的控制精度、瞬态问题的时间步长和输出频率等。
计算流体动力学（CFD)培训资料
－CFD原理及Fluent
XXXX有限公司
2021年02月05日
报告大纲
计算流体动力学(CFD)软件原理与应用
Fluent软件的基本用法相关模拟案例公XX司工业程绩的CFD模拟
CFD概述

CFD_Lecture_(Introduction_to_CFD)-CFD经典ppt

HVAC
Hydraulics
Streamlines for workstation ventilation
6
Where is CFD used?
Marine (movie) Sports
• Where is CFD used?
• • • • • • • • • •
Aerospace Automotive Biomedical Chemical Processing HVAC Hydraulics
• Viscous vs. inviscid
(Re)
• External flow or internal flow (wall bounded or not) • Turbulent vs. laminar (Re) • Incompressible vs. compressible (Ma) • Single- vs. multi-phase (Ca) • Thermal/density effects (Pr, , Gr, Ec) • Free-surface flow (Fr) and surface tension (We) • Chemical reactions and combustion (Pe, Da) • etc…
•
Modeling (governing equations)
Navier-Stokes equations (3D in Cartesian coordinates)
2u 2u 2u ˆ u u u u p u v w 2 2 2 t x y z x y z x 2v 2v 2v ˆ v v v v p u v w 2 2 2 t x y z y y z x

中科院计算流体力学最新讲义CFD第讲求代数方程组及网格生成精品文档

1 Copyright by Li Xinliang
知识回顾：有限体积法基本流程
U tIJ 1 IJ F n d s 1 IJ F vn d s0
无粘项常用方法（流过AB边的通量）：
a. 利用周围点的值，计算出(I+1/2,J) 点处的物理量；直接利用“差分格式”
n 1 n 1 n 1 n 1
2
i 1 ,j i 1 ,j i,j 1 i,j 1 i,j
i N ,N 1 .1 .;j. .N ,N 1 .1 ..
n
n+1
n+1
n
n+1
n
n+1
n+1
n+1
n
特点：两次扫描，反复迭代
Copyright by Li Xinliang
0 ann
为了计算稳定，通常使用主元消去法列主元消去法；全主元消去法计算量：乘法：n3/3n2n/3
加法：n3/3n2/2n5/6
O(n3 / 3)
xnbn/ann
n
xi [bi aikxk]/aii ki1
优点：简单精确，缺点：计算量大
Copyright by Li Xinliang
l u jk,k1,..n.
k mmj
m1
k1
lik(aik limumk)/ukk ik1,..n. m1
对角线上不能有0，计算之前先交换矩阵A 的元素，将主值交换到对角线上
Copyright by Li Xinliang
5
回代过程
Axb
LUXb
1 l21 1
y1 b1
t
x2

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

五、与FEA的对比
CFD基础讲座
六、常见CFD软件及其结构
常见商品化CFD软件
软件
Fluent CFX Star CCM+ / Star CD AVL FIRE ……
公司
美国 ANSYS
英国 CD-adapco 奥地利 AVL
CFD基础讲座
方法
有限体积法
FVM
CFDesign ……
Power FLOW
2. 建模
几何模型（Catia. Pro/E …）→ CFD 模型（面网格）。根据问题性质。常用工具：HyperMesh, ANSA, IcemCFD, CFD前处理模块 … … 汽车行业的复杂几何需要强大的建模工具
3. 生成体网格
含边界层网格。通常在CFD软件中生成。
4. 设定各种求解条件与模型
体网格与面网格相关共用壁面节点（依赖关系）
一、传统的CFD方法
History of CAE/CAD
CFD基础讲座
1940’s • First digital computers developed
1950's
• Commercial computers become available • Academic and industrial research into computer-aided drafting • 2-dimensional tools used to generate machine toolpaths
三、N-S方程处理方式
主要模拟方式
LES 大涡模拟（气动噪声）
CFD基础讲座
RANS 雷诺平均
RSM 雷诺应力模型
涡粘模型
双方程
标准 k-ε模型 RNG k-ε模型
realizable k-ε模型
k-ω模型
单方程
零方程
四、CFD 解题的一般步骤
CFD基础讲座
1. 确定问题的性质与分析目标，制定分析方案方案比较 or 绝对值？简化方式？（散热中的辐射，除霜中的相变）… …
CFD基础讲座
二、问题分类：汽车工业中的CFD问题
CFD基础讲座
从汽车工业应用角度：
外流场分析：给出气动力与流场（速度/压力场）结果。含附加装置汽车外形优化。减阻降耗。提高车辆稳定性。减小风噪。给出部件风载荷
内流分析：给出流量分配/速度场/压力场/温度场。空调风路优化，提高乘员舒适性，除霜，通风口设计
边界条件，材料属性，计算模型，求解方式，监视变量等
5. 求解
监视收敛情况，进行必要的调整
6. 提取结果，后处理
生成需要的数表与图形
7. 撰写报告
五、与FEA的对比CFFra bibliotek ≠ FEA （有限元分析）结构分析
处理对象固体结构本身
力学模型
与
数学模型
弹、塑性体
固体力学方程组
(平衡/动力学方程)
（位移、应力）
1960's
• Development of interactive computer graphics (“Sketchpad”) • Large companies develop own CAD software based on room-sized mainframes
o primarily automotive, aerospace, and government agencies • Development of finite-element analysis and computer-aided manufacturing tools
求解方法网格性质方程属性网格数量
有限单元法 (FEM) 固定于介质－拉格朗日方法线性 / 非线性几万－几十万
CFD的难点：
▪ 非线性 ▪ 计算量大（网格百万－千万）
CFD基础讲座
流动分析
流体（气体，液体，…），无固定形状，没有“大变形”概念
固体（如车）只是边界，通常不须考虑其属性
粘性流体
1970's
• US Navy begins development of 3-dimensional programs • CAD still represents "Computer-Aided Drafting" to majority of industry • Development of CFD begins in earnest
机舱分析：内外流结合，系统级热流分析结合。主要解决发动机冷却问题部件散热：给出部件/周围的速度场/压力场/温度场。
提高散热效率（制动器、大灯等）气动噪声：给出整车或部件的气动噪声。提高舒适性发动机相关：缸内燃烧、进排气道、冷却系统、旋风除尘、污染 … … 专门问题：泵、气/油路、轮胎、 … …
美国 Blue Ridge Numerics 美国 EXA
（牛顿流体与非牛顿流体）
三维N-S方程组（二阶非线性方程组）
• 动量方程 • 能量方程 • 连续性方程 • 湍流方程
• ……
（速度、压强）
多采用有限体积法 (FVM)
不固定于介质（固定于计算域）－欧拉方法
非线性
百万－千万
▪ 物理机制（湍流，分离，多相，燃烧等） ▪ 数值算法问题（有时不易收敛）
CFD基础概要
CFD基础讲座
目录
CFD基础讲座
一、传统的CFD方法二、CFD 问题分类。汽车工业中的CFD问题三、N-S方程处理方式四、CFD 解题的一般步骤五、与FEA的对比六、常见CFD软件及其结构七、常用前处理工具介绍与演示
与CFD软件的接口八、网格类型介绍九、 LBM方法简介十、部分应用算例
一、传统的CFD方法
CFD基础讲座
传统CFD方法的特点：基于连续介质力学原理认为在所考虑的空间，流体是连续分布的流体的运动规律服从N-S方程组（连续）
主要用有限体积法（FVM）离散、求解RANS方程组连续问题 →离散化→求解→近似的连续结果（少数软件采用有限元方法）
对于特定的问题添加相应的方程（连续）能量、组分、声学、燃烧、辐射等
商品化CFD软件出现于80年代，90年代后期进入中国汽车行业。
二、问题分类
从CFD角度：时间相关：定常，非定常（稳态，瞬态）热能相关：流场分析，流场+温度场分析压缩性：低速流动（如汽车），高速流动物相：连续相，离散相
单相流，多相流组分：单组分，多组分网格状态：固定网格，动网格专门问题：噪声、燃烧、除霜、制动 …… ……