【STATA精品教程】第七章 方差分析
- 格式:pptx
- 大小:961.94 KB
- 文档页数:2




stata 方差结果解读
解读Stata的方差分析结果,主要关注以下几个关键点:
1. **样本数量(Number of obs)**:这是你的样本观测值数量,用于了解你的数据规模。
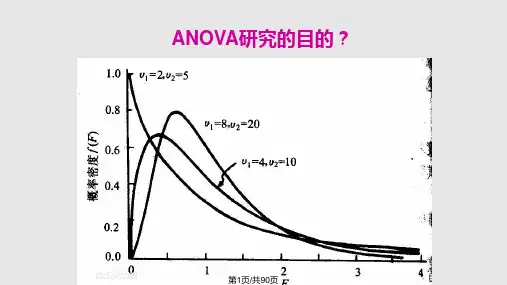
2. **F检验**:F检验用于检验方差分析中各组的总体方差是否相等。
F值越大,说明组间的方差越大,组内的方差越小。
3. **Prob>F**:这是F检验的显著性概率,如果这个值小于0.05,那么我们可以拒绝原假设(各组的总体方差相等),认为各组的总体方差不相等。
4. **R-squared(决定系数)**:这是相关系数的平方,表示模型解释的变差的比例。
一个完全的回归模型会得到1的R-squared值,意味着模型解释了所有的变差。
R-squared值越接近1,模型的拟合效果越好。
5. **Adj R-squared**:调整后的相关系数的平方,用于衡量模型的拟合优度。
与R-squared相比,Adj R-squared会随着变量的增加或减少而调整,以更准确地衡量模型的拟合优度。
6. **Root MSE**:均方根误差,表示预测值与实际值之间的平均偏差。
Root MSE越小,说明模型的预测越准确。
7. **SS(离差平方和)**:这是总偏差的来源,包括回归平方和(SSR)和残差平方和(SSE)。
回归平方和表示模型可以解释的偏差,而残差平方和表示模型无法解释的偏差。
结合这些关键点,你可以对Stata的方差分析结果进行详细的解
读。


stata的anova解读
当你使用 Stata 进行方差分析(ANOVA)后,可以通过输出结果来解读分析。
首先,Stata 的方差分析结果通常会提供一些关键的统计量和检验结果。
其中包括:
1. F 统计量:F 统计量用于检验组间差异是否显著。
如果 F 统计量的相伴概率(P 值)小于或等于显著性水平(通常为 0.05),则可以拒绝零假设,即认为至少有一个组的平均值与其他组存在显著差异。
2. 均方误差(Mean Square Error,MSE):MSE 表示每个组内的变异程度,可以用于比较不同组之间的方差。
3. 组间平方和(Sum of Squares Between Groups,SSB):SSB 表示组间差异的平方和,反映了不同组之间的变异。
4. 组内平方和(Sum of Squares Within Groups,SSW):SSW 表示组内差异的平方和,反映了每个组内部的变异。
除了这些统计量外,Stata 还会提供一些其他的信息,如组间和组内的自由度、均方(Mean Square,MS)等。
同时,Stata 还可以输出方差分析表,其中包括组间、组内和总的方差来源,以及 F 统计量和 P 值。
为了更深入地解读方差分析结果,你还可以检查各组的平均值和标准差,以及进行事后比较(post hoc comparisons)来确定哪些组之间存在显著差异。
总的来说,通过解读 Stata 的方差分析结果,你可以判断不同组之间是否存在显著差异,以及了解组内和组间的变异情况。
这些结果可以帮助你进行进一步的数据分析和解释。
如果你在解读结果时遇到问题,可以参考 Stata 的文档或相关统计书籍以获得更详细的解释。



在Stata中,求解数据的方差和协方差是非常常见和重要的数据分析操作。
通过求解方差和协方差,我们可以更深入地了解数据的变化和变量之间的关系,进而进行更准确的数据分析和预测。
本文将就Stata 中求解方差和协方差的命令进行全面评估,并深入探讨其在数据分析中的应用。
1. 方差和协方差的概念让我们简要回顾一下方差和协方差的概念。
在统计学中,方差是衡量随机变量离散程度的指标,表示一组数据离其均值的距离平方的平均值。
而协方差则是衡量两个随机变量线性关系强度和方向的指标,表示两个变量偏离其均值的乘积的平均值。
2. Stata中的方差和协方差命令在Stata中,我们可以使用“var”命令来求解变量的方差,使用“cov”命令来求解变量之间的协方差。
具体命令格式如下:``` statavar 变量名cov 变量1 变量2```通过这些命令,我们可以快速、方便地得到所需的方差和协方差结果。
3. 应用举例接下来,让我们以一个具体的应用举例,来看看如何在Stata中应用方差和协方差命令。
假设我们有一份包含两个变量(X和Y)的数据集,我们想要求解这两个变量的方差和协方差。
我们可以按照以下步骤进行操作:``` statause 数据集名var Xcov X Y```通过这些操作,我们可以得到变量X的方差和变量X与Y的协方差,从而更全面地了解这两个变量的特征和关系。
4. 个人观点和总结从个人观点来看,Stata中的方差和协方差命令非常方便实用,能够帮助我们快速获取数据的关键统计指标。
通过求解方差和协方差,我们可以更深入地了解数据的分布和变量之间的关系,为后续的数据分析和建模工作提供重要参考。
Stata中的求解方差和协方差命令是数据分析工作中必不可少的利器,通过合理使用这些命令,我们可以更全面、深刻地理解数据的特征和变量之间的关系,为数据分析工作提供有力支持。
希望本文的内容能够帮助你更好地掌握Stata中的方差和协方差求解操作,提升数据分析水平。
stata方差不齐的数据检验方法
在Stata中,可以使用多种方法来检验数据的方差不齐性。
下
面我将介绍一些常用的方法:
1. Breusch-Pagan检验,Breusch-Pagan检验是一种常用的检
验方法,用于检验回归模型的误差项的方差是否存在异方差性。
在Stata中,可以使用命令“hettest”来进行Breusch-Pagan检验。
该命令会输出LM统计量和对应的p值,用于判断是否存在异方差性。
2. White检验,White检验也是一种常用的异方差性检验方法。
在Stata中,可以使用命令“whitetest”来进行White检验。
该命
令同样会输出LM统计量和对应的p值,用于判断是否存在异方差性。
3. Park检验,Park检验是一种基于残差平方的异方差性检验
方法。
在Stata中,可以使用命令“estat hettest, park”来进行Park检验。
该命令同样会输出LM统计量和对应的p值,用于判断
是否存在异方差性。
4. 图形诊断,除了上述的统计检验方法,还可以通过绘制残差图、残差平方与自变量的散点图等图形来进行异方差性的诊断。
在
Stata中,可以使用命令“rvfplot”来绘制残差与自变量的散点图,以及命令“rvpplot”来绘制残差平方与自变量的散点图。
总之,Stata提供了多种方法来检验数据的方差不齐性,包括Breusch-Pagan检验、White检验、Park检验以及图形诊断方法。
在实际应用中,可以根据具体情况选择合适的方法进行检验。
stata协方差命令
STATA协方差分析是统计学中一种重要的工具,它可用于定性或
定量变量之间关系的分析。
它可以用来研究变量之间的关系,并对不
同变量之间影响的差异进行分析。
协方差分析使用STATA软件中的“cov”命令来完成,该命令可
以计算变量和变量之间相关的相关系数,以及变量的均值和标准差。
它同时可以确定变量的残差及其方差,以及回归系数的统计显著性等。
使用“cov”命令来进行协方差分析前,必须选择要分析的变量,所选变量必须的两两相关的关系。
协方差分析可以显示出两个变量之
间的联系程度,这有助于探究自变量和因变量之间的相关性,而不需
要考虑控制变量。
一旦确定了要进行分析的变量,协方差分析就可以开始了。
使用“cov”命令计算所选变量的平均值、标准差、相关系数、回归系数和
残差值。
若要深入了解变量之间的相关性,可以进一步检查它们的数
据分布,及其相互关系的统计显著性。
协方差分析可帮助人们理解特定变量之间的关系,并能够有效改
善研究中变量间的交互影响。
在运用STATA协方差分析之前,必须了
解要分析的变量并进行相应设置,以便得到准确可靠的结果。