17.3复数的几何意义和三角形式学习资料

复数的三角形式及乘除运算宇文皓月一、主要内容:复数的三角形式，模与辐角的概念及几何意义，用三角形式进行复数乘除运算及几何意义.二、学习要求:1．熟练进行复数的代数形式与三角形式的互化，会求复数的模、辐角及辐角主值.2．深刻理解复数三角形式的结构特征，熟练运用有关三角公式化复数为三角形式.3．能够利用复数模及辐角主值的几何意义求它们的范围（最值）.4．利用复数三角形式熟练进行复数乘除运算，并能根据乘除运算的几何意义解决相关问题.5．注意多种解题方法的灵活运用，体会数形结合、分类讨论等数学思想方法.三、重点:复数的代数形式向三角形式的转换，复数模及复数乘除运算几何意义的综合运用.四、学习建议:1．复数的三角形式是完全解决复数乘、除、乘方和开方问题的桥梁，相比之下，代数形式在这些方面显得有点力不从心，因此，做好代数形式向三角形式的转化是非常有需要的.前面已经学习过了复数的另两种暗示.一是代数暗示，即Z=a+bi(a,b∈R).二是几何暗示，复数Z既可以用复平面上的点Z(a,b)暗示，也可以用复平面上的向量来暗示.现在需要学习复数的三角暗示.既用复数Z 的模和辐角来暗示，设其模为r ，辐角为θ，则Z=r(cosθ+isinθ)(r≥0).既然这三种方式都可以暗示同一个复数，它们之间一定有内在的联系并能够进行互化.代数形式r=三角形式Z=a+bi(a,b ∈R) Z=r(cosθ+isinθ)(r≥0)复数三角形式的结构特征是:模非负，角相同，余弦前，加号连.否则不是三角形式.三角形式中θ应是复数Z 的一个辐角，纷歧定是辐角主值.五、基础知识1）复数的三角形式①定义：复数z=a+bi （a,b ∈R ）暗示成r （cos θ+ i sin θ）的形式叫复数z 的三角形式。

即z=r （cos θ+ i sin θ） 其中z r =θ为复数z 的辐角。

②非零复数z 辐角θ的多值性。

以ox 轴正半轴为始边，向量oz →所在的射线为终边的角θ叫复数z=a+bi 的辐角 因此复数z 的辐角是θ+2k π（k ∈z ）③辐角主值暗示法；用arg z 暗示复数z 的辐角主值。

高一数学复数的三角形式与指数形式复数是数学中的一个重要概念，它由实部和虚部组成，常用形式有三角形式与指数形式。

本文将介绍高一数学中复数的三角形式与指数形式，并分析它们在数学运算中的应用。

一、复数的三角形式复数的三角形式是指复数表示为幅角和模长的形式。

假设有一个复数z，可以表示为z = a + bi，其中a为实部，b为虚部，i为虚数单位。

通过对z的实部与虚部的操作，可以将复数表示为模长和幅角的形式。

令z的模长为r，幅角为θ，那么z可以表示为z = r(cosθ + isinθ)，其中r = √(a² + b²)为复数的模长，θ为复数的幅角。

复数的三角形式可以帮助我们更好地理解复数的几何意义。

在复平面上，复数z的实部对应x轴坐标，虚部对应y轴坐标。

而模长r可以表示复数z到原点的距离，幅角θ则表示复数与x轴的夹角。

二、复数的指数形式复数的指数形式是指复数表示为e的幂次方形式。

通过欧拉公式，可以将复数表示为指数形式。

假设有一个复数z，可以表示为z = a + bi。

根据欧拉公式，我们有e^(ix) = cosx + isinx，其中e为自然对数的底数。

将复数z表示为指数形式，有z = re^(iθ)，其中r为复数的模长，θ为复数的幅角。

复数的指数形式为我们进行复数的运算提供了便利。

复数的乘法可以简化为模长相乘、幅角相加，复数的除法可以简化为模长相除、幅角相减。

三、三角形式与指数形式的相互转化在数学运算中，我们常常需要将复数在三角形式和指数形式之间进行转换。

下面介绍如何将复数从三角形式转化为指数形式，以及从指数形式转化为三角形式。

1. 从三角形式转化为指数形式已知复数z = r(cosθ + isinθ)，要将其转化为指数形式，可以使用欧拉公式。

根据欧拉公式，有e^(iθ) = cosθ + isinθ。

将这个公式代入z中，可以得到z = re^(iθ)。

通过这个转化，我们可以将复数的乘法和除法转化为简单的指数运算。

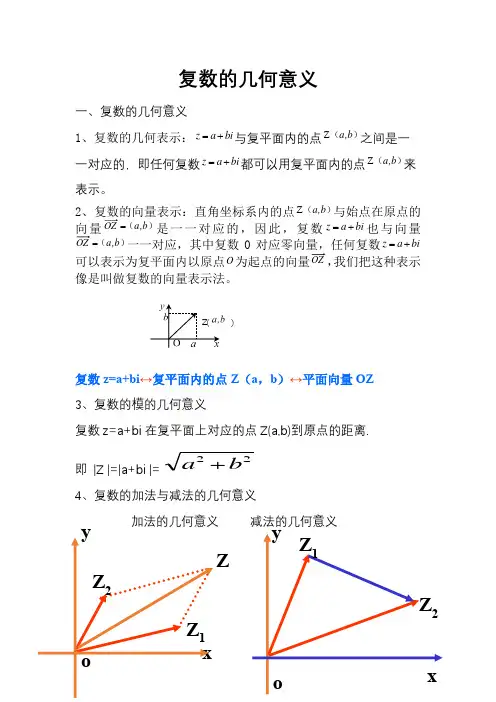
复数的几何意义一、复数的几何意义1、复数的几何表示：bi a z +=与复平面内的点）（b ,a Z 之间是一一对应的，即任何复数bi a z +=都可以用复平面内的点）（b ,a Z 来表示。

2、复数的向量表示：直角坐标系内的点）（b ,a Z 与始点在原点的向量）（b ,a OZ =是一一对应的，因此，复数bi a z +=也与向量）（b ,a OZ =一一对应，其中复数0对应零向量，任何复数bi a z +=可以表示为复平面内以原点O 为起点的向量OZ ，我们把这种表示像是叫做复数的向量表示法。

复数z=a+bi ↔复平面内的点Z （a ，b ）↔平面向量OZ 3、复数的模的几何意义复数z=a+bi 在复平面上对应的点Z(a,b)到原点的距离. 即 |Z |=|a+bi |=4、复数的加法与减法的几何意义加法的几何意义 减法的几何意义22b a + Z( )xoZ 1Z 2ZZ 2Z1yy oxz 1z 2≠0时， z 1+z 2对应的向量是以OZ 1、OZ 2、为邻边的平行四边形OZ 1ZZ 2的对角线OZ ， z 2-z 1对应的向量是Z 1Z 2 5、 复数乘法与除法的几何意义z 1=r 1（cos θ1+i sin θ1） z 2=r 2（cos θ2+i sin θ2）①乘法：z=z 1· z 2=r 1·r 2 [cos(θ1+θ2)+i sin(θ1+θ2)]如图：其对应的向量分别为oz oz oz 12→→→显然积对应的辐角是θ1+θ2 < 1 > 若θ2 > 0 则由oz 1→逆时针旋转θ2角模变为oz 1→的r 2倍所得向量便是积z 1·z 2=z 的向量oz →。

< 2 >若θ2< 0 则由向量oz 1→顺时针旋转θ2角模变为r 1·r 2所得向量便是积z 1·z 2=z 的向量oz →。

复数的三角形式及几何意义本节介绍复数的几何形式与三角形式，它们展示了复数的复平面的几何意义.通过复数的三角形式及运算，我们可以看到复数相乘（除）所对应的便是几何旋转.同时，复数的三角形式还可以有效地链接三角恒等变换，解决一些三角恒等式的计算，因此，本节内容也是强基或联赛中重点考察的对象.一．基础理论1.三角形式.复数bi a z +=（R b a ∈,）与复平面上的点),(b a Z 是一一对应的，点),(b a Z 和向量→OZ 于是一一对应的.向量→OZ 的模长称为复数bi a z +=的模||z ，即满足：22||b a z +=.进一步，复数yi x z +=在复平面内对应的点为),(y x Z .我们把向量OZ 与x 轴正方向形成的角叫做复数yi x z +=的辐角，记为Argz .取值在)2,0[π的辐角称为辐角主值，用z arg 来表示.对于非零复数，它的辐角主值是唯一的（复数0的辐角是任意的）.显然，若z arg =θ，则22sin yx y +=θ，22cos yx x +=θ，于是就可进一步得到复数的三角形式：设||OZ r =，θ为辐角，那么点P 点的坐标就可以记为)sin ,cos (θθr r ，)sin (cos θθi r z +=.2.幅角的性质.显然，若记22y x r +=则复数yi x z +=的主幅角可以表示为反三角函数的形式：xy r x r y z arctan arccos arcsinarg ====θ3.指数形式.由欧拉公式：θθθsin cos i ei +=可得到复数的指数形式：θθθi re i r z =+=)sin (cos .4.三角形式的基本运算.对于复数代数形式的加减乘除运算，属于高考数学的内容之一，这部分相对简单，此处就不再列举.我们这里重点需要强调的是复数的三角形式及运算.)sin (cos 1111θθi r z +=)sin (cos 2222θθi r z +=（1）乘法)]sin()[cos()sin )(cos sin (cos 21212122112121θθθθθθθθ+++=++=i r r i i r r z z .进一步可得：||||||2121z z z z ⋅=，2121arg arg arg z z z z +=或π2arg arg arg 2121-+=z z z z .几何意义：模翻倍，角度逆时针旋转.（可以看到，复数乘法从几何意义上讲便是旋转，这是复数的一个重要价值.）进一步，可得乘方的运算公式：设)sin (cos θθi r z +=，则)sin (cos θθn i n r z nn+=（棣莫弗定理）（2）除法)]sin()[cos(21212121θθθθ-+-=i r r z z .几何意义：模折倍，角度顺时针旋转（实则为夹角，可正可负），即||||||2121z z z z =，2121arg arg arg z z z z -=或π2arg arg arg 2121+-=z z z z.（3）开方设)sin (cos θθi r z +=，则2sin 2(cosnk i n k r z n n πθπθ+++=（1,,2,1,0-=n k ）.例如，222sin 222cos 2sin 2cos ππππππk i k i i +++=+=.可以看到，复数的n 次方根是n 个复数，它们的模都等于这个复数的模的n 次算术根，它们的幅角分别等于这个复数的幅角与π2的1,,1,0-⋅⋅⋅n 倍的和的n 分之一.5.复数的几何曲线（1）满足||||21z z z z -=-的复数z 所对应的点的轨迹为线段21Z Z 的中垂线；（2）满足r z z =-||1的复数z 所对应的点的轨迹为以1Z 为圆心，半径为r 的圆；（3）满足)2|(|,2||||2121a Z Z a z z z z <=-+-的复数z 所对应的点的轨迹为以21,Z Z 为椭圆，长轴长为a 2的椭圆.二．典例分析例1.计算下列各式的值.（1）312⎛⎫-+ ⎪ ⎪⎝⎭；（2）312⎛⎫-- ⎪ ⎪⎝⎭.解析：利用复数的三角形式可得：（1）33122cos sin cos2sin212233i i ππππ⎛⎫⎛⎫-=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭；（2）33144cos sin cos4sin41233i ππππ⎛⎫⎛⎫-=+=+= ⎪ ⎪ ⎪⎝⎭⎝⎭.点评：上述两个值是三次方程的两个单位根，其有重要的应用.例2．已知复数z 满足2240z z ++=，且arg ,2z ππ⎛⎫∈ ⎪⎝⎭，则z 的三角形式为__________．解析：由2240z z ++=可得，()213z +=-，所以11z z +=⇒=-，又arg ,2z ππ⎛⎫∈ ⎪⎝⎭，所以1z =-．因为2z ==，所以122z ⎛⎫=-=⎪ ⎪⎝⎭222cos sin 33i ππ⎛⎫+ ⎪⎝⎭．故答案为：222cos sin 33i ππ⎛⎫+ ⎪⎝⎭．例3.设11z i =+，22z i =+，33z i =+，则123arg()z z z -等于A．6πB．3πC．23πD．56π解析：由于()()()12312310z z z ii i i =+++=，∴()123arg z z z -()5arg 106i π=-=.选D.例4.（2020清华强基计划）求=++)31arcsin 103arccos1sin(arctan __________.解析：令i z i z i z +=+=+=2,3,1321，由于)arg(arg arg arg 321321z z z z z z =++，且根据复数的定义：=++31arcsin 103arccos1arctan 321arg arg arg z z z ++.另一方面：i z z z 10321=，故2)arg(321π=z z z ，则2)arg(arg arg arg 321321π==++z z z z z z ，综上，131arcsin 103arccos1sin(arctan =++.练习1．化简12arcsin 23-=______.解析：令11z =，22i z =，则有()2121211arg arg arg22z z z z +=()()1arg 42i 2⎡⎤=-+⎣⎦()13πarg 18i 24=-=.从而，12πarcsin234-=.下面我们再看复数的几何意义相关问题.例5.（2019上海竞赛）设复数z 满足4|3||3|=++-z z ，则||i z +的最大值为______.解析：显然，复数yi x z +=所对应的点的轨迹为方程为13422=+y x ，故求||i z +的最大值等价于求22)1(++y x 的最大值.利用椭圆的参数方程可求最大值为334.例6.（2020清华强基）设复数z 满足3|73|=-i z ，则iz z z +-+-1222的（）A.最大值为38 B.最大值为37 C.最小值为34 D.最小值为32解析：由3|73|=-i z 可得：1|37|=-i z ,则z 是以)37,0(i 为圆心，1为半径的圆.另一方面，|1|1222i z iz z z --=+-+-，根据几何意义可知：]38,32[|1|∈--i z .练习2.（2019中科大自主招生）若复数z 满足11+-z z 是纯虚数，则|3|2++z z 的最小值为__.答案：333.练习3.若复数z 满足1||=z ，则|))((|i z i z +-的最大值为______.答案：2练习4.若复数z 满足4|3||3|=++-z z ，则||i z +的最大值为______.答案：334练习5．（2020高联A 卷）设z 为复数．若2z z i--为实数（i 为虚数单位），则|3|z +的最小值为______．解析：设(,)z a bi a b =+∈R ，由条件知22222(2)i (2)(1)22Im Im 0i (1)i (1)(1)z a b a b ab a b z a b a b a b ⎛⎫--+---++-⎛⎫==== ⎪ -+-+-+-⎝⎭⎝⎭，故22a b +=．从而|3||(3)2|5z a b +=≥++=，即|3|z +≥．当2,2a b =-=时，|3|z +练习6.（2016山东预赛）=+++651arcsin 501arcsin 261arcsin 101arcsin_______.答案：4π.。

《7.3 复数的三角表示》复习教案7.3.1 复数的三角表示式【基础知识拓展】1．在复数的三角形式中，辐角θ的值可以用弧度表示，也可以用角度表示，可以是主值，也可以是主值加2k π或k ·360°(k ∈Z )．但为了简便起见，复数的代数形式化为三角形式时，一般将θ写成主值．2．两个非零复数相等当且仅当它们的模与辐角的主值分别相等． 【跟踪训练】1．判一判(正确的打“√”，错误的打“×”) (1)－1＝cosπ＋isinπ.( ) (2)2i ＝2⎝ ⎛⎭⎪⎫cos π2＋isin π2.( ) (3)－3(cos200°＋isin200°)是复数的三角形式．( ) 答案 (1)√ (2)√ (3)× 2．做一做(1)将复数z 1＝－1＋3i 表示成三角形式为________． (2)已知|z |＝23，arg z ＝5π3，求复数z ＝________. (3)若a <0，则a 的三角形式是________． 答案 (1)2⎝ ⎛⎭⎪⎫cos 2π3＋isin 2π3 (2)3－3i (3)－a (cosπ＋isinπ)【核心素养形成】题型一 复数的代数形式化为三角形式 例1 把下列复数的代数形式化成三角形式： (1)3＋i ；(2)1－i. [解] (1)r ＝3＋1＝2，∵3＋i 对应的点在第一象限， ∴tan θ＝13＝33，即θ＝π6，∴3＋i ＝2⎝ ⎛⎭⎪⎫cos π6＋isin π6.(2)r ＝1＋1＝ 2.∵1－i 对应的点在第四象限， 且tan θ＝－11＝－1，∴θ＝7π4， ∴1－i ＝2⎝⎛⎭⎪⎫cos 7π4＋isin 7π4. 【解题技巧】复数代数形式化为三角形式的步骤 (1)先求复数的模． (2)决定辐角所在的象限．(3)根据象限求出辐角(一般取其主值)． (4)求出复数三角形式． 【跟踪训练】把下列复数表示成三角形式． (1)－2＋2i ；(2)2⎝⎛⎭⎪⎫sin 3π4＋icos 3π4. 解 (1)原式＝22⎝ ⎛⎭⎪⎫－22＋22i ＝22⎝ ⎛⎭⎪⎫cos 3π4＋isin 3π4. (2)原式＝2⎝ ⎛⎭⎪⎫22－22i ＝2⎝⎛⎭⎪⎫cos 7π4＋isin 7π4. 题型二 判断复数三角形式的条件例2 判断下列各式是否是复数的三角形式，若不是，把它们表示成三角形式．(1)12⎝ ⎛⎭⎪⎫cos π4－isin π4；(2)－12⎝⎛⎭⎪⎫cos π3＋isin π3；⎝⎭55(4)sinπ5＋icos π5. [解] 根据复数的三角形式的结构，z ＝r (cos θ＋isin θ)，可依次作出判断． (1)不是.12⎝ ⎛⎭⎪⎫cos π4－isin π4＝12⎝ ⎛⎭⎪⎫cos7π4＋isin 7π4. (2)不是．－12⎝ ⎛⎭⎪⎫cos π3＋isin π3＝12⎝ ⎛⎭⎪⎫－12－32i＝12⎝⎛⎭⎪⎫cos 4π3＋isin 4π3.(3)不是.2⎝ ⎛⎭⎪⎫－cos π5＋isin π5＝2⎝ ⎛⎭⎪⎫cos4π5＋isin 4π5. (4)不是．sin π5＋icos π5＝cos 3π10＋isin 3π10.【解题技巧】判断复数的三角形式的条件 (1)r ≥0； (2)加号连接；(3)cos 在前，sin 在后； (4)θ前后一致，可任意值．即“模非负，角相同，余正弦，加号连”． 【跟踪训练】求复数z ＝3⎝ ⎛⎭⎪⎫sin π3－icos π3的辐角主值．解 ∵z ＝3⎝ ⎛⎭⎪⎫32－12i ＝3⎝ ⎛⎭⎪⎫cos 11π6＋isin 11π6， ∴辐角主值arg z ＝11π6. 题型三 复数三角形式化为代数形式 例3 把下列复数表示成代数形式．⎝⎭33(2)6⎝ ⎛⎭⎪⎫cos 11π6＋isin 11π6. [解] 根据a ＋b i ＝r (cos θ＋isin θ)，可得a ＝r cos θ，b ＝r sin θ，故可解．(1)4⎝ ⎛⎭⎪⎫cos π3＋isin π3＝4×12＋4×32i ＝2＋23i.(2)6⎝ ⎛⎭⎪⎫cos 11π6＋isin 11π6＝6×32＋6×⎝ ⎛⎭⎪⎫－12i ＝33－3i. 【解题技巧】将复数的三角形式化为代数形式：由z ＝r (cos θ＋isin θ)＝r cos θ＋i r sin θ， 可得a ＝r cos θ，b ＝r sin θ. 【跟踪训练】将下列复数的三角形式化成代数形式． (1)z 1＝2⎝ ⎛⎭⎪⎫cos π6＋isin π6；(2)z 2＝6(cos60°＋isin60°)． 解 (1)z 1＝2⎝ ⎛⎭⎪⎫32＋12i ＝3＋i.(2)z 2＝6⎝ ⎛⎭⎪⎫12＋32i ＝3＋33i.【课堂达标训练】1．－6的辐角主值为( ) A ．0 B.π2 C ．π D．－π2答案 C解析 －6＝6(－1＋0·i)＝6(cosπ＋isinπ)，辐角主值θ＝π.故选C. 2．下列说法正确的是( )A ．已知复数z ＝cos7π5＋isin 7π5，则z 的辐角主值为3π5B ．复数z ＝2i ＋3的虚部为2iC ．(3＋i)6＝－64D ．复数z ＝2i 的三角形式为z ＝2⎝ ⎛⎭⎪⎫cos 3π2＋isin 3π2 答案 C解析 A 项，z 的辐角主值arg z ＝7π5，错误；B 项，虚部为实数2，错误；C 项，(3＋i)6＝[(3＋i)2]3＝(2＋23i)3＝8＋3×2×(23i)2＋3×22×(23i)＋(23i)3＝－64，正确；D 项，z ＝2(0＋i)＝2⎝⎛⎭⎪⎫cos π2＋isin π2，错误．故C正确．3．复数12－32i 的三角形式是________．答案 cos 5π3＋isin 5π3解析 12－32i ＝cos 5π3＋isin 5π3，故复数12－32i 的三角形式是cos 5π3＋isin 5π3.4．设复数z ，z ＋2的辐角主值为π3，z －2的辐角主值为5π6，则z ＝________.答案 －1＋3i解析 设z ＋2＝r 1⎝ ⎛⎭⎪⎫cos π3＋isin π3＝r 12＋3r 12i ，z －2＝r 2⎝⎛⎭⎪⎫cos 5π6＋isin 5π6＝－3r 22＋r 22i.∴r 12－2＋3r 12i ＝2－3r 22＋r 22i ，易得⎩⎪⎨⎪⎧r 12－2＝2－3r 22， ①3r 12＝r 22， ②∴r 2＝3r 1，代入①得r 1＝2，∴z ＝1＋3i －2＝－1＋3i.5．设复数z 满足z －3z －的辐角主值为5π4，z ＋1的模为10，求复数z .解 设z ＝x ＋y i(x ，y ∈R )．由|z ＋1|＝10，得|(x ＋1)＋y i|＝10， ∴(x ＋1)2＋y 2＝10.①又z －3z －＝(x ＋y i)－3(x －y i)＝－2x ＋4y i ，所以 arg(z －3z －)＝5π4⇔⎩⎨⎧－2x <0，4y <0，－2x ＝4y ，②解①②，可得x ＝2，y ＝－1. 所以z ＝2－i.《7.3 复数的三角表示》课后作业7.3.1 复数的三角表示式基础巩固训练一、选择题1．如果非零复数有一个辐角为－7π4，那么该复数的( ) A ．辐角唯一 B ．辐角主值唯一 C ．辐角主值为－7π4D ．辐角主值为7π4答案 B解析 ∵辐角主值范围是[0,2π]，任何一个非零复数都有唯一的辐角主值，∴有一辐角为－7π4，则该复数有唯一的一个辐角主值，为π4.故选B.2．复数z ＝－3⎝ ⎛⎭⎪⎫sin 4π3－icos 4π3的辐角主值是( ) A.4π3 B.5π3 C.11π6 D.π6答案 C解析 z ＝－3⎝ ⎛⎭⎪⎫－sin π3＋icos π3＝3⎝ ⎛⎭⎪⎫sin π3－icos π3＝3⎝ ⎛⎭⎪⎫cos 11π6＋isin 11π6，∴arg z ＝11π6. 3．复数z ＝11＋i的辐角主值是( ) A.π4 B.3π4 C.5π4 D.7π4答案 D解析 z ＝11＋i ＝12－12i ＝22⎝ ⎛⎭⎪⎫cos 7π4＋isin 7π4，所以辐角主值是7π4，故选D.4．复数1＋3i 的三角形式是( ) A ．cos π3＋isin π3 B ．2⎝ ⎛⎭⎪⎫cos π3＋isin π3C ．cosπ6＋isin π6 D ．2⎝⎛⎭⎪⎫cos π6＋isin π6答案 B解析 1＋3i ＝2⎝ ⎛⎭⎪⎫12＋32i ＝2⎝ ⎛⎭⎪⎫cos π3＋isin π3.故选B.5．已知复数z ＝－1＋3i ，则它的共轭复数z －的三角形式为( ) A ．z ＝2⎝ ⎛⎭⎪⎫cos 4π3－isin 4π3 B ．z ＝－2⎝⎛⎭⎪⎫cos π6＋isin π6 C ．z ＝2⎝⎛⎭⎪⎫cos 4π3＋isin 4π3D ．z ＝2⎝ ⎛⎭⎪⎫cos 5π3＋isin 5π3 答案 C解析 ∵z －＝－1－3i ，∴|z －|＝2，z －＝2⎝ ⎛⎭⎪⎫－12－32i ＝2⎝⎛⎭⎪⎫cos 4π3＋isin 4π3. 6．著名数学家欧拉发现了复数的三角形式：e i x ＝cos x ＋isin x (其中i 为虚数单位，i 2＝－1)，根据这个公式，e 3i 表示的复数在复平面中所对应的点位于( )A ．第一象限B ．第二象限C ．第三象限D ．第四象限 答案 B解析 ∵e i x ＝cos x ＋isin x ，e 3i ＝cos3＋isin3,3弧度的角终边在第二象限．选B.二、填空题7．复数－2i 的实部是________，虚部是________，三角形式是________． 答案 0 －2 2⎝⎛⎭⎪⎫cos 3π2＋isin 3π2 解析 复数－2i ＝0－2i ，所以实部是0，虚部是－2，三角形式为2⎝⎛⎭⎪⎫cos 3π2＋isin 3π2.8．复数1＋i 的模是________，辐角主值是________，三角形式是________． 答案2 π42⎝⎛⎭⎪⎫cos π4＋isin π4解析 复数1＋i 的模是12＋12＝2，∵1＋i 对应的点在第一象限，且辐角的正切tan θ＝1，∴arg(1＋i)＝π4. ∴三角形式为2⎝⎛⎭⎪⎫cos π4＋isin π4.9．复数2＋i 和－3－i 的辐角主值分别为α，β，则tan(α＋β)等于________．答案 1解析 ∵复数2＋i 和－3－i 的辐角主值分别为α，β. ∴tan α＝12，tan β＝13，∴tan(α＋β)＝tan α＋tan β1－tan αtan β＝1.三、解答题10．已知复数z ＝12＋32i ，w ＝22＋22i ，求复数zw ＋zw 3的模及辐角主值．解 ∵zw ＋zw 3＝zw (1＋w 2)＝⎝ ⎛⎭⎪⎫12＋32i ⎝ ⎛⎭⎪⎫22＋22i (1＋i)＝2⎝ ⎛⎭⎪⎫－32＋12i ＝2⎝⎛⎭⎪⎫cos 5π6＋isin 5π6. ∴复数zw ＋zw 3的模为2，辐角主值为5π6. 能力提升训练1．已知复数z ＝1－sin θ＋icos θ⎝ ⎛⎭⎪⎫π2<θ<π，求z 的共轭复数z －的辐角主值．解 z ＝1＋cos ⎝ ⎛⎭⎪⎫π2＋θ＋isin ⎝ ⎛⎭⎪⎫π2＋θ＝2cos 2π2＋θ2＋2isin π2＋θ2cos π2＋θ2＝2cos π2＋θ2⎝ ⎛⎭⎪⎫cos π2＋θ2＋isinπ2＋θ2， 当π2<θ<π时，π4<3π4－θ2<π2，π2<π4＋θ2<3π4， ∴z －＝－2cos π2＋θ2⎝⎛⎭⎪⎫－cos π2＋θ2＋isin π2＋θ2＝－2cos ⎝ ⎛⎭⎪⎫π4＋θ2⎝ ⎛⎭⎪⎫cos ⎝⎛⎭⎪⎫3π4－θ2＋isin ⎝ ⎛⎭⎪⎫3π4－θ2， ∴辐角主值为3π4－θ2. 2．已知复数z ＝1＋i ，求复数z 2－3z ＋6z ＋1的模和辐角主值．解 z 2－3z ＋6z ＋1＝(1＋i )2－3(1＋i )＋61＋i ＋1＝3－i 2＋i＝1－i ，|1－i|＝12＋(－1)2＝2，因为1－i 对应的点在第四象限且辐角的正切tan θ＝－1，所以辐角的主值θ＝7π4.《7.3.2 复数乘、除运算的三角表示及其几何意义》复习教案【基础知识拓展】1．复数三角形式的乘法公式推广z 1z 2z 3…z n ＝r 1(cos θ1＋isin θ1)·r 2(cos θ2＋isin θ2)·…·r n (cos θn ＋isin θn )＝r 1r 2…r n [cos(θ1＋θ2＋…＋θn )＋isin(θ1＋θ2＋…＋θn )]．2．复数的乘方运算(棣莫佛定理)[r (cos θ＋isin θ)]n ＝r n (cos nθ＋isin nθ)．即复数的n (n ∈N *)次幂的模等于模的n 次幂，辐角等于这个复数的辐角的n 倍，这个定理称为棣莫佛定理．【跟踪训练】1．判一判(正确的打“√”，错误的打“×”) (1)在复数范围内，1的立方根是1.( ) (2)z z －＝|z |2.( )(3)2⎝ ⎛⎭⎪⎫cos π3＋isin π3·3⎝ ⎛⎭⎪⎫cos π6＋isin π6＝6i.( )答案 (1)× (2)√ (3)√ 2．做一做(1)把z ＝2－i 对应的向量OZ →，按顺时针方向旋转π2，所得向量对应的复数的代数形式为________．(2)(1＋3i)2019＝________.(3)⎣⎢⎡⎦⎥⎤12⎝ ⎛⎭⎪⎫cos π3＋isin π3÷⎣⎢⎡⎦⎥⎤6⎝ ⎛⎭⎪⎫cos π6＋isin π6＝________.答案 (1)－1－2i (2)－22019 (3)2⎝ ⎛⎭⎪⎫cos π6＋isin π6【核心素养形成】题型一 复数三角形式的乘法运算 例1 计算下列各式：(1)2⎝ ⎛⎭⎪⎫cos π12＋isin π12·3⎝ ⎛⎭⎪⎫cos5π6＋isin 5π6； (2)3cos ⎝ ⎛⎭⎪⎫π6＋isin π6·7⎝ ⎛⎭⎪⎫cos3π4＋isin 3π4； (3)⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫cos π3＋isin π3－4.[解] (1)原式＝6⎣⎢⎡⎦⎥⎤cos ⎝ ⎛⎭⎪⎫π12＋5π6＋isin ⎝ ⎛⎭⎪⎫π12＋5π6 ＝6⎝⎛⎭⎪⎫cos 11π12＋isin 11π12. (2)原式＝21⎣⎢⎡⎦⎥⎤cos ⎝ ⎛⎭⎪⎫π6＋3π4＋isin ⎝ ⎛⎭⎪⎫π6＋3π4 ＝21⎝ ⎛⎭⎪⎫cos 11π12＋isin 11π12. (3)原式＝1⎣⎢⎡⎦⎥⎤2⎝⎛⎭⎪⎫cos π3＋isin π34＝116⎝⎛⎭⎪⎫cos 4π3＋isin 4π3＝116⎝ ⎛⎭⎪⎫－12－32i ＝－12＋32i 16＝－132＋332i.【解题技巧】(1)积的模等于模的积，积的辐角等于辐角之和． (2)复数三角形式乘法运算注意向量旋转的方向．(3)做复数乘法运算时，三角形式和代数形式可以交替使用，但是结果一般保留代数形式．【跟踪训练】(1)如果向量OZ →对应复数4i ，OZ →逆时针旋转45°后再把模变为原来的2倍，得到向量OZ 1→，那么与OZ 1→对应的复数是________；(2)计算(1＋3i)6.答案 (1)－4＋4i (2)见解析 解析 (1)OZ →＝4i ＝4⎝ ⎛⎭⎪⎫cos π2＋isin π2，OZ 1→＝42⎝ ⎛⎭⎪⎫cos ⎝ ⎛⎭⎪⎫π2＋π4＋isin ⎝ ⎛⎭⎪⎫π2＋π4＝42⎝ ⎛⎭⎪⎫－22＋22i ＝－4＋4i.(2)原式＝⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫cos π3＋isin π36＝26⎝ ⎛⎭⎪⎫cos6π3＋isin 6π3＝26. 题型二 复数三角形式的除法运算例2 计算(1＋i)÷⎣⎢⎡⎦⎥⎤3⎝ ⎛⎭⎪⎫cos 3π4＋isin 3π4. [解] 因为1＋i ＝2⎝ ⎛⎭⎪⎫cos π4＋isin π4，所以原式＝2⎝⎛⎭⎪⎫cos π4＋isin π43⎝ ⎛⎭⎪⎫cos 3π4＋isin 3π4＝23⎣⎢⎡⎦⎥⎤cos ⎝ ⎛⎭⎪⎫π4－3π4＋isin ⎝ ⎛⎭⎪⎫π4－3π4＝23⎣⎢⎡⎦⎥⎤cos ⎝ ⎛⎭⎪⎫－π2＋isin ⎝ ⎛⎭⎪⎫－π2＝63(0－i) ＝－63i.【解题技巧】(1)商的模等于被除数的模除以除数的模，商的辐角等于被除数的辐角减去除数的辐角．(2)结果一般保留代数形式．(3)商的辐角主值不一定等于被除数的辐角主值减去除数的辐角主值所得的差．实际上，arg z 1z 2与arg z 1，arg z 2的关系是：arg z 1z 2＝arg z 1－arg z 2＋2k π(k ∈Z )．【跟踪训练】计算：(1)[6(cos70°＋isin70°)]÷[3(cos40°＋isin40°)]； (2)⎣⎢⎡⎦⎥⎤8⎝ ⎛⎭⎪⎫cos 2π3＋isin 2π3÷⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫cos π6＋isin π6. 解 (1)原式＝2()cos30°＋isin30°＝3＋i. (2)原式＝4⎝ ⎛⎭⎪⎫cos π2＋isin π2＝4i. 题型三 复数乘、除运算几何意义的应用例 3 如图所示，已知平面内并列八个全等的正方形，利用复数证明：∠1＋∠2＋∠3＋∠4＝π4.[证明] 如图，建立平面直角坐标系(复平面)．∠1＝arg(3＋i)， ∠2＝arg(5＋i)， ∠3＝arg(7＋i)， ∠4＝arg(8＋i)．所以∠1＋∠2＋∠3＋∠4就是乘积(3＋i)(5＋i)(7＋i)(8＋i)的辐角．而(3＋i)(5＋i)(7＋i)(8＋i)＝650(1＋i)，所以arg[(3＋i)(5＋i)(7＋i)(8＋i)]＝π4， 又因为∠1，∠2，∠3，∠4均为锐角， 于是0<∠1＋∠2＋∠3＋∠4<2π， 所以∠1＋∠2＋∠3＋∠4＝π4. 【解题技巧】复数乘、除运算的几何意义是数形结合的体现，利用复数的几何意义解题要充分挖掘题目中的已知条件．【跟踪训练】设复数z 1，z 2对应的向量为OZ 1→，OZ 2→，O 为坐标原点，且z 1＝－1＋3i ，若把OZ 1→绕原点逆时针旋转4π3，把OZ 2→绕原点顺时针旋转3π4，所得两向量恰好重合，求复数z 2.解 依题意(－1＋3i)⎝ ⎛⎭⎪⎫cos 4π3＋isin 4π3 ＝z 2cos 3π4＋isin3π4.∴z 2＝(－1＋3i)⎝ ⎛⎭⎪⎫cos 4π3＋isin 4π3⎝ ⎛⎭⎪⎫cos 3π4＋isin 3π4 ＝2⎣⎢⎡⎦⎥⎤cos ⎝⎛⎭⎪⎫2π3＋4π3＋3π4＋isin ⎝ ⎛⎭⎪⎫2π3＋4π3＋3π4 ＝2⎝⎛⎭⎪⎫cos 11π4＋isin 11π4＝－2＋2i.【课堂达标训练】1.⎝ ⎛⎭⎪⎫cos π4＋isin π410＝( )A ．iB ．－i C.22＋22i D.22－22i 答案 A解析 ⎝ ⎛⎭⎪⎫cos π4＋isin π410＝cos 10π4＋isin 10π4＝cos 5π2＋isin 5π2＝cosπ2＋isin π2＝i.故选A.2．若复数z ＝i1＋i ，则它的三角形式为( )A.12⎝ ⎛⎭⎪⎫cos π4＋isin π4B.2⎝ ⎛⎭⎪⎫cos π4＋isin π4C.22⎝⎛⎭⎪⎫cos π4＋isin π4D.22⎝⎛⎭⎪⎫cos π4－isin π4答案 C解析 ∵z ＝i 1＋i ＝12＋12i ，∴|z |＝22，复数z 对应的点是⎝ ⎛⎭⎪⎫12，12，位于第一象限，所以arg z ＝π4.故选C.3.⎝⎛⎭⎪⎫cos π6＋isin π6⎝ ⎛⎭⎪⎫cos π3＋isin π3＝( ) A ．i B ．－i C ．1 D ．－1答案 A解析 原式＝cos ⎝ ⎛⎭⎪⎫π6＋π3＋isin ⎝ ⎛⎭⎪⎫π6＋π3＝cos π2＋isin π2＝i.4．计算2÷⎝⎛⎭⎪⎫cos π4＋isin π4＝________. 答案2－2i解析 解法一：原式＝222＋22i ＝2·(1－i )22(1＋i )(1－i )＝2(1－i )2＝2－2i.解法二：原式＝2(cos0＋isin0)⎝⎛⎭⎪⎫cos π4＋isin π4 ＝2⎣⎢⎡⎦⎥⎤cos ⎝ ⎛⎭⎪⎫－π4＋isin ⎝ ⎛⎭⎪⎫－π4＝2×22＋2×⎝ ⎛⎭⎪⎫－22i＝2－2i.5．求复数z ＝1＋⎝⎛⎭⎪⎫3＋i 27的模． 解 因为32＋i 2＝cos π6＋isin π6，所以⎝ ⎛⎭⎪⎫3＋i 27＝⎝ ⎛⎭⎪⎫cos π6＋isin π67＝cos 7π6＋isin 7π6＝－32－12i ， 故z ＝1－32－12i ， |z |＝⎝⎛⎭⎪⎫1－322＋⎝ ⎛⎭⎪⎫122＝ 2－3＝4－232＝ (3－1)22＝3－12＝6－22.《7.3.2 复数乘、除运算的三角表示及其几何意义》课后作业基础巩固训练一、选择题1．复数sin40°－icos40°的辐角主值是( ) A ．40° B ．140° C ．220° D ．310°答案 D解析 ∵sin40°＝cos310°，－cos40°＝sin310°，∴sin40°－icos40°＝cos310°＋isin310°.故复数的辐角主值为310°.选D.2.⎝ ⎛⎭⎪⎫cos π4＋isin π4(1＋i)的值是( ) A ．－2i B.2i C ．2i D ．－2i 答案 B解析 解法一：原式＝⎝ ⎛⎭⎪⎫22＋22i (1＋i)＝22(1＋i)2＝22×(2i)＝2i.解法二：原式＝⎝ ⎛⎭⎪⎫cos π4＋isin π4·2⎝ ⎛⎭⎪⎫cos π4＋isin π4＝2⎝ ⎛⎭⎪⎫cos π2＋isin π2＝2i.故选B.3．计算icos120°＋isin120°的辐角主值为( )A.5π6 B.7π6 C.11π6D.5π3 答案 C解析 解法一：原式＝i －12＋32i ＝32－12i ＝cos 11π6＋isin 11π6.故选C. 解法二：原式＝cos90°＋isin90°cos120°＋isin120°＝cos(－30°)＋isin(－30°)＝cos330°＋isin330°，因为330°＝11π6.故选C.4．计算()cos36°＋isin36°－5的结果为( ) A ．－1 B ．1 C ．2 D.12答案 A 解析 原式＝1(cos36°＋isin36°)5＝1cos180°＋isin180°＝－1.选A.5．复数z ＝－3⎝ ⎛⎭⎪⎫cos π5－isin π5(i 是虚数单位)的三角形式是( )A ．3⎣⎢⎡⎦⎥⎤cos ⎝ ⎛⎭⎪⎫－π5＋isin ⎝ ⎛⎭⎪⎫－π5B ．3⎝ ⎛⎭⎪⎫cos π5＋isin π5C ．3⎝ ⎛⎭⎪⎫cos 4π5＋isin 4π5D ．3⎝ ⎛⎭⎪⎫cos 6π5－isin 6π5答案 C解析 z ＝3⎝ ⎛⎭⎪⎫－cos π5＋isin π5＝3⎝ ⎛⎭⎪⎫cos4π5＋isin 4π5.故选C. 6．计算(1＋3i)2020＝( ) A ．22019＋220193i B ．－22019＋220193i C ．22019－220193i D ．－22019－220193i答案 D解析 原式＝⎣⎢⎡⎦⎥⎤2⎝ ⎛⎭⎪⎫cos π3＋isin π32020＝22020⎝ ⎛⎭⎪⎫cos2020π3＋isin 2020π3＝22020⎝⎛⎭⎪⎫cos 4π3＋isin 4π3＝22020⎝ ⎛⎭⎪⎫－12－32i ＝－22019－220193i.选D. 二、填空题7．若复数z ＝(a ＋i)2的辐角是3π2，则实数a 的值是________．答案 －1解析 z ＝a 2－1＋2a i ，辐角为3π2，则a 2－1＝0且2a <0，故可得a ＝－1满足题意．8．在复平面内，点A 对应的复数为1，点B 对应的复数为3＋i ，将向量A B →绕A 按逆时针旋转90°，并将模扩大到原来的2倍，得向量A C →，则C 点对应的复数为________．答案 －1＋4i解析 AB →对应的复数为3＋i －1＝2＋i ，逆时针旋转90°，并将模扩大到原来的2倍，即可得A C →对应的复数为(2＋i)×2(cos90°＋isin90°)＝(2＋i)×2i＝－2＋4i.设C 点对应的复数为z ，则z －1＝－2＋4i ，故z ＝－1＋4i.9．8(cos240°＋isin240°)×[2(cos150°－isin150°)]＝________. 答案 16i解析 原式＝16(cos240°＋isin240°)×(cos210°＋isin210°) ＝16(cos90°＋isin90°)＝16i. 三、解答题10．已知复数z ＝a ＋b i(a ，b ∈R )的三角形式是r (cos θ＋isin θ)，试写出下列各复数的三角形式．(1)z 1＝－a ＋b i ；(2)z 2＝－a －b i ；(3)z 3＝a －b i.解 (1)z 1＝r (－cos θ＋isin θ)＝r [cos(π－θ)＋isin(π－θ)]． (2)z 2＝r (－cos θ－isin θ)＝r [cos(π＋θ)＋isin(π＋θ)]． (3)z 3＝r (cos θ－isin θ)＝r [cos(2π－θ)＋isin(2π－θ)]．能力提升训练1．已知|z |＝1，z 5＋z ＝1，求复数z .解 由|z |＝1，可设z ＝cos θ＋isin θ且0≤θ<2π.代入方程z 5＋z ＝1，得(cos θ＋isin θ)5＋(cos θ＋isin θ)＝1， 即(cos5θ＋cos θ－1)＋(sin5θ＋sin θ)i ＝0，所以⎩⎨⎧cos5θ＋cos θ－1＝0，sin5θ＋sin θ＝0，即⎩⎨⎧cos5θ＝1－cos θ， ①sin5θ＝－sin θ， ②两式平方后，相加得(1－cos θ)2＋(－sin θ)2＝1. 解得cos θ＝12，从而sin θ＝±32.经验证知，z ＝12±32i 都是原方程的解．故z ＝12＋32i 或z ＝12－32i.2．设z ＝r (cos θ＋isin θ)，求证1z m ＝1rm ()cos mθ－isin mθ(m ∈N *)．证明 1zm＝1r m(cos θ＋isin θ)m ＝1r m ·1cos mθ＋isin mθ＝1rm ·cos mθ－isin mθ(cos mθ＋isin mθ)(cos mθ－isin mθ)＝1rm (cos mθ－isin mθ)．得证．。

复数的三角形式及计算公式复数是数学中一个重要的概念，它可以表示为实部和虚部的和，通常用a+bi的形式表示，其中a为实部，b为虚部，i是虚数单位。

复数在数学和物理中有着广泛的应用，而复数的三角形式是表示复数的另一种形式，它可以更直观地展示复数的性质和特点。

本文将介绍复数的三角形式及其计算公式。

一、复数的三角形式。

复数的三角形式是指将复数表示为模长和幅角的形式，通常用r(cosθ + i sinθ)表示，其中r为模长，θ为幅角。

这种表示方法可以更直观地展示复数在平面直角坐标系中的位置和方向。

下面我们来看一下复数的三角形式的具体表达方式。

1.1 模长和幅角。

复数z=a+bi的模长r和幅角θ可以通过以下公式计算得出：r = |z| = √(a² + b²)。

θ = arg(z) = arctan(b/a)。

其中，|z|表示复数z的模长，arg(z)表示复数z的幅角。

1.2 复数的三角形式。

有了模长和幅角，我们就可以将复数表示为三角形式了：z = r(cosθ + i sinθ)。

这个表示方法将复数看作是一个向量，其模长r表示向量的长度，而幅角θ表示向量与实轴的夹角。

这种表示方法更直观地展示了复数在平面直角坐标系中的位置和方向。

二、复数的三角形式的计算。

下面我们来看一下如何通过复数的实部和虚部计算出其三角形式。

2.1 计算模长。

复数z=a+bi的模长可以通过以下公式计算得出：r = |z| = √(a² + b²)。

这个公式表示复数z的模长等于实部a和虚部b的平方和的平方根。

通过这个公式，我们可以很容易地计算出复数的模长。

2.2 计算幅角。

复数z=a+bi的幅角可以通过以下公式计算得出：θ = arg(z) = arctan(b/a)。

这个公式表示复数z的幅角等于虚部b与实部a的反正切值。

通过这个公式，我们可以计算出复数的幅角。

2.3 计算三角形式。

有了模长和幅角，我们就可以计算出复数的三角形式了：z = r(cosθ + i sinθ)。