线性代数第四章总结
- 格式：doc
- 大小：144.50 KB
- 文档页数：2
下载文档原格式
合集下载
线性代数之第4章.向量空间与线性变换
4.1 Rn的基与向量关于基的坐标
Rn的基与向量关于基的坐标 显然Rn的基不是唯一的，而α关于给定的基的坐标是唯 一确定的。以后，我们把n个单位向量组成的基称为自 然基或标准基。 在三维几何向量空间R3中，i, j, k是一组标准基，R3中任 一个向量α可以唯一地表示为： α＝a1i +a2j +a3k 有序数组(a1, a2, a3 )称为α在基i, j, k下的坐标。如果α的 起点在原点，(a1, a2, a3 )就是α的终点P的直角坐标（以 后我们常利用R3中向量α与空间点 P 的一一对应关系， 对Rn中的一些问题及其结论在R3中作几何解释）。
4.1 Rn的基与向量关于基的坐标
基之间的变换举例 解：由 β1 ε1 2ε2 ε3
β2 ε1 ε2 β ε ε3 3 1
即
1 1 1 ( β1 , β2 , β3 ) ( ε1 , ε2 , ε3 ) 2 1 0 1 0 1
n n
只有零解xj＝0 (j=1, 2, … , n) 。
4.1 Rn的基与向量关于基的坐标
基之间的变换 由于α1, α2, „, αn线性无关，由上式得：
a x
j 1 ij
n
j
0 i 1, 2, , n
因此，前方程只有零解（即上面齐次线性方程组只有零 解）的充要条件是上面齐次线性方程组的系数行列不等 于零，即定理中条件式成立。
4.1 Rn的基与向量关于基的坐标
基之间的变换 定义：设Rn的两组基B1={α1,α2,… ,αn}和 B2={η1,η2,… ,ηn}满足下式式的关系，
a11 a η1, η2 , , ηn α1, α2 , , αn 21 an1 a12 a1n a22 a2 n α α , , α A 1, 2 n an 2 ann
线性代数 第四章
可逆时， 的特征值。 （4） 当 A 可逆时，λ 是 A-1 的特征值。 Proof 且 x 仍是矩阵 kA， Al，g ( A) ，A-1 的分别属于特 l −1 的特征向量。 征值 k λ ，λ ， g (λ ) ， λ 的特征向量。 Note : λ，µ 为 A，B 的特征值 λ + µ，λµ 未必
−1
的特征值。 特征向量不同 特征向量不同) 是 A+B，AB 的特征值。(特征向量不同
第四章 特征值和特征向量、矩阵的相似对角化
Theorem 4.4 的证明 Proof : 由 Ax = λ x 有
(kA) x = k ( Ax) = k (λ x) = (k λ ) x
所以， 的特征值， 所以， k λ 是 kA 的特征值，且 x 也是 kA 属于
的特征向量， 用反证法 假设 x1 + x2 是A 的特征向量，则应存在数 λ
Ax1 = λ1 x1，Ax2 = λ2 x2 A( x1 + x2 ) = λ1 x1 + λ2 x2
A( x1 + x2 ) = λ ( x1 + x2 ) 使 于是 λ ( x1 + x2 ) = λ1 x1 + λ2 x2 即 (λ1 − λ ) x1 + (λ2 − λ ) x2 = 0
§1 特征值与特征向量
1.1 特征值与特征向量的概念 Definition 4.1 设 A 是 n 阶方阵，如果数 λ 和 n 维非 方阵， 零列向量 x 使关系式 对应于特征值
Ax = λ x
（1） ）
成立， 的特征值， 成立，则称 λ 为 A 的特征值，非零向量 x 称为 A 的 的特征向量。 λ 的特征向量。
说明满足 det( A − λ E ) = 0 的特征值. 是 A 的特征值. 反之 也然. 也然.
线性代数第四章
§3 向量组的秩
定义5 设有向量组 A， 如果在A中能选出 r个向量a1 , a 2 , , a r， 满足(1) 向量组A0 : a1 , a 2 , , a r 线性无关; ( 2) 向量组中 任意r 1个向量(如果A中有r 1个向量的话 )都线性相关 ， 那么称向量组 A0 是向量组 A的一个最大线性无关向 量组(简 称最大无关组 )， 最大无关组所含向量个 数r称为向量组 A 的秩， 记为RA .
a T (a1 , a2 ,, an )
二、向量的运算
三、向量组
定义 由若干个同维数的列向 量(或同维数的行向量 )构成 的集合称为向量组 . a11 a12 a1n a21 a22 a 2 n A a a a m2 mn m1 A (1 , 2 , , n ) , 其中 j (a1 j , a 2 j , , a mj )T T T A ( , , , ) , 其中 1 2 m i ( a i 1 , a i 2 , , a in )
向量组B : b1 , b2 , , bl 能由向量组向量 A : a1 , a2 , , am 线性表示 R( A) R( A, B ) 有矩阵K， 使得B AK 矩阵方程 AX B有解
例( P 86例 3) 设n维 向 量 组 A : a1 , a 2 , , a m 构 成n m 矩 阵 A ( a1 , a 2 , , a m )，n阶 单 位 矩 阵 E (e1 , e 2 , , e n )的 列 向 量 称 为n维 单 位 坐 标 向 量 .证 明 : n 维 单 位 坐 标 向 量 e1 , e 2 , , e n能 由 向 量 组 A线 性 表 示 的 充 要 条 件 是 R( A) n.
线性代数四五章知识点总结
线性代数四五章知识点总结第四章：行列式1. 行列式的定义行列式是一个数学工具，它可以用来表示一个线性变换对体积的放大倍数。
对于一个n阶（n行n列）的方阵A，它的行列式记作det(A)，行列式的元素通常用aij表示，其中i代表行号，j代表列号。
2. 行列式的性质（1）行列式中的行（列）互换，则行列式变号。
（2）行列式的某一行（列）乘以一个数k，那么行列式的值也要乘以k。
（3）行列式中的某一行（列）的元素都是两个数的和，那么行列式等于两个行列式的和。
（4）若行列式中有两行（列）完全相同，则行列式的值为0。
3. 行列式的计算（1）余子式和代数余子式对于一个n阶行列式A，如果去掉第i行和第j列的元素后，剩下来的(n-1)阶行列式就是A的余子式，用Mij表示。
而对应的代数余子式就是Mij乘上(-1)^(i+j)。
（2）拉普拉斯（Laplace）展开定理通过代数余子式的计算，可以利用拉普拉斯展开定理来计算n阶行列式的值。
即对于一个n阶行列式A，其中的元素aij乘以对应的代数余子式Mij后相加，即可得到行列式的值。
第五章：特征值和特征向量1. 特征值和特征向量的概念对于一个n阶方阵A，如果存在一个非零向量x和一个数λ，使得Ax=λx，那么λ称为A 的特征值，x称为A对应于特征值λ的特征向量。
2. 特征值和特征向量的计算寻找一个矩阵的特征值和特征向量可以通过求解方程组(A-λI)x=0来得到。
其中A是待求矩阵，λ是特征值，x是特征向量，I是单位矩阵。
3. 特征值和特征向量的性质（1）特征值的性质：一个n阶方阵A的n个特征值之和等于它的主对角线元素之和，即Tr(A)=λ1+λ2+...+λn。
（2）特征向量的性质：如果A有n个不同的特征值λ1,λ2,...,λn，那么这n个特征值对应的n个特征向量是线性无关的。
4. 特征值与对角化如果一个n阶方阵A有n个线性无关的特征向量，那么可以将它对角化成对角阵D，即找到一个可逆矩阵P，使得P^-1AP=D。
线性代数第四章复习
一般地，用正交线性替换将二次型
f ( x1 , x2 ,
…, xn ) = xTAx (其中 AT = A) 化为标准形的步骤如下:
Step1 求出二次型矩阵 A 的全部特征值
1 , 2 , … , n ;
Step2 求出正交矩阵 P，使 PTAP = diag(1 , 2 , … , n) ; Step3 作正交线性替换 x = Py ，其中 y = (x1 , x2 , … , xn )T Rn ，则二次型 f ( x1 , x2 , … , xn ) 化为标准形
det An det A 0.
实二次型正定性的判别方法 定理 4 . 7 n 元实二次型 f ( x1 , x2 , ··, xn ) 是 ·
正定二次型的充要条件是它的正惯性指数等于 n .
定理 4 . 8 实对称矩阵 A 为正定矩阵的充分
必要条件是 A 的所有特征值均为正数.
如果记
c11 c12 c1n x1 y1 c21 c22 c2 n x2 y2 n C , x R , y Rn c x y cn 2 cnn n1 n n
A AT
二次型 可以写成
f (x1 ,x2 ,,xn )
i 1
n
a x x
j 1 ij i
n
j
x Ax
T
其中 AT = A 为实对称矩阵, 称 A 为二次型的矩阵.
称矩阵 A 的秩 r(A) 为二次型的秩.
线性替换
1 定义 4.2 设 x1 , x2 , ··, xn ； y1 , y2 , ··, yn 是 · ·
求 A 对应的二次型 f (x1 , x2 , x3) .
线性代数 第四章 矩阵的特征值与特征向量
例 设 是 A 的一个特征值，证明：(1) 2 是 A2 的一个特征值；(2)当 A 可逆时， 1 是 A1 的一个 特征值.
证 设 是 A 的属于特征值 的特征向量，即 Aα α （ 0 ）
(1)在 Aα α 两边左乘 A ，得 A2α Aα 2α 所以， 2 是 A2 的一个特征值，且 是 A2 的属于特 征值 2 的特征向量.
在上述讨论中，表达式 A0 40 反映了矩阵 A 作用在向量0 上只改变了常数倍，我们把具有这 种性质的非零向量0 称为矩阵 A 的特征向量，数 4 称为对应于0 的特征向量.
定义 1 设 A 是 n 阶方阵，如果存在数 和非零 列向量 ，使得 Aα α .则称 为 A 的一个特征值， 称为矩阵 A 的属于特征值 的一个特征向量.
(2)当 A 可逆时，由 Aα α 有 α A1α ,因为 0 ， 知 0 ，故 A1α 1α ，则 1 是 A1 的一个特征值.
将此例推广为一般情况，有
结论：若 是 A 的一个特征值，则 m （ m N ） 是 Am 的一个特征值；() 是 ( A) 的特征值，其中 ( ) a0 a1 L am m ， ( A) a0 E a1 A L am Am .
例
已知向量
1 1
是
A
2 5
1 a
2 3
的一个特
1
1 b 2
征向量，试确定 a,b 及特征向量 所对应的特征值 .
解 由特征值和特征向量的定义 Aα α ，有
2 5 1
1 a b
2 3
1
1
1 1
即
2 1 1
1
2
a
b 1
于是 1 , 2 a ,b 1 所以 a 3, b 0, 1
20120525线性代数第四章小结
极大线性无关组
• • • • • • • • •
1.向量组的任意两个极大线性 无关组所含的向量个数相等。 2.向量组a1,a2,…,an-r的秩即为 矩阵A= a1,a2,…,an-r 的秩. 3.设向量组a1,a2,…,an-r的秩为 r，则向量组中任意r+1个向量 一般 （如果有）必线性相关. 情况 下 这个向量组必须是线性无关，向量 个数相等，但不唯一，（写出一个即可）
1 2 2 0
2 1 1 0
2 5 5 2
1 0 R3 R2 R34 0 0
1 2 0 0
2 1 0 0
2 5 2 0
1
'
2
'
3
'
4 . 1 即
'
2
3
' ' 初等行变换 4 1 2
实质是齐次 线性方程组 解的判断
－有非零解 －只有零解
线性相关性
• 如何判断齐次线性方程组解 • 秩 • 系数矩阵的秩与增广矩阵的秩 — • 的判断 秩(A)=秩(A) _ / • 秩(A)= (A)
/ n=m时行列式和秩的角度，n=m时两种情况的判断方法， 秩的角度（秩与变量个数之间的比较） 114 ye. 4.2. 5
1
1 2
1 0
1 1 0
所以 1 , 2 为所求的一个极大无关组，
3
1 2
且
1 1 2 ; 4 1 1 1 2
13
练习：P132 T1(2）
例 设矩阵
1 A 0 0
0 1 0
0 0 1
0 0 有 R ( A) 3 . 0
线性代数_第四章
从本例中,我们可看出,对角矩阵中的主对角
元素恰为矩阵A的特征值.相似因子阵P的各
列恰为A的对应于各特征值的特征向量.
定理7 n阶矩阵A相似于对角矩阵的充 要条件是A有n个线性无关的特征向量.
证明: (必要性)
设A相似于对角矩阵D=diag{l1, l2, …,ln} ,
则存在可逆矩阵P，使得P-1AP=D，即AP=PD。
即可求得对于该特征值的特征向量.
例4 设三阶方阵
1 2 2 A= 2 1 2 2 2 1
求A的特征值与对应于各特征值 的全部特征向量.
解: 求解特征方程|lI – A|=0,
l 1
| l I A |= 2 2 2 2 2 = (l 1) 2 (l 5) l 1
l 1
2
证明: 设A~B,则存在可逆矩阵X,使得B=X-1AX.
于是:
|B|=|X-1AX|=|X-1||A||X|=|A|
故行列式是相似不变量.
定理3
ห้องสมุดไป่ตู้
矩阵的迹是相似不变量.
定理4 矩阵的秩是相似不变量.
证明: 设矩阵A, B相似, 从而有A与B等价. 故A与B的秩相等. 因此, 矩阵的秩是相似不变量.
定理4 如果l1, l2, …,ls如(s<n)是n阶方阵A的
不同特征值,而 X , X , i1 i2
, X iri (i=1,…,s)是
A的对应于特征值li的ri个线性无关的特征向 量，那么向量组
X11 , X12 , , X1r1 , X 21, X 22 ,
, X 2r2
, X s1 , X s 2 ,
对P进行分块有：P=(X1, X2, …,Xn)，代入上式
2015线性代数第四章小结
Zhanglizhuo-2015
§4.2 向量内积
教学纲目 一、向量内积 二、向量长度 三、向量正交 教学要求 理解与掌握向量内积、长度及正交的定义及其性质。 定义 内积/长度/正交。 性质 内积/长度/正交/正交向量组的性质。
Zhanglizhuo-2015
§4.3 正 交 矩 阵
教学纲目 一、标准正交基的定义 二、正交矩阵的定义及其性质 三、标准正交基的求法 教学要求 1、理解与掌握标准正交基的定义； 2、理解与掌握正交矩阵的定义与性质； 3、理解与掌握标准正交基的求法。
定理3 Rn的一个非空子集W是Rn子空间的充分必要 条件是W关于Rn的加法和数量乘法是封闭的，即 10 对任意的, W，有+W; 20 对任意的W和实数k，有kW。
6
Zhanglizhuo-2015
命题4 如果1, 2, …,m与1, 2, …, t是线性空间Rn 的两个向量组，则 L(1, 2, …,m)=L(1, 2, …, t) 充分必要条件是向量组 {1, 2, …,m}{1, 2, …, t}。 命题5 1, 2, …,m的任一极大无关组是L(1, 2, …,m) 的一个基，且 dimL(1, 2, …,m)=rank{1, 2, …,m}。
Zhanglizhuo-2015
定义 标准正交基/正交矩阵。 性质 正交矩阵。
Zhanglizhuo-2015
命题1 设实数域上n阶矩阵A的行向量组为1, 2,…, n； 列向量组为1, 2,…, n，则 (1)A为正交矩阵当且仅当A的行向量组满足 1, 当i j , T i j 0, 当i j. (2)A为正交矩阵当且仅当A的列向量组满足 1, i j , T i j 0, i j.
线性代数第四章复习小结
α 1 , α 2 ,⋯ , α m
可由
线性相关， 线性相关，则
α1 , α 2 ,⋯ , α m 线性表示，且表示的系数唯一。 线性表示，且表示的系数唯一。
3）.若向量组 ） 若向量组 可由向量组 β 1 , β 2 , ⋯ , β
α
α1,α2 ,⋯,αr
线性表示， 线性表示，且
r>s
s
则
α1 , α 2 ,⋯ , α r 线性相关。 线性相关。
线性无关。
7）A为n阶方阵， ( A ) ） 为 阶方阵 r 阶方阵， ，又设
= n −1
η1 , η2
是非齐次线性方程组
AX = b
的两个不同的解， 的两个不同的解，证明
η1 + η2 X = k ( η1 − η2 ) + 2
为非齐次线性方程组 的通解。 的通解。其中
AX = b
K为任意常数。 为任意常数。 为任意常数
问
a, b
取何值时？（ ）有唯一解；（ ；（2）无解； 取何值时？（1）有唯一解；（ ）无解； ？（ （3）有无穷多个解，并求其解。 ）有无穷多个解，
6．设 ．
α1 , α 2 , α 3
线性无关， 线性无关，证明
β1 = α1 + α 2 , β 2 = α 2 + 2α3 ,
β 3 = α 3 + 3α1
T T
T
,3 ) ) α4 =(−1 ,2,1 ,α5 =(−2,6,4,1
T
T
3．设向量组 ．
1 4 3 2 1 , α = 0 , α = −1 , α = 1 α1 = 2 2 4 3 2 4 −2 0 1 1 3
线性代数第四章内容总结
km m
0
齐次方程组 x11 x22 xmm 0只有零解
Th4
秩R(1 , 2
, , m
)
m
(m为组中向量的个数 )
4. 讨论/证明/判定向量组相关性的方 法
法一：
将矩阵 (1, 2 , , m )化为行阶梯形，考察秩 R(1, 2 , , m )
与组中向量个数间的大 小关系。依据 Th4。 88页例5.
线性相关
定义
不全为零的数 k1, k2 ,, km , 使得k11
k2 2
km m
0
87页
至少有一个向量能由其 余m -1个向量线性表示
齐次方程组 x11 x22 xmm 0有非零解
Th4
秩R(1,
2
,,
m
)
m
(m为组中向量的个数 )
线性无关
定义
只有当k1
k2
km
0时才有k11
k2 2
1. 定义
2. 结论： 向量组与矩阵一一对应 ，也即
列向量组 1, 2 , , m 构成矩阵 A (1, 2 , , m );
行向量组
T 1
,
2
T
,
,
m
T
构成矩阵
B
(
T 1
,
2
T
,
,
m
T
)T
.
矩阵 Amn有n个m 维列向量构成的列向量 组，
有m个n维行向量构成的行向量 组。
1. 定义
1. 定义
2. 判定： 向量b由向量组1,2,,m线性表示 方程组x11 x22 xmm b有解
1. 定义. 2. 结论：
(1) 若1 ,2 ,,n-r是方程组Ax 0的基础解系，则该 方程组的任一解向量都可由1 ,2 ,,n-r线性表示.
线性代数知识点总结(第4章)
线性代数知识点总结（第4章）（一）方程组的表达形与解向量1、解的形式：(1)一般形式(2)矩阵形式：Ax=b；(3)向量形式：A=（α1，α2，…，αn）2、解的定义：若η=（c1，c2，…，c n）T满足方程组Ax=b，即Aη=b，称η是Ax=b的一个解（向量）（二）解的判定与性质3、齐次方程组：（1）只有零解←→r（A）=n（n为A的列数或是未知数x的个数）（2）有非零解←→r（A）＜n4、非齐次方程组：（1）无解←→r（A）＜r（A|b）←→r（A）=r（A）-1（2）唯一解←→r（A）=r（A|b）=n（3）无穷多解←→r（A）=r（A|b）＜n5、解的性质：（1）若ξ1，ξ2是Ax=0的解，则k1ξ1+k2ξ2是Ax=0的解（2）若ξ是Ax=0的解，η是Ax=b的解，则ξ+η是Ax=b的解（3）若η1，η2是Ax=b的解，则η1-η2是Ax=0的解【推广】（1）设η1，η2，…，ηs是Ax=b的解，则k1η1+k2η2+…+k sηs为Ax=b的解（当Σk i=1）Ax=0的解（当Σk i=0）（2）设η1，η2，…，ηs是Ax=b的s个线性无关的解，则η2-η1，η3-η1，…，ηs-η1为Ax=0的s-1个线性无关的解。
变式：①η1-η2，η3-η2，…，ηs-η2②η2-η1，η3-η2，…，ηs-ηs-1（三）基础解系6、基础解系定义：（1）ξ1，ξ2，…，ξs是Ax=0的解（2）ξ1，ξ2，…，ξs线性无关（3）Ax=0的所有解均可由其线性表示→基础解系即所有解的极大无关组注：基础解系不唯一。
任意n-r（A）个线性无关的解均可作为基础解系。
★7、重要结论：（证明也很重要）设A施m×n阶矩阵，B是n×s阶矩阵，AB=O（1）B的列向量均为方程Ax=0的解（2）r（A）+r（B）≤n（第2章，秩）8、总结：基础解系的求法（1）A为抽象的：由定义或性质凑n-r（A）个线性无关的解（2）A为数字的：A→初等行变换→阶梯型自由未知量分别取1,0,0；0,1,0；0,0,1；代入解得非自由未知量得到基础解系（四）解的结构（通解）9、齐次线性方程组的通解（所有解）设r（A）=r，ξ1，ξ2，…，ξn-r为Ax=0的基础解系，则Ax=0的通解为k1η1+k2η2+…+k n-rηn-r （其中k1，k2，…，k n-r为任意常数）10、非齐次线性方程组的通解设r（A）=r，ξ1，ξ2，…，ξn-r为Ax=0的基础解系，η为Ax=b的特解，则Ax=b的通解为η+ k1η1+k2η2+…+k n-rηn-r （其中k1，k2，…，k n-r为任意常数）（五）公共解与同解11、公共解定义：如果α既是方程组Ax=0的解，又是方程组Bx=0的解，则称α为其公共解12、非零公共解的充要条件：方程组Ax=0与Bx=0有非零公共解←→有非零解←→13、重要结论（需要掌握证明）（1）设A是m×n阶矩阵，则齐次方程A T Ax=0与Ax=0同解，r（A T A）=r（A）（2）设A是m×n阶矩阵，r（A）=n，B是n×s阶矩阵，则齐次方程ABx=0与Bx=0同解，r（AB）=r（B）。
线性代数第四章-向量空间
第四章 向量的线性相关性§1n 维向量一个含有0，1的数集P ，如果对于P 中任意两个数的四则运算结果仍在这个数集中（除数不为0），则称该数集P 为一数域。
容易验证整数集不是数域；有理数集Q 、实数集R 、复数集C 均为数域，以后分别称之为有理数域、实数域和复数域。
对于任一数域P ，有Q P C ⊂⊂。
定义1：数域P 中n 个数构成的有序数组12(,,,)n a a a L 称为数域P 上的n 维向量，向量常用希腊字母,,αβγ等表示。
其中i a 称为向量的第i 个分量。
若n 维向量12(,,,)n a a a α=L 和12(,,,)n b b b β=L 的对应分量相等，即i ia b =（1,2,i n =L ），称向量α与β相等，记为αβ=。
向量12(,,,)n a a a α=L 也称为n 维行向量。
n 维行向量可视为1n ⨯矩阵来定义加法与数乘。
矩阵中关于加法与数乘的性质也适合向量的加法与数乘。
向量有时为了方便也写成列的形式()1212,,,nn a a a a a a ⎛⎫ ⎪' ⎪= ⎪ ⎪⎝⎭L M 。
称为n 维列向量。
作为列向量时可视为1n ⨯矩阵来定义加法与数乘。
数域P 上全体n 维向量的集合对于线性运算称为数域P 上的n 维向量空间，记为n P 。
§2 线性相关性一、线性表示定义2：设12,,,s αααL 是一组n 维向量，12,,,s k k k L 是一组数，称向量1122s s k k k ααα+++L 为向量组12,,,s αααL 的一个线性组合。
如果某一向量α可表示成1122s s k k k αααα=+++L ，则称向量α可由12,,,s αααL 线性表示。
例如向量组()11,2,1α=-，()22,3,1α=-，()30,1,1α=-，有3122ααα=-，称3α可由12,αα线性表示。
注意：线性方程组AX B =的增广矩阵可写成分块矩阵形式12(,,,|)s αααβL 。
第四章-向量组及其线性组合
线性代数——第 4章
定理2 定理
向量组B能由向量组 线性表示 向量组 能由向量组A线性表示 能由向量组 ⇔ R(A) = R(A, B).
推论 向量组 A : a1 ,a2 , ...,am 与向量组 B : b1 ,b2 , ...,bn 等价⇔ 等价⇔ R(A) = R(B) = R(A, B)
定义3 定义3
设有两个向量组 A : α 1 ,α 2 ,L ,α m 及 B : β 1 , β 2 ,L , β s .
线性表示， 若 B 组中的每个向量都能由 向量组 A 线性表示，则 称 向量组 B能由向量组 A 线性表示 . 若向量组 A 与向 量组 B 能相互线性表示，则称 这两个 向量组等价． 能相互线性表示， 向量组等价．
学习本章要特别注意: 学习本章要特别注意 方程语言、矩阵语言、几何语言之间的转换。 方程语言、矩阵语言、几何语言之间的转换。 突出的典型问题是对关系式
(b1 , b2 , b3 ,⋅ ⋅ ⋅, bl ) = (a1, a2 , a3 ,⋅ ⋅ ⋅am ) K m×l
即
B = AK
所作的解释： 所作的解释： 方程语言： 是矩阵方程Ax＝ 的一个解 K是矩阵方程 的一个解； 方程语言： 是矩阵方程 ＝B的一个解； 矩阵语言： 是 与 的乘积矩阵 的乘积矩阵； 矩阵语言：B是A与K的乘积矩阵； 几何语言： 向量组B能由向量组 线性表出， 能由向量组A线性表出 几何语言： 向量组 能由向量组 线性表出， K是这一表示的系数矩阵 是这一表示的系数矩阵
同时， 同时， C的行向量组能由 B的行向量组线性表示 , A 为这一表示的系数矩阵 ：
γ 1T a11 T γ 2 a 21 M = M T γ a m m1 a12 a 22 M am 2 L a1 s β 1 T T L a 2 s β 2 M M T L a ms β s
线性代数第四章
为m个数, 称向
k11+k22+…+kmm
为向量组1, 2, …, m的一个线性组合.
15
，
定义4.2.2 设 1, 2, …, m, Rn, 如果存在数
l1, l2, …, lm 使得
=l11+l22+…+lmm
则称向量 可由向量组1, 2, …, m线性表出.
故1，2，3， 4线性相关.
31
例 2 设向量组, , 线性无关. 证明向量组
+, + , + 也线性无关.
32
小结：判定给定的一向量组1, 2, …, m是否线 性相关或线性无关，通常运用“待定系数法”，即 设待定系数 满足关系式
k11 k22 kmm O
11
二. 向量子空间
定义4.1.3 设W是的Rn一个非空子集. 如果
(i) 对任意的, ∈W，均有 + ∈W ;
(ii) 对任意的∈W 和任意的k∈R，有k∈W.
则称W是Rn的一个子空间. 子空间中向量加法和数乘向量满足向量空间定 义中的八条运算律. 从而 将向量空间和它的子空 间均称为向量空间.
中每一向量可由1, 2, …, m线性表出.
20
注. 若W=span(1, 2, …, m) , 则称1, 2, …, m
是子空间W的一组生成元, 并称W为1, 2, …, m
生成的子空间.
21
§4.3
线性相关与线性无关
一． 定义 线性相关与线性无关是线性代数中十分重要的概
利用行初等变换的方法解此方程组.
29
(1) 解. 因为
1 1 2 4 2 r1 r2 2 1 1 0 4 r1 r3 4 3 2 0
k11+k22+…+kmm
为向量组1, 2, …, m的一个线性组合.
15
，
定义4.2.2 设 1, 2, …, m, Rn, 如果存在数
l1, l2, …, lm 使得
=l11+l22+…+lmm
则称向量 可由向量组1, 2, …, m线性表出.
故1，2，3， 4线性相关.
31
例 2 设向量组, , 线性无关. 证明向量组
+, + , + 也线性无关.
32
小结：判定给定的一向量组1, 2, …, m是否线 性相关或线性无关，通常运用“待定系数法”，即 设待定系数 满足关系式
k11 k22 kmm O
11
二. 向量子空间
定义4.1.3 设W是的Rn一个非空子集. 如果
(i) 对任意的, ∈W，均有 + ∈W ;
(ii) 对任意的∈W 和任意的k∈R，有k∈W.
则称W是Rn的一个子空间. 子空间中向量加法和数乘向量满足向量空间定 义中的八条运算律. 从而 将向量空间和它的子空 间均称为向量空间.
中每一向量可由1, 2, …, m线性表出.
20
注. 若W=span(1, 2, …, m) , 则称1, 2, …, m
是子空间W的一组生成元, 并称W为1, 2, …, m
生成的子空间.
21
§4.3
线性相关与线性无关
一． 定义 线性相关与线性无关是线性代数中十分重要的概
利用行初等变换的方法解此方程组.
29
(1) 解. 因为
1 1 2 4 2 r1 r2 2 1 1 0 4 r1 r3 4 3 2 0
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
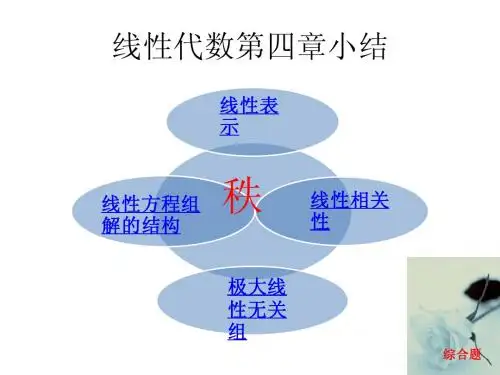
总结§4.1—§4.3
一、线性表示
1. 向量β可由向量组m ααα ,,21线性表示
⇔存在数m k k k ,,,21 使得，m m k k k αααβ ++=2211 ⇔方程组βααα=++m m x x x 2211有解（即是β=Ax 有解） ⇔
()=m R ααα ,,21()βααα,,,21m R （即是()()β,A R A R =）
2. 向量组12,,
l βββ可由向量组m ααα ,,21线性表示⇔()=m R ααα ,,21
()1212,,,,,m l R αααβββ （即是()(),R A R A B =）
向量组12,,
l βββ可由向量组m ααα ,,21线性表示⇒()12,,
l R βββ≤
()12,,m R ααα（即是()()R B R A ≤） 3. 向量组m ααα ,,21与向量组12,,
l βββ等价⇔()=m R ααα ,,21
()12,,l R βββ=()1212,,,,,m l R αααβββ （即是()()(),R A R B R A B ==）
二、线性相关与线性无关
1. 向量组m ααα ,,21线性相关⇔存在不全为零的数m k k k ,,,21 使得，
.02211=++m m k k k ααα
⇔方程组02211=++m m x x x ααα 有非零解. ⇔0=Ax 有非零解.
⇔()m R m <ααα ,,21
⇔()m A R < 其中()m A ααα ,,21=
2. 向量组m ααα ,,21线性无关⇔如果,02211=++m m k k k ααα 则有
.021====m k k k
⇔方程组02211=++m m x x x ααα 只有零解 ⇔0=Ax 只有零解 ⇔()m R m =ααα ,,21
⇔()m A R = 其中()m A ααα ,,21=
3. 向量组m ααα ,,21，如果()m A ααα ,,21=是方阵，则m ααα ,,21线性相关 （无关）().00≠=⇔A A
4.部分相关，则整体相关；整体无关，则部分无关； 1+n 个n 维向量线性相关.
5.向量组m ααα ,,21线性相关⇒其中至少有一个向量能由其余向量线性表示.
6.设向量组m ααα ,,21线性无关，则12,,,m αααβ线性相关⇔β可由向量组
m ααα ,,21线性表示. 三、最大无关组与向量组的秩 1. 最大无关组的两个等价定义：
2. 向量组的秩：向量组的秩等于它的最大无关组所包含的向量个数.
3. 定理：矩阵的秩等于它的列向量组的秩，等于它的行向量组的秩.
求法：求向量组m ααα ,,21的秩及其最大无关组，令()m A ααα ,,21=，然后对矩阵A 进行行初等变换，化到行阶梯形，行阶梯形非零行的行数即是A 的秩，也就是向量组m ααα ,,21的秩；同时行阶梯形非零行的首非零元对应于
m ααα ,,21的最大无关组.。