利用DSP实现数字滤波器
- 格式:docx
- 大小:737.72 KB
- 文档页数:18

实验三 低通、高通滤波器的幅频特性一、实验目的㈠ 进一步熟悉DSP 实验系统的结构、组成及使用方法。
㈡ 了解数字低通、高通滤波器的特点,学习数字滤波器幅频特性的测量方法。
㈢ 观察数字滤波器频响特性的周期延拓性。
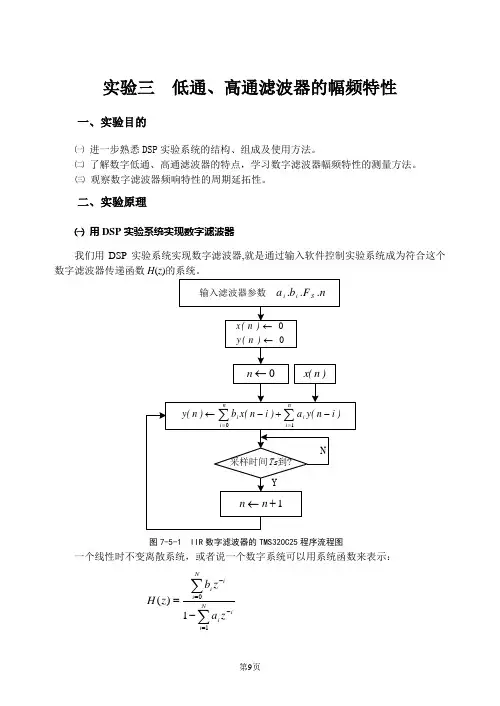
二、实验原理㈠ 用DSP 实验系统实现数字滤波器一个线性时不变离散系统,或者说一个数字系统可以用系统函数来表示:∑∑=-=--=N i ii Ni ii z a zb z H 101)(也可以用差分方程表示: ∑∑==-+-=Ni iN i ii n y a i n x b n y 1)()()(由以上两个公式中,当i a 至少有一个不为0时,表达的是一个IIR 数字滤波器;当i a 全都为0时,表达的是一个FIR 数字滤波器。
FIR 数字滤波器可以看成是IIR 数字滤波器i a 全都为0时的一个特例。
通常,我们把FIR 滤波器的系统函数表示为 H Z h n Zn N n()()==--∑01其差分方程表示为y n h i x n i i N ()()()=-=-∑01例如:已知一个用双线性变换法设计的三阶低通IIR 数字滤波器,采样频率F s =4KHz,其3dB 截止频率为1KHz,它的传递函数2321333121)(----++++=zz z z z H 为了用数字信号处理实验系统实现这个滤波器,我们对上式还需进行处理,将其化成一般表示式232123213333.0116667.05.05.016667.031161212161)(--------++++=++++=z z z z z zz z z H 由上式可知,传递函数的各系数为16667.00=b 5.01=b 5.02=b 16667.03=b 01=a 3333.02-=a 03=a相应的差分方程为)2(3333.0)3(16667.0)2(5.0)1(5.0)(16667.0)3()2()1()3()2()1()()(3213210---+-+-+=-+-+-+-+-+-+=n y n x n x n x n x n y a n y a n y a n x b n x b n x b n x b n y将以上差分方程的计算过程及采样频率Fs 、电路阶数N =3编写成TMS320Cxx 执行程序,输入实验系统,即可实现这个IIR 数字低通滤波器。


基于DSP实现的FIR低通滤波器FIR(有限脉冲响应)低通滤波器是一种常见的数字信号处理(DSP)滤波器。
它的设计和实现非常灵活,可以用于去除数字信号中高频成分,使得信号能在一定的频率范围内进行平滑处理。
FIR低通滤波器有很多种设计方法,其中最简单的方法是基于窗函数设计,例如矩形窗、汉宁窗、布莱克曼窗等。
这些窗函数的选择取决于滤波器的性能要求和频率响应的形状。
在DSP中,FIR低通滤波器的实现可以采用直接形式、级联形式、并行形式和迭代形式等多种结构。
其中直接形式是最简单和直观的实现方式,也是最容易理解和实现的一种结构。
直接形式的FIR低通滤波器由一个延迟线、一组乘法器和加法器组成。
延迟线用于延迟输入信号,乘法器用于对延迟后的信号进行调制,而加法器则将调制后的信号相加得到输出信号。
```----------------------,,,x(n) -->, Delay ,-->, Multiply,-->--+ Sum ,--> y(n)Line ,,,----------------------```在实现过程中,需要注意的是延迟线的设置和乘法器的系数。
延迟线的长度决定了滤波器的阶数,即滤波器对输入信号的响应范围。
乘法器的系数则决定了滤波器的频率响应,可以通过窗函数的选取来确定。
通常,FIR滤波器的实现可以通过查表法或者卷积法来实现。
查表法通过预先计算所有可能的输入组合,并将其存储在一张查找表中,以减少计算量。
卷积法则通过将输入信号和滤波器的冲击响应进行卷积运算来得到输出信号。
当实现FIR低通滤波器时,还需要考虑滤波器的性能指标和算法的优化。
常见的性能指标包括滤波器的截止频率、抗混叠性能、通带和阻带的幅频特性等。
算法的优化可以从以下几个方面考虑:乘法器的系数选择、滤波器结构的选择、滤波器长度的选择和存储器的优化等。
总之,基于DSP实现的FIR低通滤波器是一种常用的数字信号处理滤波器,它可以用于去除数字信号中的高频成分,平滑信号的频谱。

FIR滤波器及其DSP实现FIR(Finite Impulse Response)滤波器是一种常见的数字滤波器,它具有有限的脉冲响应。
与IIR(Infinite Impulse Response)滤波器相比,FIR滤波器具有线性相位特性,并且可以实现稳定的滤波效果。
FIR滤波器的核心是其冲激响应,即滤波器的输出响应。
FIR滤波器的输出可以通过对输入信号和滤波器的冲激响应进行卷积来实现。
为了得到所需的滤波效果,需要设计滤波器的冲激响应。
常见的方法包括频域设计和时域设计两种。
频域设计方法主要利用频率响应来设计FIR滤波器的冲激响应。
这包括将所需滤波特性转化为频率域中的理想滤波器响应,然后通过反变换得到冲激响应。
常见的频域设计方法有窗函数法、最优逼近法和频带优化法等。
窗函数法是最简单的频域设计方法之一,通过将理想滤波器的频率响应与窗函数的频率响应相乘得到FIR滤波器的冲激响应。
常用的窗函数有矩形窗、汉宁窗、汉明窗等。
窗函数法的优点是简单易用,但实现的FIR 滤波器在频域存在较大的过渡带宽。
因此,需要根据具体应用需求选择合适的窗函数。
最优逼近法是一种基于最优化理论的频域设计方法。
它通过将所需滤波特性定义为目标函数,利用优化算法来最小化目标函数与实际滤波器响应之间的差距,从而得到FIR滤波器的冲激响应。
最优逼近法能够较好地满足滤波特性的要求,但计算复杂度较高。
时域设计方法主要通过对滤波器的冲激响应进行直接设计来实现。
常见的时域设计方法有零相位响应(Zero-Phase Response,ZPR)设计和线性相位设计。
零相位响应设计方法通过首先设计一个偶对称的冲激响应,并通过反转和平移来得到滤波器的冲激响应。
这样可以实现零相位的滤波效果。
零相位响应设计方法能够保持输入信号的相位信息,适用于对相位要求较高的应用,如音频信号处理。
线性相位设计方法主要通过对滤波器的延迟进行优化来实现。
线性相位设计方法能够使得滤波器的相位响应近似为线性函数,从而实现滤波器对不同频率的信号具有相同的延迟。


基于DSP的FIR数字滤波器的设计与仿真毕业设计论文研究背景数字信号处理在现代通信、音视频处理、图像处理等领域中起着至关重要的作用,数字滤波器是数字信号处理中的重要内容。
其中FIR数字滤波器是一种常用的滤波器,其具有线性相位和稳定性等特点,在数字信号处理中应用广泛。
因此,本毕业设计将以FIR 数字滤波器为研究对象,结合DSP平台,进行数字滤波器的设计与仿真研究。
研究目标本文旨在设计一种基于DSP的FIR数字滤波器,并且研究其性能和仿真效果。
主要目标包括:1. 掌握DSP平台的开发流程和设计方法,包括硬件平台和软件开发技术。
2. 研究FIR数字滤波器的原理和特点,掌握其设计方法和计算技巧。
3. 基于DSP平台设计实现FIR数字滤波器,包括硬件和软件两个方面,满足设计要求。
4. 仿真FIR数字滤波器的性能和效果,验证设计的正确性和可行性。
5. 撰写毕业设计论文,总结设计过程和结果,体现出自己的设计思路和方法。
研究方法本研究采用如下方法:1. 研究DSP平台的开发流程和设计方法,包括使用硬件平台和软件开发技术。
2. 研究FIR数字滤波器的原理和特点,掌握其设计方法和计算技巧。
3. 基于DSP平台设计实现FIR数字滤波器,采用Verilog语言描述硬件电路,C语言编写软件程序。
4. 利用模拟工具对FIR数字滤波器进行仿真,测试性能和效果。
5. 撰写毕业设计论文,总结设计过程和结果,体现出自己的设计思路和方法。
预期结果本研究预期可以达到如下结果:1. 掌握DSP平台的开发流程和设计方法,能够应用于数字信号处理和嵌入式系统开发等领域。
2. 研究FIR数字滤波器的原理和特点,掌握其设计方法和计算技巧,能够进行数字信号处理相关工作。
3. 基于DSP平台设计实现FIR数字滤波器,满足设计要求,具有较好的性能和稳定性。
4. 仿真FIR数字滤波器的性能和效果,能够验证设计的正确性和可行性。
5. 撰写毕业设计论文,总结设计过程和结果,体现出自己的设计思路和方法,具有较好的表达和撰写能力。

基于DSP实现的FIR低通滤波器FIR(Finite Impulse Response)低通滤波器是一种数字信号处理(DSP)算法,用于滤除输入信号中高于一些截止频率的频域成分,并使输出信号只包含低于该截止频率的成分。
FIR低通滤波器通常由一组脉冲响应函数(Impulse Response)的加权和组成,其中权重决定了滤波器的频率响应。
实现FIR低通滤波器的一种常见方法是使用离散时间线性卷积运算。
滤波器的输入信号通过一个延迟线数组,然后与一组权重向量进行内积。
该内积计算的结果即为滤波器的输出。
在DSP领域,用于实现FIR低通滤波器的算法有很多种,其中最常用的是基于迭代结构(Direct Form)的算法。
此算法按照滤波器的脉冲响应函数的长度进行迭代,每次迭代处理输入信号的一个样本。
该算法的优点是实现简单、稳定可靠。
下面是一个基于DSP实现的FIR低通滤波器的伪代码示例:```python#定义滤波器的截止频率和脉冲响应函数长度def cutoff_frequency = 1000 # 截止频率为1kHzdef length = 101 # 脉冲响应函数长度为101#初始化滤波器的权重向量def weights = [0.0] * length#计算滤波器的脉冲响应函数for i in range(length):#计算当前权重对应的频率frequency = i * sampling_rate / length#如果当前频率小于截止频率,则设置权重为1,否则为0weights[i] = 1 if frequency <= cutoff_frequency else 0#初始化输入和输出信号数组def input_signal = [0.0] * signal_lengthdef output_signal = [0.0] * signal_length#循环处理输入信号的每个样本for i in range(signal_length):#延迟线数组移位,并将当前输入样本放入延迟线的第一个位置delay_line[1:] = delay_line[:-1]delay_line[0] = input_signal[i]#计算滤波器的输出output_signal[i] = sum(delay_line * weights)```这段示例代码实现了一个FIR低通滤波器,截止频率为1kHz,脉冲响应函数长度为101、首先,根据截止频率计算出权重向量。


DSP 课程实验报告—利用DSP实现实时信号IIR滤波学院:指导教师:学生:班级:DSP课程设计:实现信号IIR滤波---结题报告在信号与信息处理中,提取有用信息需要对信号进行滤波。
借助DSP数字信号处理器的高速运算能力,可以实时地对信号进行数字滤波。
本设计要求利用DSP的DMA方式进行信号采集和信号输出,同时对外部输入的信号进行数字滤波,用DSP实验工具箱实现IIR信号滤波器,调用55xdspx.lib中的IIR滤波程序iircas5(),实现信号IIR滤波仿真。
一、实验目的掌握DSP集成开发环境CCS的使用和调试方法。
掌握DSP片上资源和片外资源访问的基本方法。
通过对DSP处理器及CODEC的编程,培养C语言编程能力。
学会利用Matlab对信号进行IIR滤波,掌握Matlab的信号仿真方法。
掌握利用DSP实现信号实时IIR滤波设计方法。
提高使用DSP硬件平台实现数字信号处理算法的能力。
二、实验内容(1)用MATLAB软件产生一个两个叠加的正弦信号,并采样生成输入数据;(2)使用MATLAB软件中的工具箱设计一个IIR滤波器,获得相应系数值;(3)在CCStudio v3.3软件中建立仿真工程;(4)在DMA中断程序中,调用DSPLIB中的IIR滤波程序iircas5()实现对输入信号的滤波,观察输入输出波形。
发挥部分(1) 比较加不同窗和阶数时滤波器的滤波效果。
(2) 测试所设计滤波器的幅频特性和相频特性,并与MATLIB下的设计结果进行比较。
三、实验原理IIR 滤波原理IIR 数字滤波器差分方程的一般形式为:式中ai 、bi 为滤波系数。
当bi 全为零时,该滤波器为FIR 数字滤波器;当bi 不全为零时,则为IIR 滤波器。
IIR 数字滤波器可用直接型、级联型和并联型三种基本结构实现,其基本组成单元如图1所示。
图1.1 IIR 滤波器的二阶结构对于二阶IIR 数字滤波器,其传递函数为:H z =b 0+b 1z −1+b 2z −21−a 1z −1−a 2z −2n 时刻IIR 数字滤波器输出和输入关系为:其中x[k]是输入序列,y[k]是输出序列,ai 、bI 为滤波器系数。

DSP滤波算法设计与实现DSP(Digital Signal Processing,数字信号处理)滤波算法在信号处理领域中起到了至关重要的作用。
滤波算法可以对信号进行分析、处理和改善,去除噪音、增强信号等。
本文将介绍DSP滤波算法的设计和实现原理,以及常见的滤波器类型和应用场景。
一、滤波算法设计原理1. 数字滤波器的基本原理数字滤波器将离散时间的输入信号转换为输出信号,其基本原理是通过对输入信号进行离散化和加权求和的过程来实现。
滤波器的核心是滤波器系数的选择和滤波器结构的设计。
2. 滤波器设计方法常用的数字滤波器设计方法包括频率抽样法、模拟滤波器转换法、窗函数法和优化算法等。
频率抽样法根据滤波器的频率响应特性进行设计,模拟滤波器转换法则是将模拟滤波器的设计方法应用于数字滤波器设计。
窗函数法通过选择适当的窗函数对滤波器的频率响应进行修正。
优化算法通过数学优化模型对滤波器进行设计。
二、常见的滤波器类型1. FIR滤波器FIR(Finite Impulse Response,有限冲激响应)滤波器是一种常见的数字滤波器类型。
它的特点是只有有限个非零响应值,不存在反馈路径。
FIR滤波器具有线性相位和稳定性,适用于广义线性相位要求的应用领域。
2. IIR滤波器IIR(Infinite Impulse Response,无限冲激响应)滤波器是另一种常见的数字滤波器类型。
它的特点是存在反馈路径,具有无限长的冲激响应。
IIR滤波器具有较小的滤波器阶数,可以实现较小的延迟,适用于实时性要求较高的应用领域。
三、滤波器的应用场景1. 语音信号处理在语音信号处理中,滤波器可以用于降噪、语音增强、语音识别等任务。
通过采用合适的滤波器设计和优化算法,可以提高语音信号的清晰度和可理解性。
2. 图像处理在图像处理中,滤波器可以用于图像去噪、边缘检测、图像增强等任务。
通过采用适当的滤波器类型和参数设置,可以去除图像中的噪音,提高图像的质量和细节。
IIR 数字滤波器 (设计实验)一、实验目的1.了解IIR (Infinite Impulse Response ,无限冲激响应)滤波器原理及使用方法;2.了解使用MA TLAB 语言设计IIR 滤波器的方法;3.了解DSP 对IIR 滤波器的设计及编程方法;4.熟悉在CCS 环境下对IIR 滤波器的调试方法;二、实验原理IIR 数字滤波器的传递函数H(z)为:其对应的差分方程为:对于直接形式的二阶IIR 数字滤波器,其结构如图4.1图4.1 IIR 数字滤波器结构图编程时,可以分别开辟四个缓冲区,存放输入、输出变量和滤波器的系数,如图4.2所示。
图4.2 IIR 数字滤波器算法图三、实验内容与步骤设计一个三阶的切比雪夫Ⅰ型带通数字滤波器,其采样频率Fs =16kHz ,其通频带3.2kHz<f <4.8kHz ,内损耗不大于1dB ;f <2.4kHz 和f >5.6kHz 为阻带,其衰减大于20dB 。
输入信号频率为4000Hz 、6500Hz 的合成信号,通过所设计的带通滤波器将6500Hz 信号滤掉,余下4000Hz 的信号,达到滤波效果。
1、IIR 滤波器的MA TLAB 设计在MA TLAB 中设计IIR 滤波器,程序为: wp=[3.2,4.8];ws=[2.4,5.6];rp=1;rs=2001()1Mii i N ii i b zH z a z -=-==-∑∑01()()()MNi i i i y n b x n i a y n i ===-+-∑∑[n,wn]=cheb1ord(wp/8,ws/8,rp,rs)[b,a]=cheby1(n,rp,wn)设计结果为:N=3wn =0.4000 0.6000b0=0.0114747 a0=1.000000b1=0 a1=0b2=-0.034424 a2=2.13779b3=0 a3=0b4=0.034424 a4=1.76935b5=0 a5=0b6=-0.0114747 a6=0.539758在设计IIR滤波器时,会出现系数≥1的情况,为了用Q15定点小数格式表示系数,可以用大数去所有系数。
实验一: 通用DSP 实现IIR 滤波器1.1实验目的1.了解用数字滤波器实现模拟信号滤波的全过程;2.了解数字滤波器的实现方法及各个组成部分的功能和电路原理;3.了解一个四阶IIR 滤波器的频率特性,了解采样频率的变化对整个系统频率特性的影响。
1.2 实验原理数字滤波器的功能是将一组输入数字序列(信号)通过一定的运算后转变成另一组数字序列(信号)输出。
其输入、输出均为数字序列(信号)。
若要用数字滤波器对模拟信号进行滤波则必须配接相应的A/D ﹑D/A 转换器、保护﹑恢复滤波器。
本实验用一四阶IIR 滤波器实现对模拟信号的滤波,其框图如图1.1所示。
本实验中使用的数字信号处理器为单片式数字信号处理器,选用的是TI 公司的TMS320F206,该芯片为改进型哈佛结构的定点16位DSP 。
A/D ﹑D/A 转换器使用的也是TI 公司的TLC32044,该芯片是一个14位模拟接口集成电路,它包含了A/D ﹑D/A 单元和输入﹑输出滤波器,取样频率最高为19.2KHz ,可通过编程对采样频率进行控制,且增益可调。
电路具有模拟双断差分输入接口,其数据输入输出采用串行电路。
IIR 滤波器为无限长单位脉冲响应数字滤波器,其传递函数为以下形式:01()1mr r r nk k k b z H z a z-=-==-∑∑本实验中我们采用DSP 系统实现一个四阶的II R 滤波器,其传递函数为:12340123412341234()1b b z b z b z b z H z a z a z a z a z --------++++=----其中:012341.0, 7.4959, 24.9028, 47.8687, 58.2157b b b b b ==-==-=,123445.8645, 22.8612, 6.5933, 0.8428a a a a =-==-=。
该滤波器的频率图1.1 模拟信号的滤波特性如图1.2所示:实验中数字滤波器的结构选用直接I 型,其结构图如图1.3所示:1.3实验仪器及设备稳压电源一台,双踪示波器一台,函数发生器一台,计算机一台,仿真器一台,实验板一块。
DSP技术及应用课程设计报告课设名称:利用DSP实现数字滤波器学院:信息工程专业:通信工程班级:2012159学号:**************辅导老师:李珺陈俊峰时间:2015年12月29目录一.绪论 (1)1.1设计背景 (1)1.2设计要求 (1)1.3设计思路简介 (1)二. 系统开发平台与环境 (1)1.1CCS开发环境 (1)三 . FIR滤波器设计过程 (2)3.1FIR滤波器基本理论 (2)3.2FIR滤波器的MATLAB实现 (4)四FIR滤波器的DSP实现 (10)五. CCS仿真图及结果 (12)六. 总结 (14)七.参考文献 (15)一. 绪论1.1设计背景在信号处理中,滤波占有十分重要的地位。
数字滤波是数字信号处理的基本方法。
数字滤波与模拟滤波相比有很多优点,它除了可避免模拟滤波器固有的电压漂移、温度漂移和噪声等问题外,还能满足滤波器对幅度和相位的严格要求。
低通有限冲激响应滤波器(低通FIR滤波器)有其独特的优点,因为FIR系统只有零点,因此,系统总是稳定的,而且容易实现线性相位和允许实现多通道滤波器。
DSP(数字信号处理器)与一般的微处理器相比有很大的区别,它所特有的系统结构、指令集合、数据流程方式为解决复杂的数字信号处理问题提供了便利,本文选用TMS320C54X作为DSP处理芯片,通过对其编程来实现FIR滤波器。
对数字滤波器而言,从实现方法上,有FIR滤波器和无限冲激响应(IIR)滤波器之分。
由于FIR滤波器只有零点,因此这一类系统不像IIR系统那样易取得比较好的通带与阻带衰减特性。
但是FIR系统有自己突出的优点:①系统总是稳定的;②易实现线性相位;③允许设计多通带(阻带)滤波器。
其中后两项是IIR系统不易实现的。
1.2设计要求利用C语言在CCS环境中编写一个FIR滤波器程序,并能利用已设计好的滤波器对常用信号进行滤波处理。
1.3设计思路简介在TMS320C54x系统开发环境CCS(Code Composer Studio)下对FIR 滤波器的DSP实现原理进行讨论。
利用C语言设计相应的滤波器,通过实验仿真,从输入信号和输出信号的时域和频域曲线可看出在DSP上实现的FIR滤波器能完成预定的滤波任务。
二.系统开发平台与环境1.1 CCS开发环境CCS 提供了配置、建立、调试、跟踪和分析程序的工具,它便于实时、嵌入式信号处理程序的编制和测试,它能够加速开发进程,提高工作效率。
CCS 提供了基本的代码生成工具,它们具有一系列的调试、分析能力。
CCS支持如下图1.1所示的开发周期的所有阶段。
图 1.1三 . FIR 滤波器设计过程 3.1 FIR 滤波器基本理论(1)FIR 滤波器的特点数字滤波器的功能,就是把输入序列通过一定的运算变换成输出序列。
它的实现方法有很多,其中比较常用到的是无限长脉冲响应滤波器 IIR 和有限长脉冲响应滤波器FIR 两种。
在计算量相等的情况下,IIR 数字滤波器比FIR 滤波器的幅频特性优越,频率选择性也好。
但是,它有着致命的缺点,其相位特性不好控制。
它的相位特性)argH( )f(ωωj e =是使频率产生严重的非线性的原因。
但是在图像处理、数据传输等波形传递系统中都越来越多的要求信道具有线性的相位特性。
在这方面 FIR 滤波器具有它独特的优点,设FIR 滤波器单位脉冲响应h(n)长度为N ,其系统函数H(z)为∑-=-=1)()(N n nz n h z HH(z)是1-z 的(N-1)次多项式,它在z 平面上有(N-1)个零点,原点z=0是(N-1)阶重极点。
因此,H(z)永远稳定,它可以在幅度特性随意设计的同时,保证精确、严格的线性相位。
(2)FIR 滤波器的基本结构数字滤波是将输入的信号序列,按规定的算法进行处理,从而得到所期望的输出序列,FIR 滤波器的差分方程为:∑-=-=1)()(N k k k n x a n y对上式进行Z 变换得到FIR 滤波器的传递函数为:()()()∑-=-==10N i kk zb z X z Y z H由上式可以看出,H(z)是1-z 的N-1次多项式,它在z 平面内有N-1个零点,同时在原点处有N-1个重极点。
N 阶滤波器通常采用N 个延迟单元、N 个加法器与N+1个乘法器,取图中(a)、(b)两种结构。
图 FIR 滤波器的一般结构因为FIR 滤波器的单位抽样响应是有限长的,所以它永远是稳定的。
另外,若对 h(n)提出一些约束条件,那么可以很容易地使 H(z)具有线性相位,这在信号处理的很多领域是非常重要的。
FIR 滤波器的设计任务,是要决定一个转移函数H(z),使它的频率响应满足给定的要求。
这里所说的要求,除了通带频率p ω、阻带频率及两个带上的最大和最小衰减p ∂和s ∂外,很重要的一条是保证H(z)具有线性相位。
(3)Chebyshev 逼近法窗函数法和频率采样法设计出的滤波器的频率特性都是在不同意义上对所给理想频率特性()jwd e H 的逼近。
由数值逼近理论可知,对某个函数f(x)的逼近一般有以下三种方法:插值法(Interpolating Way)最小平方逼近法(Least Square Approaching Way) 一致逼近法(Consistent Approaching Way)切比雪夫最佳一致逼近的基本思想是,对于给定区间[a ,b]上的连续函数()x f ,在所有n 次多项式的集合n ϕ中,寻找一个多项式 p(x),使它在[a ,b]上对()x f 的偏差和其它一切属于n ϕ的多项式 p(x)对f(x)的偏差相比是最小的,即()()()()(){}x f x p x f x p-=-max min ˆmax切比雪夫逼近理论,这样的多项式是存在的,且是唯一的,并指出了构造这种最佳一致逼近多项式的方法,就是有名的“交错点组定理”。
切比雪夫逼近理论解决了p(x)的存在性、唯一性和如何构造等问题。
J.H.McClellan 、T.W.Parks 、L.R.Rabiner 等人应用切比雪夫逼近理论提出了一种设计FIR 滤波器的计算机辅助算法。
这种算法由于是在一致意义上对()jwd e H 作最佳逼近,因而获得了较好的通带和阻带性能,并能准确地指定通带和阻带的边缘。
但它的效率依赖于初始极值频率点的估计,且通带和阻带内波纹数较多,这是Chebyshev 方法的两个主要缺点。
3.2 FIR 滤波器的MATLAB 实现MATLAB 辅助DSP 实现FIR ,其总体过程为在DSP 中编写处理程序,在MATLAB 中利用滤波器设计、分析工具( FDATOOL) ,根据指定的滤波器性能快速设计一个FIR ,再把滤波器系数以头文件形式导入CCS 中,头文件中MATLAB 辅助DSP 实现FIR 数字滤波器含滤波器阶数和系数数组,在MATLAB 中调试、运行DSP 程序并显示、分析处理后的数据。
使用该方法,便于采用汇编语言来实现程序。
头文件名不变,当MATLAB 中设计的滤波器系数改变时,相应头文件中系数也改变,方便程序调试、仿真。
(1)输入信号的产生首先利用Matlab 产生导入CCS 的dat 文件,具体实现如下代码所示sl=1000;%有效信号 ns1=3000;%高频噪声 fs=20000;%采样频率 N=500; T=1/fs; n=0:N;signal=sin(2*pi*sl*n*T); noise1=0.7*sin(2*pi*ns1*n*T); x=(signal+noise1);%待滤波信号figure(1)plot(x)figure(2)y=abs(fft(x));%待滤波频谱df=n*(fs/N);plot(df,y)figure(3)plot(signal)figure(4)ysignal=abs(fft(signal));%滤波后频谱df=n*(fs/N);plot(df,ysignal) %滤波数据导出xout=x/max(x); %归一化xto_css=round(32767*xout);%数据取整xoutcss=xto_css;fid=fopen('C:\Users\zhaoyongwei\Desktop\myprojects\inpu t.dat','w'); %打开文件fprintf(fid,'1651 1 0 0 0\n');%输出文件头fprintf(fid,'%d\n',xoutcss); %输出fclose(fid);产生的时域波形如图所示:图 输入信号波形图 输入频谱经过滤波器后的预期时域波形如图:0100200300400500600-1.5-1-0.50.511.500.20.40.60.81 1.2 1.4 1.6 1.82x 10450100150200250图 输出时域波形频谱如图所示图 输出频谱100200300400500600-1-0.8-0.6-0.4-0.200.20.40.60.8100.20.40.60.81 1.2 1.4 1.6 1.82x 10450100150200250(2)滤波器的设计MATLAB集成了一套功能强大的滤波器设计工具FDATool(Filter Design & Analysis Tool),可以完成多种滤波器的设计、分析和性能评估。
a.打开Filter Design & Analysis Tool单击MATLAB主窗口下方的“Start”按钮,选择菜单“ToolBox”→“Filter Design”→“Filter Design & Analysis Tool(FDATool)”命令,打开FDATool,如图所示。
图fadatool的启动b.产生滤波器阶数为81阶,这里应填80,比阶数少1。
窗函数选择切比雪夫型(chebyshev),采样频率为20000Hz,通带截止频率为750Hz。
图滤波器的幅频特性图滤波器的相位特性c.产生滤波器系数和头文件图 滤波器系数图 头文件的产生最后将产生的头文件中的滤波器系数数组放入编写好的滤波器函数中,并在进行CCS 中进行调试与测试。
四 FIR 滤波器的DSP 实现(1)DSP 中滤波器的1-z 算法实现FIR 滤波器的输出表达式为1/2100()()()()()N N n n y n h i x n i h i s n i --===-=-∑∑式中,为滤波器系数;x(n)表示滤波器在n 时刻的输入;y(n)为n 时刻的输出。
它的基本算法是一种乘法-累加运算,即不断地输入样本x(n),经过延时后,再进行乘法-累加,最后输出滤波结果y(n)。