2019全国三卷理科数学教学提纲

绝密★启用前2019年普通高等学校招生全国统一考试理科数学注意事项：1．答卷前，考生务必将自己的姓名和准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给的四个选项中，只有一项是符合题目要求的。

(2018·新课标全国Ⅲ卷理1)1．已知集合2{1,0,1,2}{1}A B x x =-=≤，，则A B =A ．{}1,0,1-B ．{}0,1C ．{}1,1-D ．{}0,1,2【命题意图】本题考查了一元二次不等式的解法及集合的交运算，是基础题。

【答案】A【基本解法】因为{}11B x x =-≤≤，所以{}1,0,1A B =-【方法总结与拓展】集合运算是高考常考的，甚至必考的考点，属于基础题，也可以把其它知识渗透到集合中来，例如方程、不等式、向量、三角函数等，解决这类题目主要是直接法，或特值法。

集合问题主要要考虑元素的属性、运算等。

(2018·新课标全国Ⅲ卷理2)2．若(1)2z i i +=，则z = A ． 1i --B ． 1i -+C ． 1i -D ． 1i +【命题意图】本题考查了复数代数形式的四则运算， 【答案】D【基本解法】()212112i i i z i i -===++ 【方法总结与拓展】复数运算是高考常考的，甚至必考的考点，属于基础题。

(2018·新课标全国Ⅲ卷理3)3.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝，并称为中国古典小说四大名著，某中学为了解本校学生阅读四大名著的情况，随机调查了100名学生，其中阅读过《西游记》或《红楼梦》的学生共有90位，阅读过《红楼梦》的学生共有80位，阅读过《西游记》且阅读过《红楼梦》的学生共有60位，则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为（ ）A. 0.5B. 0.6C. 0.7D. 0.8【命题意图】本题考查概率与统计基本知识，考查学生对推理与计算能力，属于基础题。

2019年普通高等学校招生全国统一考试（全国 III 卷）理科数学一．选择题1、已知集合，则（ ）}1|{},2,1,0,1{2≤=-=x x B A =⋂B A A.}1,0,1{-B. B.{0,1}C. C.}1,1{-D. D.}2,1,0{答案：A 解答：，所以.}11|{}1|{2≤≤-=≤=x x x x B }1,0,1{-=⋂B A 2.若，则（ ）i i z 2)1(=+=z A.i --1B.i +-1C.i -1D.i +1答案：D 解答：,.i i z 2)1(=+i i i i i i i i i z +=-=-+-=+=1)1()1)(1()1(212 3.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝，并称为中国古典小说四大名著，某中学为了解本校学生阅读四大名著的情况，随机调查了100位学生，其中阅读过《西游记》或《红楼梦》的学生共有90位，阅读过《红楼梦》的学生共有80位，阅读过《西游记》且阅读过《红楼梦》的学生共有60位，则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为（ ）A.5.0B.6.0C.7.0D.8.0答案：C 解答：7.0100608090=+-4.的展开式中的系数为（ ）42)1)(21(x x ++3x A.12B.16C.20D.24答案：A 解答：由题意可知含的项为，所以系数为.3x 33142334121211x x C x x C =⋅⋅⋅+⋅⋅⋅125.已知各项均为正数的等比数列的前项和为，且，则（）{}n a 41553134a a a =+3a =A. 16B. 8C. 4D. 2答案：C 解答：设该等比数列的首项，公比，由已知得，，1a q 4211134a q a q a =+因为且，则可解得，又因为，10a >0q >2q =231(1)15a q q q +++=即可解得，则.11a =2314a a q ==6.已知曲线在点处的切线方程为，则（ ）x x ae y x ln +=)1(ae ，b x y +=2A.,e a =1-=b B.,e a =1=b C.,1-=e a 1=b D.,1-=e a 1-=b 答案：D 解析：令，则，，得.x x ae x f xln )(+=1ln )(++='x ae x f x21)1(=+='ae f 11-==e ea ，可得.故选D.b ae f +==2)1(1-=b7.函数在的图像大致为（ ）3222xx x y -=+[6,6]-A.B.C.D.答案：B 解析：∵，∴，∴为奇函数，32()22x x x y f x -==+332()2()()2222x x x xx x f x f x ----==-=-++()f x 排除选项C.又∵，根据图像进行判断，可知选项B 符合题意.334442424(4)8222f -⨯⨯=≈=+8.如图，点为正方形的中心，为正三角形，平面平面，是线段的中点，则（）A.，且直线，是相交直线B.，且直线，是相交直线C.，且直线，是异面直线D.，且直线，是异面直线答案：B解析：因为直线，都是平面内的直线，且不平行，即直线，是相交直线，设正方形的边长为，则由题意可得：，根据余弦定理可得：，，所以，故选B.9.执行右边的程序框图，如果输出为，则输出的值等于（）A.B.C.D.答案：C解析：第一次循环：；第二次循环：；第三次循环：；第四次循环：；…第七次循环：，此时循环结束，可得.故选C.10.双曲线：的右焦点为，点为的一条渐近线的点，为坐标原点.若C 22142x y -=F P C O 则的面积为（ ）||||PO PF =PFO ∆C:D:答案:A 解析：由双曲线的方程可得一条渐近线方程为；在中过22042x y -=y x =PFO ∆||||PO PF =点做垂直因为;所以P PH OF tan POF=∠PO =故选A;12S PFO ∆==11.若是定义域为的偶函数，且在单调递减，则（ ）()f x R (0,)+∞A. 233231(log )(2)(2)4f f f -->>B.233231(log (2)(2)4f f f -->>C.233231(2)(2)(log )4f f f -->>D.233231(2)(2)(log )4f f f -->>答案：C 解析:依据题意函数为偶函数且函数在单调递减，则函数在上单调递增；因为(0,)+∞(,0)-∞；又因为；所以3331(log )(log 4)(log 4)4f f f =-=233230221log 4--<<<<；故选C.233231(2)(2)(log )4f f f -->>12.设函数，已知在有且仅有个零点，下述四个()()sin 05f x x πωω⎛⎫=+> ⎪⎝⎭()f x []02π，5结论：在有且仅有个极大值点○1()f x ()0,2π3在有且仅有个极小值点○2()f x ()0,2π2在单调递增○3()f x 0,10π⎛⎫⎪⎝⎭的取值范围是 ○4ω1229,510⎡⎫⎪⎢⎣⎭其中所有正确结论的编号是A. B. C. D.○1○4○2○3○1○2○3○1○3○4答案：D解析：根据题意，画出草图，由图可知，[)122,x x π∈由题意可得，，解得，125565x x πωππωπ⎧+=⎪⎪⎨⎪+=⎪⎩12245295x x πωπω⎧=⎪⎪⎨⎪=⎪⎩所以，解得，故对；2429255πππωω≤<1229510ω≤<○4令得，∴图像中轴右侧第一个最值点为最大值点，故对；52x ππω+=3010x πω=>y ○1∵，∴在有个或个极小值点，故错；[)122,x x π∈()f x ()0,2π23○2∵，∴，故对.1229510ω≤<1149251051002πππππω≤⋅+<<○3二.填空题13.已知，为单位向量，且，若，则 .ab 0a b ⋅= 2c a =- cos ,a c =答案：23解析：∵，∴，()22222459c a a b b ==+-⋅= 3c =∵，∴.()2222a c a a a b ⋅=⋅=-⋅= 22cos ,133a c a c a c ⋅===⨯⋅14.记为等差数列的前项和，若，，则 .n S {}n a n 10a ≠213a a =105S S =答案：4解析：设该等差数列的公差为，∵，∴，故，d 213a a =113a d a +=()1120,0d a a d =≠≠∴.()()()1101101551102292102452452a a a d S d a a S a d d++⨯====++15.设、为椭圆的两个焦点，为上一点且在第一象限，若1F 2F 1203622=+y x C ：M C 为等腰三角形，则的坐标为________.21F MF ∆M 答案：)15,3(解析：已知椭圆可知，，，由为上一点且在第一象限，故等腰三1203622=+y x C ：6=a 4=c M C角形中，,,21F MF ∆8211==F F MF 4212=-=MF a MF 415828sin 2221=-=∠M F F ，代入可得.故的坐标为.15sin 212=∠=M F F MF y M 1203622=+y x C ：3=M x M )15,3(16.学生到工厂劳动实践，利用D 打印技术制作模型。

一．选择题1、已知集合}1|{},2,1,0,1{2≤=-=x x B A .则=⋂B A （ ） A. }1,0,1{- B. B.{0,1} C. C.}1,1{- D. D.}2,1,0{ 答案： A解答：}11|{}1|{2≤≤-=≤=x x x x B .所以}1,0,1{-=⋂B A .2.若i i z 2)1(=+.则=z （ ） A.i --1 B.i +-1 C.i -1 D.i +1 答案： D解答：i i z 2)1(=+,i i i i i i i i i z +=-=-+-=+=1)1()1)(1()1(212. 3.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝.并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况.随机调查了100位学生.其中阅读过《西游记》或《红楼梦》的学生共有90位.阅读过《红楼梦》的学生共有80位.阅读过《西游记》且阅读过《红楼梦》的学生共有60位.则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为（ ） A.5.0 B.6.0 C.7.0 D.8.0 答案： C解答：7.0100608090=+-4.42)1)(21(x x ++的展开式中3x 的系数为（ ）A.12B.16C.20D.24 答案： A解答：由题意可知含3x 的项为33142334121211x x C x x C =⋅⋅⋅+⋅⋅⋅.所以系数为12.5.已知各项均为正数的等比数列{}n a 的前4项和为15.且53134a a a =+.则3a =（） A. 16 B. 8 C. 4 D. 2 答案： C解答：设该等比数列的首项1a .公比q .由已知得.4211134a q a q a =+. 因为10a >且0q >.则可解得2q =.又因为231(1)15a q q q +++=.即可解得11a =.则2314a a q ==.6. 已知曲线x x ae y xln +=在点)1(ae ，处的切线方程为b x y +=2.则（ ） A.e a =,1-=b B.e a =,1=b C.1-=e a ,1=b D.1-=e a ,1-=b 答案： D解析：令x x ae x f xln )(+=.则1ln )(++='x ae x f x.21)1(=+='ae f .得11-==e ea .b ae f +==2)1(.可得1-=b .故选D.7.函数3222x xx y -=+在[6,6]-的图像大致为（ ）A.B.C.D.答案：B解析：∵32()22x xxy f x-==+.∴332()2()()2222x x x xx xf x f x----==-=-++.∴()f x为奇函数.排除选项C.又∵334442424(4)8222f-⨯⨯=≈=+.根据图像进行判断.可知选项B符合题意.8.如图.点为正方形的中心.为正三角形.平面平面是线段的中点.则（）A..且直线是相交直线B..且直线是相交直线C..且直线是异面直线D..且直线是异面直线答案：B解析：因为直线都是平面内的直线.且不平行.即直线是相交直线.设正方形的边长为 .则由题意可得：.根据余弦定理可得：..所以.故选B.9.执行右边的程序框图.如果输出 为 .则输出 的值等于（）A.B.C.D.答案：C解析：第一次循环：；第二次循环：；第三次循环：；第四次循环：；…第七次循环：.此时循环结束.可得.故选C.10.双曲线C：22142x y-=的右焦点为F.点P为C的一条渐近线的点.O为坐标原点.若||||PO PF=则PFO∆的面积为（）C:答案: A解析：由双曲线的方程22042x y -=可得一条渐近线方程为2y x =；在PFO ∆中||||PO PF =过点P 做PH 垂直OF 因为t a nP O F =2∠得到2PO =;所以1224S P F O∆==;故选A;11.若()f x 是定义域为R 的偶函数.且在(0,)+∞单调递减.则（ ）A. 233231(log )(2)(2)4f f f -->> B. 233231(log )(2)(2)4f f f -->>C. 233231(2)(2)(log )4f f f -->> D.233231(2)(2)(log )4f f f -->>答案： C 解析:依据题意函数为偶函数且函数在(0,)+∞单调递减.则函数在(,0)-∞上单调递增；因为3331(log )(log 4)(log 4)4f f f =-=；又因为233230221l o g4--<<<<；所以233231(2)(2)(log )4f f f -->>；故选C.12.设函数()()sin 05f x x πωω⎛⎫=+> ⎪⎝⎭.已知()f x 在[]02π，有且仅有5个零点.下述四个结论：○1()f x 在()0,2π有且仅有3个极大值点 ○2()f x 在()0,2π有且仅有2个极小值点 ○3()f x 在0,10π⎛⎫⎪⎝⎭单调递增 ○4ω的取值范围是1229,510⎡⎫⎪⎢⎣⎭其中所有正确结论的编号是A. ○1○4B.○2○3C.○1○2○3D.○1○3○4 答案： D解析：根据题意.画出草图.由图可知[)122,x x π∈.由题意可得.125565x x πωππωπ⎧+=⎪⎪⎨⎪+=⎪⎩.解得12245295x x πωπω⎧=⎪⎪⎨⎪=⎪⎩.所以2429255πππωω≤<.解得1229510ω≤<.故○4对； 令52x ππω+=得3010x πω=>.∴图像中y 轴右侧第一个最值点为最大值点.故○1对； ∵[)122,x x π∈.∴()f x 在()0,2π有2个或3个极小值点.故○2错； ∵1229510ω≤<.∴1149251051002πππππω≤⋅+<<.故○3对. 二.填空题13.已知a .b 为单位向量.且0a b ⋅=.若25c a b =-.则cos ,a c =. 答案：23解析：∵()22222545459c a ba b a b =-=+-⋅=.∴3c =.∵()225252a c a a b a a b ⋅=⋅-=-⋅=.∴22cos ,133a c a c a c⋅===⨯⋅. 14.记n S 为等差数列{}n a 的前n 项和.若10a ≠.213a a =.则105S S = . 答案：4解析：设该等差数列的公差为d .∵213a a =.∴113a d a +=.故()1120,0d a a d =≠≠.∴()()()1101101551102292102452452a a a d S d a a S a d d ++⨯====++.15.设1F 、2F 为椭圆1203622=+y x C ：的两个焦点.M 为C 上一点且在第一象限.若21F MF ∆为等腰三角形.则M 的坐标为________. 答案：)15,3(解析：已知椭圆1203622=+y x C ：可知.6=a .4=c .由M 为C 上一点且在第一象限.故等腰三角形21F MF ∆中8211==F F MF .4212=-=MF a MF ,415828sin 2221=-=∠M F F ,15sin 212=∠=M F F MF y M .代入1203622=+y x C ：可得3=M x .故M 的坐标为)15,3(.16.学生到工厂劳动实践.利用3D 打印技术制作模型。

绝密★启用前2019年普通高等学校招生全国统一考试理科数学注意事项：1．答卷前，考生务必将自己的姓名和准考证号填写在答题卡上。

2．回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。

如需改动，用橡皮擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3．考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共12小题，每小题5分，共60分。

在每小题给的四个选项中，只有一项是符合题目要求的。

1.已知集合{}{}21,0,1,21A B x x ，=-=≤，则A B ⋂=（ ） A. {}1,0,1- B. {}0,1 C. {}1,1- D. {}0,1,22.若(1i)2i z +=，则z =（ ）A. 1i --B. 1+i -C. 1i -D. 1+i3.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝，并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况，随机调查了100学生，其中阅读过《西游记》或《红楼梦》的学生共有90位，阅读过《红楼梦》的学生共有80位，阅读过《西游记》且阅读过《红楼梦》的学生共有60位，则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为（ ）A. 0.5B. 0.6C. 0.7D. 0.84.（1+2x 2 ）（1+x ）4的展开式中x 3的系数为A. 12B. 16C. 20D. 245.已知各项均为正数的等比数列{}n a 的前4项和为15，且53134a a a =+，则3a =（ ）A. 16B. 8C. 4D. 26.已知曲线e ln x y a x x =+在点()1,ae 处的切线方程为2y x b =+，则（ ）A. ,1a e b ==-B. ,1a e b ==C. 1,1a e b -==D. 1,1a e b -==-7.函数3222x x x y -=+在[]6,6-的图像大致为A. B. C.D.8.如图，点N 为正方形ABCD 的中心，ECD ∆为正三角形，平面ECD ⊥平面,ABCD M 是线段ED 的中点，则（ ）A. BM EN =，且直线,BM EN 是相交直线B. BM EN ≠，且直线,BM EN 是相交直线C. BM EN =，且直线,BM EN 是异面直线D. BM EN ≠，且直线,BM EN 是异面直线9.执行如图所示的程序框图，如果输入的ε为0.01，则输出s 的值等于（ ）A. 4122-B. 5122-C. 6122-D. 7122- 10.双曲线C ：2242x y -=1的右焦点为F ，点P 在C 的一条渐近线上，O 为坐标原点，若=PO PF ，则△PFO 的面积为A.B. C. 12x xD. 11.设()f x 是定义域为R 的偶函数，且在()0,∞+单调递减，则（ ） A. 233231log 224f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭B. 233231log 224f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭C. 23332122log 4f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭D. 23323122log 4f f f --⎛⎫⎛⎫⎛⎫>> ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭12.设函数()f x =sin （5x ωπ+）(ω＞0)，已知()f x []0,2π有且仅有5个零点，下述四个结论： ①()f x 在（0,2π）有且仅有3个极大值点②()f x 在（0,2π）有且仅有2个极小值点③()f x 在（0,10π）单调递增④ω的取值范围是[1229510，) 其中所有正确结论的编号是A. ①④B. ②③C. ①②③D. ①③④二、填空题：本题共4小题，每小题5分，共20分。

2019年普通高等学校招生全国统一考试数学(理)大纲2019年普通高等学校招生全国统一考试数学(理)大纲ⅰ．考试性质(略)ⅱ．考试要求(略)ⅲ．考试内容1．平面向量考试内容：向量．向量的加法与减法．实数与向量的积．平面向量的坐标表示．线段的定比分点．平面向量的数量积．平面两点间的距离、平移．考试要求：（1）理解向量的概念，掌握向量的几何表示，了解共线向量的概念．（2）掌握向量的加法和减法．（3）掌握实数与向量的积，理解两个向量共线的充要条件．（4）了解平面向量的基本定理，理解平面向量的坐标的概念，掌握平面向量的坐标运算．（5）掌握平面向量的数量积及其几何意义，了解用平面向量的数量积可以处理有关长度、角度和垂直的问题，掌握向量垂直的条件．（6）掌握平面两点间的距离公式，以及线段的定比分点和中点坐标公式，并且能熟练运用．掌握平移公式．2．集合、简易逻辑考试内容：集合、子集、补集、交集、并集．逻辑联结词．四种命题．充分条件和必要条件．考试要求：（1）理解集合、子集、补订、交集、交集的概念．了解空集和全集的意义．了解属于、包含、相等关系的意义．掌握有关的术语和符号，并会用它们正确表示一些简单的集合．（2）理解逻辑联结词"或"、"且"、"非"的含义．理解四种命题及其相互关系．掌握充分条件、必要条件及充要条件的意义．3．函数考试内容：映射、函数、函数的单调性、奇偶性．反函数．互为反函数的函数图像间的关系．指数概念的扩充．有理指数幂的运算性质．指数函数．对数．对数的运算性质．对数函数．函数的应用．考试要求：（1）了解映射的概念，理解函数的概念．（2）了解函数的单调性、奇偶性的概念，掌握判断一些简单函数的单调性、奇偶性的方法．（3）了解反函数的概念及互为反函数的函数图像间的关系，会求一些简单函数的反函数．（4）理解分数指数幂的概念，掌握有理指数幂的运算性质．掌握指数函数的概念、图像和性质．（5）理解对数的概念，掌握对数的运算性质．掌握对数函数的概念、图像和性质．（6）能够运用函数的性质、指数函数和对数函数的性质解决某些简单的实际问题．4．不等式考试内容：不等式．不等式的基本性质．不等式的证明．不等式的解法．含绝对值的不等式．考试要求：（1）理解不等式的性质及其证明．（2）掌握两个（不扩展到三个）正数的算术平均数不小于它们的几何平均数的定理，并会简单的应用．（3）掌握分析法、综合法、比较法证明简单的不等式．（4）掌握简单不等式的解法．（5）理解不等式|a|-|b|≤|a+b|≤|a|+|b|．5．三角函数考试内容：角的概念的推广．弧度制．任意角的三角函数．单位圆中的三角函数线．同角三角函数的基本关系式：sin2α+cos2α=1sinα/cosα=tanαtanαcotα=1 正弦、余弦的诱导公式．两角和与差的正弦、余弦、正切．二倍角的正弦、余弦、正切．正弦函数、余弦函数的图像和性质．周期函数．函数y=asin(ωx+φ)的图像．正切函数的图像和性质．已知三角函数值求角．正弦定理．余弦定理．斜三角形解法．考试要求：（1）理解任意角的概念、弧度的意义．能正确地进行弧度与角度的换算．（2）掌握任意角的正弦、余弦、正切的定义．了解余切、正割、余割的定义．掌握同角三角函数的基本关系式．掌握正弦、余弦的诱导公式．了解周期函数与最小正周期的意义．（3）掌握两角和与两角差的正弦、余弦、正切公式．掌握二倍角的正弦、余弦、正切公式．（4）能正确运用三角公式，进行简单三角函数式的化简、求值和恒等式证明．（5）了解正弦函数、余弦函数、正切函数的图像和性质，会用"五点法"画正弦函数、余弦函数和函数y=asin(ωx+φ)的简图，理解a，ω，φ的物理意义．（6）会由已知三角函数值求角，并会用符号arcsinx、arccosx、arctanx 表示．（7）掌握正弦定理、余弦定理，并能初步运用它们解斜三角形．6．数列考试内容：数列．等差数列及其通项公式．等差数列前n项和公式．等比数列及其通项公式．等比数列前n项和公式．考试要求：（1）理解数列的概念，了解数列通项公式的意义，了解递推公式是给出数列的一种方法，并能根据递推公式写出数列的前几项．（2）理解等差数列的概念，掌握等差数列的通项公式与前n项和公式，并能解决简单的实际问题．（3）理解等比数列的概念，掌握等比数列的通项公式与前n项和公式，并能解决简单的实际问题．7．直线和圆的方程考试内容：直线的倾斜角和斜率，直线方程的点斜式和两点式．直线方程的一般式．两条直线平行与垂直的条件．两条直线的交角．点到直线的距离．用二元一次不等式表示平面区域．简单的线性规划问题．曲线与方程的概念．由已知条件列出曲线方程．圆的标准方程和一般方程．圆的参数方程．考试要求：（1）理解直线的倾斜角和斜率的概念，掌握过两点的直线的斜率公式．掌握直线方程的点斜式、两点式、一般式，并能根据条件熟练地求出直线方程．（2）掌握两条直线平行与垂直的条件，两条直线所成的角和点到直线的距离公式．能够根据直线的方程判断两条直线的位置关系．（3）了解二元一次不等式表示平面区域．（4）了解线性规划的意义，并会简单的应用．（5）了解解析几何的基本思想，了解坐标法．（6）掌握圆的标准方程和一般方程，了解参数方程的概念，理解圆的参数方程．8．圆锥曲线方程考试内容：椭圆及其标准方程．椭圆的简单几何性质．椭圆的参数方程．双曲线及其标准方程．双曲线的简单几何性质．抛物线及其标准方程．抛物线的简单几何性质．考试要求：（1）掌握椭圆的定义、标准方程和椭圆的简单几何性质，理解椭圆的参数方程．（2）掌握双曲线的定义、标准方程和双曲线的简单几何性质．（3）掌握抛物线的定义、标准方程和抛物线的简单几何性质．（4）了解圆锥曲线的初步应用．9（a）．①直线、平面、简单几何体考试内容：平面及其基本性质．平面图形直观图的画法．平行直线．对应边分别平行的角．异面直线所成的角．异面直线的公垂线．异面直线的距离．直线和平面平行的判定与性质．直线和平面垂直的判定与性质．点到平面的距离．斜线在平面上的射影．直线和平面所成的角．三垂线定理及其逆定理．平行平面的判定与性质．平行平面间的距离．二面角及其平面角．两个平面垂直的判定与性质．多面体．正多面体．棱柱．棱锥．球．考试要求（1）掌握平面的基本性质，会用斜二测的画法画水平放置的平面图形的直观图．能够画出空间两条直线、直线和平面的各种位置关系的图形．能够根据图形想像它们的位置关系．（2）掌握两条直线平行与垂直的判定定理和性质定量．掌握两条直线所成的角和距离的概念，对于异面直线的距离，只要求会计算已给出公垂线时的距离．（3）掌握直线和平面平行的判定定理和性质定理．掌握直线和平面垂直的判定定理和性质定理．掌握斜线在平面上的射影、直线和平面所成的角、直线和平面的距离的概念．掌握三垂线定理及其逆定理．（4）掌握两个平面平行的判定定理和性质定理．掌握二面角、二面角的平面角、两个平行平面间的距离的概念．掌握两个平面垂直的判定定理和性质定理．（5）会用反证法证明简单的问题．（6）了解多面体、凸多面体的概念，了解正多面体的概念．（7）了解棱柱的概念，掌握棱柱的性质，会画直棱柱的直观图．（8）了解棱锥的概念，掌握正棱锥的性质，会画正棱锥的直观图．（9）了解球的概念，掌握球的性质，掌握球的表面积、体积公式．9（b）．直线、平面、简单几何体考试内容：平面及其基本性质．平面图形直观图的画法．平行直线．直线和平面平行的判定与性质．直线和平面垂直的判定．三垂线定理及其逆定理．两个平面的位置关系．空间向量及其加法、减法与数乘．空间向量的坐标表示．空间向量的数量积．直线的方向向量．异面直线所成的角．异面直线的公垂线．异面直线的距离．直线和平面垂直的性质．平面的法向量．点到平面的距离．直线和平面所成的角．向量在平面内的射影．平行平面的判定和性质．平行平面间的距离．二面角及其平面角．两个平面垂直的判定和性质．多面体．正多面体．棱柱．棱锥．球．考试要求：（1）掌握平面的基本性质，会用斜二测的画法画水平放置的平面图形的直观图；能够画出空间两条直线、直线和平面的各种位置关系的图形，能够根据图形想像它们的位置关系．（2）掌握直线和平面平行的判定定理和性质定理；理解直线和平面垂直的概念，掌握直线和平面垂直的判定定理；掌握三垂线定理及其逆定理．（3）理解空间向量的概念，掌握空间向量的加法、减法和数乘．（4）了解空间向量的基本定理；理解空间向量坐标的概念，掌握空间向量的坐标运算．（5）掌握空间向量的数量积的定义及其性质；掌握用直角坐标计算空间向量数量积的公式；掌握空间两点间距离公式．（6）理解直线的方向向量、平面的法向量、向量在平面内的射影等概念．（7）掌握直线和直线、直线和平面、平面和平面所成的角、距离的概念．对于异面直线的距离，只要求会计算已给出公垂线或在坐标表示下的距离．掌握直线和平面垂直的性质定理．掌握两个平面平行、垂直的判定定理和性质定理．（8）了解多面体、凸多面体的概念，了解正多面体的概念．（9）了解棱柱的概念，掌握棱柱的性质，会画直棱柱的直观图．（10）了解棱锥的概念，掌握正棱锥的性质，会画正棱锥的直观图．（11）了解球的概念，掌握球的性质，掌握球的表面积、体积公式．10．排列、组合、二项式定理考试内容：分类计数原理与分步计数原理．排列．排列数公式．组合．组合数公式．组合数的两个性质．二项式定理．二项展开式的性质．考试要求：（1）掌握分类计数原理与分步计数原理，并能用它们分析睡解决一些简单的应用问题．（2）理解排列的意义，掌握排列数计算公式，并能用它解决一些简单的应用问题．（3）理解组合的意义，掌握排列数计算公式和组合的性质，并能用它们解决一些简单的应用问题．（4）掌握二项式定理和二项展开式的性质，并能用它们计算和证明一些简单的问题．11．概率考试内容：随机事件的概率．等可能性事件的概率．互斥事件有一个发生的概率．相互独立事件同时发生的概率．独立重复试验．考试要求：（1）了解随机事件的发生存在着规律性和随机事件概率的意义．（2）了解等可能性事件的概率的意义，会用排列组合的基本公式计算一些等可能性事件的概率．（3）了解互斥事件、相互独立事件的意义，会用互斥事件的概率加法公式与相互独立事件的概率乘法公式计算一些事件的概率．（4）会计算事件在n次独立重复试验中恰好发生k次的概率．12．概率与统计考试内容：离散型随机变量的分布列．离散型随机变量的期望值和方差．抽样方法．总体分布的估计．正态分布．线性回归．考试要求：（1）了解离散型随机变量的意义，会求出某些简单的离散型随机变量的分布列．（2）了解离散型随机变量的期望值、方差的意义，会根据离散型随机变量的分布列求出期望值、方差．（3）会用随机抽样、系统抽样、分层抽样等常用的抽样方法从总体中抽取样本．（4）会用样本频率分布去估计总体分布．（5）了解正态分布的意义及主要性质．（6）了解线性回归的方法和简单应用．13．极限考试内容：教学归纳法．数学归纳法应用．数列的极限．函数的极限．根限的四则运算．函数的连续性．考试要求：（1）理解数学归纳法的原理，能用数学归纳法证明一些简单的数学命题．（2）了解数列极限和函数极限的概念．（3）掌握极限的四则运算法则．会求某些数列与函数的极限．（4）了解函数连续的意义，理解闭区间上连续函数有最大值和最小值的性质．14．导数考试内容：导数的概念．导数的几何意义．几种常见函数的导数．两个函数的和、差、积、商和导数．复习函数的导数．基本导数公式．利用导数研究函数的单调性和极值．函数的最大值和最小值．考试要求：（1）了解导数概念的某些实际背景（如瞬时速度、加速度、光滑曲线切线的斜率等）；掌握函数在一点处的导数的定义和导数的几何意义；理解导函数的概念．（2）熟记基本导数公式（c,xm(m为有理数)，sinx，cosx,ex,ax,ln x,logax 的导数）；掌握两个函数和、差、积、商的求导法则．了解复合函数的求导法则，会求某些简单函数的导数．（3）理解可导函数的单调性与其导数的关系；了解可导函数在某点取得极值的必要条件和充分条件（导数在极值点两则异号）；会求一些实际问题（一般指单峰函数）的最大值和最小值．15．数系的扩充--复数考试内容：复数的概念．复数的加法和减法．复数的乘法和除法．数系的扩充．考试要求：（1）了解复数的有关概念及复数的代数表示和几何意义．（2）掌握复数代数形式的运算法则，能进行复数代数形式的加法、减法、乘法、除法运算．（3）了解从自然数系列复数系的关系及扩充的基本思想．ⅳ．考试表式与试卷结构考试采用闭卷、笔试形式．全卷满分为150分，考试时间为120分钟．全试卷包括ⅰ卷和ⅱ卷．ⅰ卷为选择题；ⅱ卷为非选择题．试卷一般包括选择题、填空题和解答题等题型．选择题是四选一型的单项选择题；填空题只要求直接填写结果，不必写出计算过程或推证过程；解答题包括计算题、证明题和应用题等，解答应写出文字说明、演算步骤或推证过程．课本、报刊杂志中的成语、名言警句等俯首皆是,但学生写作文运用到文章中的甚少,即使运用也很难做到恰如其分。

一、函数、极限、连续考试内容函数的概念及表示法函数的有界性．单调性．周期性和奇偶性复合函数．反函数．分段函数和隐函数基本初等函数的性质及其图形初等函数函数关系的建立数列极限与函数极限的定义及其性质函数的左极限和右极限无穷小量和无穷大量的概念及其关系无穷小量的性质及无穷小量的比较极限的四则运算极限存在的两个准则：单调有界准则和夹逼准则两个重要极限：函数连续的概念函数间断点的类型初等函数的连续性闭区间上连续函数的性质考试要求1．理解函数的概念，掌握函数的表示法，会建立应用问题的函数关系．2．了解函数的有界性．单调性．周期性和奇偶性．3．理解复合函数及分段函数的概念，了解反函数及隐函数的概念．4．掌握基本初等函数的性质及其图形，了解初等函数的概念．5．了解数列极限和函数极限（包括左极限与右极限）的概念．6．了解极限的性质与极限存在的两个准则，掌握极限的四则运算法则，掌握利用两个重要极限求极限的方法．7．理解无穷小的概念和基本性质．掌握无穷小量的比较方法．了解无穷大量的概念及其与无穷小量的关系．8．理解函数连续性的概念（含左连续与右连续），会判别函数间断点的类型．9．了解连续函数的性质和初等函数的连续性，理解闭区间上连续函数的性质（有界性．最大值和最小值定理．介值定理)，并会应用这些性质．二、一元函数微分学考试内导数和微分的概念导数的几何意义和经济意义函数的可导性与连续性之间的关系平面曲线的切线与法线导数和微分的四则运算基本初等函数的导数复合函数．反函数和隐函数的微分法高阶导数一阶微分形式的不变性微分中值定理洛必达（L'Hospital）法则函数单调性的判别函数的极值函数图形的凹凸性．拐点及渐近线函数图形的描绘函数的最大值与最小值考试要求1．理解导数的概念及可导性与连续性之间的关系，了解导数的几何意义与经济意义（含边际与弹性的概念），会求平面曲线的切线方程和法线方程．2．掌握基本初等函数的导数公式．导数的四则运算法则及复合函数的求导法则，会求分段函数的导数会求反函数与隐函数的导数．3．了解高阶导数的概念，会求简单函数的高阶导数．4．了解微分的概念，导数与微分之间的关系以及一阶微分形式的不变性，会求函数的微分．5．理解罗尔（Rolle）定理．拉格朗日( Lagrange)中值定理．了解泰勒定理．柯西（Cauchy)中值定理，掌握这四个定理的简单应用．6．会用洛必达法则求极限．7．掌握函数单调性的判别方法，了解函数极值的概念，掌握函数极值、最大值和最小值的求法及其应用．8．会用导数判断函数图形的凹凸性（注：在区间内，设函数具有二阶导数．当时，的图形是凹的；当时，的图形是凸的），会求函数图形的拐点和渐近线．9．会描述简单函数的图形．三、一元函数积分学考试内容原函数和不定积分的概念不定积分的基本性质基本积分公式定积分的概念和基本性质定积分中值定理积分上限的函数及其导数牛顿一莱布尼茨（Newton- Leibniz）公式不定积分和定积分的换元积分法与分部积分法反常（广义）积分定积分的应用考试要求1．理解原函数与不定积分的概念，掌握不定积分的基本性质和基本积分公式，掌握不定积分的换元积分法和分部积分法．2．了解定积分的概念和基本性质，了解定积分中值定理，理解积分上限的函数并会求它的导数，掌握牛顿一莱布尼茨公式以及定积分的换元积分法和分部积分法．3．会利用定积分计算平面图形的面积．旋转体的体积和函数的平均值，会利用定积分求解简单的经济应用问题．4．了解反常积分的概念，会计算反常积分．四、多元函数微积分学考试内容多元函数的概念二元函数的几何意义二元函数的极限与连续的概念有界闭区域上二元连续函数的性质多元函数偏导数的概念与计算多元复合函数的求导法与隐函数求导法二阶偏导数全微分多元函数的极值和条件极值．最大值和最小值二重积分的概念．基本性质和计算无界区域上简单的反常二重积分考试要求1．了解多元函数的概念，了解二元函数的几何意义．2．了解二元函数的极限与连续的概念，了解有界闭区域上二元连续函数的性质．3．了解多元函数偏导数与全微分的概念,会求多元复合函数一阶、二阶偏导数，会求全微分,会求多元隐函数的偏导数．4．了解多元函数极值和条件极值的概念，掌握多元函数极值存在的必要条件，了解二元函数极值存在的充分条件，会求二元函数的极值，会用拉格朗日乘数法求条件极值，会求简单多元函数的最大值和最小值，并会解决简单的应用问题．5．了解二重积分的概念与基本性质，掌握二重积分的计算方法（直角坐标．极坐标）．了解无界区域上较简单的反常二重积分并会计算．五、无穷级数考试内容常数项级数收敛与发散的概念收敛级数的和的概念级数的基本性质与收敛的必要条件几何级数与级数及其收敛性正项级数收敛性的判别法任意项级数的绝对收敛与条件收敛交错级数与莱布尼茨定理幂级数及其收敛半径．收敛区间（指开区间）和收敛域幂级数的和函数幂级数在其收敛区间内的基本性质简单幂级数的和函数的求法初等函数的幂级数展开式考试要求1．了解级数的收敛与发散．收敛级数的和的概念．2．了解级数的基本性质和级数收敛的必要条件，掌握几何级数及级数的收敛与发散的条件，掌握正项级数收敛性的比较判别法和比值判别法．3．了解任意项级数绝对收敛与条件收敛的概念以及绝对收敛与收敛的关系，了解交错级数的莱布尼茨判别法．4．会求幂级数的收敛半径、收敛区间及收敛域．5．了解幂级数在其收敛区间内的基本性质（和函数的连续性、逐项求导和逐项积分），会求简单幂级数在其收敛区间内的和函数6．了解．．．及的麦克劳林（Maclaurin）展开式．六、常微分方程考试内容常微分方程的基本概念变量可分离的微分方程齐次微分方程一阶线性微分方程线性微分方程解的性质及解的结构定理二阶常系数齐次线性微分方程及简单的非齐次线性微分方程差分与差分方程的概念差分方程的通解与特解一阶常系数线性差分方程微分方程的简单应用考试要求1．了解微分方程及其阶、解、通解、初始条件和特解等概念．2．掌握变量可分离的微分方程．齐次微分方程和一阶线性微分方程的求解方法．3．会解二阶常系数齐次线性微分方程．4．了解线性微分方程解的性质及解的结构定理，会解自由项为多项式．指数函数．正弦函数．余弦函数的二阶常系数非齐次线性微分方程．5．了解差分与差分方程及其通解与特解等概念．6．了解一阶常系数线性差分方程的求解方法．7．会用微分方程求解简单的经济应用问题．线性代数一、行列式考试内容行列式的概念和基本性质行列式按行（列）展开定理考试要求1.了解行列式的概念，掌握行列式的性质．2.会应用行列式的性质和行列式按行（列）展开定理计算行列式．二、矩阵考试内容矩阵的概念矩阵的线性运算矩阵的乘法方阵的幂方阵乘积的行列式矩阵的转置逆矩阵的概念和性质矩阵可逆的充分必要条件伴随矩阵矩阵的初等变换初等矩阵矩阵的秩矩阵的等价分块矩阵及其运算考试要求1．理解矩阵的概念，了解单位矩阵、数量矩阵、对角矩阵、三角矩阵的定义及性质，了解对称矩阵、反对称矩阵及正交矩阵等的定义和性质．2．掌握矩阵的线性运算、乘法、转置以及它们的运算规律，了解方阵的幂与方阵乘积的行列式的性质．3.理解逆矩阵的概念，掌握逆矩阵的性质以及矩阵可逆的充分必要条件，理解伴随矩阵的概念，会用伴随矩阵求逆矩阵.4.了解矩阵的初等变换和初等矩阵及矩阵等价的概念，理解矩阵的秩的概念，掌握用初等变换求矩阵的逆矩阵和秩的方法．5.了解分块矩阵的概念，掌握分块矩阵的运算法则．三、向量考试内容向量的概念向量的线性组合与线性表示向量组的线性相关与线性无关向量组的极大线性无关组等价向量组向量组的秩向量组的秩与矩阵的秩之间的关系向量的内积线性无关向量组的正交规范化方法考试要求1．了解向量的概念，掌握向量的加法和数乘运算法则．2．理解向量的线性组合与线性表示、向量组线性相关、线性无关等概念，掌握向量组线性相关、线性无关的有关性质及判别法．3．理解向量组的极大线性无关组的概念，会求向量组的极大线性无关组及秩．4．理解向量组等价的概念，理解矩阵的秩与其行（列）向量组的秩之间的关系．5．了解内积的概念．掌握线性无关向量组正交规范化的施密特（Schmidt）方法．四、线性方程组考试内容线性方程组的克莱姆（Cramer）法则线性方程组有解和无解的判定齐次线性方程组的基础解系和通解非齐次线性方程组的解与相应的齐次线件方程组（导出组）的解之间的关系非齐次线性方程组的通解考试要求1.会用克莱姆法则解线性方程组．2.掌握非齐次线性方程组有解和无解的判定方法．3.理解齐次线性方程组的基础解系的概念，掌握齐次线性方程组的基础解系和通解的求法．4.理解非齐次线性方程组解的结构及通解的概念．5.掌握用初等行变换求解线性方程组的方法．五、矩阵的特征值和特征向量考试内容矩阵的特征值和特征向量的概念、性质相似矩阵的概念及性质矩阵可相似对角化的充分必要条件及相似对角矩阵实对称矩阵的特征值和特征向量及相似对角矩阵考试要求1.理解矩阵的特征值、特征向量的概念，掌握矩阵特征值的性质，掌握求矩阵特征值和特征向量的方法．2.理解矩阵相似的概念，掌握相似矩阵的性质，了解矩阵可相似对角化的充分必要条件，掌握将矩阵化为相似对角矩阵的方法．3.掌握实对称矩阵的特征值和特征向量的性质．六、二次型考试内容二次型及其矩阵表示合同变换与合同矩阵二次型的秩惯性定理二次型的标准形和规范形用正交变换和配方法化二次型为标准形二次型及其矩阵的正定性考试要求1.了解二次型的概念，会用矩阵形式表示二次型，了解合同变换与合同矩阵的概念．2.了解二次型的秩的概念，了解二次型的标准形、规范形等概念，了解惯性定理，会用正交变换和配方法化二次型为标准形．3.理解正定二次型．正定矩阵的概念，并掌握其判别法．概率论与数理统计一、随机事件和概率考试内容随机事件与样本空间事件的关系与运算完备事件组概率的概念概率的基本性质古典型概率几何型概率条件概率概率的基本公式事件的独立性独立重复试验考试要求1．了解样本空间（基本事件空间）的概念，理解随机事件的概念，掌握事件的关系及运算．2．理解概率、条件概率的概念，掌握概率的基本性质，会计算古典型概率和几何型概率，掌握概率的加法公式、减法公式、乘法公式、全概率公式以及贝叶斯（Bayes）公式等．3．理解事件的独立性的概念，掌握用事件独立性进行概率计算；理解独立重复试验的概念，掌握计算有关事件概率的方法．二、随机变量及其分布考试内容随机变量随机变量的分布函数的概念及其性质离散型随机变量的概率分布连续型随机变量的概率密度常见随机变量的分布随机变量函数的分布考试要求1．理解随机变量的概念，理解分布函数的概念及性质，会计算与随机变量相联系的事件的概率．2．理解离散型随机变量及其概率分布的概念，掌握0－1分布、二项分布、几何分布、超几何分布、泊松（Poisson）分布及其应用．3．掌握泊松定理的结论和应用条件，会用泊松分布近似表示二项分布．4．理解连续型随机变量及其概率密度的概念，掌握均匀分布、正态分布、指数分布及其应用，其中参数为的指数分布的概率密度为5．会求随机变量函数的分布．三、多维随机变量的分布考试内容多维随机变量及其分布函数二维离散型随机变量的概率分布、边缘分布和条件分布二维连续型随机变量的概率密度、边缘概率密度和条件密度随机变量的独立性和不相关性常见二维随机变量的分布两个及两个以上随机变量的函数的分布考试要求1．理解多维随机变量的分布函数的概念和基本性质．2．理解二维离散型随机变量的概率分布和二维连续型随机变量的概率密度、掌握二维随机变量的边缘分布和条件分布．3．理解随机变量的独立性和不相关性的概念，掌握随机变量相互独立的条件，理解随机变量的不相关性与独立性的关系．4.掌握二维均匀分布和二维正态分布，理解其中参数的概率意义．5．会根据两个随机变量的联合分布求其函数的分布，会根据多个相互独立随机变量的联合分布求其函数的分布．四、随机变量的数字特征考试内容随机变量的数学期望（均值）、方差、标准差及其性质随机变量函数的数学期望切比雪夫（Chebyshev）不等式矩、协方差、相关系数及其性质考试要求1．理解随机变量数字特征（数学期望、方差、标准差、矩、协方差、相关系数）的概念，会运用数字特征的基本性质，并掌握常用分布的数字特征．2．会求随机变量函数的数学期望．3．了解切比雪夫不等式．五、大数定律和中心极限定理考试内容切比雪夫大数定律伯努利（Bernoulli）大数定律辛钦（Khinchine）大数定律棣莫弗—拉普拉斯（De Moivre－Laplace）定理列维—林德伯格（Levy－Lindberg）定理考试要求1．了解切比雪夫大数定律、伯努利大数定律和辛钦大数定律（独立同分布随机变量序列的大数定律）．2．了解棣莫弗—拉普拉斯中心极限定理（二项分布以正态分布为极限分布）、列维—林德伯格中心极限定理（独立同分布随机变量序列的中心极限定理），并会用相关定理近似计算有关随机事件的概率．六、数理统计的基本概念考试内容总体个体简单随机样本统计量经验分布函数样本均值样本方差和样本矩分布分布分布分位数正态总体的常用抽样分布考试要求1．了解总体、简单随机样本、统计量、样本均值、样本方差及样本矩的概念，其中样本方差定义为2．了解产生变量、变量和变量的典型模式；了解标准正态分布、分布、分布和分布得上侧分位数，会查相应的数值表．3．掌握正态总体的样本均值．样本方差．样本矩的抽样分布．4.了解经验分布函数的概念和性质．七、参数估计考试内容点估计的概念估计量与估计值矩估计法最大似然估计法考试要求1．了解参数的点估计、估计量与估计值的概念．2．掌握矩估计法（一阶矩、二阶矩）和最大似然估计法希望以上资料对你有所帮助，附励志名3条：1、积金遗于子孙，子孙未必能守；积书于子孙，子孙未必能读。

2019年高考理科数学全国三卷一、前言2019年高考理科数学全国三卷是国家统一高考中的一部分，是考生们完成高中学业的最后一次考试。

数学是一门普遍被认为难度较大的科目，而高考数学试卷又是考生们最关注的考试科目之一。

对于本次高考数学试卷的分析和总结，具有一定的参考价值。

本文将对2019年高考理科数学全国三卷进行全面的分析，包括试卷结构、题型特点、考查重点等方面的内容，旨在帮助广大考生更好地理解试卷，为今后的高考复习和备战提供有益的参考。

二、试卷结构1. 选择题部分：选择题部分占据了本次高考数学试卷的相当比例。

包括单项选择题和多项选择题，分别涉及到代数、几何、函数、数列等多个知识点。

2. 填空题部分：填空题部分体现了对考生计算能力和解题方法的考查，题目艰深且富有技巧，考生需要有扎实的基本知识和较高的解题能力。

3. 主观题部分：主观题部分包括了解答题和证明题，考查了考生对知识的掌握程度和运用能力。

三、题型特点1. 难度适中：整体来看，本次高考数学试卷的难度适中，与往年相比并无明显增加。

选择题考查的知识点广泛，但均属基础知识，填空题和主观题也未涉及特别深奥和复杂的内容。

2. 知识点覆盖全面：本次试卷的题目覆盖了高中数学范围内的各个知识点，涉及代数、几何、函数、概率统计等多个大类，考查了考生的综合解题能力。

3. 语言表述精准：试卷的题目语言表述精确，无歧义，且有规范化的表述和符号，考生易于理解和掌握题意。

四、考查重点1. 代数知识的应用：本次试卷中，代数知识的应用是一个明显的考查重点。

涉及到了方程与不等式、函数及其性质、数列等多个知识点，要求考生熟练掌握代数知识，并能够熟练应用到实际问题中。

2. 几何图形的性质：几何知识在本次试卷中也得到了较多的考查。

要求考生熟悉各种几何图形的性质和计算方法，能够灵活运用几何知识解决实际问题。

3. 数学建模能力：本次试卷的一些主观题设置了较多的实际问题，考查了考生的数学建模能力，要求考生具备将数学知识与实际问题相结合的能力。

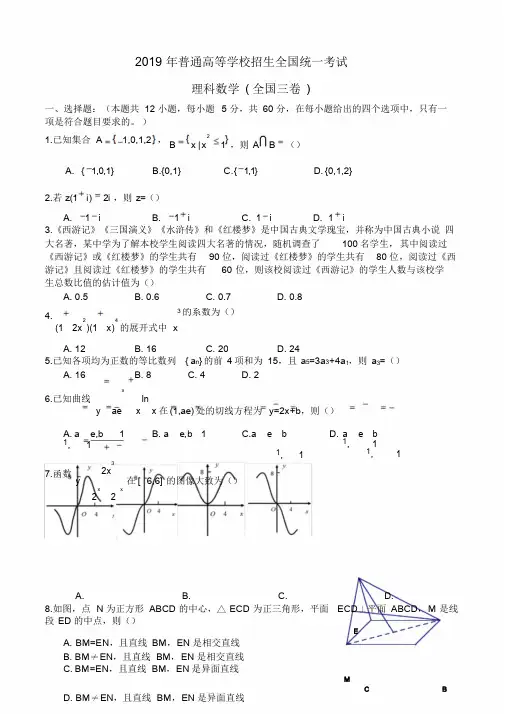
2019 年普通高等学校招生全国统一考试理科数学( 全国三卷)一、选择题：（本题共12 小题，每小题 5 分，共60 分，在每小题给出的四个选项中，只有一项是符合题目要求的。

）1.已知集合 A 1,0,1,2 ， 2B x |x 1 ，则A B （）A. { 1,0,1}B.{0,1}C.{ 1,1}D. {0,1,2}2.若z(1 i) 2i ，则z=（）A. 1 iB. 1 iC. 1 iD. 1 i3.《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝，并称为中国古典小说四大名著，某中学为了解本校学生阅读四大名著的情况，随机调查了100名学生，其中阅读过《西游记》或《红楼梦》的学生共有90 位，阅读过《红楼梦》的学生共有80 位，阅读过《西游记》且阅读过《红楼梦》的学生共有60 位，则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为（）A. 0.5B. 0.6C. 0.7D. 0.84. 3 的系数为（）2 4(1 2x )(1 x) 的展开式中xA. 12B. 16C. 20D. 245.已知各项均为正数的等比数列{ a n}的前4 项和为15，且a5=3 a3+4a1，则a3=（）A. 16B. 8C. 4D. 2x6.已知曲线lny ae x x 在(1,ae) 处的切线方程为y=2x +b，则（）A. a e,b 1B. a e, b 1C.a e bD. 1, 11, 1 a e b1, 11, 17.函数32xy 在[ 6,6] 的图像大致为（）x x2 2A. B. C. D.8.如图，点N 为正方形ABCD 的中心，△ECD 为正三角形，平面ECD⊥平面ABCD，M 是线段ED 的中点，则（）EA. BM=EN，且直线BM，EN 是相交直线B. BM≠EN，且直线BM，EN 是相交直线C. BM =EN，且直线BM，EN 是异面直线MC BD. BM≠EN，且直线BM，EN 是异面直线ND A9.执行右边的程序框图，如果输入的ε为0.01，则输出s 的值等于（）1 A.2 421B. 2 521C. 2 621D. 2 7210.双曲线C：2 2x y4 21 的右焦点为F，点P 在C 的一条渐近线上，O为坐标原点.若|PO|=|PF|，则△PFO 的面积为（）A. 3 24B.3 22C. 2 2D.3 211.设f(x)是定义域为R 的偶函数，且在(0,+ ∞单)调递减，则（）A.3 212 3f (log ) f (2 ) f (2 ) B.342 313 2f (log ) f (2 ) f (2 )34C.3 21f 2 f f D.(2 ) (2 ) (log )3342 313 2f (2 ) f (2 ) f (log )3412.设函数 f ( x) sin( x )( 0) ，已知f ( x)在[0,2 π有]且仅有 5 个零点，下述四个结论：① f5(x)在(0,2 π有)且仅有 3 个极大值点；②f (x)在(0,2 π有)且仅有 2 个极小值点；③f (x)在(0, )10单调递增；④的取值范围是12 29[ , )5 10.其中所有正确结论的编号是（）A.①④B.②③C.①②③D.①③④二、填空题：本题共 4 小题，每小题 5 分，共20分.13.已知a，b为单位向量，且a·b=0，若c2a5b，则cos<a,c>=_____________.14.记S n 为等差数列{a n} 的前n 项和，若a1≠0，a2=3 a1，则S10S5=_____________.15.设F1，F2 为椭圆C：2 2x y36 201的两个焦点，M 为C 上一点且在第一象限，若△MF1F2 为等腰三角形，则M 的坐标为______________.D1C1G 16.学生到工厂劳动实践，利用3D 打印技术制作模型，如图，该模型为长方体ABCD- A1B1C1D1 挖去四棱锥O- EFGH 后所得的几何体，其中O 为长方体的中心，E，F，G，H 分别为所在棱的A1O中点，AB=BC=6cm，AA1=4cm.3D 打印所用的材料密度为HDB1FC EA B3，不考虑打印损耗，制作该模型所需原料的质量为__________g.0.9g/cm三、解答题：共70分，解答应写出文字说明、证明过程或演算步骤.第17~21 题为必考题，每个试题考生都必须作答。