立体几何中的翻折问题资料
- 格式:ppt
- 大小:323.00 KB
- 文档页数:33

翻折问题立体几何在高中数学中是培养学生的空间想象能力的重要载体,其中翻折问题学生学习是一个难点,同时也是近年来高考的热点。
翻折问题实质是图形由平面到立体变化中一些线、面之间发生了变化,因此本节内容从正三角形、正方形、矩形、梯形、五边形等图形进行翻折,以便学生能更清楚熟悉模型,同时还列举了翻折模型中的平行、垂直、线线角、线面角、二面角、长度等问题。
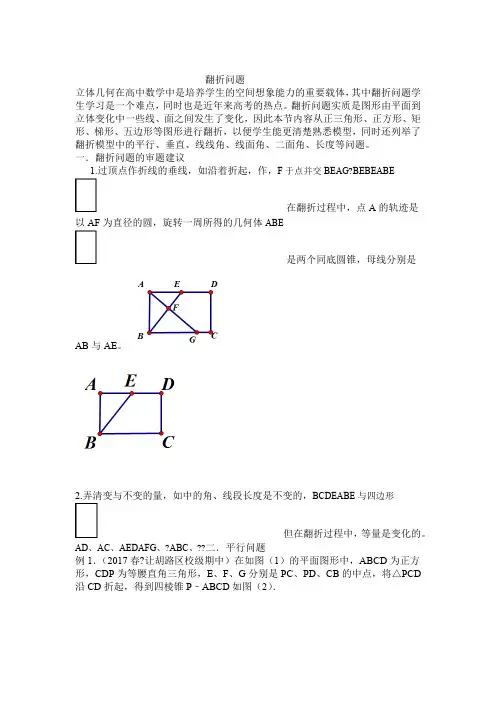
一.翻折问题的审题建议1.过顶点作折线的垂线,如ABE沿着BE折起,作G BE F⊥并交于点,A BE在翻折过程中,点A的轨迹是以AF为直径的圆,ABE旋转一周所得的几何体是两个同底圆锥,母线分别是AB与AE。
2.弄清变与不变的量,如ABE BCDE与四边形中的角、线段长度是不变的,但在翻折过程中,AFG ABC AED AC AD∠∠∠、、、、等量是变化的。
二.平行问题例1.(2017春•让胡路区校级期中)在如图(1)的平面图形中,ABCD为正方形,CDP为等腰直角三角形,E、F、G分别是PC、PD、CB的中点,将△PCD 沿CD折起,得到四棱锥P﹣ABCD如图(2).求证:在四棱锥P﹣ABCD中,AP∥平面EFG.【分析】连接E、F,连接E、G,可得EF∥平面PAB.EG∥平面PAB.即可证平面PAB∥平面EFG【解答】证明:连接E、F,连接E、G,在四棱锥PABCD中,E,F分别为PC,PD的中点,∴EF∥CD.∵AB∥CD,∴EF∥AB.∵EF⊄平面PAB,AB⊂平面PAB,∴EF∥平面PAB.同理EG∥平面PAB.又EF∩EG=E,∴平面PAB∥平面EFG.又AP⊂平面PAB,∴AP∥平面EFG.【点评】本题考查了空间线面平行的判定,属于中档题.【变式训练1】(2017•闵行区校级模拟)如图,正△ABC的边长为4,CD是AB边上的高,EF分别是AC和BC的中点,现将△ABC沿CD翻折成直二面角A﹣DC﹣B.(1)证明:AB∥平面DEF;(2)在线段BC上是否存在点P,使AP⊥DE?如果存在,求出的值;如果不存在,请说明理由.【分析】(1)由E、F分别是AC、BC的中点,得EF∥AB,由此证明AB∥平面DEF;(Ⅱ)以点D为坐标原点,以直线DB、DC、DA分别为x轴、y轴、z轴,建立空间直角坐标系,利用向量法找出在线段BC上存在点P,使AP⊥DE.【解答】解:(1)证明:如图(2),在△ABC中,∵E、F分别是AC、BC的中点,∴EF∥AB,又AB⊄平面DEF,EF⊂平面DEF,∴AB∥平面DEF;(2)以点D为坐标原点,以直线DB、DC、DA分别为x轴、y轴、z轴,建立空间直角坐标系,如图(3)所示;则A(0,0,2),B(2,0,0),C(0,2,0),E(0,,1),F(1,,0),=(2,0,﹣2),=(﹣2,2,0),=(0,,1),=(1,,0);设=λ,则=+=(2﹣2λ,2λ,﹣2),由AP⊥DE得•=0,∴×2λ+1×(﹣2)=0,解得λ=,∴在线段BC上存在点P,使AP⊥DE,且=.【点评】本题考查了直线与平面平行的证明与满足条件的点是否存在的判断问题,阶梯式要注意向量法的合理运用.二.垂直问题例2.(2017春•三元区校级月考)如图,在四形边ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使CD⊥平面ABD,构成三棱锥A﹣BCD.则在三棱锥A﹣BCD中,下列结论正确的是()A.AD⊥平面BCD B.AB⊥平面BCDC.平面BCD⊥平面ABC D.平面ADC⊥平面ABC【分析】由题意推出CD⊥AB,AD⊥AB,推出AB⊥平面ADC,可得平面ABC ⊥平面ADC.【解答】解:∵在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°∴BD⊥CD又平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD故CD⊥平面ABD,则CD⊥AB,又AD⊥AB故AB⊥平面ADC,所以平面ABC⊥平面ADC.故选D.【点评】本题考查平面与平面垂直的判定,考查逻辑思维能力,是中档题.例3.(2016•杨浦区校级模拟)已知矩形ABCD,AB=1,BC=2,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折的过程中()A.存在某个位置,使得直线AB和直线CD垂直B.存在某个位置,使得直线AC和直线BD垂直C.存在某个位置,使得直线AD和直线BC垂直D.无论翻折到什么位置,以上三组直线均不垂直【分析】假设各选项成立,根据线面位置关系推导结论,若得出矛盾式子,则假设错误,得出正确选项.【解答】解:对于A,若存在某个位置,使得直线AB与直线CD垂直,∵CD⊥BC,∴CD⊥平面ABC,∴平面ABC⊥平面BCD,过点A作平面BCD的垂线AE,则E在BC上,∴当A在平面BCD上的射影在BC上时,AB⊥CD.故A正确;对于B,若存在某个位置,使得直线AC与直线BD垂直,作AF⊥BD,则BD⊥平面AFC,∴BD⊥EC,显然这是不可能的,故B错误;对于C,若存在某个位置,使得直线AD与直线BC垂直,则BC⊥平面ACD,BC⊥AC,∴AB>BC,即1>2,显然这是不可能的,故C错误.故选:A.【点评】本题主要考查了空间的线面和面面的垂直关系,翻折问题中的变与不变,空间想象能力和逻辑推理能力,有一定难度,属中档题.【变式训练2】(2017春•辛集市校级月考)如图,在正方形ABCD中,E、F 分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方形折成一个空间图形,使B、C、D三点重合,重合后的点记为H,那么,在这个空间图形中必有()A.AG⊥△EFH所在平面B.AH⊥△EFH 所在平面C.HF⊥△AEF所在平面D.HG⊥△AEF所在平面【分析】本题为折叠问题,分析折叠前与折叠后位置关系、几何量的变与不变,可得HA、HE、HF三者相互垂直,根据线面垂直的判定定理,可判断AH与平面HEF的垂直.【解答】解:根据折叠前、后AH⊥HE,AH⊥HF不变,∴AH⊥平面EFH,B 正确;∵过A只有一条直线与平面EFH垂直,∴A不正确;∵AG⊥EF,EF⊥AH,∴EF⊥平面HAG,∴平面HAG⊥AEF,过H作直线垂直于平面AEF,一定在平面HAG内,∴C不正确;∵HG不垂直于AG,∴HG⊥平面AEF不正确,D不正确.故选B【点评】本题考查直线与平面垂直的判定,一般利用线线⇔线面⇔面面,垂直关系的相互转化判断.【变式训练3】(2016秋•杭州期末)如图所示,四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使面ABD⊥面BCD,连结AC,则下列命题正确的是()A.面ABD⊥面ABC B.面ADC⊥面BDC C.面ABC⊥面BDC D.面ADC⊥面ABC【分析】证明CD⊥平面ABD,因此有AB⊥CD.又因为AB⊥AD,AD∩DC=D,所以AB⊥平面ADC,即可得到平面ADC⊥平面ABC.【解答】解:由题意知,在四边形ABCD中,CD⊥BD.在三棱锥A﹣BCD中,平面ABD⊥平面BCD,两平面的交线为BD,所以CD⊥平面ABD,因此有AB⊥CD.又因为AB⊥AD,AD∩DC=D,所以AB⊥平面ADC,于是得到平面ADC⊥平面ABC.故选D.【点评】本题考查线面垂直、面面垂直的判定,考查学生分析解决问题的能力,属于中档题.三.线线角例4.(2017•浙江模拟)矩形ABCD中,,BC=1,将△ABC与△ADC 沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为()A.B.C.D.【分析】求出两个特殊位置,直线AD与直线BC成的角,即可得出结论.【解答】解:由题意,初始状态,直线AD与直线BC成的角为0,DB=时,AD⊥DB,AD⊥DC,∴AD⊥平面DBC,AD⊥BC,直线AD与直线BC成的角为,∴在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为[0,].故选:C.【点评】本题考查两直线所成的角的范围的求法,考查学生的计算求解能力、推理论证能力、空间思维能力,考查数形结合思想、分类讨论思想、转化化归思想,是中档题.例5.(2017春•涵江区校级期中)正方形ABCD,沿对角线BD折成直二面角A ﹣BD﹣C,则折后的异面直线AB与CD所成的角的大小为()A.30°B.45°C.60°D.90°【分析】取BD中点O,连结AO、CO,以O为原点,OC为x轴,OD为y轴,OA为z轴,建立空间直角坐标系,利用向量法能求出折后的异面直线AB与CD所成的角.【解答】解:取BD中点O,连结AO、CO,设正方形ABCD边长为,∵沿对角线BD折成直二面角A﹣BD﹣C,∴AO⊥BD,CO⊥BD,AO⊥CO,以O为原点,OC为x轴,OD为y轴,OA为z轴,建立空间直角坐标系,A(0,0,1),B(0,﹣1,0),C(1,0,0),D(0,1,0),=(0,﹣1,﹣1),=(﹣1,1,0),设折后的异面直线AB与CD所成的角为θ,则cosθ=|cos<>|===,∴θ=60°.∴折后的异面直线AB与CD所成的角为60°.故选:C.【点评】本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.(2016•浙江一模)如图四边形ABCD,AB=BD=DA=2.BC=CD=,【变式训练4】现将△ABD沿BD折起,使二面角A﹣BD﹣C的大小在[,],则直线AB与CD所成角的余弦值取值范围是()A.[0,]∪(,1)B.[,]C.[0,]D.[0,]【分析】取BD中点O,连结AO,CO,以O为原点,OC为x轴,OD为y轴,过点O作平面BCD的垂线为z轴,建立空间直角坐标系,利用向量法能求出直线AB与CD所成角的余弦值取值范围.【解答】解:取BD中点O,连结AO,CO,∵AB=BD=DA=2.BC=CD=,∴CO⊥BD,AO⊥BD,且CO=1,AO=,∴∠AOC是二面角A﹣BD﹣C的平面角,以O为原点,OC为x轴,OD为y轴,过点O作平面BCD的垂线为z轴,建立空间直角坐标系,B(0,﹣1,0),C(1,0,0),D(0,1,0),设二面角A﹣BD﹣C的平面角为θ,则,连AO、BO,则∠AOC=θ,A(),∴,,设AB、CD的夹角为α,则cosα==,∵,∴cos,∴|1﹣|∈[0,].∴cos.故选:D.【点评】本题考查异面直线所成角的取值范围的求法,是中档题,解题时要认真审题,注意向量法的合理运用.【变式训练5】(2016•浙江二模)如图,边长为1的菱形ABCD中,∠DAB=60°,沿BD将△ABD翻折,得到三棱锥A﹣BCD,则当三棱锥A﹣BCD体积最大时,异面直线AD与BC所成的角的余弦值为()A.B.C.D.【分析】菱形ABCD中,∠DAB=60°,△ABD、△CBD为边长为1的等边三角形,将△ABD沿BD翻折过程中,点A在底面BDC的投影在∠DCB的平分线上,三棱锥的高最大时,平面ABD⊥平面BCD.【解答】解:△ABD、△CBD为边长为1的等边三角形,将△ABD沿BD翻折形成三棱锥A﹣BCD如图:点A在底面BDC的投影在∠DCB的平分线CE上,则三棱锥A﹣BCD的高为△AEC过A点的高;所以当平面ABD⊥平面BCD时,三棱锥A﹣BCD的高最大,体积也最大,此时AE⊥平面BCD;求异面直线AD与BC所成的角的余弦值:平移BC到DC′位置,|cos∠ADC′|即为所求,AD=DC=1,AE=,EC′=,AC′=|cos∠ADC′|=||=,所以异面直线AD与BC所成的角的余弦值为,故选B.【点评】本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.【变式训练6】(2016•丽水校级模拟)如图,长方形ABCD,M,N分别为AB,AD上异于点A的两点,现把△AMN沿着MN翻折,记AC与平面BCD所成的角为θ1,直线AC与直线MN所成的角为θ2,则θ1与θ2的大小关系是()A.θ1=θ2B.θ1>θ2C.θ1<θ2D.不能确定【分析】作AO⊥平面BCD,垂足是O,连接CO,过点C作直线l∥MN,在l上取点H,令CH=CO,在△AOC和△AHC 中,CO=CH,AO⊥平面BCD,从而AO<AH,由此能求出θ1<θ2.【解答】解:作AO⊥平面BCD,垂足是O,连接C过点C作直线l∥MN,在l上取点H,令CH=CO,在△AOC和△AHC中,CO=CH,AO⊥平面BCD,∴AO<AH,∴∠ACO<∠ACH,∵AC与平面BCD所成的角为θ1,直线AC与直线MN所成的角为θ2,AO⊥平面BCD,CH∥MN,∴∠ACO=θ1,∠ACH=θ2。
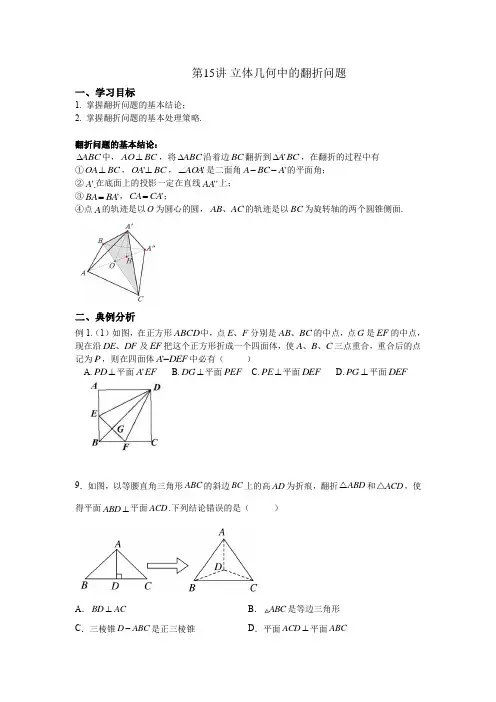
第15讲 立体几何中的翻折问题一、学习目标1. 掌握翻折问题的基本结论;2. 掌握翻折问题的基本处理策略.翻折问题的基本结论:ABC ∆中,BC AO ⊥,将ABC ∆沿着边BC 翻折到BC A '∆,在翻折的过程中有 ①BC OA ⊥,BC OA ⊥','AOA ∠是二面角'A BC A --的平面角; ②'A 在底面上的投影一定在直线''AA 上; ③'BA BA =,'CA CA =;④点A 的轨迹是以O 为圆心的圆,AC AB 、的轨迹是以BC 为旋转轴的两个圆锥侧面.二、典例分析例1.(1)如图,在正方形ABCD 中,点F E 、分别是BC AB 、的中点,点G 是EF 的中点,现在沿DF DE 、及EF 把这个正方形折成一个四面体,使C B A 、、三点重合,重合后的点记为P ,则在四面体DEF A -'中必有( )A.⊥PD 平面EF A 'B.⊥DG 平面PEFC.⊥PE 平面DEFD.PG ⊥平面DEF9.如图,以等腰直角三角形ABC 的斜边BC 上的高AD 为折痕,翻折ABD △和ACD △,使得平面ABD ⊥平面ACD .下列结论错误的是( )A .BD AC ⊥B .ABC 是等边三角形 C .三棱锥D ABC -是正三棱锥D .平面ACD ⊥平面ABC【答案】(1)C ; (2)D. 变式:(1)已知正三角形ABC 的中线AF 与中位线DE 相交于点G ,ED A '∆是AED ∆绕DE 旋转过程中的一个图形,则下列结论错误的是( )A.动点'A 在平面ABC 上的射影在线段AF 上B.三棱锥FED A -'的体积有最大值C.恒有平面⊥GF A '平面BCEDD.异面直线E A '与BD 不可能互相垂直【答案】D(2)如图,在矩形ABCD 中,AD AB 2=,E 为AB 的中点,将ADE ∆沿直线DE 翻折成DE A '∆,若M 是线段C A 1的中点,则在ADE ∆翻折的过程中,下列命题正确的是( )A.BM 是定值B.M 的轨迹是一段圆弧C.//BF 平面DE A 'D.存在某个位置,使得C A DE 1⊥【答案】D例2.(1)已知矩形ABCD ,1,2AB BC ==ABD ∆沿矩形的对角线BD 所在的直线经翻折,在翻折过程中( )A.存在某个位置,使得直线AC 与BD 垂直B.存在某个位置,使得直线AB 与CD 垂直C.存在某个位置,使得直线AD 与BC 垂直D.对任意位置,三对直线“AC 与BD ”,“AB 与CD ”,“AD 与BC ”均不垂直(2)如图,在菱形ABCD 中,︒=∠60BAD ,线段BD AD ,的中点分别为F E ,,现将ABD ∆沿对角线BD 翻折,则异面直线BE 与CF 所成角的取值范围是( )A.)3,6(ππ B.]2,6(ππ C.]2,3(ππ D.)32,3(ππ【答案】(1)B ; (2)C.. 变式:1.在正方形ABCD 中,点F E 、分别是AD BC 、的中点,将ABF ∆沿BF 所在的直线进行翻折,将CDE ∆沿DE 所在的直线进行翻折,在翻折的过程中,( ) A.点A 与点C 在某一位置可能重合 B.点A 与点C 的最大距离为AB 3 C.直线AB 与直线CD 可能垂直 D.直线AF 与直线CE 可能垂直【答案】D2.如图,在ABC Rt ∆中,1=AC ,x BC =,D 是斜边AB 的中点,将BCD ∆沿直线CD 翻折,若在翻折过程中存在某个位置,使得AD CB ⊥,则x 的取值范围是( ) A.]3,0( B.]2,22( C.]32,3( D.]4,2( 【答案】A例3.(1)如图,在长方形ABCD 中,3,1AB BC ==,E 为线段DC 上一动点,现将AED ∆沿AE 折起,使得点D 在面ABC 上的射影K 在直线AE 上,当E 从D 运动到C ,则K 所形成的轨迹的长度是__________.(2)如图,在长方形ABCD 中,2AB =,1BC =,E 为DC 的中点,F 为线段EC (端点除外)上一动点.现将AFD ∆沿AF 折起,使平面ABD ⊥平面ABC .在平面ABD 内过点D 作DK AB ⊥,K 为垂足.设AK t =,则t 的取值范围是 .【答案】(1)3π; (2))1,21(. 变式:1.在矩形ABCD 中,3=AB ,1=BC ,E 为DC 的三等分点(靠近C 处),F 为线段EC 上一动点(包括端点),现将AFD ∆沿AF 折起,使D 点在平面内的射影恰好落在边AB 上,则当F 运动时,二面角B AF D --的余弦值的取值范围是________.【答案】]41,91[例4.如图,在平行四边形ABCD 中,2AB BC =,120ABC ∠=︒,E 为线段AB 的中点,将ADE ∆沿直线DE 翻折成'A DE ∆,使平面'A DE ⊥平面BCD ,F 为线段'A C 的中点。
翻折问题立体几何在高中数学中是培养学生的空间想象能力的重要载体,其中翻折问题学生学习是一个难点,同时也是近年来高考的热点。
翻折问题实质是图形由平面到立体变化中一些线、面之间发生了变化,因此本节内容从正三角形、正方形、矩形、梯形、五边形等图形进行翻折,以便学生能更清楚熟悉模型,同时还列举了翻折模型中的平行、垂直、线线角、线面角、二面角、长度等问题。
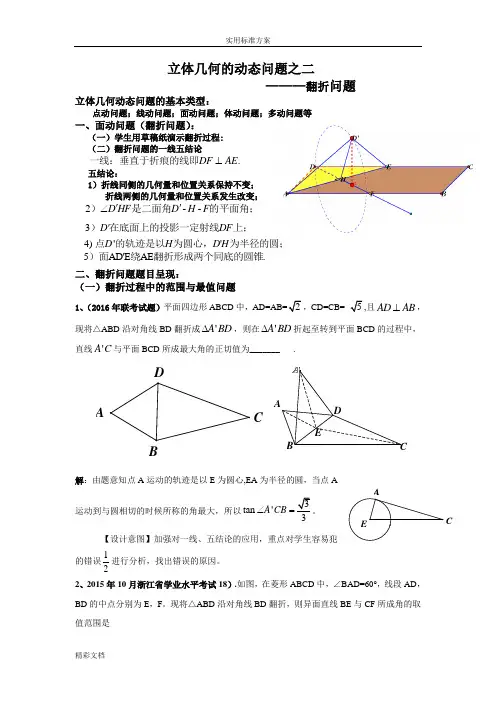
一.翻折问题的审题建议1.过顶点作折线的垂线,如沿着折起,作,F于点并交BEAG?BEBEABE在翻折过程中,点A的轨迹是以AF为直径的圆,旋转一周所得的几何体ABE是两个同底圆锥,母线分别是AB与AE。
2.弄清变与不变的量,如中的角、线段长度是不变的,BCDEABE与四边形但在翻折过程中,等量是变化的。
AD、AC、AEDAFG、?ABC、??二.平行问题例1.(2017春?让胡路区校级期中)在如图(1)的平面图形中,ABCD为正方形,CDP为等腰直角三角形,E、F、G分别是PC、PD、CB的中点,将△PCD 沿CD折起,得到四棱锥P﹣ABCD如图(2).求证:在四棱锥P﹣ABCD中,AP∥平面EFG.【分析】连接E、F,连接E、G,可得EF∥平面PAB.EG∥平面PAB.即可证平面PAB∥平面EFG,PC分别为F,E中,PABCD,在四棱锥G、E,连接F、E【解答】证明:连接.PD的中点,∴EF∥CD.∵AB∥CD,∴EF∥AB.∵EF?平面PAB,AB?平面PAB,∴EF∥平面PAB.同理EG∥平面PAB.又EF∩EG=E,∴平面PAB∥平面EFG.又AP?平面PAB,∴AP∥平面EFG.【点评】本题考查了空间线面平行的判定,属于中档题.【变式训练1】(2017?闵行区校级模拟)如图,正△ABC的边长为4,CD是AB 边上的高,EF分别是AC和BC的中点,现将△ABC沿CD翻折成直二面角A﹣DC﹣B.(1)证明:AB∥平面DEF;?如果存在,求出的值;如果AP⊥DE2)在线段BC上是否存在点P,使(不存在,请说明理由.∥平ABAB,由此证明BC的中点,得EF∥、【分析】(1)由E、F分别是AC;面DEF轴,建zyx轴、轴、DBD为坐标原点,以直线、DC、DA分别为(Ⅱ)以点.DEAP ⊥,使立空间直角坐标系,利用向量法找出在线段BC上存在点P中,),在△ABC)证明:如图(【解答】解:(12,∥EFAB、、EF分别是ACBC的中点,∴∵,平面EFDEF?又AB平面,?DEF∴AB∥平面DEF;(2)以点D为坐标原点,以直线DB、DC、DA分别为x轴、y轴、z轴,;建立空间直角坐标系,如图(3)所示),2,00,0),C(0,(则A0,0,2),B(2,),,0F(1E(0,,,1),2,=),(﹣,0),2,0,﹣22=(,,10=(0,,1);),=(2,﹣2λ,则2=),+=(设2=λ,﹣λ=0,?得由AP⊥DEλ=,解得,×)21×(﹣2=0λ+∴,且DEP,使AP⊥=.∴在线段BC上存在点【点评】本题考查了直线与平面平行的证明与满足条件的点是否存在的判断问题,阶梯式要注意向量法的合理运用.二.垂直问题例2.(2017春?三元区校级月考)如图,在四形边ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°.将△ADB沿BD折起,使CD⊥平面ABD,构成三棱锥A﹣BCD.则在三棱锥A﹣BCD中,下列结论正确的是()A.AD⊥平面BCD B.AB⊥平面BCDC.平面BCD⊥平面ABC D.平面ADC⊥平面ABC【分析】由题意推出CD⊥AB,AD⊥AB,推出AB⊥平面ADC,可得平面ABC ⊥平面ADC.【解答】解:∵在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°∴BD⊥CD又平面ABD⊥平面BCD,且平面ABD∩平面BCD=BD故CD⊥平面ABD,则CD⊥AB,又AD⊥AB故AB⊥平面ADC,所以平面ABC⊥平面ADC.故选D.【点评】本题考查平面与平面垂直的判定,考查逻辑思维能力,是中档题.例3.(2016?杨浦区校级模拟)已知矩形ABCD,AB=1,BC=2,将△ABD沿矩形的对角线BD所在的直线进行翻折,在翻折的过程中()A.存在某个位置,使得直线AB和直线CD垂直垂BDAC和直线B.存在某个位置,使得直线直垂和直线BCC.存在某个位置,使得直线AD直.无论翻折到什么位置,以上三组直线均不垂直D【分析】假设各选项成立,根据线面位置关系推导结论,若得出矛盾式子,则假设错误,得出正确选项.垂直,与直线CDA,若存在某个位置,使得直线AB【解答】解:对于,⊥平面ABCBC,∴CD∵CD⊥上,BC,则E在,过点A作平面BCD的垂线AE∴平面ABC⊥平面BCD正确;ACD.故上的射影在BC上时,AB⊥∴当A在平面BCD垂直,与直线BD对于B,若存在某个位置,使得直线AC错误;B⊥EC,显然这是不可能的,故AFC⊥BD,则BD⊥平面,∴BD作AF 垂直,BCAD与直线对于C,若存在某个位置,使得直线,⊥AC⊥平面ACD,BC则BC错误.,显然这是不可能的,故C1>BC,即>2AB∴.A故选:翻折问题中的变与不变,本题主要考查了空间的线面和面面的垂直关系,【点评】空间想象能力和逻辑推理能力,有一定难度,属中档题.【变式训练2】(2017春?辛集市校级月考)如图,在正方形ABCD中,E、F分别是BC、CD的中点,G是EF的中点,现在沿AE、AF及EF把这个正方形折成一个空间图形,使B、C、D三点重合,重合后的点记为H,那么,在这个空间图形中必有()A.AG⊥△EFH所在平面B.AH⊥△EFH 所在平面C.HF⊥△AEF所在平面D.HG⊥△AEF所在平面【分析】本题为折叠问题,分析折叠前与折叠后位置关系、几何量的变与不变,可得HA、HE、HF三者相互垂直,根据线面垂直的判定定理,可判断AH与平面HEF的垂直.【解答】解:根据折叠前、后AH⊥HE,AH⊥HF不变,∴AH⊥平面EFH,B 正确;∵过A只有一条直线与平面EFH垂直,∴A不正确;∵AG⊥EF,EF⊥AH,∴EF⊥平面HAG,∴平面HAG⊥AEF,过H作直线垂直于平面AEF,一定在平面HAG内,∴C不正确;∵HG不垂直于AG,∴HG⊥平面AEF不正确,D不正确.故选B【点评】本题考查直线与平面垂直的判定,一般利用线线?线面?面面,垂直关系的相互转化判断.,BC∥AD中,ABCD杭州期末)如图所示,四边形?秋2016】(3【变式训练.AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使面ABD⊥面BCD,连结AC,则下列命题正确的是()A.面ABD⊥面ABC B.面ADC⊥面BDC C.面ABC⊥面BDC D.面ADC⊥面ABC【分析】证明CD⊥平面ABD,因此有AB⊥CD.又因为AB⊥AD,AD∩DC=D,所以AB⊥平面ADC,即可得到平面ADC⊥平面ABC.【解答】解:由题意知,在四边形ABCD中,CD⊥BD.在三棱锥A﹣BCD中,平面ABD⊥平面BCD,两平面的交线为BD,所以CD⊥平面ABD,因此有AB⊥CD.又因为AB⊥AD,AD∩DC=D,所以AB⊥平面ADC,于是得到平面ADC⊥平面ABC.故选D.【点评】本题考查线面垂直、面面垂直的判定,考查学生分析解决问题的能力,属于中档题.三.线线角中,,BC=1,将△浙江模拟)矩形ABCDABC与△ADC例4.(2017?沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为().D..B .AC【分析】求出两个特殊位置,直线AD与直线BC成的角,即可得出结论.【解答】解:由题意,初始状态,直线AD与直线BC成的角为0,DB=时,AD⊥DB,AD⊥DC,∴AD⊥平面DBC,AD⊥BC,成的角为BC,直线AD与直线,[0AD与直线BC成的角范围(包含初始状态)为].∴在翻折过程中直线故选:C.【点评】本题考查两直线所成的角的范围的求法,考查学生的计算求解能力、推理论证能力、空间思维能力,考查数形结合思想、分类讨论思想、转化化归思想,是中档题.例5.(2017春?涵江区校级期中)正方形ABCD,沿对角线BD折成直二面角A ﹣BD﹣C,则折后的异面直线AB与CD所成的角的大小为()90°.60°DB.45°C.30°A.O,以AO、CO【分析】取BD中点O,连结轴,zOA为轴,x轴,OD为y为原点,OC为利用向量法能求出折后的建立空间直角坐标系,所成的角.CDAB 与异面直线,COAO、【解答】解:取BD中点O,连结,﹣CBDBD折成直二面角A设正方形ABCD﹣边长为,∵沿对角线,⊥CO⊥BD,AO∴AO⊥BD,CO轴,建立空间直角坐标系,为zy轴,OA为原点,OC为x轴,OD为以O ),,10D(0,,,10),C(1,00),(,(A0,01),B0,﹣),0,1,1,﹣11),=(﹣,﹣=(0,所成的角为θAB设折后的异面直线与CD=>|cos<|cosθ=则,==.∴θ=60°.所成的角为CD60°与∴折后的异面直线AB.故选:C【点评】本题考查异面直线所成角的余弦值的求法,是基础题,解题时要认真审题,注意向量法的合理运用.BC=CD=,AB=BD=DA=2.浙江一模)如图四边形ABCD,【变式训练4】(2016?,的大小在][,则直线折起,使二面角ABD沿BDA﹣BD﹣C现将△)所成角的余弦值取值范围是(AB与CD,0]D..[0[,,∪(1)B.][,].A[0C,]【分析】取BD中点O,连结AO,CO,以O为原点,OC为x轴,OD为y轴,轴,建立空间z作平面BCD的垂线为过点OCD与直角坐标系,利用向量法能求出直线AB所成角的余弦值取值范围.,COAO,O【解答】解:取BD中点,连结,BDCOAB=BD=DA=2.⊥BC=CD=,∴∵,AO=CO=1AO⊥BD,且,的平面角,﹣CBDAOC是二面角A﹣∴∠轴,yx轴,OD为以O为原点,OC为建立空间直角坐标系,轴,BCD的垂线为z过点O作平面),1,0),D(0,00B(0,﹣1,),C(1,0,,则﹣C的平面角为θ,设二面角A﹣BD)(,、连AOBO,则∠AOC=θ,A,∴,,αAB设、CD的夹角为,则cosα==.[∈∵﹣1,∴|,∴cos|,0].cos∴.故选:D【点评】本题考查异面直线所成角的取值范围的求法,是中档题,解题时要认真审题,注意向量法的合理运用.(2016?浙江二模)如图,边长为1的菱形ABCD中,∠DAB=60°,【变式训练5】沿BD将△ABD翻折,得到三棱锥A﹣BCD,则当三棱锥A﹣BCD体积最大时,异面直线AD与BC所成的角的余弦值为().DC .B..A【分析】菱形ABCD中,∠DAB=60°,△ABD、△CBD为边长为1的等边三角形,将△ABD沿BD翻折过程中,点A在底面BDC的投影在∠DCB的平分线上,三棱锥的高最大时,平面ABD⊥平面BCD.【解答】解:△ABD、△CBD为边长为1的等边三角形,将△ABD沿BD翻折形成三棱锥A﹣BCD如图:点A在底面BDC的投影在∠DCB的平分线CE上,则三棱锥A﹣BCD的高为△AEC过A点的高;所以当平面ABD⊥平面BCD时,三棱锥A﹣BCD的高最大,体积也最大,此时AE⊥平面BCD;求异面直线AD与BC所成的角的余弦值:平移BC到DC′位置,|cos∠ADC′|即为所求,AC′=EC′=AE=,AD=DC=1,,=,||||cos∠ADC′=所成的角的余弦值为,AD与BC所以异面直线故选B.【点评】本题考查异面直线所成角的余弦值的求法,是中档题,解题时要认真审题,注意向量法的合理运用.【变式训练6】(2016?丽水校级模拟)如图,长方形ABCD,M,N分别为AB,AD上异于点A的两点,现把△AMN沿着MN翻折,记AC与平面BCD所成的角为θ,直线AC与直线MN所成的角为θ,则θ与θ的大小关系是()2211=θB.θ>θC.θ<θA.θD.不能确定212112【分析】作AO⊥平面BCD,垂足是O,连接CO,过点C作直线l∥MN,在l上取点H,令CH=CO,在△AOC和△AHC 中,CO=CH,AO⊥平面BCD,从而AO<AH,由此能求出θ<1θ.2【解答】解:作AO⊥平面BCD,垂足是O,连接C过点C作直线l∥MN,在l上取点H,令CH=CO,,⊥平面BCD中,CO=CH,AOAHC在△AOC和△,<AH∴AO,<∠ACH∴∠ACO,θ所成的角为,直线AC与直线MN∵AC与平面BCD所成的角为θ21,MNBCD,CH∥AO⊥平面.Cθ<θ.故选:∴∠ACO=θ,∠ACH=θ∴2211。
立体几何的动态问题之二———翻折问题立体几何动态问题的基本类型:点动问题;线动问题;面动问题;体动问题;多动问题等一、面动问题(翻折问题):(一)学生用草稿纸演示翻折过程: (二)翻折问题的一线五结论.D F A E ⊥一线:垂直于折痕的线即五结论:1)折线同侧的几何量和位置关系保持不变;折线两侧的几何量和位置关系发生改变; 2--D H F D H F ''∠)是二面角的平面角;3D D F ')在底面上的投影一定射线上;二、翻折问题题目呈现:(一)翻折过程中的范围与最值问题1、(2016年联考试题)平面四边形ABCD 中,CD=CB=且A D A B ⊥,现将△ABD 沿对角线BD 翻折成'A B D ∆,则在'A B D ∆折起至转到平面BCD 的过程中,直线'A C 与平面BCD 所成最大角的正切值为_______ .解:由题意知点A 运动的轨迹是以E 为圆心,EA 为半径的圆,当点A运动到与圆相切的时候所称的角最大,所以ta n '3A CB ∠=【设计意图】加强对一线、五结论的应用,重点对学生容易犯的错误12进行分析,找出错误的原因。
2、2015年10月浙江省学业水平考试18).如图,在菱形ABCD 中,∠BAD=60°,线段AD ,BD 的中点分别为E ,F 。
现将△ABD 沿对角线BD 翻折,则异面直线BE 与CF 所成角的取值范围是DABECDABC4) ''D H D H 点的轨迹是以为圆心,为半径的圆;5A D 'E A E .)面绕翻折形成两个同底的圆锥CA.(,)63ππB. (,]62ππC. (,]32ππD. 2(,)33ππ分析:这是一道非常经典的学考试题,本题的解法非常多,很好的考查了空间立体几何线线角的求法。
方法一:特殊值法(可过F 作FH 平行BE,找两个极端情形) 方法二:定义法:利用余弦定理:222254c o s 243F HF CC HF H C C HF H F C+-∠==-,有344C H ≤≤11c o s ,22C F H ⎡⎤∴∠∈-⎢⎥⎣⎦异面直线BE 与CF 所成角的取值范围是(,]32ππ 方法三:向量基底法:111()()222B E FC B A BD F C B A F C B F F A F C=+==+111c o s ,c o s ,,222B E F C F C F A ⎡⎤<>=<>∈-⎢⎥⎣⎦方法四:建系:3、(2015年浙江·理8)如图,已知ABC ∆,D 是AB 的中点,沿直线CD 将ACD ∆折成A CD '∆,所成二面角A CDB '--的平面角为α,则 ( B )A. A DB α'∠≤B. A DB α'∠≥C. A CB α'∠≥D. A CB α'∠≤方法一:特殊值方法二:定义法作出二面角,在进行比较。




立体几何中的折叠问题1.概念:将平面图形沿某直线翻折成立体图形,再对折叠后的立体图形的线面位置关系和某几何量进行论证和计算,就是折叠问题.2.折叠问题分析求解原则:(1)折叠问题的探究须充分利用不变量和不变关系;(2)折叠前后始终位于折线的同侧的几何量和位置关系保持不变。
(最值问题)1、把正方形ABCD 沿对角线AC 折起,当以A 、B 、C 、D 四点为顶点的三棱锥体积最大时,直线BD 和平面ABC 所成角的大小为_______.(两点间距离,全品83页)2、把长宽分别为2的长方形ABCD 沿对角线AC 折成60o 的二面角,求顶点B 和D 的距离。
3、(全品70页)给出一边长为2的正三角形纸片,把它折成一个侧棱长与底面边长都相等的三棱锥,并使它的全面积与原三角形面积相等,设计一种折叠方法,并用虚线标在图中,并求该三棱锥的体积。
4、(2005江西文)矩形ABCD 中,AB=4,BC=3,沿AC 将矩形ABCD 折成一个直二面角B —AC —D ,则四面体ABCD 的外接球的体积为 ( ) A .π12125B .π9125C .π6125D .π3125A BCEMN解决折叠问题的关键是弄清折叠前后哪些量没有变化,折叠后位置关系怎样变化,通过空间想象折叠成的几何体的形状来分析已知和待求,是培养空间想象能力的很好的题型。
高考题中的折叠问题1、在正方形SG 1G 2G 3中E 、F 分别是G 1G 2及G 2G 3的中点,D 是EF 的中点,现在沿SE 、SF 及EF 把这个正方形折成一个四面体,使G 1、G2、G 3三点重合,重合后的点记为G.那么,在四面体S —EFG 中必有(A)SG ⊥△EFG 所在平面 (B)SD ⊥△EFG 所在平面 (C)GF ⊥△SEF 所在平面 (D)GD ⊥△SEF 所在平面 2、如图,在正三角形ABC 中,D ,E ,F 分别为各边的中点, G ,H ,I ,J 分别为AF ,AD ,BE ,DE 的中点.将△ABC 沿DE , EF ,DF 折成三棱锥以后,GH 与IJ 所成角的度数为( ) A .90° B .60° C .45° D .0°3、(2005浙江理科)12.设M 、N 是直角梯形ABCD 两腰的中点,DE ⊥AB 于E (如下图).现将△ADE 沿DE 折起,使二面角A -DE -B 为45°,此时点A 在平面BCDE 内的射影恰为点B ,则M 、N 的连线与AE 所成角的大小等于_____.4、(2006山东)如图,在等腰梯形ABCD 中,AB=2DC=2,∠DAB =60°,E 为AB 的中点,将△ADE 与△BEC 分别沿ED 、EC 向上折起,使A 、B 重合于点P ,则P -DCE 三棱锥的外接球的体积为(A)2734π (B)26π (C)86π (D)246π5、(2009浙江)如图,在长方形ABCD 中,2AB =,1BC =,E 为DC 的中点,F 为线段EC (端点除外)上一动点.现将AFD ∆沿AF 折起,使平面ABD ⊥平面ABC .在平面ABD 内过点D 作DK AB ⊥,K 为垂足.设AK t =,则t 的取值范围是 .6.(2010上海)在边长为4的正方形纸片ABCD 中,AC 与BD 相交于O,剪去AOB V ,将剩余部分沿OC 、OD 折叠,使OA 、OB 重合,则以A 、(B )、C 、D 、O 为顶点的四面体的体积为 。

翻折视角下的立体几何试题1.筝形的翻折筝形是指有一条对角线所在直线为对称轴的四边形,与菱形的定义相对应。
菱形是特殊的筝形。
筝形的一条对角线所在的直线垂直平分另一条对角线。
在筝形平面到空间变换的研究中,常常沿着其中一条对角线进行翻折。
在翻折的过程中,两条对角线的垂直关系保持不变,高考命题中常常利用两个对应的等腰三角形来描述空间筝形。
此类高考试题极为丰富。
例:2013年新课标1文科19题)如图,三棱柱111ABC A B C -中,CA CB =,1AB AA =,160BAA ∠= 。
(Ⅰ)证明:1AB A C ⊥;(Ⅱ)若2AB CB ==,16AC =,求三棱柱111ABC A B C -的体积。
2.梯形的翻折:1)等腰梯形的翻折等腰梯形的翻折主要强调对腰的翻折,即保持底面的矩形特征,两腰向中间翻折,这里就有两底的端点是否合拢的问题。
例:2016全国卷1理科18题)如图,在以A ,B ,C ,D ,E ,F 为顶点的五面体中,面ABEF 为正方形,AF =2FD ,90AFD ∠= ,且二面角D -AF -E 与二面角C -BE -F 都是60 .(I )证明:平面ABEF ⊥平面EFDC ;(II )求二面角E -BC -A 的余弦值例:2017年全国卷1理科18题)如图,在四棱锥P−ABCD 中,AB//CD ,且90BAP CDP ∠=∠= .(1)证明:平面PAB⊥平面PAD;(2)若PA=PD=AB=DC,90APD∠= ,求二面角A−PB−C的余弦值.2)直角梯形的翻折在直角梯形中有一类由两个直角三角形,特别的,其中一个是等腰直角三角形,拼接而成的直角梯形的翻折问题考查热点。
这类的翻折问题一般都是沿着两个三角形的公共边AC进行翻折,翻折的位置往往强调两个面互相垂直,这样容易考查线面垂直与面面垂直的判定定理和性质定理。
具体操作时要注意翻折前后的点与线、线与线位置关系的变与不变,数量关系的变与不变。
立体几何专题——翻折问题
1、已知矩形ABCD ,AB=1,BC=。
将△ABD 沿矩
形的对角线BD 所在的直线进行翻折,在翻折过程中。
A.存在某个位置,使得直线AC 与直线BD 垂直.
B.存在某个位置,使得直线AB 与直线CD 垂直.
C.存在某个位置,使得直线AD 与直线BC 垂直.
D.对任意位置,三对直线“AC 与BD ”,“AB 与CD ”,
“AD 与BC ”均不垂直
2、如图,在长方形ABCD 中,AB=2,BC=1,E 为DC 的中点,F 为线段EC(端点除外)上一动点,现将 AFD 沿AF 折起,使平面AFD ⊥平面ABC,在平面ABD 内过点D 作DK ⊥AB,K 为垂足,设AK=t,则t 的取值范围是_______.
3、如图, 在矩形ABCD 中,点,E F 分别在线段,AB AD 上,243AE EB AF FD ===
=.沿直线EF 将AEF V 翻折成'A EF V ,使平面'
A EF BEF ⊥平面.
(Ⅰ)求二面角'A FD C --的余弦值; (Ⅱ)点,M N 分别在线段,FD BC 上,若沿直线MN 将四边形MNCD 向上翻折,使C 与'A 重合,求线段FM 的长'A。
高考数学难点突破八--------立体几何中的翻折问题一、知识储备翻折问题就是把平面图形经过折叠变成一个空间图形,实际上,折叠问题就是轴对称的问题,折痕就是对称轴,重合的即是全等图形,解决折叠问题时,要把运动着的空间图形不断地与原平面图形进行对照,看清楚其中哪些量在变化,哪些量没有变化,从而寻找出解决问题的方法,达到空间问题与平面问题相互转化的目的。
核心是抓牢折痕就是翻折前与翻折后平面图形的公共底边,折痕与公共底边上两高所在平面垂直。
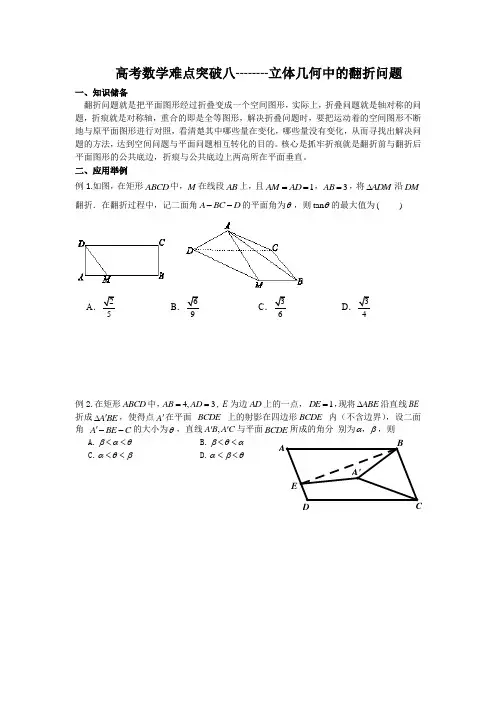
二、应用举例例1.如图,在矩形ABCD 中,M 在线段AB 上,且1AM AD ==,3AB =,将ADM ∆沿DM 翻折.在翻折过程中,记二面角A BC D --的平面角为θ,则tan θ的最大值为( )ABCD例2.在矩形ABCD 中,4,3AB AD ==,E 为边AD 上的一点,1DE =,现将ABE ∆沿直线BE 折成A BE '∆,使得点A '在平面 BCDE 上的射影在四边形BCDE 内(不含边界),设二面角 A BE C '--的大小为θ,直线,A B A C ''与平面BCDE 所成的角分 别为αβ,,则 A.βαθ<< B.βθα<< C.αθβ<< D.αβθ<<例3.如图,矩形ABCD 中心为, O BC AB >,现将DAC 沿着对角线AC 翻折成EAC ,记BOE a ∠=,二面角B AC E --的平面角为β,直线DE 和BC 所成角为γ,则( )A. ,2a ββγ>>B. ,2a ββγ><C. ,2a ββγ<>D. ,2a ββγ<<例4.如图,在ABC △中,1AB =,22BC =,4B π=,将ABC △绕边AB 翻转至ABP △,使面ABP ⊥面ABC ,D 是BC 中点,设Q 是线段PA 上的动点,则当PC 与DQ 所成角取得最小值时,线段AQ 的长度为( ) A .5 B .25C .35D .25例5.已知在矩形ABCD 中,2AD AB =,沿直线BD 将ABD ∆ 折成'A BD ∆,使得点'A 在平面BCD 上的射影在BCD ∆内(不含边界),设二面角'A BD C --的大小为θ,直线','A D A C 与平面BCD 所成的角分别为,αβ,则( )A. αθβ<<B. βθα<<C. βαθ<<D. αβθ<<Q DPCBA例6、(嘉兴市2020年1月期终)已知矩形ABCD ,4AB =,2BC =,E 、F 分别为AB 、CD 的中点,沿直线DE 将ADE △翻折成PDE △,在点P 从A 至F 的运动过程中,CP 的中点G 的轨迹长度为 .例7、(宁波市2020年1月期终)已知平面四边形ABCD 中,90A C ∠=∠=︒,BC CD =,AB AD >,现将ABD △沿对角线BD 翻折得到三棱锥A BCD '-,在此过程中,二面角A BC D '--、A CDB '--的大小分别为α,β,直线A B '与平面BCD 所成角为γ,直线A D '与平面BCD 所成角为δ,则( )A .γδβ<<B .γαβ<<C .αδβ<<D .γαδ<<例8、(柯桥一中2020年1月期终)已知在矩形ABCD 中,2AB =,4AD =,E ,F 分别在边AD ,BC 上,且1AE =,3BF =,如图所示, 沿EF 将四边形AEFB 翻折成A EFB '',则在翻折过程中,二面角B CD E '--的大小为θ,则tan θ的最大值为( ) A.5C.4例9、(2020年3月名校合作体)已知C 为ABD Rt ∆斜边BD 上一点,且ACD ∆为等边三角形,现将ABC ∆沿AC 翻折至C B A '∆,若在三棱锥ACD B -'中,直线B C '和直线B A '与平面ACD 所成角分别为βα,,则( )A. βα<<0B.βαβ2≤<C.βαβ32≤≤D.βα3≥例10、(2020年1月嘉兴期终)已知矩形ABCD ,4AB =,2BC =,E 、F 分别为AB 、CD 的中点,沿直线DE 将ADE △翻折成PDE △,在点P 从A 至F 的运动过程中,CP 的中点G 的轨迹长度为 .例11、(2020年4月温州模拟)如图,在ABC ∆中,点M 是边BC 的中点,将ABN ∆沿着AM 翻折成M B A '∆,且点B '不在平面AMC 内,点P 是线段C B '上一点,若二面角B AM P '--与二面角C AM P --的平面角相等,则直线AP 经过C B A '∆的( ) A. 重心 B. 垂心 C. 内心 D.外心B DACG PFD C B A例12、(2020年嘉兴一模)将边长为1的正方形ABCD 沿对角线BD 翻折,使得二面角A BD C --的平面角的大小为π3,若点E ,F 分别是线段AC 和BD 上的动点,则BE CF 的取值范围为 ( )A .[1,0]-B .1[1,]4-C .1[,0]2-D . 11[,]24-例13、(2020年5月暨阳联考)如图:ABC ∆中,︒=∠⊥90,ACB BC AB ,D 为AC 的中点,ABD ∆沿BD 边翻折过程中,直线AB 与BC 直线所成的最大角,最小角分别记为11βα,,直线AD 与直线BC 所成的最大角,最小角分别记为22βα,,则有( )A. ββαα≤<121,B. 2121ββαα><,C. 2121ββαα≤≥,D.2121ββαα>≥,例14、(2020年4月台州二模)如下图①,在直角梯形ABCD 中,90=∠=∠=∠DAB CDB ABC , 30=∠BCD ,4=BC ,点E 在线段CD 上运动,如下图②,沿BE 将BEC ∆折至C BE '∆,使得平面⊥'C BE 平面ABED ,则C A '的最小值为 .⇒例15、(2020年9月嘉兴基础知识测试)如图,矩形ABCD 中,2,1==BC AB ,点E 为AD 中点,将ABE ∆沿BE 折起,在翻折过程中,记二面角B DC A --的平面角大小为α,则当α最大时,=αtan ( ) A. 22 B. 32 C. 31 D.21。
立体几何大题题型二:翻折问题1.已知四边形满足,,是的中点,将△沿着翻折成△,使面面,分别为的中点.(1)求三棱锥的体积;(2)证明:平面;(3)证明:平面平面.思路分析:对于翻折问题要注意翻折后的图形与翻折前的图形中的变与不变量.(1)求棱锥的体积一般找棱锥高易求的进行转换.由题意知,且,∴四边形为平行四边形,∴,即为等边三角形.由面面的性质定理,连结,则,可知平面.所以即可;(2)本题利用线面平行的判定定理去做.因为为的中点,注意利用中位线;(3)本题利用面面垂直的判定定理证明.因为∥,只需证明平面即可。
连结,则.又△为等边三角形,则,得证.本题注意体现了转化的思想.ABCD AD BC 12BA AD DC BC a ====E BC BAE AE 1B AE 1B AE ⊥AECD ,F G 1,B D AE 1E ACB -1B E ACF 1B GD ⊥1B DC AD EC AD EC =ADCE AE DC a ==E AB 1∆1B AE ⊥AECD 1B G 1B G AE ⊥1B G ⊥AECD 11E ACB B AEC V V --=F 1B D AE CD AE ⊥1B GD GD DG AE ⊥ABE 1B G AE ⊥C A B D AB 1CD E GF(2)连接交于,连接,∵为菱形,且为的中点,∴.又面,平面,∴平面(3)连结,则.又,,∴平面.又,∴平面.又平面,∴平面平面. 点评:本题考查了直线与平面平行、平面与平面垂直的判定和几何体的体积,以折叠问题为载体,折叠问题是考查学生空间想象能力的较好载体。
如本题,不仅要求学生象解常规立几综合题一样懂得线线,线面和面面垂直的判定方法及相互转化,还要正确识别出△沿折叠而成的空间图形,更要识得折前折后有关线线、线面位置的变化情况以及有关量(边长与角)的变化情况,否则无法正确解题.这正是折叠问题的价值之所在.2.(2015·山东聊城二模)如图(1)所示,正△ABC 的边长为4,CD 是AB 边上的高,E ,F 分别是AC 和BC 边的中点,现将△ABC 沿CD 翻折成直二面角A -DC -B .(如图(2))ED AC O OF AEDC F 1B D 1FO B E 1B E ⊄ACF FO ⊂ACF 1B E ACF GD DG AE ⊥1B G AE ⊥1B G GD G = AE ⊥1B GD AE DC DC ⊥1B GD DC ⊂1B DC 1B GD ⊥1B DC BAE AE A BCD E GF(1)试判断直线AB 与平面DEF 的位置关系,并说明理由;(2)求二面角E -DF -C 的余弦值; (3)在线段BC 上是否存在一点P ,使AP ⊥DE ?如果存在,求出BP BC的值;如果不存在,请说明理由.【解】 (1)平行.在△ABC 中,由E 、F 分别是AC 、BC 中点,得EF ∥AB ,又AB ⊄平面DEF ,EF ⊂平面DEF ,∴AB ∥平面DEF .(2)以点D 为坐标原点,以直线DB 、DC 、DA 分别为x 轴、y 轴、z 轴,建立空间直角坐标系,则A (0,0,2),B (2,0,0),C (0,23,0),E (0,3,1),F (1,3,0),DF →=(1,3,0),DE→=(0,3,1),DA →=(0,0,2).平面CDF 的法向量为DA →=(0,0,2),设平面EDF 的法向量为n =(x ,y ,z ),则⎩⎪⎨⎪⎧DF →·n =0,DE →·n =0,即⎩⎨⎧x +3y =0,3y +z =0, 取n =(3,-3,3),cos 〈DA →,n 〉=DA →·n |DA →||n |=217, 所以二面角E -DF -C 的余弦值为217. (3)存在.设P (s ,t ,0),有AP →=(s ,t ,-2),则AP →·DE →=3t -2=0,∴t =233, 又BP →=(s -2,t ,0),PC →=(-s ,23-t ,0), ∵BP →∥PC →,∴(s -2)(23-t )=-st ,∴3s +t =2 3.把t =233代入上式得s =43,∴BP →=13·BC →, ∴在线段BC 上存在点P ,使AP ⊥DE .此时,BP BC =13. 3.(2015·陕西高考)如图1,在直角梯形 ABCD 中,AD ∥BC ,∠BAD =π2,AB =BC =12AD =a ,E 是AD 的中点,O 是AC 与BE 的交点.将△ABE 沿BE 折起到图2中△A 1BE 的位置,得到四棱锥A 1BCDE .(1)证明:CD ⊥平面A 1OC ;(2)当平面A 1BE ⊥平面BCDE 时,四棱锥A 1BCDE 的体积为362,求a 的值.【解】 (1)证明:在图1中,因为AB =BC =12AD =a ,E 是AD 的中点. ∠BAD =π2,所以BE ⊥AC . 即在图2中,BE ⊥A 1O ,BE ⊥OC .从而BE ⊥平面A 1OC ,又CD ∥BE ,所以CD ⊥平面A 1OC .(2)由已知,平面A 1BE ⊥平面BCDE ,且平面A 1BE ∩平面BCDE =BE ,又由(1),A 1O ⊥BE ,所以A 1O ⊥平面BCDE ,即A 1O 是四棱锥A 1BCDE 的高.由图1知,A 1O =22AB =22a ,平行四边形BCDE 的面积S =BC ·AB =a 2. 从而四棱锥A 1BCDE 的体积为V =13×S ×A 1O =13×a 2×22a =26a 3, 由26a 3=362,得a =6. 4.(2015·宁夏银川一中二模)如图1,在直角梯形ABCD 中,∠ADC =90°,CD ∥AB ,AD =CD =12AB =2,点E 为AC 中点.将△ADC 沿AC 折起,使平面ADC ⊥平面ABC ,得到几何体D —ABC ,如图2所示.(1)在CD 上找一点F ,使AD ∥平面EFB ;(2)求点C 到平面ABD 的距离.【解】 (1)取CD 的中点F ,连结EF ,BF ,在△ACD 中,∵E ,F 分别为AC ,DC 的中点,∴EF 为△ACD 的中位线,∴AD ∥EF ,∵EF ⊂平面EFB ,AD ⊄平面EFB ,∴AD ∥平面EFB .(2)设点C 到平面ABD 的距离为h ,在Rt △ADC 中,AD =CD =2,∴AC =AD 2+CD 2=22,易求得BC =22, ∵AB =4,∴AC 2+BC 2=AB 2,∴AC ⊥BC .∵平面ADC ⊥平面ABC ,平面ADC ∩平面ABC =AC ,且BC ⊂平面ABC , ∴BC ⊥平面ADC ,∴BC 是三棱锥B —ADC 的高,BC ⊥AD ,又AD ⊥DC ,DC ∩BC =C ,∴AD ⊥平面BCD ,∴AD ⊥BD .∴S △ABD =12AD ·BD =12×2×23=23, 由V C -ABD =V B -ACD ,得13·S △ABD ·h =13·S △ACD ·BC ,即13·23·h =13·12×2×2·22, 解得h =263. ∴点C 到平面ABD 的距离为263.。
立体几何中翻折问题(微专题)一、题型选讲题型一、展开问题1(2022·广东佛山·高三期末)长方体ABCD-A1B1C1D1中,AB=1,AD=AA1=2,E为棱AA1上的动点,平面BED1交棱CC1于F,则四边形BED1F的周长的最小值为()A.43B.213C.2(2+5)D.2+42【答案】B【分析】将几何体展开,利用两点之间直线段最短即可求得截面最短周长.【详解】解:将长方体展开,如图所示:当点E为BD1与AA1的交点,F为BD1与CC1的交点时,截面四边形BED1F的周长最小,最小值为2BD1=222+(1+2)2=213.故选:B.1.(2022·湖北武昌·高三期末)已知四面体ABCD的一个平面展开图如图所示,其中四边形AEFD是边长为22的菱形,B,C分别为AE,FD的中点,BD=22,则在该四面体中()A.BE⊥CDB.BE与平面DCE所成角的余弦值为21015D.四面体ABCD的外接球表面积为9πC.四面体ABCD的内切球半径为10530【答案】ACD【分析】几何体内各相关线段的计算即可.【解析】由题意得,展开图拼成的几何体如下图所示,AB=CD=2,AD=BD=BC=AC=22,取AB中点M,CD中点N,MN中点O,连MN、OA,过O作OH⊥CM于H,则OH是内切球的半径,OA是外接球的半径.所以AM=CN=12AB=22,CM=AN=AC2-CN2=222-222=302MN=CM2-CN2=3022-22 2=7对于A:AN⊥CD,BN⊥CD,AN∩BN=N,故CD⊥平面ABN,而BE⊂平面ABN,所以BE⊥CD,故A正确;对于B:由于CD⊂平面ACD,故平面ABN⊥平面ACD,故∠BAN是BE与平面DCE所成角,故cos∠BAN=AMAN=22×230=1515,故B错误;对于C:OH=CNCM12MN=22×230×12×7=10530,故C正确;对于D:OA2=AM2+12MN2=22 2+72 2=94所以外接球的表面积为9π,故D正确.故选:ACD2.【2020年高考全国Ⅰ卷理数】如图,在三棱锥P-ABC的平面展开图中,AC=1,AB=AD= 3,AB⊥AC,AB⊥AD,∠CAE=30°,则cos∠FCB=.【答案】-14【解析】∵AB ⊥AC ,AB =3,AC =1,由勾股定理得BC =AB 2+AC 2=2,同理得BD =6,∴BF =BD =6,在△ACE 中,AC =1,AE =AD =3,∠CAE =30°,由余弦定理得CE 2=AC 2+AE 2-2AC ⋅AE cos30°=1+3-2×1×3×32=1,∴CF =CE =1,在△BCF 中,BC =2,BF =6,CF =1,由余弦定理得cos ∠FCB =CF 2+BC 2-BF 22CF ⋅BC=1+4-62×1×2=-14.故答案为:-14.题型二、折叠问题2(2022·河北唐山·高三期末)如图,四边形ABCD 是边长为2的正方形,E 为AB 的中点,将△AED 沿DE 所在的直线翻折,使A 与A 重合,得到四棱锥A -BCDE ,则在翻折的过程中()A.DE ⊥AAB.存在某个位置,使得A E ⊥CDC.存在某个位置,使得A B ∥DED.存在某个位置,使四棱锥A -BCDE 的体积为1【答案】AB 【分析】过A 作A O ⊥DE ,垂足为O ,证得DE ⊥平面A AO ,可判定A 正确;取DC 的中点G ,连接EG ,A G ,当A 在平面ABCD 上的投影在FG 上时,可判定B 正确;连接A B ,由直线A B 与DE 是异面直线,可判定C错误;求得A O=25,结合体积公式求可判定D错误.【详解】对于A中,如图所示,过A 作A O⊥DE,垂足为O,延长AO交BC于点F,因为DE⊥AO,且AO∩A O=O,所以DE⊥平面A AO,又因为A A⊂平面A AO,所以DE⊥AA ,所以A正确;对于B中,取DC的中点G,连接EG,A G,当A 在平面ABCD上的投影在FG上时,此时DC⊥平面A EG,从而得到A E⊥CD,所以B正确;对于C中,连接A B,因为E⊂平面A BE,D⊄平面A BE,所以直线A B与DE是异面直线,所以不存在某个位置,使得A B∥DE,所以C错误;对于D中,由V A -BCDE=13×12×(1+2)×2×h=1,解得h=1,由A 作A O⊥DE,可得A O=A E⋅A DDE=1×25=25,即此时四棱锥的高h∈0,25 5,此时25<1,所以不存在某个位置,使四棱锥A -BCDE的体积为1,所以D错误.故选:AB.1.(2022·江苏宿迁·高三期末)如图,一张长、宽分别为2,1的矩形纸,A,B,C,D分别是其四条边的中点.现将其沿图中虚线折起,使得P1,P2,P3,P4四点重合为一点P,从而得到一个多面体,则()A.在该多面体中,BD=2B.该多面体是三棱锥C.在该多面体中,平面BAD⊥平面BCDD.该多面体的体积为112【答案】BCD利用图形翻折,结合勾股定理,确定该多面体是以A ,B ,C ,D 为顶点的三棱锥,利用线面垂直,判定面面垂直,以及棱锥的体积公式即可得出结论.【解析】由于长、宽分别为2,1,A ,B ,C ,D 分别是其四条边的中点,现将其沿图中虚线折起,使得P 1,P 2,P 3,P 4四点重合为一点P ,且P 为BD 的中点,从而得到一个多面体ABCD ,所以该多面体是以A ,B ,C ,D 为顶点的三棱锥,故B 正确;AB =BC =CD =DA =32,AC =BD =1,AP =CP =22,故A 不正确;由于22 2+22 2=1,所以AP ⊥CP ,BP ⊥CP ,可得BD ⊥平面ACP ,则三棱锥A -BCD 的体积为13×BD ×S △ACP =13×1×12×22×22=112,故D 正确;因为AP ⊥BP ,AP ⊥CP ,所以AP ⊥平面BCD ,又AP ⊂平面BAD ,可得平面BAD ⊥平面BCD ,故C 正确.故选:BCD2.(2022·江苏海安·高三期末)如图,ABCD 是一块直角梯形加热片,AB ∥CD ,∠DAB =60°,AB =AD =4dm .现将△BCD 沿BD 折起,成为二面角A -BD -C 是90°的加热零件,则AC 间的距离是dm ;为了安全,把该零件放进一个球形防护罩,则球形防护罩的表面积的最小值是dm 2.(所有器件厚度忽略不计)【答案】4设E 为BD 的中点,由题可得AE ⊥平面BCD ,进而可求AC ,再结合条件可得△DAB 的中心为棱锥C -ABD 的外接球的球心,即求.【解析】∵ABCD 是一块直角梯形加热片,AB ∥CD ,∠DAB =60°,AB =AD =4dm .∴△DAB 为等边三角形,BC =23dm ,DC =2dm ,设E 为BD 的中点,连接AE ,CE ,则AE ⊥BD ,又二面角A -BD -C 是90°,∴AE ⊥平面BCD ,CE ⊂平面BCD ,∴AE ⊥CE ,又CE =2dm ,AE =23dm ,∴AC =AE 2+CE 2=4dm ,设△DAB 的中心为O ,则OE ⊥平面BCD ,又E 为BD 的中点,△BCD 为直角三角形,∴OB =OC =OD =OA ,即O 为三棱锥C -ABD 的外接球的球心,又OA =23×23=433dm ,故球形防护罩的表面积的最小值为4π⋅OA 2=64π3dm 2.故答案为:4,64π3.3.(2022·河北保定·高三期末)如图,DE 是边长为4的等边三角形ABC 的中位线,将△ADE 沿DE 折起,使得点A 与P 重合,平面PDE ⊥平面BCDE ,则四棱雉P -BCDE 外接球的表面积是.【答案】52π3求出四边形BCDE 外接圆的圆半径,再设四棱锥P -BCDE 外接球的球心为O ,由R 2=OO 2+O B 2求出半径,代入球的表面积公式即可.【解析】如图,分别取BC ,DE 的中点O ,F ,连接PF ,O F .因为△ABC 是边长为4的等边三角形,所以PF =O F =3,所以O B =O C =O D =O E =2,则四边形BCDE 外接圆的圆心为O ,半径r =2.设四棱锥P -BCDE 外接球的球心为O ,连接OO ,过点O 作OH ⊥PF ,垂足为H .易证四边形HFO O 是矩形,则HF =OO ,OH =O F =3.设四棱锥P -BCDE 外接球的半径为R ,则R 2=OO 2+O B 2=OH 2+PH 2=O F 2+PF -OO 2,即R 2=OO 2+22=3 2+3-OO 2,解得R 2=133,故四棱锥P -BCDE 外接球的表面积是4πR 2=52π3.故答案为:52π3题型三、折叠的综合性问题3(2022·江苏扬州·高三期末)在边长为6的正三角形ABC 中M ,N 分别为边AB ,AC 上的点,且满足AM AB =ANAC=λ,把△AMN 沿着MN 翻折至A ′MN 位置,则下列说法中正确的有()A.在翻折过程中,在边A ′N 上存在点P ,满足CP ∥平面A ′BMB.若12<λ<1,则在翻折过程中的某个位置,满足平面A ′BC ⊥平面BCNMC.若λ=12且二面角A ′-MN -B 的大小为120°,则四棱锥A ′-BCNM 的外接球的表面积为61πD.在翻折过程中,四棱锥A ′-BCNM 体积的最大值为63【答案】BCD 【分析】通过直线相交来判断A 选项的正确性;通过面面垂直的判定定理判断B 选项的正确性;通过求四棱锥A -BCNM 外接球的表面积来判断C 选项的正确性;利用导数来求得四棱锥A -BCNM 体积的最大值.【详解】对于选项A,过P作PQ⎳MN⎳BC,交AM于Q,则无论点P在A′N上什么位置,都存在CP与BQ相交,折叠后为梯形BCQP,则CP不与平面A′BM平行,故选项A错误;对于选项B,设D,E分别是BC,MN的中点,若12<λ<1,则AE>DE,所以存在某一位置使得A′D⊥DE,又因为MN⊥A′E,MN⊥DE,且A′E∩DE=E,所以MN⊥平面A′DE,所以MN⊥A′D,DE∩MN=E,所以A′D⊥平面BCNM,所以A′BC⊥平面BCNM,故选项B正确;对于选项C,设D,E分别是BC,MN的中点,若λ=12且二面角A′-MN-B的大小为120°,则△AMN为正三角形,∠BMN=120°,∠C=60°,则BCNM四点共圆,圆心可设为点G,其半径设为r,DB=DC=DM=DN=3,所以点G即为点D,所以r=3,二面角A′-MN-B的平面角即为∠A′ED=120°,过点A′作A′H⊥DE,垂足为点H,EH=334,DH=934,A′H=94,DH2=24316,设外接球球心为O,由OD2+32=R294-OD2+24316=R2,解得R2=614,所以外接球的表面积为S=4πR2=61π,故选项C正确;对于选项D,设D,E分别是BC,MN的中点,设h是四棱锥A -BCNM的高.S△AMN=12×6λ×6λ×32=93λ2,S△ABC=12×6×6×32=93,所以S四边形BCNM=93(1-λ2),则V A′-BCNM=13×93(1-λ2)×h≤33(1-λ2)×A′E=33(1-λ2)×33λ=27(-λ3+λ),λ∈(0,1),可设f(λ)=27(-λ3+λ),λ∈(0,1),则f λ =27(-3λ2+1),令f λ =0,解得λ=33,则函数f(λ)在0,33上单调递增,在33,1上单调递减,所以f(λ)max=f33=63,则四棱锥A′-BCN体积的最大值为63,故选项D正确.故选:BCD1.(2021·山东滨州市·高三二模)已知正方形ABCD的边长为2,将△ACD沿AC翻折到△ACD 的位置,得到四面体D -ABC,在翻折过程中,点D 始终位于△ACD所在平面的同一侧,且BD 的最小值为2,则下列结论正确的是()A.四面体D -ABC的外接球的表面积为8πB.四面体D -ABC体积的最大值为63C.点D的运动轨迹的长度为22π3D.边AD旋转所形成的曲面的面积为22π3【答案】ACD【解析】对ABCD各选项逐一分析即可求解.【详解】解:对A:∵∠ABC=90o,∠AD C=90o,∴AC中点即为四面体D -ABC的外接球的球心,AC为球的直径,∴R=2,∴SD -ABC =4πR2=4π22=8π,故选项A正确;对B:当平面AD C⏊平面ABC时,四面体D -ABC体积的最大,此时高为2,∴V D -ABCmax=13×12×2×2×2=223,故选项B错误;对C :设方形ABCD 对角线AC 与BD 交于O ,由题意,翻折后当BD 的最小值为2时,△OD B 为边长为2的等边三角形,此时∠D OB =π3,所以点D 的运动轨迹是以O 为圆心2为半径的圆心角为2π3的圆弧,所以点D 的运动轨迹的长度为2π3×2=22π3,故选项C 正确;对D :结合C 的分析知,边AD 旋转所形成的曲面的面积为以A 为顶点,底面圆为以O 为圆心OD =2为半径的圆锥的侧面积的13,即所求曲面的面积为13πrl =13π×2×2=22π3,故选项D 正确.故选:ACD .2.【2022·广东省深圳市宝安区第一次调研10月】如图甲是由正方形ABCD ,等边△ABE 和等边△BCF 组成的一个平面图形,其中AB =6,将其沿AB ,BC ,AC 折起得三棱锥P -ABC ,如图乙.(1)求证:平面PAC ⊥平面ABC ;(2)过棱AC 作平面ACM 交棱PB 于点M ,且三棱锥P -ACM 和B -ACM 的体积比为1:2,求直线AM 与平面PBC 所成角的正弦值.【答案】(1)证明见解析;(2)427.【分析】(1)取AC 的中点为O ,连接BO ,PO ,证明PO ⊥AC ,PO ⊥OB ,即证PO ⊥平面ABC ,即证得面面垂直;(2)建立如图空间直角坐标系,写出对应点的坐标和向量AM 的坐标,再计算平面PBC 法向量n,利用所求角的正弦为cos AM ,n即得结果.【解析】(1)证明:如图,取AC 的中点为O ,连接BO ,PO .∵PA =PC ,∴PO ⊥AC .∵PA =PC =6,∠APC =90°,∴PO =12AC =32,同理BO =32.又PB =6,∴PO 2+OB 2=PB 2,∴PO ⊥OB .∵AC ∩OB =O ,AC ,OB ⊂平面ABC ,11∴PO ⊥平面ABC .又PO ⊂平面PAC ,∴平面PAC ⊥平面ABC ;(2)解:如图建立空间直角坐标系,根据边长关系可知,A 32,0,0 ,C -32,0,0 ,B 0,32,0 ,P 0,0,32 ,∴CB =32,32,0 ,CP =32,0,32.∵三棱锥P -ACM 和B -ACM 的体积比为1:2,∴PM :BM =1:2,∴M 0,2,22 ,∴AM =-32,2,22 .设平面PBC 的法向量为n =x ,y ,z ,则32x +32y =032x +32z =0 ,令x =1,得n =1,-1,-1 .设直线AM 与平面PBC 所成角为θ,则sin θ=cos AM ,n =-6227⋅3 =427.∴直线AM 与平面PBC 所成角的正弦值为427.。