气体的等温变化

气体的等温、等容、等压变化一、简要知识点：1、等温变化过程、玻意尔定律；2、气体的等温变化图象、玻意尔定律的微观解释；3、应用玻意尔定律解题的一些特殊方法；4、气体的等容变化、查里定律；5、气体等容变化的图象及其微观解释；6、气体的等压变化、盖.吕萨克定律；7、热力学温标。

二、基本概念：（一）、气体的等温变化、玻意尔定律：1、一定质量的气体在温度不变时，压强随体积的变化而变化，这种变化叫做等温变化。

判断一定质量的气体是否是等温变化，要看它在状态变化过程中温度是否始终保持不变，而不能只看始末状态温度相同。

2、玻意尔定律：（1）内容：一定质量的气体，在温度不变的情况下，它的压强跟体积成反比。

（2）公式：P 1V 1=P 2V 2=恒量 ；（3）适用条件：压强不太大（与大气压相比）温度不太低（与室温相比）。

3、应用玻意尔定律解题的一般步骤：（1）首先确定研究对象，即某一定质量的气体，有时也常假设有一无形袋，从而使变质量气体问题转变为等质量气体的问题。

（2）然后确定始末两个状态的压强与体积，并统一单位（不一定都要用国际单位）。

（3）最后用玻意尔定律列方程求解，必要时还要考虑解答结果是否合理。

4、应用玻意尔定律时的几个注意问题：（1）解题时一定要充分挖掘题意中包含的隐含条件。

（2）常用假设法研究气体的等温变化，一种是假设物理现象（先假设某些量不变，然后利用已知的物理规律进行分析推理，从而肯定或否定所做的假设，得出正确的判断）；另一种是假设物理过程（用一个或多个较简单的变化过程等效替代原来的物理过程）。

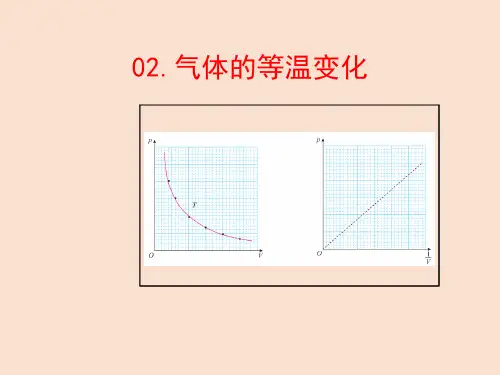
5、气体的等温变化图象：（1）横坐标为体积V ，纵坐标为P ；（2）等温图象的特点：等温线是双曲线，温度越高，其等温线离原点越远。

如图所示：两条曲线分别对应的温度为：T 1<T 2 ；（3）在P －V1图象中为一条过原点的直线，同理T 2>T 1 。

（二）、气体的等容变化、查里定律：1、质量一定的气体，在体积不变的情况下所发生的状态变化过程，压强随着温度的升高而增大、随温度的降低而减小。

气体等温等压变化计算公式在研究气体的性质和行为时，等温等压变化是一个重要的概念。

等温等压变化是指在恒定的温度和压力下，气体所发生的变化。

在这种情况下，气体的体积和其他性质会随着其他因素的改变而发生变化。

为了计算等温等压变化，我们可以使用一些基本的公式。

首先，让我们来看一下理想气体状态方程，它描述了气体的状态与温度、压力和体积之间的关系。

理想气体状态方程可以表示为：PV = nRT。

其中，P是气体的压力，V是气体的体积，n是气体的摩尔数，R是气体常数，T是气体的温度。

根据理想气体状态方程，我们可以推导出气体的等温等压变化计算公式。

首先，让我们来看一下气体的等温变化。

等温变化是指在恒定的温度下，气体的体积和压力发生变化。

根据理想气体状态方程，我们可以得到气体的等温变化计算公式：P1V1 = P2V2。

在这个公式中，P1和V1分别是气体的初始压力和体积，P2和V2分别是气体的最终压力和体积。

这个公式告诉我们，当气体的温度保持不变时，它的压力和体积呈反比关系。

也就是说，当气体的体积增大时，它的压力会减小，反之亦然。

接下来，让我们来看一下气体的等压变化。

等压变化是指在恒定的压力下，气体的体积和温度发生变化。

根据理想气体状态方程，我们可以得到气体的等压变化计算公式：V1/T1 = V2/T2。

在这个公式中，V1和T1分别是气体的初始体积和温度，V2和T2分别是气体的最终体积和温度。

这个公式告诉我们，当气体的压力保持不变时，它的体积和温度呈正比关系。

也就是说，当气体的体积增大时，它的温度也会增大，反之亦然。

通过这两个等温等压变化计算公式，我们可以计算气体在等温等压条件下的体积、压力和温度的变化。

这些计算公式在工程、化学和物理等领域都有广泛的应用。

例如，在工业生产中，我们可以利用这些公式来设计和优化气体的生产过程；在科学研究中，我们可以利用这些公式来研究气体的性质和行为。

总之，气体的等温等压变化是一个重要的概念，它描述了在恒定的温度和压力下，气体的体积和其他性质所发生的变化。

气体的等温变化
气体是一种物质，它们可以在不同温度和压力条件下改变状态及性质，而等温变化就是这样一种变化。

气体在特定温度下改变状态和性质时会受到等温变化的影响。

在热力学理论中，等温变化是指在一定温度下，物质的温度、压力和体积是固定的，这一点在等温变化中也得到了证明。

例如，当一个物质的温度上升时，压力会增加，而体积会减少；当一个物质的温度下降时，压力和体积都会降低。

等温变化对于热力学系统来说是一个重要的概念，因为它可以用来描述物质在温度和压力条件下的变化。

它还可以帮助我们理解复杂的热力学系统，如热压力研究，改变等热力学系统的变化可以通过研究等温变化来实现。

此外，等温变化也可以用来描述气体在特定温度下的变化。

例如，在某温度下，当气体的压力减小时，它的体积也会减小，反之亦然。

因此，当气体进行等温变化时，它的体积和压力都会发生变化，但温度保持不变。

另一方面，等温变化也可以描述气体在特定体积下的变化。

当气体体积变化时，它的温度和压力也会发生变化。

因此，当气体进行等温变化时，它的体积和温度都会发生变化，但压力保持不变。

等温变化还会受到温度的影响。

例如，在高温下，气体的温度和压力都会升高，而体积会降低；在低温下，气体的温度和压力都会降低，而体积会增加。

本文讨论了气体等温变化的概念，以及它如何受到温度的影响。

等温变化可以帮助我们更好地理解热力学系统，并有助于改善气体热力学性质的计算和分析。

除此之外，等温变化也可以帮助我们了解复杂的气体变化，如温度、压力和体积变化。

因此，等温变化是一个重要的概念，它也可以帮助我们更好地理解气体的特性。

第1节气体的等温变化1.一定质量的气体，在温度不变的条件下，其压强与体积变化时的关系，叫做气体的等温变化。

2．玻意耳定律：一定质量的某种气体，在温度不变的情况下，压强p 与体积V 成反比，即pV ＝C 。

3．等温线：在p -V 图像中，用来表示温度不变时，压强和体积关系的图像，它们是一些双曲线。

在p -1V 图像中，等温线是倾斜直线。

一、探究气体等温变化的规律 1．状态参量研究气体性质时，常用气体的温度、体积、压强来描述气体的状态。

2．实验探究二、玻意耳定律1．内容一定质量的某种气体，在温度不变的情况下，压强与体积成反比。

2．公式pV＝C或p1V1＝p2V2。

3．条件气体的质量一定，温度不变。

4．气体等温变化的p -V图像气体的压强p随体积V的变化关系如图8-1-1所示，图线的形状为双曲线，它描述的是温度不变时的p -V关系，称为等温线。

一定质量的气体，不同温度下的等温线是不同的。

图8-1-11．自主思考——判一判(1)一定质量的气体压强跟体积成反比。

(×)(2)一定质量的气体压强跟体积成正比。

(×)(3)一定质量的气体在温度不变时，压强跟体积成反比。

(√)(4)在探究气体压强、体积、温度三个状态参量之间关系时采用控制变量法。

(√)(5)玻意耳定律适用于质量不变、温度变化的气体。

(×)(6)在公式pV＝C中，C是一个与气体无关的参量。

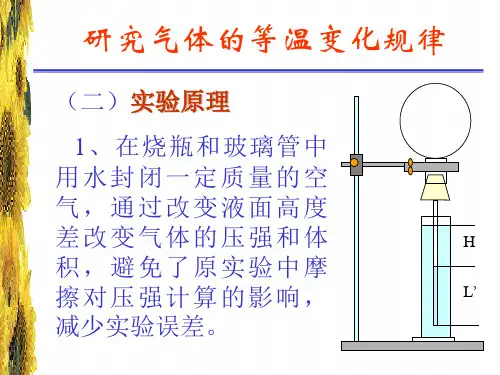
(×)2．合作探究——议一议(1)用注射器对封闭气体进行等温变化的实验时，在改变封闭气体的体积时为什么要缓慢进行？提示：该实验的条件是气体的质量一定，温度不变，体积变化时封闭气体自身的温度会发生变化，为保证温度不变，应给封闭气体以足够的时间进行热交换，以保证气体的温度不变。

(2)玻意耳定律成立的条件是气体的温度不太低、压强不太大，那么为什么在压强很大、温度很低的情况下玻意耳定律就不成立了呢？提示：①在气体的温度不太低、压强不太大时，气体分子之间的距离很大，气体分子之间除碰撞外可以认为无作用力，并且气体分子本身的大小也可以忽略不计，这样由玻意耳定律计算得到的结果与实际的实验结果基本吻合，玻意耳定律成立。

气体的等温变化汇总气体的等温变化。

气体的等温变化是指在恒定的温度下，气体发生的体积、压强和密度的变化。

在等温条件下，气体分子的平均动能保持不变，因此气体的性质会随着压强和体积的变化而发生变化。

本文将对气体的等温变化进行探讨，包括等温膨胀和等温压缩两个方面。

等温膨胀。

等温膨胀是指在恒定温度下，气体的体积发生变化的过程。

根据查理定律，等温条件下，气体的体积与压强成反比，即PV=常数。

当气体的体积增大时，压强会减小，反之亦然。

这个规律可以用来解释气球的膨胀现象。

当气球被吹气时，气球内的气体体积增大，压强减小，从而使得气球膨胀起来。

等温膨胀的过程可以用来做功。

根据气体的做功公式W=PΔV，当气体膨胀时，对外界做正功，而当气体被压缩时，对外界做负功。

因此，等温膨胀可以用来做功，比如汽车引擎的工作过程就是利用气体的等温膨胀来驱动汽车。

等温压缩。

等温压缩是指在恒定温度下，气体的体积减小的过程。

根据查理定律，等温条件下，气体的体积与压强成反比。

因此，当气体的体积减小时，压强会增大。

这个规律可以用来解释液化气的储存和运输。

液化气是将气体通过压缩变成液体的过程，这就是利用等温压缩的原理来实现的。

等温压缩的过程需要对气体做功。

根据气体的做功公式W=PΔV，当气体被压缩时，对外界做负功。

因此，等温压缩需要外界对气体做功，比如液化气罐的充装过程就是需要外界对气体做功，将气体压缩成液体。

气体的等温变化不仅在日常生活中有着重要的应用，而且在工业生产和科学研究中也有着广泛的应用。

通过对气体的等温变化的研究，可以更好地理解和利用气体的性质，为人类的生产和生活带来更多的便利和效益。

总结。

气体的等温变化是指在恒定温度下，气体的体积、压强和密度的变化。

等温膨胀和等温压缩是气体在等温条件下发生的两种变化，它们都遵循查理定律。

气体的等温变化不仅在日常生活中有着重要的应用，而且在工业生产和科学研究中也有着广泛的应用。

通过对气体的等温变化的研究，可以更好地理解和利用气体的性质，为人类的生产和生活带来更多的便利和效益。

气体的等温变化的知识点以气体的等温变化为题，我们来探讨一下这个有趣的话题。

什么是等温变化呢？等温变化是指气体在恒定温度下的变化过程。

在等温变化中，气体的温度保持不变，但其他性质如压强、体积等可能发生变化。

等温变化的一个重要定律是盖吕萨克定律，也被称为玻意耳-马略特定律。

这个定律表明，在等温条件下，气体的压强与体积呈反比关系。

也就是说，当气体体积增大时，压强减小；当气体体积减小时，压强增大。

这个定律在实际应用中非常重要，例如在气体容器的设计和气体压缩等领域。

等温变化还可以用等温线来表示。

等温线是在压强-体积坐标系中表示等温变化的曲线。

根据盖吕萨克定律，等温线是一个反比例函数。

在等温线上，任意两点的体积和压强的乘积是相等的，即PV=常数。

这个常数被称为等温过程的等温系数，它与气体的性质有关。

在等温变化中，气体的分子之间发生的碰撞不会改变分子的平均动能，因此气体的温度保持不变。

这是因为在等温变化中，系统与外界之间有热量的交换，以保持系统温度的恒定。

等温变化的一个重要应用是理想气体状态方程。

根据理想气体状态方程，等温变化中，气体的压强和体积满足以下关系：PV= nRT，其中P是气体的压强，V是气体的体积，n是气体的摩尔数，R是理想气体常量，T是气体的温度。

根据这个方程，我们可以计算出等温变化中气体的压强和体积的变化。

在等温变化中，气体的压强和体积的变化是相互关联的。

当压强增大时，气体的体积减小，反之亦然。

这是因为在等温变化中，气体的温度保持不变，分子的平均动能也不变，而压强和体积的变化是由分子之间的碰撞引起的。

当分子碰撞的频率增加时，压强增大，体积减小；当分子碰撞的频率减小时，压强减小，体积增大。

总结一下，等温变化是指气体在恒定温度下的变化过程。

在等温变化中，气体的温度保持不变，但压强和体积可能发生变化。

等温变化可以用盖吕萨克定律来描述，也可以用等温线来表示。

在等温变化中，气体的压强和体积满足反比关系。

气体的等温变化气体的等温变化是热力学中的一个重要概念，它描述的变化涉及气体的物理性质和物理状态。

根据它的定义，气体的等温变化是指当给定的压强的条件下，气体的温度以恒定的速率变化，而温度变化时，气体体积也随之发生变化。

讨论气体的等温变化必须从热力学的基本原理出发。

根据热力学第一定律，温度在显式加热或者卸载热量的情况下将保持恒定。

热力学第二定律指出，当加热气体时，温度将以恒定的速率升高，当卸载热量时，温度将以恒定的速率下降。

当气体处于恒定的压强时，流体体积会随着温度的变化而变化，而流体的密度会随温度的变化而变化，这就是气体的等温变化。

气体的等温变化表明，当压强恒定时，温度将以恒定速率变化，而体积也将随着温度的变化而变化，而且随着温度变化，流体的密度也将随之变化。

另外，由于气体的热容和温敏性有关，所以气体的密度的变化随着温度的变化而变化。

当气体温度变化时，体积也会随之变化，这正是热力学第四定律的结果。

气体的等温变化受到许多因素的影响，包括气体的特性，温度，压强和物质的特性。

温度对气体的等温变化有重要影响，当气体降温时，气体的体积会减小，而当气体升温时，气体的体积会增大。

温度和压强也会影响气体的等温变化，当压强升高时，气体的等温变化会变得更明显，而当压强降低时，气体的等温变化会降低。

物质的特性也会影响气体的等温变化，不同物质具有不同的热容和温度比热，从而影响等温变化的程度。

气体的等温变化虽然简单，但是它对于理解气体的行为具有重要意义，它不仅可以解释气体在受到热量刺激时温度和体积发生变化的原因，而且还可以帮助我们更好地理解热力学中其它概念，比如热容、热导率和温度比热等。

总之，气体的等温变化是热力学中的一个重要概念，它的概念和原理对于理解气体受到外力刺激时的行为具有重要意义。

另外，气体的等温变化受到许多因素的影响，因此，人们在分析气体的等温变化时应该考虑到这些因素。