学案15：抛物线(一)

抛物线及其标准方程学案知识目标：1. 能从数学实验中抽象出抛物线的模型并总结出抛物线的定义；2. 会利用坐标法推导抛物线的标准方程；3. 能利用数形结合的思想方法准确得出焦点、准线、方程的对应关系。

过程与方法：掌握开口向右的抛物线标准方程的推导过程，进一步理解解析法，培养学生解决数学问题时的观察、分析、计算能力。

情感态度价值观：通过数学抽象、直观想象、数学运算逐渐形成数学核心素养。

重点：抛物线的定义及标准方程。

难点：从抛物线的画法中抽象概括出抛物线的定义一、创设情景，引入新课在初中我们已经从函数的角度学习了抛物线，日常生活中也有美丽的抛物线的实例，然后抛出问题，以问题为引领开始教学。

二、新课探究探究一：抛物线定义实验一：学生动手操作实验实验二：学生观察画抛物线的过程（反复演示后），请学生归纳抛物线的定义，并思考抛物线有怎样的几何特征，教师总结。

探究二：求抛物线的标准方程1．学生思考讨论建系的各种形式。

2．学生根据定义求抛物线的标准方程。

3．学生讨论得出抛物线四种形式，完成下表。

1三、例题讲解例1、（1）已知抛物线的标准方程是xy2=6，求它的焦点坐标和准线方程；（2）已知抛物线的方程是y =-x26,求它的焦点坐标和准线方程（3）已知抛物线的焦点坐标是F（0，-2），求它的标准方程四、小结1.抛物线的定义。

2.抛物线的标准方程。

五、目标测试、1、根据下列条件，写出抛物线的标准方程：（1）焦点是F（3，0）；（2）准线方程是x=14 -；（3）焦点到准线的距离是2。

2、求下列抛物线的焦点坐标和焦点坐标：（1）y2 = 20x （2）x2=12y2 2六、作业2。

抛物线及其标准方程一、教材分析新课程标准要求1．了解圆锥曲线的实际背景，感受圆锥曲线在刻画现实世界和解决实际问题中的作用。

2．经历从具体情境中抽象出椭圆、抛物线模型的过程，掌握它们的定义、标准方程、几何图形及简单性质。

3．能用坐标法解决一些与圆锥曲线有关的简单几何问题（直线与圆锥曲线的位置关系）和实际问题。

4．通过圆锥曲线的学习，进一步体会数形结合的思想。

二、教学目标1．知识与技能：理解抛物线定义；掌握抛物线图形及其方程；会运用抛物线性质解决问题；2．过程与方法：通过思维导图让学生对抛物线的基本知识形成知识框架；通过典型例题剖析总结出通性通法。

3．情态与价值：通过本节课的学习，体会数学数形结合的思想、方程思想及分类讨论思想。

【教学重点】抛物线定义及其方程；抛物线性质的综合应用。

【教学难点】抛物线性质的综合应用；三、教学方法这一节与椭圆、双曲线几何性质的知识结构相似，研究方法为学生所熟悉，这使学生的自主探究活动具备良好的基础。

但是学生思维的全面性、深刻性，以及数形结合思想有待进一步培养加强。

基于以上分析，本节课我采用启发探究式的教学方法，以问题的提出、问题的解决为主线，充分体现以学生为主体的教学理念。

为了展现丰富生动的教学内容，我利用多媒体技术进行辅助教学。

四、教学过程通过历年抛物线在高考全国卷的比对，让学生把握抛物线的考察重点及其方向。

【师生活动】引导学生回顾抛物线的定义。

一、抛物线的定义课堂探究一：抛物线的定义【例1】 若抛物线y 2＝2x 的焦点是F ，点P 是抛物线上的动点，又有点A (3，2)，则|P A |＋|PF |取最小值时点P 的坐标为________.解析：将x ＝3代入抛物线方程 y 2＝2x ，得y ＝± 6.∵6>2，∴A 在抛物线内部，如图.设抛物线上点P 到准线l ：x ＝－12的距离为d ，由定义知|P A |＋|PF |＝|P A |＋d ，当P A ⊥l 时，|P A |＋d 最小，最小值为72，此时P 点纵坐标为2，代入y 2＝2x ，得x ＝2，∴点P 的坐标为(2，2).【共同归纳】应用抛物线定义的两个关键点(1)由抛物线定义，把抛物线上点到焦点距离与到准线距离相互转化.(2)注意灵活运用抛物线M上一点P (x 0，y 0)到焦点F 的距离|PF |＝|x 0|＋p 2或|PF |＝|y 0|＋p2. 通过题组分析总结出最值的规律方法。

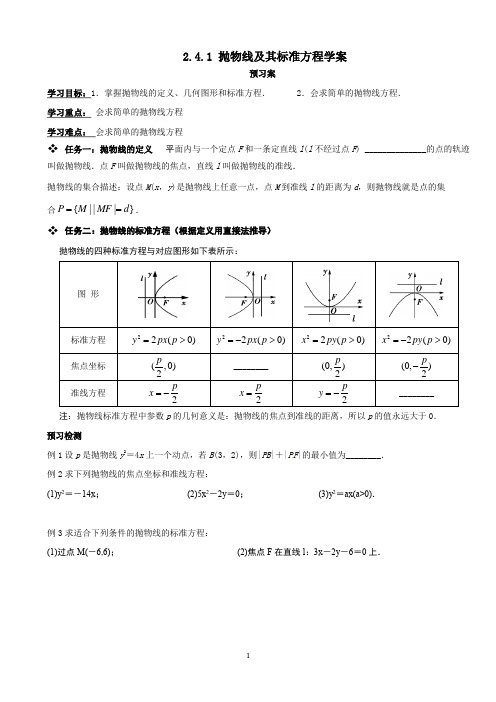
2.4.1 抛物线及其标准方程学案预习案 学习目标：1．掌握抛物线的定义、几何图形和标准方程． 2．会求简单的抛物线方程． 学习重点： 会求简单的抛物线方程学习难点： 会求简单的抛物线方程❖ 任务一：抛物线的定义 平面内与一个定点F 和一条定直线l (l 不经过点F ) ______________的点的轨迹 叫做抛物线．点F 叫做抛物线的焦点，直线l 叫做抛物线的准线．抛物线的集合描述：设点M (x ，y )是抛物线上任意一点，点M 到准线l 的距离为d ，则抛物线就是点的集合|{}||P M MF d ==．❖ 任务二：抛物线的标准方程（根据定义用直接法推导）抛物线的四种标准方程与对应图形如下表所示： 图 形标准方程22(0)y px p => 22(0)y px p =-> 22(0)x py p => 22(0)x py p =-> 焦点坐标(,0)2p ________ (0,)2p (0,)2p - 准线方程 2p x =- 2p x = 2p y =- ________注：抛物线标准方程中参数p 的几何意义是：抛物线的焦点到准线的距离，所以p 的值永远大于0． 预习检测例1设p 是抛物线y 2＝4x 上一个动点，若B (3，2)，则|PB |＋|PF |的最小值为________．例2求下列抛物线的焦点坐标和准线方程：(1)y 2＝－14x ； (2)5x 2－2y ＝0； (3)y 2＝ax(a>0)．例3求适合下列条件的抛物线的标准方程：(1)过点M(－6,6)； (2)焦点F 在直线l ：3x －2y －6＝0上．巩固练习一、选择题1．准线与x 轴垂直，且经过点(1，－2)的抛物线的标准方程是 ( )A ．y 2＝－2xB ．y 2＝2xC ．x 2＝2yD ．x 2＝－2y2．已知抛物线的顶点在原点，对称轴为x 轴，焦点在双曲线x 24－y 22＝1上，则抛物线的方程为( ) A ．y 2＝8x B ．y 2＝4x C ．y 2＝2x D ．y 2＝±8x3．设抛物线y 2＝8x 上一点P 到y 轴的距离是4，则点P 到该抛物线焦点的距离是 ( )A ．4B ．6C ．8D ．124．已知点A (－2,3)在抛物线C ：y 2＝2px 的准线上，记C 的焦点为F ，则直线AF 的斜率为 ( )A ．－43B ．－1C ．－34D ．－12二、填空题5．抛物线y ＝2x 2的准线方程为________．6．抛物线y ＝－14x 2上的动点M 到两定点F (0，－1)，E (1，－3)的距离之和的最小值为________． 7．抛物线y 2＝2x 上的两点A ，B 到焦点的距离之和是5，则线段AB 的中点到y 轴的距离是________．8．在抛物线y 2＝－12x 上，与焦点的距离等于9的点的坐标是________．三、解答题9．如图2­4­4，已知抛物线y 2＝2px (p >0)的焦点为F ，A 是抛物线上横坐标为4，且位于x 轴上方的点，点A 到抛物线准线的距离等于5，过点A 作AB 垂直于y 轴，垂足为点B ，OB 的中点为M .(1)求抛物线的方程； (2)过点M 作MN ⊥F A ，垂足为N ，求点N 的坐标.。

第7节 抛物线考试要求 1.了解抛物线的实际背景，了解抛物线在刻画现实世界和解决实际问题中的作用；2.掌握抛物线的定义、几何图形、标准方程及简单几何性质. 知识梳理 1.抛物线的定义(1)平面内与一个定点F 和一条定直线l (F ∉l )的距离相等的点的轨迹叫做抛物线.点F 叫做抛物线的焦点，直线l 叫做抛物线的 .(2)其数学表达式：{M ||MF |＝d }(d 为点M 到准线l 的距离). 2.抛物线的标准方程与几何性质图形标准方程y 2＝2px(p >0)y 2＝－2px(p >0)x 2＝2py(p >0)x 2＝－2py(p >0)p 的几何意义：焦点F 到准线l 的距离性质顶点对称轴焦点离心率准线方程 y ＝p2 范围 开口方向向左3.设AB 是过抛物线y 2＝2px (p >0)焦点F 的弦，若A (x 1，y 1)，B (x 2，y 2)，则 (1)x 1·x 2＝p 24.(2)y 1·y 2＝－p 2.(3)|AB |＝x 1＋x 2＋p ＝2psin 2α(α是直线AB 的倾斜角).(4)1|AF |＋1|BF |＝2p 为定值(F 是抛物线的焦点). 自主检测1.顶点在原点，且过点P (－2，3)的抛物线的标准方程是________________.2. 抛物线y 2＝8x 上到其焦点F 距离为5的点的个数为________.3.若抛物线y 2＝2px (p >0)的焦点是椭圆x 23p ＋y 2p＝1的一个焦点，则p ＝( ) A.2 B.3 C.4 D.84.已知F 是抛物线y 2＝x 的焦点，A ，B 是抛物线上的两点，且|AF |＋|BF |＝3，则线段AB 的中点到y 轴的距离为( )A.34B.1C.54D.745.已知抛物线方程为y 2＝8x ，若过点Q (－2，0)的直线l 与抛物线有公共点，则直线l 的斜率的取值范围是________. 典型例题考点一 抛物线的定义、标准方程及其性质【例1】 (1)已知抛物线C 与双曲线x 2－y 2＝1有相同的焦点，且顶点在原点，则抛物线C 的方程是( ) A.y 2＝±22x B.y 2＝±2x C.y 2＝±4x D.y 2＝±42x(2)设抛物线y 2＝4x 的焦点为F ，准线为l ，P 为该抛物线上一点，P A ⊥l ，A 为垂足，若直线AF 的斜率为－3，则△P AF 的面积为( ) A.2 3 B.4 3 C.8 D.8 3(3)动圆过点(1，0)，且与直线x ＝－1相切，则动圆的圆心的轨迹方程为__________.【训练1】 (1)设抛物线y 2＝2px 的焦点在直线2x ＋3y －8＝0上，则该抛物线的准线方程为( ) A.x ＝－4 B.x ＝－3 C.x ＝－2 D.x ＝－1(2)已知抛物线x 2＝2py (p ＞0)的焦点为F ，准线为l ，点P (4，y 0)在抛物线上，K 为l 与y 轴的交点，且|PK |＝2|PF |，则y 0＝________.考点二 与抛物线有关的最值问题 角度1 到焦点与定点距离之和(差)最值问题【例2－1】 点P 为抛物线y 2＝4x 上的动点，点A (2，1)为平面内定点，F 为抛物线焦点，则： (1)|P A |＋|PF |的最小值为________；(2)(多填题)|P A |－|PF |的最小值为________，最大值为________. 角度2 到点与准线的距离之和最值问题【例2－2】 设P 是抛物线y 2＝4x 上的一个动点，则点P 到点A (－1，1)的距离与点P 到直线x ＝－1的距离之和的最小值为________.角度3 动弦中点到坐标轴距离最短问题【例2－3】 已知抛物线x 2＝4y 上有一条长为6的动弦AB ，则AB 的中点到x 轴的最短距离为( ) A.34 B.32 C.1 D.2角度4 焦点弦中距离之和最小问题【例2－4】 已知抛物线y 2＝4x ，过焦点F 的直线与抛物线交于A ，B 两点，过A ，B 分别作y 轴的垂线，垂足分别为C ，D ，则|AC |＋|BD |的最小值为________.角度5 到定直线的距离最小问题【例2－5】 抛物线y ＝－x 2上的点到直线4x ＋3y －8＝0距离的最小值是________.【训练2】 (1)若在抛物线y 2＝－4x 上存在一点P ，使其到焦点F 的距离与到A (－2，1)的距离之和最小，则该点的坐标为( ) A.⎝⎛⎭⎫－14，1 B.⎝⎛⎭⎫14，1 C.(－2，－22) D.(－2，22)(2)已知P 为抛物线y 2＝4x 上一个动点，Q 为圆C ：x 2＋(y －4)2＝1上一个动点，那么点P 到点Q 的距离与点P 到抛物线准线的距离之和的最小值是________. 考点三 直线与抛物线的综合问题【例3】 已知抛物线C ：y 2＝3x 的焦点为F ，斜率为32的直线l 与C 的交点为A ，B ，与x 轴的交点为P .(1)若|AF |＋|BF |＝4，求直线l 的方程； (2)若AP →＝3PB →，求|AB |.【训练3】 如图所示，抛物线关于x 轴对称，它的顶点在坐标原点，点P (1，2)，A (x 1，y 1)，B (x 2，y 2)均在抛物线上.(1)写出该抛物线的方程及其准线方程；(2)当P A 与PB 的斜率存在且倾斜角互补时，求y 1＋y 2的值及直线AB 的斜率.当堂检测1.已知抛物线y 2＝2px (p ＞0)，点C (－4，0)，过抛物线的焦点作垂直于x 轴的直线，与抛物线交于A ，B 两点，若△CAB 的面积为24，则以直线AB 为准线的抛物线的标准方程是( ) A.y 2＝4x B.y 2＝－4x C.y 2＝8x D.y 2＝－8x2.设抛物线C ：y 2＝3x 的焦点为F ，点A 为C 上一点，若|F A |＝3，则直线F A 的倾斜角为( ) A.π3 B.π4 C.π3或2π3 D.π4或3π43.设F 为抛物线y 2＝2x 的焦点，A ，B ，C 为抛物线上三点，若F 为△ABC 的重心，则|F A →|＋|FB →|＋|FC →|的值为________.4.已知双曲线C 1：x 2a 2－y 2b 2＝1(a >0，b >0)的离心率为2.若抛物线C 2：x 2＝2py (p >0)的焦点到双曲线C 1的渐近线的距离为2，则抛物线C 2的方程为________.5.已知P 为抛物线C ：y ＝x 2上一动点，直线l ：y ＝2x －4与x 轴、 y 轴交于M ，N 两点，点A (2，－4)且AP →＝λAM →＋μAN →，则λ＋μ的最小值为________.6.设A ，B 为曲线C ：y ＝x 24上两点，A 与B 的横坐标之和为4.(1)求直线AB 的斜率；(2)设M 为曲线C 上一点，C 在M 处的切线与直线AB 平行，且AM ⊥BM ，求直线AB 的方程.7.已知过抛物线y 2＝2px (p >0)的焦点，斜率为22的直线交抛物线于A (x 1，y 1)，B (x 2，y 2)(x 1<x 2)两点，且|AB |＝9.(1)求该抛物线的方程；(2)O 为坐标原点，C 为抛物线上一点，若OC →＝OA →＋λOB →，求λ的值.。

2.3.2抛物线的简单几何性质（第一课时）(人教A版普通高中教科书数学选择性必修第一册第三章)一、教学目标1.掌握抛物线的简单几何性质：范围、对称性、顶点、离心率；2.能根据抛物线的几何性质对抛物线方程进行讨论；3.对通径、焦半径公式进行初步探索；4.进一步理解数形结合的思想方法在解析几何中的应用。

二、教学重难点1.教学重点：抛物线的简单几何性质、利用抛物线的几何性质求方程、对通径与焦半径公式的初步探究。

2.教学难点：利用数形结合法对通径、焦半径公式的探究。

三、教学过程1.利用数形结合的思想探究抛物线的简单几何性质1.1 知识回顾，温故知新【学生活动】学生完成学案内容，对抛物线的四种方程、图形、焦点坐标、准线方程进行复习。

【设计意图】之前学过椭圆、双曲线的几何性质，都是通过图形和方程两方面进行研究的，因此引导学生对抛物线的四种方程、图形、焦点坐标、准线方程进行复习，有利于对抛物线性质的进一步探索。

1.2 数形结合，类比探究问题1：类比用标准方程研究椭圆、双曲线几何性质的过程与方法，请思考：我们要研究抛物线的哪些几何性质？如何研究这些性质？【预设答案】前面我们学习了椭圆、双曲线的范围、对称性、顶点、离心率，在双曲线中还学习了渐近线。

我们是通过“数”和“形”两方面对椭圆、双曲线的几何性质进行探究的。

【设计意图】类比椭圆、双曲线几何性质的研究思路，为接下来用数形结合法研究抛物线的几何性质进行铺垫。

问题2：观察图形，你能发现抛物线横、纵坐标的取值范围吗？【预设答案】通过观察图形，学生很容易得到开口向右的抛物线中横、纵坐标的取值范围，即为问题3：从数的角度，也就是从抛物线方程的角度，怎样得到抛物线中横纵坐标的取值范围呢？【预设答案】在方程中，并无限制，因此。

而因为，且，所以。

【设计意图】让学生从“数”和“形”两个角度探索抛物线的范围。

问题4：观察图形，抛物线有几条对称轴？是否有对称中心？【预设答案】学生观察图形容易得到开口向右的抛物线关于轴对称，没有对称中心。

《抛物线及其标准方程（第一课时）》教学实录师：（投影幻灯片1）这是我自创的一首散文诗：《你们最重要》。

（教师深情朗诵）没有校领导与老师们的指导，数学学习如同没有阳光的冬日，谢谢你们对本班的厚爱；生：（学生用掌声感谢来听课的领导和老师）师：没有经验老道依然年轻的我，数学学习如同腰折的泰坦尼克号；没有本班全体同学一颗颗渴望的求知心，数学学习迎来的将是无奈与孤寂，美丽的梦会灰飞烟没，你们最重要。

哦，全靠你们了！先让我们穿越时空隧道，来到初中。

（投影幻灯片2）在初中,我们知道二次函数y=ax2(a>0)的图像是一条抛物线。

当a>0时，抛物线开口向什么方向？生：开口向上。

师：当a＜0时，抛物线开口向什么方向？生：开口向下。

师：而且我们还知道抛物线的顶点、对称轴等等，但你知道抛物线的准确定义？师：（投影幻灯片3）我们一起来探究。

请看题。

（教师读题，学生看题）师：（打开几何画板演示动点M的轨迹，学生观察几何画板演示）拖动点H，点M随之运动。

点M的轨迹是这条红色的曲线，它是一条什么曲线？生：它是一条抛物线。

师：在点M运动的整个过程中，点M始终位于线段FH的垂直平分线上，我们知道：线段平分线上的点到线段两端点的距离相等。

所以，点M满足的几何条件是什么？生：线段|MF|=|MH|。

师：很好，全班同学都观察得很仔细。

（再投影幻灯片3）对，用我们的文字语言来表述：动点M到定点F的距离=动点M到定直线L的距离。

满足这个几何条件的点的轨迹就是抛物线。

从这，我们可知抛物线的定义。

师：（投影幻灯片4展示抛物线的定义）请大家边读边理解定义。

师：根据定义可知，定点是焦点，动点是抛物线上一点，所以抛物线上任一点满足的几何条件是什么？生：动点M到焦点F的距离=动点M到准线L的距离。

师：我们知道了抛物线的定义，那它的方程呢？这是我们这节课要研究的重要问题。

师：（投影幻灯片5和6，师引导学生看学习目标、重点、难点）师：先轻松一下，看看生活中的抛物线的魅力。

《抛物线及其标准方程》教案《抛物线及其标准方程》教案教案是教师为顺利而有效地开展教学活动，根据课程标准，教学大纲和教科书要求及学生的实际情况，以课时或课题为单位，对教学内容、教学步骤、教学方法等进行的具体设计和安排的一种实用性教学文书。

下面是小编整理的《抛物线及其标准方程》教案，欢迎大家分享。

《抛物线及其标准方程》教案篇1一、目标1.掌握抛物线的定义、几何图形,会推导抛物线的标准方程2.能够利用给定条件求抛物线的标准方程3.通过“观察”、“思考”、“探究”与“合作交流”等一系列数学活动，培养学生观察、类比、分析、概括的能力以及逻辑思维的能力，使学生学会数学思考与推理，学会反思与感悟，形成良好的数学观。

并进一步感受坐标法及数形结合的思想二、重点抛物线的定义及标准方程三、教学难点抛物线定义的形成过程及抛物线标准方程的推导（关键是坐标系方案的选择）四、教学过程（一）复习旧知在初中，我们学习过了二次函数，知道二次函数的图象是一条抛物线。

例如：（1），（2）的图象（展示两个函数图象）：（二）讲授新课1.课题引入在实际生活中，我们也有许多的抛物线模型，例如1965年竣工的密西西比河河畔的萨尔南拱门,它就是用不锈钢铸成的抛物线形的建筑物。

到底什么样的曲线才可以称做是抛物线？它具有怎样的几何特征？它的方程是什么呢？这就是我们今天要研究的内容.（板书：课题2.4.1抛物线及其标准方程）2.抛物线的定义信息技术应用（课堂中展示画图过程）先看一个实验：如图：点F是定点，是不经过点F的定直线，H是上任意一点，过点H作，线段FH的垂直平分线交MH于点M。

拖动点H，观察点M的轨迹，你能发现点M满足的几何条件吗？（学生观察画图过程，并讨论）可以发现，点M随着H运动的过程中，始终有MH=MF,即点M 与定点F和定直线的距离相等。

（也可以用几何画板度量MH，MF的值）（定义引入）：我们把平面内与一个定点F和一条定直线（不经过点F）距离相等的点的轨迹叫做抛物线，点F叫做抛物线的焦点，直线叫做抛物线的准线。

数学教案模板高中抛物线
教学目标：学生能够了解抛物线的定义、性质和应用，掌握抛物线的标准方程和一般方程，能够解决相关的计算题目。

教学重点：抛物线的定义、性质及应用。

教学难点：抛物线的一般方程及相关计算题目的解决。

教学准备：教师准备PPT、黑板、彩色粉笔、教材等。

教学过程：
一、导入
请学生回顾圆的性质，并提问什么是抛物线？抛物线有哪些性质？
二、讲解
1. 抛物线的定义：横坐标和纵坐标的平方成正比。

2. 抛物线的性质：焦点、准线、对称轴、顶点等。

3. 抛物线的标准方程和一般方程。

三、练习
1. 计算抛物线的焦点和准线。

2. 给出抛物线上一点的坐标，求该点到焦点的距离。

四、拓展
1. 抛物线与直线的交点求解。

2. 抛物线的应用：如抛物线天花板的设计、射击运动等。

五、总结
让学生总结抛物线的性质和方程，并强化知识点。

六、作业
1. 完成教材上相关练习题。

2. 仿照课堂上的例题，设计自己的抛物线计算题目。

教学反思：本节课内容涵盖抛物线的定义、性质、方程以及应用，教师应注重学生的实际运用能力和分析问题的能力，通过讲解、训练和练习，帮助学生掌握相关知识。