2011学年度闸北区第二学期高二数学学科期中练习卷及答案

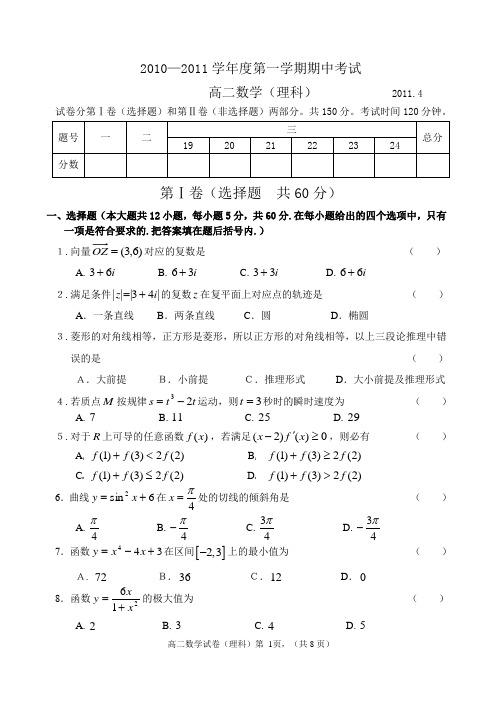
2010—2011学年度第一学期期中考试高二数学（理科） 2011.4试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分。

共150分。

考试时间120分钟。

第Ⅰ卷（选择题 共60分）一、选择题（本大题共12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合要求的.把答案填在题后括号内.） １.向量)6,3(=对应的复数是 （ ）A .i 63+B .i 36+C .i 33+D .i 66+ ２.满足条件||||z i =+34的复数z 在复平面上对应点的轨迹是 （ ）A ．一条直线B ．两条直线C ．圆D ．椭圆３.菱形的对角线相等，正方形是菱形，所以正方形的对角线相等，以上三段论推理中错误的是 （ ） Ａ．大前提 Ｂ．小前提Ｃ．推理形式D ．大小前提及推理形式４.若质点M 按规律t t s 23-=运动，则3=t 秒时的瞬时速度为 （ ）A .7B .11C .25D .29５.对于R 上可导的任意函数)(x f ，若满足0)()2(≥'-x f x ，则必有 （ ）A )2(2)3()1(f f f <+B )2(2)3()1(f f f ≥+C )2(2)3()1(f f f ≤+D )2(2)3()1(f f f >+6．曲线6sin 2+=x y 在4π=x 处的切线的倾斜角是 （ ）A .4πB .4π-C .43πD .43π-7．函数344+-=x x y 在区间[]2,3-上的最小值为 （ ）Ａ. 72 Ｂ．36 Ｃ．12 D ．08．函数216x xy +=的极大值为 （ ） A .2B .3C .4D .59．曲线x y 4=和x x y 232-=所围成图形的面积 （ ）A ．2B ．4C ．6D ．810．定义在R 上的函数)(x f 满足：)2()2(x f x f -=+,若方程0)(=x f 有且只有三个不等实根，且0是其中之一，则方程的另外两个根必是 （ ） A .2-，2 B . 1-，4 C .1，1- D . 2，4 11．已知整数按如下规律排成一列：)1,1(、)2,1(、)1,2(、)3,1(、)2,2(、)1,3(、)4,1(、)3,2(、)2,3(、)1,4(、……则第60个数对是 （ ） Ａ．)1,10( Ｂ．)10,2( Ｃ．)7,5( Ｄ．)5,7(12．设函数xx x f )21(log )(21-=，xx x f 21(log )(212-=的零点分别为21,x x ，则（ ）Ａ．1021<<x x Ｂ．121=x x Ｃ．2121<<x x Ｄ．221≥x x第Ⅱ卷（非选择题 共90分）二、填空题（本大题共6小题，每小题5分，共30分．把答案填在题中横线上．）13．设C z ∈，且i z i 34)21(+=+（i 为虚数单位），则_______=z ，=||z . 14. 用反证法证明命题“如果b a >，那么33b a >” 时，应假设 . 15.函数x x y ln -=的单调减区间为 .16.曲线xy e =在点2(2)e ，处的切线与坐标轴所围三角形的面积为 . 17.若三角形内切圆半径是r ，三边长为,,,c b a 则有三角形面积r c b a S )(21++=.根据类比思想，若四面体内切球半径是R ，四面体四个面的面积是,,,,4321S S S S 则四面体的体积=V .18．已知函数cx bx x x f ++=23)(的图象如图所示，则=+2221x x .三、解答题（本大题共6小题，共60分．解答应写出文字说明，演算步骤或证明过程.） 19．（本题9分）已知复数)1(216)2(2i imm i z ----+=. （Ⅰ）当实数m 取什么值时，复数z 是:①实数； ②虚数；③纯虚数； （Ⅱ）在复平面内，若复数z 所对应的点在第二象限，求m 的取值范围. 解：20．（本题9分）（Ⅰ）已知0>a 0,0>>c b ,求证:abc b a c c a b c b a 6)()()(222222≥+++++. 证明：（Ⅱ）已知3≥a ，求证：321---<--a a a a .证明：21. （本题9分）已知数列}{n a 满足nn a a a a -==+21,11.（Ⅰ）依次计算5432,,,a a a a ；（Ⅱ）猜想n a 的表达式，并用数学归纳法进行证明. 解：22．（本题9分）将直径为d 的圆木锯成长方体横梁，横截面为 矩形，横梁的强度同它的断面高的平方与宽x 的积成 正比（强度系数为k ，0 k ）．要将直径为d 的圆木锯 成强度最大的横梁，断面的宽x 应是多少？ 解：dx横梁断面图已知函数,)(2ax e x x f =其中e a ,0≥为自然对数的底数.(Ⅰ)讨论函数)(x f 的单调性；(Ⅱ)求函数)(x f 在区间]0,1[-上的最大值. 解：已知三次函数),,()(23R c b a cx bx ax x f ∈++=.（Ⅰ）若函数)(x f 过点)2,1(-且在点))1(,1(f 处的切线方程为02=+y ，求函数)(x f的解析式；（Ⅱ）在（Ⅰ）的条件下，若]2,3[,21-∈∀x x ，都有t x f x f ≤-|)()(|21，求实数t 的最小值；（Ⅲ）当11≤≤-x 时，1|)(|≤'x f ，试求a 的最大值，并求a 取得最大值时)(x f 的表达式. 解：2010—2011学年度第二学期期中考试参考答案 高二数学（理科） 2011.4一、选择题（本大题共12小题，每小题6分，共60分.）二、填空题（本大题共6小题，每小题5分，共30分．）13.i +2，5 14.33b a ≤ 15.)1,0( 16.221e17.)(314221S S S S R V +++= 18．38三、解答题（本大题共6小题，共60分．）19．（本题9分）已知复数)1(216)2(2i imm i z ----+=. （Ⅰ）当实数m 取什么值时，复数z 是:①实数； ②虚数；③纯虚数； （Ⅱ）在复平面内，若复数z 所对应的点在第二象限，求m 的取值范围. 解：（Ⅰ）)1(2)1(3)2(2i i m i z --+-+=i m m m m )23()232(22+-+--=. …………………………………1分①当0232=+-m m 时，即1=m 或2=m 时，复数z 为实数. …………2分②当0232≠+-m m 时，即1≠m 且2≠m 时，复数z 为虚数. …………3分③当⎪⎩⎪⎨⎧≠+-=--023023222m m m m 时，解得⎪⎩⎪⎨⎧≠≠=-=21221m m m m 且或， 即21-=m 时，复数z 为纯虚数. …………………………………………5分 （Ⅱ）若复数z 所对应的点在第二象限，则⎪⎩⎪⎨⎧>+-<--023023222m m m m . …………7分解得⎪⎩⎪⎨⎧><<<-21221m m m 或，所以121<<-m .所以， m 的取值范围)1,21(-. …9分20．（本题9分）（Ⅰ）已知0>a 0,0>>c b ,求证:abc b a c c a b c b a 6)()()(222222≥+++++ 证明：因为0,222>≥+a bc c b ， …………………………………………1分 所以abc c b a 2)(22≥+. …………………………………………2分同理abc c a b 2)(22≥+.abc b a c 2)(22≥+. …………………………………………………3分所以abc b a c c a b c b a 6)()()(222222≥+++++. ……………………4分（Ⅱ）已知3≥a ，求证：321---<--a a a a证明：要证321---<--a a a a ，只需证明213-+-<-+a a a a ， ……………………5分两边平方得212323232-⋅-+-<-⋅+-a a a a a a ，……6分 只需证明213-⋅-<-⋅a a a a ， …………………………7分两边平方得23322+-<-a a a a ，…………………………………8分 即20<，所以原不等式成立 ……………………………………9分 21. （本题9分）已知数列}{n a 满足nn a a a a -==+21,11.（Ⅰ）依次计算5432,,,a a a a ；（Ⅱ）猜想n a 的表达式，并用数学归纳法进行证明解：（Ⅰ）因为n n a a -=+211， 所以a a -=212， a a a 2323--=，aa a 34234--=， ………………3分 （Ⅱ）猜想：an n a n n a n )1()2()1(-----=. ……………………………5分 证明：①当1=n 时， a a =1显然成立.， ………………………………6分②假设k n =时，a k k a k k a k )1()2()1(-----=，……………………………7分 当1+=k n 时，ak k a k k a a k k )1()2()1(21211------=-=+ ])2()1[(])1([2)1(a k k a k k a k k --------= kak a k k -+--=)1()1(.…………8分 故当1+=k n 时，结论成立.由①、②可知，对N n ∈，都有a n n a n n a n )1()2()1(-----=成立. . …………19分 22．（本题9分）将直径为d 的圆木锯成长方体横梁，横截面为矩形，横梁的强度同它的断面高的平方与宽x 的积成正比（强度系数为k ，0>k ）．要将直径为d 的圆木锯成强度最大的横梁，断面的宽x 应是多少？解：设断面高为h ，则222x d h -=．横梁的强度函数2)(xh k x f ⋅=， d x 横梁断面图所以)()(22x d x k x f -⋅= ，d x <<0． ……………………………3分 所以)3()(22x d k x f -⋅='．令0)(='x f 解得d x 33±=（舍负）． ……5分 当d x 330<<时，0)(>'x f ；当d x d <<33时，0)(<'x f ． ……6分 因此，函数)(x f 在定义域),0(d 内只有一个极大值点d x 33=．………………7分 所以)(x f 在d x 33=处取最大值，就是横梁强度的最大值． ……………8分 即当断面的宽为d 33时，横梁的强度最大． ……………………9分 23．（本题10分）已知函数,)(2ax e x x f =其中e a ,0≥为自然对数的底数．(Ⅰ)讨论函数)(x f 的单调性；(Ⅱ)求函数)(x f 在区间]0,1[-上的最大值．解：(Ⅰ).)2()(ax e ax x x f +=' ……………………………………………………1分 ①当0=a 时，令)(x f '=0, 得0=x ．若0>x 则0)(>'x f ,从而)(x f 在),0(+∞上单调递增；若0<x 则0)(<'x f ,从而)(x f 在)0,(-∞上单调递减． ………………3分 ②当0>a 时,令0)(='x f ,得0)2(=+ax x ,故0=x 或a x 2-=． ………4分 若a x 2-<,则0)(>'x f ，从而)(x f 在)2,(a --∞上单调递增； ………5分 若,02<<-x a 则0)(<'x f ，.从而)(x f 在)0,2(a -)上单调递减；……6分若0>x ， 则0)(>'x f ，从而)(x f ),0(+∞上单调递增． ……………7分 (Ⅱ)①当0=a 时, )(x f 在区间]0,1[-上的最大值是1)1(=-f . …………8分 ②当20<<a 时, )(x f 在区间]0,1[-上的最大值是a e f -=-)1(.………9分 ③当2≥a 时, )(x f 在区间]0,1[-上的最大值是224)2(e a a f =-．………10分 24．（本题14分）已知三次函数),,()(23R c b a cx bx ax x f ∈++=．（Ⅰ）若函数)(x f 过点)2,1(-且在点))1(,1(f 处的切线方程为02=+y ，求函数)(x f的解析式；（Ⅱ）在（Ⅰ）的条件下，若]2,3[,21-∈∀x x ，都有t x f x f ≤-|)()(|21，求实数t 的最小值；（Ⅲ）当11≤≤-x 时，1|)(|≤'x f ，试求a 的最大值，并求a 取得最大值时)(x f 的表达式.解：（Ⅰ）∵函数)(x f 过点)2,1(-，∴2)1(=-+-=-c b a f ， ①……………1分又c bx ax x f ++='23)(2，函数)(x f 点))1(,1(f 处的切线方程为02=+y ， ∴⎩⎨⎧='-=0)1(2)1(f f ，即⎩⎨⎧=++-=++0232c b a c b a ， ②……………3分 由①和②解得3,0,1-===c b a ，故 x x x f 3)(3-=． ……………4分 （Ⅱ）由（Ⅰ）33)(2-='x x f ，令0)(='x f ，解得1±=x ， ……………5分 ∵2)2(,2)1(,2)1(,18)3(=-==--=-f f f f ， …………………………6分 ∴在区间[]3,2-上max ()2f x =，min ()18f x =-， …………………………7分 ∴对]2,3[,21-∈∀x x ，都有20|)()(|21≤-x f x f ，∴20≥t ，从而t 的最小值为20． ………………………………………8分（Ⅲ）∵c bx ax x f ++='23)(2，则 ⎪⎩⎪⎨⎧++='+-=-'='c b a f c b a f c f 23)1(23)1()0(，可得)0(2)1()1(6f f f a '-'+-'=．……………10分 ∵当11≤≤-x 时，1|)(|≤'x f ，∴1|)1(|≤-'f ，1|)0(|≤'f ，1|)1(|≤'f ． ∴4|)0(|2|)1(||)1(||)0(2)1()1(|||6≤'+'+-'≤'-'+-'=f f f f f f a ． ∴32≤a ，故a 的最大值为32． …………………………………………………12分 当32=a 时，⎪⎩⎪⎨⎧=++='=+-=-'=='1|22||)1(|1|22||)1(|1|||)0(|c b f c b f c f ，解得1,0-==c b ．∴a 取得最大值时x x x f -=332)(． …………………………………………14分。

高二年级第二学期期中考试数学参考答案1．22．3503．164．55．53 6．10.5亿元7．8．（2）9．8-10．(1)2m m + 11．解：（1）A={3，4，5，6，7}，B={4，5，6，7，8}，A ∪B={3，4，5，6，7，8}…3分 （2）C 63=20（个） ……6分 （3）A 中取3有C 31A 53种 ；A 中不取3，有A 54种∴共有C 31A 53+A 54=300（种） ……10分12．解：（1）设(,)z a bi a b R =+∈，则2(2)z i a b i +=++， ()(2)2222(2)(2)55z a bi a bi i a b a b i i i i i +++-+===+---+， ……2分 ∵2z i +和2z i -都是实数，∴20205b a b +=⎧⎪+⎨=⎪⎩，解得42a b =⎧⎨=-⎩， ……4分∴42z i =-． ……5分 （2）由（1）知42z i =-，∴222()[4(2)]16(2)8(2)z ai a i a a i +=+-=--+-， ……6分 ∵2()z ai +在复平面上对应的点在第四象限， ∴216(2)08(2)0a a ⎧-->⎨-<⎩， ……7分 即241202a a a ⎧--<⎨<⎩，∴262a a -<<⎧⎨<⎩， ∴22a -<<，即实数a 的取值X 围是(2,2)-．……10分13………… (2分)(2)提出假设H 0: 人的脚的大小与身高之间没有关系.……………… (3分)根据上述列联表可以求得2220(51212)8.802614713χ⨯⨯-⨯=≈⨯⨯⨯. …… (5分)当H 0成立时,27.879χ>的概率约为0.005,而这里8.802>7.879,所以我们有99.5%的把握认为: 人的脚的大小与身高之间有关系.………… (6分) (3) ①抽到12号的概率为141369P ==……………………………… (8分)②抽到“无效序号(超过20号)”的概率为261366P ==…………………… (10分) 14．解：可以猜得第n 个式子是： 121......4131211-+++++n ＞2n （n ≥1,N n ∈）……3分证明：用数学归纳法（1）当n=1 时，1>21，即当n=1 时，猜想成立………4分 （2）假设当n=k （n ≥1,N n ∈）时，命题成立，即2121......4131211kk >-+++++……5分则当n=k+1时，121......12121121 (312111)-+++++-+++++k k k k ……6分 ＞kk k k k 21121......121212-++++++ ＞kkk k k 2221......2212212⋅++⋅+⋅+ =212122222+=+=⋅+k k k kk 这就是说当n=k+1时，猜想成立 ………9分综合（1）（2）有，对一切N n n ∈≥,1命题都成立． ………10分15．解：根据题意，设该项为第r +1项，则有1111C 22C 2,5C 2C 2,6r r r r n n r r r r n n --++⎧=⎪⎨=⎪⎩………1分即11C C ,5C C 3rr n n r r n n-+⎧=⎪⎨=⎪⎩， 亦即21,!5!,!()!3(1)!(1)!n r n n r n r r n r =-⎧⎪⎨=⎪-+--⎩解得 4,7.r n =⎧⎨=⎩…………3分 （1）所有项的二项式系数和为72128=．……5分 （2）展开式的通项为217C 2,7r rrr T x r r +=≤∈N 且． 于是当r =0,2,4,6时，对应项为有理项，………6分即有理项为：00017C 21T x ==，2237C 284T x x ==，442257C 2560T x x ==， 663377C 2448T x x ==．……10分16．解：（1）在252910012910(22)(1)(1)(1)(1)x x a a x a x a x a x ++=+++++++++中，令1x =-，得01a =．……………………………2分 令0x =，得5012910232a a a a a +++++==． …………………4分所以101210131n n a a a a ==+++=∑． ……………………5分（2）等式252910012910(22)(1)(1)(1)(1)x x a a x a x a x a x ++=+++++++++两边对x 求导，得2489129105(22)(22)2(1)9(1)10(1)x x x a a x a x a x ++⋅+=+++++++．…………7分 在2489129105(22)(22)2(1)9(1)10(1)x x x a a x a x a x ++⋅+=+++++++中，令x =0，整理，得105129101291052160n n na a a a a ==++++=⋅=∑．…………10分17．解：将四棱台ABCD －A ′B ′C ′D ′补为四棱锥V －ABCD ， 设点V 到面A ′B ′C ′D ′的距离为h ′．由212''(),,''S h h S h h h h ==++'.h h=………4分 所以212121111(')'()'3333V S h h S h S S h S h =+-=-+台………6分212111()333S h S S h =+=， 所以四棱台ABCD －A ′B ′C ′D ′的体积为121()3S S h +．………10分18．解析：（1）设考生甲、乙正确完成实验操作的题数分别为ξ、η， 则ξ取值分别为1，2，3；η取值分别为0，1，2，3. (1分)51)1(362214===ξC C C P ，53)2(361224===ξC C C P ，51)3(360234===ξC C C P (4分) ∴考生甲正确完成题数的概率分布列为2513532511=⨯+⨯+⨯=ξE . (5分)∵==)0(ηP 271)321(33=-C ， 同理：276)1(==ηP ，2712)2(==ηP ，278)3(==ηP . (9分)∴考生乙正确完成题数的概率分布列为：227832712227612710=⨯+⨯+⨯+⨯=ηE . (10分) （2）∵5251)32(53)22(51)12(222=⨯-+⨯-+⨯-=ξD ， 32278)32(2712)22(276)12(271)02(2222=⨯-+⨯-+⨯-+⨯-=ηD . （或3231323=⨯⨯==ηnpq D ） ∴η<ξD D . (12分) ∵8.05153)2(=+=≥ξP ，74.02782712)2(≈+=≥ηP ，∴)2()2(≥η>≥ξP P . 从做对题数的数学期望考察，两人水平相当；从做对题数的方差考察，甲较稳定；从至少完成2题的概率考察，甲获得通过的可能性大.因此可以判断甲的实验操作能力较强．(15分)19．解：(1))21()21(f f +=1…………………1分 ()()1211223363331222211333336312 1.33aaa a a a f f a a a a a a a ⋅+=+=+=+=⎛+++ ⎝…………4分 (2)一般性规律是:1)()1(=+-x f x f …………5分1(1)()x x x f x f x --+=+=1x =+==. ………………7分于是20081122008()()()()2009200920092009i i f f f f ==+++∑=200810042=． (8)分(3) n n b a ====．…………9分 当a =2时，2n b n >不能对任意n ∈N 都成立.………………10分猜想当a =3时，2n a n >对任意n ∈N 都成立．………………12分方法一:①当n =0时，0230>，不等式成立，n =1时，1231>，不等式成立，当n =2时，2232>，不等式成立．…………13分②假设当n =k (k ≥2)时，不等式成立，即23k k >， 则当n =k +1时，123333k k k +=⋅>， 而223(1)k k -+=22212(1)1k k k k --=--．又2k ≥，则223(1)3k k -+≥，223(1)0k k ∴-+>，即223(1)k k >+. 即n =k +1时，不等式成立．由①②可知，23n n >对任意的n ∈N 都成立．………………15分另证:3n =(1+2)n =1+n n n n n n C C C 222211221+⋅++⋅+⋅-- 22221222n n C C n n >=+>.。

高二数学第二学期期中考试卷本卷满分100分,考试时间90分钟一、填空题（本大题共有11小题，每小题4分，共44分）1．直线y =－3x +1的倾斜角为 .2．过点A(1,－4),且与直线2350x y ++=垂直的直线方程为 . 3．两平行直线3450x y ++=与34250x y +-=间的距离是 ． 4．若方程x 2+y 2+2kx+4y+3k+8=0表示一个圆,则k 的取值范围是___________.5．与双曲线116922=-y x 有共同的渐近线，且一顶点为(0，8)的双曲线的方程 是 .6．已知圆C 的方程(x-2)2+y 2=4,过原点与圆C 相交的弦的中点轨迹是__________.7．设12,F F 为椭圆2212516x y +=的两个焦点，直线过1F 交椭圆于,A B 两点，则2AF B ∆的周长是 ．8．已知双曲线b 2x 2－a 2y 2=a 2b 2的两渐近线的夹角为2α，则c:a ＝ .9．椭圆1222=+y x 和双曲线1222=-y x 有相同的焦点，则实数n 的值是10. 等腰直角三角形的直角顶点是（4，-1），斜边在直线3x -y +2=0上，两条直角边所在的直线方程是 .11. 已知椭圆方程为221499x y +=中，F 1, F 2分别为它的两个焦点，则下列说法：①焦点在x 轴上，其坐标为(±7, 0)；② 若椭圆上有一点P 到F 1的距离为10，则P 到F 2的距离为4；③焦点在y 轴上，其坐标为(0, ±2)；④ a =49,b =9,c =40，正确的有 .二、选择题：（本大题共4小题;每小题4分,共16分）12．直线320x y ++=与直线4210x y +-=夹角是 （ ） A.34π B. 4πC. 2arctgD. arctg 12. 3k >是方裎22131x y k k +=--表示双曲线的条件是 （ ） A.充分但不必要 B. 必要但不充分 C.充要 D.既不充分也不必要14.直线1y x =-上的点到圆224240x y x y ++-+=的最近距离是 （ ） A.1 B. 1+ D. 115. 椭圆13422=+y x 上有n 个不同的点: P 1, P 2, …, P n , 椭圆的右焦点为F . 数列｛|P n F |｝是公差大于1001的等差数列, 则n 的最大值是 ( )A 、198B 、199C 、200D 、20110三、解答题：（本大题共6小题，共40分）P 射出，被x轴反射，反射光线经过点Q(7,1)，16.（6分）已知光线从点(1,5)求入射光线所在的直线方程．21的17. (6分)已知中心在原点，顶点A1、A2在x轴上，焦距与长轴长的比为3双曲线过点P(6，6) 求双曲线方程18. (6分)求过点(1,6)M 且与圆22230x y x ++-=相切的切线方程．19. （7分）过椭圆141622=+y x 内一点M （2，1）内引一条弦，使弦被M 点平分，求这条弦所在直线的方程.20.（7分）斜率为2的直线l 被双曲线x y 22321-=截得的弦长为2515，求直线l 的方程.21.（8分）已知动点P 到直线4x =的距离等于到定点1(1,0)F 的距离的2倍， （１） 求动点P 的轨迹方程；（２） 过1(1,0)F 且斜率1k =的直线交上述轨迹于C 、D 两点，已知(2,0)A ，求ACD ∆的面积S ．高二数学参考答案1．120° 2. 3x －2y －11=0 3. 6 4．(-∞,-1)∪(4,+∞)5．1366422=-x y 6. x 2+y 2-2x=0 7．２０ ８. αsec ９. 3± １０．2x+y-7=0或x-2y-6=0 １１. ② １2. Ｂ １3.Ａ １4.Ｄ １5. C16. 解：点B 关于x 轴对称点为C(7,－1), 入射光线所在的直线为AC43-=AC k入射光线所在的直线方程为3x+4y －17=0．17.解：设双曲线方程为2222by a x -=1由已知得321,16622222222=+==-ab a e b a ,解得a 2=9,b 2=12所以所求双曲线方程为12922y x -=1 18.解：设直线的方程为y=k(x －1)+6,圆心(－1,0)到直线的距离等于半径221622=++-k k ,解得k=34切线方程为46(1)3y x -=-或10x -= 19.解：设直线与椭圆的交点为（x 1 , y 1）,（x 2 , y 2）,M(2,1)为AB 的中点故x 1+x 2= 4, y 1+y 2 = 2 ，由于点 A 、B 在椭圆上，则 x 12 + 4y 12 = 16, x 22 +4y 22 =16 两式相减得 ∴k AB =-=--2121x x y y 21244)(42121-=⨯-=++y y x x故所求直线方程为x +2y – 4 =020. 解：设直线l 的方程为y x m =+2 将y x m =+2代入23622x y -=得232622x x m -+=() 整理得101232022x mx m +++=()设直线l 与双曲线的两个交点坐标为P x y 111(,)，P x y 222(,)∴+=-=+x x m x x m 12122653102,()·由P P kx x 122121=+-得()()()[]25151225155422122212212⎛⎝ ⎫⎭⎪=+-⎛⎝ ⎫⎭⎪=+-x x x x x x1255654310222=-⎛⎝ ⎫⎭⎪-⨯+⎡⎣⎢⎢⎤⎦⎥⎥m m () 解得m m 21223==±,∴所求的直线方程是y x =±22321.（１）设动点(,)P x y ，由题设知4x -=化简得动点(,)P x y 的轨迹方程是22143x y +=． （２）过1(1,0)F 且斜率1k =的直线方程为1y x =-代入椭圆方程消去y ， 得 27880x y --=．设1122(,),(,)C x y D x y ，则12127y y x x -=-==而11211122ACD S AF y y ∆=⋅-=⨯=。

高二下学期期中考试数学试卷-附带参考答案和解析本试卷共5页 22小题 满分150分.考试用时120分钟.考生注意事项：1．试卷分第Ⅰ卷和第Ⅰ卷 第Ⅰ卷用2B 铅笔涂在答题卡上 第Ⅰ卷用黑色钢笔 签字笔在答题卡上作答2．质量监测时间120分钟 全卷满分150分．一、选择题：本大题共8小题 每小题5分 共40分 每小题只有一项是符合题目要求的．1．已知集合(){}2log 20A x x =∈-≤N {A x y =∈N ，则A B ⋃=（ ）A ．{}0,1,2B ．{}1,2C ．{}0,1D ．{}1【答案】C【分析】根据对数的单调性 一元二次不等式的解法 结合并集的定义进行求解即可. 【详解】由(){}2log 20021121x x x A -≤⇒<-≤⇒≤<⇒=由{}210110,1x x B -≥⇒-≤≤⇒=所以A B ⋃={}0,1 故选：C2．复数z 满足()1i i z += i 为虚数单位，则下列说法正确的是（ ） A ．1z = B ．z 在复平面内对应的点位于第二象限 C ．z 的实部为12D ．z 的虚部为1i 2【答案】C【分析】根据复数的除法运算求出复数z 即可求得其模以及实部和虚部 以及对应的点所在象限 一一判断各选项 即得答案.【详解】因为()1i i z += 故i i (1i)11i 1i (1i)(1i)22z ⋅-===+++-则z ==A 错误 z 在复平面内对应的点为11(,)22位于第一象限 B 错误z 的实部为12C 正确z 的虚部为12D 错误故选：C ．3．在ABC 中 点D 是线段AB 上靠近B 的四等分点 点E 是线段CD 上靠近D 的三等分点，则AE =（ ）A ．2133CA CB -+ B ．1526CA CB -C ．1233CA CB -+D 5162CA CB -+．【答案】D【分析】方法一：利用平面向量基本定理得到答案方法二：设ABC 是等腰直角三角形 且4CA CB == 建立空间直角坐标系 写出点的坐标 设m A CA nCB E =+ 从而得到方程组 求出答案.【详解】方法一：如图 由题意得23CE CD = 34AD AB =故()22123333AE AC CE AC CD AC AD AC AC AD =+=+=+-=+()111151323262AC AB CA CB CA CA CB =+=-+-=-+方法二：不妨设ABC 是等腰直角三角形 且4CA CB == 以C 为坐标原点建立平面直角坐标系 如图所示 则()()()()20,0,0,4,4,0,3,1,2,3C A B D E ⎛⎫ ⎪⎝⎭则()()0,4,4,0CA CB == 设m A CA nCB E =+故()()102,0,44,03m n ⎛⎫-=+ ⎪⎝⎭所以1042,43n m ==- 解得51,62m n =-=故5162CA C A B E -=+．故选：D ．4．函数()()()2sin 0,ππf x x ωϕωϕ=+>-<<的部分图像如图所示，则ω ϕ的值分别是（ ）A ．2 π6- B ．2 π3-C ．2π3D ．4 5π6-【答案】B【分析】根据三角函数图像与性质求ω ϕ的值即可. 【详解】设()f x 的周期为T则由图像知35π9π3πππ4123124T T ⎛⎫=--==⇒= ⎪⎝⎭所以2π2Tω==，则()()2sin 2f x x ϕ=+ 因为()f x 在5π12x =处取得最大值 所以5π2π2π,Z 122k k ϕ⨯+=+∈ 得π2π,Z 3k k ϕ=-+∈因为ππϕ-<< 所以π0,3k ϕ==-.故选：B5．在数列{}n a 中的相邻两项n a 与()*1n a n +∈N 之间插入一个首项为1n a n- 公差为1n -的等差数列的前n 项记构成的新数列为{}n b 若21n a n =+，则{}n b 前65项的和为（ ） A ．252-B ．-13C ．272-D ．-14【答案】A【分析】根据题意 得到数列{}n b 中n a 及其后面n 项的和为n S ()()1112n n n n S n a n+=+-⨯求解. 【详解】解：数列{}n b 为：1122233331121,1,,,1,,,,1,,,233n n a a a a a a a a a a a n-------1231,,,,1,,n n n n n n a a a a a n nn+-----设n a 及其后面n 项的和为n S ，则()()()1111123222n n n n n S n a n n ++=+-⨯=-=- 所以数列{}n S 是以1为首项 公差为12-的等差数列.所以{}n b 前65项的和为1210710125222S S S ⎛⎫- ⎪⎝⎭+++==-故选：A.6．冬季是流感高发期 其中甲型流感病毒传染性非常强．基本再生数0R 与世代间隔T 是流行病学基本参考数据．某市疾控中心数据库统计分析 可以用函数模型()2rtW t =来描述累计感染甲型流感病毒的人数()W t 随时间t Z t ∈（单位：天）的变化规律 其中指数增长率r 与基本再生数0R 和世代间隔T 之间的关系近似满足01R rT =+ 根据已有数据估计出04R =时 12T =．据此回答 累计感染甲型流感病毒的人数增加至()0W 的3倍至少需要（参考数据：lg 20.301≈ lg30.477≈）（ ）A ．6天B ．7天C ．8天D ．9天【答案】B【分析】先求得r 然后根据“()0W 的3倍”列方程 化简求得需要的时间. 【详解】依题意 01R rT =+ 且04R =时 12T =即14112,4r r =+⨯= 所以()142tW t = ()10W =令()1423tW t == 两边取以10为底的对数得14lg 340.477lg 2lg 3, 6.34lg 20.301t t ⨯==≈≈ 所以至少需要7天. 故选：B7．如图 在长方形ABCD 中 2AB = 1BC = E 为DC 的中点 F 为线段EC （端点除外）上的动点．现将AFD △沿AF 折起 使平面ABD ⊥平面ABC 在平面ABD 内过点D 作DK AB ⊥ K 为垂足．设AK t ，则t 的取值范围是（ ）A ．10,4⎛⎫ ⎪⎝⎭B ．11,42⎛⎫ ⎪⎝⎭C ．1,12⎛⎫ ⎪⎝⎭D ．51,4⎛⎫ ⎪⎝⎭【答案】C【分析】设DF x = 求得x 关于t 的表达式 根据x 的取值范围求得t 的取值范围. 【详解】如图 在平面ADF 内过点D 作DH AF ⊥垂足为H 连接HK ．过点F 作//FP BC 交AB 于点P ．设FAB θ∠= AE AC == 所以cos θ∈⎝⎭．设DF x =，则12x <<．因为平面ABD ⊥平面ABC 平面ABD ⋂平面ABC AB =DK AB ⊥ DK ⊂平面ABD 所以DK ⊥平面ABC又AF ⊂平面ABC 所以DK AF ⊥． 又因为DHAF ⊥DKDH D = DK DH ⊂平面DKH 所以AF ⊥平面DKH 所以AF HK ⊥ 即AH HK ⊥．在Rt ADF 中 AF DH因为ADF △和APF 都是直角三角形 PF AD = 所以Rt Rt ADF FPA ≌△△ AP DF x ==．因为AHD ADF ∽△△,1AH DH AH AH AD DF ===所以cos AH AP AK AF θ=== 得1x t=． 因为12x << 所以112t<< 所以112t <<．故选：C【点睛】方法点睛：线面垂直 面面垂直转化的过程中 要从线面垂直得到面面垂直 需要“经过一个平面的垂线” 要从面面垂直得到线面垂直，则需要“在一个平面内 垂直于交线” 在答题过程中 要注意使用正确的符号语言.8．在直角坐标系xOy 内 圆22:(2)(2)1C x y -+-= 若直线:0l x y m ++=绕原点O 顺时针旋转90后与圆C 存在公共点，则实数m 的取值范围是（ ）A．⎡⎣ B．44⎡--⎣C．22⎡--⎣D．2⎡-⎣【答案】A【分析】由题意首先得出旋转后的直线为1:0l x y m 然后由直线与圆的位置关系列出不等式即可求解. 【详解】连接OP 设POx θ∠=（即以x 轴正方向为始边 OP 为终边的角）由题意对于直线:0l x y m ++=上任意一点(),P x y存在R a θ=∈ 使得()cos ,sin P a a θθ 则直线:0l x y m ++=绕原点O 顺时针旋转90后 点()cos ,sin P a a θθ对应点为1ππcos ,sin 22P a a θθ⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭ 即()1sin ,cos Pa a θθ- 因为()cos ,sin P a a θθ在直线:0l x y m ++=上 所以满足cos sin 0a a m θθ++= 设11sin ,cos x a y a θθ==- 所以110y x m -++= 即()1sin ,cos P a a θθ-所在直线方程为1:0l xy m而圆22:(2)(2)1C x y -+-=的圆心 半径分别为()2,2,1r = 若直线:0l x y m ++=绕原点O 顺时针旋转90后与圆C 存在公共点所以圆心()2,2C 到直线1:0l x y m 的距离1d r =≤= 解得m ≤故选：A.【点睛】关键点睛：关键是求出旋转后的直线 从而即可顺利得解.二 多选题9．某校举行演讲比赛 6位评委对甲 乙两位选手的评分如下： 甲：7.5 7.5 7.8 7.8 8.0 8.0 乙：7.5 7.8 7.8 7.8 8.0 8.0 则下列说法正确的是（ ）A ．评委对甲评分的平均数低于对乙评分的平均数B ．评委对甲评分的方差小于对乙评分的方差C ．评委对甲评分的40%分位数为7.8D ．评委对乙评分的众数为7.8 【答案】ACD【分析】由平均数 方差 百分位数 众数的概念及求法分别求解判断即可. 【详解】选项A 评委对甲评分的平均数7.57.57.87.88.08.017.87.8630x +++++==-<甲评委对乙评分的平均数7.57.87.87.88.08.017.87.8660x +++++==+>乙所以x x <甲乙 故A 正确选项B 由A 知 两组数据平均数均约为7.8且纵向看 甲组数据与乙组数据仅一组数据7.5,7.8不同 其余数据相同 又甲组数据7.5与平均数的差明显大于乙组数据7.8与平均数的差 且差距较大 故与平均数比较 甲组数据波动程度明显大些即评委对甲评分的方差大于对乙评分的方差 故B 错误 选项C 由640% 2.4⨯=不是整数则评委对甲评分的40%分位数为从小到大第3个数据 即：7.8 故C 正确 选项D 评委对乙评分中最多的数据 即众数为7.8 故D 正确.故选：ACD.10．下列说法正确的是（ ）A ．“α为第一象限角”是“2α为第一象限角或第三象限角”的充分不必要条件 B ．“π2π6k α=+ Z k ∈”是“1sin 2α=”的充要条件C ．设ππ,Z 4M k k αα⎧⎫==±∈⎨⎬⎩⎭ π,Z 4k N k αα⎧⎫==∈⎨⎬⎩⎭，则“M θ∈”是“N θ∈”的充分不必要条件D ．“sin 0θ>”是“θtan 02>”的必要不充分条件 【答案】AC【分析】对于A 利用象限角 求得角α的范围 可判定充分性 取π3α= 验证必要性即可 对于B 考查1sin 2α=时 α的取值范围 可判定必要性不成立 对于C 根据集合M N 的关系即可判定 对于D 根据条件求得α的取值范围即可判断. 【详解】对于A,因为α为第一象限角 所以π2π2π,Z 2k k k α<<+∈ 则πππ,Z 4k k k α<<+∈, 当k 为偶数时 α为第一象限角 当k 为奇数时 α为第三象限角 所以充分性成立 当π3α=时 α为第一象限角，则2π23α= 为第二象限角 即必要性不成立 故A 正确 对于B 当π2π6k α=+ Z k ∈时 1sin 2α=成立，则充分性成立当1sin 2α=时 π2π6k α=+或5π2π6k α=+ Z k ∈, 故必要性不成立，则B 错误对于C ()41πππ,Z ,Z 44k M k k k αααα⎧⎫⎧⎫⎪⎪==±∈==∈⎨⎬⎨⎬⎩⎭⎪⎪⎩⎭而π,Z 4k N k αα⎧⎫==∈⎨⎬⎩⎭则MN 故则“M θ∈”是“N θ∈”的充分不必要条件 故C 正确对于D,当sin 0θ>时 2π2ππ,Z k k k θ<<+∈, 则πππ,Z 22k k k θ<<+∈ 则θtan 02> 故充分性成立 当θtan02>时 πππ,Z 22k k k θ<<+∈则2π2ππ,Z k k k θ<<+∈ 则sin 0θ>成立 所以“sin 0θ>”是“θtan 02>”的充要条件 故D 错误 故选：AC.11．椭圆C 的标准方程为22121,,82x y F F +=为椭圆的左 右焦点 点()2,1P ．12PF F △的内切圆圆心为(),I I I x y 与1212,,PF PF F F 分别相切于点,,D E H ，则（ ）A ．126PF F S =△ B ．13x C ．1233y = D ．226PD PE ==【答案】BCD【分析】根据椭圆中焦点三角形的性质求解12PF F S再结合三角形内切圆的几何性质逐项判断即可得结论.【详解】椭圆C ：22182x y +=，则22,2,826a b c ===-= 所以()()126,0,6,0F F又()2,1P 所以点P 再椭圆上 连接12,,,,,ID IE IH IP IF IF则121211122PF F p SF F y =⋅=⨯ 故A 不正确由椭圆的定义可得122PF PF a +==又12PF F △的内切圆圆心为(),I I I x y 所以内切圆半径I r y = 由于121212PF F IF F IF PIF PSSSS=++()(121212121111122222I I I I I F F y PF y PF y y F F PF PF y =⨯⨯+⨯⨯+⨯⨯=⋅++=⋅故3I r y === 故C 正确又1122,,PD PE DF F H EF HF ===所以12121212PF PF PD DF PE EF PD F H PE HF PD PE F F +=+++=+++=++=则2PD = 所以PD PE == 故D 正确又2PF == 所以222HF EF PF PE ==-又H I x x = I x = 即1x 故B 正确. 故选：BCD.12．已知函数()()e xf x a x =+ ()()lng x x a x =+，则下列说法正确的是（ ）A ．若函数()y f x =存在两个极值，则实数a 的取值范围为21,e ⎛⎫-∞ ⎪⎝⎭B ．当1a =时 函数()y g x =在(0,)+∞上单调递增C ．当1a =时 若存在1x ≥ 使不等式()()2()ln f mx fxx x ≥+成立，则实数m 的最小值为0D ．当1a =时 若()()12(0)f x g x t t ==>，则()121ln x x t +⋅的最小值为1e【答案】BC【分析】对A 选项：由极值点的性质结合导数讨论单调性即可得 对B 选项：结合导数讨论单调性即可得 对C 选项：结合()f x 单调性 可转化为当1x ≥时 有()1ln m x x ≥+成立 求出()1ln x x +最小值即可得 对D 选项：采用同构法可确定12e xx = 再将多变量化为单变量后结合导数讨论单调性即可得.【详解】对A 选项：()()()e e 1e x x xf x x a x a +=+'=++若函数()y f x =存在两个极值，则函数()f x '必有两个变号零点令()()1e 0x f x x a =++='，则()1e xa x =-+令()()1e xh x x =-+，则()()2e xh x x +'=-则当2x >-时 ()0h x '< 当<2x -时 ()0h x '> 故()h x 在(),2∞--上单调递增 在()2,∞-+上单调递减故()()()221221e e h x h -≤-=--+=又当1x >-时 ()()1e 0xh x x =-+<恒成立当x →-∞时 ()0h x →故当210,e a ⎛⎫∈ ⎪⎝⎭函数()f x '有两个变号零点即若函数()y f x =存在两个极值，则实数a 的取值范围为210,e⎛⎫ ⎪⎝⎭故A 错误对B 选项：当1a =时 ()(1)ln g x x x =+ ()11ln ln 1x g x x x x x='+=+++ 令()()x g x μ='，则()22111x x x x xμ'-=-= 则当()0,1x ∈时 ()0x μ'< 当()1,x ∞∈+时 ()0x μ'> 故()x μ在()0,1上单调递减 在()1,∞+上单调递增故()()120g x g '='≥> 故函数()y g x =在(0,)+∞上单调递增 故B 正确对C 选项：当1a =时 ()()e 1xf x x =+()()()e e 11e 1x x x f x x x =++=++'令()()m x f x ='，则()()2e xm x x +'=则当<2x -时 ()0m x '< 当2x >-时 ()0m x '> 故()m x 在(),2∞--上单调递减 在()2,∞-+上单调递增故()()2212e 110e f x f -≥-=-+=-'>' 故()f x 在R 上单调递增则存在1x ≥ 使不等式()()2()ln f mx fxx x ≥+成立等价于存在1x ≥ 使不等式()2ln mx x x x ≥+成立则当1x ≥时 有()1ln m x x ≥+成立由当1a =时 ()(1)ln g x x x =+ 且()y g x =在(0,)+∞上单调递增 故()11ln10m ≥+= 即实数m 的最小值为0 故C 正确对D 选项：当1a =时 由B C 可知 ()f x ()g x 均为定义域上的增函数 由()00f = ()10g = 故有1>0x 21x >由()()12f x g x =，则()()1122e 11ln xx x x +=+即()()()111122e 1e 1ln e 1ln x x x x x x +=+=+ 故12e xx =又()()111e 10xf x t x ==+> 故()121ln ln x x t t t +⋅=令()ln n x x x =，则()1ln n x x x ='+ 令()()1ln p x n x x x==+'则()22111x p x x x x='-=- 则当()0,1x ∈时 ()0p x '< 当()1,x ∞∈+时 ()0p x '> 故()p x 在()0,1上单调递减 在()1,∞+上单调递增 即()()10n x n ''≥= 故()n x 在()0,∞+上单调递增 故()n x 无最小值 即()121ln x x t +⋅无最小值 故D 错误. 故选：BC.【点睛】思路点睛：本题考查导数在研究函数中的综合应用问题 其中D 选项中涉及到多变量问题的求解 求解此类问题的基本思路是根据已知中的等量关系 将多变量转化为单变量的问题 从而将其转化为函数最值问题的求解. 三 填空题13．()622x x y y ⎛⎫+- ⎪⎝⎭的展开式中42x y 的系数为 ．（用数字作答）【答案】40-【分析】由二项式定理得到()62x y -的通项公式 结合2xy+得到34,T T 得到42x y 的系数. 【详解】()62x y -的通项公式为()()66166C 2C 2rrr r r r r r T x y x y --+=-=-令2r =得 ()22424236C 260T x y x y =-= 此时4242602120x y x y ⋅=令3r =得 ()33333346C 2160T x y x y =-=- 此时3342160160xx y x y y-⋅=- 故42x y 的系数为12016040-=- 故答案为：40-14．设数列{}n a 满足12a = 26a = 且2122n n n a a a ++-+= 若[]x 表示不超过x 的最大整数，则122021202120212021a a a ⎡⎤+++=⎢⎥⎣⎦． 【答案】2020【分析】根据题意 得到()()2112n n n n a a a a +++---= 得到{}1n n a a +-为等差数列 求得其通项公式 结合累加法 得到(1)n a n n =+ 求得2021112021()1n a n n =-+ 再利用裂项求和 求得12202120212021202120212021(2020,2021)2022a a a +++=⨯∈ 即可求解. 【详解】因为2122n n n a a a ++-+= 可得()()2112n n n n a a a a +++---= 又因为12a = 26a = 可得214a a -=所以数列{}1n n a a +-是首项为4 公差为2的等差数列 所以14(1)222n n n a n a +-=+-⨯=+ 当2n ≥时 112211()()()n n n n n a a a a a a a a ---=-+-++-+(1)22(1)2222(1)2n n n n n n +=+-++⨯+=⨯=+ 且当1n =时 12a =也成立 所以()1n a n n =+ 所以202111120212021()(1)1n a n n n n =⨯=-++ 所以122021202120212021111112021[(1)()()]22320212022a a a +++=-+-++- 120212021(1)2021(2020,2021)20222022=-=⨯∈所以1220212021202120212020a a a ⎡⎤+++=⎢⎥⎣⎦. 故答案为：2020.15．已知椭圆 22221(0)x y C a b a b+=>>：的左右焦点为12,F F ．直线y kx =与椭圆C 相交于,P Q 两点 若112PF QF = 且12π3PFQ ∠= ，则椭圆C 的离心率为． 【分析】由椭圆的对称性可得四边形12PFQF 为平行四边形 再根据椭圆的定义求出12,PF PF 再在12PF F △中 利用余弦定理求出,a c 的关系即可得解.【详解】由椭圆的对称性可得四边形12PFQF 为平行四边形，则21PF QF =由12π3PFQ ∠= 得12π3F PF ∠= 因为112PF QF = 所以122PF PF = 又122PF PF a += 所以1242,33a aPF PF == 在12PF F △中 由余弦定理得222121212122cos F F PF PF PF PF F PF =+-∠ 即2222164421442993323a a a a ac =+-⨯⨯⨯=所以c a =即椭圆的离心率c e a ==16．已知A M N 是棱长为1的正方体表面上不同的三点，则·AM AN 的取值范围是 ． 【答案】1,32⎡⎤-⎢⎥⎣⎦【分析】根据正方体的性质可得·3cos ,a AM AN AM AN =≤结合夹角的定义可得3a ≤ 可得其最大值 根据数量积的运算可知24≥-MN a 可得其最小值.【详解】正方体表面上任意两点间距不超过体对角线长度d 则,AM AN d ≤ 故·3cos ,a AM AN AM AN =≤ 而[]cos ,1,1AM AN ∈- 故3a ≤如图建立空间直角坐标系 取()0,0,0A ,M N 重合为()1,1,1时 则()()1,1,11,1,13a =⋅= 取得最大值3由对称性 设A 在下底面 (),,AM x y z = (),,AN a b c =由A 在下底面知0,0,0z c zc ≥≥≥ 当且仅当,M N 也在下底面时取等 此时,,A M N 共面时 设MN 中点为E ，则EM EN =-()()()()()2222··4MN a AM AN AE EM AE EN AE EN EN==++=-≥-=-当且仅当,A E 重合时取等又因为2MN ≤ 可得2142-≥-≥a MN 例如11,,022A ⎛⎫ ⎪⎝⎭ ()()1,0,0,0,1,0M N ，则11111·,,0,,022222a AM AN ⎛⎫⎛⎫==--=- ⎪⎪⎝⎭⎝⎭所以·AM AN 的取值范围是1,32⎡⎤-⎢⎥⎣⎦. 故答案为：1,32⎡⎤-⎢⎥⎣⎦.四 解答题（共70分）17．（本题10分）如图 在ABC 中 6AB AC == 点D 是边BC 上一点且,cos AD AB CAD ∠⊥=2AE EB =(1)求BCE 的面积 (2)求线段AD 的长. 【答案】(1)(2)=AD【分析】（1）根据13BCE ABC S S =△△求解即可（2）解法1：在ABC 中根据余弦定理求出BC 结合等腰三角形的性质求cos B 在ABD △中勾股定理求AD 即可 解法2：由A BCABDACDSSS=+求得AD .【详解】（1）12,3BCEABCAE EB SS =∴=而11πsin 66sin 222ABCSAB AC BAC CAD ⎛⎫=⋅⋅∠=⨯⨯⨯∠+ ⎪⎝⎭ 18cos 18CAD =∠== 1423BCEABCSS ∴==（2）解法1：()1cos 0,π,sin 3CAD CAD CAD ∠=∠∈∴∠= π1cos cos sin 23CAB CAD CAD ⎛⎫∴∠=∠+=-∠=- ⎪⎝⎭在ABC 中 22212cos 3636266963BC AB AC AB AC CAB ⎛⎫=+-⋅⋅∠=+-⨯⨯⨯-= ⎪⎝⎭BC ∴=∴在等腰ABC 中12cos BCB BA ==∴Rt ABD △中6cos ,BA BBD BD BD===∴=AD ∴==解法2：()1cos 0,π,sin 3CAD CAD CAD ∠=∠∈∴∠== 由A BCABDACDSSS=+得1166sin 22AD AD CAD =⨯⨯+⨯⨯⋅∠,即()11166223AD AD =⨯⋅+⋅⋅⋅解得=AD18．（本题12分）已知数列{}n a 的前n 项和为n S 11a = 且满足()()11112n n n S nS n n ++=-+.(1)求数列{}n a 的通项公式(2)设()23cos πn a n n b a n =+⋅ 求数列{}n b 的前n 项和n T .【答案】(1)n a n =(2)()()()()11133,,24133,.24n n n n n n T n n n ++⎧++--⎪⎪=⎨++-⎪--⎪⎩为偶数为奇数【分析】（1）利用构造法和等差数列的定义与通项公式可得()12n n n S +=结合1n n n a S S -=-即可求解（2）由（1）知()()213nnn b n =-+- 利用分组求和法计算即可求解. 【详解】（1）根据题意 ()()11112n n n S nS n n ++=-+ 所以1112n n S S n n +-=+由于1111S a ==，则n S n ⎧⎫⎨⎬⎩⎭是以首项为1 公差为12的等差数列所以()111122n S n n n +=+-⨯= 所以()12n n n S += 当2n ≥时 1(1)(1)22n n n n n n na S S n -+-=-=-=. 验证1n =时11a =满足通项公式 故数列{}n a 的通项公式为n a n =.（2）由（1）知()()()223cos π13n n na n nb a n n =+⋅=-+-.设()21nn -的前n 项和为n A ，则当n 为偶数时 ()22222212341n A n n =-+-+-⋅⋅⋅--+()()()()()()2121434311n n n n ⎡⎤⎡⎤=-++-++⋅⋅⋅+--+-⎣⎦⎣⎦ ()()1123412n n n n +=++++⋅⋅⋅+-+=. 当n 为奇数时 ()()2211122n n n n n n A A n n --+=-=-=-设()3n-的前n 项和为n B ，则()()()131333134nn nB +⎡⎤-⋅-----⎣⎦==+. 因为=+n n n T A B 所以()()()()11133,,24133,.24n n n n n n T n n n ++⎧++--⎪⎪=⎨++-⎪--⎪⎩为偶数为奇数 19．（本题12分）如图 在四棱锥P ABCD -中 PAD 为等边三角形 AD CD ⊥ //AD BC 且22AD BC ==CD =PB = E 为AD 中点．(1)求证：平面PAD ⊥平面ABCD(2)若线段PC 上存在点Q 使得二面角Q BE C --的大小为60︒ 求CQCP的值． 【答案】(1)证明见解析 (2)12【分析】（1）首先连接PE 根据线面垂直的判定定理证明PE ⊥平面ABCD 再利用面面垂直的判定定理证明平面PAD ⊥平面ABCD . （2）设()01CQ CP λλ=≤≤,再利用向量法求二面角Q BE C --的平面角 再列方程得到12λ= 即得CQCP 的值．【详解】（1）证明：连接PEPAD 是边长为2的等边三角形 E 是AD 的中点PE AD ⊥∴PE =//DE BC DE BC = AD CD ⊥ ∴四边形BCDE 是矩形BE CD ∴==222PE BE PB ∴+= PE BE ∴⊥又AD BE E = AD BE ⊂平面ABCDPE ∴⊥平面ABCD又PE ⊂平面PAD∴平面PAD ⊥平面ABCD ．（2）以E 为原点 以EA EB EP 为坐标轴建立空间直角坐标系 如图所示：则(00P()C -()0B ()0,0,0E ()0EB ∴=， ()100BC =-，，(1CP = 设()01CQCPλλ=≤≤则()1BQ BC CQ BC CP λλ=+=+=- 设平面QBE 的法向量为(),,m x y z =则00m EB m BQ ⎧⋅=⎪⎨⋅=⎪⎩即()010x y z λ⎧=⎪⎨-=⎪⎩，，令1z = 得()301m λλ=-，，又PE ⊥平面ABCD()001n ∴=，，为平面BEC 的一个法向量cos 3m n m n m nλ⋅∴==，二面角Q BE C --的大小为60︒12= 解得12λ=． 12CQ CP ∴=． 20．（本题12分）2023年秋末冬初 呼和浩特市发生了流感疾病. 为了彻底击败病毒 人们更加讲究卫生讲究环保. 某学校开展组织学生参加线上环保知识竞赛活动 现从中抽取200名学生 记录他们的首轮竞赛成绩并作出如图所示的频率直方图 根据图形 请回答下列问题：(1)若从成绩低于60分的同学中按分层抽样方法抽取5人成绩 求5人中成绩低于50分的人数 (2)以样本估计总体 利用组中值估计该校学生首轮竞赛成绩的平均数(3)首轮竞赛成绩位列前10%的学生入围第二轮的复赛 请根据图中信息 估计入围复赛的成绩（记为K ）. 【答案】(1)2人 (2)71 (3)88K ≥【分析】（1）利用分层抽样的定义求解即可 （2）利用平均数公式求解即可（3）根据题意设入围复赛的成绩的临界值为[)80,90K ∈，则()900.0250.050.1K -⨯+= 求出K 的值即可. 【详解】（1）成绩在[)40,50的人数为0.011020020⨯⨯=（人） 成绩在[)50,60的人数为0.0151020030⨯⨯=（人） 则按分层抽样方法从成绩低于60分的同学中抽取5人成绩低于50分的人数为20522030⨯=+（人）. 故5人中成绩低于50分的人数为2人（2）由()0.010.0150.0150.0250.005101a +++++⨯= 得0.030a = 则平均数450.1550.15650.15750.3850.25950.0571x =⨯+⨯+⨯+⨯+⨯+⨯=故该校学生首轮竞赛成绩的平均数约为71分（3）根据频率分布直方图可知：[]90,100的频率为0.005100.05⨯= [)80,90的频率为0.025100.25⨯=所以入围复赛的成绩一定在[)80,90可知入围复赛的成绩的临界值为[)80,90K ∈则()900.0250.050.1K -⨯+= 解得88K =故估计入围复赛的成绩为88K ≥分.21．（本题12分）已知椭圆2222:1(0)x y C a b a b +=>> 斜率为2的直线l 与x 轴交于点M l 与C 交于A B 两点 D 是A 关于y 轴的对称点．当M 与原点O 重合时 ABD △面积为169． (1)求C 的方程(2)当M 异于O 点时 记直线BD 与y 轴交于点N 求OMN 周长的最小值．【答案】(1)22142x y += (2)2【分析】（1）设出各点坐标 表示出面积后 结合面积与离心率计算即可得（2）要求OMN 的周长，则需把各边长一一算出 即需把M x N y 算出 设出直线方程与椭圆方程联立得与横坐标有关韦达定理 借助韦达定理表示出M x N y 可得OMN 各边边长 结合基本不等式即可求得最值.【详解】（1）当M 与原点O 重合时 可设()00,A x y ，则有()00,B x y -- ()00,D x y -且002y x = 即有AD BD ⊥, 则()()00001116229ABD S AD BD x x y y =⋅=++=即201649x = 又00x > 故023x =，则043y = 即有22416199a b +=即c a =则22222a c b c ==+ 故222a b = 即有224161189b b += 解得22b = 故24a = 即C 的方程为22142x y +=（2）设直线l 方程为2y x t =+ 令0y = 有2t x =- 即2M t x =- 设点()11,A x y ()22,B x y ，则()11,D x y - 联立直线与椭圆方程：222142y x t x y =+⎧⎪⎨+=⎪⎩ 消去y 有2298240x tx t ++-= ()222Δ64362414480t t t =--=->即t -<有1289t x x -+= 212249t x x -= BD l 为()122212y y y x x y x x -=-+-- 令0x = 故21222122122221122121212N x y x y x y x y x y x y x y x y y y x x x x x x -+-+++=+==--++ 由2y x t =+ 故()()2112211212121212224x x t x x t x y x y x x t x x x x x x ++++==++++ 其中2121224198429t x x t t x x t -==-+-+ 即12442N t y t t t ⎛⎫=-++= ⎪⎝⎭则22OMN N M t C y x t =+=+2≥=当且仅当2t =±时等号成立故OMN周长的最小值为2+【点睛】本题考查了椭圆的方程 在求解直线与椭圆的位置关系问题时 常用方法是设而不求 借助韦达定理等手段 将多变量问题转变为单变量问题 再用基本不等式或函数方式求取范围或最值.22．（本题12分）已知函数21()ln 2f x x x ax =+-． (1)当12a =时 求在曲线()y f x =上的点(1,(1))f 处的切线方程 (2)讨论函数()f x 的单调性(3)若()f x 有两个极值点1x 2x 证明：()()121222f x f x a x x -<--． 【答案】(1)3230x y --=(2)详见解析(3)详见解析.【分析】（1）根据导数的几何意义求出（2）求出导函数()1(0)f x x a x x '=+-> 在定义域()0,∞+内分类讨论解含参不等式即可求出 （3）由题意得2a > 12x x a += 121=x x 而()()1212f x f x x x --1212ln ln 12x x a x x -=-- 只需证明1212ln ln 2x x x x -<- 即证：11111ln ln 2x x x x ⎛⎫+<- ⎪⎝⎭ 即证：1111ln x x x <-对任意的1(1,)x ∈+∞恒成立即可． 【详解】（1）由题可知 当12a =时 211()ln 22f x x x x =+- ()112f x x x ∴=+-' ∴(1)0f = 3(1)2f '= ∴切点为(1,0) 切线的斜率为32 ∴切线方程为：30(1)2y x -=- 即3230x y --=（2）对函数()f x 求导可得 ()1(0)f x x a x x '=+->． 当2a ≤时 ()120f x x a a x=+-≥-≥'．则()f x 在(0,)+∞上单调递增． 当2a >时 ()2110x ax f x x a x x -+=+-=='．则1x =2x = 令()0f x '>，则10x x << 或2x x >．()0f x '<，则12x x x <<综上：当2a ≤时 ()f x 在(0,)+∞上单调递增当2a >时 ()f x在⎛ ⎝⎭和∞⎫+⎪⎪⎝⎭上单调递增 ()f x在⎝⎭上单调递减． （3）()f x 有两个极值1x 2x1x ∴ 2x 是方程210x ax -+=的两个不等实根则2a > 12x x a += 121=x x()()2211122212121211ln ln 22x x ax x x ax f x f x x x x x ⎛⎫+--+- ⎪-⎝⎭=-- ()()()121212*********ln ln ln ln 122x x x x x x a x x x x a a x x x x -+-+---==+--- 1212ln ln 12x x a x x -=--． 要证：()()121222f x f x a x x -<--．即证：1212ln ln 2x x x x -<-． 不妨设1210x x >>> 即证：11111ln ln 2x x x x ⎛⎫+<- ⎪⎝⎭． 即证：1111ln x x x <-对任意的1(1,)x ∈+∞恒成立． 令1()ln f x x x x =-+ (1)x >．则()22211110x x f x x x x -+=--=-<'． 从而()f x 在(1,)+∞上单调递减 故()(1)0f x f <=．所以()()121222f x f x a x x -<--．【点睛】本题考查了切线方程问题考查函数的单调性问题考查导数的应用以及分类讨论思想训练了构造函数法证明不等式的成立属难题.。

高二下学期数学期中考试试卷时量：120分钟 总分：150分一、选择题：本大题共12小题，每小题5分，共60分. 在每小题给出的四个选项中，只有一项是符合题目要求的。

1. 设全集R I =，集合}1|{},3,log |{A 3-==>==x y x B x x y y ，则（ ）A ．B A ⊆ B ．A B A =⋃C ．φ=⋂B AD ．φ≠⋂)(B C A I 2.已知i 是虚数单位，复数z 满足i z i 2)1(=-，则z 的虚部是（ ） A ．1 B ．i C ．－1 D ．－i3. 函数x x f 3log )(=的图象与函数()sin g x x π=的图象的交点个数是( ) A ．2 B ．3 C ．4 D ．54. 若向量,a b 的夹角为32π，且1||,2||==b a ，则向量b a 2+与向量a 的夹角为（ ） A ．6π B ．3π C. 23π D ．56π5. 已知0a >，0b >，若不等式313ma b a b+≥+恒成立，则m 的最大值为（ ）A ．9B ．12C ．18D ．246.已知21)4tan(=-πα，且0<<-απ，则αα2sin 22sin +等于（ ）A ．B ．25-C ．25D ．5127.已知直三棱柱ABC ﹣A 1B 1C 1，AB ⊥BC ，AB=BC=AA 1=2，若该三棱柱的所有顶点都在同一球面上，则该球的表面积为（ ）A ．π48B ．π32C ．π12D ．π8 8. 已知定义在R 上的函数()21x mf x -=- （m 为实数）为偶函数，记)3(log 5.0f a =,),2(),5(log 2m f c f b ==则,,a b c 的大小关系为（ ）A ．a b c <<B ．a c b <<C ．c a b <<D ．c b a <<9.直线02=++y x 分别与轴轴，y x 交于B A ,两点，点P 在圆2)2(22=+-y x 上，则ABP ∆面积的取值范围是（ ）A ．]6,2[B ．]8,4[ C. ]23,2[ D ．]23,22[ 10. 执行如图所示的程序框图，则输出的k 值为（ ） A ．4B ．5C ．7D ．911.已知函数)(x f 是定义在R 上的偶函数，设函数)(x f 的导数为)(x f '，若对任意的0>x 都有0)()(2>'+x f x x f 成立，则（ ）A ．)3(9)2(4f f <-B ． )3(9)2(4f f >-C ．)2(3)3(2->f fD ．)2(2)3(3-<-f f12.设双曲线)0,0(12222>>=-b a by a x C ，：的左、右焦点分别为1F 、2F 。

2011年上海市闸北区中考数学二模试卷一、选择题（共6小题，每小题4分，满分24分）1．根据国家统计局1月28日发布《2010年国民经济和社会发展统计公报》，去年全年国内生产总值﹙GDP﹚为亿元．用科学记数法保留三个有效数字为（）A．3.97×105亿元B．0.39×105亿元C．3.98×105亿元D．3.98×104亿元10分）：这次听力测试成绩的众数是（）A．5分B．6分C．9分D．10分3．（2010•宁波）下列各图是选自历届世博会徽中的图案，其中是中心对称图形的是（）A．B．C．D．4．（2010•嘉兴）设a＞0，b＞0，则下列运算错误的是（）A．=•B．=+C．（）2=a D．=5．（2006•宜昌）下列四边形①等腰梯形，②正方形，③矩形，④菱形的对角线一定相等的是（）A．①②③B．①②③④C．①②D．②③6．（2010•绍兴）已知P1（x1，y1），P2（x2，y2），P3（x3，y3）是反比例函数y=的图象上的三点，且x1＜x2＜0＜x3，则y1、y2、y3的大小关系是（）A．y3＜y2＜y1B．y1＜y2＜y3C．y2＜y1＜y3D．y2＜y3＜y1二、填空题（共12小题，每小题4分，满分48分）7．计算：=_________．8．（2011•南昌）因式分解：x3﹣x=_________．9．不等式组的解是_________．10．方程的解是_________．11．如果函数，那么=_________．12．将二次函数y=﹣x2+2的图象向右平移1个单位后，所得图象的函数解析式是_________．13．（2010•丽水）玉树地震灾区小朋友卓玛从某地捐赠的2种不同款式的书包和2种不同款式的文具盒中，分别取一个书包和一个文具盒进行款式搭配，则不同搭配的可能有_________种．14．如果与是互为相反向量，那么=_________．15．如图，边长为（m+3）的正方形纸片剪出一个边长为m的正方形之后，剩余部分又剪拼成一个矩形（不重叠无缝隙），若拼成的矩形一边长为3，则另一边长是_________．16．已知在△ABC中，AB=AC=5，BC=8，点G为重心，那么GA=_________．17．（2009•鸡西）如图，一条公路的转弯处是一段圆弧（图中的），点O是这段弧的圆心，C是上一点，OC⊥AB，垂足为D，AB=300m，CD=50m，则这段弯路的半径是_________m．18．（2010•金华）如图在边长为2的正方形ABCD中，E，F，O分别是AB，CD，AD的中点，以O为圆心，以OE为半径画弧EF．P是上的一个动点，连接OP，并延长OP交线段BC于点K，过点P作⊙O的切线，分别交射线AB于点M，交直线BC于点G．若=3，则BK=_________．三、解答题（共7小题，满分78分）19．计算：．20．解方程：21．（2010•荆州）2010年，世博会在我国的上海举行，在网上随机调取了5月份中的某10天持票入园参观的人数，绘成下面的统计图．根据图中的信息回答下列问题：（1）求出这10天持票入园人数的平均数、中位数和众数；（2）不考虑其它因素的影响，以这10天的数据作为样本，估计在世博会开馆的184天中，持票入园人数超过30万人的有多少天？22．（1）如图，给出四个条件：①AE平分∠BAD，②BE平分∠ABC，③AE⊥EB，④AB=AD+BC．请你以其中三个作为命题的条件，写出一个能推出AD∥BC的正确命题，并加以证明；（2）请你判断命题“如图，AE平分∠BAD，BE平分∠ABC，E是CD的中点，则AD∥BC．”是否正确，并说明理由．23．如图，已知矩形ABCD中，BC=6，AB=8，延长AD到点E，使AE=15，连接BE交AC于点P．（1）求AP的长；（2）若以点A为圆心，AP为半径作⊙A，试判断线段BE与⊙A的位置关系并说明理由；（3）已知以点A为圆心，r1为半径的动⊙A，使点D在动⊙A的内部，点B在动⊙A的外部，求动⊙A的半径r1的取值范围．24．（2010•金华）已知点P的坐标为（m，0），在x轴上存在点Q（不与P点重合），以PQ为边作正方形PQMN，使点M落在反比例函数y=﹣的图象上．小明对上述问题进行了探究，发现不论m取何值，符合上述条件的正方形只有两个，且一个正方形的顶点M在第四象限，另一个正方形的顶点M1在第二象限．（1）如图所示，若反比例函数解析式为y=﹣，P点坐标为（1，0），图中已画出一符合条件的一个正方形PQMN，请你在图中画出符合条件的另一个正方形PQ1M1N1，并写出点M1的坐标；M1的坐标是_________．（2）请你通过改变P点坐标，对直线M1M的解析式y﹦kx+b进行探究可得k﹦_________，若点P的坐标为（m，0）时，则b﹦_________；（3）依据（2）的规律，如果点P的坐标为（6，0），请你求出点M1和点M的坐标．25．直线分别交x轴、y轴于A、B两点，△AOB绕点O按逆时针方向旋转90°后得到△COD，抛物线y=ax2+bx+c经过A、C、D三点．（1）写出点A、B、C、D的坐标；（2）求经过A、C、D三点的抛物线表达式，并求抛物线顶点G的坐标；（3）在直线BG上是否存在点Q，使得以点A、B、Q为顶点的三角形与△COD相似？若存在，请求出点Q的坐标；若不存在，请说明理由．2011年上海市闸北区中考数学二模试卷参考答案与试题解析一、选择题（共6小题，每小题4分，满分24分）1．根据国家统计局1月28日发布《2010年国民经济和社会发展统计公报》，去年全年国内生产总值﹙GDP﹚为亿元．用科学记数法保留三个有效数字为（）A．3.97×105亿元B．0.39×105亿元C．3.98×105亿元D．3.98×104亿元考点：科学记数法与有效数字。

上海交通大学附属中学2010-2011学年度第二学期高二数学期中试卷本试卷共有22道试题，满分100分，考试时间90分钟。

请考生用钢笔或圆珠笔将答案写在答题卷上一、填空题（本大题满分42分）本大题共有14题，只要求直接填写结果，每个空格填对得3分，否则一律得零分。

1. 1001001i i+= .2. 抛物线280y x +=的焦点坐标为 .3. 双曲线2238x y -=的两条渐近线的夹角为 .4. 从甲、乙、丙三名学生中任意安排2名学生参加数学、外语两个课外活动小组的活动，有 种不同的安排方案。

5. 若复数214tz t i+=-+在复平面上对应的点在第四象限，则实数t 的取值范围是 6. 6名学生排成一排，其中甲不在排头，乙不在排尾，则共有 种排法。

7. 已知双曲线221y x a-=的一条渐近线与直线230x y -+=垂直，则实数a = . 8. 在抛物线220y x =上有一点P ，且P 与焦点的距离等于15，,则P 点坐标为 . 9. 复数2)2321(i z -=是实系数方程012=++bx ax 的根，则=⨯b a . 10. 某抛物线形拱桥的跨度为20米，拱高是4米，在建桥时，每隔4米需用一根支柱支撑，其中最高支柱的高度是 米．（答案保留两位小数．．．．．．．．） 11. 已知焦点为(0,3)的双曲线方程是2288kx ky -=，则k = .12. 某高校食堂供应午饭，每位学生可以在食堂提供的菜肴中任选2荤2素共4种不同的品种。

现在食堂准备了5种不同的荤菜，若要保证每位学生有200种以上不同的选择，则食堂至少还需要准备不同的素菜品种 种.（结果用数值表示）13. 从抛物线24y x =上一点P 引其准线的垂线，垂足为M ，设抛物线的焦点为F ，且||5PF =，则MPF ∆的面积为 .14. 已知双曲线2222:1x y C a b-=，1F 、2F 分别为左右焦点，P 为C 上的任意一点，若122F PF π∠=，且124F PF S ∆=，则双曲线的虚轴长为 .二、选择题（本大题满分16分）本大题共有4题，每题都给出代号为(A)、(B)、(C)、(D)的四个结论，其中有且只有一个结论是正确的，必须把正确结论的代号写在对应的空格内，选对得4分，不选、选错或者选出的代号超过一个（不论是否都写在空格内），一律得零分。

上海南汇中学 2011 学年第二学期期中考试高二数学（答案）满分： 100 分完成时间： 90 分钟命题人：吴世星周华审核人：潘静红一、填空题（每小题 3 分，共 36 分）1、直线x 3y 1 0 的倾斜角.62、若椭圆的长轴长为12，一个焦点是(0, 2)，则椭圆的标准方程为___ x2 y2 1_________.32 363、经过点A(1,0)且与直线x y 1 0 平行的直线 l 的方程为x y 1 0 _.x2 y21的虚轴长是9 _.4、双曲线4 95、已知直线2x y 2 0和3x y 1 0 的夹角是4_.6、直线x y 1被圆x2 y2 1所截得的弦长等于 2 _.7、已知方程x2 y 21表示双曲线，则实数k 的取值范围为___ k 4或 k 10 .10 k k 48、过点(1,2)且与圆x2y21 3x 4 y 5 0或 x 1_.相切的直线的方程是9、已知双曲线x2 y2 1的两个焦点分别为F1、F2, P 为双曲线上一点，且F1PF2 ,4 2 则F1PF2的面积是 4 .10、设F为抛物线y2 4x 的焦点，A, B, C为该抛物线上三点，若点A(1,2) ，ABC 的重心与抛物线的焦点 F 重合，则 BC 边所在直线方程为2x y 1 0 .11、若方程x k 1 x2 0 只有一个解，则实数k 的取值范围是[ 1,1) { 2}.12、下列五个命题：①直线l 的斜率 k [ 1,1]，则直线 l 的倾斜角的范围是[ , ] ；4 4②直线 l : y kx 1 与过 A( 1,5) ， B(4, 2) 两点的直线相交，则k 4 或 k 3 ；43，那么y的最大值为③如果实数 x, y 满足方程( x 2)2 y2 3 ；x④直线 y kx 1 与椭圆x2 y2 1恒有公共点，则m 的取值范围是m 1；5 m⑤方程 x2 y 2 4mx 2 y 5m 0 表示圆的充要条件是m 1 或 m 1 ；4正确的是 _____② _③_⑤ ___ _.二、选择题（每小题 3 分，共 12 分）13、直线3x 2 y m 0 与直线 2x 3y 1 0 的位置关系是,,,,,,,,,, （ A ）（ A）相交（B）平行（ C）重合（ D）由 m决定14、若椭圆x2 y 2 1与双曲线x4 a 2 a2y 2 a为,,,, （ C ）21有相同的焦点，则实数2（ A ） 1 （B ） 1 （C） 1 （D ）不确定15、已知抛物线C : y2 x 与直线l : y kx 1，“k 0 ”是“直线l与抛物线C有两个不同交点”的,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,,, （ B ）（ A ）充分不必要条件（ B）必要不充分条件（C）充要条件（ D）既不充分也不必要条件16、已知曲线C： x | x | y | y | 1 ，下列叙述中错误的是 ,,,,,,,,,,,, （ C ）2 2 ．．a b（ A ）垂直于x轴的直线与曲线 C 只有一个交点（ B ）直线y kx m （k, m R）与曲线C最多有三个交点（ C）曲线 C 关于直线y x 对称y1 y2（ D）若P1( x1, y1)，P2( x2, y2)为曲线 C 上任意两点，则有x2x1三、解答题（第 17、18 题各 8 分，第 19 题 10 分，第 20 题 12 分，第 21 题 14 分，共 52 分）17、已知△ ABC 的三个顶点是A(3, 4) 、 B(0,3) 、 C ( 6,0) ，求（ 1）BC 边所在直线的一般式方程；(4 分 )（ 2）BC 边上的高 AD 所在直线的一般式方程. (4 分 )解；（ 1）BC ( 6, 3) 是BC边所在直线的方向向量故 l BC : x y 3，即 l BC : x 2 y 6 0 ,,,,,,,,,, 4 分6 3（ 2）BC ( 6, 3) 高 AD 所在直线的法向量故 l AD : 6( x 3) 3( y 4) 0 ，即 l AD :2x y 2 0 ,,,,,,,,,, 8 分18、求经过A( 3,0) ,且与圆C : ( x 3)2 y2 64 内切的圆的圆心M 的轨迹方程. (8 分 ) 解：根据题意得，MA MC 8 AC , ,,,,,,,,,,,,,, 2 分由椭圆定义得 a 4, c 3 ，所以 b2 7 ,,,,,,,,,,,,,,,, 4 分所以所求的圆心M 的轨迹方程为x2 y2 1 ,,,,,,,,,,,,,, 8 分16 719、已知双曲线C1 ： x2 y2 14（ 1）求与双曲线C1有相同的焦点，且过点P(4, 3) 的双曲线 C2的标准方程；（5分）（ 2）直线l：y x m 分别交双曲线C1的两条渐近线于A、B两点。

2011学年第一学期期中考试 (2011. 11)高二数学试卷(参考答案)考生注意：l ．本试卷共3页．满分100分．考试时间90分钟．全卷包括三大题，共21题．第一大题为填空题．第二大题为选择题．第三大题为解答题．2．所有题目均做在答题卷上．3．答卷前，务必在答题卷上将班级、姓名、学号、准考证号等填写清楚．友情提示：细心耐心，沉着冷静，诚信应考，收获自信！一、填空题(本大题满分36分) 本大题共有12题，考生应在答题卷的相应编号的空格内直接填写结果，每题填对得3分，否则一律得零分． 1．等差数列{}n a 中，36a =，98a =，则公差d =132．求极限22341lim 2n n n n n →∞+-=- 32-3．无穷等比数列{}n a 的首项为3，公比13q =-，则{}n a 的各项和S =944．数列{}n a 的前n 项和2*10()n S n n N =-∈，则n a = 9,112,2n n n =⎧⎨-≥⎩5．等比数列前n 项和123nn S k ⎛⎫=⋅+ ⎪⎝⎭，则常数k 的值为 2-6．已知两等差数列{}{},n n a b 的前n 的和分别为,n S T 3742n n S n T n +=-，则1010a b = ．32377．若12lim 02nn n n a+→∞=+，则实数a 的取值范围是 ()(),22,-∞-+∞U8．如图给出的是计算111124620++++L 的值的一个程序框图，其中判断框内应填入的条件是_______________．20≤n 或10≤i 9．若11111()1234212f k k k=-+-++--L ，则(1)()f k f k +=+11.2122k k -++ 10．对数列{}n a ，已知lim(2)1n n na →∞=，则[]lim (1)n n n a →∞-= ．12- 11．已知数列{}n a 满足133a =，12n n a a n +-=,则n a n 的最小值为 ．21212．将全体正整数排成一个三角形数阵：1 2 3 4 5 6 7 8 9 10． ． ． ． ． ． ．按照以上排列的规律，第n 行（3n ≥）从左向右的第3个数为 ． 262n n -+二、选择题（本大题满分12分）本大题共有4题，每题有且只有一个正确答案，考生应在答题卷的相应编号的空格内直接填写选项，每题选对得3分，否则一律得零分．13．一套共五册的丛书，计划每两年出版一册，若各书的出版年份之和为10030，则出齐这套书的年份是（ ）()A 2008 ()B 2010()C 2011()D 2012 答案()B14．数列1，（1+2），（1+2+22），⋅⋅⋅，（1+2+22+⋅⋅⋅+2n），⋅⋅⋅的前99项之和是（ ）()A 99299- ()B 100299- ()C 992101- ()D 1002101-答案()D15．已知等比数列{}n a 中21a =，则其前3项的和3S 的取值范围是( )()A (],1-∞- ()B ()(),01,-∞+∞U()C [)3,+∞()D (][),13,-∞-+∞U 答案()D16．已知数列{}n a 的首项10a ≠，其前n 项的和为n S ，且112n n S S a +=+,则limnn na S →∞=( )()A 0 ()B 12()C 1 ()D 2 答案()B三、解答题（本大题满分52分）本大题共有5题，解答下列各题必须在答题卷的相应编号规定区域内写出必要的步骤． 17．（本题满分8分），L的前n项和．解：12na==………………4分)112nS⎡⎤∴=-++++⎣⎦L)112=………………4分18．（本题满分10分）本题共有2个小题，第1小题满分4分，第2小题满分6分．已知{}n a是首项119a=，公差2d=-的等差数列，nS为{}n a的前n项和.⑴求通项na及nS；⑵设{}n nb a-是首项为1，公比为3的等比数列，求数列{}n b的通项公式及其前n项和n T．解：⑴2212,20n na n S n n=-=-+………………………4分⑵13221nnb n-=-+，1231(133)202nnn nT S n n--=++++=-++L……………4分19．（本题满分8分）数列}{na中，nnna⎪⎭⎫⎝⎛+=109)2(，试问n取何值时，na取最大值，并求此最大值．解：假设第k项最大．…………………………1分⎪⎪⎩⎪⎪⎨⎧≥≥-+1111kkkkaaaa⎩⎨⎧≤≥⇒87kk∴7=k或8 …………………………5分∴第7项或第8项最大，最大值为=7a788109=a．…………………………2分20．（本题满分12分）本题共有2个小题，第1小题满分6分，第2小题满分6分．已知数列{}n a满足：()*1131,,03nn nnaa a a n Na+==≠∈+，计算234,,a a a的值，根据计算的结果猜想{}n a 的通项公式，并用数学归纳法．．．．．加以证明． 解：2343313,,4526a a a ====……………………3分猜想：32n a n =+ ……………………3分 证明：⑴当1n =时，11a = ，猜想成立. ……………………1分 ⑵假设当*(,1)n k k N k =∈≥时，猜想成立，即32k a k =+， ……………………1分 则当1n k =+时，193332=== ,333(1)232k k k a k a a k k k ++=++++++猜想也成立. …2分由⑴和⑵，可知32n a n =+对任何*n N ∈都成立． ………1分21．（本题满分14分）第1小题4分，第2小题5分，第3小题5分．记数列}{n a 的前n 项和为n S ，所有奇数项之和为'S ，所有偶数项之和为''S ． （1）若}{n a 是等差数列，项数n 为偶数，首项11=a ，公差32d =，且-''S 15S '=，求n S ； （2）若无穷数列}{n a 满足条件：①n S 531S 1n -=+)(*∈N n ，②'''S S =．求}{n a 的通项； （3）若}{n a 是等差数列，首项01>a ，公差*d N ∈，且36S '=，27S ''=，请写出所有满足条件的数列．解：（1）若数列}a {n 项数n 为偶数，由已知，得-''S 22315S 'n⋅==，…………2分 解得20=n ，…………………………………………………………………1分.3052321920201S n =⨯⨯+⨯=……………………………………………1分 （2）n S 531S 1n -=+Θ)(*∈N n ① 1n 531S --=∴n S )2(≥∈*n N n ， ②①减去②得：531-=+n n a a ． ……………………………………………1分 所以数列}a {n 是从第二项开始的无穷等比数列，公比53-=q ，且1||0<<q由题意，得221'1S q q a a -+=，22''1S qa -=，……………………………………………1分Θ'''S S =，221251a q a a =+=∴， ……………………………………………1分 又n S 531S 1n -=+Θ)(*∈N n ，55821=+∴a a 211=∴a ……………………………1分所以，对应的数列的通项为⎪⎪⎩⎪⎪⎨⎧≥-==-2)53(511212n n a n n ………………………………1分（3）假设数列}a {n 项数n 为偶数，-''S 02S '>⋅=d n与9S '''-=-S 矛盾．故数列}a {n 项数n 不为偶数，………………1分解法1：设数列}a {n 项数12n +=k （N k ∈），则)1(2S 1211231'+⋅+=+⋅⋅⋅++=++k a a a a a k kk a a a a a kk ⋅+=+⋅⋅⋅++=2S 22242''k k a a a a 22121+=++Θ，27361'''=+=∴k k S S ，解得3k =，项数7132n =+⨯=， ……………………………………………2分d a S S S ⋅⨯+==+=2677631'''7Θ，931=+∴d a ，0391>-=d a Θ，3<∴d ．又*N d ∈，所以，1=d 或2=d ． 当1d =时，6a 1=，此时，51)1(6+=⋅-+=n n a n ， 所以，该数列为：6，7，8，9，10，11，12．……………………………………………1分 当2d =时，3a 1=，此时，122)1(3+=⋅-+=n n a n所以，该数列为：3，5，7，9，11，13，15．……………………………………………1分解法2：⎪⎪⎩⎪⎪⎨⎧=⋅-++=⋅-++++27221()(362211)(1()1(11d k k d a k d k k a k ））⎩⎨⎧=⋅+=+++2736)1()1(211d k ka kd k a k ，解得3=k ，项数7132n =+⨯=，……………………2分 d a S S S ⋅⨯+==+=2677631'''7Θ， 931=+∴d a ，0391>-=d a Θ，3<∴d ．又*N d ∈，所以，1=d 或2=d ． 当1d =时，6a 1=，此时，51)1(6+=⋅-+=n n a n ，所以，该数列为：6，7，8，9，10，11，12．……………………………………………1分 当2d =时，3a 1=，此时，122)1(3+=⋅-+=n n a n所以，该数列为：3，5，7，9，11，13，15．……………………………………………1分。

上海市高二下学期期中考试数学试卷一. 填空题1. 从甲地到乙地有2条路可走，从乙地到丙地有3条路可走，从甲地到丁地有4条路可走，从丁地到丙地有2条路可走，从甲地到丙地共有 种不同的走法2. 3600有 个正约数3. 有一组统计数据共10个，它们是2、4、4、5、5、6、7、8、9、x ，已知这组数据的平均数为6，则这组数据的方差为4. 在正方体1111ABCD A B C D -中，异面直线1A B 与11B D 所成角是5. 0到9这10个数字，可以组成 个没有重复数字的三位数6. 在正方体1111ABCD A B C D -中，二面角1A BC D --的大小是7. 直线3445x t y t =+⎧⎨=-⎩（t 为参数）的斜率为 8. 从5个男生，4个女生中任意选两个，则至少有一个女生的概率是9. 如图，已知AB 是平面α的一条斜线，B 为斜足，AO α⊥，O 为垂足，BC 为α内的一条直线，60ABC ∠=︒，45OBC ∠=︒，则斜线AB 和平面α所成角是10. 若将五本不同的书全部分给三个同学，每人至少一本，则有 种不同的分法11. 已知2624120126(243)(1)(1)(1)x x a a x a x a x ++=+++++⋅⋅⋅++，则0246a a a a +++=12. 已知从1n +个球（其中n 个白球，1个黑球）的口袋中取出m 个球（0m n <<，,m n ∈*N ），共有1m n C +种取法，在这1m n C +种取法中，可以分成两类：一类是取出的m 个球全部为白球，另一类是取出1个黑球和1m -个白球，共有01111m m n n C C C C -+种取法，即有等式01m n C C +1111m m n n C C C -+=成立，试根据上述思想，化简下列式子：1122m m m k m k n k n k n k n C C C C C C C ---+++⋅⋅⋅+= （1k m n ≤<≤，*,,k m n ∈N ）二. 选择题13. 若532m m P P =，则m 的值为（ ）A. 5B. 3C. 6D. 714.“直线l 垂直于平面α内的无数条直线”是“l α⊥”的（ ）A. 充分非必要条件B. 必要非充分条件C. 充要条件D. 既不充分也不必要条件15. 关于直角AOB 在定平面α内的射影有如下判断：①可能是的0°角；②可能是锐角；③可能是直角；④可能是钝角；⑤可能是180°的角；其中正确判断的序号是（ ）A. ②③⑤B. ①②③C. ①④⑤D. ①②③④⑤16. 一辆单向行驶的汽车，满载为25人，全程共设14个车站，途中每个车站均可上下乘客，由不同的起点到达不同的终点的乘客应购买不同的车票，在一次单程行驶中，车上最多卖出不同的车票的个数是（） A. 63 B. 65 C. 67 D. 69三. 解答题17. 三个女生和五个男生排成一排.（1）如果女生必须全排在一起，有多少种不同的排法；（2）如果女生必须全分开，有多少种不同的排法.18. 在长方体1111ABCD A B C D -中，2AB =，2BC =，14CC =，M 为棱1CC 的中点.（1）求证：BM ⊥平面11A B M ；（2）求异面直线BM 和1B A 所成的角的大小.19. 某办公室有5位教师，只有3台电脑供他们使用，教师是否使用电脑是相互独立的.（1）若上午某一时段A 、B 、C 三位教师需要使用电脑的概率分别是14、23、25，求这一时段A 、B 、C 三位教师中恰有2位教师使用电脑的概率；（2）若下午某一时段每位教师需要使用电脑的概率都是13，求这一时段办公室电脑数无法满足需求的概率.20. 已知在33()2n x x -的展开式中，第6项为常数项.（1）求n ；（2）求含2x 的项的系数；（3）求展开式中所有的有理项.21. 设四边形ABCD 为矩形，点P 为平面ABCD 外一点，且PA ⊥平面ABCD ，若1PA AB ==，2BC =.（1）求PC 与平面PAD 所成角的大小；（2）在BC 边上是否存在一点G ，使得点D 到平面PAG 的距离为2，若存在，求出BG 的值，若不存在，请说明理由；（3）若点E 是PD 的中点，在△PAB 内确定一点H ，使CH EH +的值最小，并求此时 HB 的值.参考答案一. 填空题1. 142. 453. 5.64. 3π5. 6486. 4π7. 54-8. 13189. 45° 10. 150 11. 61(31)2+ 12. m n k C + 二. 选择题13. A 14. B 15. D 16. C三. 解答题17.（1）4320；（2）14400.18.（1）证明略；（2）10arccos. 19.（1）13；（2）11243. 20.（1）10n =；（2）454；（3）2223101()2T C x =-，556101()2T C =-，8829101()2T C x -=-. 21.（1）5arctan ；（2）存在，1BG =； （3）延长CB 到C '，使得C B CB '=，连结C E '，过E 作EE AD '⊥于E '，∴22141104CH EH C H EH C E EE C E '''''+=+≥=+=+=， 当且仅当C '、H 、E 三点共线时等号成立，∴min 41()2CH EH +=， 过H 作HH AB '⊥于H '，连结HB ，∴在Rt △HH B '中，13HH '=，23H B '=，2222125()()33HB HH H B ''=+=+=.上海市高二第二学期期中数学试卷一、填空题：（本大题共14小题，每小题5分，共70分）1. 在正方体1111ABCD A B C D -中，异面直线1A B 与AD 所成角的大小为 .2. 已知向量()()23,2,3,4,2,a x b x x =+=-，若a b ⊥，则实数x 的值是 .3.球的表面积为216cm π，则球的体积为 .4.一条直线上的3个点A,B,C 到平面M 的距离为1，这条直线和平面的关系是 .5．正四面体侧面与底面所成二面角的余弦值为 .6.圆柱的轴截面是正方形，且面积为4，则圆柱的侧面积为 .7.如图是三角形ABC 的直观图，ABC ∆则平面图形是 .8.把地球看作半径为R 到额球，A 点位于北纬30，东经20，B 点位于北纬30，东经80，则A,B 两点的球面距离是 .9.下面命题：（1）n 条斜线段长相等，则它们在平面内的射影长也相等；（2）直线a,b 不在平面α内，它们在平面α内的射影是两条平行直线，则a//b ；（3）与同一平面所成角相等的两条直线平行；（4）一条直线与一个平面所成角为θ，那么它与平面内任何其它直线所成的角都不小于θ.其中正确的命题序号为 .10.由曲线222,2,2,2x y x y x x ==-==-围成的图形绕y 轴旋转一周所得旋转体的体积为1V ，满足()()2222224,11,11x y x y x y +≤+-≥++≥的点组成的图形绕y 轴旋转一周所得的旋转体的体积为2V ，试写出1V 与2V 的一个关系式 .11.如图，空间四边形OABC 中，,M N 分别是对边,OA BC 的中点，点G 在线段MN 上，分MN 所成的比为2，OG xOA yOB zOC =++,则,,x y z 的值分别为 .12.如图，1111ABCD A B C D -是棱长为1的正方体，任作平面α与对角线1AC 垂直，使得α与正方体的每个面都有公共点，这样得到的截面多边形的面积为S ，周长为l 的范围是为 .（用集合表示） 二、选择题：13．已知,m n 是异面直线，m ⊂平面α，n ⊂平面β，l αβ=，则l 与A.与,m n 相交B.至少与,m n 中的一条相交C. 与,m n 都不相交D. 至多与,m n 中的一条相交14．已知某几何体的三视图如图所示，则该几何体的体积为A. 83πB. 3πC. 103πD. 6π15．连接球面上两点的线段称为球的弦.半径为4的球的两条弦AB ，CD 的长度分别等于27,43，M,N 分别为AB,CD 的中点，每条弦的两端都在球面上运动.下列四个命题：①弦AB,CD 可能相交于点M ；②弦AB,CD 可能相交于点N ；③MN 的最大值为5；④MN 的最小值为1.其中真命题的个数是A. 1个B. 2个C. 3个D. 4个16．四棱锥P ABCD -底面是正方形，侧面PAD 为等边三角形，且侧面PAD ⊥底面ABCD ，点M 在底面正方形ABCD 内运动，且满足MP MC =，则点M 在平面ABCD 内的轨迹一定是三、解答题：本大题共6小题，共90分.解答应写出必要的文字说明或推理、验算过程.17.（本题满分14分）三棱柱111ABC A B C -的底面是等腰直角三角形，190,2,22,BAC AB AC AA ∠====,E F 分别是1,BC AA 的中点，求：（1）FE 与底面所成角的大小；（2）异面直线FE 和1A B 所成角的大小.18.（本题满分14分）图1是某储蓄罐的平面展开图，其中90GCD EDC F ∠=∠=∠=，且,AD CD DE CG FG FE ====，若将五边形CDEFG 看成底面，AD 为高，则该储蓄罐是一个直五棱柱.（1）图2为面ABCD 的直观图，请以此为底面将该储蓄罐的直观图画完整；（2）已知该储蓄罐的容积为31250V cm =求制作该储蓄罐所需材料的总面积S ，（精确到整数位，材料厚度，按键及投币口的面积忽略不计）.19.（本题满分14分）如图，在正四棱柱1111ABCD A B C D -中，14,8AB AA ==（1）求异面直线1B C 与11A C 所成角的大小；（2）若E 是线段1DD 上（不含线段的两端点）的一个动点，请提出一个与三棱锥体积有关的数学问题（注：三棱锥需以点E 和已知四棱柱八个顶点中的三个为顶点构成），并解答所提出的问题.20.（本题满分16分）如图，在底面是菱形的四棱锥P ABCD -中，60,,2.ABC PA AC a PB PD a ∠=====点E 在PD 上，且:2:1PE ED =.（1）证明：PA ⊥平面ABCD ；（2）在棱PB 上是否存在一点F ，使得三棱锥F ABC -是正三棱锥？证明你的结论；（3）求以AC 为棱，EAC 与DAC 为面的二面角θ的大小.21.（本题满分16分）已知圆锥的侧面展开图是一个半圆..（1）求圆锥的母线与底面所成角的大小；（2）过底面中心1O且平行于母线AB的平面，若截面与圆锥侧面的交线是焦参数（焦点到准线的距离）为p的抛物线，求圆锥的全面积；（3）过底面点C作垂直于母线AB的截面，若截面与圆锥侧面的交线是长轴为2a的椭圆，求椭圆的面积（椭圆22221x ya b+=的面积公式为S abπ=）.高二下学期期中考试数学试卷一、填空题（40分）：1.若161615144m P =⨯⨯⨯⨯，则正整数m =_______________；2.已知一个正四面体的棱长为2，则它的高是_______________；3.某校共有师生1800人，现用分层抽样的方法，从所有师生中抽取一个容量为150的样本，已知从学生中抽取的人数为140，则该学校的教师人数是_______________；4.由0，1，2，3组成的没有重复数字的四位数有_______________个；5.某高中元旦晚会有一节目是现代舞，选了5位男生和4位女生参加，舞蹈老师在排练前，让他们男女间隔排列，则排列的方式有_______________种；6.已知正三角形ABC 的边长43，则到三个顶点的距离都为2的平面有_______________个；7.如图，已知正三棱柱111ABC A B C -的各条棱长都是2，M 是1BB 的中点，则异面直线1AC 与CM 所成角的大小是_______________；8.从0、1、2、6、8中任意选择3个不同数作为一元二次方程20ax bx c ++=的三个系数，则所得到的一元二次方程有实数根的概率是_______________；9.设集合{}1,2,3,,2020A =，选择A 的两个非空子集B 和C ，要使C 中最小的数大于B 中的最大数，则不同的选择方法有_______________；10.a ，b 为空间两条互相垂直的直线，直角三角形ABC 的直角边AC 所在直线与a ，b 都垂直，斜边AB 以AC 为旋转轴旋转，30ABC ∠=︒，有下列结论：①当直线AB 与a 成60°角时，AB 与b 成30°角；②当直线AB 与a 成60°角时，AB 与b 成45°角；⑤直线AB 与a 所成角的最大值为60°；④直线AB 与a 所成角的最大值为30°；其中正确的是_______________.（填写所有正确结论的编号）二、选择题（16分）11.已知一组数据6、7、8、x 、y 的平均数是7，则这组数据的中位数是（ ）A.6B.7C.8D.不确定12.已知两个不同的平面α、β，A 、B 、C 是三个不同线的三个点，且它们都在平面α内，则“A 、B 、C 到平面β距离相等”是“平面//α平面β”的（ ）条件A.充要B.充分非必要C.必要非充分D.非充分非必要 13.从集合{}1,2,3,4,,15中任意选择三个不同的数，使得这三个数组成等差数列，这样的等差数列有（ ）个A.98B.56C.84D.49 14.以长方体1111ABCD A B C D -的任意三个顶点为顶点作三角形，从中随机取出2个三角形，则这2个三角形不共面的情兄有（ ）种A.1480B.1468C.1516D.1492三、解答题（10+10+12+12=44分）15.在二项式()32nx -的展开式中.（1）若前3项的二项式系数和等于67，求二项式系数最大的项；（2）若第3项的二项式系数等于第18项的二项式系数，求奇次项系数和.16.2020年初，新型冠状病毒疫情牵动着全国人民的心，某市根据上级要求，在本市某人民医院要选出护理外科、心理治疗方面的专家4人与省专家组一起赶赴武汉参加救助工作，该医院完中现有3名护理专家1A ，2A ，3A ，5名外科专家1B ，2B ，3B ，4B ，5B ，2名心理治疗专家1C ，2C .（1）求1人中有1位外科专家，1位心理治疗师的概率；（2）求至少含有2位外科专家，且外科专家1B 和护理专家1A 不能同时被选的概率.17.如图所示的几何体ABCDEF 中，四边形ABCD 为菱形，//AF DE ，AF ⊥平面ABCD ，BAD α∠=.（1）求证：//BF 平面CDE ；（2）若60α=︒，求直线AE 与平面CDE 所成角的正弦值；（3）若90α=︒，P 是EAC △内的一点，求点P 到平面ABCD ，平面EDA ，平面EDC 的距离的平方和最小值.18.如图，已知正方体1111ABCD A B C D -内接于球O ，且球的半径为3，P ，Q 分别是BC ，1BC 上的动点.（1）求正方体1111ABCD A B C D -的棱长；（2）求1PQ QD +的最小值；（3）若平面1PAB 与平面11ADC B 所成二面角的大小为α，平面1PDC 与平面11ADC B 所成二面角的大小+的最小值，及此时P点的位置. 为β，试求αβ参考答案：1.13；2.3；3.120；4.18；5.2880；6.8；7.90°；8.1124； 9.2019100921⨯+；10.②④；11.B ；12.C ；13.A ；14.B ；。