当前位置：文档之家 › 阻抗和导纳9-1-7

阻抗和导纳9-1-7

  • 格式：ppt
  • 大小：712.50 KB
  • 文档页数：62

下载文档原格式

  / 62

合集下载

其阻抗和导纳为倒数关系

其阻抗和导纳为倒数关系

L XL 2mH
例.

I1
*
*W
+
US
V
–
V1
R jX 1
+
+
U 1
– A2 A3
jX 2 jX 3 U 2


I2
I3
–
正弦稳态电路如图示，已知电压表V读数为220V，V1读数 为100 2 V，电流表A2读数30A，A3的读数 20A ，功率表读 数1000W。求各元件参数R、X1、X2和X3。
U L
R 10 X1 10 1 45 U1 100 2 V
U
2 S

U
2 2

U
2 1
2U1U2
cos 135
U S 220V
U
2 2

2

100
2 (
2 2 )U2 (100
2 )2 2202 0
U
2 2

200U 2

28400

0
,
U2 96V（负值舍去）

318.47 103 90 1049.5 17.7
303.45 72.3 92.11 j289.13
Z2 R2 jL 10 j157
I1 I2 R1
I3
j 1 C
+
R2
Z Z1 Z2 92.11 j289.13 10 j157
另: Z通常为ω的函数 Z(jω)= R(ω) +jX(ω), R(ω)称为电阻分量,X(ω)称为电抗分量 。
二、导纳
1. 定义 • 阻抗Z的倒数定义为导纳,用Y表示

电路第9章 正弦稳态电路的分析

电路第9章 正弦稳态电路的分析

I 1 Y G jC j G jB Y y U L
§9-1
阻抗和导纳
Y—复导纳；|Y| —复导纳的模；y—
导纳角； G —电导(导纳的实部)；
B —电纳(导纳的虚部)；
| Y | G 2 B 2 转换关系： 或 B y arctan G
I
相量图：选电压为参考向量，
u 0
y
IG
.
IB U
I I G2 I B2 I G2 (I C I L )2
注意
RLC并联电路会出现分电流大于总电流的现象
§9-1
阻抗和导纳
+ I R U -
等效电路
IR
1 jC eq
I B
（3）wC<1/wL，B<0，y<0，电路为感性，电流落后电压；
1 Y 0.0128 50.20 Z 78.150.20 0.0082 j0.0098 S 1
R’
L’
1 1 1 0.102mH R 122 L 0.0098 G 0.0082
§9-1
阻抗和导纳
① 一端口N0的阻抗或导纳是由其内部的参数、
y
IG
I
.
U
.
I I I I (I L IC )
2 G 2 B 2 G
2
IC .
IL
§9-1
阻抗和导纳
I
+
IR
R
j Leg
等效电路
I B
U -
（4）wC=1/wL，B=0，j y =0，电路为电阻性， 电流与电压同相。
I
C
IL
I IG

电路邱关源第三版第九章

电路邱关源第三版第九章

+ +
U1
1 jω C
Us U S U1 U 2 200 V U S、U1、U 2 三个相量构成一个等边三角形。 U S 200 60 V U 2 200 0 V， 1 200 120 V U
+
U2
-
(U 2 ) U1
作出相量模型电路图后，仿照直流电路进行分析。 2. 仿直分析：
二、相量图解法：
1. 参考相量的选取原则： 串联： 选电流相量； 并联： 选电压相量。 2. 应非常熟悉单个元件上或一条支路上电压、电流在相位和 幅度上的关系。 直角三角形； 3. 数学工具： 一般三角形：余弦、正弦定理等。
8
例 列图示电路的结点电压方程。
Z3
I3
解： 以结点2为参考结点。
U 结点1： n1 U S 2
1
+
2
U S 3_
3 Z4
+
Z1
_
US2
I 3
4
Z5
结点3： Y3U n1 (Y3 Y4 Y5 )U n3 Y5U n 4 Y3U S 3 结点4： Y1U n1 Y5U n 3 (Y1 Y5 )U n 4 I 3 另有： 3 Y3 (U n1 U S 3 U n 3 ) I
即虚部为零，故 I 与 U S 同相。
+ I
1 j C
I1
j L
IC
令 U S 380 0 V 则 I 2.590 A， I C jCU S j9.66 A
设 I1 I1 1A， 则由KCL有： .590 j9.66 I1 1， 2 9.66 2 2 10 A I1 1 2.590 j9.66 2.59 9.66 arctan 2.59 ∴A1读数为10A。 12

9章_正弦稳态电路的分析n

9章_正弦稳态电路的分析n
9 正弦稳态电路的分析
9-1 阻抗和导纳 9-2 电路的相量图 9-3 正弦稳态电路的分析 9-4 正弦稳态电路的功率 9-5 复功率 9-6 最大功率传输
一、复阻抗Z
9-1 阻抗和导纳
I
+
U
无源 线性
-
I
+
U
Z
-
正弦激励下的无独立源线性网络，定义其入端等效复阻抗Z:
Z

UI
U I
(u
Z 2Ω I=8A ?
两个阻抗并联时,在什么情况下:
1 1 1 成立。
Z Z1 Z2
1. 图示电路中,已知 X L XC R 2Ω 电流表A1的读数为3A,
试问(1)A2和A3的读数为多少? + A1 A2 A3 (2)并联等效阻抗Z为多少? U L R C -
2. 如果某支路的阻抗 Z (8 j6)Ω, 则其导纳
阻抗三角形(impedance triangle)
|Z|
z
R
z > 0
X或
R
z
X |Z|
z < 0

| Z |
R2 X 2

φ arctan X R
R = |Z|cos z X = |Z|sin z
阻抗Z可以用加压求流法计算（含受控源），也可以用复阻 抗的串并联等效计算。
UL超 前I90°
由相量图可求得：
V 读数为141V
UL
100I1 10
U
45°I 45°
100UAB
10 2 I2
练习题
一、 如图电路中，已知：
i
u(t) 10cos(400π t 60o) V

9正弦稳态电路的分析

9正弦稳态电路的分析

一、瞬时功率(instantaneous power)
吸收
p( t ) ui
网络N0吸收能量 O
i、 u 、 p
p( t ) 0
p( t ) 0 网络N0释放能量
• 有正有负，表明有能量交换; 正大于负,表明耗能。
2019/1/23
ωt
Z
24
二、平均功率(average power) ：+
I L
j17.3
-j10
20
10
I 10 A, L: I L 1 17.390 V U
L
I 2
I 1
10 j17.3 V, I U / 20 160 A 20电阻：U R2 R2 2
I I 1.73230 A, U j10 I 17.32 60 V C: I C 1 2 C C
I
+ U Y
对于无源网络N0: + U
I
R
jX
Z Y 1
I
+ U -
| Z | | Y | 1
2019/1/23
0
Z Y
G
jB
8
R、L、C元件的阻抗与导纳
I
+ U R + U -
I
jL
+ U -
I
1 j C
ZR
Y G
22
U n3
2019/1/23
例2：求图示电路的戴维南等效电路。
50 5 I j300 I 解： 6000 50 I 1 1 1
j300 I U OC 1
60 UO C 30 2450 1 j

第九章正弦稳态电路的分析课本部分习题

第九章正弦稳态电路的分析课本部分习题

第九章正弦稳态电路的分析正弦稳态电路的分析应用相量法。

通过引入相量法，建立了阻抗和导纳的概念，给出了KCL，KVL和欧姆定律的相量形式，由于它们与直流电路的分析中所用的同一公式在形式上完全相同，因此能够把分析直流电路的方法，原理，定律，例如，网孔法（回路法），结点法，叠加定理，戴维宁定理，等效电源原理等等直接应用于分析正弦电路的相量模型，其区别仅在于：（1）不直接引用电压电流的瞬时表达式来表征各种关系，而是用对应的向量形式来表征各种关系；（2）相应的运算不是代数运算，而是复数的运算，因而运算比直流复杂。

但根据复数运算的特点，可画出向量图，利用向量图的几何关系来帮助分析和简化计算，从而扩大了求解问题的思路和方法。

（3）引入了一些新的概念，如平均功率，无功功率，视在功率，复功率，最大功率传输，谐振等。

认识以上区别，对正弦稳态电路的分析是有益的。

9-1试求图示各电路的输入阻抗Z和导纳Y。

解：（a）Z=1+=1+=Y====S(b) Z==Y=（c） Y=SZ=题9-1图设端口电压相量为，根据KVL，得所以输入阻抗为导纳设端口电压，电流相量为，，根据KCL，得且有所以输入阻抗导纳注：本题的求解过程说明，引入阻抗和导纳的概念以后，正弦电路的输入阻抗（或导纳）的定义与计算和直流电路输入电阻（或电导）的定义与计算是相似的。

即输入阻抗若有n个阻抗串联，等效阻抗若有n个导纳并联，等效导纳为只不过Ｚ和Ｙ是复数。

９－２已知图示电路中，。

试求电路中合适的元件值（等效）。

解：把u用余弦函数表示有u和I的相量形式为,根据入端导纳的定义，有既图示的两并联元件为电导和电容，其参数为注：以上计算表明，导纳的模等于电流与电压的模值之比，导纳角等于电流与电压的相位差，若导纳角，表示电流超前电压，导纳为电容性，反之为电感性。

9-3 附图中N为不含独立源的一端口，端口电压u，电流I分别如下列各式所示。

试求没一种情况下的输入阻抗Z和导纳Y，并给出等效电路图（包括元件的参数值）。

第九章 正弦稳态电路的分析

第九章正弦稳态电路的分析 §9－1阻抗和导纳§9－2阻抗(导纳)的串联和并联§9－3正弦稳态电路的分析§9－4正弦稳态电路的功率§9－5复功率§9－6最大传输功率§9－7串联电路的谐振§9－8并联电路的谐振串、并联谐振的特性比较§9－1阻抗和导纳一、阻抗1、阻抗的定义无源线性一端口网络等效电路§9－1阻抗和导纳2、单个元件的阻抗电阻电容电感§9－1阻抗和导纳3、RLC 串联电路的阻抗或§9－1阻抗和导纳对于RLC 串联电路：（1）当ωL ＞1/ωC 时§9－1阻抗和导纳（2）当ωL ＜1/ωC时§9－1阻抗和导纳（3）当ωL ＝1/ωC时§9－1阻抗和导纳二、导纳1、导纳的定义无源线性一端口网络等效电路§9－1阻抗和导纳2、单个元件的导纳电阻电容电感§9－1阻抗和导纳3、RLC 并联电路的导纳或§9－1阻抗和导纳对于RLC 并联电路：（1）当ωL ＞1/ωC时§9－1阻抗和导纳（2）当ωL ＜1/ωC 时§9－1阻抗和导纳（3）当ωL = 1/ωC时§9－1阻抗和导纳三、复阻抗和复导纳的等效互换同一个两端口电路阻抗和导纳可以互换，互换的条件为：即：§9－1阻抗和导纳串联电路和其等效的并联电路它的阻抗为：其等效并联电路的导纳为：即等效电导和电纳为：§9－1阻抗和导纳同理，对并联电路，它的导纳为其等效串联电路的阻抗为：即等效电阻和电抗为：§9－1阻抗和导纳)60sin(25 +=t u ωHz f 4103⨯=例9-1电路如图(a)所示，已知：R =15Ω,L =0.3mH,C =0.2μF, ，。

求i ,u R ,u L ,u C 。

VU 605∠=•解：电路的相量模型如图（b ）所示，其中：§9－1阻抗和导纳C j L j R Z ωω1-+=A Z U I 4.3149.04.6354.33605-∠=∠∠==••V I L j U L 4.8642.84.3149.0905.56∠=-∠⨯∠==••ωV I R U R 4.3235.24.3149.015-∠=-∠⨯==••V I Cj U C 4.9395.34.3149.0905.261-∠=-∠⨯-∠==••ω因此总阻抗为总电流为电感电压为电阻电压为电容电压为相量图如图（c ）所示，各量的瞬时式为：§9－1阻抗和导纳例9-2 RL 串联电路如图（a ）所示，求在ω＝106rad/s 时的等效并联电路图（b ）。

第九章-正弦稳态电路的分析

（举例略）
例：9-4-2如图，列出节点电压相量方程
33
-j5Ω
1
2
5Ω 10o A
j12Ω
j5Ω -j10Ω
10Ω -j0.5A
设节点与参考节 点如图
(1 5
1 j10
1 j12
1 )U j5 1
(
1 - j5
1 )U j12 2
00
A
I 2
3
.
1
4
-
300
A
I 3.14300 A
R jωL IU2S（略）
练习9-7
习题：9-1 （b）、（e）
23
9-3 （4）
9-7 9-11
说明：9-7 求R、L时，习题解答单纯根据相量电 路列方程求解较麻烦，借助相量图分析得 到电流电压相量，然后，由
Z
R
jωL
U I
部分答案参考：
9 （1 b)Zin 2 j, Yin 0.4 j0.2
=2A。求电流表 A 读数
1
I
解：利用KCL建立电路方程
+
U
-
A
R1
-j 1
A1 I1
I2 A2
R2
1、设I2 20O
I 1
R1
U
j1 ωC
U00
1 ωC
j1 ωC
I1 1A
I1 14 5O
I14 5O
ωC
2 、I I1 I2 0 . 7 0 7 j 0 . 7 0 7 2 I 2 . 7 0 72 0 . 7 0 72 2.8( A )
Yeq Y1 Y2 Yn — 端口等效导纳
两个阻抗并联，则等效导纳：
Y
Y 1

单元电路(串联阻抗、并联导纳、无耗传输线)的基本网络参量(Z矩阵、Y矩阵、A矩阵、S矩阵、T巨矩阵)

单元电路的网络参量，可以直接根据未归一化网络参量的 定义求得。

也可以根据网络参量间的互换关系，由另一组网络参量转推得到。

一、串联阻抗图 1 串联阻抗由图 1，根据基尔霍夫定律，有：12121I I U U ZI =-⎧⎨=+⎩ (1-1) 1.1 Y 矩阵根据导纳矩阵定义：11111222211222I Y U Y U I Y U Y U =+⎧⎨=+⎩ (1.1-1)将式（1-1）代入，有2111011U I Y U Z ===，1112021U I Y U Z ===-，2221011U I Y U Z===-，1222021U I Y U Z===则[]11122122111=11Y Y Y Y Y Z -⎡⎤⎡⎤=⎢⎥⎢⎥-⎣⎦⎣⎦(1.1-2)1.2 A 矩阵根据转移矩阵定义：11121221212222U A U A I I A U A I =-⎧⎨=-⎩ (1.2-1)将式（1-1）代入，有2111021I U A U ===，211202-U U A Z I ===，2121020I I A U ===，2122021U I A I ===-则[]111221221=01A A Z A A A ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ (1.2-2)1.3 S矩阵根据S矩阵和a矩阵的转换关系：[]11121112212211221221212211122122111221222()12()21=12221111S S a a a a a a a aSS S a a a aa a a aZZ ZZZR ZR Z Z R+---⎡⎤⎡⎤==⎢⎥⎢⎥--+-+++⎣⎦⎣⎦⎤⎥⎥⎢⎥⎢⎢⎣⎡⎤⎥⎥=⎥⎢⎢⎣⎡⎤+-=⎢⎥++-+⎢⎥⎣⎦(1.3-1)考虑Z01=Z02情况，此时R=1，则[]2122ZSZ Z⎡⎤=⎢⎥+⎢⎥⎣⎦(1.3-2) 1.4 T矩阵根据S矩阵和T矩阵的转换关系：[]2211212111111(1)(1)41(1)1111STS SSZ RZ R ZR Z R Z Z R RR Z R ZR Z R ZR Z R Z-⎡⎤=⎢⎥-⎣⎦⎡⎤-+-⎢⎥++⎥=⎥+--+--++⎥++++⎢⎥⎣⎦⎡⎤++--=⎥+--+⎥⎦(1.4-1)考虑Z01=Z02情况，此时R=1，则[]2122Z ZTZ Z⎡⎤+-=⎢⎥-⎢⎥⎣⎦(1.4-2)二、并联导纳图 2 并联导纳由图 2，根据基尔霍夫定律，有：12121U U I I YU =⎧⎨+=⎩ (2-1) 2.1 Z 矩阵根据阻抗矩阵定义，有：11111222211222U Z I Z I U Z I Z I =+⎧⎨=+⎩ (2.1-1) 将式（2-1）代入，有2111011I U Z I Y===，1112021I U Z I Y ===，2221011I U Z I Y ===，1222021I U Z I Y===(2.1-2)即[]1112212211111ZZ Z Z Z Y ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦(2.1-3)2.2 A 矩阵根据转移矩阵定义：11121221212222U A U A I I A U A I =-⎧⎨=-⎩ (2.2-1)将式（1-1）代入，有2111021I U A U ===，2112020-U U A I ===，212102I I A Y U ===，2122021U I A I ===-则[]1112212210=1AA A A A Y ⎡⎤⎡⎤=⎢⎥⎢⎥⎣⎦⎣⎦ (2.2-2)2.3 S矩阵根据S矩阵和a矩阵的转换关系：[]11121112212211221221212211122122111221222()12()21=12221111S S a a a a a a a aSS Sa a a aa a a aYRYRR YRR YR R YR+---⎡⎤⎡⎤==⎢⎥⎢⎥--+-+++⎣⎦⎣⎦⎤⎥⎢⎥⎢⎢⎣⎡⎤⎥⎥=⎥⎢⎢⎣⎡⎤--=⎢++--⎢⎣⎦⎥⎥(2.3-1)考虑Y01=Y02情况，此时R=1，则[]2122YSY Y⎡⎤-=⎢⎥+-⎢⎥⎣⎦(2.3-2) 2.4 T矩阵根据S矩阵和T矩阵的转换关系：[]2211212111111(1)(1)41(1)1111STS SSYR RYR R YRR YR R YR YR R RR YR R YRR YR R YRR YR R YR-⎡⎤=⎢⎥-⎣⎦⎡⎤+-⎢⎥++⎥=⎥------+--⎢⎥++++⎢⎥⎣⎦⎡⎤+++-=⎥---+⎥⎦(2.4-1)考虑Y01=Y02情况，此时R=1，则[]2122Y YTY Y⎡⎤+=⎢⎥--⎢⎥⎣⎦(2.4-2)三、无耗传输线段图 3 无耗传输线段根据传输线方程的解：00()cos sin ()cos sin L L L L U z U z jI Z z U I z I z j z Z ββββ=+⎧⎪⎨=+⎪⎩(3-1)根据传输线方程的关系，22,,L L z U U I I θβ===-，则12202120cos sin sin cos U U jI Z U I j I Z θθθθ=-⎧⎪⎨=-⎪⎩(3-2) 3.1 Z 矩阵根据阻抗矩阵定义，有：11111222211222U Z I Z I U Z I Z I =+⎧⎨=+⎩ (3.1-1)将式（3-2）代入有：212110021cos cot sin I U U Z jZ U I j Z θθθ====- (3.1-2)11120csc I U Z jZ I θ===- (3.1-3)2221001csc I U Z jZI θ===-(3.1-6) 1222002cot I U Z jZ I θ===- (3.1-7)即[]001112002122cot csc csc cot jZ jZ ZZ Z jZ jZ Z Z θθθθ--⎡⎤⎡⎤==⎢⎥⎢⎥--⎣⎦⎣⎦(3.1-8)3.2 Y 矩阵根据导纳矩阵定义：11111222211222I Y U Y U I Y U Y U =+⎧⎨=+⎩ (3.2-1)将式（3-2）代入，根据定义，U 2=0时，将式（3-2）两式相除，有2121101200cos 1cot sin U I I Y j U jI Z Z θθθ====- (3.2-2)根据定义，U 1=0时，由式（3-2_1）有22200cos 1cot sin U I j j U Z Z θθθ=-=-，代入式（3-2_2）有221200011sin (cot )cos sin U U I j j U j Z Z Z θθθθ=--=，进而1112021csc U I Y jU Z θ=== (3.2-3) 根据定义，U 2=0时，由式（3-2_1）有 2221011csc U I Y jU Z θ=== (3.2-4) 根据定义，U 1=0时，由式（3-2_1）有12220200cos 1cot sin U I Y j U jZ Z θθθ====- (3.2-5)由式（3.2-2）-式（3.2-5）有：[]00111221220011cot csc =11csc cot j j Z Z Y Y Y Y Y j j Z Zθθθθ⎡⎤-⎢⎥⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦-⎢⎥(3.2-6)将式（3.1-8）和式（3.2-6）相乘，有 [][]00000000222211cot csc cot csc csc cot 11csc cot 10csc cot 0010csc cot j jZ Z jZ jZ Z Y jZ jZ j j Z Z θθθθθθθθθθθθ⎡⎤-⎢⎥--⎡⎤⎢⎥=⎢⎥⎢⎥--⎣⎦-⎢⎥⎣⎦⎡⎤-⎡⎤==⎢⎥⎢⎥-⎣⎦⎣⎦ (3.2-14)根据式（3-2）以及A 矩阵定义，有211102cos I U A U θ===，2112002sin -U U A jZ I θ===，21210201sin I I A jU Z θ===，212202cos U I A I θ===-。

正弦稳态电路的分析

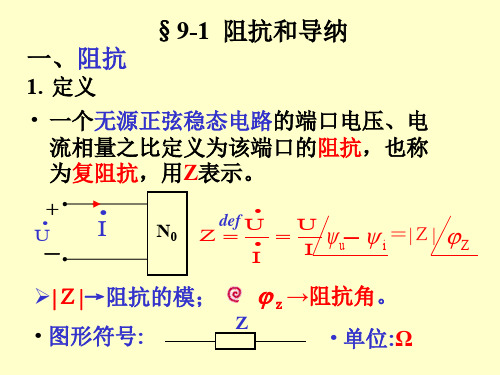
第九章正弦稳态电路的分析本章内容1．阻抗和导纳的概念2．阻抗的串并联及电路的相量图3．正弦稳态电路的分析4．瞬时功率、有功功率、无功功率、视在功率、复功率及最大输出功率5．串联和并联谐振本章重点：正弦量的向量正表示; 正弦电路中的阻抗和导纳;正弦电路的分析串联谐振的谐振条件及特征; 并联谐振的谐振条件及特征本章重点：正弦电路参数的分析及最大功率输出的分析§9-1 阻抗和导纳阻抗和导纳是正弦电流电路分析的重要内容一、阻抗在无源的线性网络中，端口的电压相量与电流相量的比值定义为该一端口的阻抗（复阻抗），用Z表示。

式中：•U=U∠ϕu•I=I∠ϕI阻抗的模：Z= U/I，阻抗角：ϕZ= ϕu-ϕi 阻抗的代数式： Z=R+jX式中：R—电阻 X—电抗1．若网络N 0内只含单一元件，则单一元件的复阻抗（1）电阻的复阻抗：Z R =R（2）电感的复阻抗：Z L =ωj L=jX L X L =ωL —感抗 （3）电容的复阻抗：Z C =cj ω1=c jω1-=jX C X C =cω1-—容抗 2．若网络N 0内为RLC 串联，则阻抗为（1）阻抗：Z=•U /•I = R+ωj L+cj ω1=R+j(ωL-Cω1)=R+jx=Z ϕ∠Z可见：阻抗Z 的实部为电阻R （R=Z cos ϕZ ），阻抗Z 的虚部为电抗X （X= R=Z sin ϕZ ），三者构成阻抗三角形 （2） 阻抗的模：Z =22)(C L X X R -+=22X R +=U/I （3）阻抗角：ϕZ =arctanR X X C L -=RX=ϕu -ϕi X 〉0 ωL>C ω1电路呈电感性 X<0 ωL<Cω1电路呈电容性X=0 电路呈电阻性一、 导纳：复阻抗的倒数定义为复导纳（电流相量与对应端口的电流相量的比值），用Y 表示 Y=Z 1=••UI =)(u i U Iϕϕ-∠=Y Y ϕ∠导纳的模： Y =U I导纳角： Y ϕ=u i ϕϕ- 导纳的代数式： Y=G+JB式中：G —电导 B —电纳1．若网络N 0内只含单一元件，则单一元件的复阻抗 （1） 电阻的复导纳：Y R =G=1/R （2） 电感的复导纳：Y L =Lj ω1=L jω1- =jB L B L =Lω1-—感纳 （3）电容的复导纳：Z C ==ωj C =jB C B C =ωC —容纳2．若网络N 0内为RLC 并联，则导纳为(1)导纳Y=••UI基尔霍夫电流定律的相量形式：∑•I =0•I =•I R +•I L +•I C =⎥⎦⎤⎢⎣⎡-+)1(1L C j R ωω•U =G+j(B C +B L )•UY=R 1+L j ω1+ωj C=R1+)1(L C j ωω-=G+jB可见：导纳Y 的实部为电导G （G=Y cos ϕY ），导纳Y 的虚部为电纳B （B= Y sin ϕY ），三者构成导纳三角形 （2）导纳的模：Y =22)(L C B B G -+=22B G +=I/U （3）阻抗角：ϕY =arctanG B B L C -=GB=ϕi -ϕu B 〉0 ωC>L ω1电路呈电容性 B<0 ωC<Lω1电路呈电感性B=0 电路呈电阻性二、阻抗和导纳相互转换（自学）§9-2 阻抗（导纳）串联和并联阻抗的串并联与电阻的串并联的计算规则相同，只是要把电阻换成阻抗。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

三、正弦量的有效值 一直流电流I和一交流电流i分别通过同一电阻R, 一直流电流I和一交流电流i 内所产生的热量相等， 在同一个周期T内所产生的热量相等， 那么这个 直流电流I的数值就叫做交流电流i的有效值。 直流电流I的数值就叫做交流电流i的有效值。 由此得出 交流电流的有效值为
I
2
RT
= 1 T 1 T
= α ( cos θ + j sin θ ) = α e jθ = α∠θ
三角形式 指数形式 极坐标形式
或
这四种形式可以互换， 这四种形式可以互换，例如 cosθ α1=αcosθ，α2=αsinθ sinθ
α2 α = α1 + α 2 ,θ = tan α1
2 2 −1
uA—uB 。
相量直接求和。 相量直00 = 220 + j0V uB ←→U B = 220/ − 1200 = 220(cos(−1200 ) + j220sin(−1200 ) = −110 − j110 3V uA + uB ←→U A + U B = 110 − j110 3 = 220/ 600V uA − uB ←→U A − U B = 330 + j110 3 = 380/ 60 V
X=
.
.
.
−1 α 0ω x (t ) = sin ωt + ϕ − tan 2 2 α1 α1 + (α 0ω ) 2A = 2A
α12 + (α 0ω ) 2
sin (ωt + ϕ − θ )
α 0ω θ = tan α1
−1
x (t ) =
2A
(α
2 − α 0ω
2 2
（４）反相关系
φ12= φ
1
-φ
2
称这两个正弦量反相。 ＝π, 称这两个正弦量反相。
判断下图正弦量的相位关系： 例：判断下图正弦量的相位关系：
u i u i 0 u1 u2 u i1 i2 i u i u i
ωt ϕ2 ϕ1
0
ωt
0
ωt
π 2
0
ωt
ϕu ϕi
ϕ1 ϕ2
(a)
(b)
(c)
(d)
(a)u和 同相； 解：(a)u和i同相； (b)u1超前u2； 超前u2 (b)u1超前u2； (c)i1和i2反相 反相； (c)i1和i2反相； (d)u和 正交。 (d)u和i正交。
m
sin(ωt+φ)
2π ω= = 2πf T
角频率ω 2. 角频率ω 角频率ω表示正弦量在单位时间内变化的弧度数, 角频率ω表示正弦量在单位时间内变化的弧度数,单位 为rad/s或1/s rad/s或 其中“ 表示正弦量变化一周所需的时间 称为周期。 表示正弦量变化一周所需的时间， 其中“T”表示正弦量变化一周所需的时间，称为周期。 为秒(s)。 为秒(s)。 (s) 单位
0 . . . . .
.
uA + uB = 220 2 (sinωt − 600 )V uA − uB = 380 2 (sinωt + 300 )V
§9－4 相量的线性性质和微分性质
相量法的基础是数学上的变换概念和复数运算。 相量法的基础是数学上的变换概念和复数运算。 相量法可将原来表达正弦量之间关系的微分方 或微分-积分方程） 程（或微分-积分方程）变为联系复数之间关系的代 数方程；将求解微分方程（或微分-积分方程） 数方程；将求解微分方程（或微分-积分方程）变为 求解复数时代数方程。 求解复数时代数方程。只要再对复数的代数方程的 解答进行反变换，便可得出所欲求的正弦量。 解答进行反变换，便可得出所欲求的正弦量。
i(t)=I
m
sin(ωt+φ)
一、正弦量的三要素 1.振幅（最大值） 1.振幅（最大值） 振幅 正弦量瞬时值中的最大值, 正弦量瞬时值中的最大值, 叫振幅 也叫峰值。 用大写字母带下标“ 值, 也叫峰值。 用大写字母带下标“m” 表示, 表示, 如Um、Im等。
i(t)=I
m
sin(ωt+φ)
i(t)=I
一阶
dx α 0 + α1 x = 2 A sin (ωt + ϕ ) dt
d x dx α 0 2 + α1 + α 2 x = 2 A sin (ωt + ϕ ) dt dt
dnx d n −1 x dx α 0 n + α1 n −1 + L + α n −1 + α n x = 2 A sin (ωt + ϕ ) dt dt dt
3. 初相 正弦量解析式中的ωt+φ称为相位角。 称为相位角。
t=0时， 相位为φ， 称其为正弦量的初 =0时
相。
如下图正弦量的三要素： 如下图正弦量的三要素：幅值为Um、 角频率为 ω = 2π = 2πf T 初相为０ 初相为０
u
Um π 0 (T ) 2 2π (T)
α/t
二、相位差 相位差指两个同频率正弦量的相位之差。 相位差指两个同频率正弦量的相位之差。 两个同频率的正弦量
u 1(t)=U u 2(t)=U
1m 2m
sin(ωt+φ1) sin(ωt+φ2)
相位差 φ12 =(ωt+ φ 1 )―(ωt+ φ2 )= φ1 ― φ2 由此得：相位差＝ 由此得：相位差＝初相之差
同频率正弦量的几种相位关系： 同频率正弦量的几种相位关系： （１）超前关系
φ12= φ1-φ2>0且|φ12|≤π弧度， >0且 |≤π弧度， 弧度
由此得出有效值和最大值关系： 由此得出有效值和最大值关系：
Im I= = 0.707 I m 2 Um U= = 0.707U m 2
例：电压有效值为２２０V，则最大值为： 电压有效值为２２０V 则最大值为： ２２０
U m = 220 2 = 311V
原来的 问题 变换域中较 易的问题
原来问题 的解答 变换域问 题的解答
)
+ α12ω 2
−1
sin (ωt + ϕ − θ )
a1ω θ = tan a2 − a0ω 2
x( t ) = 2A sin (ωt +ϕ −θ )
∫ ∫
T 0 T
i 2 R dt i 2 dt
I =
0
同理， 交流电压的有效值为 U = 同理，
∫
T 0
u
2
dt
正弦交流电流的有效值为
1 I= T
∫
T
0
I sin ωtdt =
2 m 2
I T
2 m
∫
T
0
1 − cos 2ωt dt 2
2 2 Im T Im T Im = ( ∫ dt − ∫ cos 2ωtdt ) = (T − 0) = 0 2T 0 2T 2
2
二阶
n阶 阶 任意角频率相同的正弦量以及任意个这种正 弦量的任意阶导数的代数和， 弦量的任意阶导数的代数和，仍为一个同频 率的正弦量
dx α 0 + α1 x = 2 A sin (ωt + ϕ ) dt
α 0 jω X + α1 X = A∠ϕ
αω A A∠ϕ A∠ϕ ∠ϕ = = ∠(ϕ − tan−1 0 ) αω α0 jω +α1 α1 α12 +(α0ω)2 α02ω2 +α12 ∠tan−1 0 α1
２、相量图 相量图就是把正弦量的相量画在复平面上。 相量图就是把正弦量的相量画在复平面上。
Um ej ωt则是一个复值函数。 则是一个复值函数。
+j
f (t )
•
ω t2
0
F
ϕ
2 F = Fm
+1
0 ϕ
•
•
ω t2
2π
ωt
例： 已知正弦电压u1(t)=141 cos(ωt+π/3) V， V， V， u2(t)=70.5cos(ωt-π/6) V， 写出u1和u2的有 效值相量， 并画出相量图。 效值相量， 并画出相量图。 解：
变换的基本思路： 变换的基本思路： 1、把原来的问题变换为一个较容易处理的 问题。 问题。 在变换域中求解问题。 2、在变换域中求解问题。 3、把变换域中求得的解答反变换为原来问 题的解答。 题的解答。
§9－2
A = α1 + jα 2
复数
代数形式
对复数我们早已熟悉，它有四种表达形式， 对复数我们早已熟悉，它有四种表达形式，即
方法： 方法： (1) 写出相应的相量， 并表示为代数形式。 写出相应的相量， 并表示为代数形式。
按复数运算法则进行相量相加， 求出和的相量。 (2) 按复数运算法则进行相量相加， 求出和的相量。 (3) 作相量图， 按照矢量的运算法则求相量和。 作相量图， 按照矢量的运算法则求相量和。
例uA(t)=220sinωt V， )=220sin 220 )=220 220sin( 120° 120 )V， uB(t)=220sin(ωt—120°)V， 求uA+uB和 解:
第九章
阻抗和导纳
§9－1 变换方法的概念 §9－2 复数 §9－3 相量 §9－4 相量的线性性质和微分性质 §9－5 基尔霍夫定理的相量形式 三种基本电路元件VCR VCR的相量形式 §9－6 三种基本电路元件VCR的相量形式 § 9－ 7 VCR向量形式的统一 阻抗和导纳 VCR向量形式的统一—阻抗和导纳 向量形式的统一
称第一量超前第二量 （２）滞后关系 φ12= φ
1
-φ
2
<0且 |≤π弧度 弧度， <0且|φ12|≤π弧度，