计算理论导引习题答案[第2版]CHAP7new
- 格式:pdf
- 大小:382.68 KB
- 文档页数:5

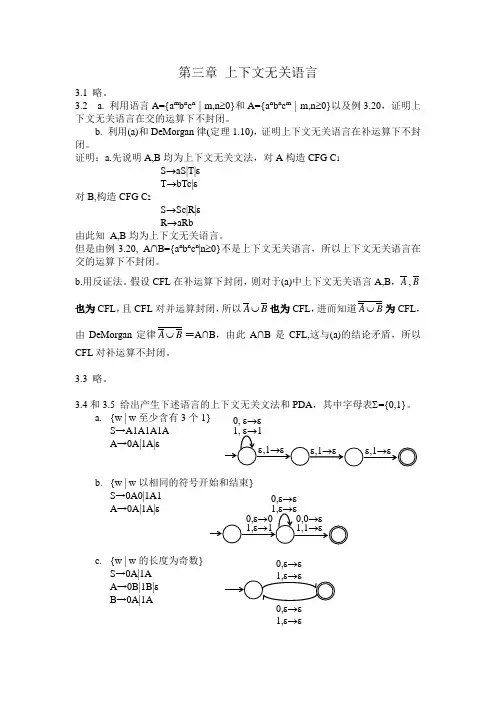
第三章 上下文无关语言3.1 略。
3.2 a. 利用语言A={a m b n c n | m,n ≥0}和A={a n b n c m | m,n ≥0}以及例3.20,证明上下文无关语言在交的运算下不封闭。
b. 利用(a)和DeMorgan 律(定理1.10),证明上下文无关语言在补运算下不封闭。
证明:a.先说明A,B 均为上下文无关文法,对A 构造CFG C 1S →aS|T|εT →bTc|ε对B,构造CFG C 2S →Sc|R|εR →aRb由此知 A,B 均为上下文无关语言。
但是由例3.20, A ∩B={a n b n c n |n ≥0}不是上下文无关语言,所以上下文无关语言在交的运算下不封闭。
b.用反证法。
假设CFL 在补运算下封闭,则对于(a)中上下文无关语言A,B ,A ,B 也为CFL ,且CFL 对并运算封闭,所以B A ⋃也为CFL ,进而知道B A ⋃为CFL ,由DeMorgan 定律B A ⋃=A ∩B ,由此A ∩B 是CFL,这与(a)的结论矛盾,所以CFL 对补运算不封闭。
3.3 略。
3.4和3.5 给出产生下述语言的上下文无关文法和PDA ,其中字母表∑={0,1}。
a. {w | w 至少含有3个1} S →A1A1A1AA →0A|1A|εb. {w | w 以相同的符号开始和结束}S →0A0|1A1 A →0A|1A|εc. {w | w 的长度为奇数} S →0A|1A A →0B|1B|εB →0A|1A0, ε→ε0,ε→ε 0,ε→ε 1,ε→ε 0,ε→εd. {w | w 的长度为奇数且正中间的符号为0}S →0S0|1S1|0S1|1S0|0e. {w | wS →A1A A →0A1|1A0|1A|AA|εf. {w | w=w R }S →0S0|1S1|1|0g.空集S →S3.6 给出产生下述语言的上下文无关文法:a . 字母表{a,b}上a 的个数是b 的个数的两倍的所有字符串组成的集合。
![计算理论导引习题答案[第2版]CHAP5new](https://uimg.taocdn.com/14a23d6565ce0508773213a8.webp)
5.1 证明EQ CFG 是不可判定的。
解:只须证明ALL CFG ≤m EQ CFG 即可。
构造CFG G 1,使L(G 1)=∑*。
设计从ALL CFG 到EQ CFG 的归约函数如下: F=“对于输入<G >,其中G 是CFG :1)输出<G ,G 1>。
”若<G >ALL CFG ,则<G ,G 1>EQ CFG 。
若<G >ALL CFG ,则<G , G 1>EQ CFG 。
F 将ALL CFG 归约到EQ CFG 即ALL CFG ≤m EQ CFG∵ALL CFG 是不可判定的,∴EQ CFG 是不可判定的。
5.2证明EQ CFG 是补图灵可识别的。
证明:注意到A CFG ={<G,w>|G 是能派生串w 的CFG}是可判定的。
构造如下TM : F=“输入<G ,H>,其中G ,H 是CFG ,1) 对于字符串S 1, S 2,,重复如下步骤。
2) 检测S i 是否可以由G 和H 派生。
3) 若G 和H 中有一个能派生w ,而另一个不能,则接受。
”F 识别EQ CFG 的补。
5.3 略。
5.4 如果A m B 且B 是正则语言,这是否蕴涵着A 也是正则语言?为什么? 解:否。
例如:对非正则语言A={0n 1n |n 0}和正则语言B={0},可以构造一个可计算函数f 使得:f(w)=⎩⎨⎧≠=n n nn 10w 1,10w 0, 于是w A f(w)B,故A m B 。
5.5 证明A TM 不可映射规约到E TM 。
证明:反证法假设A TM m E TM , 则有TM m TM E A ≤。
而A TM 的补不是图灵可识别的,从而可知E TM 的补也不是图灵可识别的。
下面构造一个识别E TM 的补的图灵机S :S=“输入<M>,M 是TM,1) 对i=1,2,…重复下一步。
2) 对S 1,S 2,…,S i 模拟M 运行i 步,若有接受,则接受。

第1章概述习题(答案)一.选择题1. D2. B3. CD4. C5. ABC6. A7. B8. B9. ABCD 10. ABCDE二.简答题1.什么是计算机系统?计算机系统是一种能够按照事先存储的程序,自动、高速地对数据进行输入、处理、输出和存储的系统,由计算机硬件系统和计算机软件系统两大部分组成。
2.请解释冯•诺依曼所提出的“存储程序”概念。
把程序和数据都以二进制的形式统一存放在存储器中,由机器自动执行。
不同的程序解决不同的问题,实现了计算机通用计算的功能。
3.控制器的主要功能是什么?控制器基本功能就是从内存中取出指令和执行指令,即控制器按程序计数器指出的指令地址从内存中取出该指令进行译码,然后根据该指令功能向有关部件发出控制命令,执行该指令。
另外,控制器在工作过程中,还要接受各部件反馈回来的信息。
4.简述CPU和主机的概念。
通常把运算器、控制器做在一个大规模集成电路块上称为中央处理器,又称CPU(Central Processing Unit)。
通常把内存储器、运算器和控制器合称为计算机主机,也可以说主机是由CPU与内存储器组成的,而主机以外的装置称为外部设备,外部设备包括输入/输出设备,外存储器等。
5.什么是计算机软件?计算机软件的分类有哪些?软件是指用来指挥计算机运行的各种程序的总和以及开发、使用和维护这些程序所需的技术文档。
计算机软件系统分为系统软件和应用软件。
计算机系统软件由操作系统、语言处理系统、以及各种软件工具等组成,指挥、控制计算机硬件系统按照预定的程序运行、工作,从而达到预定的目标。
应用软件是用户利用计算机软、硬件资源为解决各类应用问题而编写的软件,包括用户程序及其说明性文件资料。
6.计算机有哪些主要的特点?(1)运算速度快、精度高计算机的字长越长,其精度越高,现在世界上最快的计算机每秒可以运算几十万亿次以上。
一般计算机可以有十几位甚至几十位(二进制)有效数字,计算精度可由千分之几到百万分之几,是任何计算工具所望尘莫及的。

计算机导论(第 2 版)【清华大学出版社】课后习题答案第一章绪论一、简答题1.什么是计算机?(P1)计算机是一种能够按照事先存储的程序,自动、高速的对数据进行输入、处理、输出和存储的系统。
一个计算机系统包括硬件和软件两大部分。
2.解释冯•诺依曼所提出的“存储程序”概念。
(P6)把计算机程序与数据都以二进制的形式统一存放在存储器中,由机器自动执行。
不同的程序解决不同的问题,实现了计算机通用计算的功能。
3.计算机有哪些主要的特点?(P3-P4)○1运算速度快○2运算精度高○3具有记忆能力○4具有逻辑判断能力○5存储程序4.计算机有哪些主要的用途?(P4-P5)○1科学计算○2数据处理○3实时控制○5人工智能○5计算机辅助工程和辅助教育○6娱乐与游戏5.计算机发展中各个阶段的主要特点是什么?(P6-P8)第一代计算机(1946 年—1957 年)○1逻辑器件使用电子管○2用穿孔卡片机作为数据和指令的输入设备○3用磁鼓或磁带作为外存储器○4使用机器语言编译第二代计算机(1958 年—1964 年)○1用晶体管代替了电子管○2内存储器采用了磁心体○3引入了寄存器和浮点运算硬件○4利用I/O处理机提高了输入输出能力○5在软件方面配置了子程序库和批处理管理程序,并且推出了FORTRAN、COBOL、ALGOL 等高级程序设计语言及相应的编译程序第三代计算机(1965 年—1971 年)○1用小规模或中小规模的集成电路来代替晶体管等分立元件○2用半导体存储器代替磁心存储器○3使用微程序设计技术简化处理机的结构○4在软件方面则广泛引入多道程序、并行处理、虚拟存储系统以及功能完备的操作系统,同时还提供了大量的面向用户的应用程序第四代计算机(1972 年至今)○1使用了大规模和超大规模集成电路○2使用了大容量的半导体存储器作为内存储器○3在体系结构方面进一步发展了并行处理、多机系统、分布式计算机系统和计算机网络系统○4在软件方面则推出了数据库系统、分布式操作系统以及软件工程标准等第五代计算机主要特征是人工智能,具有一些人类智能的属性。

第三章上下文没关语言略。
a. 利用语言 A={a m b n c n | m,n0} 和 A={a n b n c m | m,n0} 以及例,证明上下文没关语言在交的运算下不关闭。
b.利用 (a) 和 DeMorgan律( 定理,证明上下文没关语言在补运算下不关闭。
证明: a. 先说明 A,B 均为上下文没关文法,对 A 结构 CFG C1S aS|T|T bTc|对 B, 结构 CFG C2S Sc|R|R aRb由此知 A,B 均为上下文没关语言。
0} 不是上下文没关语言,所以上下文无可是由例 , A ∩B={a n b n c n|n 关语言在交的运算下不关闭。
b. 用反证法。
假定 CFL在补运算下关闭,则对于 (a) 中上下文没关语言A,B,A , B也为 CFL,且 CFL对并运算关闭,所以A B也为 CFL,从而知道 A B 为CFL,由DeMorgan定律 A B =A∩B,由此A∩B是CFL,这与 (a) 的结论矛盾,所以 CFL对补运算不关闭。
略。
和给出产生下述语言的上下文没关文法和PDA,其中字母表={0,1} 。
a.{w | w起码含有3个1}0,1,1S→A1A1A1A,1,1,1 A→0A|1A|b.{w | w以同样的符号开始和结束}S→0A0|1A10,1,A→0A|1A|0,00,01,11,1c. {w | w的长度为奇数}0,1,0,1,S →0A|1AA →0B|1B|B →0A|1Ad. {w | w 的长度为奇数且正中间的符号为 0}S →0S0|1S1|0S1|1S0|00, 0 0,0 1,1,0,$ 0,,$e. {w | w 中 1 比 0 多}1,00,1 0S →A1A0, ,11,1 ,$,1,$A →0A1|1A0|1A|AA|f. {w | w=w R }S →0S0|1S1|1|00, 0 0,0 1, 1 1,1 ,1, ,$$ 0,,g. 空集S →S给出产生下述语言的上下文没关文法:a .字母表 {a,b} 上 a 的个数是b 的个数的两倍的全部字符串构成的会合。


定义概念题目:第三章:1. 图灵机:是一种精确的通用计算机模型,能模拟实际计算机的所有计算行为,它的核心是转移函数δ,它说明了机器如何从一个格局走到下一个格局。
对于图灵机,δ的形式如下:Q×Γ→Q×Γ{L,R},图灵机是一个7元组(Q,∑,Γ,δ,q 0,q accept,q reject).其中Q,∑,Γ都是有穷集合,并且1)Q是状态集;2)∑是输入字母表,不包括特殊空白符号凵,3)Γ是带字母表,其中凵∈Г,∑∈Г4)δ2. 格局:图灵机的计算过程中,当前状态,当前内容和读写头当前位置组合在一起。
例如:1011q701111:当前状态q7,当前读写头位置在第二个0上。
定义3.2 如果一个语言能被某一个图灵机识别,则称该语言是图灵可识别的(递归可枚举语言)定义3.2 如果一个语言能被某一个图灵机判定,则称该语言是图灵可判定的简称可判定的(递归语言)3.图灵机的变形:多带图灵机、非确定型图灵机、枚举器。
每个4.枚举器:他是图灵机的一种变形,是带有打印机的图灵机,图灵机把打印机当作输出设备,从而可以打印串,每当图灵机想在打印序列中增加一个串时,就把此串送到打印机。
一个语言是图灵可识别的,当且仅当有枚举器枚举它。
5.图灵机的术语:形式化描述,实现描述,高水平描述。
第四章:1.可判定的语言有:(A DFA、A NFA、A REX、E DFA、EQ DFA 是正则语言)、(A CFG、E CFG 是上下无关语言)❶每个上下文无关语言都是可判定的。
2.不可判定的语言有::EQ CFG、A TM 、停机问题、HALT TM 、E TM、REGULAR TM 、EQ TM 、 E LBA 、ALL CFG 、PCPA TM ={<M,ω>|M是TM,ω是串,M接受ω}是不可判定的。
证明:假设证A TM 是可判定的,下面将由之导出矛盾。
设H是A TM 的判定器。
令M是一个TM,ω是一个串。
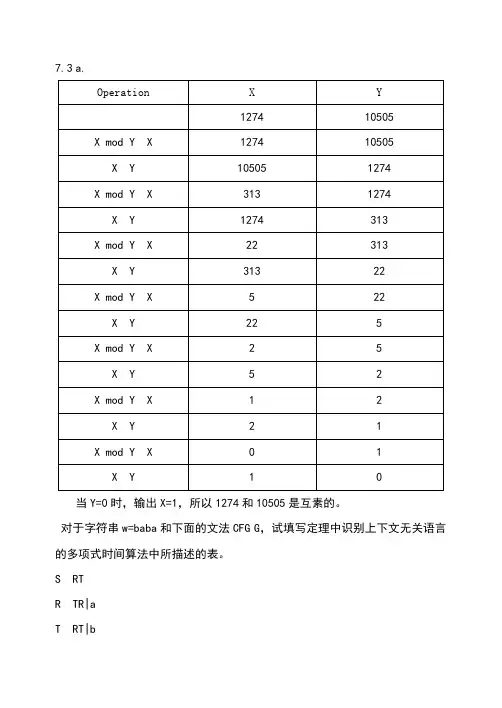
Operation X Y127410505 X mod Y X127410505X Y105051274 X mod Y X3131274X Y1274313 X mod Y X22313X Y31322X mod Y X522X Y225X mod Y X25X Y52X mod Y X12X Y21X mod Y X01X Y10当Y=0时,输出X=1,所以1274和10505是互素的。
对于字符串w=baba和下面的文法CFG G,试填写定理中识别上下文无关语言的多项式时间算法中所描述的表。
S RTR TR|aT RT|bT R,T S R,T,SR S ST R,TR下面的公式是可满足得吗=(x y)(x y)(x y)( x y)解:(x,y)共有四种取值:(true, true),(true, false),(false, true),(false, false).分别将其带入公式得:若(x,y)=(true, true),=(true true) (true false) (false true) (false false)=false若(x,y)=(true, false),=(true false) (true true) (false false) (false true)=false若(x,y)=(false, true),=(false true) (false false) (true true) (true false)=false若(x,y)=(false, false),=(false false) (false true) (true false) (true true)=false所以原公式不可满足。
证明P在并、连接和补运算下封闭。
(1) 并:对任意 L1, L2P,设有n a时间图灵机M1和n b时间图灵机M2判定它们,且c=max{a,b}。
对L1L2构造判定器M:M=“对于输入字符串w :1)在w上运行M1,在w上运行M2。
![计算理论导引习题答案[第2版]CHAP9new](https://uimg.taocdn.com/4af91adb79563c1ec4da7111.webp)
9.1 证明TIME(2n)=TIME(2n+1).证明:2n=O(2n+1)TIME(2n)TIME(2n+1).2n+1=O(2n)TIME(2n+1)TIME(2n).所以TIME(2n)=TIME(2n+1).9.2证明TIME(2n)TIME(22n)。
注:这里“”是严格包含。
证明:令f(n)=22n,则f(n)/logf(n)=22n/2n, 由时间层次定理有TIME(o(22n/2n))TIME(22n).又由于2n=o(22n/2n),TIME(2n)TIME(o(22n/2n)),所以TIME(2n)TIME(22n).9.3 证明NTIME(n)PSPACE.证明:NTIME(n)NSPACE(n)SPACE(n2)SPACE(n3)PSPACE.9.6 证明若A P,则P A=P。
证明:首先P P A。
这是因为不带谕示即可。
下面证明P A P。
任取A P,则存在多项式图灵机T判定A。
设B P A,则存在带语言A的谕示的多项式时间图灵机M A判定B。
如下构造不带谕示的图灵机D:D=“对于输入串w:1)在w上运行M A。
2)每当M A要在谕示带上写下某个字符串x,则在x上运行T,若T接受,则代替谕示回答x属于A,否则代替谕示回答x不属于A。
3)若M A接受,则接受;否则,拒绝。
”设M A的运行时间是n a,T的运行时间是n b。
谕示带上写下的字符串的长度不会超过n a,询问谕示带的次数也不会超过n a。
D的运行时间是n a (n a)b=n a+ab,所以A P。
9.7 给出带指数的正则表达式,产生如下在字母表{0,1}上的语言:a.所有长为500的字符串. (01)500。
b.所有长度不超过500的字符串.(01)500.c.所有不少于500的字符串. (01)500(01)*.d.所有长度不等于500的字符串. (01)499(01)501(01)*.e.所有恰好包含500个1的字符串. 0*(10*)500.f.所有包含至少500个1的字符串. (01)*(1(01)*)500.g.包含至多500个1的字符串. 0*((1)0*)500.h.所有长度不少于500并且在第500个位置上是0的字符串. (01)4990(01)*.i.所有包含两个0并且其间至少相隔500个符号的字符串。

武汉科学与技术学院计算机技术系大学计算机基础实验与习题第二版参考答案供教师参考第1~3、5、7章张葵;第4、9章吴志芳;第6章丁胜;第8章王思鹏张葵整理若有建议及意见,请发邮件至zhangkui@,谢谢您!2015年11月目录第1章概述习题 (1)第2章计算机系统习题 (2)第3章信息在计算机中的表示习题 (7)第4章操作系统基础习题 (10)第5章计算机网络基础习题 (13)第6章程序设计基础习题 (17)第7章数据结构与常用算法习题 (26)第8章数据库技术基础习题 (32)第9章信息安全基础习题 (39)第1章概述习题一、单项选择题1~5 DBCCD 6~10 DCCBB 11~12 AA答案解析:3.除C选项外,其余的关于ENIAC的描述都是正确的。
冯•诺依曼提出的计算机实现的基本思想在ENIAC 计算机之后,所以ENIAC计算机那时还没有采用“程序存储”的思想。
4. 计算机的“存储程序控制”的思想是计算机区别于其他计算机器的主要特征。
A、B、D选项都是计算机的特征,但不是计算机自动工作的主要原因。
5. 早期的计算机都是用于数值计算,随着计算机的普及和发展,才逐渐应用到人工智能、过程控制、信息处理等领域。
6. MIPS表示每秒兆个指令,是表示计算机的运算速度的指标。
8.性价比低和体积小不是所有计算机的特征。
9.计算机的发展历程用第几代来表示,主要以所用的电子元器件来划分的。
12.对计算机的一种分类是依据计算机的CPU的型号来划分的。
B、C、D都不是划分的依据。
二、简答题1. 计算机的定义是什么?答:计算机定义:计算机是一种能按照事先存储的程序,自动、高速地进行大量数值计算和各种信息处理的现代化智能电子装置。
2. 计算机的特点有哪些?答:计算机的特点是:(1)运算速度快;(2)计算精度高;(3)记忆力强;(4)具有逻辑判断能力;(5)可靠性高、通用性强。
3. 计算机有哪些发展趋势?答:计算机的发展趋势:(1)高性能计算;(2)普适计算;(3)云计算;(4)生物计算;(5)智能计算;(6)未来互联网技术。
计算机科学导论第二版答案【篇一:计算机科学导论习题答案】题(答案)一.选择题1. d2. b3. cd4. c5. abc6. a7. b8. b9. abcd 10. abcde二.简答题1.什么是计算机系统?计算机系统是一种能够按照事先存储的程序,自动、高速地对数据进行输入、处理、输出和存储的系统,由计算机硬件系统和计算机软件系统两大部分组成。
2.请解释冯?诺依曼所提出的“存储程序”概念。
把程序和数据都以二进制的形式统一存放在存储器中,由机器自动执行。
不同的程序解决不同的问题,实现了计算机通用计算的功能。
3.控制器的主要功能是什么?控制器基本功能就是从内存中取出指令和执行指令,即控制器按程序计数器指出的指令地址从内存中取出该指令进行译码,然后根据该指令功能向有关部件发出控制命令,执行该指令。
另外,控制器在工作过程中,还要接受各部件反馈回来的信息。
4.简述cpu和主机的概念。
通常把运算器、控制器做在一个大规模集成电路块上称为中央处理器,又称cpu(central processing unit)。
通常把内存储器、运算器和控制器合称为计算机主机,也可以说主机是由cpu与内存储器组成的,而主机以外的装置称为外部设备,外部设备包括输入/输出设备,外存储器等。
5.什么是计算机软件?计算机软件的分类有哪些?软件是指用来指挥计算机运行的各种程序的总和以及开发、使用和维护这些程序所需的技术文档。
计算机软件系统分为系统软件和应用软件。
计算机系统软件由操作系统、语言处理系统、以及各种软件工具等组成,指挥、控制计算机硬件系统按照预定的程序运行、工作,从而达到预定的目标。
应用软件是用户利用计算机软、硬件资源为解决各类应用问题而编写的软件,包括用户程序及其说明性文件资料。
6.计算机有哪些主要的特点?(1)运算速度快、精度高计算机的字长越长,其精度越高,现在世界上最快的计算机每秒可以运算几十万亿次以上。
一般计算机可以有十几位甚至几十位(二进制)有效数字,计算精度可由千分之几到百万分之几,是任何计算工具所望尘莫及的。
第3章数的表示一、复习题1.如何把十进制数转换成二进制数?答:除2逆向取余。
2.如何把二进制数转换成十进制数?答:将每个二进制位乘以它的位权,将所有结果相加得到对应的十进制数。
3.在二进制系统中,每一位是哪一个数的幂?答:2。
4.在十进制系统中,每一位是哪个数的幂?答:10。
5.表示有符号整数有哪三种方法?答:(1)符号加绝对值(原码)(2)二进制反码(3)二进制补码6.最大的无符号整数的含义是什么?答:计算机中分配用于保存无符号整数的二进制位数所确定的最大无符号整数,最大无符号整数取决于计算机中分配用于保存无符号整数的二进制位数N,无符号整数范围:0~ (2N-1)。
7.位数分配指什么?答:用以表示整数的二进制位数.8.为什么不可以将十进制数256存储在8位存储单元中?答:八位存储单元最大存储到255,存储256会产生溢出。
9.试述无符号整数的两种用途?答:(1)计数。
计数时,不需要负数,可以从0或1开始。
(2)寻址。
因为地址是从0开始到整个存储器的总字节数的正数。
10.将十进制数130以符号加绝对值表示法存储在8位存储单元中会怎样?答:会溢出。
因为符号加绝对值表示法在八位存储单元中存储数据的的范围是:-127到+127. 11.分析比较正整数在符号加绝对值、二进制反码、二进制补码三种表示法中的异同。
答:没有不同。
12.分析比较负整数在符号加绝对值、二进制反码、二进制补码三种表示法中的异同。
答:相同点:最左边的位定义的都是符号。
如果为0,则表示正数,如果为1,则表示负数。
不同点:首先将整数的绝对值转换成二进制数,若是负数,符号加绝对值是将最左边的位置1,其余不变;反码是将所有二进制位中的0变为1。
即按位取反。
补码是最右边连续的0和首次出现的1保持不变,其余位逐位取反。
13.分析比较0在符号加绝对值,二进制反码,二进制补码三种表示方法中的异同。
答:符号加绝对值:有两个0,正0(00000000)和负0(10000000)二进制反码:有两个0,正0(00000000)和负0(11111111)二进制补码:只有一个0(00000000)14. 分析比较符号加绝对值,二进制反码,二进制补码三种表示方法中可以表示的数的范围。