当前位置：文档之家 › 运筹学整数规划指派问题

运筹学整数规划指派问题

  • 格式：pptx
  • 大小：435.78 KB
  • 文档页数：34

下载文档原格式

  / 34

合集下载

[理学]运筹学教案整数规划与指派问题

[理学]运筹学教案整数规划与指派问题
6
x2
6
X1<=3
X1>=3+1
5

4


3



(3.25, 2.5)

2



1





o

1
2
3

4

5
67Fra bibliotekx1加上附加约束将问题分为两枝，即两个线性规划问 题，而且保证不丢失正数解。 7
B1：B
xj<=[bj] 分别求解问题B1与B2
B2：B
xj>=[bj]+1
4、定界：以当前目标值最大而又未分枝的子问题 的目标值为上界，当前最好的整数解目标值（若 还没有则选择为负无穷大）为下界。 5、逐步分枝，并求各分技问题，修改上下界，上 界将逐步减小，下畀将逐步增加，直到二者相等， 则得到原整数规划问题的解。 注意：分枝的优先顺序和剪技（不再继续分技） 的条件。以书上例子加以说明。
运筹学教案
整数规划
陈安明
1
4.1 整数规划问题及特点
4.1.1 整数规划的概念
1、整数规划的定义： 决策变量要求取整数的线性规划。 2、整数规划的分类： 纯整数规划：全部决策变量均要求取整数。 混合整数规划：只要部分决策变量要求取整数。 0,1规划：一类变量只取0,1特殊的整数规划问题。 3、整数规划的性质： （1）可行解域为点集。 （2）整数最优解的目标值劣于同问题非整数最优解 的目标值。
max z 3 x1 2 x2 2 x1 3 x2 14 4 x 2 x 18 1 2 x1 , x2 0 x1 , x2为整数 (1) ( 2) (3) ( 4)

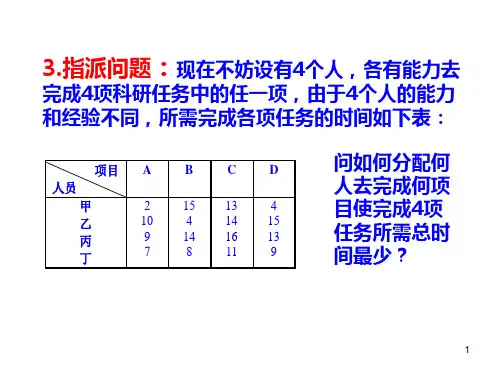
整数规划-案例1-指派问题

整数规划-案例1-指派问题
i 1 j 1
3
4
4
故模型为： min z
ci Βιβλιοθήκη 1 j 144ij
xij
4 xij 1, i 1,2,3,4 j 1 4 xij 1, j 1,2,34 i 1 xij 0 or 1(i, j 1,2,3,4)
设ijx表示第i个人去完成第j项任务则????项任务时个人不去完成第当第项任务时个人去完成第当第jijixij01?项任务时个人不去完成第当第ji0每个人去完成一项任务的约束为????????????1112423222114131211xxxxxxxx每一项任务必有一人完成的约束
3.指派问题：现在不妨设有4个人，各有能力
记 系 数 矩 阵 为
2 15 11 4 10 4 14 15 cij 9 14 16 13 7 8 11 9
称其为效益（价值）矩阵.
cij 表示第 i 个人去完成 第 j 项任务时有关的效
益 （时间、 费用、 价值等） 。 则目标函数可表示为
min z cij xij
4
用lingo求解后，可知让甲去完成任 务D，乙完成任务B，丙完成任务A， 丁完成任务C，所用时间最少为28.
5
x11 x 21 x31 x 41 1 x x x x 1 12 22 32 42 x13 x 23 x33 x 43 1 x14 x 24 x34 x 44 1
2
目标函数：
min z 2 x11 15x12 13x13 4 x14 10x21 4 x22 14x23 15x24 9 x31 14x32 16x33 13x34 7 x41 8 x42 11x43 9 x44

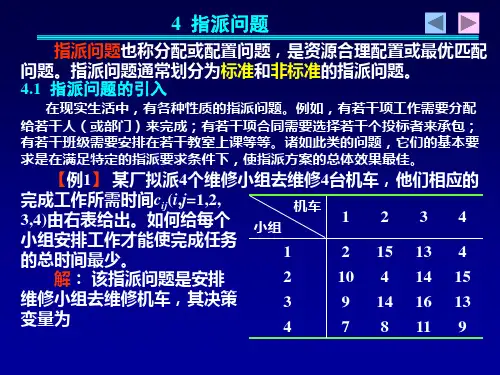
第4章整数规划——指派问题

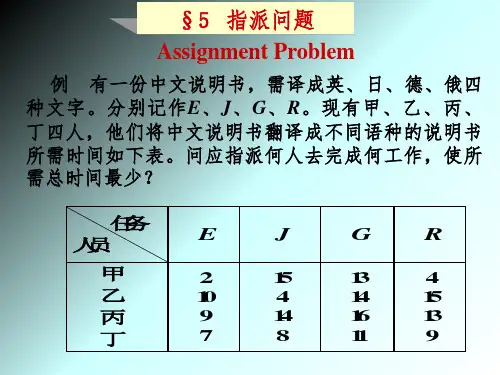
第4章整数规划——指派问题

4 指派问题
解： 可行解｛c12=0， c24 =0， c31 =0， c43 =0｝是一个独立零元素组， c12=0， c24 =0， c31 =0， c43 =0分别称 为独立零元素； ｛c12=0， c23 =0， c31 =0， c44 =0｝也 是一个独立零元素组，而｛c14=0， c23 =0， c31 =0， c44 =0｝就不是独立零元素 组.
4 指派问题
1）对新矩阵中所有不含“*”元素的行打√ ； 2）对打√的行中，所有打×零元素所在的列打√； 3）对所有打√列中标记“*”元素所在行打√； 4）重复上述2），3）步，直到不能进一步打√为止； 5）对未打√的每一行划一直线，对已打√的每一列划一纵线， 即得到覆盖当前0元素的最少直线数。 第四步：对矩阵未被直线覆盖过的元素中找最小元素，将打 √行的各元素减去这个最小元素，将打√列的各元素加上这个最小 元素（以避免打√行中出现负元素），这样就增加了零元素的个 数，返回第二步。 【例5】 求解例1和例2
X (2)
都是指派问题的最优解。
4 指派问题
4.3 指派问题的求解 指派问题既是一类特殊的整数规划问题，又是特殊的运输问 题，因此可以用多种相应的解法来求解，然而这些解法都没有充 分利用指派问题的特殊性质，有效地减少计算量，直到1955年库 恩（W. W. Kuhn）提出的匈牙利法才有效地解决了指派问题。 匈牙利法的理论基础 定义2 独立零元素组 在效率矩阵中，有一组在不同行不同 列的零元素，称为独立零元素组，其每个元素称为独立零元素。 5 0 2 0 2 3 0 0 C 【例4】 已知效率矩阵 0 5 6 7 4 8 0 0 求其独立零元素组。
0 , 不 指 派 Ai 承 建 商 店 B j x ij ( i , j 1, 2 ,3, 4 ,5 ) 1, 指 派 Ai 承 建 商 店 B j

第5章 整数规划(工作指派问题)

第5章 整数规划(工作指派问题)

36
2. “圈0”：
0 10 16 13 6 0 6 3 2 13 13 0 12 2 0 4
37
可以看到，打圈的0的个数为4，正好是矩阵 的阶数。从而得最优解：
• x11=1,x22=1,x34=1,x43=1
相应地，要使机器发挥的总效率最大，我们 应做如下安排：
• • • • 机器A1安排在工地B1； 机器A2安排在工地B2； 机器A3安排在工地B4； 机器A4安排在工地B3。
0
11 2 0
8
0 3 11
2
5 0 4
5
4 0 5
0 11
2 0
8 0
3 11
2 5
0 4
5ห้องสมุดไป่ตู้4
0 5
10
如果在效率系数矩阵中，位于不同行不同 列的零元素的个数与效率系数矩阵(cij)n×n 的阶数n相同，则只要令对应于这些零元 素位置的xij=1，其余的xij=0 ，则此解就 是问题的最优解。
0 0 0 1
为什么只圈出 三个0？？？
30
匈牙利法求工作指派问题步骤小结
1. 2. 3. 4. 5. 6. 列表 约简（包括行约简和列约简） 圈0（也是检验最优解的过程） 画线（画0元素的最少覆盖线） 增0（矩阵变换） 重复3～5（必要的话）
31
求极大值的匈牙利法（P131）
当目标函数为求极大值时，不能用通常改变 系数的符号而成为极小化问题的办法求解， 即如果指派问题的目标函数为： Max z=ΣΣcijxij 我们不能用求解 Min z’=-ΣΣcijxij 的办法来解剖原问题。因为匈牙利法要求效 率系数矩阵的每个元素都是非负的。
3. xij=1 或 0

运筹学第5章：整数规划

运筹学第5章：整数规划
1 xj 0 对项目j投资 对项目j不投资 （j 1， ，n） 2，
则问题可表示为：
max z c j x j
j 1 n
n a j x j B j 1 x1 x2 0 s.t. x3 x4 1 x x x 2 7 5 6 x j 0或1 j 1,2, , n 【例5-3】工厂A1和A2生产某种物资，由于该种物资供不应 求，故需要再建一家工厂，相应的建厂方案有A3和A4两个。这 种物资的需求地有B1、B2、B3、B4四个。各工厂年生产能力、各 地年需求量、各厂至各需求地的单位物资运费cij(j=1,2,3,4) 见表5-2。
三、割平面法的算法步骤
步骤1：将约束条件系数及右端项化为整数，用单纯形法求 解整数规划问题(ILP)的松弛问题(LP)。设得到最优基B，相应 的基最优解为X*。 步骤2：判别X*的所有分量是否全为整数？如是，则X*即为 (ILP)的最优解，算法终止；若否，则取X*中分数最大的分 量 x * ，引入割平面(5.7)。
表5-2
Ai cij A1 A2 Bj B1 2 8 B2 9 3 B3 3 5 B4 4 7 生产能力 (千吨/年) 400 600
A3
A4 需求量(千吨/年)
7
4 350
6
5 400
1
2 30025 150200200工厂A3或A4开工后，每年的生产费用估计分别为1200万元或 1500万元。现要决定应该建设工厂A3还是A4，才能使今后每年 的总费用(即全部物资运费和新工厂生产费用之和)最少。
一般来说，整数线性规划可分为以下几种类型：
1. 纯整数线性规划(Pure Integer Linear Programming)： 指全部决策变量都必须取整数值的整数线性规划，也称为全整 数规划。 2. 混合整数线性规划(Mixed Integer Linear Programming)：指决策变量中一部分必须取整数值，而另一部 分可以不取整数值的整数线性规划。 3. 0-1整数线性规划(Zero-one Integer Linear Programming)：指决策变量只能取0或1两个值的整数线性规划。

整数规划指派问题

整数规划指派问题

丙
9
14
16
13
丁
7
8
11
9
§5 指派问题
Assignment Problem
有n项任务，分派给n个人承担，每人承担一项。
第i 人完成第j 项任务的花费(时间或费用等)为cij， 如何分派使总花费最省？
nn
minz cijxij
第j项工作只由 一个人完成
i1 j1
n
xij 1
( j 1,,n)
i1
4 增加0元素的个数，但不出现负元素
设无直线覆盖的元素中最小的元素为a，对 所有打“√”的行中各元素减去a； 所有打“√”的列中各元素加上a。
再重新试派，直至得到最优解。
整理ppt
8
例8．求表中所示效率矩阵的指派问题的最小解。
任务 A
B
C
D
E
人
甲 12
7
9
6
6
6
丙
7
17 12 14
9
丁 15 14
§5 指派问题
Assignment Problem
例 有一份中文说明书，需译成英、日、德、俄四 种文字。分别记作E、J、G、R。现有甲、乙、丙、 丁四人，他们将中文说明书翻译成不同语种的说明书 所需时间如下表。问应指派何人去完成何工作，使所 需总时间最少？
任务
人员
E
J
G
R
甲
2
15
13
4
乙
10
4
14
15
经行运算即可得每行每列都有 0 元素的系数矩阵，
试派：
5 0 2 0 2
2
3
0
0
0
0 10 5 7 2

第五讲-整数规划与指派问题_图文

固定成本及总运输费用最小的目标为
产量限制约束条件：
销量限制约束条件： （2）增加约束条件
二、整数规划的求解方法概述
整数线性规划，是要求整数解的线性规划， 包括上班的人数、设备的台数、材料的件数等 。
问题：
最优整数解是否可以对非整数 解进行四舍五入法或者去尾法呢？
线性规划的最优解为： 整数规划的最优解为：
同解变化
四、匈牙利解法（续）
定理：覆盖一个方阵内所有0元的最小直线数 等于该阵中位于不同行、列的0元的最多个数 ；
基本思想（反复应用同解变换）
成本矩阵（效益矩阵）的每一行及每一列减去该行或列的 最小数，使每行每列至少有一个0，假如能够从中找出n个位 于不同行、列的0元，则为最优阵，对应最优解。
设
分别为甲、乙两种货物托运的件数，其数学
规划模型如下：
一、整数规划的案例（续 ）
案例2：固定成本问题
高压容器公司制造小、中、大三种尺寸的金属容 器，所用资源为金属板、劳动力和机器设备，制造 一个容器所需的各种资源的数量如下表：
资源
小号容器
中号容器
大号容器
金属板
2
4
8
劳动力
2
34Biblioteka 机器设备12
3
不考虑固定费用，每种容器售出一只所得的利润
三、指派问题
指派问题（Assignment problem）
又称分配问题，研究如何给n个人（或单位） 分配n项工作，使得完成全部工作所消耗的总资 源（时间、费用）最少。
s.t.
例：有一份中文说明书，需译成英、日、德、 俄四种文字。分别记作E、J、G、R。现有甲、 乙、丙、丁四人。他们将中文说明书翻译成不 同语种的说明书所需时间如表所示。问应指派 何人去完成何工作，使所需总时间最少?

运筹学第五章 整数规划

第五章 整数规划主要内容：1、分枝定界法； 2、割平面法； 3、0－1型整数规划； 4、指派问题。

重点与难点：分枝定界法和割平面法的原理、求解方法，0－1型规划模型的建立及求解步骤，用匈牙利法求解指派问题的方法和技巧。

要 求：理解本章内容，熟练掌握求解整数规划的方法和步骤，能够运用这些方法解决实际问题。

§1 问题的提出要求变量取为整数的线性规划问题，称为整数规则问题（简称IP ）。

如果所有的变量都要求为（非负）整数，称之为纯整数规划或全整数规划；如果仅一部分变量要求为整数，称为混合整数规划。

例1 求解下列整数规划问题211020max x x z += ⎪⎪⎩⎪⎪⎨⎧≥≤+≤+为整数21212121,0,13522445x x x x x x x x 如果不考虑整数约束，就是一个线性规划问题（称这样的问题为原问题相应的线性规划问题），很容易求得最优解为：96max ,0,8.421===z x x 。

50用图解法将结果表示于图中画“+”号的点都是可行的整数解，为满足要求，将等值线向原点方向移动，当第一次遇到“+”号点（1,421==x x ）时得最优解为1,421==x x ，最优值为z=90。

由上例可看出，用枚举法是容易想到的，但常常得到最优解比较困难，尤其是遇到变量的取值更多时，就更困难了。

下面介绍几种常用解法。

§2 分枝定界法分枝定界法可用于解纯整数或混合的整数规划问题。

基本思路：设有最大化的整数规划问题A ，与之相应的线性规划问题B ，从解B 开始，若其最优解不符合A 的整数条件，那么B 的最优值必是A 的最优值*z的上界，记为z；而A 的任意可行解的目标函数值是*z的一个下界z，采取将B 的可行域分枝的方法，逐步减少z 和增大z ，最终求得*z 。

现举例说明： 例2 求解A219040max x x z +=⎪⎪⎩⎪⎪⎨⎧≥≤+≤+为整数21212121,0,702075679x x x x x x x x 解：先不考虑条件⑤，即解相应的线性规划B （①--④），得最优解=1x 4.81, =2x 1.82, =0z 356（见下图）。

整数规划2-指派问题


原来的 0 元素不变。这样得到新系数矩阵（其最优解和原问
题相同）。若得到 n 个独立的 0 元素，则已得最优解，否则 重复该步骤继续变换系数矩阵。
匈牙利解法的一般步骤：
5 2 0 9 0
0 3 10 8 6
2 0 5 0 3
0 0 7 0 6
2 0 2 4 5
7 4
0 3 8 8 4
2 0 3 0 1
匈牙利解法:
匈牙利解法的关键是利用了指派问题最优解的如下性质： 若从指派问题的系数矩阵 C = （ cij ）n×n 的某行（或某列）
各元素分别减去一个常数 k ，得到一个新的系数矩阵C’ = （ c’ij ）,
则以 C 和 C’ 为系数矩阵的两个指派问题有相同的最优解。
匈牙利解法的一般步骤:
步骤一： 变换系数矩阵。使其每行及每列至少有一个零元素，同 时不出现负元素。 步骤二： 进行试指派，即确定独立零元素。 步骤三： 继续变换系数矩阵，然后返回步骤二。
5)
对没有打√号的行画一横线，对打√号的列画一竖线， 这样就得到能覆盖所有零元素的最少直线数目的直 线集合。
匈牙利解法的一般步骤：
5
0
2
0
2
2
0
3
10
0
5
0
7
02√源自9086
0
3
0
6
4
5
√
√
匈牙利解法的一般步骤：
继续变换系数矩阵。其方法是在未被直线覆盖的元素中
找出一个最小元素。然后在打√号行各元素都减去这一最小 元素，而在打√号列的各元素都加上这一最小元素，以保证
11 10 7 4 4
2 11 4 2 2
0 6 0 0

06运筹学教案(整数规划与指派问题)


第一步：变换目标函数和约束方程组
B1 A1 A2 2 8 B2 9 3 B3 3 5 B4 4 7 年生产能力 400 600
A3
A4 年需求量
7
4 350
6
5 400
1
2 300
2
5 150
200
200
23
工厂A3或A4开工后，每年的生产费用估计分别为 1200万或1500万元。现要决定应该建设工厂A3还是 A4，才能使今后每年的总费用最少。 解：由于事先不知选择A3还是A4，故可引入0，1 决策变量表述。
即
17
用上述方法构造的线性规划问题的割平面具有 P51两个性质。 4.3.3 割平面法求解整数规划问题的计算步骤： 一、求解其伴随规划问题 若得到整数最优解则终止，否则，选择任一不取 整数的基所在约束行构造割平面方程 二、将此约束标准化，加到最优表中，整理得 一可用对偶单纯形法求解的计算表 三、用对偶单纯形法求解 转一步。 详细见P51~P53例子。
28
y y
i 1
i
i
求解方法： （1）穷举法：以各种组合情况代入约束，计算 约束成立的组合解的目标函数，并得到最优解， 但此法因计算量太大而无效。 （2）各种隐枚举法：增加过滤（约束）条件， 隐去大量不满足过滤条件的组合，减少枚举数量 的方法。
以下介绍一种方法
29
按目标值从优到劣依次列出组合，逐个检验其 可行性，最先满足所有约束据条件的组合为最优解 ，劣于最优解的组合，即使可行，也不列出检验， 隐去。
max z 3 x1 2 x2 2 x1 3 x2 14 4 x 2 x 18 1 2 x1 , x2 0 x1 , x2为整数 (1) ( 2) (3) ( 4)
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

c11 c12
C
c21
c22
c1n c2n
cn1 cn2 cnn
则指派问题的数学模型为
nn
min Z
cij xij
i1 j 1
n
xij 1
i 1,2,n
j1
s.t. n xij 1 j 1,2,ni1源自xij0或1
注：指派问题是一种特殊的LP问题，是一种特殊的运输问题。
cij xij ckj xkj t xkj
i1 j1
j 1
ik
i1 j1
j 1
j 1
ik
n
注意到
xij 1
j 1
nn
所以原式
cij xij t.1 Z t
i1 j1
因此有 min Z min(Z t) min Z t
推论 若将指派问题的效率矩阵每一行及每一列分别减去各 行各列的最小元素，则得到的新的指派问题与原指派问题有 相同的最优解。
指派问题的数学模型
引进0-1变量
1 表示安排第i个人完成第j项工作 xij 0 表示不安排第i个人完成第j项工作
决策变量矩阵可表示为：
x11
X
x21
x12
x22
x1n x2n
xn1 xn2 xnn
用 cij 表示第i个人完成第j项工作所需的资源数，称之为效率
系数（或价值系数）。表示为
0
4
1
-4 -7 -6 -6
1 0 0 0 0
0 0 0 0 1
X
*
0
0
0
1
0
0 1 0 0 0
0
0
1
0
0
-7 从而导出匈牙利解法的思想：
二匈牙利解法 1955年,由库恩（W.W.Kuhn）根据匈牙利数学家狄·考尼 格（d.konig)关于矩阵中独立零元素的定理发明的。
匈牙利法的基本原理： 定理1 将效率矩阵的某一行（或某一列）的各个元素都减去 同一个常数t (t可正可负），得到新的矩阵，则以新矩阵为 效率矩阵的指派问题与原指派问题的最优解相同。但其最 优值比原最优值减少t 。 解：设效率矩阵C为
c11 c21
c12 c22
c1n c2n
C ck1
ck 2
ckn
cn1 cn2 cnn
c11 c21
c12 c22
c1n c2n
C ck1 t
ck 2 t
ckn t
cn1
cn2 cnn
记新指派问题的目标函数为 Z ，
nn
B1 B2 B3 B4 B5
A1 4 8 7 15 12
C
A2 A3
7
6
9 9
17 12
14 6
7
10
A4 6 7 14 8 10
A5
6
9
6
10
8
这是一个标准的指派问题。若设0-1变量
1 xij 0
当 Ai 承建 B j 时 当 Ai 不承建 B j 时
则问题的数学模型为
min Z 4x11 8x12 10 x54 6x55
注：当 cij=0 时，从第i行看，它表示第i人去干第j项工作 效率（相对）最好，而从第j列来看，它表示第j项工作让第i 人来干效率（相对）最高。
问题是：能否找到位于不同行、不同列的n个0元素？ 定义 在效率矩阵C中，有一组处于不同行、不同列的零元素， 称为独立零元素组，此时其中每个元素称为独立零元素。
5
xij 1
i 1,2,5
j1
s.t. 5 xij 1 j 1,2,5
i1
xij
0
或1
B1 B2 B3 B4 B5
A1 4 8 7 15 12
C A2
A3
7
6
9 9
17 12
14 6
7 10
A4 6 7 14 8 10
A5
6
9
6
10
8
如何分派工作?
1 0 0 0 0
nn
n
Z
cij xij
cij xij ckj xkj
i1 j1
i1 j1
j 1
ik
nn
n
nn
n
n
cij xij (ckj t)xkj
cij xij ckj xkj t xkj
i1 j1
j 1
ik
i1 j1
j 1
j 1
ik
nn
n
nn
n
n
cij xij (ckj t)xkj
也是一个独立零元素组。
5 0 2 0
C
2
0 4
3 5 8
0 6 0
0
7 0
不是一个独立零元素组。
定理 效率矩阵C中独立零元素的最多个数等于能覆盖所 有零元素的最少直线数。
本定理由匈牙利数学家狄·考尼格证明的。
例 已知矩阵
5 0 2 0
C
2 0 4
3 5 8
0 6 0
0
7 0
5 0 2 0
C
2
0 4
3 5 8
0 6 0
7 03
例 现有一个4×4的指派问题，其效率矩阵为：
2 15 13 4
C
10
9 7
4 14 8
14 16 11
15 193
求解该指派问题。
步骤1：变换系数矩阵，使得每行及每列至少产生一个零元 素。
2 15 13 4
第三节 0－1型整数规划
0－1变量： 在整数规划问题中，有一类特殊的整数规
划，不仅要求解为整数，而且要求只能取得0 和1两个整数值，这类整数规划称之为0－1型 整数规划，该类解称为0－1变量。
一 指派问题
由n项不同的工作或任务，需要n个人去完成（每人只 能完成一项工作）。由于每人的知识、能力、经验等 不同，故各人完成不同任务所需的时间（或其它资源） 不同。 问应指派哪个人完成何项工作所消耗的总资源最少？
例 已知
5 0 2 0
C
2 0 4
3 5 8
0 6 0
0 70
则 {c12 0, c24 0, c31 0, c43 0} 是一个独立零元素组，
c12 0, c24 0, c31 0, c43 0 分别称为独立零元素。
5 0 2 0
C
2
0 4
3 5 8
0 6 0
0
7 0
0 0 0 0 1
X
*
0
0
0
1
0
0 1 0 0 0
0
0
1
0
0
B1 B2 B3 B4 B5
A1
C A2
A3 A4
4
7
6
6
8 9 9 7
7 17 12 14
15 14 6 8
12 7
10 10
0
3
2
2
1 2 2 0
1 11 6 8
9 8 0 2
5 0
3 3
A5
6
9
6
10
8
2
2
目前认为最简洁的方法—匈牙利法。
例 某商业公司计划开办五家新商店。为了尽早建成
营业，商业公司决定由5家建筑公司分别承建。已知建筑
公司 Ai (i 1,2,,5) 对新商店 Bj ( j 1,2,,5) 的建造
报价（万元）为cij (i, j 1,2,,5) ，商业公司应当对5
家建筑公司怎样分配建筑任务，才能使总的建筑费用最 少？