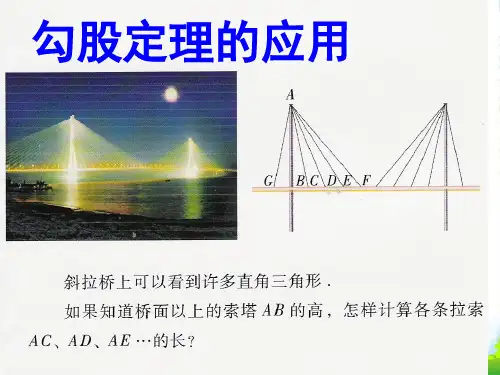
勾股定理与应用1．勾股定理：直角三角形中，斜边的平方等于两条直角边的平方和．2．勾股定理的逆定理：有一条边的平方等于其他两边的平方和的三角形是直角三角形．勾股定理最早的文字记载见于欧几里得（公元前三世纪）的《几何原本》第一卷命题47,“直角三角形斜边上的正方形面积等于两直角边上正方形面积之和”．勾股定理是数学史上一颗璀璨的明珠,在西方又称毕达哥拉斯定理,它是欧几里得几何的重要定理之一，有的数学家形象地称勾股定理为欧氏几何的“拱心石”．数学大师陈省身先生说：“欧几里得几何的主要结论有两个，一个是毕达哥拉斯定理,一个是三角形内角之和等于1800．”华罗庚教授曾建议把它送入其他星球，作为地球人与“外星人"交谈的语言，以探索宇宙的奥妙．到目前为止,勾股定理已有300多种证法．勾股定理揭示了直角三角形的三边之间的关系，对于线段的计算，常可由勾股定理列方程进行求解；对于涉及平方关系的等式证明，可根据勾股定理进行论证；对于已知三角形的三边的长，要判断其形状，则可根据勾股定理的逆定理通过计算进行判定．如果在问题的条件中发现与勾股定理极为类似的形式，就应设法将所涉及的线段集中于一个直角三角形中,或者设法构作出这个直角三角形，再进行证明．我国汉代数学家赵爽著《勾股圆方图》全文530余字，在我国第一次明确给出了勾股定理的理论证明，“案弦图又可以勾股相乘为朱实二，倍之，为朱实四,以勾股之差自相乘为中黄实,加差实亦成弦实”．证明勾股定理的“弦图”,其中“弦实”是弦平方的面积,“弦图"以弦为边作正方形（如正方形ABCD），然后在“弦图"内部作四个直角三角形(如△AHB，△BEC，△CDF，△DAG）．设a，b,c为四个直角三角形的勾、股、弦，则根据“出入相补原理"就有c2＝4×12ab＋（b－a）2c2＝2ab＋b2－2ab＋a2,c2＝a2＋b2．即c2＝2ab＋b2－2ab＋a2，即c2＝a2＋b2．从而巧妙地证明了勾股定理．这是中国古代数学家独立于西方毕达哥拉斯和欧几里得发明的证法．后人沿用“出入相补原理”，也就是割补原理解决了许多数学问题，也创造了“勾股定理”的许多新证法．事实上每位初中同学学了勾股定理，只要用心思考,一定会用割补法想出更新的证明勾股定理的方法．下面的几例拓展,希望细细体会．拓展设a，b，c分别为直角三角形的勾、股、弦．（1）在图 2中，有a2＋b2＝（S3＋S5）＋(S1＋S2＋S4）＝（S4＋S5)＋（S1＋S2＋S3）＝2S2＋S1＋S3＝c2．（2）在图3中，有a2＋b2＝（S3＋S4）＋(S1＋S2)＝S1＋S3＋S4＋S＇2＋S5＝c2（3）在图 4中，有a2＋b2＝（S＋S5)＋（S1＋S3＋S4）2＝S1＋S2＋S3＋S4＋S5＝c2．（4)在图5中,有a2＋b2＝（S′＋S5）＋(S1＋S3＋S4)2＝(S＇2＋S4）＋（S1＋S3＋S5)＝S1＋S2＋S3＋S5＝c2．在课内我们学过了勾股定理及它的逆定理．早在3000年前,我国已有“勾广三，股修四,径阳五”的说法．关于勾股定理，有很多证法,在我国它们都是用拼图形面积方法来证明的．下面的证法1是欧几里得证法．证法1 如图6所示．在Rt△ABC的外侧，以各边为边长分别作正方形ABDE,BCHK，ACFG，它们的面积分别是c2,a2，b2．下面证明，大正方形的面积等于两个小正方形的面积之和．过C引CM∥BD，交AB于L，连接BG，CE．因为AB＝AE，AC＝AG，∠CAE＝∠BAG，所以△ACE≌△AGB（SAS)．而S＝错误!AE×ME＝错误! S AEML，△ACES＝错误!AG×GF＝错误! S ACFG＝错误!b2,△ABG所以 S AEML＝b2．①同理可证 S BLMD＝a2．②①＋②得S ABDE＝S AEML＋S BLMD＝b2＋a2，即c2＝a2＋b2．证法2 如图7所示．将Rt△ABC的两条直角边CA，CB分别延长到D,F，使AD=a,BF=b．构成正方形CDEF(它的边长为a+b)，又在DE上截取DG=b,在EF上截取EH=b,连接AG,GH,HB．由作图易知△ADG≌△GEH≌△HFB≌△ABC，所以AG＝GH＝HB＝AB＝c，∠BAG＝∠AGH＝∠GHB＝∠HBA＝90°，因此，AGHB为边长是c的正方形．显然，正方形CDEF的面积等于正方形AGHB的面积与四个全等的直角三角形(△ABC,△ADG，△GEH，△HFB）的面积和，即（a＋b）2＝c2＋4×错误!ab，化简得a2＋b2＝c2．证法3 如图8在直角三角形ABC的斜边AB上向外作正方形ABDE，延长CB，自E作EG⊥CB延长线于G，自D作DK⊥CB延长线于K，又作AF，DH分别垂直EG于F，H．由作图不难证明,下述各直角三角形均与Rt△ABC全等：△AFE≌△EHD≌△BKD≌△ACB．设五边形ACKDE的面积为S，一方面S＝S ABDE＋2S，①△ABC另一方面S＝S ACGF＋S HGKD＋2S．②△ABC由①，②c2＋2×错误!ab＝b２＋a２＋2×错误!ab，所以c2＝a2＋b2．利用勾股定理，在一般三角形中,可以得到一个更一般的结论．拓展在三角形中，锐角(或钝角)所对的边的平方等于另外两边的平方和，减去（或加上)这两边中的一边与另一边在这边(或其延长线)上的射影的乘积的2倍．证（1)设角C为锐角，如图8所示．作AD⊥BC于D，则CD就是AC在BC上的射影．在直角三角形ABD中,AB2＝AD2＋BD2, ①在直角三角形ACD中，AD2＝AC2－CD2，②又BD2＝(BC-CD)2，③②，③代入①得AB2＝（AC2－CD2)＋(BC－CD）2＝AC2－CD2＋BC2＋CD2－2BC·CD＝AC2＋BC2－2BC·CD,即c2＝a2＋b2－2a·CD．④(2）设角C为钝角，如图10所示．过A作AD与BC延长线垂直于D,则CD就是AC在BC(延长线）上的射影．在直角三角形ABD中，AB2＝AD2＋BD2, ⑤在直角三角形ACD中，AD2＝AC2－CD2，⑥又BD2＝(BC＋CD)2，⑦将⑥,⑦代入⑤得AB2＝（AC2－CD2）＋(BC＋CD）2＝AC2－CD2＋BC2＋CD2＋2BC·CD＝AC2＋BC2＋2BC·CD，即c2＝a2＋b2＋2a·cd．⑧综合④，⑧就是我们所需要的结论c2＝a2＋b2±2a·CD．特别地,当∠C＝90°时，CD＝0，上述结论正是勾股定理的表述：c2＝a2＋b2．因此，我们常又称此定理为广勾股定理（意思是勾股定理在一般三角形中的推广)．由广勾股定理我们可以自然地推导出三角形三边关系对于角的影响．在△ABC中,（1)若c2＝a2＋b2，则∠C＝90°；(2)若c2＜a2＋b2，则∠C＜90°；（3)若c2＞a2＋b2,则∠C＞90°．勾股定理及广勾股定理深刻地揭示了三角形内部的边角关系，因此在解决三角形(及多边形）的问题中有着广泛的应用．尊敬的读者：本文由我和我的同事在百忙中收集整编出来，本文稿在发布之前我们对内容进行仔细校对，但是难免会有不尽如人意之处，如有疏漏之处请指正，希望本文能为您解开疑惑,引发思考。
