对外经济贸易大学 金融计算数值计算
- 格式：pdf
- 大小：469.68 KB
- 文档页数：50
下载文档原格式
合集下载
对外经济贸易大学815经济学综合宏观名词解释总结
对外经济贸易⼤学815经济学综合宏观名词解释总结对外经济贸易⼤学815经济学综合宏观名词解释总结适合科⽬：815经济学1. 国内⽣产总值国内⽣产总值是指经济社会（⼀国或地区）在⼀定时期内运⽤全部⽣产要素所⽣产的全部最终产品的市场价值。
国内⽣产总值是⼀个地域概念。
2. 国民⽣产总值国民⽣产总值是指某国国民所拥有的全部⽣产要素所⽣产的最终产品的市场价值。
国民⽣产总值是⼀个国民概念。
国民⽣产总值核算的⽅法有⽣产法，⽀出法和收⼊法。
3. 消费物价指数CPI消费物价指数也称零售物价指数，是反映消费品价格⽔平变动状况的⼀种价格指数，⼀般是⽤通过对若⼲种主要消费品的零售价格以及服务费⽤进⾏加权平均来编制。
⽤公式表⽰为：CPI=（⼀组固定商品按当期价格计算的价值/⼀组固定商品按基期价格计算的价值）*100%4. 潜在产出潜在产出是指经济中实现了充分就业时所达到的产量⽔平。
它不是⼀个实际产出量，⼀般认为只有在充分就业时，才有可能实现潜在国内⽣产总值，增加潜在产出的途径是增加劳动、资本等⽣产要素投⼊，实现技术进步。
5. GDP 平减指数GDP 平减指数是按当年价格计算的国内⽣产总值和按不变价格计算的国内⽣产总值的⽐率。
⽤公式表⽰为：GDP 平减指数=报告期价格计算的当期国内⽣产总值/基期价格计算的当期国内⽣产总值GDP 平减指数的优点是范围⼴泛，能⽐较准确地反映⼀般物价⽔平的变动趋向。
6. 相对收⼊消费理论相对收⼊消费理论由美国经济学家杜森贝利提出，他认为消费者会受⾃⼰过去的消费习惯以及周围消费⽔准的影响来决定消费。
从⽽消费是相对地决定的。
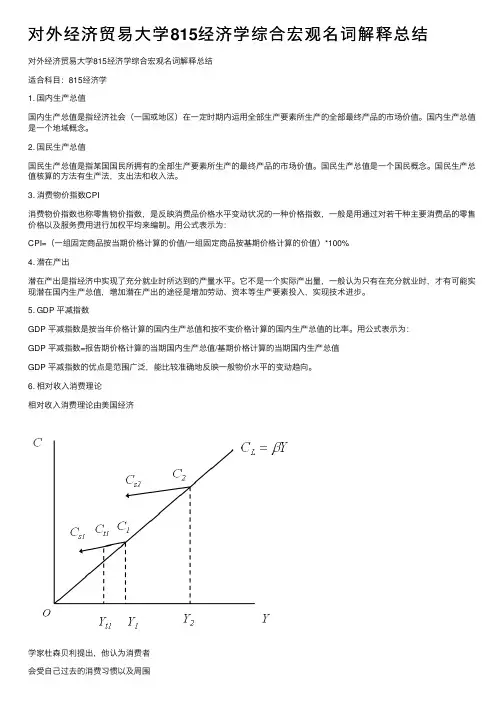
按他的看法，消费与所得在长期维持⼀固定⽐率，故长期消费函数是从原点出发的直线，但短期消费函数则为有正截距的曲线。
如图所⽰，当经济稳定增长时，消费为收⼊的固定⽐率，故长期消费函数为Y C L β=，但当经济景⾊变动时，短期消费函数有着不同形态，例如原先收⼊为Y 1时，消费为C 1，当收⼊由Y 1减少时，消费不遵循C L 途径，⽽是循C S1途径变动，1111Y C Y C t t >，即平均消费倾向变⼤，反之，当收⼊由Y t1逐渐恢复时，消费循着C S1的路径变动，直到达到原来的最⼤⽔平，当经济稳定增长时，⼜⾛Y C L β=的途径，如此，便形成了长期与短期消费函数的区别：长期：Y C L β=，短期：cYC C s +=0 。
对外经济贸易大学保险学院精算学专业（精算与风险管理实验班）人才培养方案
对外经济贸易⼤学保险学院精算学专业（精算与风险管理实验班）⼈才培养⽅案对外经济贸易⼤学保险学院精算学专业(精算与风险管理实验班)培养⽅案⼀、培养⽬标本实验班旨在培养适应建设社会主义现代化国家需要，德、智、体全⾯发展，具有扎实的数学、英语功底，宽厚的经济学、⾦融学、保险学、统计学等相关领域基础知识，熟练掌握最新的精算与风险管理理论、⽅法，具备从事精算与风险管理专业研究的优良素质以及实践⼯作的良好技能，具有国际化、前瞻性专业视⾓的现代精算与风险管理⾼端⼈才。
⼆、专业要求1.具有较宽的基础知识⾯，对于政治、历史、⽂化和⾃然科学等⽅⾯有较深刻的了解；2. ⾄少熟练掌握⼀门外国语，在听、说、读、写、译以及与国外交流等⽅⾯达到较⾼的⽔平；3. 具备扎实的数学、统计学等数量基础，掌握必要的计算机技能，具有较全⾯的经济学、⾦融学、保险学和财务分析能⼒；4. 具有扎实的专业基础，熟练掌握精算与风险管理的基本理论和实务技能；5. 通过听课、课堂讨论、参加研讨会、国际合作交流等多种途径，培养创新的思维意识、国际化视野、研究素质和解决实际问题的能⼒。
三、学分要求学⽣毕业所应取得的最低总学分为173学分，其中包括课程学分和实践教学学分。
要求修读不少于2门暑期学校课程。
⑴学⽣必须完成学校要求的实践教学环节，取得相应学分。
⑵实践教学环节学时学分计算规则：社会实践50学时计1学分；专业实习30学时计1学分；毕业论⽂20学时计1学分。
⑶学⽣在教师的指导下，完成毕业论⽂并通过论⽂答辩。
学院⿎励学⽣进⾏创业类毕业设计，培养⼤学⽣创新创业意识，提⾼学⽣的创业能⼒和实践能⼒。
四、通识通修课程选修要求（专业⼊门课程）五、主要课程1六、授予学位理学学⼠七、考核学⽣成绩考核严格按照《对外经济贸易⼤学学分管理条件》、《对外经济贸易⼤学本科⽣学籍管理办法》及《对外经济贸易⼤学本科⽣成绩管理办法》的有关规定执⾏。
⼋、精算学专业(精算与风险管理实验班)教学计划1《对外经济贸易⼤学学⼠学位授予办法》学⼠学位授予条件要求主要课程平均积点达到2.0。
国际金融计算题常用公式总结
间接标价法下，较小的数值为卖出汇率，较大数值为买入汇率如：巴黎（直接标价法）：USD1=EUR0.7145-0.7165伦敦（间接标价法）：GBP1=USD1.5782-1.5803F=S[1+i/1+i f]：1+i 本国1+i*外国•在直接标价法下，所报点数的小数在前，大数在后，表示升水；相反是贴水•在间接标价法下，所报点数的小数在前，大数在后，表示贴水；相反是升水升水（贴水）数=即期汇率×俩种货币的利率差×天数/360（利率平价原理）•同边相乘：采用不同标价方法时•交叉相除：采用同样的标价法时（基础货币和报价货币相同时）•If S(PHP/USD)=49.9000-50.0000S (PHP/AUD)?•S(AUD/USD)=6.8475-6.8525相同的报价方法/报价货币形同，交叉相除直接标价法下，较小的数值为买入汇率，较大数值为卖出汇率间接标价法下，较小的数值为卖出汇率，较大数值为买入汇率如：巴黎（直接标价法）：USD1=EUR0.7145-0.7165伦敦（间接标价法）：GBP1=USD1.5782-1.5803F=S[1+i/1+i f]：1+i 本国1+i*外国•在直接标价法下，所报点数的小数在前，大数在后，表示升水；相反是贴水•在间接标价法下，所报点数的小数在前，大数在后，表示贴水；相反是升水升水（贴水）数=即期汇率×俩种货币的利率差×天数/360（利率平价原理）•同边相乘：采用不同标价方法时•交叉相除：采用同样的标价法时（基础货币和报价货币相同时）•If S(PHP/USD)=49.9000-50.0000S (PHP/AUD)?•S(AUD/USD)=6.8475-6.8525相同的报价方法/报价货币形同，交叉相除间接标价法下，较小的数值为卖出汇率，较大数值为买入汇率如：巴黎（直接标价法）：USD1=EUR0.7145-0.7165伦敦（间接标价法）：GBP1=USD1.5782-1.5803F=S[1+i/1+i f]：1+i 本国1+i*外国•在直接标价法下，所报点数的小数在前，大数在后，表示升水；相反是贴水•在间接标价法下，所报点数的小数在前，大数在后，表示贴水；相反是升水升水（贴水）数=即期汇率×俩种货币的利率差×天数/360（利率平价原理）•同边相乘：采用不同标价方法时•交叉相除：采用同样的标价法时（基础货币和报价货币相同时）•If S(PHP/USD)=49.9000-50.0000S (PHP/AUD)?•S(AUD/USD)=6.8475-6.8525相同的报价方法/报价货币形同，交叉相除直接标价法下，较小的数值为买入汇率，较大数值为卖出汇率间接标价法下，较小的数值为卖出汇率，较大数值为买入汇率如：巴黎（直接标价法）：USD1=EUR0.7145-0.7165伦敦（间接标价法）：GBP1=USD1.5782-1.5803F=S[1+i/1+i f]：1+i 本国1+i*外国•在直接标价法下，所报点数的小数在前，大数在后，表示升水；相反是贴水•在间接标价法下，所报点数的小数在前，大数在后，表示贴水；相反是升水升水（贴水）数=即期汇率×俩种货币的利率差×天数/360（利率平价原理）•同边相乘：采用不同标价方法时•交叉相除：采用同样的标价法时（基础货币和报价货币相同时）•If S(PHP/USD)=49.9000-50.0000S (PHP/AUD)?•S(AUD/USD)=6.8475-6.8525相同的报价方法/报价货币形同，交叉相除。
2018对外经济贸易大学431金融硕士真题
，免费领取 16 所名校金融硕士真题汇编。 凯程金融硕士的黄埔军校！
2018 对外经济贸易大学 431 金融硕士真题
选择题： 泰勒公式 2011.10 之后，成为准货币的有 货币层次划分 名词解释： 影子银行 久期分析 成本推动型通货膨胀 资本预算 优先股 计算题： 1.货币供给存款 5000，现金 1000，法定存款率百分之十，准备金 700 ①求超额率，货币乘数，基础货币； ②法定率上调 25 个基本点，超额率不变，现金率不变，求基础货币和货币乘数，均保留 两位小数 。 2.设备成本六十万，安装费四千，做调研六千。直线折旧，10 年账面变 0，10 年后能卖 5 万 。开始使用要 3 万零件，然后每年销售收入 2 万，维修费用 2 万，减少人工成本 15 万，资本成本率为百分之 10，税率 33，作现金流量表和估算要不要投资 简答题: 1.请画出 cml 与 sml 的图形，写出方程式，并比较二者不同； 2.为什么有些公司选择回收股票而不是发放股利 3.通货膨胀目标制的内容和优缺点 4.央行作为最后贷款人有哪些手段工具 5.为什么公司更希望发放债券，而不是发放股票，请分析！ 论述题： 1.请简述非常规货币政策的种类与作用，说出它的优缺点。 2.（1）什么是汇率的逆周期性 （2）我国为什么会存在汇率顺周期性 （3）材料中提到的“汇率超调”是什么 （4）用什么措施避免汇率超调 3.简述有效市场有效的三个假设，并说明行为金融如何对这三个假设提出质疑。
2018 对外经济贸易大学 431 金融硕士真题
选择题： 泰勒公式 2011.10 之后，成为准货币的有 货币层次划分 名词解释： 影子银行 久期分析 成本推动型通货膨胀 资本预算 优先股 计算题： 1.货币供给存款 5000，现金 1000，法定存款率百分之十，准备金 700 ①求超额率，货币乘数，基础货币； ②法定率上调 25 个基本点，超额率不变，现金率不变，求基础货币和货币乘数，均保留 两位小数 。 2.设备成本六十万，安装费四千，做调研六千。直线折旧，10 年账面变 0，10 年后能卖 5 万 。开始使用要 3 万零件，然后每年销售收入 2 万，维修费用 2 万，减少人工成本 15 万，资本成本率为百分之 10，税率 33，作现金流量表和估算要不要投资 简答题: 1.请画出 cml 与 sml 的图形，写出方程式，并比较二者不同； 2.为什么有些公司选择回收股票而不是发放股利 3.通货膨胀目标制的内容和优缺点 4.央行作为最后贷款人有哪些手段工具 5.为什么公司更希望发放债券，而不是发放股票，请分析！ 论述题： 1.请简述非常规货币政策的种类与作用，说出它的优缺点。 2.（1）什么是汇率的逆周期性 （2）我国为什么会存在汇率顺周期性 （3）材料中提到的“汇率超调”是什么 （4）用什么措施避免汇率超调 3.简述有效市场有效的三个假设，并说明行为金融如何对这三个假设提出质疑。
国际金融计算公式总结
国际金融计算公式总结国际金融计算是金融领域中重要的分支之一，它主要研究跨国公司、国际金融市场和国际金融机构等与国际金融活动相关的各种问题。
在国际金融计算中，有一些重要的公式被广泛应用于金融分析、决策和风险管理等领域。
本文将对一些常用的国际金融计算公式进行总结，以便读者更好地了解和应用这些公式。
一、货币兑换公式货币兑换公式是国际金融计算的基础公式之一、它用于计算不同货币之间的兑换率。
1、直接报价 currency A / currency B = direct exchange rate直接报价是指以一种货币来衡量另一种货币的价格。
2、间接报价 currency B / currency A = indirect exchange rate间接报价是指以一种货币来表示所需的另一种货币的价格。
3、交叉汇率 cross exchange rate = (direct exchange rate of currency A / direct exchange rate of currency B)交叉汇率是指通过两个货币直接汇率计算出的两个不同货币之间的汇率。
二、利息计算公式利息计算公式用于计算借款或存款的利息。
简单利息计算公式是利用固定利率和借贷时间计算利息的公式。
复合利息计算公式是利用不同计息方式计算出的利息。
三、现金流量计算公式现金流量计算公式用于计算现金流入和流出的金额。
1、净现值计算公式 net present value = present value of cash inflows - present value of cash outflows净现值计算公式是用于衡量项投资项目现金流量的总体价值。
2、内部收益率计算公式 internal rate of return = discount rate at which the net present value equals zero内部收益率计算公式是用于计算投资项目的收益率。
对外经济贸易大学金融专硕431金融学综合复习指导参考书目(1.
对外经济贸易大学金融专硕 431金融学综合复习指导参考书目(120分高分研究生分享一:前言各位同学,大家好!很荣幸有这个机会能和大家探讨考研对外经济贸易大学金融专硕 431的学习,因为在 13年考研中专业课取得了 120分的成绩,现在被外经贸金融学院金融专硕拟录取。
因而想着能为大家分享一些我的经历, 帮助大家在考研外经贸的专业课中取得好的成绩。
我写这个经验谈有两个目的, 第一个目的, 真诚的希望能够提供一些信息帮助到同学们。
第二个目的是毛遂自荐, 我现在在惠园教育兼职考研对外经贸专业课的辅导讲师, 我很乐意这份工作,有需要的同学可以通过惠园教育联系我。
下面我来跟大家详细的探讨专业课应当如何复习的问题, 这里补充一下, 这只是我个人的复习经历和一些感受,作为借鉴,希望大家能够结合自己的特点选择性的吸收。
二、专业课先介绍下我的个人情况,高中是理科生,本科是武汉的工科院校,专业也是工科专业,属于跨地区跨专业考研。
专业知识方面,本科阶段我只初略的看过一点经济和管理相关的书籍, 可以说从考研才开始真正认真学习经济和金融的相关知识, 在初试的复习阶段, 相对于本科是经济或者相关专业的同学来说, 很多知识对我来说都是全新和陌生的, 刚开始学习起来也比较吃力,但最后坚持下来,很多方面感觉收获很大。
所以想告诉大家的是,努力去付出, 就一定会有收获,如果你也是跨地区跨专业考研,坚定信心,找到适合自己的学习方法,坚持下去, 一样可以取得好的成绩; 而对于不是跨考的学生, 也一定不能因为自己本科学过相关的一些知识,就掉以轻心。
考研的专业课的应试,是在大纲限定的知识范围内,有针对性的系统学习, 超纲的范围一般来说不会超过 20%, 而超纲的内容, 不管你本科是不是学经济的,也可能在你的知识范围之外,所以集中时间和精力,主攻下占 80%的基础内容,就可以取得比较好的成绩。
下面介绍我所使用过的参考书目:《货币金融学》 ,中国人民大学出版社,米什金著,郑艳文,荆国勇译 + 米什金版《货币金融学》的课后习题指导书(看了至少三遍,第一遍看课本和指导书,做指导书上的习题,做错的习题重点标记;第二遍看课本,整理知识点,归纳成笔记;第三遍结合整理的笔记和指导书上的知识点看课本和重点习题;后期记忆笔记。
公式推导：投资乘数和对外贸易乘数
投资乘数和对外贸易乘数：假定、结论和政策含义乘数理论是现代西方经济学的重要经济理论之一，最早于1931年由英国经济学家卡恩（凯恩斯的学生）提出，后被凯恩斯加以利用和完善，并把乘数与边际消费倾向(Marginal propensity of Consume ,MPC )结合，作为国民收入决定理论的一个重要组成部分，后来被广泛推广应用于税收、对外贸易等研究领域。
1 ）投资乘数的推导投资乘数指国民收入变动量与引起这种变动的投资量的比率。
如果以△I 代表投资增量，△Y 代表国民收入增量，k 代表投资乘数，则有Y k I ∆=⨯∆（1）直接推演方法 假定国民经济有新增投资量△I ，其中有不变的比例c （0＜c ＜1）用于国民消费(该比例即为边际消费倾向)，则随着投资在国民经济中的连锁效应，国民收入会不断增加：1）国民收入的第一轮增加△I ，意味着新雇工人的收入增加△I ，形成1Y I ∆=∆2）国民收入的第二轮增加：工人用收入的c 比例去购买棉布，带动了棉布的生产，使生产棉布的工人的收入增加：2Y I c c I ∆=∆⨯=∆；3）国民收入的第三轮增加：生产棉布的工人用他们收入的c 比例去购买自行车，使生产自行车的工人收入增加：23Y c I c c I ∆=∆⨯=∆ ；……4）将以上加总，得到：因为0＜c ＜1，所以当n 因为0＜c ＜1，-1＜－c即为投资乘数。
c 是边际消费倾向，(1-c)是边际储蓄倾向(Marginal propensity of Saving ,MPS ，常以s 表示):（2）公式推导方法在两部门经济中（国内经济只有消费和储蓄，没有对外贸易等活动，经济封闭）从总供给角度有：Y=C+S （国民收入=消费+储蓄）从总需求角度有：Y=C+I （国民收入=消费+投资）所以S= I （储蓄=投资）而S=Y-C得△S=△Y -△C设边际消费倾向为c ，即:则:即：投资乘数是1减边际消费倾向的差的倒数，或是边际储蓄倾向(Marginal propensity of Saving ,MPS，以s表示)的倒数。
对外经济贸易大学金融专业考研(米什金)《货币金融学》辅导讲义9
三种类型：1. 一级信贷，又称常备贷款便利，短期，隔夜，向财务健全的银行发放。 2. 二级信贷，给陷入困境的银行，惩罚性的高利率。 3. 季节性信贷。
5. 货币政策工具的变动如何影响联邦基金利率 1）公开市场操作：影响取决于市场最初均衡的位置，两种情况见下图 结论：公开市场购买导致联邦基金利率下跌，公开市场出售相反。 准备金利率是联邦基金利率的下限。 2）贴现贷款：（通过贴现窗口）贴现率一般远大于目标联邦基金率， 因此大部分贴现利率变动不会影响联邦基金率。 3）法定准备金率：提高法定准备金率，任何给定利率水平上准备金需求量增加， 需求曲线右移，联邦基金率上升；反之下降。
一方面抵押品价值增加导致更容易的借款， 另一方面金融机构资本价值增加导致放贷能力增加。 结果是贷款扩张，资产需求增加，继续推高资产价格。 2. 单纯由非理性繁荣驱动的泡沫：来自过分乐观的预期，与信贷无关。
危险性小但几乎无法确认。 2）货币政策是否应该试图刺破资产价格泡沫？——否 1. 加息对资产价格的影响具有高度不确定性。可能导致泡沫突然破裂，加剧破坏力。 2. 某时期泡沫可能只出现在部分资产中。货币政策可能影响所有资产价格，过于生硬。 3. 刺破泡沫的货币政策会危及整体经济。高利率会导致经济放缓等，引发巨额成本。
有些同学对某一回答要点展开说反复说表面看答了不少如小企业对环境适应性强对环境反应敏感船小好掉头利于根据市场调整产品结构等等如此之多只踩对了一个环境方面的得分点应该将回答的要点面扩宽语言要简洁即使答的简练也可得分不要过多叙述解释
对外经济贸易大学金融专业考研（米什
金）《货币金融学》辅导讲义 9
第十三章 中央银行与联邦储备体系
7. 欧洲的中央银行 1）盯住的利率指标被称为目标融资率。 2）公开市场操作：主要再融资操作 + 较长期限再融资操作。 3）贴现率为边际贷款利率，通过边际贷款便利提供贷款。 4）逆向操作，相当于美联储的防御性公开市场操作。
5. 货币政策工具的变动如何影响联邦基金利率 1）公开市场操作：影响取决于市场最初均衡的位置，两种情况见下图 结论：公开市场购买导致联邦基金利率下跌，公开市场出售相反。 准备金利率是联邦基金利率的下限。 2）贴现贷款：（通过贴现窗口）贴现率一般远大于目标联邦基金率， 因此大部分贴现利率变动不会影响联邦基金率。 3）法定准备金率：提高法定准备金率，任何给定利率水平上准备金需求量增加， 需求曲线右移，联邦基金率上升；反之下降。
一方面抵押品价值增加导致更容易的借款， 另一方面金融机构资本价值增加导致放贷能力增加。 结果是贷款扩张，资产需求增加，继续推高资产价格。 2. 单纯由非理性繁荣驱动的泡沫：来自过分乐观的预期，与信贷无关。
危险性小但几乎无法确认。 2）货币政策是否应该试图刺破资产价格泡沫？——否 1. 加息对资产价格的影响具有高度不确定性。可能导致泡沫突然破裂，加剧破坏力。 2. 某时期泡沫可能只出现在部分资产中。货币政策可能影响所有资产价格，过于生硬。 3. 刺破泡沫的货币政策会危及整体经济。高利率会导致经济放缓等，引发巨额成本。
有些同学对某一回答要点展开说反复说表面看答了不少如小企业对环境适应性强对环境反应敏感船小好掉头利于根据市场调整产品结构等等如此之多只踩对了一个环境方面的得分点应该将回答的要点面扩宽语言要简洁即使答的简练也可得分不要过多叙述解释
对外经济贸易大学金融专业考研（米什
金）《货币金融学》辅导讲义 9
第十三章 中央银行与联邦储备体系
7. 欧洲的中央银行 1）盯住的利率指标被称为目标融资率。 2）公开市场操作：主要再融资操作 + 较长期限再融资操作。 3）贴现率为边际贷款利率，通过边际贷款便利提供贷款。 4）逆向操作，相当于美联储的防御性公开市场操作。
2023全国前十金融数学专业大学院校排名
2023全国前十金融数学专业大学院校排名全国前十金融数学专业大学院校排名北京大学(排名第1)、中国人民大学(排名第2)、中央财经大学(排名第3)、对外经济贸易大学(排名第4)、东北财经大学(排名第5)、上海财经大学(排名第6)、厦门大学(排名第7)、清华大学(排名第8)、南开大学(排名第9)、复旦大学(排名第10)。
金融数学专业介绍金融数学又称数理金融学、数学金融学、分析金融学，是利用数学工具研究金融，进行数学建模、理论分析、数值计算等定量分析，以求找到金融学内在规律并用以指导实践。
金融数学也可以理解为现代数学与计算技术在金融领域的应用，因此，金融数学是一门新兴的交叉学科，发展很快，是目前十分活跃的前沿学科之一。
金融数学专业培养掌握数学科学的基本理论与基本方法、基本技能，掌握金融理论基础并接受严格数理金融思维训练，具备运用数学金融知识、使用计算机技术解决实际问题的能力，受到严格科学思维训练，能凭借坚实的数学基础和金融基础，在金融证券、投资、保险等部门从事经济分析、经济建模、金融产品设计工作的专门人才。
金融数学专业就业方向金融数学专业学生毕业后可以到投资银行工作，或者进行商品贸易或国际贸易的公司(能源公司、航空公司、大型钢铁公司、矿业公司及国际大公司)处理商品价格风险及外汇风险数据分析师、管理培训生、数据分析经理、金融工程师、交易员、软件工程师、分析师、数据分析专员、精算师、产品经理、期货交易员、软件测试工程师等。
绝大部分的金融数学家为国际性的投资银行工作。
顶尖的管理咨询公司也雇用金融数学家为那些本身未聘请金融数学家的公司提供服务。
金融数学专业旨在为金融业提供具有定量分析财务能力的专业人才，它着重应用数学和统计学在金融系统中的应用。
该专业在利物浦大学已有多年历史，而且证明毕业生受业面广，极受银行、保险公司等金融机构的欢迎。
该专业在中国首次出现，它将为中国乃至世界金融行业的快速发展提供急需的金融人才。
对外经济贸易大学815经济学综合考研真题详解
跨考网独家整理最全经济学考研真题资料库，您可以在这里查阅历年经济学考研真题，经济学考研资料，经济学参考书等内容，更有跨考考研历年辅导的经济学学哥学姐的经济学考研经验，从前辈中获得的经验对初学者来说是宝贵的财富，这或许能帮你少走弯路，躲开一些陷阱。
以下内容为跨考网独家整理，如您还需更多考研资料，可选择经济学一对一在线咨询进行解答。
2008年对外经济贸易大学815经济学综合考研真题详解一、名词解释（每小题3分，共12分）1．范围经济答：当单个企业的联合产出超过各生产一种产品的两个企业所能达到的总产量时（两个企业分配到相等的投入要素），存在范围经济，即由于产品种类的增加而导致平均成本下降的情况。
企业采用联合生产的方式可以通过使多种产品共同分享设备或其他投入物而获得产出或成本方面的好处，也可以通过统一的营销计划或统一的经营管理获得成本方面的好处。
范围经济的程度可以通过研究企业的成本来确定。
测度范围经济的公式为：()()()()121212C q C q C q q SC C q q +-=，，其中，()1C q 、()2C q 分别表示生产1q 和2q 的产出所耗费的成本；()12C q q ，是生产两种产出所耗费的联合生产成本。
在范围经济的情况下，0SC >；当范围不经济时，0SC <。
总之，SC 的值越大，范围经济的程度就越高。
2．帕累托改进答：帕累托改进是指通过某种方式对既定的资源配置状态予以改变，可以使至少一个人的境况变好，同时其他人的境况至少不变坏，从而增加了社会福利的情况。
利用帕累托最优标准和帕累托改进，可以定义最优资源配置，即如果对于既定的资源配置状态，所有的帕累托改进都不存在，在该状态下，任意改变都不可能使至少有一个人的状况变好而又不使任何人的状况变坏，则这种资源配置状态为帕累托最优状态。
3．成本推动通货膨胀答：成本推动通货膨胀又称为成本通货膨胀或供给通货膨胀，指在没有超额需求的情况下，由于供给方面成本的提高所引起的一般价格水平持续和显著地上涨。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第二章：数值计算简介数值计算的基本概念数值算法优劣的判断数值算法内容介绍2010-9-17金融学院－－金融计算22010-9-17金融学院－－金融计算3§1 数值计算的基本概念软件的核心就是算法。
20 世纪最伟大的科学技术发明---计算机计算机是对人脑的模拟，强化了人的思维智能；没有软件的支持，超级计算机只是一堆废铁而已；算法犹如乐谱，软件犹如CD 盘片，而硬件如同CD 唱机。
什么叫算法？算法定义：由基本运算及运算顺序的规定所构成的完算法。
它可以直接转整的解题步骤，称为算法换为计算机程序。
2010-9-17金融学院－－金融计算42010-9-17金融学院－－金融计算5算法的描述：日常语言和数学语言结合描述程序流程图程序语言例：求解二元一次联立方程组⎩⎨⎧=+=+22221211212111b x a x a b x a x a2010-9-17金融学院－－金融计算6用行列式解法：首先判别12212211a a a a D −=（1）如果，则令计算机计算0≠D () , 1222211D a b a b x −=()Da b a b x 2111122−=输出计算的结果x 1，x 2。
（2）如果D = 0，则或是无解，或有无穷多组解。
是否为零，存在两种可能：日常语言描述2010-9-17金融学院－－金融计算712212211D a a a a −=令通过求解过程，可以总结出算法步骤如下：S2 计算12212211D a a a a −=S3 如果0D =则输出原方程无解或有无穷多组解的信息;否则0D ≠ D 1212112b a b a x −= D 2121221b a b a x −=S1 输入2122211211,,,,,b b a a a a S4 输出计算的结果21,x x 算法语言2010-9-17金融学院－－金融计算8输入2122211211,,,,,b b a a a a D=a 11a 22-a 12a 21D=0开始Da b a b x Da b a b x /)(/)(21111221222211−=−=输出x 1, x 2结束No 输出无解信息Yes 程序流程图现代科学研究的三大支柱理论研究科学实验科学计算计算数学2010-9-17金融学院－－金融计算921世纪信息社会的两个主要特征：“计算机无处不在”“数学无处不在”21世纪信息社会对科技人才的要求：--会“用数学”解决实际问题--会用计算机进行科学计算2010-9-17金融学院－－金融计算102010-9-17金融学院－－金融计算11建立数学模型选取计算方法编写上机程序计算得出结果金融模型的量化过程分析金融问题分析结果解释问题数值计算过程在建立了数学模型之后，并不能立刻用计算机直接求解，由于计算机能够进行加、减、乘、除及逻辑运算，每个解数学问题的算法只能通过计算机能够执行的运算来表示，所以必须将数学模型中的连续变量离散化，编制出计算机可以识别的指令组合，称之为算法，再上机计算得出满意的数值结果。
2010-9-17金融学院－－金融计算121、定义数值计算的定义数值计算方法，是数学的一个分支，对象是研究建立各种数学问题数值计算算法的方法与理论，任务是提供在计算机上可行的、理论可靠的、计算复杂性好的各种常用算法。
2010-9-17金融学院－－金融计算13但并不是所有的问题都可以编制算法进行计算，那些可以编制算法进行计算的问题称为可计算问题，否则称为不可计算的问题，同时可以编制算法的问题也不是全部可以利用计算机实现，有些问题算法太复杂，计算量过大，以致找不到有效的算法，这种问题称为不可处理问题。
2010-9-17金融学院－－金融计算14第二章：数值计算简介数值计算的基本概念数值算法优劣的判断数值算法内容介绍2010-9-17金融学院－－金融计算15§2判断标准评价算法的两个主要标准：速度和精度一个面向计算机,计算复杂性好,存储量少，逻辑结构简单，精度高，又有可靠理论分析的算法就是一个好算法.2010-9-17金融学院－－金融计算161、计算的复杂度：计算复杂性包括时间复杂性和空间复杂性时间复杂性即计算量：一个算法所需基本运算总次数. （包括四则运算，逻辑运算）一个算法所需的乘除运算总次数。
空间复杂性即存储量，指计算过程中需要的存储数量。
2010-9-17金融学院－－金融计算17算法复杂度比较实例1255x例1计算254 A:x255=x.x (x)算法A: (SAS程序) data;x=2;y=x;do i=1 to 254; y=y*x;end;put y;run;计算结果：y=5.7896045E76计算量：N=256存储量：3开始X=2,y=x,i=1i>254Y=y*xi=i+1输出y结束YN2010-9-17金融学院－－金融计算182010-9-17金融学院－－金融计算19实例1（续）B:x 255=x ·x 2·x 4·x 8·x 16·x 32·x 64·x128计算结果：y=5.7896045E76计算量：N=17存储量：4算法B （SAS ）:Data;x=2; s=x;y=x;do i=1 to 7;s=s*s; y=y*s;end;put y;run;算法B复杂度更小，更好！2010-9-17金融学院－－金融计算2032()34262p x x x x =+−+计算多项式例：的值。
231,x x x 由计算法：算出后再算。
需乘法5次，加法3次，存储单元7个。
()[(34)22]6p x x x x =+−+算法：需乘法3次，加法3次，存储单元6个。
算法复杂度比较实例22010-9-17金融学院－－金融计算21算法2、秦九韶算法（1247）(Horner 算法1819)算法1、需乘法2n-1次，加法n次，存储单元n+4个。
0111)(a x a xa x a x P n n n n n ++++=−−L 一般地，计算n 次多项式的值需乘法n次，加法n次，存储单元n+3个。
计算如下例2（续）2010-9-17金融学院－－金融计算22有递推公式1210()(((())n n n n P x x x x x a x a a a a −−=+++++L L nn a s =k k k a xs s +=+10)(s x P n =()0,1,2,,1L −=n k 例2（续）复杂度的度量关键相比较来说，随着计算机的发展，时间复杂性是我们更关注的。
无论是时间复杂度的度量还是空间复杂度的度量，最重要的不是它的精确复杂度，而是复杂度的增长速度，这个速度可以用无穷大阶数来表示。
对于前面两个例子，虽然算法2相对算法1复杂度更小一些，但是就无穷大的阶数来讲是同阶的0(n)，因此，在计算机计算时他们所需要的时间差别并不大。
2010-9-17金融学院－－金融计算232010-9-17金融学院－－金融计算24一、误差的背景介绍1. 来源与分类¾从实际问题中抽象出数学模型——模型误差例3:请描述股票价格与时间之间的关系。
}21exp{2000t W ut s S s S dW S dt S dS t t t t t t σσσμ−+=⇒=+=其中μ为期望收益率,σ为收益波动率。
2.计算精度的度量－－误差2010-9-17金融学院－－金融计算25¾通过测量得到模型中参数的值——观测误差¾求近似解——截断误差¾机器字长有限——舍入误差π= 3.1415926…L 3333.031=x = 8.12345数值计算研究的误差！431()4!xe S x x −=+L2010-9-17金融学院－－金融计算26二、绝对误差、相对误差1．绝对误差与绝对误差限例4:若用以厘米为最小刻度的尺去量桌子的长，大约为1.45米，求1.45米的绝对误差。
1.45米的绝对误差=？不知道！定义1：设x 是准确值，x *为x 的一个近似值，称*)(x x x e −=是近似值x 的绝对误差绝对误差,简称为误差误差。
2010-9-17金融学院－－金融计算27但实际问题往往可以估计出不超过某个正数ε，即，则称ε为绝对误差限，有了绝对误差限就可以知道x 范围为)(x e ε≤−*x x ε±=*x x ],[**εε+−x x 即x 落在内。
在应用上，常常采用下列写法来刻划x *的精度。
εε+≤≤−**x x x2010-9-17金融学院－－金融计算282．相对误差和相对误差限xx x x e *−=定义2：设x 是准确值，x *是近似值，称rxxx ε≤−*满足为近似值x 的相对误差相对误差，相应地，若正数，r ε则称为x 的相对误差限相对误差限。
r ε2010-9-17金融学院－－金融计算293．有效数字则说x*近似表示x 精确到小数后第n 位，并从这第n 位起直到最左边的非零数字之间的一切数字都称为有效数字有效数字，并把有效数字的位数称为有效位数有效位数。
定义3：如果nx x −×≤−1021*410211416.3−×≤−π5102114159.3−×≤−π由上述定义0015926.014.3=−π有效数位为3位0000074.01416.3−=−π有效数位为5位0000926.01415.3=−π有效数位为4位例、误差的传播与积累例5：蝴蝶效应——纽约的一只蝴蝶翅膀一拍，风和日丽的北京就刮起台风来了？！NY BJ以上是一个病态问题2010-9-17金融学院－－金融计算30度量误差的原则当某个量的准确值很小或很大时，相对误差比绝对误差更能反映准确数与近似数的差异。
在数值计算中，尽可能多地保留近似数的有效数字，有效数字越多，相对误差越小，计算结果越精确。
2010-9-17金融学院－－金融计算312010-9-17金融学院－－金融计算323、数值计算减小误差的方法1．要使用数值稳定的算法例6：求（n = 0, 1, 2, …, 8）的值。
∫+=10dx 5x x I nn 解：由于nx x x x I I n n n n n 1dx dx 5551011011==++=+∫∫−−−初值)2.1ln(5ln 6ln dx 51100=−=+=∫x I2010-9-17金融学院－－金融计算33递推公式⎪⎩⎪⎨⎧=−==−)8,,2,1(,51)2.1ln(10L n I n I I n n 按上式就可以逐步算出09.05101≈−=I I 05.052112≈−=I I Whathappened?!025.155145≈−=I I 952.456156−≈−=I I 不稳定的算法！……….2010-9-17金融学院－－金融计算34这就是误差传播所引起的危害!改变公式：n I I n n 151=+−将公式变为不妨设I 9 ≈I 10，于是由10951501I I −=可求得I 9 ≈0.017，按上式可逐次求得)1,,1,( 51511L −=−=−n n K I K I K k2010-9-17金融学院－－金融计算35I 8 ≈0.019I 7 ≈0.021I 6 ≈0.024I 5 ≈0.028I 4 ≈0.034I 3 ≈0.043I 2 ≈0.058I 1 ≈0.088I 0 ≈0.182稳定的算法！2．要避免两个相似数相减在数值计算中，两个相近的数作减法时有效数字会损失。