2019年(新人教版)八年级数学上册期末复习提纲

人教版八年级数学上学期期末复习：第13章《轴对称》填空题精选一．填空题（共30小题）1．（2020春•渝中区校级期末）如图，P为△ABC内一点，过点P的线段MN分别交AB、BC于点M、N，且M、N分别在P A、PC的中垂线上．若∠ABC＝80°，则∠APC的度数为．2．（2020春•沙坪坝区期末）如图，在Rt△ABC中，∠C＝90°，∠A＝30°，AB＝6，BD是△ABC的角平分线，点P，点N分别是BD，AC边上的动点，点M在BC上，且BM＝1，则PM+PN的最小值为．3．（2019秋•九龙坡区校级期末）已知△ABC为等腰三角形，AB＝AC＝10，BC＝8，BD为∠ABC的平分线，点P 为线段BD上的一动点，过点P作线段AB的垂线，垂足为点M，连接AP，则PM+P A的最小值为．4．（2020春•沙坪坝区校级期末）如图所示，在等腰△ABC中，AB＝AC，∠B＝50°，D为BC的中点，点E在AB 上，∠AED＝73°，若点P是等腰△ABC的腰上的一点，则当△EDP为以DE为腰的等腰三角形时，∠EDP的度数是．5．（2019秋•渝中区校级期末）如图所示，在△ABC中，∠C＝90°，DE垂直平分AB，交BC于点E，垂足为点D，BE＝6cm，∠B＝15°，则AC等于．6．（2019秋•渝中区校级期末）在平面直角坐标系中，若点A（a，b）与点B（1，﹣2）关于y轴对称，则a+b＝．7．（2019秋•巴南区期末）如图，△ABC中，∠ABC的平分线与∠ACB的外角平分线相交于点D，点E，F分别在线段BD、CD上，点G在EF的延长线上，△EFD与△EFH关于直线EF对称，若∠A＝60°，∠BEH＝84°，∠HFG＝n°，则n＝．8．（2019秋•开州区期末）如图，△ABC中边AB的垂直平分线分别交BC、AB于点D、E，AE＝4cm，△ADC的周长为10cm，则△ABC的周长是cm．9．（2019秋•两江新区期末）如图，在△ABC中，DB和DC分别平分∠ABC和∠ACB，过D作EF∥BC，分别交AB、AC于点E、F，若EF＝5，BE＝3，则线段CF的长为．10．（2019秋•江津区期末）如图，在等腰△ABC的两腰AB、BC上分别取点D和E，使DB＝DE，此时恰有∠ADE= 12∠ACB，则∠A的度数是．11．（2019秋•九龙坡区期末）在平面直角坐标系中，点P（1，﹣5）关于x轴对称点的点的坐标是．12．（2019秋•梁平区期末）如图，△ABC是等边三角形，D，E分别是BC，AB的中点，且AD＝4cm．F是AD上一动点，则BF+EF的最小值为cm．13．（2019秋•江北区期末）如图，在△ABC中，AB＝AC，点D，E都在边BC上，∠BAD＝∠CAE，若BD＝7，则CE的长为．14．（2019秋•万州区期末）如图，已知：∠BAC的平分线与BC的垂直平分线相交于点D，DE⊥AB，DF⊥AC，垂足分别为E、F，AB＝6，AC＝3，则BE＝．15．（2019秋•长寿区期末）在线段、直角、等腰三角形、直角三角形中，成轴对称图形的是．16．（2019秋•长寿区期末）等腰三角形一边长为4，另一边长为9，则它的周长是．17．（2019春•南岸区期末）如图，在△ABC中，过A作DE∥BC交∠ABC的平分线BD于点D、交∠ACB的平分线CE于点E．若BC＝7，DE＝9，则△ABC的周长为．18．（2018秋•南岸区期末）如图，在平面直角坐标系中，将△ABC三个顶点的横坐标分别乘以﹣1，而纵坐标保持不变，得到△A′B′C′，则△A′B′C′和△ABC关于对称（横线上填“x轴”、“y轴”或“原点”）．19．（2019春•渝中区校级期末）如图，△ABC中，AC＝BC，CE为△ABC的中线，BD为AC边上的高，BF平分∠CBD交CE于点G，连接AG交BD于点M，若∠AFG＝63°，则∠AMB的度数为°．20．（2018秋•渝中区期末）如图，已知∠BAC＝65°，D为∠BAC内部一点，过D作DB⊥AB于B，DC⊥AC于C，设点E、点F分别为AB、AC上的动点，当△DEF的周长最小时，∠EDF的度数为．21．（2018秋•合川区期末）如图，在△ABC中，∠ACB＝90°，CD是AB边上的高，∠BCD＝60°，若BD＝3cm，则AD＝cm．22．（2018秋•渝北区期末）如图，∠ABC＝20°，点D，E分别在射线BC，BA上，且BD＝3，BE＝3，点M，N 分别是射线BA，BC上的动点，求DM+MN+NE的最小值为．23．（2018秋•巴南区期末）如图，BE、CD分别是等边△ABC的高和角平分线，点O是它们的交点，若∠BOC＝m°，则m＝．24．（2018秋•江北区期末）在等腰△ABC中，一腰上的高与另一腰的夹角为26°，则底角的度数为．25．（2019春•沙坪坝区校级期末）如图，已知△ABC是等边三角形，点B、C、D、F在同一直线上，CD＝CE，DF＝DG，则∠F＝度．26．（2019春•南岸区校级期末）如图，在等腰△ABC中，AB＝BC，∠B＝120°，线段AB的垂直平分线分别交AB、AC于点D、E，若AC＝12，则DE＝．27．（2019春•沙坪坝区校级期末）如图，在直角三角形ABC中，∠A＝90°，AB＝8，AC＝15，BC＝17．D，P分别是线段AC，BC上的动点，则BD+DP的最小值是．28．（2019春•渝中区校级期末）在△ABC中，AB＝AC，AC的垂直平分线与AB所在直线相交所得的锐角为40°，∠C＝．29．（2019春•渝中区校级期末）如图，△ABC中，AC＝BC＝5，AB＝6，CD＝4，CD为△ABC的中线，点E、点F分别为线段CD、CA上的动点，连接AE、EF，则AE+EF的最小值为．30．（2018秋•九龙坡区校级期末）在平面直角坐标系中，点P（﹣2，﹣3）关于x轴对称点的坐标为．参考答案一．填空题（共30小题）1．【解答】解：∵∠ABC ＝80°，∴∠BMN +∠BNM ＝100°，∵M 、N 分别在P A 、PC 的中垂线上，∴MA ＝MP ，NP ＝NC ，∴∠MP A ＝∠MAP =12∠BMN ，∠NPC ＝∠NCP =12∠BNM ，∴∠MP A +∠NPC =12×100°＝50°，∴∠APC ＝180°﹣50°＝130°， 故答案为：130°．2．【解答】解：如图所示，作点M 关于BD 的对称点M '，连接PM '，则PM '＝PM ，BM ＝BM '＝1， ∴PN +PM ＝PN +PM '，当N ，P ，M '在同一直线上，且M 'N ⊥AC 时，PN +PM '的最小值等于垂线段M 'N 的长，此时，∵Rt △AM 'N 中，∠A ＝30°，∴M 'N =12AM '=12（6﹣1）=52，∴PM +PN 的最小值为52， 故答案为：52．3．【解答】解：如图，过点P 作PK ⊥BC 于K ，过点A 作AH ⊥BC 于H ．∵AB ＝AC ＝10，AH ⊥BC ，∴BH ＝CH ＝4，∴∠AHB ＝90°，∴AH =√AA 2−AA 2=√102−42=2√21，∵BD 平分∠ABC ，PM ⊥AB ，PK ⊥BC ，∴PM ＝PK ，∴P A +PM ＝P A +PK ≥AH ，∴P A +PM ≥2√21，∴P A +PM 的最小值为2√21．4．【解答】解：∵AB ＝AC ，∠B ＝50°，∠AED ＝73°，∴∠EDB ＝23°，∵当△DEP 是以DE 为腰的等腰三角形，①当点P 在AB 上，∵DE ＝DP 1，∴∠DP 1E ＝∠AED ＝73°，∴∠EDP 1＝180°﹣73°﹣73°＝34°，②当点P 在AC 上，∵AB ＝AC ，D 为BC 的中点，∴∠BAD ＝∠CAD ，过D 作DG ⊥AB 于G ，DH ⊥AC 于H ，∴DG ＝DH ，在Rt △DEG 与Rt △DP 2H 中，{AA =AA 2AA =AA， ∴Rt △DEG ≌Rt △DP 2H （HL ），∴∠AP 2D ＝∠AED ＝73°，∵∠BAC ＝180°﹣50°﹣50°＝80°，∴∠EDP 2＝134°，③当点P 在AC 上，同理证得Rt △DEG ≌Rt △DPH （HL ），∴∠EDG ＝∠P 3DH ，∴∠EDP 3＝∠GDH ＝180°﹣80°＝100°，④当点P 在AB 上，EP ＝ED 时，∠EDP =12（180°﹣73°）＝53.5°．故答案为：34°或53.5°或100°或134°．5．【解答】解：∵在△ABC 中，∠ACB ＝90°，∠B ＝15°，∴∠BAC＝90°﹣15°＝75°，∵DE垂直平分AB，BE＝6cm，∴BE＝AE＝6cm，∴∠EAB＝∠B＝15°，∴∠EAC＝75°﹣15°＝60°，∵∠C＝90°，∴∠AEC＝30°，∴AC=12AE=12×6cm＝3cm，故答案为：3cm．6．【解答】解：∵点A（a，b）与点B（1，﹣2）关于y轴对称，∴a＝﹣1，b＝﹣2，∴a+b＝﹣3，故答案为：﹣3．7．【解答】解：∵∠ABC的平分线与∠ACB的外角平分线相交于点D，∴∠ABD＝∠DBC，∠ACD＝∠DCM，设∠ABD＝∠DBC＝x，∠ACD＝∠DCM＝y，∵∠A+∠ABC＝∠ACM，∴12∠A+12∠ABC=12∠ACM，即30°+x＝y，∵∠D+∠DBC＝∠DCM，∴∠D+x＝y，∴∠D＝30°，∵EFD与△EFH关于直线EF对称，∠BEH＝84°，∴∠DEG＝∠HEG=180°−84°2=48°，∴∠HFG＝n°＝∠DFG＝48°+30°＝78°则n＝78．故答案为：78．8．【解答】解：∵DE是△ABC中边AB的垂直平分线，∴AD＝BD，AB＝2AE＝2×4＝8（cm），∵△ADC的周长为10cm，即AD+AC+CD＝BD+CD+AC＝BC+AC＝10cm，∴△ABC的周长为：AB+AC+BC＝8+10＝18（cm）．故答案为：18．9．【解答】解：∵BD平分∠ABC，∴∠ABD＝∠CBD，∵EF∥BC，∴∠EDB＝∠DBC，∴∠ABD＝∠EDB，∴BE＝ED，同理DF＝CF，∴EF＝3+CF＝5，∴CF＝2，故答案为：2．10．【解答】解：设∠B＝x．∵DB＝DE，∴∠DEB＝∠B＝x，∴∠ADE＝∠DEB+∠B＝2x，∴∠ACB＝2∠ADE＝4x．∵AB＝BC，∴∠ACB＝∠A＝4x．在△ABC中，∵∠A+∠B+∠C＝180°，∴4x+x+4x＝180°，∴x＝20°．即∠B＝20°∴∠A＝4x＝80°故答案为：80°11．【解答】解：点P（1，﹣5）关于x轴对称点的点的坐标是：（1，5）．故答案为：（1，5）．12．【解答】解：过C作CE⊥AB于E，交AD于F，连接BF，则BF+EF最小（根据两点之间线段最短；点到直线垂直距离最短），由于C和B关于AD对称，则BF+EF＝CE，∵等边△ABC中，BD＝CD，∴AD⊥BC，∴AD是BC的垂直平分线（三线合一），∴C和B关于直线AD对称，∴CF＝BF，即BF+EF＝CF+EF＝CE，∵AD⊥BC，CE⊥AB，∴∠ADB ＝∠CEB ＝90°，在△ADB 和△CEB 中，{∠AAA =∠AAAAAAA =AAAA AA =AA，∴△ADB ≌△CEB （AAS）， ∴CE ＝AD ＝4cm ，即BF +EF ＝4cm ．故答案为：4．13．【解答】解：∵AB ＝AC ，∴∠B ＝∠C ，在△BAD 和△CAE 中，{∠AAA =∠AAA AA =AAAA =AA ，∴△BAD ≌△CAE （ASA ），∴BD ＝CE ＝7，故答案为：7．14．【解答】解：连接CD ，BD ，∵AD 是∠BAC 的平分线，DE ⊥AB ，DF ⊥AC ，∴DF ＝DE ，∠F ＝∠DEB ＝90°，∠ADF ＝∠ADE ， ∴AE ＝AF ，∵DG 是BC 的垂直平分线，∴CD ＝BD ，在Rt △CDF 和Rt △BDE 中，{AA =AA AA =AA， ∴Rt △CDF ≌Rt △BDE （HL ），∴BE ＝CF ，∴AB ＝AE +BE ＝AF +BE ＝AC +CF +BE ＝AC +2BE ， ∵AB ＝6，AC ＝3，∴BE ＝1.5．故答案为：1.5．15．【解答】解：线段的垂直平分线所在的直线是对称轴，是轴对称图形，符合题意；直角的角平分线所在的直线就是对称轴，是轴对称图形，符合题意；等腰三角形底边中线所在的直线是对称轴，是轴对称图形，符合题意；直角三角形不一定是轴对称图形，不符合题意．故成轴对称图形的是：线段、直角、等腰三角形．故答案为：线段、直角、等腰三角形．16．【解答】解：当等腰三角形的三边为：4、4、9时，不符合三角形三边关系，因此这种情况不成立；当等腰三角形的三边为：4、9、9时，符合三角形三边关系，则三角形的周长为：4+9+9＝22．因此等腰三角形的周长为22．故填22．17．【解答】解：∵DE∥BC，∴∠E＝∠ECB，∠D＝∠DBC，∵CE平分∠ACB，BD平分∠ABC，∴∠ECB＝∠ACE，∠DBC＝∠ABD，∴∠E＝∠ACE，∠D＝∠ABD，∴AE＝AC，AB＝AD，∵AB+AC＝AD+AE＝DE＝9，BC＝7，∴△ABC的周长为AB+AC+BC＝DE+BC＝9+7＝16．故答案为16．18．【解答】解：∵横坐标乘以﹣1，∴横坐标相反，又纵坐标不变，∴关于y轴对称．故答案为：y轴．19．【解答】解：∵BD为AC边上的高，∴BD⊥AC，∴∠BDF＝90°，∵∠AFG＝63°，∴∠DBF＝90°﹣63°＝27°，∵BF平分∠CBD交CE于点G，∴∠CBD＝2∠DBF＝54°，∴∠ACB＝90°﹣∠CBD＝36°，∵AC＝BC，∴∠CAB＝∠CBA=12（180°﹣36°）＝72°，∴∠ABD＝72°﹣54°＝18°，∴∠ABG＝27°+18°＝45°，∵CE为△ABC的中线，∴CE⊥AB，∴CE垂直平分AB，∴AG＝BG，∴∠GAB＝∠GBA＝45°，∴∠AMB＝180°﹣45°﹣18°＝117°，故答案为：117．20．【解答】解：如图所示：延长DB和DC至M和N，使MB＝DB，NC＝DC，连接MN交AB、AC于点E、F，连接DE、DF，此时△DEF的周长最小．∵DB⊥AB，DC⊥AC，∴∠ABD＝∠ACD＝90°，∠BAC＝65°，∴∠BDC＝360°﹣90°﹣90°﹣65°＝115°，∴∠M+∠N＝180°﹣115°＝65°根据对称性质可知：DE＝ME，DF＝NF，∴∠EDM＝∠M，∠FDN＝∠N，∴∠EDM+∠FDN＝65°，∴∠EDF＝∠BDC﹣（∠EDM+∠FDN）＝115°﹣65°＝50°．故答案为50°．21．【解答】解：∵在△ABC中，∠ACB＝90°，CD是AB边上的高，∠BCD＝60°，BD＝3cm，∴BC＝2CD，可得：BC2﹣CD2＝4CD2﹣CD2＝9，解得：CD=√3cm，∴BC＝2√3cm，∴AC=AA√3=2cm，∴AB＝4cm，∴AD＝4﹣3＝1cm．故答案为：122．【解答】解：如图所示：作点D关于AB的对称点G，作点E关于BC的对称点H，连接GH交AB于点M、交BC于点N，连接DM、EN，此时DM+MN+NE的值最小．根据对称的性质可知：DB＝BG＝3，∠GBE＝∠DBE＝20°，BH＝BE＝3，∠HBD＝∠EBD＝20°，∴∠GBH＝60°，∴△BGH是等边三角形，∴GH＝GB＝HB＝3，∴DM+MN+NE的最小值为3．故答案为3．23．【解答】解：∵BE、CD分别是等边△ABC的高和角平分线，∴∠ODB＝90°，∠ABE＝30°，∴∠BOC＝∠ODB+∠DBE＝90°+30°＝120°，故答案为：12024．【解答】解：①∵AB＝AC，∠ABD＝26°，BD⊥AC，∴∠A＝64°，∴∠ABC＝∠C＝（180°﹣64°）÷2＝58°．②∵AB＝AC，∠ABD＝26°，BD⊥AC，∴∠BAC＝26°+90°＝116°∴∠ABC＝∠C＝（180°﹣116°）÷2＝32°．故答案为：58°或32°．25．【解答】解：∵△ABC是等边三角形，∴∠ACB＝60°，∠ACD＝120°，∵CE＝CD，∴∠CDE＝30°，∠FDG＝150°，∵DF＝DG，∴∠F＝15°．故答案为：15．26．【解答】解：连接BE，∵AB＝BC，∠B＝120°，∴∠A＝∠C＝30°，∵DE是线段AB的垂直平分线，∴EA＝EB，∴∠EBA＝∠A＝30°，∴∠CBE＝90°，又∠C＝30°，∴BE=12EC，∴AE=12EC，∴AE=13AC＝4，在Rt△ADE中，∠A＝30°，∴DE=12AE＝2，故答案为：2．27．【解答】解：作B关于AC的对称点E，过E作EP⊥BC于P，交AD于D，则AE＝AB＝8，此时，BD+DP的值最小，BD+DP的最小值＝EP，∵∠BAC＝∠BPE＝90°，∠C＝∠E，∴△ABC∽△PBE，∴AAAA=AAAA，∴1617=AA 15，∴PE =24017， 故答案为：24017．28．【解答】解：当△ABC 为锐角三角形时，如图1，设AC 的垂直平分线交线段AB 于点D ，交AC 于点E ，∵∠ADE ＝40°，DE ⊥AC ，∴∠A ＝90°﹣40°＝50°，∵AB ＝AC ，∴∠C =12（180°﹣∠A ）＝65°；当△ABC 为钝角三角形时，如图2，设AC 的垂直平分线交AC 于点E ，交AB 于点D ，∵∠ADE ＝40°，DE ⊥AC ，∴∠DAC ＝50°，∵AB ＝AC ，∴∠B ＝∠C ，∵∠B +∠C ＝∠DAB ，∴∠C ＝25°；综上可知∠C 的度数为65°或25°，故答案为：65°或25°．29．【解答】解：过B 作BF ⊥AC 于F ，交CD 于E ， 则BF 的长即为AE +EF 的最小值，∵AC ＝BC ＝5，CD 为△ABC 的中线，∴AD =12AB ＝3，∵S △ABC =12AB •CD =12AC •BF ，∴BF =6×45=245， ∴AE +EF 的最小值为245， 故答案为：245．30．【解答】解：点P （﹣2，﹣3）关于x 轴对称点的坐标为：（﹣2，3）． 故答案为：（﹣2，3）．。

2019-2020年人教版八年级上册数学期末复习常考填空题汇总训练（含解析）二、填空题1. 如图，在正六边形ABCDEF中，连接AE，DF，则∠1=∘．2. 如图，是一个不规则的五角星，则∠A+∠B+∠C+∠D+∠E=（用度数表示）．3. 如果将一副三角尺按如图方式叠放，那么∠1=．4. 在三角形的三个外角中，锐角最多有个．5. 在△ABC中，若∠A:∠B:∠C=2:3:5，这个三角形为三角形（按角分类）．6. 如图，已知△ABC中，∠C=90∘，那么∠1+∠2=∘．7. 已知在△ABC中，∠A:∠B:∠C=3:2:5，那么△ABC是．（填“锐角三角形”“直角三角形”或“钝角三角形”）8. 若等腰三角形的两条边长分别为7cm和14cm，则它的周长为cm．9. 如图所示，已知△ABC为直角三角形，∠C=90∘，若沿图中虚线剪去∠C，则∠1+∠2=．10. 如图，一辆汽车由A点出发向前行驶100米到B处，向左转45度，继续向前行驶同样的路程到C处，再向左转45度，按这样的行驶方法，回到A点总共行驶了米．11. 如图，为了使一扇旧木门不变形，木工师傅在木门的背后加钉了一根木条，这样做的道理是．12. 如图，在△ABC中，∠A=50∘，∠ABC=70∘，BD平分∠ABC，则∠BDC的度数是．13. 如图，AB∥CD，AD与BC交于点E，若∠B=35∘，∠D=45∘，则∠AEC=．14. 如图，在△ABC中，∠C=90∘，延长AB到D，延长CB到F．设∠A=x+10∘，∠CBA=x−10∘，∠ABF=y，则x=度，y=度．15. 将一副直角三角尺按如图所示的方式放置，若AE∥BC，则∠AFD的度数是．16. 如图，∠A +∠B +∠C +∠D +∠E +∠F 的度数 = ．17. 请从以下两个小题中任选一个作答，若多选，则按第一题计分． A ．正 n 边形的一个内角等于 135∘，则从这个多边形的一个顶点出发可引 条对角线． B ．运用科学计算器计算：(13)3×tan78∘≈ ．（结果精确到 0.01）18. 一个等腰三角形的两边长分别是 2 cm ，5 cm ，则它的周长为 cm ．19. 如图，BC ⊥ED 于点 M ，∠A =27∘，∠D =20∘，则 ∠ABC = ．20. 将一副直角三角板如图放置，使含 30∘ 角的三角板的短直角边和含 45∘ 角的三角板的一条直角边重合，则 ∠1 的度数为 度．21. 下列说法中：① 如果两个三角形可以依据“AAS ”来判定全等，那么一定也可以依据“ASA ”来判定它们全等；② 如果两个三角形都和第三个三角形不全等，那么这两个三角形也一定不全等；③ 要判断两个三角形全等，给出的条件中至少要有一对边对应相等．正确的是 ．22. 如图，AC=BC，请你添加一对边或一对角相等的条件，使AD=BE．你所添加的条件是．23. 在△ABC中，AB=AC，点E，F分别在AB，AC上，AE=AF，BF与CE相交于点P，则相等的线段有．24. 如图，在△ABC和△DEF中，已知CB=DF，∠C=∠D，要使△ABC≌△EFD，还需添加一个条件，那么这个条件可以是．25. 如图，AB与CD相交于点O，且OA=OB，要添加一个条件，才能使得△AOC≌△BOD，那么，方法一：可以添加的一个条件是，判断三角形全等的依据是；方法二：可以添加的一个条件是，判断三角形全等的依据是；方法三：可以添加的一个条件是，判断三角形全等的依据是．26. 在△ABC中，点D是BC的中点，作射线AD，在线段AD及其延长线上分别取点E，F，连接CE，BF，添加一个条件，使得△BDF≌△CDE，你添加的条件是（不添加辅助线）．27. 如图，已知∠ABC=∠DEF，AB=DE，要说明△ABC≌△DEF，（1）若以“SAS”为依据，还需添加的一个条件为；（2）若以“ASA”为依据，还需添加的一个条件为；（3）若以“AAS”为依据，还需添加的一个条件为．28. 如图，在下列各组条件中，能够判断△ABC和△DEF全等的有．①AB=DE，AC=DF，BC=EF；②AB=DE，BC=EF，∠B=∠E；③∠A=∠D，∠B=∠E，AB=DE；④∠A=∠D，AB=DE，BC=EF．29. 如图，已知∠AOB．小明按如下步骤作图：①以点O为圆心，任意长为半径画弧，交OA于点D，交OB于点E．②分别以D，E为圆心，大于DE长为半径画弧，在∠AOB的内部两弧交于点C．③画射线OC．所以射线OC为所求∠AOB的平分线．根据上述作图步骤，回答下列问题：（1）写出一个正确的结论：．（2）如果在OC上任取一点M，那么点M到OA，OB的距离相等．依据是：．30. 如图所示，已知∠1=∠2，请你添加一个条件，使△ABC≌△BAD，你的添加条件是（填一个即可）．31. 已知△ABC，现将△ABC绕点B逆时针旋转，使点A落在射线BP上，求作△AʹCʹB．作法：在BP上截BAʹ=BA，以点B为圆心、BC为半径作弧，以点Aʹ为圆心、AC为半径作弧，两弧在射线BP右侧交于点Cʹ，则△AʹCʹB即为所求．请用文字语言描述上述操作的作图原理：．32. 如图，AC，BD相交于点O，∠A=∠D．请补充一个条件，使△AOB≌△DOC，你补充的条件是（填出一个即可）．33. 如图，AC=DC，BC=EC，请你添加一个适当的条件：，使得△ABC≌△DEC．34. 如图，AB=AC，要使△ABE≌△ACD，应添加的条件是（添加一个条件即可）.35. 如图，点B，A，D，E在同一直线上，BD=AE，BC∥EF，要使△ABC≌△DEF，则只需添加一个适当的条件是．（只填一个即可）36. 如图，BC=EF，∠1=∠F．请你添加一个适当的条件，使得△ABC≌△DEF（只需填一个答案即可）．37. 如图，在平面直角坐标系中，以O为圆心，适当长为半径画弧，交x轴于点M，交y轴于点N，MN的长为半径画弧，两弧在第二象限内交于点P(a,b)，则再分别以点M，N为圆心，大于12a与b的数量关系是．38. 如图，在△ABC中，∠ACB=80∘，∠ABC=60∘．按以下步骤作图：①以点A为圆心，小于ACEF的长为半径的长为半径画弧，分别交AB，AC于点E，F；②分别以点E，F为圆心，大于12画弧，两弧相交于点G；③作射线AG交BC于点D．则∠ADB的度数为∘．39. 已知OC是∠AOB的平分线，点P在OC上，PD⊥OA，PE⊥OB，垂足分别为点D，E，PD=10，则PE的长度为．40. 如图，△ACB≌△AʹCBʹ，∠BCBʹ=30∘，则∠ACAʹ的度数为．41. 已知△ABC是边长为1的等边三角形，△DBC是以BC为斜边的等腰直角三角形，那么点B到直线AD的距离为．42. 数学课上，王老师布置如下任务：如图1，△ABC中，BC>AB>AC，在BC边上取一点P，使∠APC=2∠ABC．小路的作法如下，如图2：①作AB边的垂直平分线，交BC于点P；②连接AP，所以，∠APC=2∠ABC．小路的作图依据是．43. 下面是“已知底边及底边上的高线作等腰三角形”的尺规作图过程．已知：线段a．求作：等腰△ABC，使AB=AC，BC=a，BC边上的高为2a．作法：如图，（1）作线段BC=a：（2）作线段BC的垂直平分线DE交BC于点F：（3）在射线FD上顺次截取线段FG=GA=a，连接AB，AC．所以△ABC即为所求作的等腰三角形．请回答：得到△ABC是等腰三角形的依据是：①；②．44. 阅读下面材料：在数学课上，老师提出如下问题：尺规作图：作一条线段的垂直平分线．已知：线段AB．求作：线段AB的垂直平分线．小红的作法如下：AB的长为半径作弧，两弧相交于点C；如图，①分别以点A和点B为圆心，大于12AB的长为半径（不同于①中的半径）作弧，两弧相交于②再分别以点A和点B为圆心，大于12点D，使点D与点C在直线AB的同侧；③作直线CD．所以直线CD就是所求作的垂直平分线．老师说：“小红的作法正确．”请回答：小红的作图依据是．45. 等腰三角形的对称轴是．46. 已知，在△ABC中，AB=AC=2，BC=2√3，那么∠A的度数是．47. 如图，已知△ABC是等边三角形，点B，C，D，E在同一直线上，且CG=CD，DF=DE，则∠E=度．48. 在△ABC中，AB=AC，若∠A=30∘，则∠B=．49. 在平面直角坐标系中，点A的坐标是(2,−3)，作点A关于x轴的对称点，得到点Aʹ，再作点Aʹ关于y轴的对称点，得到点Aʺ，则点Aʺ的坐标是．50. 如图，在△ABC中，∠C=90∘，∠CAB=60∘，按以下步骤作图：AB的长为半径作弧，两弧相交于点P和点Q．①分别以A，B为圆心，以大于12②作直线PQ交AB于点D，交BC于点E，连接AE．若CE=4，则AE=．51. 如图，在△ABC中，∠C=90∘，∠CAB=62∘，按以下步骤作图：AB的长为半径作弧，两弧相交于点P和Q．①分别以A，B为圆心，以大于12②作直线PQ交AB于点D，交BC于点E，连接AE，则∠AEC=．52. 如图，△ABC为等边三角形，BD⊥AB，BD=AB，则∠DCB=．53. 如图所示，在△ABC中，AB=AC，D，E是△ABC内两点，AD平分∠BAC，∠EBC=∠E=60∘．若BE=7，DE=3，则BC=．54. 如图，在Rt△ABC中，∠C=90∘，∠B=15∘，DE是AB的中垂线，垂足为D，交BC于点E．若BE=4，则AC=．55. 如图所示，△ABC的角平分线相交于点D，过点D作EF∥BC，交AB于点E，交AC于点F．若△AEF的周长为30cm，则AB+AC=cm．56. 如图所示，已知AD是等边△ABC的角平分线，过点D作DE⊥AB于点E．若AD=8，则DE=．57. 尺规作图：已知∠AOB，试在∠AOB内确定一点P，使点P到OA，OB的距离相等，并且到M，N两点的距离也相等，要求保留作图痕迹，并简要说明理由．理由：．58. 如图，等腰△ABC底边BC的长为4cm，面积是12cm2，腰AB的垂直平分线EF交AC于点F，若D为BC边上的中点，M为线段EF上一动点，则△BDM的周长最小值为cm．59. “直角”在初中几何学习中无处不在．课堂上李老师提出一个问题：如图，已知 ∠AOB ．判断 ∠AOB 是否为直角（仅限用直尺和圆规）．小丽的方法：如图，在 OA ，OB 上分别取点 C ，D ，以点 C 为圆心，CD 长为半径画弧，交 OB的反向延长线于点 E ．若 OE =OD ，则 ∠AOB =90∘．李老师说小丽的作法正确，请你写出她作图的依据： ．60. 如图，在已知的 △ABC 中，按以下步骤作图：①分别以 B ，C 为圆心，以大于 12BC 的长为半径作弧，两弧相交于两点 M ，N ；②作直线 MN 交 AB 于点 D ，连接 CD ． 若 CD =AC ，∠A =50∘，则 ∠ACB 的度数为 度．61. 运算种类公式(用字母表示)法则(文字叙述)a m ⋅a n (m 、n 是正整数)(a m )n (m 、n 是正整数)(a ⋅b )n (n 是正整数)a m ÷a n (a ≠0,m 、n 是正整数,m >n)62. 若3n=2，3m=5，则32m+3n−1的值为．63. （1）若m+n=10，mn=24，则m2+n2=；（2）若a−b=13，a2−b2=39，则(a+b)2=．64. （1）若a m=2，则(3a m)2−4(a3)m=；（2）若2m=9，3m=6，则62m−1=．65. 分解因式：27x2+18x+3=；2x2−8=．66. 因式分解：4a2−4−c2+4c=．x2)=；−(−2a2)4=．67. 计算：3x3⋅(−1968. 把多项式4−a2−2ab−b2分解因式的结果是．69. 已知a2+2a=−2，则2a(2a+1)+(a+4)2的值为．70. 如果x−y=√2，那么代数式(x+2)2−4x+y(y−2x)的值是．71. 把4x2+1加上一个单项式，使其成为一个完全平方式．请你写出符合条件的单项式：．（写出一个即可）72. 课本上，公式(a−b)2=a2−2ab+b2是由公式(a+b)2=a2+2ab+b2推导得出的．已知(a+b)4=a4+4a3b+6a2b2+4ab3+b4，则(a−b)4=．73. 无论x、y取任何实数，多项式x2+y2−2x−4y+16的值总是数．74. 分解因式：2x3−8x=．75. 已知2x−3y−2=0，则(10x)2÷(10y)3=．76. 直接写出因式分解的结果：（1）6a2−8ab=；（2）y3−y=；（3）(a+b)2−8a−8b+16=；（4）x2−2x−15=．77. 已知：(x−2)0无意义，请你计算(2x+1)2−(2x+5)(2x−5)=．78. 已知x2+x−5=0，则代数式(x−1)2−x(x−3)+(x+2)(x−2)=．79. 已知a m=−4，a n=5，则a3m−n=．80. 计算（直接写出结果）．①a⋅a3=；②(b3)4=；③(2ab)3=；④3x2y⋅(−2x3y2)=．81. （1）分式x−1x+1的值为零，则x的值为；（2）使分式2x+12x−1无意义的x的值是；（3）化简：aa−b −ba−b=；（4）(x2y )3÷(y2−x)−2=．82. 已知1x −1y=3，则代数式2x−14xy−2yx−2xy−y的值为．83. 若关于x的方程axx−2=4x−2+1无解，则a的值是．84. 在课外活动跳绳时，相同时间内小林跳了90下，小群跳了120下．已知小群每分钟比小林多跳20下，设小林每分钟跳x下，则可列关于x的方程为．85. （1）如果分式2−xx的值为0，那么x=；（2）当x≠时，分式x−1x+2有意义；（3）x2x2−y2−y2x2−y2=；（4）(y6x2)−2÷(−4xy2)2=．86. （1）当x时，分式1+2x1−2x有意义．（2）当x时，分式x−3x+3的值为零．87. 已知x=−2时，分式x−bx+a无意义，x=4时此分式值为0，则a+b=；88. 已知分式x−nx+m，当x=−5时，该分式没有意义，当x=−6时，该分式的值为0，则(m+ n)2015=．89. 计算：xx−1−1x−1=．90. 1xy ，−y4x3，16xyz的最简公分母是．91. 计算：x−yx ÷(x−2xy−y2x)=．92. 若分式x+1x+2÷x+3x+4有意义，则x的取值范围是．93. 当分式1x2−1−2x+1−1x−1的值等于零时，则x=．94. 若分式方程x−ax+1=a无解，则a的值为．95. 对于分式x2−2x−3x−3，当x=时，分式无意义；当x=时，分式值为零．96. 当分式x−22x+1的值为0时，x的值为．97. 分式x2−9x−3，当x时分式的值为零．98. 已知3x=4y，则xy=．99. 若分式x2−9x+3的值为0，则x=．100. 若a+3b=0，则(1−ba+2b )÷a2+2ab+b2a2−4b2=．答案第一部分1. 1202. 180∘3. 105∘4. 15. 直角6. 2707. 直角三角形8. 359. 270∘10. 800【解析】由题意可得，这个多边形的每个外角都为45∘，∴边数为360∘÷45∘=8，∴总共行驶了8×100=800米．11. 利用三角形的稳定性12. 85∘13. 80∘14. 45，14515. 75∘16. 360∘17. 5，0.17【解析】A．∵正多边形的外角和为360∘，正n边形的一个内角等于135∘，则这个正n边形的每个外角为180∘−135∘=45∘，=8，∴n=360∘45∘∴这个多边形的边数为8，又过正n(n>3)边形的一个顶点，可引n−3条对角线，则从这个多边形的一个顶点出发可引8−3=5条对角线；B．按键顺序为，显示结果为0.174245559，结果四舍五入约等于0.17．18. 1219. 43∘20. 75【解析】如图．∵∠3=60∘，∠4=45∘，∴∠1=∠5=180∘−∠3−∠4=75∘．21. ①③22. ∠A=∠B或∠ADC=∠BEC或CE=CD【解析】因为AC=BC，∠C=∠C，所以添加∠A=∠B或∠ADC=∠BEC或CE=CD，可得△ADC与△BEC全等，利用全等三角形的性质得出AD=BE．23. PB=PC，BF=CE，PF=PE，BE=CF24. AC=ED或∠A=∠FED或∠ABC=∠F【解析】要使△ABC≌△EFD，已知CB=DF，∠C=∠D，则可以添加AC=ED，运用SAS来判定其全等；也可添加一组角∠A=∠FED或∠ABC=∠F运用AAS来判定其全等．25. OC=OD，SAS，∠A=∠B，ASA，∠C=∠D，AAS26. DE=DF（或CE∥BF或∠ECD=∠DBF或∠DEC=∠DFB）【解析】由已知可得CD=BD，又∠EDC=∠FDB，因为三角形全等条件中必须是三个元素，并且一定有一组对应边相等，所以，添加的条件可以是一组对应边相等，也可以是一组对应角相等或者是能推导出边相等或角相等的条件．27. BC=EF（或BE=CF），∠A=∠D，∠ACB=∠F28. ①②③29. OD=OE或DC=EC或OC平分∠AOB等等均可，角平分线上的点到角两边距离相等30. BC=AD或∠C=∠D或∠ABD=∠BAC31. 三边分别相等的两个三角形全等【解析】∵在△ABC和△AʹBCʹ中，{AʹB=AB, BCʹ=BC, AʹCʹ=AC,∴△ABC≌△AʹBCʹ(SSS)．32. AB=DC或OA=OD或OB=OC33. 答案不唯一，如AB=DE（或∠ACD=∠BCE，∠ACB=∠DCE等）34. ∠B=∠C（答案不唯一）35. BC=EF或∠BAC=∠EDF36. AC=DF（或∠A=∠D或∠B=∠DEF）37. a+b=038. 10039. 1040. 30∘41. 12【解析】由题意可得AB=AC，DB=DC，∴AD所在的直线垂直平分BC，BC=1．∴点B到直线AD的距离为1242. 线段垂直平分线上的点到线段两个端点的距离相等；等腰三角形两底角相等；三角形的一个外角等于于它不相邻的两个内角之和．43. 线段垂直平分线上的点到线段两个端点的距离相等，有两条边相等的三角形是等腰三角形44. 到线段两个端点距离相等的点在这条线段的垂直平分线上；两点确定一条直线【解析】如图，∵由作图可知，AC=BC=AD=BD，∴直线CD就是线段AB的垂直平分线．45. 顶角平分线（底边上的中线，底边上的高）所在的直线或者写“底边的中垂线”46. 120∘47. 1548. 75∘49. (−2,3)50. 851. 56∘52. 15∘53. 10【解析】如图所示，作AQ⊥BC，延长ED交BC于点F，因为∠EBC=∠E=60∘．所以∠QFD=60∘．因为BE=7，DE=3，所以DF=4．DF=2，在Rt△DQF中，QF=12所以BQ=5．所以BC=2BQ=10．54. 255. 3056. 457. 如图，点P即为所求.理由是：角平分线上一点到角两边距离相等；线段垂直平分线上的点到线段两端的距离相等．58. 8【解析】连接AD，因为△ABC是等腰三角形，点D是BC边的中点，所以AD⊥BC，所以S△ABC=12BC⋅AD=12×4×AD=12，解得AD=6cm，因为EF是线段AB的垂直平分线，所以点B关于直线EF的对称点为点A，所以AD的长为BM+MD的最小值，所以△BDM的周长最短=(BM+MD)+BD=AD+12BC=6+12×4=6+2=8(cm).59. 两条边相等的三角形为等腰三角形，等腰三角形的三线合一60. 10561.运算种类公式(用字母表示)法则(文字叙述)a m⋅a n(m、n是正整数)a m⋅a n=a m+n同底数幂相乘,底数不变指数相加(a m)n(m、n是正整数)(a m)n=a mn幂的乘方,底数不变,指数相乘(a⋅b)n(n是正整数)(a⋅b)n=a n b m积的乘方,等于把积的每一个因式分别乘方,再把所得的幂相a m÷a n(a≠0,m、n是正整数,m>n)a m÷a n=a m−n同底数幂相除,底数不变,指数相减62. 200363. 52，964. 4，48665. 3(3x+1)2，2(x+2)(x−2)66. (2a+c−2)(2a−c+2)x5，−16a867. −1368. (2−a−b)(2+a+b)69. 670. 671. 4x（答案不唯一）72. a4−4a3b+6a2b2−4ab3+b473. 正74. 2x(x+2)(x−2)75. 10076. （1）2a(3a−4b)，（2）y(y+1)(y−1)，（3）(a+b−4)2，（4）(x−5)(x+3)77. 3478. 2【解析】原式=x2−2x+1−x2+3x+x2−4=x2+x−3．因为x2+x−5=0，所以x2+x=5，所以原式=x2+x−3=5−3=2．79. −64580. a4，b12，8a3b3，−6x5y3，（3）1，（4）x4y81. （1）1，（2）1282. 483. 1或2【解析】提示：分式方程无解有两种情况：由分式方程化成的整式方程无解；整式方程的解是原分式方程的增根．84. 120x+20=90x（其他答案正确也给分）85. （1）2，（2）−2，（3）1，（4）9x2y2486. （1）≠12，（2）=387. 688. −189. 190. 12x3yz91. 1x−y92. x≠−2且x≠−3且x≠−493. 2394. −1或195. 3，−1【解析】依题意得：x−3=0，解得x=3，所以x=3时，分式无意义；依题意得：x2−2x−3=0且x−3≠0，即(x−3)(x+1)=0，且x−3≠0，所以x+1=0，解得x=−1．96. 297. x=−398. 4399. 3100. 52。

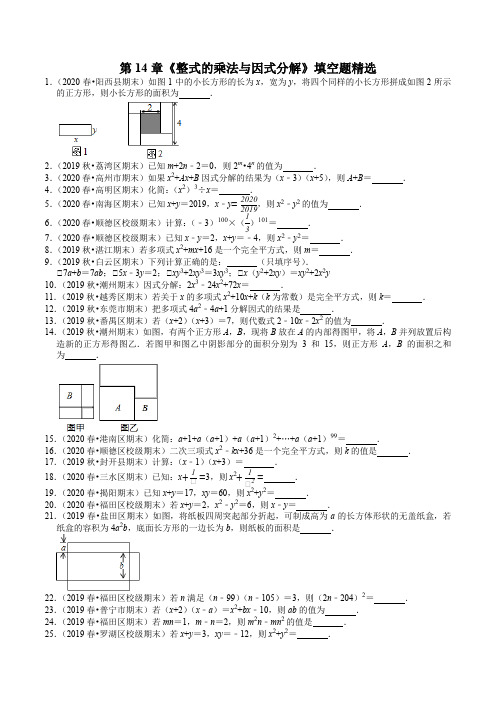
第14章《整式的乘法与因式分解》填空题精选1．（2020春•阳西县期末）如图1中的小长方形的长为x ，宽为y ，将四个同样的小长方形拼成如图2所示的正方形，则小长方形的面积为 ．2．（2019秋•荔湾区期末）已知m +2n ﹣2＝0，则2m •4n 的值为 ．3．（2020春•高州市期末）如果x 2+Ax +B 因式分解的结果为（x ﹣3）（x +5），则A +B ＝ ．4．（2020春•高明区期末）化简：（x 2）3÷x ＝ ．5．（2020春•南海区期末）已知x +y ＝2019，x ﹣y =20202019，则x 2﹣y 2的值为 ．6．（2020春•顺德区校级期末）计算：（﹣3）100×（13）101＝ ．7．（2020春•顺德区校级期末）已知x ﹣y ＝2，x +y ＝﹣4，则x 2﹣y 2＝ ．8．（2019秋•湛江期末）若多项式x 2+mx +16是一个完全平方式，则m ＝ ．9．（2019秋•白云区期末）下列计算正确的是： （只填序号）．①7a +b ＝7ab ；①5x ﹣3y ＝2；①xy 3+2xy 3＝3xy 3；①x （y 2+2xy ）＝xy 2+2x 2y10．（2019秋•潮州期末）因式分解：2x 3﹣24x 2+72x ＝ ．11．（2019秋•越秀区期末）若关于x 的多项式x 2+10x +k （k 为常数）是完全平方式，则k ＝ ．12．（2019秋•东莞市期末）把多项式4a 2﹣4a +1分解因式的结果是 ．13．（2019秋•番禺区期末）若（x +2）（x +3）＝7，则代数式2﹣10x ﹣2x 2的值为 ．14．（2019秋•潮州期末）如图，有两个正方形A ，B ，现将B 放在A 的内部得图甲，将A ，B 并列放置后构造新的正方形得图乙．若图甲和图乙中阴影部分的面积分别为3和15，则正方形A ，B 的面积之和为 ． 15．（2020春•港南区期末）化简：a +1+a （a +1）+a （a +1）2+…+a （a +1）99＝ ．16．（2020春•顺德区校级期末）二次三项式x 2﹣kx +36是一个完全平方式，则k 的值是 ．17．（2019秋•封开县期末）计算：（x ﹣1）（x +3）＝ ．18．（2020春•三水区期末）已知：x +1x =3，则x 2+1x 2= ． 19．（2020春•揭阳期末）已知x +y ＝17，xy ＝60，则x 2+y 2＝ ．20．（2020春•福田区校级期末）若x +y ＝2，x 2﹣y 2＝6，则x ﹣y ＝ ．21．（2019春•盐田区期末）如图，将纸板四周突起部分折起，可制成高为a 的长方体形状的无盖纸盒，若纸盒的容积为4a 2b ，底面长方形的一边长为b ，则纸板的面积是 ． 22．（2019春•福田区校级期末）若n 满足（n ﹣99）（n ﹣105）＝3，则（2n ﹣204）2＝ ．23．（2019春•普宁市期末）若（x +2）（x ﹣a ）＝x 2+bx ﹣10，则ab 的值为 ．24．（2019春•福田区期末）若mn ＝1，m ﹣n ＝2，则m 2n ﹣mn 2的值是 ．25．（2019春•罗湖区校级期末）若x +y ＝3，xy ＝﹣12，则x 2+y 2＝ ．26．（2019春•南海区期末）若2x＝5，2y＝3，则2x+y＝．27．（2018秋•中山市期末）已知m+2n+2＝0，则2m•4n的值为．28．（2018秋•天河区期末）若（x+p）与（x+5）的乘积中不含x的一次项，则p＝．29．（2018秋•白云区期末）一个正方形的边长增加了2cm，它的面积就增加44cm2，这个正方形的边长是：．30．（2019春•大埔县期末）若5x﹣3y＝2，则105x÷103y＝．31．（2019春•南海区期末）若（x+y）2＝49，xy＝12，则x2+y2＝．32．（2019春•天桥区期末）已知x2+mx+25是完全平方式，则m＝．33．（2018秋•番禺区期末）计算：（x+1）（x+2）＝．34．（2019春•罗湖区期末）n为正整数，若a9÷a n＝a5，则n＝．35．（2019春•顺德区期末）若x2+mx+1是完全平方式，则m＝．36．（2019秋•端州区期末）分解因式：4x3﹣9x＝．37．（2019秋•越秀区期末）点（﹣3，4）与点（a2，b2）关于y轴对称，则（a+b）（a﹣b）＝．38．（2019秋•潮州期末）计算：（2xy）2（﹣5x2y）＝．39．（2020春•顺德区校级期末）若a+b＝10，ab＝11，则代数式a2﹣ab+b2＝．40．（2020春•顺德区校级期末）计算：（a+2b）2＝．41．（2020春•顺德区校级期末）化简：（2x﹣y）（x+3y）＝．第14章《整式的乘法与因式分解》填空题精选参考答案与试题解析一．填空题（共41小题）1．【解答】解：由图2可知， {x +x =4x −x =2， 解得：{x =3x =1， 则小长方形的面积为xy ＝3．故答案为：3．2．【解答】解：由m +2n ﹣2＝0得m +2n ＝2，∴2m •4n ＝2m •22n ＝2m +2n ＝22＝4．故答案为：4．3．【解答】解：x 2+Ax +B ＝（x ﹣3）（x +5）＝x 2+2x ﹣15，得A ＝2，B ＝﹣15，∴A +B ＝2﹣15＝﹣13．故答案为：﹣13．4．【解答】解：（x 2）3÷x ＝x 6÷x ＝x 5，故答案为：x 5．5．【解答】解：x 2﹣y 2＝（x +y ）（x ﹣y ）＝2019×20202019=2020， 故答案为：2020．6．【解答】解：（﹣3）100×（13）101 ＝3100×（13）100×13 =(3×13)100×13=1100×13=1×13 =13． 故答案为：13． 7．【解答】解：∵x ﹣y ＝2，x +y ＝﹣4，∴x 2﹣y 2＝（x ﹣y ）（x +y ）＝2×（﹣4）＝﹣8．故答案为：﹣8．8．【解答】解：∵x 2+mx +16＝x 2+mx +42，∴mx ＝±2×4×x ，解得m ＝±8．故答案为：±8．9．【解答】解：∵7a 与b 、5x 与3y 都不是同类项，不能加减，故①①不正确； ∵xy 3与2xy 3是同类项，xy 3+2xy 3＝3xy 3，故①正确；∵x （y 2+2xy ）＝xy 2+2x 2y ，故①正确．故答案为：①①10．【解答】解：原式＝2x （x 2﹣12x +36）＝2x （x ﹣6）2，故答案为：2x （x ﹣6）211．【解答】解：∵关于x 的多项式x 2+10x +k 是完全平方式，∴x 2+10x +k ＝x 2+2•x •5+52，∴k ＝52＝25，故答案为：25．12．【解答】解：原式＝（2a ﹣1）2，故答案为：（2a ﹣1）2．13．【解答】解：∵（x +2）（x +3）＝7，∴x 2+5x ＝1，∴2﹣10x ﹣2x 2＝﹣2（x 2+5x ）+2＝﹣2×1+2＝0，故答案为：0．14．【解答】解：如图所示：设正方形A 、B 的边长分别为x ，y ，依题意得：{x 2−x 2−2(x −x )x =3(x +x )2−x 2−x 2=15， 化简得：{x 2−2xx +x 2=3x 2xx =15x 由①+①得：x 2+y 2＝18，∴x x +x x =x 2+x 2=18，故答案为18．15．【解答】解：原式＝（a +1）[1+a +a （a +1）+a （a +1）2+…+a （a +1）98] ＝（a +1）2[1+a +a （a +1）+a （a +1）2+…+a （a +1）97]＝（a +1）3[1+a +a （a +1）+a （a +1）2+…+a （a +1）96]＝…＝（a +1）100．故答案为：（a +1）100．16．【解答】解：∵二次三项式x 2﹣kx +36是一个完全平方式，∴k ＝±12，故答案为：±1217．【解答】解：（x ﹣1）（x +3）＝x 2+3x ﹣x ﹣3＝x 2+2x ﹣3．故答案为：x 2+2x ﹣3．18．【解答】解：∵x +1x =3，∴（x +1x ）2＝x 2+2+1x 2=9， ∴x 2+1x 2=7， 故答案为：7．19．【解答】解：∵x +y ＝17，xy ＝60，∴x 2+y 2＝（x +y ）2﹣2xy ＝172﹣2×60＝169．故本题答案为：169．20．【解答】解：∵x +y ＝2，x 2﹣y 2＝（x +y ）（x ﹣y ）＝6，∴x ﹣y ＝3，故答案为：3．21．【解答】解：根据题意得：4a 2b ÷ab ＝4a ，则纸板的面积为4a •b +4a •a •2+a •b •2＝4ab +8a 2+2ab ＝6ab +8a 2． 故答案为：6ab +8a 2．22．【解答】解：设t ＝n ﹣99，则n ＝t +99，∵（n ﹣99）（n ﹣105）＝3，∴t （t ﹣6）＝3，即t 2﹣6t ＝3，∴t 2﹣6t +9＝12，∴（t ﹣3）2＝12，∴原式＝4（n ﹣102）2＝4（t ﹣3）2＝4×12＝48．故答案为48．23．【解答】解：已知等式整理得：x 2+（2﹣a ）x ﹣2a ＝x 2+bx ﹣10， 可得2﹣a ＝b ，﹣2a ＝﹣10，解得：a ＝5，b ＝﹣3，则ab ＝﹣15，故答案为：﹣1524．【解答】解：∵mn ＝1，m ﹣n ＝2，∴m 2n ﹣mn 2＝mn （m ﹣n ）＝1×2＝2故答案为：2．25．【解答】解：∵x +y ＝3，xy ＝﹣12，∴x 2+y 2＝（x +y ）2﹣2xy ＝32﹣2×（﹣12）＝33．26．【解答】解：∵2x ＝5，2y ＝3，∴2x +y ＝2x ×2y ＝15．故答案为：15．27．【解答】解：∵m +2n +2＝0，∴m +2n ＝﹣2，∴2m •4n ＝2m •22n ＝2m +2n ＝2﹣2=14． 故答案为：14．28．【解答】解：（x +p ）（x +5）＝x 2+5x +px +5p ＝x 2+（5+p ）x +5p ， ∵乘积中不含x 的一次项，∴5+p ＝0，解得p ＝﹣5，故答案为：﹣5．29．【解答】解：设正方形的边长是xcm ，根据题意得：（x +2）2﹣x 2＝44，解得：x ＝10．故答案为：10cm ．30．【解答】解：∵5x ﹣3y ＝2，∴105x ÷103y ＝105x ﹣3y ＝102＝100．故答案为：100．31．【解答】解：∵（x +y ）2＝49，xy ＝12，∴x 2+y 2＝（x +y ）2﹣2xy ＝49﹣24＝25，故答案为：2532．【解答】解：∵x 2+mx +25＝x 2+mx +52是完全平方式，∴m＝±2×5＝±10．故答案为：±10．33．【解答】解：原式＝x2+2x+x+2＝x2+3x+2，故答案为：x2+3x+234．【解答】解：∵a9÷a n＝a5，∴9﹣n＝5，n＝4．故答案为：4．35．【解答】解：由于（x±1）2，＝x2±2x+1，＝x2+mx+1，∴m＝±2．故答案为：±2．36．【解答】解：原式＝x（4x2﹣9）＝x（2x+3）（2x﹣3），故答案为：x（2x+3）（2x﹣3）37．【解答】解：∵点（﹣3，4）与点（a2，b2）关于y轴对称，∴a2＝3，b2＝4．∴（a+b）（a﹣b）＝a2﹣b2＝3﹣4＝﹣1．故答案为：﹣1．38．【解答】解：原式＝4x2y2•（﹣5x2y）＝﹣20x4y3．故答案为：﹣20x4y3．39．【解答】解：当a+b＝10，ab＝11时，原式＝（a+b）2﹣3ab＝100﹣33＝67．故答案为：67．40．【解答】解：原式＝a2+4ab+4b2＝a2+4ab+4b2，故答案为：a2+4ab+4b2．41．【解答】解：原式＝2x2+6xy﹣xy﹣3y2＝2x2+5xy﹣3y2．故答案为：2x2+5xy﹣3y2．。

历史八年级上册期末复习提纲第一单元中国开始沦为半殖民地半封建社会第1课鸦片战争（1840-1842）（道光帝在位）一、鸦片走私与林则徐禁烟（一）鸦片走私1、原因：19世纪上半期，英国成为最强大的资本主义国家。

为开辟国外市场、推销工业品、掠夺廉价的工业原料，英国把侵略矛头指向中国。

2、根本目的：打开中国市场3、直接原因：扭转对华贸易的逆差4、危害：经济上：使白银外流造成清政府财政危机政治上：官吏更加腐败军事上：军队的战斗力削弱④生活上：毒害中国人民的身心健康（二）林则徐禁烟1、背景：白银大量外流，直接威胁到清政府的财政；腐蚀统治机构，清政府更加腐败；削弱了军队的战斗力；毒害中国人民的身心健康。

2、目的：维护清王朝的封建统治。

3、林则徐虎门销烟的经过（1）人物：1838 年底，道光帝派林则徐为钦差大臣赴广州查禁鸦片。

（2）时间：1839年6月3日至25日（3）林则徐禁烟措施：①派人暗访密查②缉拿烟贩③强迫外商交出鸦片二百多万斤④虎门销烟（4）虎门销烟：（1）时间：1839年6月领导人：林则徐地点：广州虎门海滩（2）意义（影响）：是中国人民禁烟斗争的伟大胜利，显示了中华民族反对外来侵略的坚强意志。

振奋了民族精神，维护了民族尊严，林则徐是当之无愧的民族英雄。

二、英国发动侵略战争1、时间：1840.6～1842.82、直接原因（借口、导火线）：中国的禁烟运动（虎门销烟）3、根本原因：英国为打开中国市场4、第一阶段：1840年6月---1841年5月英军封锁珠江口→陷定海→逼天津→道光帝将林则徐撤职查办第二阶段： 1841年6月---1842年8月英军占香港、进攻虎门炮台、占四方炮台（关天培——中国近代牺牲的第一位清军将领）→占厦门、定海、宁波、吴松、镇江到南京下关江面（陈化成吴淞之战牺牲）三、《南京条约》的签订★★★★★1、时间：1842年8月29日2、内容：①割香港岛给英国；②赔款2100万元；③开放广州、厦门、福州、宁波、上海五处为通商口岸；④英商进出口货物应纳税款，必须经过双方协议。

第12章全等三角形一．选择题（共12小题）1．下列各组的两个图形属于全等图形的是（）A．B．C．D．2．下列说法中，正确的是（）A．全等图形是形状相同的两个图形B．全等三角形是指面积相同的两个三角形C．等边三角形都是全等三角形D．全等图形的周长、面积都相等3．如图，若△ABC≌△CDA，则下列结论错误的是（）A．∠2＝∠1 B．AC＝CA C．∠B＝∠D D．BC＝DC4．如图，△ABC≌△ADE，点D落在BC上，且∠EDC＝70°，则∠B的度数等于（）A．50°B．55°C．60°D．65°5．如图，∠C＝∠D，那么补充下列一个条件后，仍无法判定△ABC≌△BAD的是（）A．AD＝BC B．AC＝BD C．∠CAB＝∠DBA D．∠ABC＝∠BAD 6．如图，小明书上的三角形被墨水污染了，他根据所学知识画出了完全一样的一个三角形，他的依据是（）A．ASA B．SAS C．SSS D．AAS7．如图，点A，D，C，E在同一条直线上，AB∥EF，AB＝EF，∠B＝∠F，AE＝10，AC＝7，则AD的长为（）A．5.5 B．4 C．4.5 D．38．如图，已知AB⊥BC于B，CD⊥BC于C，BC＝13，AB＝5，且E为BC上一点，∠AED＝90°，AE＝DE，则BE＝（）A．13 B．8 C．6 D．59．如图，在△ABC中，AC⊥BC，AE为∠BAC的平分线，ED⊥AB于点D，AB＝7cm，AC＝3cm，则BD的长为（）A．3cm B．4cm C．1cm D．2cm10．小明不慎将一块三角形的玻璃碎成如图所示的四块（图中所标1、2、3、4），你认为将其中的哪一块带去，就能配一块与原来大小一样的三角形玻璃？应该带第_____块去，这利用了三角形全等中的_____原理（）A．1；SAS B．2；ASA C．3；ASA D．4；SAS11．如图，△ABC中，∠C＝90°，∠BAC的角平分线交BC于点D，DE⊥AB于点E．若CD＝2，AB＝7，则△ABD的面积为（）A．3.5 B．7 C．14 D．2812．有一块三角形的草坪，现要在草坪上建一座凉亭供大家休息，要使凉亭到草坪三条边的距离相等，则凉亭的位置应选在（）A．△ABC三条角平分线的交点B．△ABC三边的垂直平分线的交点C．△ABC三条中线的交点D．△ABC三条高所在直线的交点二．填空题（共4小题）13．如图，△ABD≌△ACE，AD＝8cm，AB＝3cm，则BE＝cm．14．如图，已知△ABC≌△DEF，A和D是对应顶点，若∠A＝80°，∠B＝65°，则∠F°．15．如图，点P是∠AOB平分线OC上一点，PE⊥OA，PF⊥OB，垂足分别是点E，F，若PE ＝3．则PF＝．16．利用两块完全相同的直角三角板测量升旗台的高度．首先将两块完全相同的三角板按图1放置，然后交换两块三角板的位置，按图2放置．测量数据如图所示，则升旗台的高度是cm．三．解答题（共5小题）17．如图，利用尺规，在△ABC的边AC上方作∠CAE＝∠ACB，在射线AE上截取AD＝BC，连接CD，并证明：CD∥AB（尺规作图要求保留作图痕迹，不写作法）18．如图，已知AB，CD相交于O，△ACO≌△BDO，AE＝BF，求证：CE＝FD．19．如图，在△ABC中，AB＝AC，CD⊥AB于点D，BE⊥AC于点E．求证：BD＝CE．20．如图，∠A＝∠B＝90°，E是AB上的一点，且AD＝BE，∠1＝∠2，求证：Rt△ADE≌Rt△BEC．21．如图，在△ABC和△DEF中，AB∥DE，点A，F，C，D在同一直线上，AF＝CD，∠AFE＝∠BCD．试说明：（1）△ABC≌△DEF；（2）BF∥EC．参考答案与试题解析一．选择题（共12小题）1．下列各组的两个图形属于全等图形的是（）A．B．C．D．【分析】根据全等形是能够完全重合的两个图形进行分析判断．【解答】解：A、两个图形能够完全重合，故本选项正确．B、圆内两条相交的线段不能完全重合，故本选项错误；C、两个正方形的边长不相等，不能完全重合，故本选项错误；D、两只眼睛下面的嘴巴不能完全重合，故本选项错误；故选：A．2．下列说法中，正确的是（）A．全等图形是形状相同的两个图形B．全等三角形是指面积相同的两个三角形C．等边三角形都是全等三角形D．全等图形的周长、面积都相等【分析】根据全等形是能够完全重合的两个图形进行分析判断．【解答】解：A、全等图形是指形状相同、大小相等的两个图形，故本选项错误；B、全等三角形是指能够完全重合的两个三角形，故本选项错误；C、等边三角形的形状相同、但是大小不一定相等，所以不一定都是全等三角形，故本选项错误；D、全等图形的周长、面积相等，故本选项正确；故选：D．3．如图，若△ABC≌△CDA，则下列结论错误的是（）A．∠2＝∠1 B．AC＝CA C．∠B＝∠D D．BC＝DC【分析】直接利用全等三角形的性质得出对应角以及对应边相等进而得出答案．【解答】解：∵△ABC≌△CDA，∴∠1＝∠2，AC＝CA，∠B＝∠D，BC＝AD，故只有选项D，BC＝DC错误．故选：D．4．如图，△ABC≌△ADE，点D落在BC上，且∠EDC＝70°，则∠B的度数等于（）A．50°B．55°C．60°D．65°【分析】直接利用全等三角形的性质得出AB＝AD，∠B＝∠ADE，进而利用已知得出答案．【解答】解：∵△ABC≌△ADE，∴AB＝AD，∠B＝∠ADE，∴∠B＝∠ADB，∴∠BDA＝∠ADE，∵∠EDC＝70°，∴∠BDA＝∠ADE＝×（180°﹣70°）＝55°．故选：B．5．如图，∠C＝∠D，那么补充下列一个条件后，仍无法判定△ABC≌△BAD的是（）A．AD＝BC B．AC＝BD C．∠CAB＝∠DBA D．∠ABC＝∠BAD 【分析】根据全等三角形的判定方法即可一一判断．【解答】解：A、SSA无法判断三角形全等，故本选项符合题意；B、根据ASA即可判断△ACO≌△BDO，得OC＝OD，OA＝OB，再用SAS可得三角形全等，故本选项不符合题意；C、根据AAS即可判断三角形全等，故本选项不符合题意；D、根据AAS即可判断三角形全等，故本选项不符合题意；故选：A．6．如图，小明书上的三角形被墨水污染了，他根据所学知识画出了完全一样的一个三角形，他的依据是（）A．ASA B．SAS C．SSS D．AAS【分析】根据图形，未污染的部分两角与这两角的夹边可以测量，然后根据全等三角形的判定方法解答即可．【解答】解：小周书上的三角形被墨水污染了，他根据所学知识画出了完全一样的一个三角形，他根据的定理是：两角及其夹边分别相等的两个三角形全等（ASA）．故选：A．7．如图，点A，D，C，E在同一条直线上，AB∥EF，AB＝EF，∠B＝∠F，AE＝10，AC＝7，则AD的长为（）A．5.5 B．4 C．4.5 D．3【分析】证明△ABC≌△EFD可得DE＝AC＝10，根据AD＝AE﹣DE可求解．【解答】解：∵AB∥EF，∴∠A＝∠E．又AB＝EF，∠B＝∠F，∴△ABC≌△EFD（ASA）．∴AC＝DE＝10．∴AD＝AE﹣DE＝10﹣7＝3．故选：D．8．如图，已知AB⊥BC于B，CD⊥BC于C，BC＝13，AB＝5，且E为BC上一点，∠AED＝90°，AE＝DE，则BE＝（）A．13 B．8 C．6 D．5【分析】证明△ABE≌△ECD得到CE值，则BE可求．【解答】解：在△ABE和△ECD中∴△ABE≌△ECD（AAS）．∴CE＝AB＝5．∴BE＝BC﹣CE＝13﹣5＝8．故选：B．9．如图，在△ABC中，AC⊥BC，AE为∠BAC的平分线，ED⊥AB于点D，AB＝7cm，AC＝3cm，则BD的长为（）A．3cm B．4cm C．1cm D．2cm【分析】根据垂直的定义得到∠C＝∠ADE＝90°，利用AAS定理证明△ACE≌△ADE，根据全等三角形的性质计算即可．【解答】解：∵AC⊥BC，ED⊥AB，∴∠C＝∠ADE＝90°，在△ACE和△ADE中，，∴△ACE≌△ADE（AAS），∴AD＝AC＝3cm，∴BD＝AB﹣AD＝4cm，故选：B．10．小明不慎将一块三角形的玻璃碎成如图所示的四块（图中所标1、2、3、4），你认为将其中的哪一块带去，就能配一块与原来大小一样的三角形玻璃？应该带第_____块去，这利用了三角形全等中的_____原理（）A．1；SAS B．2；ASA C．3；ASA D．4；SAS【分析】根据全等三角形的判断方法解答．【解答】解：由图可知，带第4块去，符合“角边角”，可以配一块与原来大小一样的三角形玻璃．故选：B．11．如图，△ABC中，∠C＝90°，∠BAC的角平分线交BC于点D，DE⊥AB于点E．若CD＝2，AB＝7，则△ABD的面积为（）A．3.5 B．7 C．14 D．28【分析】根据角平分线的性质得出DE＝CD＝2，根据三角形的面积公式求出即可．【解答】解：∵△ABC中，∠C＝90°，∠BAC的角平分线交BC于点D，DE⊥AB于点E，CD＝2，∴DE＝CD＝2，∵AB＝7，∴△ABD的面积是：＝＝7，故选：B．12．有一块三角形的草坪，现要在草坪上建一座凉亭供大家休息，要使凉亭到草坪三条边的距离相等，则凉亭的位置应选在（）A．△ABC三条角平分线的交点B．△ABC三边的垂直平分线的交点C．△ABC三条中线的交点D．△ABC三条高所在直线的交点【分析】根据角平分线的性质解答即可．【解答】解：∵三角形角平分线上的点到角两边的距离相等，∴亭的位置应选在三角形三条角平分线的交点上．故选：A．二．填空题（共4小题）13．如图，△ABD≌△ACE，AD＝8cm，AB＝3cm，则BE＝ 5 cm．【分析】由△ABD≌△ACE可得AD＝AE，AC＝AB，因为BE＝AE﹣AB，即可AE的长度．【解答】解：∵△ABD≌△ACE，∴AD＝AE，AC＝AB，又AD＝8cm，AB＝3cm，∵BE＝AE﹣AB＝8﹣3＝5，∴BE＝5cm．故填5．14．如图，已知△ABC≌△DEF，A和D是对应顶点，若∠A＝80°，∠B＝65°，则∠F＝35 °．【分析】利用三角形内角和定理可得∠ACB，再根据全等三角形的性质可得∠F＝∠ACB ＝35°．【解答】解：∵∠A＝80°，∠B＝65°，∴∠ACB＝180°﹣80°﹣65°＝35°，∵△ABC≌△DEF，∴∠F＝∠ACB＝35°，故答案为：＝35．15．如图，点P是∠AOB平分线OC上一点，PE⊥OA，PF⊥OB，垂足分别是点E，F，若PE ＝3．则PF＝ 3 ．【分析】根据角平分线的性质直接写出结论即可．【解答】解：∵点P是∠AOB平分线OC上一点，PE⊥OA，PF⊥OB，∴PE＝PF，∵PE＝3，∴PF＝PE＝3，故答案为：3．16．利用两块完全相同的直角三角板测量升旗台的高度．首先将两块完全相同的三角板按图1放置，然后交换两块三角板的位置，按图2放置．测量数据如图所示，则升旗台的高度是69 cm．【分析】设升旗台的高度是zcm，AC＝xcm，BC＝ycm．构建方程组即可解决问题．【解答】解：设升旗台的高度是zcm，AC＝xcm，BC＝ycm．由题意：，①+②可得，2z＝138，∴z＝69，故答案为69．三．解答题（共5小题）17．如图，利用尺规，在△ABC的边AC上方作∠CAE＝∠ACB，在射线AE上截取AD＝BC，连接CD，并证明：CD∥AB（尺规作图要求保留作图痕迹，不写作法）【分析】利用尺规作∠EAC＝∠ACB即可，先证明△ACD≌△CAB，再证明CD∥AB即可．【解答】解：图象如图所示，∵∠EAC＝∠ACB，∴AD∥CB，∵AD＝BC，AC＝CA，∴△ACD≌△CAB，∴∠ACD＝∠CAB，∴AB∥CD．18．如图，已知AB，CD相交于O，△ACO≌△BDO，AE＝BF，求证：CE＝FD．【分析】首先根据△ACO≌△BDO得到CO＝OD，AO＝OB，进而得到OE＝OF，再证明△COE ≌△DOF，即可得到结论．【解答】解：∵△ACO≌△BDO，∴CO＝OD，AO＝OB，∵AE＝BF，∴OE＝OF，∴△COE≌△DOF，∴CE＝DF．19．如图，在△ABC中，AB＝AC，CD⊥AB于点D，BE⊥AC于点E．求证：BD＝CE．【分析】根据垂直的定义可得∠BDC＝∠CEB＝90°，根据等腰三角形的性质可得∠ABC ＝∠ACB，再有公共边BC，利用AAS可得△BCD≌△CBE，据此可得BD＝CE．【解答】证明：∵CD⊥AB，BE⊥AC，∴∠BDC＝∠CEB＝90°，∵AB＝AC，∴∠ABC＝∠ACB，在△BCD和△CBE中，∠BDC＝∠CEB，∠DBC＝∠ECB，BC＝CB，∴△BCD≌△CBE（AAS），∴BD＝CE．20．如图，∠A＝∠B＝90°，E是AB上的一点，且AD＝BE，∠1＝∠2，求证：Rt△ADE≌Rt△BEC．【分析】根据已知条件，利用直角三角形的特殊判定方法可以证明题目结论．【解答】证明：∵∠1＝∠2，∴DE＝CE．∵AD∥BC，∠A＝∠B＝90°，∴△ADE和△EBC是直角三角形，而AD＝BE．∴Rt△ADE≌Rt△BEC（HL）21．如图，在△ABC和△DEF中，AB∥DE，点A，F，C，D在同一直线上，AF＝CD，∠AFE＝∠BCD．试说明：（1）△ABC≌△DEF；（2）BF∥EC．【分析】（1）由角边角可证明△ABC和△DEF全等；（2）证明△BFC和△ECF全等，可得∠BFC＝∠ECF，继而可得BF∥EC．【解答】证：（1）∵AB∥DE，∴∠A＝∠D∵AF＝CD，∴AF+FC＝CD+FC即AC＝DF∵∠AFE＝∠BCD，∴∠DFE＝∠ACB在△ABC和△DEF中，∴△ABC≌△DEF（ASA）（2）∵△ABC≌△DEF∴BC＝EF在△BCF和△EFC中，∴△BCF≌△EFC（SAS）∴∠BFC＝∠ECF∴BF∥EC。

第11章《三角形》解答题精选1．（2019秋•花都区期末）如图，在四边形ABCD 中，∠C +∠D ＝210°（1）∠DAB +∠CBA ＝ 度；（2）若∠DAB 的角平分线与∠CBA 的角平分线相交于点E ，求∠E 的度数．2．（2019秋•南海区期末）阅读下面的材料，并解决问题．（1）已知在△ABC 中，∠A ＝60°，图1﹣3的△ABC 的内角平分线或外角平分线交于点O ，请直接求出下列角度的度数．如图1，∠O ＝ ；如图2，∠O ＝ ；如图3，∠O ＝ ；如图4，∠ABC ，∠ACB 的三等分线交于点O 1，O 2，连接O 1O 2，则∠BO 2O 1＝ ．（2）如图5，点O 是△ABC 两条内角平分线的交点，求证：∠O ＝90°+12∠A ． （3）如图6，△ABC 中，∠ABC 的三等分线分别与∠ACB 的平分线交于点O 1，O 2，若∠1＝115°，∠2＝135°，求∠A 的度数．3．（2019秋•普宁市期末）某校八年级数学兴趣小组对“三角形内角或外角平分线的夹角与第三个内角的数量关系”进行了探究．（1）如图1，在△ABC 中，∠ABC 与∠ACB 的平分线交于点P ，∠A ＝64°，则∠BPC ＝ ；（2）如图2，△ABC 的内角∠ACB 的平分线与△ABC 的外角∠ABD 的平分线交于点E ．其中∠A ＝α，求∠BEC ．（用α表示∠BEC ）；（3）如图3，∠CBM 、∠BCN 为△ABC 的外角，∠CBM 、∠BCN 的平分线交于点Q ，请你写出∠BQC 与∠A 的数量关系，并证明．4．（2019秋•东莞市期末）如图，在△ABC 中，AD 是高，AE 是角平分线，∠B ＝70°，∠DAE ＝10°，求∠C 的度数．5．（2020春•东湖区期末）（1）已知一个正多边形的每个内角比它的每个外角的4倍多30°，求这个多边形的边数；（2）一个多边形的外角和是内角和的27，求这个多边形的边数．6．（2019秋•越秀区期末）如图所示，在△ABC 中，D 是BC 边上一点∠1＝∠2，∠3＝∠4，∠BAC ＝69°，求∠DAC 的度数．7．（2019秋•揭阳期末）探究与发现：如图①，在△ABC 中，∠B ＝∠C ＝45°，点D 在BC 边上，点E 在AC 边上，且∠ADE ＝∠AED ，连接DE ．（1）当∠BAD ＝60°时，求∠CDE 的度数；（2）当点D 在BC （点B 、C 除外）边上运动时，试猜想∠BAD 与∠CDE 的数量关系，并说明理由．（3）深入探究：如图①，若∠B ＝∠C ，但∠C ≠45°，其他条件不变，试探究∠BAD 与∠CDE 的数量关系．8．（2019秋•江城区期末）如图，Rt △ABC 中，∠C ＝90°，∠B ＝3∠A ，求∠B 的度数．9．（2019春•龙门县期末）如图，在四边形ABCD 中，AD ∥BC ，连接BD ，点E 在BC 边上，点F 在DC 边上，且∠1＝∠2．（1）求证：EF ∥BD ；（2）若DB 平分∠ABC ，∠A ＝130°，求∠2的度数．10．（2019春•番禺区期末）（1）如图1，已知AB ∥CD ，求证：∠EGF ＝∠AEG +∠CFG ．（2）如图2，已知AB ∥CD ，∠AEF 与∠CFE 的平分线交于点G ．猜想∠G 的度数，并证明你的猜想．（3）如图3，已知AB ∥CD ，EG 平分∠AEH ，EH 平分∠GEF ，FH 平分∠CFG ，FG 平分∠HFE ，∠G ＝95°，求∠H 的度数．11．（2019春•南海区期末）如图1，在△ABC 中，∠A ＝80°，BD 、CE 分别平分∠ABC 、∠ACB ，BD 与CE 交于点F ．（1）求∠BFC 的度数；（2）如图2，EG、DG分别平分∠AEF、∠ADF，EG与DG交于点G，求∠EGD的度数．12．（2018秋•澄海区期末）如图，已知AD，AE是△ABC的高和角平分线，∠B＝44°，∠C＝76°，求∠DAE的度数．13．（2018秋•越秀区期末）如图，六边形ABCDEF的内角都相等，∠F AD＝60°．（1）求∠ADE的度数；（2）求证：EF∥BC．14．（2018秋•揭西县期末）CE是△ABC的一个外角∠ACD的平分线，且EF∥BC交AB于点F，∠A＝60°，∠CEF＝50°，求∠B的度数．15．（2018秋•普宁市期末）已知，直线PQ∥MN，△ABC的顶点A与B分别在直线MN与PQ上，点C在直线AB 的右侧，且∠C＝45°，设∠CBQ＝∠α，∠CAN＝∠β．（1）如图1，当点C落在PQ的上方时，AC与PQ相交于点D，求证：∠β＝∠α+45°．请将下列推理过程补充完整：证明：∵∠CDQ是△CBD的一个外角（三角形外角的定义），∴∠CDQ＝∠α+∠C（三角形的一个外角等于和它不相邻的两个内角的和）∵PQ∥MN（），∴∠CDQ＝∠β（）．∴∠β＝（等量代换）．∵∠C＝45°（已知），∴∠β＝∠α+45°（等量代换）（2）如图2，当点C落在直线MN的下方时，BC与MN交于点F，请判断∠α与∠β的数量关系，并说明理由．16．（2017春•石狮市期末）如图，在△ABC中，点D在BC边上，点E在AC边上，连接AD，DE，∠B＝60°（1）若∠3＝60°，试说明∠1＝∠2；（2）∠C＝40°，∠1＝50°，且∠3＝∠4，求∠2的度数．17．（2019春•潮南区期末）如图，在四边形ABCD中，AD∥BC，∠ABC的平分线交CD于点E．（1）若∠A＝70°，求∠ABE的度数；（2）若AB∥CD，且∠1＝∠2，判断DF和BE是否平行，并说明理由．18．（2018秋•大埔县期末）如图，在△ABC中，∠ABC和∠ACB的平分线相交于点O，若∠A＝42°．（1）求∠BOC的度数；（2）把（1）中∠A＝42°这个条件去掉，试探索∠BOC和∠A之间有怎样的数量关系．19．（2019春•南海区期末）已知：如图，在△ABC中，∠BAC＝80°，AD⊥BC于D，AE平分∠DAC，∠B＝60°；求∠AEC的度数．20．（2018秋•禅城区期末）叙述并证明“三角形的内角和定理”．（要求根据下图写出已知、求证并证明）21．（2018春•福田区期末）完成下列推理说明．如图，在三角形ABC中，点D、F在BC边上，点E在AB边上，点G在AC边上，∠CDG＝∠B，∠1+∠FEA ＝180°，试说明：∠BFE＝∠ADF．理由：因为∠CDG＝∠B（已知）所以DG∥AB（）所以＝∠BAD（）因为∠1+∠FEA＝180°（已知）所以+∠FEA＝180°（等量代换）所以AD∥EF（）所以∠BFE＝（）22．（2018春•海珠区期末）已知点C（﹣10，10），直线CE∥x轴交y轴于点B，点A是x轴的负半轴上的动点，作AD⊥AC交线段BO于点D（点D不与点O、B重合），MD⊥AD交CE于点M，∠EMD，∠OAD的角平分线MN，AN交于点N（1）直接写出OB的长度；（2）求出∠MNA的度数；（3）若NH⊥x轴于点H，求∠ANH的取值范围．23．（2017秋•潮安区期末）如图，AB、ED分别垂直于BD，点B、D是垂足，且∠ACB＝∠CED．求证△ACE是直角三角形．24．（2017秋•白云区期末）如图，在△ABC中，AD⊥BC，垂足为D，∠1＝∠B，∠C＝67°，求∠BAC的度数．25．（2018春•澄海区期末）（1）如图①，在四边形ABCD中，AD∥BC，点E是线段CD上一点．求证：∠AEB＝∠DAE+∠CBE；（2）如图①，若AE平分∠DAC，∠CAB＝∠CBA．①求证：∠ABE+∠AEB＝90°；①如图①，若∠ACD的平分线与BA的延长线交于点F，与AE交于点P，且∠F＝65°，求∠BCD的度数．26．（2018春•白云区期末）已知：在四边形ABCD中，连接AC、BD，∠1＝∠2，∠3＝∠4．求证：∠ABC＝∠ADC．27．（2018春•越秀区期末）如图1，已知∠A+∠E+∠F+∠C＝540°．（1）试判断直线AB与CD的位置关系，并说明理由（2）如图2，∠P AB＝3∠P AQ，∠PCD＝3∠PCQ，试判断∠APC与∠AQC的数量关系，并说明理由．28．（2018春•东莞市期末）如图，AC、BD相交于点O，∠A＝∠ABC，∠DBC＝∠D，BD平分∠ABC，点E在BC 的延长线上．（1）求证：CD∥AB；（2）若∠D＝38°，求∠ACE的度数．29．（2018春•茂名期末）已知：△ABC，∠A、∠B、∠C之和为多少？为什么？解；∠A+∠B+∠C＝180°理由：作∠ACD＝∠A，并延长BC到E∵∠ACD＝∠（已作）AB∥CD（）∴∠B＝（）而∠ACB+∠ACD+∠DCE＝180°∴∠ACB++＝180°（）30．（2018春•香洲区期末）如图1，线段AB⊥BC于点B，CD⊥BC于点C，点E在线段BC上，且AE⊥DE．（1）求证：∠EAB＝∠CED；（2）如图2，AF、DF分别平分∠BAE和∠CDE，EH平分∠DEC交CD于点H，EH的反向延长线交AF于点G．①求证EG⊥AF；①求∠F的度数．【提示：三角形内角和等于180度】第11章《三角形》解答题精选参考答案与试题解析一．解答题（共30小题）1．【解答】解：（1）∵∠DAB+∠CBA+∠C+∠D＝360°，∴∠DAB+∠CBA＝360°﹣（∠C+∠D）＝360°﹣210°＝150°．故答案为：150；（2）∵∠DAB与∠ABC的平分线交于四边形内一点E，∴∠EAB=12∠DAB，∠EBA=12∠ABC，∴∠E＝180°﹣（∠EAB+∠EBA）＝180°−12（∠DAB+∠CBA）＝180°−12（360°﹣∠C﹣∠D）=12（∠C+∠D），∵∠C+∠D＝210°，∴∠E=12（∠C+∠D）＝105°．2．【解答】解；（1）如图1，∵BO平分∠ABC，CO平分∠ACB∴∠OBC=12∠ABC，∠OCB=12∠ACB∴∠OBC+∠OCB=12（∠ABC+∠ACB）=12（180°﹣∠BAC）=12（180°﹣60°）＝60°∴∠O＝180°﹣（∠OBC+∠OCB）＝120°；如图2，∵BO平分∠ABC，CO平分∠ACD∴∠OBC=12∠ABC，∠OCD=12∠ACD∵∠ACD＝∠ABC+∠A∴∠OCD=12（∠ABC+∠A）∵∠OCD＝∠OBC+∠O ∴∠O＝∠OCD﹣∠OBC=12∠ABC+12∠A−12∠ABC=12∠A ＝30°如图3，∵BO 平分∠EBC ，CO 平分∠BCD∴∠OBC =12∠EBC ，∠OCB =12∠BCD∴∠OBC +∠OCB=12（∠EBC +∠BCD ）=12（∠A +∠ACB +∠BCD ）=12（∠A +180°）=12（60°+180°）＝120°∴∠O ＝180°﹣（∠OBC +∠OCB ）＝60°如图4，∵∠ABC ，∠ACB 的三等分线交于点O 1，O 2∴∠O 2BC =23∠ABC ，∠O 2CB =23∠ACB ，O 1B 平分∠O 2BC ，O 1C 平分∠O 2CB ，O 2O 1平分BO 2C ∴∠O 2BC +∠O 2CB=23（∠ABC +∠ACB ） =23（180°﹣∠BAC ）=23（180°﹣60°） ＝80°∴∠BO 2C ＝180°﹣（∠O 2BC +∠O 2CB ）＝100°∴∠BO 2O 1=12∠BO 2C ＝50°故答案为：120°，30°，60°，50°；（2）证明：∵OB 平分∠ABC ，OC 平分∠ACB ，∴∠OBC =12∠ABC ，∠OCB =12∠ACB ，∠O ＝180°﹣（∠OBC +∠OCB ）＝180°−12（∠ABC +∠ACB ）＝180°−12（180°﹣∠A ）＝90°+12∠A ． （3）∵∠O 2BO 1＝∠2﹣∠1＝20°∴∠ABC ＝3∠O 2BO 1＝60°，∠O 1BC ＝∠O 2BO 1＝20°∴∠BCO 2＝180°﹣20°﹣135°＝25°∴∠ACB ＝2∠BCO 2＝50°∴∠A ＝180°﹣∠ABC ﹣∠ACB ＝70°或由题意，设∠ABO 2＝∠O 2BO 1＝∠O 1BC ＝α，∠ACO 2＝∠BCO 2＝β， ∴2α+β＝180°﹣115°＝65°，α+β＝180°﹣135°＝45°∴α＝20°，β＝25°∴∠ABC +∠ACB ＝3α+2β＝60°+50°＝110°，∴∠A ＝70°．3．【解答】解：（1）∵BP 、CP 分别平分∠ABC 和∠ACB ，∴∠PBC =12∠ABC ，∠PCB =12∠ACB ，∴∠BPC ＝180°﹣（∠PBC +∠PCB ）＝180°﹣（12∠ABC +12∠ACB ）， ＝180°−12（∠ABC +∠ACB ），＝180°−12（180°﹣∠A ）， ＝180°﹣90°+12∠A ， ＝90°+32°＝122°，故答案为：122°；（2）∵CE 和BE 分别是∠ACB 和∠ABD 的角平分线，∴∠1=12∠ACB ，∠2=12∠ABD ，又∵∠ABD 是△ABC 的一外角，∴∠ABD ＝∠A +∠ACB ，∴∠2=12（∠A +∠ABC ）=12∠A +∠1，∵∠2是△BEC 的一外角，∴∠BEC ＝∠2﹣∠1=12∠A +∠1﹣∠1=12∠A =α2；（3）∠QBC =12（∠A +∠ACB ），∠QCB =12（∠A +∠ABC ）， ∠BQC ＝180°﹣∠QBC ﹣∠QCB ，＝180°−12（∠A +∠ACB ）−12（∠A +∠ABC ），＝180°−12∠A −12（∠A +∠ABC +∠ACB ），结论∠BQC ＝90°−12∠A ． 4．【解答】解：∵AD 是高，∠B ＝70°，∴∠BAD ＝20°，∴∠BAE ＝20°+10°＝30°，∵AE 是角平分线，∴∠BAC ＝60°，∴∠C ＝180°﹣70°﹣60°＝50°．5．【解答】解：（1）设这个多边形的每个内角是x °，每个外角是y °， 则得到一个方程组{α=4α+30α+α=180 解得{α=150α=30， 而任何多边形的外角和是360°，则多边形内角和中的外角的个数是360÷30＝12，则这个多边形的边数是12边形；（2）设这个多边形的边数为n ，依题意得：27（n ﹣2）180°＝360°，解得n ＝9，答：这个多边形的边数为9．6．【解答】解：设∠1＝∠2＝x °，则∠3＝∠4＝2x °，∵∠2+∠4+∠BAC＝180°，∴x+2x+69＝180，解得x＝37，即∠1＝37°，∴∠DAC＝∠BAC﹣∠1＝69°﹣37°＝32°．7．【解答】解：（1）∵∠ADC是△ABD的外角，∴∠ADC＝∠BAD+∠B＝105°，∠DAE＝∠BAC﹣∠BAD＝30°，∴∠ADE＝∠AED＝75°，∴∠CDE＝105°﹣75°＝30°；（2）∠BAD＝2∠CDE，理由如下：设∠BAD＝x，∴∠ADC＝∠BAD+∠B＝45°+x，∠DAE＝∠BAC﹣∠BAD＝90°﹣x，∴∠ADE＝∠AED=90°+α2，∴∠CDE＝45°+x−90°+α2=12x，∴∠BAD＝2∠CDE；（3）设∠BAD＝x，∴∠ADC＝∠BAD+∠B＝∠B+x，∠DAE＝∠BAC﹣∠BAD＝180°﹣2∠C﹣x，∴∠ADE＝∠AED＝∠C+12 x，∴∠CDE＝∠B+x﹣（∠C+12x）=12x，∴∠BAD＝2∠CDE．8．【解答】解：∵∠B＝3∠A，∴∠A=13∠B，∵∠C＝90°，∴∠A+∠B＝90°，∴13∠B+∠B＝90°，解得∠B＝67.5°．9．【解答】（1）证明：如图，∵AD∥BC（已知），∴∠1＝∠3（两直线平行，内错角相等）．∵∠1＝∠2，∴∠3＝∠2（等量代换）．∴EF∥BD（同位角相等，两直线平行）．（2）解：∵AD∥BC（已知），∴∠ABC+∠A＝180°（两直线平行，同旁内角互补）．∵∠A＝130°（已知），∴∠ABC＝50°．∵DB平分∠ABC（已知），∴∠3=12∠ABC＝25°．∴∠2＝∠3＝25°．10．【解答】证明：（1）如图1，过点G作GH∥AB，∴∠EGH＝∠AEG．∵AB∥CD，∴GH∥CD．∴∠FGH＝∠CFG．∴∠EGH+∠FGH＝∠AEG+∠CFG．即：∠EGF＝∠AEG+∠CFG；（2）如图2所示，猜想：∠G＝90°；证明：由（1）中的结论得：∠EGF＝∠AEG+∠CFG，∵EG、FG分别平分∠AEF和∠CEF，∴∠AEF＝2∠AEG，∠CEF＝2∠CFG，∵AB∥CD，∴∠AEF+∠CFE＝180°，∴2∠AEG+2∠CFG＝180°，∴∠AEG+∠CFG＝90°，∴∠G＝90°；（3）解：如图3，∵EG平分∠AEH，EH平分∠GEF，FH平分∠CFG，FG平分∠HFE，∴∠AEG＝∠GEH＝∠HEF=13αααα，∠CFH＝∠HFG＝∠EFG=13αααα，由（1）可知，∠G＝∠AEG+∠CFG，∠H＝∠AEH+∠CFH，∴∠G=13∠AEF+23∠CFE＝95°，∵AB∥CD，∴∠AEF+∠CFE＝180°，∴13（∠AEF+∠CFE）+13αCFE＝95°，∴∠CFE＝105°，∴∠AEF＝75°，∴∠H=23∠AEF+13∠CFE=23×75°+13×105°=85°．11．【解答】解：（1）∵BD、CE分别平分∠ABC、∠ACB∴∠CBD=12∠CBA，∠BCE=12∠ACB，∵∠CBA +∠BCA ＝180°﹣80°＝100°，∴∠BFC ＝180°−12（∠CBA +∠ACB ）＝130°．（2）∵EG 、DG 分别平分∠AEF 、∠ADF∴∠GEF =12∠AEF ，∠GDF =12∠ADF ，∵∠AEF +∠ADF ＝360°﹣80°﹣130°＝150°，∴∠GEF +∠GDF =12×150°＝75°，∴∠EGD ＝360°﹣（∠GEF +∠GDF ）﹣∠EFD ＝360°﹣75°﹣130°＝155°．12．【解答】解：∵∠B ＝44°，∠C ＝76°，∴∠BAC ＝180°﹣∠B ﹣∠C ＝60°，∵AE 是角平分线，∴∠EAC =12∠BAC ＝30°．∵AD 是高，∠C ＝76°，∴∠DAC ＝90°﹣∠C ＝14°，∴∠DAE ＝∠EAC ﹣∠DAC ＝30°﹣14°＝16°．13．【解答】解：（1）∵六边形ABCDEF 的内角都相等，∴∠BAF ＝∠B ＝∠C ＝∠CDE ＝∠E ＝∠F =(6−2)×180°6=120°， ∵∠F AD ＝60°，∴∠F +∠F AD ＝180°，∴EF ∥AD ，∴∠E +∠ADE ＝180°，∴∠ADE ＝60°；（2）∵∠BAD ＝∠F AB ﹣∠F AD ＝60°，∴∠BAD +∠B ＝180°，∴AD ∥BC ，∴EF ∥BC ．14．【解答】解：∵EF ∥BC ，∴∠CEF ＝∠ECD ＝50°，∵CE 平分∠ACD ，∴∠ACE ＝∠ECD ，∴∠ACD ＝∠ACE +∠ECD ＝100°，∴∠ACB ＝180°﹣∠ACD ＝180°﹣100°＝80°，∴∠B ＝180°﹣（∠A +∠ACB ）＝180°﹣60°﹣80°＝40°．15．【解答】解：（1）证明：∵∠CDQ 是△CBD 的一个外角（三角形外角的定义），∴∠CDQ ＝∠α+∠C （三角形的一个外角等于和它不相邻的两个内角的和）∵PQ ∥MN （已知），∴∠CDQ ＝∠β（两直线平行，同位角相等）．∴∠β＝∠α+∠C （等量代换）．∵∠C ＝45°（已知），∴∠β＝∠α+45°（等量代换）；故答案为：已知，两直线平行，同位角相等，∠α+∠C ，（2）证明：∵∠CFN 是△ACF 的一个外角（三角形外角的定义），∴∠CFN ＝∠β+∠C （三角形的一个外角等于和它不相邻的两个内角的和），∵PQ ∥MN （已知），∴∠CFN ＝∠α（两直线平行，同位角相等）∴∠α＝∠β+∠C （等量代换）．∵∠C ＝45°（已知），∴∠α＝∠β+45°（等量代换）．16．【解答】解：（1）∠B ＝60°，∠3＝60°，∴△ABD 中，∠1＝180°﹣∠B ﹣∠ADB ＝120°﹣∠ADB ，又∵∠2＝180°﹣∠3﹣∠ADB ＝120°﹣∠ADB ，∴∠1＝∠2；（2）∵∠C ＝40°，∠B ＝60°，∴∠BAC ＝80°，又∵∠1＝50°，∴∠DAE＝30°，又∵∠3＝∠4，∴∠4＝75°，∴∠2＝∠4﹣∠C＝75°﹣40°＝35°．17．【解答】（1）解：∵AD∥BC，∠A＝70°，∴∠ABC＝180°﹣∠A＝110°，∵BE平分∠ABC，∴∠ABE=12∠ABC＝55°；（2）证明：DF∥BE．∵AB∥CD，∴∠A+∠ADC＝180°，∠2＝∠AFD，∵AD∥BC，∴∠A+∠ABC＝180°，∴∠ADC＝∠ABC，∵∠1＝∠2=12∠ADC，∠ABE=12∠ABC∴∠2＝∠ABE，∴∠AFD＝∠ABE，∴DF∥BE．18．【解答】解：（1）∵∠A＝42°，∴∠ABC+∠ACB＝180°﹣∠A＝138°，∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线，∴∠1=12∠ABC，∠2=12∠ACB，∴∠1+∠2=12（∠ABC+∠ACB）=12×138°=69°，∴∠BOC＝180°﹣（∠1+∠2）＝180°﹣69°＝111°；（2）∠BOC＝90°+12∠A，∵BO、CO分别是△ABC的角∠ABC、∠ACB的平分线，∴∠1=12∠ABC，∠2=12∠ACB，∴∠1+∠2=12（∠ABC+∠ACB）=12（180°﹣∠A），∴∠BOC＝180°﹣（∠1+∠2）＝180−12(180°−αα)=90°+12αα．19．【解答】解：∵AD⊥BC，∠B＝60°，∴∠BAD＝90°﹣∠B＝90°﹣60°＝30°，∵∠BAC＝80°，∴∠DAC＝∠BAC﹣∠BAD＝80°﹣30°＝50°，∵AE平分∠DAC，∴∠DAE=12∠DAC=12×50°＝25°，∴∠BAE＝30°+25°＝55°，∴∠AEC＝∠BAE+∠B＝55°+60°＝115°．20．【解答】已知：△ABC中，求证：∠A+∠B+∠C＝180°．证明：过点A作直线MN，使MN∥BC．∵MN∥BC，∴∠B＝∠MAB，∠C＝∠NAC（两直线平行，内错角相等）∵∠MAB+∠NAC+∠BAC＝180°（平角定义）∴∠B+∠C+∠BAC＝180°（等量代换）即∠A+∠B+∠C＝180°．21．【解答】解：∵∠CDG＝∠B（已知），∴DG∥AB（同位角相等，两直线平行），∴∠1＝∠BAD（两直线平行，内错角相等），∵∠1+∠FEA＝180°（已知），∴∠BAD+∠FEA＝180°（等量代换），∴AD∥EF（同旁内角互补，两直线平行），∴∠BFE＝∠ADF（两直线平行，同位角相等），故答案为：同位角相等，两直线平行，∠1，两直线平行，内错角相等，∠BAD，同旁内角互补，两直线平行，∠ADF，两直线平行，同位角相等．22．【解答】解：（1）∵C（﹣10，10），CE∥x轴，∴B（0，10），∴OB＝10．（2）连接AM．∵AD⊥DM，∴∠DAM+∠DMA＝90°，∵EC∥AH，∴∠EMA+∠HAM＝180°，∴∠EMD+∠HAD＝90°，∵MN平分∠EMD，AN平分∠DAH，∴∠EMN+∠NAH＝45°，∴∠NMA+∠NAM＝135°，∴∠MNA＝180°﹣135°＝45°．（3）由题意：0°＜∠DAO＜45°，∵AN平分∠DAO，∴0°＜∠NAH＜22.5°，∵NH⊥AH，∴∠AHN＝90°，∴∠ANH＝90°﹣∠NAH，∴67.5°＜∠ANH＜90°．23．【解答】证明：∵AB⊥BD，ED⊥BD，∴∠ABC＝∠CDE＝90°，∴∠ACB+∠BAC＝90°，∠CED+∠DCE＝90°．∵∠ACB＝∠CED，∴∠BAC＝∠DCE，∴∠ACB+∠DCE＝90°，∴∠ACE＝180°﹣（∠ACB+∠DCE）＝90°．∴△ACE是直角三角形．24．【解答】解：∵AD⊥BC，∴∠ADB＝90°，∴∠1＝∠B＝45°，又∵∠C＝67°，∴∠BAC＝180°﹣∠B﹣∠C＝68°．25．【解答】（1）证明：如图①，过E作EF∥AD，∵AD∥BC，∴EF∥BC，∴∠DAE＝∠AEF，∠CBE＝∠BEF，∴∠AEB＝∠DAE+∠CBE；（2）①证明：∵AD∥BC，∴∠DAC＝∠ACB．∵AE平分∠DAC，∴∠EAC=12∠DAC=12∠ACB，∵∠ABC＝∠BAC，∠ABC+∠BAC+∠ACB＝180°，∴∠BAC+∠EAC＝90°，∴∠ABE+∠AEB＝90°；①解：如图（3），由①知∠BAE＝90°，∴∠F AE＝90°．∵∠F＝65°，∴∠APC＝90°+60°＝155°．∴∠P AC+∠ACP＝25°．∵AE平分∠DAC，CF平分∠ACD，∴∠DAC+∠ACD＝2（∠P AC+∠ACP）＝50°，∴∠D＝180°﹣50°＝130°．∵AD∥BC，∴∠BCD＝180°﹣∠D＝180°﹣130°＝50°．26．【解答】证明：方法1：∵∠1＝∠2，∴AB∥CD，∴∠ABC+∠DCB＝180°，∵∠3＝∠4，∴AD∥BC，∴∠ADC+∠DCB＝180°，∴∠ABC＝∠ADC．方法2：∵∠1＝∠2，∴AB∥CD，∵∠3＝∠4，∴AD∥BC，∴ABCD是平行四边形，∴∠ABC＝∠ADC．27．【解答】解：（1）AB∥CD，理由是：分别过点E、F作EM∥AB，FN∥AB，∵EM∥AB，FN∥AB，∴EM∥FN∥AB，∴∠1+∠A＝180°，∠3+∠4＝180°，∵∠A+∠E+∠F+∠C＝540°，∴∠2+∠C＝540°﹣180°﹣180°＝180°，∴FN∥CD，∵FN∥AB，∴AB∥CD；（2）设∠P AQ＝x，∠PCD＝y，∵∠P AB＝3∠P AQ，∠PCD＝3∠PCQ，∴∠P AB＝3x，∠BAQ＝2x，∠PCD＝3y，∠QCD＝2y，过P作PG∥AB，过Q作QH∥AB，∵AB∥CD，∴AB∥CD∥PG∥GH，∴∠AQH＝∠BAQ＝2x，∠QCD＝∠CQH＝2y，∴∠AQC＝2x+2y＝2（x+y），同理可得：∠APC＝3x+3y＝3（x+y），∴αααααααα=23，即∠AQC=23∠APC．28．【解答】解：（1）∵BD平分∠ABC，∴∠ABD＝∠DBC，∵∠DBC＝∠D，∴∠ABD＝∠D，∴CD∥AB，（2）∵∠D＝38°，∴∠ABD＝∠D＝38°，∵BD平分∠ABC，∴∠ABC＝2∠ABD＝76°，∴∠ABC＝∠A＝76°，∵CD∥AB，∴∠ACD＝∠A＝76°，∠ABC＝∠DCE＝76°，∴∠ACE＝∠ACD+∠DCE＝76°+76°＝152°29．【解答】解；∠A+∠B+∠C＝180°．理由：作∠ACD＝∠A，并延长BC到E∵∠ACD＝∠A（已作）∴AB∥CD（内错角相等，两直线平行）∴∠B＝∠DCE（两直线平行，同位角相等）而∠ACB+∠ACD+∠DCE＝180°∴∠ACB+∠A+∠B＝180°（等量代换）故答案为：A，内错角相等，两直线平行，∠DCE，两直线平行，同位角相等，∠A，∠B，等量代换．30．【解答】解：（1）∵AB⊥BC，∴∠EAB+∠AEB＝90°，∵AE⊥ED，∴∠CED+∠AEB＝90°，∴∠EAB＝∠CED．（2）①∵AF平分∠BAE，∴∠EAG=12∠EAB，∵EH平分∠CED，∴∠HED=12∠CED，∵∠EAB＝∠CED，∴∠HED＝∠EAG，∴∠HED+∠AEG＝90°，∴∠EAG+∠AEG＝90°，∴∠EGA＝90°，∴EG⊥AF．①作FM∥CD．∵AB⊥BC，CD⊥BC，∴AB∥CD，∴FM∥AB，∴∠DFM＝∠CDF=12∠CDE，∠AFM＝∠F AB=12∠EAB，∵∠CDE+∠CED＝90°，∴∠CDE+∠EAB＝90°，∴∠DF A＝∠DFM+∠AFM=12∠CDE+12∠EAB=12（∠CDE+∠EAB）＝45°．。

2019-2020学年人教版上册八年级期末（代数部分）常考解答题专题复习因式分解、整式化简求值、乘法公式几何背景、分式方程、分式化简求值一、解答题1.把下列多项式分解因式：（1）a 2x 2-a 2y 2 （2）4x 2-8xy+4y 22.分解因式:（1）mx²-6mx ＋9m （2）a²(x －y)＋b²(y －x) （3）(x －1)(x －3)＋13.把下面各式分解因式：（1）ax 3－9ax ； （2）x 2＋2x(x －3y)＋(x －3y)2.4.因式分解：（1）am −an +ap （2）2a(b +c)−3(b +c)（3）4x 4−4x 3+x 2 （4）x 4−165.分解因式：（1）2a(x −y)+6(y −x) ； （2）a 3−4ab 2 .6.因式分解：（1）(a 2+1)2 - 4a 2 （2）2x 2(x-y)+50y 2(y-x)7.先化简，再求值：（m +2﹣ 5m−2 ）÷ m−33m 2−6m ，其中m 满足m 2+3m ﹣1＝0．8.先化简： (3x+1−x +1)+x 2−4x+4x+1 ，然后从 −1≤x ≤2 中选一个合适的整数作为x 的值代入求值。

9.先化简( 3a+1 －a ＋1)÷a 2−4a+4a+1 ，并从0，－1，2中选一个合适的数作为a 的值代入求值. 10.先化简再求值：化简m −2m 2−1÷(m 2−m m 2−2m+1−2m−1) ，并0，-1，1，2四个数中，取一个合适的数作为m 的值代入求值. 11.先化简，再求值： (1−1a+1)÷a 2−a a+1 ，其中 a =12 . 12.解分式方程： 1−x x−2=12−x −213.解方程： 1x−2=1−x 2−x −3 .14.解方程： 1x−2+3=1−x 2−x .15.解方程：（1）1x−3=1+x x−3（2）3x+2+4x−2=16x 2−4 .16.解方程：（1）5x−2+1=0 （2）2x 2−1+1=x x−117.解方程（1）3x =4x−2（2）23+x3x−1=19x−318.解方程：31−x =xx−1−5．19.已知(x2+px+8)(x2-3x+q)的展开式中不含x2，x3项，求p、q的值.20.已知m−n=−3，mn=4.（1）求(3−m)(3+n)的值；（2）求m4+n4的值.21.已知：多项式A=b3﹣2ab（1）请将A进行因式分解：（2）若A=0且a≠0，b≠0，求(a−1)2+b2−12b2的值．22.已知x﹣y=3，求[（x﹣y）2+（x+y）（x﹣y）]÷2x的值．23.先化简，再求值．2（x﹣3）（x+2）﹣（3+a）（﹣a+3），其中，a=﹣2，x=1．24.已知M是含字母x的单项式，要使多项式4x2+M+1是某一个多项式的平方，求M的表达式．25.先化简再求值：4（m+1）2﹣（2m+5）（2m﹣5），其中m=﹣3．26.先化简再求值：4a（a+1）﹣（a+1）（2a﹣1），其中a=2．27.先化简，再求值：（2a+b）（﹣b+2a）﹣（2a﹣3b）2﹣5b（3a﹣2b），其中a=﹣12，b= 13．28.先化简，再求值：x（x﹣1）+2x（x+1）﹣（3x﹣1）（2x﹣5），其中x=2．29.有一张边长为a厘米的正方形桌面，因为实际需要，需将正方形边长增加b厘米，木工师傅设计了如图所示的三种方案：小明发现这三种方案都能验证公式：a2+2ab+b2=（a+b）2，对于方案一，小明是这样验证的：a2+ab+ab+b2=a2+2ab+b2=（a+b）2请你根据方案二、方案三，写出公式的验证过程．方案二：方案三：30.请认真观察图形，解答下列问题：（1）根据图中条件，用两种方法表示两个阴影图形的面积的和（只需表示，不必化简）；（2）由（1），你能得到怎样的等量关系？请用等式表示；（3）如果图中的a，b（a＞b）满足a2＋b2＝53，ab＝14，求：①a＋b的值；②a4－b4的值．参考答案及解析一、解答题1.【答案】（1）解：原式=a2(x2-y2)=a2(x+y)(x-y)（2）解：原式=4(x2-2xy+y2)=4（x-y）2【解析】【分析】（1）对式子先利用提公因式法，再利用公式法进行因式分解得到答案即可；（2）将式子提出公因式4，再将括号内的式子利用完全平方公式进行因式分解即可。