2019小学数学几何专题(奥数)一~十归总
- 格式:doc
- 大小:508.00 KB
- 文档页数:17

小学奥数必备:10大几何图形解法!数学老师强力推荐!
小学数学是打基础的阶段,内容还比较简单,学有余力的孩子其实可以参加一下小学数学的奥数竞赛,锻炼一下孩子们的脑力。
没有参加过小学奥数的人生,算不上一个学霸的人生。
老师在课堂上讲的方法,是为了照顾孩子的大多数,不可能讲一些超纲的、课程内容之外的东西。
这对于一些成绩普普通通的孩子来说还无所谓,但对于那些成绩比较好的,还有更进一步的发挥余地的孩子们而言,无疑是一种脑力的浪费。
脑子是越转越灵活的,适当的来一些挑战,会让孩子的大脑越来越优秀!
今天我就给大家整理一篇小学数学10大几何图形的解法,有些比较基础,有些则可能属于奥数的范畴。
几何是非常锻炼孩子的空间想象能力的,通过巧妙的辅助线,往往会让孩子的大脑豁然开朗,对开动孩子们的脑力绝对有所帮助。

新编小学奥数试题学奥数更聪明归一、归总问题(二)1、2只兔子3天能吃12千克萝卜,照这样计算,5只兔子7天能吃多少千克萝卜?2、一辆汽车从甲地开往乙地,前3小时行了210千米,照这样的速度,再行5小时可以到达目的地。
甲地到乙地有多少千米?3、5箱蜜蜂一年可以酿75千克蜂蜜,照这样计算,酿300千克蜂蜜要增加几箱蜜蜂?4、某大学新生军训,4小时走16千米,为了在天黑前到达目的地,每小时多走了1千米,剩下的20千米路程几小时可以到达?5、一个养牛专业户养牛100头,这些牛一星期(7天)用去饲料2800千克。
照这样计算,卖出30头牛后,现在有2000千克饲料用一个星期够不够?6、某工厂车间计划8人在5天里加工80个零件,生产时又增加了任务,在工作效率不变的情况下,需要10人做9天才能完成。
增加的任务是多少个零件?7 、一辆汽车从甲地开往乙地,每小时行60千米,预计4小时可以到达。
如果要提前一小时到达,每小时要行多少千米?8、5台拖拉机24天耕地12000公亩。
要18天耕完54000公亩土地,需要增加同样拖拉机多少台?9、加工9600套服装,30人10天完成了3600套,又增加了20人,剩下的还需要几天完成?10、4辆大卡车运沙土,7次共运走沙土336吨。
现在有沙土360吨,要求5次运完。
问:需要增加同样的卡车多少辆?11、小豪家有个书架共5层,每层放36本书,现在要空出一层放碟片,把这些书放入4层中,每层比原来多放多少本?12、学校买了12张办公桌和若干把椅子,共用去2440元,其中买办公桌用去1440元。
又知每张办公桌比每把椅子贵70元。
问一共买了多少把椅子?13、解放军训练,4小时走16千米,为了在天黑前到达目的地,每小时多走1千米,剩下的20千米可在几小时之内到达?14、筑路队修一条36千米长的路,15天修了4500米,以后加快速度每天多修75米,这条路共修多少天?15、面粉厂用5台磨面机6小时磨面粉30000千克,现在增加2台同样的磨面机,用几小时可磨完56000千克的面粉?16、4个工人5天挖土方200方,如果工作时间和工作效率不变,要挖土方300方,需增加多少人?17、毛衣加工厂计划每天加工毛衣25件,30天完成一批加工任务。

小学奥数几何知识点讲解几何是数学的一个重要分支,主要研究空间形状、大小、相对位置等概念及其性质和关系。
在小学奥数竞赛中,几何是一个常见的考察内容。
下面我将为大家讲解一些小学奥数几何知识点,希望能够帮助大家更好地应对几何题目。
1.点、线、面的概念在几何中,点是没有大小和形状的,只有位置的概念。
线是由无数个点组成的,没有宽度、长度、厚度等,可以用箭头表示方向。
面是由无数个点和线组成的,是平面上的一个二维图形。
2.正方形、长方形、三角形正方形是一种四条边都相等且角都是直角的四边形,它拥有四条对称轴。
长方形是一种拥有两组相等的对边和四个直角的四边形,它有两条对称轴。
三角形是一种由三条边和三个角组成的图形。
3.圆和半圆圆是由等距离圆心的所有点组成的集合,圆心到圆上任意一点的距离都相等。
半圆是圆的一半,由圆周上的一个弧和两条半径组成。
4.平行线和垂直线平行线是在同一个平面内永远不会相交的两条直线。
垂直线是与另一条线段相交时,两条线段之间的角度为90度的线。
5.直角、锐角和钝角直角是一个角度为90度的角,锐角是小于90度的角,钝角是大于90度小于180度的角。
6.对称和中心对称对称是指两个物体在一些轴线上镜像重合的关系,中心对称是指一个图形可以通过一些点进行旋转180度后重合。
7.面积和周长面积是指一个二维图形所占的空间大小,通常用平方单位表示,如平方厘米、平方米等。
周长是指一个图形的边缘长度。
8.直角三角形和勾股定理直角三角形是一种其中一个角为90度的三角形。
勾股定理是指在直角三角形中,直角边的平方之和等于斜边的平方,即a²+b²=c²。
9.分数、比例和相似分数是表示一个整体被分成几等份的表达方式。
比例是指两个或多个数之间的等比关系。
相似是指两个图形有相同的形状,但是可能有不同的大小。
10.正多边形和不规则图形正多边形是指所有边和角都相等的多边形。
不规则图形是指边和角都不相等的图形。
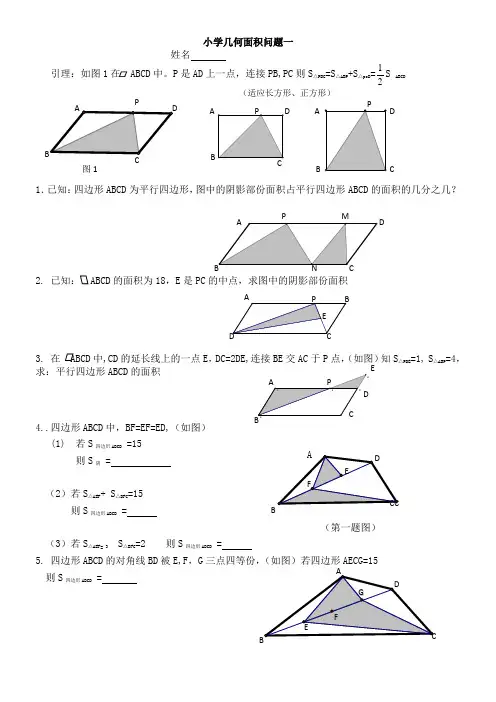
小学几何面积问题一姓名引理:如图1在 ABCD中。
P 是AD 上一点,连接PB,PC 则S △PBC =S △ABP +S△pcD =21S ABCD1.已知:四边形ABCD 为平行四边形,图中的阴影部份面积占平行四边形ABCD 的面积的几分之几?2. 的面积为18,E 是PC 的中点,求图中的阴影部份面积3. 在中,CD 的延长线上的一点E ,DC=2DE,连接BE 交AC 于P 点,(如图)知S △PDE =1, S △ABP =4,求:平行四边形ABCD 的面积4..四边形ABCD 中,BF=EF=ED,(如图)(1) 若S 四边形ABCD =15则S 阴 = (2)若S △AEF + S △BFC =15 则S 四边形ABCD =(第一题图)(3)若S △AEF= 3 S △BFC =2 则S 四边形ABCD =5. 四边形ABCD 的对角线BD 被E,F ,G 三点四等份,(如图)若四边形AECG=15 则S 四边形ABCD =E P图1ADCB(适应长方形、正方形)BGB F C A E D6.四边形ABCD的对角线BD被E,F,G三点四等份,(如图)若阴影部份面积为15则S四边形ABCD=7.若ABCD为正方形,F是DC的中点,已知:S△BFC= 1(1)则S四边形ADFB=(2) S△DFE=(3) S△AEB=8.直角梯形ABCD中.AE=ED,BC=18,AD=8,CD=6,且BF=2FC,S△GED=S△GFC.求S阴=小学几何面积问题二姓名1.如图S△AEF= 2, AB=3AE CF=3EF则S△ABC=2. 如图S△BDE=30 ,AB=2AE, DC=4AC则S△ABC=3.正方形ABCD中,E,F,G为BC边上四等份点,M,N,P为对角线AC上的四等份点(如图)若S正方形ABCD=32 则S△NGP=4.已知:S△ABC=30 D是BC的中点AE=2ED 则S△BDE=A CBD第1题第2题5. 已知:AD=DB DE=3EC AF=3FE 若S △ABC =160 求S △EFC =6.已知:在△ABC 中,FC=3AF EC=2BE BD=DF 若S △DFE=3则S △ABC=7.ABCD 为平行四边形,AG=GC,BE=EF=FC,若S △GEF =2,则S ABCD =8.ABCD 是梯形,AD // BC(如图)则S △AOB= S △AOD= (第8题)9. ABCD 是梯形,AD // BC(如图)则S △DOC= S △BOC= (第9题)10.ABCD 是梯形,AD // BC(如图),且BO=3OD, S △AOB=15则S 梯ABCD=(第10题)BACACC CCCCBC B CL 2L 1N11. 如图BD=DE, EC=3EF AF=2FD若△DFE 的面积等于1 则△ABC 的面积为(第11题)小学几何面积问题三姓名1.在梯形ABCD 中,AD//BC,图中阴影部分的面积为4,OC=2AO, 求 S 梯ABCD =2在梯形ABCD 中,AD//BC,S △BOC=14 OC=2AO 求 S 梯ABCD =3. 在梯形ABCD 中,AD//BC,S △AOB=14 OC=3AO 求 S 梯ABCD =4.在梯形ABCD 中,AD//BC,图中阴影部分的面积为30,OC=3AO,S △AOB =6求S 空=5.读一读:A 若直线L 1//L 2 (如图一)一.当高不变,底扩大(或缩小)K 倍。

小学奥数知识点分类小学奥数大约80 个知识点,可分成5 大类,数论和行程是重点也是难点。
基础知识和差倍、年龄、植树、周期、鸡兔、方阵、逻辑、容斥、排列组合等计算能力速算与巧算、分数百分数、循环小数、分数拆分、四则混合运算等等行程问题相遇、追及、行程、流水、过桥、时钟、圆周、发车间隔等等数论问题平方数、奇数、偶数、约数、倍数、质数、合数、整除、余数、进制图形问题平面图形、立体图形、几何计数、周长面积、表面积体积、阴影面积第一部分基础知识基础知识点列表1 归一归总9 鸡兔问题17 加法乘法原理2 和差问题10 方阵问题18 排列与组合3 和倍问题11 抽屉问题19 商品利润4 差倍问题12 容斥问题20 存款利息5 植树问题13 逻辑问题21 浓度问题6 年龄问题14 数字谜22 工程问题7 盈亏问题15 等差数列23 正反比例8 周期问题16 一笔画24 牛吃草问题第二部分计算能力万丈高楼平地起,计算能力任何时候都是学好数学的根基,必须高度重视!第三部分数论知识数论由于比较抽象,是小学数学的重点也是难点,而且小学数论与中学的代数学有着密切的联系,因此我们必须高度重视。
数论知识点列表1 定义新运算 6 整数进制2 约数倍数7 数的整除3 奇数偶数8 余数与同余4 质数合数9 高斯取整5 平均数10 不定方程第四部分图形知识图形属于小学奥数三大专题之一,主要考察学生们对平面图形和立体图形的认识、建构、以及对周长、面积、表面积、体积的计算等方面的知识,图形问题的重点在于等积变换的直线型面积数论知识点列表1 几何计数 4 体积与表面积2 周长与面积 5 阴影面积3 长方体与正方体 6 直线型面积第五部分行程问题行程问题是研究物体运动的速度、时间、路程三者之间的关系.基本公式:路程=速度×时间;路程÷时间=速度;路程÷速度=时间关键问题:确定运动过程中的位置。
相遇问题:速度和×相遇时间=相遇路程(请写出其他公式)追及问题:追及时间=路程差÷速度差(写出其他公式)过桥问题:关键是确定物体所运动的路程,参照以上公式。


奥数知识点解析之归一归总问题(1)来源:武汉巨人学校作者:小学数学部奥数知识点解析之归一归总问题(1)应用题是小学数学学习的一项重要内容,解题关键在于掌握数量关系,找出应用题中条件及条件和问题之间的联系,解决问题。
传统的分析应用题的方法有两种:分析法和综合法。
分析法是从题目的问题出发,寻找需要的条件,逐步向已知条件靠拢;综合法是从题目的已知条件出发,顺藤摸瓜,逐步推导出所求的问题。
实际解题时,往往是综合使用这两种分析方法,从两头往中间凑,在已知条件与问题之间搭建一座桥梁。
归一问题:在解答某些应用题时,常常需要先找出“单位量”,再以这个“单位量”为标准,根据其它条件求出所求数量,这类应用题被称为归一问题。
这里的“单位量”常指单位时间的工作量、单价、单产量、速度等。
归一问题可以分为两类:用一步运算就能求出“单位量”的归一问题称为“单归一;用两步运算才能求出“单位量”的归一问题称为“双归一”。
归总问题:是指解答某些应用题时,需要先找出“总量”,再根据其它条件求出所求数量。
这里“总量”是指总路程、总产量、工作总量、总价等。
数量关系:单位量×份数=总量;总量&pide;份数=单位量;总量&pide;单位量=份数。
解决归一问题的关键是抓住单位量不变,总量随着份数的变化而变化,其中蕴藏着正比例函数关系;解决归总问题的关键是抓住总量不变,单位量随着份数的变化而变化,其中蕴藏中反比例函数关系。
通过列表找出数量间的对应关系,是解决这类问题的比较好的策略。
同一道题可以采取不同的方法解答,而同一种解题策略可以解决不同类型的应用题。
解答应用题时,要根据题目的需要选择合适方法、策略,在理解的基础上灵活解题,切忌“记题型,套方法”,生搬硬套。
【题目1】:筑路队修一条36千米长的路,15天修了4500米,以后加快速度每天多修75米,这条路共修多少天?【解析】:运用分析法解题。
从所求问题出发,寻找需要的条件,逐步向已知条件靠拢,可以画出如下示意图,理清分析的思路。

小学奥数:经典21道题型(数学思维)题型一:归一问题【含义】在解题时先求出一份是多少(即单一量),然后以单一量为标准,求出所要求的数量。
【数量关系】总量÷份数=单一量单一量×所占份数=所求几份的数量或总量A÷(总量B÷份数B)=份数A【解题思路】先求出单一量,以单一量为标准,求出所要求的数量。
【例】买5支铅笔需要0.6元钱,买同的铅笔16支,需要多少钱?解:先求出一支铅笔多少钱—0.6÷5=0.12(元)再求买16支铅笔需要多少钱——0.12×16=1.92(元)综合算式:0.6÷5×16=0.12×16=1.92(元)题型二:归总问题【含义】解题时先找出“总数量”,再根据已知条件解决问题的题型。
所谓“总数量”可以指货物总价、几天的工作量、几亩地的总产量、几小时的总路程等。
【数量关系】1份数量×份数=总量总量÷一份数量=份数【解题思路】先求出总数量,再解决问题。
【例】服装厂原来做一套衣服用布3.2米,改进剪裁方法后,每套衣服用布2.8米。
问原来做791套衣服的布,现在可以做多少套衣服?解:先求这批布总共多少米——3.2×791=2531.2(米)再求现在可以做多少套——2531.2÷2.8=904(套)综合算式:3.2×791÷2.8=904(套)题型三:和差问题【含义】已知两个数量的和与差,求这两个数量各是多少。
【数量关系】大数=(和+差)÷2小数=(和一差)÷2【解题思路】简单题目直接套用上述公式,复杂题目变通后再套用公式。
【例】甲乙两班共有学生98人,甲班比乙班多6人,求两班各有多少人?解:直接套用公式一—甲班人数=(98+6)÷2=52(人)乙班人数=(98-6)÷2=46(人)题型四:和倍问题【含义】已知两个数的和及“大数是小数的几倍(或小数是大数的几分之几)”,求这两个数各是多少。

数学专项复习小升初典型奥数之归一归总问题在小升初的数学学习中,归一归总问题是一类常见且重要的题型。
掌握这类问题的解题方法,对于提高数学思维能力和应对考试都具有重要意义。
归一问题是指在解题时,先求出一份是多少(即单一量),然后以单一量为标准,求出所要求的数量。
而归总问题则是先求出总数是多少,然后再根据其他条件求出每份数或者份数。
我们先来看归一问题的例子。
比如,一辆汽车 3 小时行驶了 180 千米,照这样的速度,5 小时行驶多少千米?在这个问题中,首先要算出汽车每小时行驶的速度,也就是单一量。
180÷3 = 60(千米/小时),这就是汽车每小时行驶的路程。
然后再用这个速度乘以 5 小时,就能得出 5 小时行驶的路程:60×5 = 300(千米)。
再来看一个归一问题:小明买 5 个本子花了 20 元,照这样计算,买 8 个本子需要多少钱?先算出一个本子的价格,20÷5 = 4(元),这就是单个本子的价格。
那么买 8 个本子需要的钱数就是 4×8 = 32(元)。
接下来看看归总问题。
例如,工厂有一批原料,原计划每天用8 吨,可以用 30 天。
实际每天节约了 2 吨,这批原料实际可以用多少天?首先,我们要算出这批原料的总量,8×30 = 240(吨)。
然后,由于实际每天节约了 2 吨,所以实际每天用的量是 8 2 = 6(吨)。
最后用总量除以实际每天用的量,240÷6 = 40(天),这就是实际可以用的天数。
又如,一项工程,原计划 10 人 20 天完成,现在增加 5 人,多少天可以完成?先算出这项工程的总量,假设每人每天的工作量为 1 份,那么总量就是 10×20×1 = 200 份。
现在人数增加到 10 + 5 = 15 人,那么完成的天数就是 200÷(15×1)= 40 / 3(天)。
在解决归一归总问题时,关键是要理解题目中给出的条件,找出单一量或者总量。


新编小学奥数试题学奥数更聪明归一、归总问题(一)1、电视电话5秒扫描25幅图像,照这样计算,通话45秒电视电话要扫描多少幅图像?2、一个修路队修一条路,3天修了180千米,照这样计算,一个星期(7天)能修多少千米?3、小刚3分钟走了180米,照这样的速度,他从家到学校要走15分钟。
他家离学校有多远?4、欢欢45分钟做了5道应用题,照这样计算,欢欢做10道应用题需要多少分钟?5、5头牛吃了30千克青草,照这样计算,480千克青草够机头能吃?6、一种农药3克需加水24千克,照这样计算,64千克水中可以加多少克农药?7、一辆汽车4小时行120千米,照这样计算,①5小时行多少千米?②行180千米要用几小时?8、每30千克鲜葡萄可以晒成6千克葡萄干,现有50千克鲜葡萄,可以晒多少千克葡萄干?9、有一条360米长的路需要整修,修路队前3天整修了120米。
照这样计算,剩下路需要整修多少天?10、织布厂要织布3600米,8小时织了960米,照这样计算,再织几小时能完成任务?11、一台机器4小时加工160个零件,照这样计算,再加工240个零件,一共需要几小时?12、2台拖拉机4天耕地32公顷,照这样计算,5台拖拉机7天耕地多少公顷?”13、2台拖拉机4天耕地32公顷,照这样计算,5台这样的拖拉机,耕200公顷需几天?”14、一辆汽车从甲地开往乙地,每小时行60千米,5小时到达。
若要4小时到达,则每小时需要多行多少千米?15、小华和小刚读同样的一本书,小华每天读12页,6天读完;小刚要8天读完,平均每天要读多少页?16、服装厂8个工人6天可以加工720件服装,照这样计算,如果增加2个人,15天可以加工多少件服装?17、2台拖拉机3天耕地18公顷,照这样计算,9天耕地81公顷,需要几台同样的拖拉机?。
奥数思维拓展:归一、归总问题一.选择题(共6小题)1.一盒6支装的钢笔138元,李老师买了3盒这样的钢笔,付给售货员500元。
李老师买了多少支钢笔?要解决这个问题,需要用到的数学信息是()。
A.一盒6支,138元,3盒,500元B.138元,3盒,500元C.一盒6支,138元,3盒D.一盒6支,3盒2.算式30÷2×12是解决下面()问题的。
A.小美每天写2页毛笔字,每页写12个,30天写了多少个?B.小美第一天写了2页毛笔字,每页12个字,第2天写了30个,一共写了多少个字?C.小美第一天写了30个毛笔字,第2天写了12个,这两天一共写了多少个字?D.小美2天写了30页毛笔字,照这样计算,12天能写多少个字?3.1000粒小麦的质量大约是50克,照这样推算,1000000000粒小麦的质量大约是()。
A.5吨B.50吨C.500吨4.王处长从东北捎来一袋苹果分给甲乙两个科室的人员,每人可分得6个,如果只分给甲科,每人可分得10个.问如果只分给乙科,每人可分得多少个?()A.8个B.12个C.15个D.16个5.花花12元买了6瓶饮料,玲玲3元买了一瓶饮料,买一瓶饮料()花钱少。
A.花花B.玲玲C.花花和玲玲一样6.整修一段公路,6人11天可以完成,照这样计算,如果要提前5天完成,应增加()人。
A.2B.3C.4D.5二.填空题(共6小题)7.小兵计划在暑假里看完一部小说。
如果每天看36页,第13天可以看完;如果每天看40页,第12天可以看完。
这本书最多可能有页。
8.某种砖2块重5千克,200块重千克。
9.5个人能搬2套桌椅。
那么,人能搬8套桌椅,40人能搬套桌椅。
10.有种浓缩型洗衣液,在6升水里加入8毫升的洗衣液,效果达到最佳。
妈妈在洗衣机里放了24升水,需要倒入毫升的洗衣液,效果才能达到最佳。
11.某文具店用744元进了62个文具盒,如果想至少赚得124元,那么该怎么给文具盒定价,至少定价为元.12.王亮原计划5天读完一本100页的书,实际每天比原计划多读了5页。
小学奥数。
归总问题精选练习例题含答案解析(附知识点拨及考点)本节课研究归总问题,了解其类型和解决方法,掌握基本关系式并应用到实际问题中。
归总问题是找出“总量”,如总路程、总产量、工作总量、物品总价等。
与归一问题类似,但归一问题是找出“单一量”。
例1:“走美比萨店”共有5名员工,其中2名厨师每周分别工作36小时,每小时工资10美元;3名服务生每周工作30小时,每小时工资5美元。
老板每周应向员工支付1170美元的工资。
例2:某车间需要加工3960个零件,3名工人10小时加工了1320个,其余的要求在15小时内完成,需要增加1名工人。
例3:___有50名学生帮学校搬砖,要搬2000块,4次搬了一半。
再增加50名学生,还需要2次运完。
例4:一辆汽车从甲地开往乙地,每小时行60千米,5小时到达。
若要4小时到达,则每小时需要多行15千米。
考点】复杂的归总问题【难度】3星【题型】解答解析】原计划60人工作,80天完成,说明这条公路的总工作量有:60×80=4800人天,工作20天后,已经完成了60×20=1200人天的工作量,剩下的工作量为:4800-1200=3600人天。
现在增加了30人,总共工作人数为60+30=90人,所以剩下的工作再用多少天可以完成为:3600/90=40天。
【答案】40天一个工人在森林中锯木头,他用12分钟把一根树干锯成了4段,那么锯一次需要12÷3=4(分钟)。
现在要把每段木头再锯成两段,也就是要锯4-1=3(下),需要时间为:4×3=12(分钟)。
所以,要把每段木头再锯成两段,还需要12分钟。
关键词】比较思想方法解析】根据题意,可以列出以下两个方程组:4x + 3y = 24.(妈妈买的情况)3x + 5y = 29.(上星期妈妈买的情况)将第一个方程乘以3,得到12x + 9y = 72,再将第二个方程乘以4,得到12x + 20y = 116.然后将两个方程相减,得到11y = 44,即y = 4.将y代入第一个方程,得到4x + 3(4) = 24,解得x = 3.因此,小梦龙每支3元,可爱多冰淇淋每支4元。
小学几何奥数知识点几何是数学的一个重要分支,也是小学数学中的一个重要内容。
它可以培养学生的观察力、空间想象力和逻辑思维能力。
在小学奥数竞赛中,几何题常常是难点和关键。
下面将介绍一些小学几何奥数的知识点。
1. 直线、线段和射线:- 直线:由无数个点连成的路径,没有起点和终点,可以用两个点表示一条直线。
- 线段:直线上的两个点及其之间的部分,有起点和终点,可以用线段的两个端点表示。
- 射线:直线上的一个点及其一侧的部分,有起点但没有终点,可以用射线的起点和其中一点表示。
2. 角和三角形:- 角:由两条射线共享一个端点所围成的图形。
角的大小可以用度数或弧度表示。
- 直角:角的度数为90°,即两条相互垂直的直线所围成的角。
- 锐角:角的度数小于90°。
- 钝角:角的度数大于90°。
- 三角形:由三条线段组成的图形。
根据边长和角度的关系,三角形可以分为等边三角形、等腰三角形、直角三角形等。
3. 平行和垂直:- 平行线:在同一个平面上,永远不会相交的直线。
- 垂直线:两条直线相交时,相交的角为直角。
4. 四边形和多边形:- 四边形:有四条边的多边形。
常见的四边形有矩形、正方形、平行四边形、菱形等。
- 多边形:有多条边的封闭图形。
根据边的长度和角的大小,多边形可以分为等边多边形、等角多边形等。
5. 相似和全等:- 相似:两个图形的形状相似,但大小可能不同。
相似的图形具有相等的角度比例和对应边的比例关系。
- 全等:两个图形形状和大小完全相同。
6. 对称和轴对称:- 对称:一个图形可以绕某个中心点旋转、翻转或旋转加翻转,使得图形完全重合。
- 轴对称:一个图形可以沿着一条线对折,两边完全重合。
以上是小学几何奥数的一些基础知识点。
通过掌握和理解这些知识点,小学生可以提升自己的数学技能和解题能力,更好地应对几何题目。
在学习几何的过程中,培养学生的观察力和创造力也是非常重要的。
希望同学们通过勤奋学习和练习,能够在小学几何奥数中取得优异的成绩!。
本讲主要学习归总问题.通过本节课的学习,学生应了解归总问题的类型,以及解决归总问题的一般方法,掌握归总问题的基本关系式,并会将这种方法应用到一些实际问题中.归总问题 与归一问题类似的是归总问题,归一问题是找出“单一量”,而归总问题是找出“总量”,再根据其它条件求出结果.所谓“总量”是指总路程、总产量、工作总量、物品的总价等.模块一、简单的归总问题【例 1】 “走美比萨店”共有5名员工,2名厨师每周分别工作36小时,每小时工资10美元;3名服务生每周工作30小时,每小时工资5美元。
如果你是“走美比萨店”的老板,你每周该向员工制服的工资一共为 美元。
【考点】简单的归总问题 【难度】1星 【题型】填空【关键词】走美杯,3年级,初赛【解析】 2361033057204501170⨯⨯+⨯⨯=+=(美元)【答案】1170美元【例 2】 某车间需要加工3960个零件,3个工人10小时加工了1320个,其余的要求在15小时内完成,需要增加多少个工人?【考点】简单的归总问题 【难度】2星 【题型】解答【解析】 每个工人每小时加工:132031044÷÷=(个),现在还剩下:396013202640-=(个)零件,15小时内完成需要工人264044154÷÷=(个),即需要增加1个工人.【答案】1个工人【例 3】 光明小学有50个学生帮学校搬砖,要搬2000块,4次搬了一半。
照这样算,再增加50个学生,还要几次运完?【考点】简单的归总问题 【难度】2星 【题型】解答【解析】 先求出每个学生每次运的砖数: 1200045052⨯÷÷=(块). 再求出现在的学生一次过运的砖数: (50+50)×5=500(块).最后求出还要运的次数: 1200050022⨯÷= (次),简便方法: 4÷[(50+50)÷50]=2(次)。
小学数学典型应用题1.归一问题:能够根据已知条件,先求出一个单位量的数值,然后再根据题中的条件和问题求出结果叫做归一问题。
解决归一问题的关键是求出单位量的数值。
【数量关系】总份量÷份数=1份量1份数量×所占份数=所求几份的数量另一总量÷(总量÷份数)=所求份数【解题思路和方法】先求出单一量,以单一量为标准,求出所要求的数量。
例一:买5支铅笔要0.6元钱,买同样的铅笔16支,需要多少钱?解:(1)买1支铅笔多少钱?0.6÷5=0.12(元)(2)买16支铅笔需要多少钱?0.12×16=1.92(元)列成综合算式0.6÷5×16=0.12×16=1.92(元)答:需要1.92元。
例二:3台拖拉机3天耕地90公顷,照这样计算,5台拖拉机6天耕地多少公顷?解(1)1台拖拉机1天耕地多少公顷?90÷3÷3=10(公顷)(2)5台拖拉机6天耕地多少公顷?10×5×6=300(公顷)列成综合算式90÷3÷3×5×6=10×30=300(公顷)答:5台拖拉机6天耕地300公顷。
例三:5辆汽车4次可以运送100吨钢材,如果用同样的7辆汽车运送105吨钢材,需要运几次?解(1)1辆汽车1次能运多少吨钢材?100÷5÷4=5(吨)(2)7辆汽车1次能运多少吨钢材?5×7=35(吨)(3)105吨钢材7辆汽车需要运几次?105÷35=3(次)列成综合算式105÷(100÷5÷4×7)=3(次)答:需要运3次。
例四:3头牛4天吃了24千克的草料,照这样计算5头牛6天吃草_____千克。
解:1.根据题意先算出1头牛1天吃草料的质量:24÷3÷4=2(千克)。
小学几何面积问题一姓名引理:如图1在ABCD 中。
P 是AD 上一点,连接PB,PC 则S △PBC =S △ABP +S △pcD =21S ABCD1.已知:四边形ABCD 为平行四边形,图中的阴影部份面积占平行四边形ABCD 的面积的几分之几?2. 的面积为18,E 是PC 的中点,求图中的阴影部份面积3. 在中,CD 的延长线上的一点E ,DC=2DE,连接BE 交AC 于P 点,(如图)知S △PDE =1, S △ABP =4,求:平行四边形ABCD 的面积4..四边形ABCD 中,BF=EF=ED,(如图)(1) 若S 四边形ABCD =15则S 阴 = (2)若S △AEF + S △BFC =15 则S 四边形ABCD =(第一题图)(3)若S △AEF= 3 S △BFC =2 则S 四边形ABCD =5. 四边形ABCD 的对角线BD 被E,F ,G 三点四等份,(如图)若四边形AECG=15 则S 四边形ABCD =E P图1ADCB(适应长方形、正方形)BGB F C A E D6.四边形ABCD 的对角线BD 被E,F ,G 三点四等份,(如图)若阴影部份面积为15 则S 四边形ABCD =7.若ABCD 为正方形,F 是DC 的中点,已知:S △BFC = 1 (1)则S 四边形ADFB =(2) S △DFE =(3) S △AEB =8.直角梯形ABCD 中.AE=ED,BC=18,AD=8,CD=6,且BF=2FC,S △GED =S △GFC .求S 阴=小学几何面积问题二姓名 1.如图S △AEF= 2, AB=3AE CF=3EF 则S △ABC=2. 如图S △BDE=30 ,AB=2AE , DC=4AC 则S △ABC=3.正方形ABCD 中,E,F,G 为BC 边上四等份点, M,N,P 为对角线AC 上的四等份点(如图) 若S 正方形ABCD=32 则S △NGP=4.已知:S △ABC=30 D 是BC 的中点 AE=2ED 则S △BDE=ACBD第1题第2题5. 已知:AD=DB DE=3EC AF=3FE 若S △ABC =160 求S △EFC =6.已知:在△ABC 中,FC=3AF EC=2BE BD=DF 若S △DFE=3则S △ABC=7.ABCD 为平行四边形,AG=GC,BE=EF=FC,若S △GEF =2,则S ABCD =8.ABCD 是梯形,AD // BC(如图)则S △AOB= S △AOD= (第8题)9. ABCD是梯形,AD // BC(如图)则S △DOC= S △BOC= (第9题)10.ABCD 是梯形,AD // BC(如图),且BO=3OD, S △AOB=15则S 梯ABCD=(第10题)BACACC CCCCBC B CL 2L 111. 如图BD=DE, EC=3EF AF=2FD若△DFE 的面积等于1 则△ABC 的面积为(第11题)小学几何面积问题三姓名1.在梯形ABCD 中,AD//BC,图中阴影部分的面积为4,OC=2AO, 求 S 梯ABCD =2在梯形ABCD 中,AD//BC,S △BOC=14 OC=2AO 求 S 梯ABCD =3. 在梯形ABCD 中,AD//BC,S △AOB=14 OC=3AO 求 S 梯ABCD =4.在梯形ABCD 中,AD//BC,图中阴影部分的面积为30,OC=3AO,S △AOB =6求S 空=5.读一读:A 若直线L 1//L 2 (如图一)一.当高不变,底扩大(或缩小)K 倍。
其面积也同时扩大(或缩小)K 倍例:BC=2 AB=4 AB 是BC 扩大2倍而得ABC ⅡⅠACBC 所以面积Ⅰ就是面积Ⅱ的2倍.若直线L 1//L 2 (如图二)二.当底不变,高扩大(或缩小)K 倍。
其面积也同时扩大(或缩小)K 倍例:AC=BC H 1=2H 2 (图二) 那么:S △NBC =2S △MAC练一练:1如图(一):L 1//L 2 AB=10 BC=5若S △HAB =2.如图(二)△ACM 的AC 边上的高H 1是△NCB 的CB 边上的高H 2的一半,且AC=CB, 若S △NBC =100 则S △ACM =3.把下面的三角形分成三个小三角形,使它们的面积的比为1:2:34.△ABC 是等边三角形,AD 是BC 边上的高,若S △ABC =2,则S △ADC =5. △ABC 是等边三角形,D 是AB 的中点,且DH 垂直于BC ,H 为垂足. 若S △BDH =2,则S △ABC =_ C_ _EAFCDBB C 小学几何面积问题四姓名1.在△ABC 中,AE=BE,BD=2DC,FC=3AF 若△ABC 的面积为1,则S △EFD =2.△ABC 中,三边BC,CA,AB 上分别有点D,E,F,且BC=3CD AB=2BE AC=4AF 若△ABC 的面积为240平方厘米,则S △DEF 平方厘米.3.. 如图BD=DE, EC=3EF AF=2FD若△DFE 的面积等于1 则△ABC 的面积为4.两个正方形拼成如图,则阴影部分的面积为______。
5.两个正方形拼成如图,则阴影部分的面积为______。
6D CFE BA6.三个正方形拼成如图,求阴影部分的面积为______。
7.如图ABCD是矩形,EF∥AB如果S矩形ABCD=24 则S阴=8.在平行四边形ABCD中,EF∥AC,若△AED的面积为72平方厘米,则S△DCF=9.ABCD是平行四边形.直线CF与AB交于E,与DA的延长线交于F,连BF,若三角形BEF的面积等于4cm2,那么三角形EDA(阴影部分)的面积是 cm2小学几何面积问题五姓名1.有两种自然放法,将正方形内接于等腰直角三角形.如果按左图的放法,那么可求得这个正方形面积为441. 如果按右图的放法,那么可求得这个正方形面积应为2.下图是一块长方形的草地,长方形的长是18米.宽是10米.中间有两条宽2米的路,一条是长方形,另一条是平行四边形,那么草地的面积是平方米.44 5jF(第2题图)3.如图大正方形的边长是20厘米.E,F,G,H 分别是各边中点,问:中间小正方形的面积是 平方厘米.4.“十字架”由五个边长相等的正方形拼成,若AB=20厘米.求:这个“十字架”的面积是 平方厘米.5.一个边长为21厘米的正方形,被分成了四个长方形(如图)它们的面积分别是这个正方形面积的101,51,103,52在占52的这一块长方形里有一个小正方形是阴影部分.求这个阴影部分的面积为 平方厘米.6.一个面积小于100的整数的长方形中,它的内部有三个小正方形,边长都是整数.已知正方形(二)的边长是长方形长的2/5,正方形(一)的边长是长方形宽的1/8。
那么图中阴影部分的面积为 (平方单位)cmCBC1厘米CBDA7. 如图所示ABCD 为正方形,且AB//EF ,BF=1厘米 则:阴影部分的面积= 平方厘米.、8.在长方形ABCD 中,长是宽的4倍,对角线BD=17厘米,求该长方形的面积是 .小学几何面积问题六 姓名1.一个长方形ABCD ,向它的形外分别作正方形(如图)若所作的四边形的周长之和为264厘米,面积之和是1378平方厘米,求原来的长方形的面积是 平方厘米.2. 两个长方形叠放如图,小长方形宽是2厘米,A 是大长方形一边的中点,△ABC 是等腰直角三角形,图中阴影部分的面积和为 平方厘米.3.在边长为10的正方形的四边上分别取E,F,G,H.已知E 与G 的水平距离是5厘米,H 与F 的水平距离是4厘米,求四边形EFGH 的面积为 平方厘米.EDCBFABA10厘米FED'C'B'A'DCBA8平方厘米6平方厘米DCBAPDCBA684.长方形ABCD 的长DC 是8厘米,宽AD 是4厘米. EFCA 也是长方形,它的面积是多少平方厘米?答:是 平方厘米.5.如图在直角梯形中,AB=10厘米,阴影部分的面积是这个直角梯形面积的一半.求这个直角梯形面积是 平方厘米6.已知:ABCD 是平行四边形,P 在AD 上, BP ⊥CP,且BP=8厘米,CP=6厘米。
求图中的阴影部分的面积 平方厘米.7. 梯形ABCD 与梯形A /B /C /D /大小相同,如图重合(叠) 若EC=4厘米,D /C /=24厘米,高EF=5厘米. 求阴影部分的面积是 平方厘米.8.在一个梯形内,有两个三角形的面积分别是6平方厘米和8平方厘米,梯形的下底长是上底长的2倍,求:阴影部分的面积和是 平方厘米.8平方厘米12厘米4厘米EDCBA24cm28cm2EDCBAGC7厘米C21厘米小学几何面积问题七姓名1.求图中阴影部分的面积2. 求图中阴影部分的面积3.已知:EF 是梯形ABCD 的中位线,求梯形ABCD 的面积4.求梯形的面积5.求下图四边形的面积B'EDFA6.在下图中,长方形内有一个钝角三角形,按照图示的数,求这个三角形的面积.7.三个边长为10厘米、12厘米、8厘米的正方形拼放在一起,直线BC 将整个图形面积平分,求线段AB 的长.8. 如图有两个边长都是10厘米的正方形ABCD 和A /B /C /D /,且正方形A /B /C /D /的顶点A /恰好是正方形ABCD 的中心,那么:阴影部分的面积是 平方厘米.小学几何面积问题八姓名1. 平行四边形ABCD 的面积是32厘米,AD=8厘米,∠B=45○,求阴影部分的面积是 平方厘米.2.如图所示平行四边形ABCD 中,CH=DE=FB=GC ,如果阴影部分的面积为7平方厘米,那么,这个平行四边形的面积是 平方厘米.D354913FEDCBA3.平行四边形ABCD 已知:三角形AHB 的面积是8平方厘米,三角形DFC 的面积是6平方厘米.求阴影部分的面积是 平方厘米.4. 平行四边形ABCD 中有一点E ,已知,三角形ABE 的面积是73平方厘米,三角形BEC 的面积是10平方厘米。
求阴影部分三角形BED 的面积是 平方厘米.5.一个45度的直角三角板.最长边为12厘米,那么,它的面积为 平方厘米.6.如图长方形内画了一些直线,已知边上有三块面积分别为13平方厘米,35平方厘米,49平方厘米,那么图中的阴影部分面积是 平方厘米.7.在长方形ABCD 中,DE,DF 把这个长方形平均分成了三份,即三角形ADE 的面积等于三角形DFC的面积等于四边形BEDF 的面积.如果这个长方形的面积是54平方厘米,那么三角形BEF 的面积是 平方厘米.FB10厘米E6厘米DCFCB8.如图三角形ABC 是等腰直角三角形.它与一个正方形叠放在一起。