人教版七年级数学上册整式的加减知识点专题复习与典型例题(无答案)

1．把有理数a 代入|a +4|﹣10得到a 1，称为第一次操作，再将a 1作为a 的值代入得到a 2，称为第二次操作，…，若a ＝23，经过第2020次操作后得到的是（ ） A ．﹣7B ．﹣1C ．5D ．11A解析：A【分析】先确定第1次操作，a 1=|23+4|-10=17；第2次操作，a 2=|17+4|-10=11；第3次操作，a 3=|11+4|-10=5；第4次操作，a 4=|5+4|-10=-1；第5次操作，a 5=|-1+4|-10=-7；第6次操作，a 6=|-7+4|-10=-7；…，后面的计算结果没有变化，据此解答即可．【详解】解：第1次操作，a 1=|23+4|-10=17；第2次操作，a 2=|17+4|-10=11；第3次操作，a 3=|11+4|-10=5；第4次操作，a 4=|5+4|-10=-1；第5次操作，a 5=|-1+4|-10=-7；第6次操作，a 6=|-7+4|-10=-7；第7次操作，a 7=|-7+4|-10=-7；…第2020次操作，a 2020=|-7+4|-10=-7．故选：A ．【点睛】本题考查了绝对值和探索规律．解题的关键是先计算，再观察结果是按照什么规律变化的．探寻规律要认真观察、仔细思考，善用联想来解决这类问题．2．某文具店三月份销售铅笔100支，四、五两个月销售量连续增长．若月平均增长率为x ，则该文具店五月份销售铅笔的支数是（ ）A ．100（1+x ）B ．100（1+x ）2C ．100（1+x 2）D ．100（1+2x ）B 解析：B【解析】试题分析：设出四、五月份的平均增长率，则四月份的市场需求量是100（1+x ），五月份的产量是100（1+x ）2．故答案选B.考点：列代数式.3．已知5a b +=，4ab =，则代数式()()35834ab a b a ab +++-的值为（ ） A ．36B ．40C ．44D ．46A 解析：A【分析】原式去括号整理后，将已知等式代入计算即可求出值．【详解】∵a+b=5，ab=4，∴原式=3ab+5a+8b+3a−4ab=8(a+b)−ab=40−4=36，故选A.【点睛】本题考查的是代数式的求值，熟练掌握先化简再求值是解题的关键.4．已知322x y 和m 2x y -是同类项，则式子4m 24-的值是（ ）A ．21-B ．12-C ．36D ．12B解析：B【分析】根据同类项定义得出m 3=，代入求解即可．【详解】解：∵322x y 和m 2x y -是同类项， ∴m 3=，∴4m 24432412-=⨯-=-，故选B ．【点睛】本题考查了对同类项定义的应用，注意：所含字母相同，并且相同字母的指数也分别相等的项，叫同类项，常数也是同类项．5．一列数123,,n a a a a ⋅⋅⋅，其中11a =-，2111a a =- ，3211a a =- ，……，111n n a a -=- ，则1232020a a a a ⨯⨯⋅⋅⋅⨯=（ ） A ．1 B ．-1 C ．2020 D ．2020- A 解析：A【分析】首先根据11a =-，可得()21111,1112a a ===---32112,1112a a ===--43111112a a ===---，…，所以这列数是-1、12、2、−1、12、2…，每3个数是一个循环；然后用2020除以3，求出一共有多少个循环，还剩下几个数，从而可得答案．【详解】 解： 11a =-，()21111,1112a a ===--- 32112,1112a a ===--43111112a a ===---， 所以这列数是-1、12、2、−1、12、2…，发现这列数每三个循环， 由202036731,÷= 且()1231121,2a a a ⨯⨯=-⨯⨯=- 所以：()()123206732011 1.a a a a =-⨯-⨯⨯⋅⨯=⋅⋅故选A ．【点睛】 本题主要考查了探寻数列规律问题，同时考查了有理数的加减乘除乘方的运算，注意观察总结规律，并能正确的应用规律，解答此题的关键是判断出：这列数是-1、12、2、−1、12、2…，每3个数是一个循环． 6．已知有理数1a ≠,我们把11a-称为a 的差倒数,如:2的差倒数是1112=--,1-的差倒数是()11112=--.如果12a =-,2a 是1a 的差倒数,3a 是2a 的差倒数,4a 是3a 的差倒数…依此类推,那么2020a 的值是（ ）A ．2-B ．13C ．23D ．32A 解析：A【分析】求出数列的前4个数，从而得出这个数列以-2，13，32依次循环，用2020除以3，再根据余数可求a 2020的值．【详解】 ∵a 1=-2， ∴2111(3)3a ==--，3131213a ==-， 412312a ==-- ∴每3个结果为一个循环周期∵2020÷3=673⋯⋯1，∴202012a a ==-故选：A.【点睛】本题考查了规律型：数字的变化类：通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．7．下列同类项合并正确的是（ ）A ．x 3+x 2＝x 5B ．2x ﹣3x ＝﹣1C ．﹣a 2﹣2a 2＝﹣a 2D ．﹣y 3x 2+2x 2y 3＝x 2y 3D解析：D【分析】 根据合并同类项系数相加字母及指数不变，可得答案．【详解】解：A 、x 3与x 2不是同类项，不能合并，故A 错误；B 、合并同类项错误，正确的是2x ﹣3x ＝﹣x ，故B 错误；C 、合并同类项错误，正确的是﹣a 2﹣2a 2＝﹣3a 2，故C 错误；D 、系数相加字母及指数不变，故D 正确；故选：D ．【点睛】本题考查了合并同类项，熟记合并同类项的法则，并根据合并同类项的法则计算是解题关键．8．下列各式中，去括号正确的是（ ）A ．2(1)21x y x y +-=+-B ．2(1)22x y x y --=++C ．2(1)22x y x y --=-+D ．2(1)22x y x y --=-- C解析：C【分析】各式去括号得到结果，即可作出判断．【详解】解：2(1)22x y x y +-=+-，故A 错误； 2(1)22x y x y --=-+，故B,D 错误，C 正确.故选：C ．【点睛】此题考查了去括号与添括号，熟练掌握去括号法则是解本题的关键．9．式子5x x-是（ ）. A ．一次二项式B ．二次二项式C ．代数式D ．都不是C 解析：C【分析】根据代数式以及整式的定义即可作出判断．【详解】 式子5x x-分母中含有未知数，因而不是整式，故A 、B 错误，是代数式，故C 正确． 故选：C ．【点睛】 本题考查了代数式的定义，就是利用运算符号把数或字母连接而成的式子，单独的数或字母都是代数式．10．若a 、b 互为相反数，c 、d 互为倒数，m 的绝对值等于1，则()2a b cd m +-+的值是（ ）.A ．0B ．-2C ．0或-2D ．任意有理数A解析：A【分析】根据相反数的定义得到0a b +=，由倒数的定义得到cd=1，根据绝对值的定义得到|m|=1，将其代入()2a b cd m +-+进行求值． 【详解】∵a ，b 互为相反数，∴0a b +=，∵c ，d 互为倒数，∴cd =1，∵m 的绝对值等于1，∴m =±1，∴原式=0110-+=故选：A.【点睛】本题考查代数式求值，相反数，绝对值，倒数.能根据相反数，绝对值，倒数的定义求出+a b ，cd 和m 的值是解决此题的关键.11．在3a ，x+1，-2，3b -，0.72xy ，2π，314x -中单项式的个数有（ ） A ．2个B ．8个C ．4个D ．5个C 解析：C【分析】根据单项式的定义逐一判断即可.【详解】3a中，分母含未知数，是分式，不是单项式， x+1是多项式，不是单项式，-2是单项式，3b -是单项式， 0.72xy 是单项式，2π是单项式， 314x -=3144x -，是多项式，∴单项式有-2、3b -、0.72xy 、2π，共4个， 故选C.【点睛】 本题考查单项式的定义，熟练掌握定义是解题关键.12．下列说法：①在数轴上表示a -的点一定在原点的左边；②有理数a 的倒数是1a；③一个数的相反数一定小于或等于这个数；④如果a b >，那么22a b >；⑤235x y 的次数是2；⑥有理数可以分为整数、正分数、负分数和0；⑦27m ba -与2abm 是同类项.其中正确的个数为( )A ．1个B ．2个C ．3个D ．4个A解析：A【分析】根据字母可以表示任意数可判断①，根据特殊例子0没有倒数可判断②，根据负数的相反数可判断③，根据特殊例子a=1，b=-2，可判断④，根据单项式次数的定义可判断⑤，根据有理数的分类判断⑥，根据同类项的概念判断⑦.【详解】字母可以表示任意数，当a ＜0时，-a ＞0，故①错误；0没有倒数，故②错误；负数的相反数是正数，正数大于负数，故③错误；若a=1，b=-2，a b >，但是22a b <，故④错误； 235x y 的次数是3，故⑤错误； 0属于整数，故⑥这种分类不正确；27m ba -与2abm 是同类项，⑦正确，故选A.【点睛】本题考查有理数和代数式的相关概念，熟记这类知识点是解题的关键.13．小明乘公共汽车到白鹿原玩，小明上车时，发现车上已有（6a ﹣2b ）人，车到中途时，有一半人下车，但又上来若干人，这时车上共有（10a ﹣6b ）人，则中途上车的人数为（ ）A ．16a ﹣8bB ．7a ﹣5bC ．4a ﹣4bD ．7a ﹣7b B解析：B【分析】根据题意表示出途中下车的人数，再根据车上总人数即可求得中途上车的人数．【详解】由题意可得：（10a ﹣6b ）﹣[（6a ﹣2b ）﹣（3a ﹣b ）]＝10a ﹣6b ﹣6a +2b +3a ﹣b＝7a ﹣5b ．故选B ．【点睛】本题考查了整式加减的应用，根据题意正确列出算式是解决问题的关键.14．一列数：0，1，2，3，6，7，14，15，30，___，___，___这串数是由小能按照一定规则写下来的，他第一次写下“0，1”，第二次按着写“2，3”，第三次接着写“6，7”第四次接着写“14，15”，就这样一直接着往下写，那么这串数的最后三个数可能是下面的 A ．31，63，64B ．31，32，33C ．31，62，63D ．31，45，46C 解析：C【分析】本题通过观察可知下一组数的第一个数是前一组数的第二个数的两倍，在同一组数中的前后两个数相差1．由此可写出最后的3个数．【详解】解：本题通过观察可知下一组数的第一个数是前一组数的第二个数的两倍，在同一组数中的前后两个数相差1，所以这串数最后的三个数为31，62，63．故选：C ．【点睛】本题是一道找规律的题目，这类题型在中考中经常出现．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．15．下列说法错误的是（ ）A ．23-2x y 的系数是32- B ．数字0也是单项式 C ．-x π是二次单项式D ．23xy π的系数是23πC 解析：C【分析】根据单项式的有关定义逐个进行判断即可．【详解】 A. 23-2x y 的系数是32-，故不符合题意； B. 数字0也是单项式 故不符合题意；C. -x π是一次单项式 ，故原选项错误D. 23xy π的系数是23π，故不符合题意. 故选C ．【点睛】本题考查对单项式有关定义的应用，能熟记单项式的有关定义是解此题关键．1．观察下列顺序排列的等式：9×0+1 = 1，9×1+2 = 11，9×2+3=21， 9×3+4=31，9×4+5=41，……，猜想：第n 个等式（n 为正整数）用n 表示，可表示成_________．【分析】根据数据所显示的规律可知：第一数列都是9第2数列开始有顺序且都是所对序号的数减去1加号后的数据有顺序且与所在的序号项吻合等号右端是的规律所以第n 个等式（n 为正整数）应为【详解】根据分析：即第解析：109n -【分析】根据数据所显示的规律可知：第一数列都是9，第2数列开始有顺序且都是所对序号的数减去1，加号后的数据有顺序且与所在的序号项吻合，等号右端是()10?11n -+的规律，所以第n 个等式（n 为正整数）应为()()9110?11n n n -+=-+．【详解】根据分析：即第n 个式子是()()9110?11109n n n n -+=-+=-．故答案为：109n -．【点睛】本题主要考查了数字类规律探索题．对于找规律的题目首先应找出哪些部分发生了变化，是按照什么规律变化的．通过分析找到各部分的变化规律后直接利用规律求解． 2．在同一平面中，两条直线相交有一个交点，三条直线两两相交最多有3个交点，四条直线两两相交最多有6个交点……由此猜想，当相交直线的条数为n 时，最多可有的交点数m 与直线条数n 之间的关系式为：m =_____.（用含n 的代数式填空）【分析】根据题意3条直线相交最多有3个交点4条直线相交最多有6个交点5条直线相交最多有10个交点而3=1+26=1+2+310=1+2+3+4故可猜想n 条直线相交最多有1+2+3+…+（n-1）=个解析：()12n n - 【分析】根据题意，3条直线相交最多有3个交点，4条直线相交最多有6个交点，5条直线相交最多有10个交点．而3=1+2，6=1+2+3，10=1+2+3+4，故可猜想，n 条直线相交，最多有1+2+3+…+（n-1）=()12n n -个交点． 【详解】解：∵3条直线相交最多有3个交点，4条直线相交最多有6个交点．而3=1+2，6=1+2+3，10=1+2+3+4，∴可猜想，n 条直线相交，最多有1+2+3+…+（n-1）=()12n n - 个交点．即()12n n m -= 故答案为：()12n n -．【点睛】本题主要考查了相交线，图形的规律探索，此题着重培养学生的观察、实验和猜想、归纳能力，掌握从特殊向一般猜想的方法．3．已知123112113114,,,...,1232323438345415a a a =+==+==+=⨯⨯⨯⨯⨯⨯依据上述规律，则 99a =________．【解析】试题解析：1009999. 【解析】试题 等号右边第一式子的第一个加数的分母是从1开始，三个连续的数的积，分子是1；第二个加数的分子是1，分母是2，结果的分子是2，分母是1×3=3；等号右边第二个式子的第一个加数的分母是从2开始，三个连续的数的积，分子是1；第二个加数的分子是1，分母是3，结果的分子是3，分母是2×4=8；等号右边第三个式子的第一个加数的分母是从3开始，三个连续的数的积，分子是1；第二个加数的分子是1，分母是4，结果的分子是4，分母是3×5=15．所以a 99=991100991019999+=⨯. 考点：规律型：数字的变化类．4．如图，图1是“杨辉三角”数阵；图2是（a+b ）n 的展开式（按b 的升幂排列）．若（1+x ）45的展开式按x 的升幂排列得：（1+x ）45＝a 0+a 1x+a 2x 2+…+a 45x 45，则a 2＝_____．990【分析】根据图形中的规律即可求出（1+x ）45的展开式中第三项的系数为前44个数的和计算得到结论【详解】解：由图2知：（a+b ）1的第三项系数为0（a+b ）2的第三项的系数为：1（a+b ）3的解析：990【分析】根据图形中的规律即可求出（1+x ）45的展开式中第三项的系数为前44个数的和，计算得到结论．【详解】解：由图2知：（a+b ）1的第三项系数为0，（a+b ）2的第三项的系数为：1，（a+b ）3的第三项的系数为：3＝1+2，（a+b ）4的第三项的系数为：6＝1+2+3，…∴发现（1+x ）3的第三项系数为：3＝1+2；（1+x ）4的第三项系数为6＝1+2+3；（1+x ）5的第三项系数为10＝1+2+3+4；不难发现（1+x ）n 的第三项系数为1+2+3+…+（n ﹣2）+（n ﹣1），∴（1+x ）45＝a 0+a 1x+a 2x 2+...+a 45x 45，则a 2＝1+2+3+ (44)44(441)2⨯+＝990； 故答案为：990．【点睛】本题考查了完全平方式，也是数字类的规律题，首先根据图形中数字找出对应的规律，再表示展开式：对应（a+b ）n 中，相同字母a 的指数是从高到低，相同字母b 的指数是从低到高．5．m ，n 互为相反数，则（3m –2n ）–（2m –3n ）=__________．0【解析】由题意m+n=0所以(3m －2n)－(2m －3n)=3m-2n-2m+3n=m+n=0【点睛】本题考查相反数去括号法则等解题的关键是根据题意得出m+n=0然后再对所求的式子进行去括号合并同解析：0【解析】由题意m+n=0，所以(3m －2n)－(2m －3n)=3m-2n-2m+3n=m+n=0.【点睛】本题考查相反数、去括号法则等，解题的关键是根据题意得出m+n=0，然后再对所求的式子进行去括号，合并同类项，整体代入数值即可.6．一个关于x 的二次三项式，一次项的系数是1，二次项的系数和常数项都是－12，则这个二次三项式为________________________．【解析】根据题意要求写一个关于字母x 的二次三项式其中二次项是x2一次项是-x 常数项是1所以再相加可得此二次三项式为 解析：21122x x -+-【解析】根据题意，要求写一个关于字母x 的二次三项式，其中二次项是x 2，一次项是-12x ，常数项是1，所以再相加可得此二次三项式为211x x 22-+-． 7．关于x 的二次三项式的一次项的系数为5，二次项的系数是－3，常数项是－4.按照x 的次数逐渐减小排列，这个二次三项式为____．－3x2＋5x －4【分析】由于多项式是由单项式组成的而多项式的次数是多项式中次数最高的项的次数而关于x 的二次三项式的二次项系数是-3一次项系数是5常数项是-4根据前面的定义即可确定这个二次三项式【详解析：－3x2＋5x－4【分析】由于多项式是由单项式组成的，而多项式的次数是“多项式中次数最高的项的次数”，而关于x的二次三项式的二次项系数是-3，一次项系数是5，常数项是-4，根据前面的定义即可确定这个二次三项式．【详解】∵关于x的二次三项式，二次项系数是-3，∴二次项是-3x2，∵一次项系数是，∴一次项是5x，∵常数项是-4，∴这个二次三项式为：-3x2+5x-4．故答案为：-3x2+5x-4【点睛】本题考查了多项式的知识，多项式是由单项式组成的，本题首先要确定是由几个单项式组成，要记住常数项也是一项，单项式前面的符号也应带着．8．礼堂第一排有a个座位，后面每排都比第一排多1个座位，则第n排座位有________________．【分析】有第1排的座位数看第n排的座位数是在第1排座位数的基础上增加几个1即可【详解】解：∵第一排有个座位∴第2排的座位为a+1第3排的座位数为a+2…第n排座位有（a+n-1）个故答案为：（a+n解析：a n1+-【分析】有第1排的座位数，看第n排的座位数是在第1排座位数的基础上增加几个1即可．【详解】解：∵第一排有a个座位，∴第2排的座位为a+1，第3排的座位数为a+2，…第n排座位有（a+n-1）个．故答案为：（a+n-1）．【点睛】考查列代数式；得到第n排的座位数与第1排座位数的关系式的规律是解决本题的关键．9．观察下列各等式中的数字特征：53-58=53×58，92-911=92×911，107-1017=107×1017，…将所发现的规律用含字母a，b的等式表示出来是_____．-=×【分析】从大的方面看两个数的差等于两个数的积从小的方面看所有的分子都相同可设两个分母分别为ab分子用ab表示即可【详解】观察发现都是两个分数的差等于两个分数的积设第一个分式为则第二个分式的分子 解析：a b -a a b +=a b ×a a b+ 【分析】 从大的方面看，两个数的差等于两个数的积．从小的方面看，所有的分子都相同，可设两个分母分别为a ，b ，分子用a ，b 表示即可．【详解】观察发现，都是两个分数的差等于两个分数的积． 设第一个分式为a b，则第二个分式的分子与第一个分式的分子相同，而分母恰好是a b +，∴用含字母a b ，的等式表示出来是a b -a a b +=a b ×a a b +． 故答案为：a b -a a b +=a b ×a a b +． 【点睛】本题考查了数字类规律的探索，解决此类探究性问题，关键在观察、分析已知数据，寻找它们之间的相互联系，探寻其规律．10．若单项式322m x y -与3-x y 的差仍是单项式，则m 的值为__________．【分析】根据题意可知单项式与是同类项从而可求出m 的值【详解】解：∵若单项式与的差仍是单项式∴这两个单项式是同类项∴m-2=1解得：m=3故答案为：3【点睛】本题考查合并同类项和单项式解题关键是能根据解析：3【分析】根据题意可知单项式322m x y-与3-x y 是同类项，从而可求出m 的值． 【详解】解：∵若单项式322m x y -与3-x y 的差仍是单项式， ∴这两个单项式是同类项，∴m-2=1解得：m=3.故答案为：3.【点睛】本题考查合并同类项和单项式，解题关键是能根据题意得出m=3．11．列式表示：(1)三个连续整数的中间一个是n ，用代数式表示它们三个数的和为______；(2)三个连续奇数的中间一个是n ，其他两个数用代数式表示为______；(3)设n 表示任意一个整数，试用含n 的式子表示不能被3整除的数为______.(1)或；(2)和；(3)和【分析】（1）易得最小的整数为n-1最大的整数为n+1把这3个数相加即可；（2）易得最小的奇数为n-2最大的奇数为n+2；（3）余数为1或2的数都不能被3整除从而列出代数解析：(1)()()11n n n -+++或3n ； (2)2n -和2n +； (3)31n +和32n +.【分析】（1）易得最小的整数为n-1，最大的整数为n+1，把这3个数相加即可；（2）易得最小的奇数为n-2，最大的奇数为n+2；（3）余数为1或2的数都不能被3整除，从而列出代数式.【详解】解： (1)由题意可知，最小的整数为n-1，最大的整数为n+1，∴它们的和为()()11n n n -+++=3n ；(2) 三个连续奇数的中间一个是n ，其他两个数用代数式表示为2n -和2n +；(3)3n 能被3整除，余数为1或2的数都不能被3整除，∴不能被3整除的数为31n +和32n +.【点睛】本题考查了列代数式及代数式化简的知识，；用到的知识点为：连续整数之间间隔1，连续奇数之间相隔2，余数为1或2的数都不能被3整除．1．观察下列各式：13+23=1+8=9，而（1+2）2=9，∴13+23=（1+2）2；13+23+33=36，而（1+2+3）2=36，∴13+23+33=（1+2+3）2；13+23+33+43=100，而（1+2+3+4）2=100，∴13+23+33+43=（1+2+3+4）2；∴13+23+33+43+53=（______ ）2= ______ ．根据以上规律填空：（1）13+23+33+…+n 3=（______ ）2=[ ______ ]2．（2）猜想：113+123+133+143+153= ______ ．解析：1+2+3+4+5；225；1+2+…+n ；()n n 12+；11375 【解析】分析：观察题中的一系列等式发现，从1开始的连续正整数的立方和等于这几个连续正整数和的平方，根据此规律填空；(1)、根据上述规律填空，然后把1+2+…+n 变为2n 个(n+1)相乘，即可化简；(2)、对所求的式子前面加上1到10的立方和，然后根据上述规律分别求出1到15的立方和与1到10的立方和，求出的两数相减即可求出值．详解：由题意可知：13+23+33+43+53=（1+2+3+4+5）2=225(1)、∵1+2+…+n=（1+n ）+[2+（n-1）]+…+[n 2+（n-n 2+1）]=()n n 12+， ∴13+23+33+…+n 3=（1+2+…+n ）2=[()n n 12+]2；(2)、113+123+133+143+153=13+23+33+...+153-（13+23+33+ (103)=（1+2+…+15）2-（1+2+…+10）2 =1202-552=11375．点睛：此题要求学生综合运用观察、想象、归纳、推理概括等思维方式，探索问题，获得解题途径．考查了学生善于观察，归纳总结的能力，以及运用总结的结论解决问题的能力．2．数a 、b 、c 在数轴上对应的位置如图所示，化简a c c b a b +-++-．解析：0；【分析】由数轴可得a ＞0＞b ＞c ，并从数轴上可得出a ，b ，c 绝对值的大小，从而可以得出各项式子的正负，去绝对值可得出答案. 【详解】 解：由数轴得，c b 0a <<<，且c a b >>，a c cb a b +-++-a c cb a b =--+++- 0=．【点睛】本题考查了数轴上数的大小，去绝对值，熟悉掌握定义是解决本题的关键.3．数学课上，老师出示了这样一道题目:“当1,22a b ==-时，求多项式3233233733631061a a b a a b a b a a b +++----的值”．解完这道题后，张恒同学指出:“1,22a b ==-是多余的条件”师生讨论后，一致认为这种说法是正确的，老师及时给予表扬，同学们对张恒同学敢于提出自己的见解投去了赞赏的目光．（1）请你说明正确的理由；（2）受此启发，老师又出示了一道题目,“无论x 取任何值，多项式2233x mx nx x -++-+的值都不变，求系数m 、n 的值”．请你解决这个问题． 解析：（1）见解析；（2）3n =，1m =.【分析】（1）将原式进行合并同类项，然后进一步证明即可；（2）将原式进行合并同类项，根据“无论x 取任何值，多项式值不变”进一步求解即可.【详解】（1）3233233733631061a a b a a b a b a a b +++----=3332233731033661a a a a b a b a b a b +-+-+--=1-，∴该多项式的值与a 、b 的取值无关，∴1,22a b ==-是多余的条件. （2）2233x mx nx x -++-+=2233x nx mx x -++-+=2(3n)(1)3x m x -++-+∵无论x 取任何值，多项式值不变，∴30n -+=，10m -=，∴3n =，1m =.【点睛】本题主要考查了多项式运算中的无关类问题，熟练掌握相关方法是解题关键. 4．已知一个多项式加上223x y xy -得222x y xy -，求这个多项式． 佳佳的解题过程如下：解：222223x y xy x y xy ---①224x y xy =-②请问佳佳的解题过程是从哪一步开始出错的？并写出正确的解题过程． 解析：是从第①步开始出错的，见解析【分析】根据多项式的加减运算法则进行运算即可求解．【详解】解：佳佳是从第①步开始出错的，正确的解题过程如下：根据题意，得：()()222223x y xy x y xy ---222223x y xy x y xy =--+222x y xy =+，∴这个多项式为222x y xy +．故答案为222x y xy +．【点睛】本题考查了多项式的加减混合运算，注意：只有同类项才能进行加减运算．。

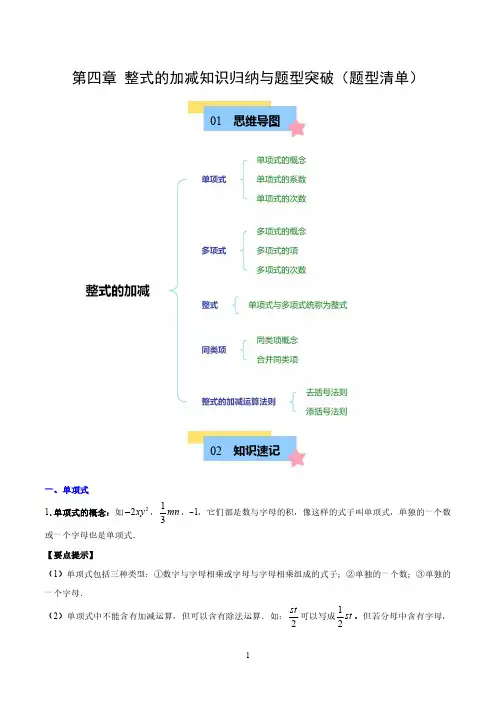
第四章整式的加减知识归纳与题型突破（题型清单）01思维导图02知识速记一、单项式1.单项式的概念：如22xy ，13mn ，-1，它们都是数与字母的积，像这样的式子叫单项式，单独的一个数或一个字母也是单项式．【要点提示】（1）单项式包括三种类型：①数字与字母相乘或字母与字母相乘组成的式子；②单独的一个数；③单独的一个字母．（2）单项式中不能含有加减运算，但可以含有除法运算．如：2st 可以写成12st 。

但若分母中含有字母，如5m就不是单项式，因为它无法写成数字与字母的乘积．2.单项式的系数：单项式中的数字因数叫做这个单项式的系数．【要点提示】（1）确定单项式的系数时，最好先将单项式写成数与字母的乘积的形式，再确定其系数；（2）圆周率π是常数．单项式中出现π时，应看作系数；（3）当一个单项式的系数是1或-1时，“1”通常省略不写；（4）单项式的系数是带分数时，通常写成假分数，如：2114x y 写成254x y ．3.单项式的次数：一个单项式中，所有字母的指数的和叫做这个单项式的次数．【要点提示】单项式的次数是计算单项式中所有字母的指数和得到的，计算时要注意以下两点：（1）没有写指数的字母，实际上其指数是1，计算时不能将其遗漏；（2）不能将数字的指数一同计算．二、多项式1.多项式的概念：几个单项式的和叫做多项式．【要点提示】“几个”是指两个或两个以上．2.多项式的项：每个单项式叫做多项式的项，不含字母的项叫做常数项．【要点提示】（1）多项式的每一项包括它前面的符号．（2）一个多项式含有几项，就叫几项式，如：2627x x --是一个三项式．3.多项式的次数：多项式里次数最高项的次数，叫做这个多项式的次数．【要点提示】（1）多项式的次数不是所有项的次数之和，而是多项式中次数最高的单项式的次数．（2）一个多项式中的最高次项有时不止一个，在确定最高次项时，都应写出．三、整式单项式与多项式统称为整式．【要点提示】（1）单项式、多项式、整式这三者之间的关系如图所示．即单项式、多项式必是整式，但反过来就不一定成立．（2）分母中含有字母的式子一定不是整式．四、同类项用运算符号把数或表示数的字母连结而成的式子叫做代数式.单独的一个数或字母也是代数式.【要点提示】1)判断是否同类项的两个条件：①所含字母相同；②相同字母的指数分别相等，同时具备这两个条件的项是同类项，缺一不可．(2)同类项与系数无关，与字母的排列顺序无关．(3)一个项的同类项有无数个，其本身也是它的同类项．五、合并同类项1.概念：把多项式中的同类项合并成一项，叫做合并同类项．2．法则：合并同类项后，所得项的系数是合并前各同类项的系数的和，且字母部分不变．【要点提示】合并同类项的根据是乘法分配律的逆运用，运用时应注意：(1)不是同类项的不能合并，无同类项的项不能遗漏,在每步运算中都含有．(2)合并同类项，只把系数相加减，字母、指数不作运算.六、去括号法则如果括号外的因数是正数，去括号后原括号内各项的符号与原来的符号相同；如果括号外的因数是负数，去括号后原括号内各项的符号与原来的符号相反．【要点提示】(1)去括号法则实际上是根据乘法分配律推出的：当括号前为“+”号时，可以看作+1与括号内的各项相乘；当括号前为“-”号时，可以看作-1与括号内的各项相乘．（2）去括号时，首先要弄清括号前面是“+”号，还是“-”号，然后再根据法则去掉括号及前面的符号．(3)对于多重括号，去括号时可以先去小括号，再去中括号，也可以先去中括号．再去小括号．但是一定要注意括号前的符号．（4）去括号只是改变式子形式，但不改变式子的值，它属于多项式的恒等变形．七、添括号法则添括号后，括号前面是“+”号，括到括号里的各项都不变符号；添括号后，括号前面是“-”号，括到括号里的各项都要改变符号．【要点提示】(1)添括号是添上括号和括号前面的符号，也就是说，添括号时，括号前面的“+”号或“-”号也是新添的，不是原多项式某一项的符号“移”出来得到的．(2)去括号和添括号是两种相反的变形，因此可以相互检验正误：如：()a b c a b c +-+- 添括号去括号，()a b c a b c -+-- 添括号去括号八、整式的加减运算法则一般地，几个整式相加减，如果有括号就先去括号，然后再合并同类项．【要点提示】（1）整式加减的一般步骤是：①先去括号；②再合并同类项．（2）两个整式相加减时，减数一定先要用括号括起来．(3)整式加减的最后结果中：①不能含有同类项，即要合并到不能再合并为止；②一般按照某一字母的降幂或升幂排列；③不能出现带分数，带分数要化成假分数．03题型归纳题型一单项式、多项式、整式的判断例题：（23-24七年级上·全国·课堂例题）把下列式子分别填在相应的大括号内：222123,,,7,9,335n p a b m n x a m -----．单项式：{…}；多项式：{…}整式：{…}．巩固训练1.（23-24七年级上·云南文山·阶段练习）在式子23x y +，2a，0.5，2x -，23a b ，b 22+中，单项式的个数是（）A ．2个B ．3个C ．4个D ．5个2．（23-24七年级上·江苏苏州·期末）下列式子13ab ，2a b +，12x y +，23x x +-中，多项式有（）A ．1个B ．2个C ．3个D ．4个3．（23-24七年级上·吉林松原·阶段练习）下列式子中：a -，23abc ，x y -，3x ，22872x x -+，整式有（）A ．2个B ．3个C ．4个D ．5个4．（22-23七年级上·安徽六安·阶段练习）对下列式子进行分类．2131,3,,,,,0,,3,4,3.141,23325b xy ab n x m a b d xy a b++->-=+．单项式：（）；多项式：（）；整式：（）．题型二同类项的判断例题：（23-24七年级上·海南儋州·期末）下列各式中，与325x y 是同类项的是（）A ．53xB ．232x y C ．3213x y-D ．512y -巩固训练1．（22-23七年级上·河北唐山·单元测试）下列各选项中的两个单项式，不是同类项的是()A ．23x y 与22yx -B ．22ab 与2ba -C ．3xy与5xy D ．23a 与32a2．（23-24七年级上·江苏徐州·期末）不是同类项的是（）A ．3xy 和4xyB ．2x y -和25xy C ．234x y 和232x y D ．35xy 和3y x3．（23-24七年级上·山东青岛·期末）下列各组中的两项不是同类项的是（）A ．232x y 与233x y -B ．3210a b c 与2310a b c C ．5xy 与yxD ．13-与12题型三单项式的系数、次数例题：（23-24七年级下·青海西宁·开学考试）单项式35x y-的系数是，次数是．巩固训练1．（23-24七年级上·四川成都·阶段练习）π3xyz -的系数是，次数是．2．（23-24七年级上·湖北荆门·单元测试）单项式2223xy z π-的系数是，次数是．3．（23-24七年级上·四川内江·期末）单项式325x y zπ-的系数是，次数是；题型四多项式的项、项数或次数例题：（23-24七年级上·上海·单元测试）多项式2233241x y xy x y -+-+是次项式，其中最高次项的系数是．巩固训练1．（23-24七年级上·上海青浦·期中）多项式3224534x x y xy --+是次项式，常数项是．2．（23-24七年级上·湖南怀化·期末）多项式2323217x y xy --的次数最高项的系数是，常数项是．3．（23-24六年级下·全国·假期作业）多项式33248715a b ab a b -+-的二次项系数是，三次项系数是，常数项是，次数最高项的系数是．题型五写出满足某些特征的单项式、多项式例题：（23-24七年级下·广东东莞·期中）写出一个含有字母x 、y 的五次单项式：．巩固训练1．（23-24七年级上·云南德宏·期末）写出系数为1-，含有字母x ，y 的三次单项式．2．（23-24七年级下·河南洛阳·开学考试）请你写出一个关于x 的二次三项式，使得它的二次项系数为21-，则这个二次三项式是．3．（23-24七年级上·河南新乡·期末）一个关于字母m 的二次三项式，它的常数项是1-，请写出一个满足条件的多项式．题型六将多项式按某个字母升幂（降幂）排列例题：（23-24七年级上·上海·阶段练习）把多项式235632x x y x --+按字母x 的降幂排列：．巩固训练1．（23-24七年级上·四川宜宾·期末）把多项式332223a b ab a b +--按a 的降幂排列为．2．（23-24七年级上·四川乐山·阶段练习）将多项式323274x x y y xy --+-按y 的降幂重新排列为：．3．（23-24七年级上·福建泉州·期末）将多项式322525m n mn n m --+按字母m 升幂排序：．题型七整式的加减运算例题：（2024七年级上·全国·专题练习）化简：(1)2222(542)(322)a ab b a ab b -++--；(2)222(456)3(256)x x x x ----+．巩固训练1．（23-24七年级上·四川宜宾·期末）化简下列式子：(1)2253215m m m m -+--+；(2)()2222523433x xy y x xy y ⎛⎫-+--+ ⎪⎝⎭．2．（23-24六年级上·山东青岛·期末）化简：(1)()()22225327a a b ab b ab ---(2)222963()3x x x x +--3．（23-24七年级上·江西吉安·期中）计算：(1)()()5273310x y x y ---；(2)22223355a b ab a b a b⎛⎫-+- ⎪⎝⎭4．（23-24六年级下·黑龙江大庆·期中）化简：(1)()()193213y y -++；(2)221123422⎛⎫⎛⎫-+--+ ⎪ ⎪⎝⎭⎝⎭x x x x ．题型七整式加减运算中先化简再求值例题：（23-24七年级下·宁夏固原·开学考试）先化简，再求值：()22122332x x x y x y ⎛⎫-+-++ ⎪⎝⎭，其中2x =-，3y =．巩固训练1．（22-23七年级上·辽宁沈阳·阶段练习）先化简，再求值：()()()22243521a b ab a b ab ba -+-+---，其中2a =，12b =.2．（23-24七年级下·河南濮阳·开学考试）先化简，再求值：()()222234a b ab a b ab a b +---，其中1a =，1b =-．3．（23-24七年级上·安徽·单元测试）先化简、再求值：()()2222232xy x y xy x y xy xy --+--，其中1x =、1y =-4．（23-24七年级下·广西南宁·开学考试）先化简后求值：226(3)3(2)20a b a b a a b a -+-++，其中3a =-，12b =-．5．（23-24七年级下·重庆·开学考试）化简求值：()22222222a b ab a b ab ab ⎡⎤----⎣⎦，其中130a b -++=．(1)求a ，b 的值(2)化简并求出()22222222a b ab a b ab ab ⎡⎤----⎣⎦的值．题型八整式的加减运算中错解复原问题例题：（23-24七年级上·广东江门·阶段练习）小明化简22(426)2(225)a a a a -----的过程如下，请指出他化简过程中的错误，写出对应的序号，并写出正确的化简过程：解：22(426)2(225)a a a a -----22426445a a a a =---++①2(44)(24)(65)a a =-+-++-+②21a =-③(1)他化简过程中出错的是第________步（填序号）；(2)请写出正确的解答过程巩固训练1．（23-24七年级上·宁夏吴忠·期中）下面是小明同学进行整式化简的过程，请认真阅读并完成相应任务．()22231223ab a b a b ab ⎛⎫++-- ⎪⎝⎭()()2232324ab a b a b ab =++--第一步2232324ab a b a b ab=++--第二步3ab=-第三步任务一：填空：①以上化简步骤中，第一步的依据是________；②第________步开始出现错误，这一步错误的原因是_________；任务二：请直接写出该整式化简后的正确结果________．2．（23-24七年级上·河南周口·阶段练习）下面是小林同学化简的一道题，其解答过程如下：化简：()()22332x x y x y -++-+⎡⎤⎣⎦，解：原式()22632x x y x y =-+-+第一步22632x x y x y =--++第二步34x y =-第三步(1)小林同学开始出现错误是在第______步，错误的原因是__________．(2)请给出正确的解答过程．3．（23-24七年级上·贵州黔东南·期中）下面是马小虎同学做的一道题：化简：22113122323x x y x y ⎛⎫⎛⎫--+-+ ⎪ ⎪⎝⎭⎝⎭．解：原式22113122323x x y x y =---+………………第一步22131122233x x x y y ⎛⎫⎛⎫=--+-+ ⎪ ⎪⎝⎭⎝⎭…………………第二步4x =-………………………………………………………第三步(1)上面的解题过程中最早出现错误的步骤是第步；(2)请写出正确的解题过程．4．（22-23七年级上·广西南宁·期中）下面是小帆同学进行整式化简的过程，认真阅读并完成相应的问题．()211142824x x x ⎛⎫--+-+- ⎪⎝⎭2111822x x x ⎛⎫=-++-+- ⎪⎝⎭…………第一步2111822x x x =-+-+-………………第二步27x =--………………………………第三步(1)以上化简步骤中，第__________步开始出现错误，错误的原因是__________；(2)请写出正确的化简过程，并计算当12x =-时该整式的值．第四章整式的加减知识归纳与题型突破（题型清单）01思维导图02知识速记一、单项式1.单项式的概念：如22xy ，13mn ，-1，它们都是数与字母的积，像这样的式子叫单项式，单独的一个数或一个字母也是单项式．【要点提示】（1）单项式包括三种类型：①数字与字母相乘或字母与字母相乘组成的式子；②单独的一个数；③单独的一个字母．（2）单项式中不能含有加减运算，但可以含有除法运算．如：2st 可以写成12st 。

1 第十三讲：整式的加减复习 姓名：_________日期：_________ 课前热身 1．若a－b＝2，b－c＝－3，则a－c等于( ) A．1 B．－1 C．5 D．－5 3．计算： (1) 2(x－y)＋3y＝____； (2)(3a2＋b2－5ab)＋(4ab－b2＋7a2)＝____________________； (3)－(m－2n)－(－m＋n)＝____； (4)(7a2－7ab－6)＋(2－4a2)＝____． 4．已知长方形的周长为4a＋2b，其一边长为a－b，则另一边长为________． 5．计算： (1)(－6x2＋5xy)－12xy－(2x2－9xy)；

(2)3a－[－2b＋(4a－3b)]． 6．先化简，再求值： (x2－2x3＋1)－(－1＋2x3＋2x2)，其中x＝2. 2

考点汇编 类型之一 字母表示数 1．某企业今年3月份产值为a万元，4月份比3月份减少了10%，5月份比4月份增加了15%，则5月份的产值是( ) A．(a－10%)(a＋15%)万元 B．(1－90%)(1＋85%)a万元 C．(1－10%)(1＋15%)a万元 D．(1－10%＋15%)a万元 2．今年“五一”假期，张老师一家四口开着一辆轿车去长春市净月潭森林公园度假．若门票每人a元，进入园区的轿车每辆收费20元，则张老师一家开轿车进净月潭森林公园园区所需的费用是___元(用含a的代数式表示)． 3．体育委员带了500元钱去买体育用品，已知一个足球a元，一个篮球b元，则代数式500－3a－2b表示的意义为_________________________________． 4．定义新运算“⊗”，规定：a⊗b＝13a－4b，则12⊗(－1)＝____． 类型之二 整式的概念 5．在式子ab5c，－4x，－23abc，π，2a－13，x＋5y，0，－ab2π，a2－b2中，单项式与多项式各有( ) A．5个，1个 B．5个，2个 C．4个，1个 D．4个，2个 6．下列说法中，正确的是( ) A．－43x2yz的系数是43 B．12ab2c的次数是2 C．－5x2与0.5x2不是同类项 D．3x2y2－y3＋8是四次三项式 7．已知关于x的多项式3x4－(m＋5)x3＋(n－1)x2－5x＋3不含x3和x2项，则( ) A．m＝－5，n＝－1 B．m＝5，n＝1 C．m＝－5，n＝1 D．m＝5，n＝－1 8．若式子－7x3－(2n－2)x2＋(3＋m)x－11不含二次项与一次项，求m与n的值．

第1课 有理数及整式的加减（易混易错题）一、计算：1、（﹣15）+（+9） 2、（﹣15a ）+9a3、﹣13﹣74、﹣13y ﹣7y5、﹣13﹣（﹣7）6、﹣13b ﹣（﹣7b ）7、214- 8、2)16(- 2、计算：注意：()24223,132,3--⎪⎭⎫ ⎝⎛-- （1）])2()32(3[23322-+-⨯-⨯-[]24)3(331)5.12(1)2(--⨯⨯---3、实数a 、b 在数轴上的位置如图所示，则化简b a +的结果为4、 已知有理数a ，b 所对应的点在数轴上如图所示，化简b a -=5、若()0422=-++b a ，则ba6、若a 是最小的自然数，b=++c b a 2 .7、已知a 与b 互为相反数，c 与d 互为倒数，m 的绝对值为6，则mcd mb a +-+的值为 .8、观察图中正方形四个顶点所标的数字规律，可知数2015应标在（ ）A ．第503个正方形的左上角B ．第503个正方形的右上角C ．第504个正方形的左上角D ．第504个正方形的右上角 9、观察下面一列有规律的数： ,486,355,244,153,82,31， 根据这个规律可知第n 个数是 （n 是正整数）10.如图是棋子按某种规律摆成的一串“六”字，按照这种规律，第n 个“六”字中的棋子个数是（ ）A. 4n+1B. 4n+2C. 4n+3D. 4n+411、观察下列版式：2210101-=+=；2221213-=+=；2232325-=+=；2243437-=+=； 2254549-=+= ……若字母n 表示自然数，请把你观察到的规律用含n 的式子表示出来： .12、有理数c b a ,,在数轴的位置如图所示，化简：c b a c b a a +--++-13、若M ＝4x 2－2009x ＋10，N ＝3x 2－2009x ＋9，则M________N (填“＞”、“＜”或“＝”)．14．如图是一个简单的数值运算程序，当输入n 的值为3时，则输出的结果15.计算:(1) )5(3)23(---a a （2）(2)()xy y y yx ---+；（3）2237(43)2x x x x ⎡⎤----⎣⎦； （4）22225(3)2(7)a b ab a b ab ---；16、化简求值：（1）)23()3(222x x x x +++-，其中2-=x（2）4y x 2－[6xy －2（4xy －2）－y x 2]＋1，其中x =－21y =1.17.先阅读下面的问题，并填空，解题。

整式的加减专题复习——规律探究（解析版）第一部分典例剖析+针对训练类型一数式规律典例1（2021秋•南岗区校级期中）有一列数，按一定规律排列而成：﹣1，3，﹣9，27，﹣81，243，…，其中某三个相邻数的和是1701，则这三个数中最小的数是．思路引领：设三个数中最前面的数为x，则另外两个数分别为﹣3x，9x，根据三个数之和为1701，即可得出关于x的一元一次方程，解之即可得出x的值，再将其代入﹣3x和9x 中，取其中最小值即可得出结论．解：设三个数中最前面的数为x，则另外两个数分别为﹣3x，9x，依题意，得：x﹣3x+9x＝1701，解得：x＝243，∴﹣3x＝﹣729，9x＝2187．∵﹣729＜243＜2187，故答案为：﹣729．总结升华：本题考查了一元一次方程的应用以及规律型：数字的变化类，找准等量关系，正确列出一元一次方程是解题的关键．典例2（2022秋•涟水县校级月考）观察下面三行数，并按规律填空：①﹣2，4，﹣8，16，﹣32，64，，，…；②0，6，﹣6，18，﹣30，66，，…；③﹣3，3，﹣9，15，﹣33，63，，…．（1）按第①行数的规律，分别写出第7和第8个数；（2）请你分别写出第②③行的第7个数；（3）取每行数的第9个数，计算这三个数的和．思路引领：（1）根据已知数据都是前一个数乘2的到得，再利用第奇数个系数为负数即可得出答案；（2）根据3行数据关系分别分析得出即可；（3）根据（2）得出的规律分别求出每行第9个数，再把它们相加即可．解：（1）∵①﹣2，4，﹣8，16，﹣32，64，∴第7个数是﹣128，第八个数是256；（2）第②行数是第①行数加上2，第③行数正好比第①行数少1得到的，即第二行的第7个数是﹣128+2＝﹣126，第三行的第7个数是﹣128﹣1＝﹣129；（3）根据以上所求得出：第一行第9个数为﹣512，第二行第9个数为﹣512+2＝﹣510，第三行第9个数为﹣512﹣1＝﹣513，则这三个数的和是：﹣512﹣510﹣513＝﹣1535．总结升华：此题主要考查了数字变化规律，根据已知数据得出得数字第②行数是第①行数加上2，第③行数正好比第①行数少1得到的是解题关键．针对训练11．（2021•武汉）按照一定规律排列的n个数：﹣2、4、﹣8、16、﹣32、64、…，若最后三个数的和为768，则n为（）A．9B．10C．11D．12思路引领：观察得出第n个数为（﹣2）n，根据最后三个数的和为768，列出方程，求解即可．解：由题意，得第n个数为（﹣2）n，那么（﹣2）n﹣2+（﹣2）n﹣1+（﹣2）n＝768，当n为偶数：整理得出：3×2n﹣2＝768，解得：n＝10；当n为奇数：整理得出：﹣3×2n﹣2＝768，则求不出整数．故选：B．总结升华：此题考查规律型：数字的变化类，找出数字的变化规律，得出第n个数为（﹣2）n是解决问题的关键．2．（2021秋•新洲区期中）有一串数：﹣2018，﹣2014，﹣2010，﹣2006，﹣2002…按一定的规律排列，那么这串数中前个数的和最小．思路引领：根据题目中数据的特点，可以写出第n个数，然后令第n个数等于0，即可得到相应的n的值，从而可以解答本题．解：∵有一串数：﹣2018，﹣2014，﹣2010，﹣2006，﹣2002…∴这串数的第n个数为﹣2018+4（n﹣1）＝4n﹣2022，当4n﹣2022＝0时，解得，n＝505…2，∴那么这串数中前505个数的和最小，故答案为：505．总结升华：本题考查数字的变化类，解答本题的关键是明确题意，发现数字的变化特点，求出第多少个数的值为0．类型二数阵、数表规律典例3（2020秋•江汉区月考）将全体正偶数排成一个三角形数阵：按照以上规律排列，第25行第20个数是．思路引领：观察数字的变化，第n行有n个偶数，求出第n行的第一个数，结论可得．解：观察数字的变化可知：第n行有n个偶数．∵第1行的第一个数是：2＝1×0+2；第2行第一个数是：4＝2×1+2；第3行第一个数是：8＝3×2+2；第4行第一个数是：14＝4×3+2；•∴第n行第一个数是：n（n﹣1）+2．∴第25行第一个数是：25×24+2＝602．∴第25行第20个数是：602+2×19＝640．故答案为：640．总结升华：本题主要考查了数字的变化的规律，有理数的混合运算．准确找出数字的变化规律是解题的关键．典例4（2019秋•江汉区期中）有这样一对数，如下表，第n+3个数比第n个数大2（其中n是正整数）第1个第2个第3个第4个第5个……a b c（1）第5个数表示为；第7个数表示为；（2）若第10个数是5，第11个数是8，第12个数为9，则a＝，b＝，c＝；（3）第2019个数可表示为．思路引领：（1）根据第n+3个数比第n个数大2，即可求解；（2）根据第n+3个数比第n个数大2，分别求出第10、11、12个数即可求出结果；（3）根据数字的变化规律，解：（1）∵第n+3个数比第n个数大2，∴第5个数比第2个数大2，∴第5个数为b+2．∵第4个数比第1个数大2，∴第4个数为a+2，∴第7个数比第4个数大2，∴第7个数为a+4．故答案为b+2、a+4．（2）∵第10个数为a+6，第11个数为b+6，第12个数为c+6，∴a+6＝5，b+6＝8，c+6＝9解得a＝﹣1，b＝2，c＝3．故答案为﹣1、2、3．（3）第一组数是a、b、c第二组数是a+2、b+2、c+2第三组数是a+4、b+4、c+4第四组数是a+6、b+6、c+6…第n组数的第三个数是c+（2n﹣2）2019÷3＝673，第2019个数是第673组的第三个数，∴第673组的第三个数是c+2×673﹣2＝c+1344．故答案为c+1344．总结升华：本题考查了数字的变化类，解决本题的关键是寻找数字的变化规律．针对训练21．（2021秋•播州区期中）如表被称为“杨辉三角”或“贾宪三角”．其规律是：从第三行起，每行两端的数都是“1”，其余各数都等于该数“两肩”上的数之和．表中两平行线之间的一列数：1，3，6，10，15，…，我们把第一个数记为a1，第二个数记为a2，第三个数记为a3，…，第n个数记为a n，则a6＝，a2020＝．思路引领：根据题目中的数据，可以写出前几项，从而可以数字的变化特点，然后即可得到a6和a2020的值．解：由题意可得，a1＝1，a2＝1+2＝3，a3＝1+2+3＝6，a4＝1+2+3+4＝10，a5＝1+2+3+4+5＝15，…，∴a n＝1+2+3+…+n=n(n+1)2，∴当n＝6时，a6=6×72=21，当n＝2020时，a2020=2020×20212=2041210，故答案为：21，2041210．总结升华：本题考查数字的变化类，解答本题的关键是明确题意，发现数字的变化特点，求出所求项的值．2．（2018秋•江夏区期中）已知一列数：1、﹣2、3、﹣4、5、﹣6、……，将这列数排成下列形式：按照上述规律排列下去，第10行数的第1个数是（）A．﹣46B．﹣36C．37D．45思路引领：观察排列规律得到第1行有1个数，第2行有2个数，第3行有1个数，…，第9行有9个数，则可计算出前9行的数的个数45，而数字的序号为偶数时，数字为负数，于是可判断第10行数的第1个数为﹣46．故选A．解：第1行有1个数，第2行有2个数，第3行有1个数，…，第9行有9个数，所以前9行的数的个数为1+2+3+…+9＝45，而数字的序号为奇数时，数字为正数，数字的序号为偶数时，数字为负数，所以第10行数的第1个数为﹣46．故选：A．总结升华：本题考查了规律型：数字的变化类：认真观察、仔细思考，利用数字与序号数的关系解决这类问题．3．（2017秋•海淀区校级期中）如图，从左边第一个格子开始向右数，在每个小格子中都填入一个整数，使得其中任意三个相邻格子中所填整数之和都相等．（1）可求得x＝，第2017个格子中的数为．（2）判断：前m个格子中所填整数之和是否可能为2018？若能，求出m的值，若不能，请说明理由．（3）若取前3格子中的任意两个数记作a、b，且a≥b，那么所有的|a﹣b|的和可以通过计算|9﹣★|+|9﹣☆|+|★﹣☆|得到，其结果为；若a、b为前19格子中的任意两个数记作a、b，且a≥b，则所有的|a﹣b|的和为．思路引领：（1）根据三个相邻格子的整数的和相等列式求出x的值，再根据第9个数是2可得☆＝2，然后找出格子中的数每3个为一个循环组依次循环，在用2014除以3，根据余数的情况确定与第几个数相同即可得解；（2）可先计算出这三个数的和，再照规律计算．（3）由于是三个数重复出现，因此可用前三个数的重复多次计算出结果．解：（1）∵任意三个相邻格子中所填整数之和都相等，∴9+★+☆＝★+☆+x，解得：x＝9，★+☆+x＝☆+x﹣6，∴★＝﹣6，所以，数据从左到右依次为9、﹣6、☆、9、﹣6、☆、…，第9个数与第三个数相同，即☆＝2，所以，每3个数“9、﹣6、2”为一个循环组依次循环，∵2017÷3＝672…1，∴第2017个格子中的整数与第1个格子中的数相同，为9．故答案为：9，9；（2）9﹣6+2＝5，2018＝2015+3＝2015+9﹣6，2015÷5＝403，403×3＝1209，所以是第1209+1+1＝1211个数，即m＝1211，故前1211个数的和为2018；（3）∵取前3格子中的任意两个数，记作a、b，且a≥b，∴所有的|a﹣b|的和为：|9﹣（﹣6）|+|9﹣2|+|﹣6﹣2|＝30．∵由于是三个数重复出现，那么前19个格子中，这三个数，9出现了7次，﹣6和2各出现了6次．∴代入式子可得：|9﹣（﹣6）|×7×6+|9﹣2|×7×6+|2﹣（﹣6）|×6×6＝1212．故答案为：30，1212．总结升华：本题主要考查数字的变化规律，解答的关键是找出数字间的关系，得出规律．类型三图形的增长规律典例4（2021•汉川市模拟）古希腊著名的毕达哥拉斯学派把1、3、6、10、…，这样的数称为“三角形数”，而把1、4、9、16、…，这样的数称为“正方形数”．从图中可以发现，任何一个大于1的“正方形数”都可以看作两个相邻“三角形数”之和．则第10个图形中右下方的“三角形数”中的所有点数是．思路引领：观察图象中点的个数的规律有第一个图形是4＝1+3，第二个图形是9＝3+6，第三个图形是16＝6+10，…则按照此规律得到第10个图形的规律即可．解：∵第1个图形是4＝1+（1+2），第2个图形是9＝（1+2）+（1+2+3），第3个图形是16＝（1+2+3）+（1+2+3+4），…∴第10个图形是112＝（1+2+3+4+5+6+7+8+9+10）+（1+2+3+4+5+6+7+8+9+10+11）＝55+66．故答案为：66．总结升华：此题考查图形的变化规律，通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．典例5（2020秋•江夏区期中）按照如图所示的方法排列黑色小正方形地砖，则第14个图案中黑色小正方形地砖的数量是（）A．360B．363C．365D．369思路引领：观察图形可知，黑色与白色的地砖的个数的和是连续奇数的平方，而黑色地砖比白色地砖多1个，求出第n个图案中的黑色与白色地砖的和，然后求出黑色地砖的块数，再把n＝14代入进行计算即可．解：第1个图案只有（2×1﹣1）2＝12＝1块黑色地砖，第2个图案有黑色与白色地砖共（2×2﹣1）2＝32＝9，其中黑色的有12（9+1）＝5块，第3个图案有黑色与白色地砖共（2×3﹣1）2＝52＝25，其中黑色的有12（25+1）＝13块，…第n 个图案有黑色与白色地砖共（2n ﹣1）2，其中黑色的有12[（2n ﹣1）2+1]，当n ＝14时，黑色地砖的块数有12×[（2×14﹣1）2+1]=12×730＝365．故选：C ．总结升华：本题考查图形的变化规律，观察图形找出黑色与白色地砖的总块数与图案序号之间的关系是解题的关键． 针对训练31．（2021秋•中山市期中）观察下列图中所示的一系列图形，它们是按一定规律排列的，依照此规律，第10个图形共有 个〇．思路引领：观察图形的变化先得前几个图形中圆圈的个数，可以发现规律：第n 个图形共有（3n +1）个〇，进而可得结果． 解：观察图形的变化可知： 第1个图形共有1×3+1＝4个〇； 第2个图形共有2×3+1＝7个〇； 第3个图形共有3×3+1＝10个〇； …所以第n 个图形共有（3n +1）个〇； 所以第10个图形共有10×3+1＝31个〇； 故答案为：31．总结升华：本题考查了规律型：图形的变化类，解决本题的关键是根据图形的变化寻找规律．2．（2018秋•硚口区期中）对于大于或等于2的整数的平方进行如下“分裂”，如下分别将22、32、42分裂成从1开始的连续奇数的和，依此规律，则20182的分裂数中最大的奇数是 ．思路引领：由题意可知：每个数中所分解的最大的奇数是前边底数的2倍减去1．由此得出答案即可．解：自然数n2的分裂数中最大的奇数是2n﹣1．20182分裂的数中最大的奇数是2×2018﹣1＝4035，故答案为：4035．总结升华：此题考查数字的变化规律，注意根据具体的数值进行分析分解的最大的奇数和底数的规律，从而推广到一般．3．（2022•仙居县校级开学）如图，都是由棱长为1的正方体叠成的立体图形，例如第（1）个图形由1个正方体叠成，第（2）个图形由4个正方体叠成，第（3）个图形由10个正方体叠成，依次规律，第（10）个图形由（）个正方体叠成．A．120B．165C．220D．286思路引领：根据图形的变换规律，可知第n个图形中的正方体的个数为1+3+6+⋯+ n(n+1)2，据此可得第（6）个图形中正方体的个数．解：由图可得：第（1）个图形中正方体的个数为1；第（2）个图形中正方体的个数为4＝1+3；第（3）个图形中正方体的个数为10＝1+3+6；第（4）个图形中正方体的个数为20＝1+3+6+10；故第n个图形中的正方体的个数为1+3+6+⋯+n(n+1)2，∴第10个图形中正方体的个数为1+3+6+10+15+21+28+36+45+55＝220．故选：C．总结升华：本题主要考查了图形变化类问题，解决问题的关键是依据图形得到变换规律．解题时注意：第n个图形中的正方体的个数为1+3+6+⋯+n(n+1)2．类型四乘方规律典例6（2022•内蒙古）观察下列等式：70＝1，71＝7，72＝49，73＝343，74＝2401，75＝16807，…，根据其中的规律可得70+71+72+…+72022的结果的个位数字是（ ） A ．0B ．1C ．7D ．8思路引领：由已知可得7n 的尾数1，7，9，3循环，则70+71+…+72022的结果的个位数字与70+71+72的个位数字相同，即可求解．解：∵70＝1，71＝7，72＝49，73＝343，74＝2401，75＝16807，… ∴7n 的尾数1，7，9，3循环， ∴70+71+72+73的个位数字是0， ∵2023÷4＝505…3，∴70+71+…+72022的结果的个位数字与70+71+72的个位数字相同， ∴70+71+…+72022的结果的个位数字是7， 故选：C ．总结升华：本题考查数的尾数特征，能够通过所给数的特点，确定尾数的循环规律是解题的关键．典例7（2022秋•东港区校级月考）求1+2+22+23+……+22007的值，可令S ＝1+2+22+23+……+22007，则2S ＝2+22+23+24+……+22008，因此2S ﹣S ＝22009﹣1，即S ＝22009﹣1，仿照以上推理，计算出1+3+32+33+……+32022值为32023−12．思路引领：令S ＝1+3+32+33+……+32022，则3S ＝3+32+33+……+32023，作差求出S 即可． 解：令S ＝1+3+32+33+……+32022， 则3S ＝3+32+33+……+32023， ∴3S ﹣S ＝32023﹣1， 则S =32023−12，即1+3+32+33+……+32022=32023−12．故答案为：32023−12．总结升华：本题考查数字的变化规律，通过观察所给的求和方法，灵活应用此方法求和是解题的关键． 针对训练41．（2021秋•罗湖区期中）观察等式：2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2；……，已知按一定规律排列的一组数：2501，2502，2503，……，2999，21000．若2500＝a ，用含a 的式子表示这组数之和是（ ） A ．2a 2﹣2aB ．2a 10﹣2a 5﹣2C ．2a 2﹣aD ．2a 20﹣a思路引领：把所求的数列的各数提取2500，可得：2500×（2+22+23+…+2499+2500），利用所给的等式的规律求解即可．解：∵2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2；…， ∴2+22+23+…+2n ＝2n +1﹣2， ∴2501+2502+2503+…+2999+21000 ＝2500×（2+22+23+…+2499+2500） ＝2500×（2500+1﹣2） ＝2500×（2×2500﹣2）， ∵2500＝a ， ∴原式＝a （2a ﹣2） ＝2a 2﹣2a ． 故选：A ．总结升华：本题主要考查了规律型：数字的变化类，有理数的混合运算，解答的关键是由所给的等式总结出规律．2．（2019秋•汾阳市期末）任意大于1的正整数m 的三次幂均可“分裂”成m 个连续奇数的和，如：23＝3+5，33＝7+9+11，43＝13+15+17+19，…按此规律，若m 3分裂后，其中有一个奇数是203，则m 的值是（ ） A ．13B ．14C ．15D ．16思路引领：观察可知，分裂成的奇数的个数与底数相同，然后求出到m 3的所有奇数的个数的表达式，再求出奇数203的是从3开始的第101个数，然后确定出101所在的范围即可得解．解：∵底数是2的分裂成2个奇数，底数为3的分裂成3个奇数，底数为4的分裂成4个奇数，∴m 3分裂成m 个奇数，所以，到m 3的奇数的个数为：2+3+4+…+m =(m+2)(m−1)2，∵2n +1＝203，n ＝101，∴奇数203是从3开始的第101个奇数， ∵(13+2)(13−1)2=90，(14+2)(14−1)2=104，∴第101个奇数是底数为14的数的立方分裂的奇数的其中一个， 即m ＝14． 故选：B ．总结升华：本题是对数字变化规律的考查，观察出分裂的奇数的个数与底数相同是解题的关键，还要熟练掌握求和公式．3．在求两位数的平方时，可以用“列竖式”的方法进行速算，求解过程如图所示：则第4个方框中x+y的值是（）A．11B．12C．13D．14思路引领：找出求解过程图中的规律，利用此规律求得m，n，x，y的值，将相应字母的值代入即可得出结论．解：求解过程图中的表格中的规律为：第一行前两个格为十位数字的平方，后两个格为个位数字的平方，平方后不是两位数，十位数字用0代替，第二行从第二个格开始表示的是两位数中个位数字与十位数字的乘积的2倍，第三行为从右开始将一二行数字相加的和，足10进1，∵62＝36，∴m＝3，n＝6，∵6×7×2＝84，∴x＝8，y＝4，∴x+y＝12．故选：B．总结升华：本题主要考查了有理数的乘方，求代数式的值，找出求解过程图中的规律是解题的关键．类型五幻方规律典例8（2021秋•江阴市期中）小学时候大家喜欢玩的幻方游戏，老师稍加创新改成了“幻圆”游戏，现在将﹣1、2、﹣3、4、﹣5、6、﹣7、8分别填入图中的圆圈内，使横、竖以及内外两圈上的4个数字之和都相等，老师已经帮助同学们完成了部分填空，则图中a+b的值为（）A．﹣6或﹣3B．﹣8或1C．﹣1或﹣4D．1或﹣1思路引领：由于八个数的和是4，所以需满足两个圈的和是2，横、竖的和也是2．列等式可得结论．解：设小圈上的数为c，大圈上的数为d，﹣1+2﹣3+4﹣5+6﹣7+8＝4，∵横、竖以及内外两圈上的4个数字之和都相等，∴两个圈的和是2，横、竖的和也是2，则﹣7+6+b+8＝2，得b＝﹣5，6+4+b+c＝2，得c＝﹣3，a+c+4+d＝2，a+d＝1，∵当a＝﹣1时，d＝2，则a+b＝﹣1﹣5＝﹣6，当a＝2时，d＝﹣1，则a+b＝2﹣5＝﹣3，故选：A．总结升华：本题考查了有理数的加法．解决本题的关键是知道横竖两个圈的和都是2．典例9（2020•冷水江市一模）我国的《洛书》中记载着世界上最古老的一个幻方：将1～9这九个数字填入3×3的方格内，使三行、三列、两对角线上的三个数之和都相等．如图的幻方中，m＝．思路引领：根据“每行、每列、每条对角线上的三个数之和相等”解答即可．解：1+2+3+…+9＝45，根据“每行、每列、每条对角线上的三个数之和相等”，可知三行、三列、两对角线上的三个数之和都等于15，∴第一列第三个数为：15﹣2﹣5＝8，第三列第二个数为：15﹣3﹣5＝7，第三个数为：15﹣2﹣7＝6，如图所示：∴m＝15﹣8﹣6＝1．故答案为：1．总结升华：本题考查数的特点和有理数的加法，抓住每行、每列、每条对角线上的三个数之和相等，数的对称性是解题的关键．针对训练51．（2021秋•南安市期中）现有七个数﹣1，﹣2，﹣2，﹣4，﹣4，﹣8，﹣8将它们填入图1（3个圆两两相交分成7个部分）中，使得每个圆内部的4个数之积相等，设这个积为m，如图2给出了一种填法，此时m＝64，在所有的填法中，m的最大值为256．思路引领：观察图象，可得这7个数，有的被乘了1次，2次，3次．要使得每个圆内部的4个数之积相等且最大所以﹣8，﹣8必须放在被乘两次的位置．与﹣8，﹣8同圆的只能为﹣1，﹣4，其中﹣4m＝256解：观察图象，可得这7个数，有的被乘了1次，2次，3次．要使得每个圆内部的4个数之积相等且最大所以﹣8，﹣8必须放在被乘两次的位置．与﹣8，﹣8同圆的只能为﹣1，﹣4，其中﹣4放在中心位置，如图∴m＝（﹣8）×（﹣8）×（﹣1）×（﹣4）＝256总结升华：本题考查有理数的乘法，关键是找到两个（﹣8）的位置．2．将9个数填入幻方的九个方格中，使处于同一横行、同一竖列、同一斜对角线上的三个数的和相等，如表一：按此规律将满足条件的另外6个数填入表二，则表二中这9个数的和为（用含a的整式表示）．表一492357816表二a+5a+1a﹣1思路引领：根据同一横行、同一竖列、同一斜对角线上的三个数的和相等作出图形，根据题意列出关于a与x的方程，可得x＝a+2，进一步求出这9个数的和即可．解：如图所示：4+x+a﹣1+a+3＝a﹣3+a+1+a+3，解得x＝a﹣5，a+3+x+a+3＝2a+6+a﹣5＝3a+1，3（3a+1）＝9a+3．故答案为：9a+3．总结升华：此题考查了列代数式，整式的加减，熟练掌握运算法则是解本题的关键．类型六其他规律典例10（2019秋•武昌区校级期中）某初中七（5）班学生军训排列成7×7＝49人的方阵，做了一个游戏，起初全体学生站立，教官每次任意点4个不同学号的学生，被点到的学生，站立的蹲下，蹲下的站立，且学生都正确完成指令，同一名学生可以多次被点，则15次点名后蹲下的学生人数可能是（）A．3B．27C．49D．以上都不可能思路引领：假设站立记为“+1”，则蹲下为“﹣1”．原来49个“+1”，乘积为“+1”，每次改变其中的4个数，即每次运算乘以4个“﹣1”，即乘以了“+1”，乘积为“+1”，即可得出结论．解：假设站立记为“+1”，则蹲下为“﹣1”．原来49个“+1”，乘积为“+1”，每次改变其中的4个数， 即每次运算乘以4个“﹣1”，即乘以了“+1”， 15次点名后，乘积仍然是“+1”， 所以，最后出现“﹣1”的个数为偶数， 即蹲下的学生人数为偶数， 选项A ，B ，C 都不符合题意， 故选：D ．总结升华：此题主要考查了奇数与偶数，有理数乘法中积的符号的判断，解决本题的关键是利用有理数的乘法进行解决． 针对训练61．（2019秋•硚口区期中）把几个不同的数用大括号括起来，相邻两个数之间用逗号隔开，如：{1，2}；{1，4，7}；…我们称之为集合，其中的每一个数称为该集合的元素．规定：当整数x 是集合的一个元素时，100﹣x 也必是这个集合的元素，这样的集合又称为黄金集合，例如{﹣1，101}就是一个黄金集合．若一个黄金集合所有元素之和为整数m ，且1180＜m ＜1260，则该黄金集的元素的个数是（ ） A ．23B ．24C ．24或25D ．26思路引领：由黄金集合的定义，可知一个整数是x ，则必有另一个整数是100﹣x ，则这两个整数的和为x +100﹣x ＝100，只需判断1180＜m ＜1260内100的个数即可求解． 解：在黄金集合中一个整数是x ，则必有另一个整数是100﹣x ， ∴两个整数的和为x +100﹣x ＝100， 由题意可知，1180＜m ＜1260时， 100×12＝1200，100×13＝1300， ∴这个黄金集合的个数是24或25个； 故选：C ．总结升华：本题考查有理数，新定义；理解题意，通过两个对应元素和的特点，结合m 的取值范围，进而确定元素个数是解题关键．第二部分 专题提优训练1．观察下面一列数：1，12，2，13，1，3，14，23，32，4，15，12，1，2，5，16，…（已写出了第1至第16个数）．（1）第7，第8，第9，第10个数的积是 ，前16个数的积是 ； （2）按此规律，第30个数是 ；（3）在上面这列数中，从左起第m 个数记为F （m ），当F （m ）=92020时，求m 的值． 思路引领：（1）根据规律直接写出数计算即可；（2）根据题意将数字从左边开始分别以1个数，2个数，3个数，…，为一组，每组数据的积为1，且分子递增1，分母递减1，然后根据规律得出第30个数即可； （3）根据F （m ）=92020判断出F （m ）是第几组第几个数即可得出m 的值． 解：（1）根据题意知，第7，第8，第9，第10个数的积是14×23×32×4＝1，前16个数的积是1×（12×2）×（13×1×3）×（14×23×32×4）×（15×24×1×42×5）×16=16，故答案为：1，16；（2）由（1）知，将数字从左边开始分别以1个数，2个数，3个数，…，为一组，每组数据的积为1，且分子递增1，分母递减1， ∵1+2+3+4+5+6+7＝28，∴第30个数在第8组的第2个数，即1+18−1=27，故答案为：27；（3）∵F （m ）=92020，2020+9＝2029，∴F （m ）是第2028组第9个数，前面有2027组数， ∴m ＝（1+2+3+4+…+2027）+9=1+20272×2027+9=2055387． 总结升华：本题主要考查数字的变化规律，根据数字的变化分组分析规律是解题的关键．2．（2021秋•丹江口市期中）观察一列数：1，﹣2，3，﹣4，5，﹣6，7，…，将这列数排成下列形式：（1）在表中，第12行第6个数是 ；（2）在表中，“2021”是其中的第 行，第 个数；（3）将表中第i 行的最后一个数记为a i ，如第1行的最后一个数记为a 1，即a 1＝1，第2行的最后一个数记为a 2，即a 2＝3，如此下去，a 3＝﹣6，a 4＝﹣10，…，第n 行的最后一个数记为a n ，则用含n 的式子表示|a n |为 ； （4）在（3）的条件下，计算1a 1+1a 2−1a 3−1a 4+1a 5+1a 6−1a 7−1a 8+1a 9+1a 10．思路引领：（1）先求出前11行一共有66，即可求解；（2）求出前n 行共有n(n+1)2个数，再求前63行共有2016个数，即可求2021的位置；（3）由题意可得，1+2+3+......+n =n(n+1)2，即可求解； （4）原式=2(1−12+12−13+13−14+......+19−110+110−111)，再运算即可． 解：（1）由题可知，第一行1个数，第二行2个数，…，第n 行n 个数， ∴前11行一共有1+2+3+…+11＝66， ∴第12行第一个数是67， ∴第12行第6个数是﹣72， 故答案为：﹣72；（2）由题意可得，前n 行共有n(n+1)2个数，∴当n ＝63时，前63行共有2016个数， ∴2021时第64行的第5个数， 故答案为：64，5；（3）由题意可得，1+2+3+......+n =n(n+1)2， ∴|a n |=n(n+1)2， 故答案为：n(n+1)2； （4）1a 1+1a 2−1a 3−1a 4+1a 5+1a 6−1a 7−1a 8+1a 9+1a 10=11+13+16+110+......+145=2(11×2+12×3+13×4+......+19×10+110×11) =2(1−12+12−13+13−14+......+19−110+110−111)=2(1−111) =2011．总结升华：本题考查数字的变化规律，根据题意探索数字的排列规律是解的关键． 3．（2022•东莞市校级一模）找出以下图形变化的规律，则第2022个图形中黑色正方形的数量是 3033 ．思路引领：仔细观察图形并从中找到规律，然后利用找到的规律即可得到答案． 解：∵当n 为偶数时第n 个图形中黑色正方形的数量为n +12n 个；当n 为奇数时第n 个图形中黑色正方形的数量为n +12（n +1）个，∴当n ＝2022时，黑色正方形的个数为2022+1011＝3033个． 故答案为：3033．总结升华：本题考查了图形的变化类问题，解题的关键是仔细的观察图形并正确的找到规律．4．（2020秋•西城区校级期中）古希腊毕达格拉斯学派的数学家常用小石子在沙滩上摆成各种形状来研究各种多边形数，比如：他们研究过图1中的1，3，6，10，…．由于这些数能够表示成三角形，将其称为三角形数；类似的，称图2中的1，4，9，16，…，这样的数为正方形数．（1）请你写出一个既是三角形数又是正方形数的自然数 ．（2）类似地，我们将k 边形数中第n 个数记为N （n ，k ）（k ≥3）．以下列出了部分k 边形数中第n 个数的表达式： 三角形数：N （n ，3）=12n 2+12n 正方形数：N （n ，4）＝n 2 五边形数：N （n ，5）=32n 2−12n 六边形数：N （n ，6）＝2n 2﹣n …根据以上信息，得出N （n ，k ）＝ ．（用含有n 和k 的代数式表示）思路引领：（1）由题意得第8个图的三角形数是36，所以既是三角形数又是正方形数，且大于1的最小正整数为36；（2）由已知等式进行变形进而可推出结果．解：（1）由题意第8个图的三角形数为12×8（8+1）＝36，∴既是三角形数又是正方形数，且大于1的最小正整数为36， 故答案为36．（2）∵N （n ，3）=n 2+n 2=(3−2)n 2+(4−3)n2，N （n ，4）＝n 2=2n 2+0×n 2=(4−2)n 2+(4−4)n2， N （n ，5）=32n 2−12n =(5−2)n 2+(4−5)n2，N （n ，6）＝2n 2﹣n =4n 2−2n 2=(6−2)n 2+(4−6)n2， 由此推断出N （n ，k ）=(k−2)n 2+(4−k)n2（k ≥3）．故答案为：(k−2)n 2+(4−k)n2（k ≥3）．总结升华：本题考查三角形数、正方形数的规律、完全平方数与归纳推理等知识，观察已知式子的规律并改写形式是解决问题的关键．5．（2020秋•江夏区校级月考）观察下列等式：12＝1，22＝4，32＝9，42＝16，52＝25，…，若12+22+32+42+52+…+n 2的个位数字是1（0＜n ≤2020，且n 为整数），下列选项中，n 的最大值是（ ） A ．2001B ．2006C ．2011D ．2019思路引领：通过计算发现每10个数，末位数字循环一次，再结合选项进行判断即可求解． 解：∵12＝1，22＝4，32＝9，42＝16，52＝25，62＝36，72＝49，82＝64，92＝81，102＝100，112＝121，122＝144，132＝169，…， ∴每10个数，末位数字循环一次， ∴1+4+9+6+5+6+9+4+1+0＝45， ∵2001÷10＝200……1， ∴200×45+1＝9001； ∵2006÷10＝200……6， ∴200×45+1+4+9+6+5+6＝9031； ∵2011÷10＝201……1， ∴201×45+1＝9046； ∵2019÷10＝201……9， ∴202×45＝9090； ∵2006＞2001， ∴n 的最大值为2006， 故选：B ．总结升华：本题考查数字的变化规律，通过探索每个数的尾数的循环规律，并运用规律求解是解题的关键．6．（2021•碧江区 模拟）观察等式：2+22＝23﹣2：2+22+23＝24﹣2；2+22+23+24＝25﹣2，…已知按一定规律排列的一组数：250、251、252、…、299、2100，若250＝a，则用含a的式子表示这组数的和是．思路引领：由等式：2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2，得出规律：2+22+23+…+2n＝2n+1﹣2，那么250+251+252+…+299+2100＝（2+22+23+…+2100）﹣（2+22+23+…+249），将规律代入计算即可．解：∵2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2；…∴2+22+23+…+2n＝2n+1﹣2，∴250+251+252+…+299+2100＝（2+22+23+...+2100）﹣（2+22+23+ (249)＝（2101﹣2）﹣（250﹣2）＝2101﹣250，∵250＝a，∴2101＝（250）2•2＝2a2，∴原式＝2a2﹣a．故答案为：2a2﹣a．总结升华：本题是一道找规律的题目，要求学生通过观察，分析、归纳发现其中的规律，并应用发现的规律解决问题．解决本题的难点在于得出规律：2+22+23+…+2n＝2n+1﹣2．7．（2019秋•武汉期中）如图，在边长为1厘米的正方形网格有12个格点，用这些格点做三角形顶点，一共可以连成面积为2平方厘米的三角形个数为（）A．24B．32C．28D．12思路引领：根据面积等于底乘以高依次分情况分析既可以得到三角形个数．解：①如图以AB为底时，与对边CF的四个顶点都可以构成面积等于2平方厘米的三角形，类似这样的三角形共有16个，②如图以AC为底与线段BE上的三个点可以构成面积等于2平方厘米的三角形，类似这样的三角形共有12个，其中有四个直角三角形是重复的，故三角形总个数：16+12﹣4＝24个，。