有理数的运算复习课初一数学

有理数及其运算（复习）一、正负数有理数的分类：_____________统称整数，试举例说明。

_____________统称分数，试举例说明。

____________统称有理数。

正确理解非负数和非正数。

练习：1、把下列各数填在相应额大括号内：1，－0.1，-789，25，0，-20，-3.14，-590，6/7正整数集｛ …｝；正有理数集｛ …｝；负有理数集｛ …｝ 负整数集｛ …｝；自然数集｛ …｝；正分数集｛ …｝ 负分数集｛ …｝2、某种食用油的价格随着市场经济的变化涨落，规定上涨记为正，则-5.8元的意义是 ；如果这种油的原价是76元，那么现在的卖价是 。

二、数轴规定了 、 、 的直线，叫数轴练习：1、如图所示的图形为四位同学画的数轴，其中正确的是（ ）2、在数轴上画出表示下列各数的点，并按从大到小的顺序排列，用“>”号连接起来。

4，-|-2|， -4.5， 1， 03、下列语句中正确的是（ ）Ａ数轴上的点只能表示整数Ｂ数轴上的点只能表示分数Ｃ数轴上的点只能表示有理数Ｄ所有有理数都可以用数轴上的点表示出来4、①比－3大的负整数是_______； ②已知ｍ是整数且-4<m<3，则ｍ为_______________。

③有理数中，最大的负整数是 ，最小的正整数是 。

最大的非正数是 。

④与原点的距离为三个单位的点有_ _个，他们分别表示的有理数是 _和_ _。

5、在数轴上点A 表示-4,如果把原点O 向负方向移动1个单位,那么在新数轴上点A 表示的数是( ) A.-5， B.-4 C.-3 D.-26、画出数轴，把下列各组数分别在数轴上表示出来，并按从大到小的顺序排列，用“>”连接起来：⑴ 1，－2，3，－4 ⑵31，0，3，－0.2三、相反数1、像2和-2、-5和5、2.5和-2.5这样，只有 不同的两个数叫做互为相反数。

0的相反数是 。

一般地：若a 为任一有理数，则a 的相反数为-a2、相反数的相关性质：a 、相反数的几何意义：表示互为相反数的两个点（除0外）分别在原点O 的两边，并且到原点的距离相等。

初一数学上册第一章有理数复习教案最新3篇篇一：数学《有理数》教案篇一一、教材分析：（一）教材的地位和作用：本节课的内容是《新人教版七年级数学》教材中的第一章第四节，“有理数的乘除法”是把“有理数乘法”和“有理数除法”的内容进行整合，在“有理数的加减混合运算”之后的一个学习内容。

在本章教材的编排中，“有理数的乘法”起着承上启下的作用，它既是有理数加减的深入学习，又是有理数除法、有理数乘方的基础，在有理数运算中有很重要的地位。

“有理数的乘法”从具体情境入手，把乘法看做连加，通过类比，让学生进行充分讨论、自主探索与合作交流的形式，自己归纳出有理数乘法法则。

通过这个探索的过程，发展了学生观察、归纳、猜测、验证的能力，使学生在学习的过程中获得成功的体验，增强了自信心。

所以本节课的学习具有一定的现实地位。

（二）学情分析：因为学生在小学的学习里已经接触过正数和0的乘除法，对于两个正数相乘、正数与0相乘、两个正数相除、0与正数相除的情况学生已经掌握。

同时由于前面学习了有理数的加减法运算，学生对负数参与运算有了一定的认识，但仍还有一定的困难。

另外，经过前一阶段的教学，学生对数学问题的研究方法有了一定的了解，课堂上合作交流也做得相对较好。

（三）教学目标分析：基于以上的学情分析，我确定本节课的教学目标如下1、知识目标：让学生经历学习过程，探索归纳得出有理数的乘除法法则，并能熟练运用。

2、能力目标：在课堂学习过程中，使学生经历探索有理数乘除法法则的过程，发展观察、猜想、归纳、验证、运算的能力，同时在探索法则的过程中培养学生分类和归纳的数学思想。

3、情感态度和价值观：在探索过程中尊重学生的学习态度，树立学生学习数学的自信心，培养学生严谨的数学思维习惯。

4、教学重点：会进行有理数的乘除法运算。

5、教学难点：有理数乘除法法则的探索与运用。

确定教学目标的理由依据是：新课标中指出课堂教学中应体现知识与技能、过程与方法、情感态度与价值观的三维目标，同时也基于本节内容的地位与作用。

知识点总结知识点1 常规计算有理数混合运算的运算顺序：1、先乘方，再乘除，最后加减；2、同级运算，从左到右进行；3、如有括号，先做括号内的运算，按小括号、中括号、大括号的顺序依次进行.【方法总结】根据有理数的混合运算顺序和运算法则计算即可．本题主要考查有理数的混合运算，熟练掌握有理数的混合运算的顺序和法则是解题的关键．注意：绝对值符号有括号的作用.知识点2 运算律、规律计算有理数的混合运算中，常用的运算律有：加法交换律、加法结合律、乘法交换律、乘法结合律、乘法对加法的分配律、加法对乘法的分配律. 【方法总结】本题主要考察了有理数混合运算的运算顺序和分配律的使用，（1）和（3）是乘法分配律的正用，（2）是乘法分配律的逆用，熟练掌握运算律的使用是解本题的关键．知识点3 求代数式的值重要结论：互为相反数的两数和为0，相反数等于自身的数是0；互为倒数的两数积为1，倒数等于自身的数有-1,1，倒数等于自身的自然数是1；最大的负整数是-1，最小的正整数是1，绝对值最小的有理数是0；有理数的混合运算:1.有理数混合运算顺序：先算乘方，再算乘除，最后算加减;同级运算，应按从左到右的顺序进行计算;如果有括号，要先做括号内的运算。

2.进行有理数的混合运算时，注意各个运算律的运用，使运算过程得到简化。

有理数混合运算的四种运算技巧：(1)转化法：一是将除法转化为乘法，二是将乘方转化为乘法，三是在乘除混合运算中，通常将小数转化为分数进行约分计算.(2)凑整法：在加减混合运算中，通常将和为零的两个数，分母相同的两个数，和为整数的两个数，乘积为整数的两个数分别结合为一组求解.(3)分拆法：先将带分数分拆成一个整数与一个真分数的和的形式，然后进行计算.(4)巧用运算律：在计算中巧妙运用加法运算律或乘法运算律往往使计算更简便.知识要点1.计算的基本法则：包括:有理数的加法、减法、乘法、除法、乘方①加法：同号两数相加，取相同的符号，并把绝对值相加. 异号两数相加，取绝对值大的数的符号，并用较大的绝对值减去较小的绝对值. 一个数同0相加，仍得这个数。

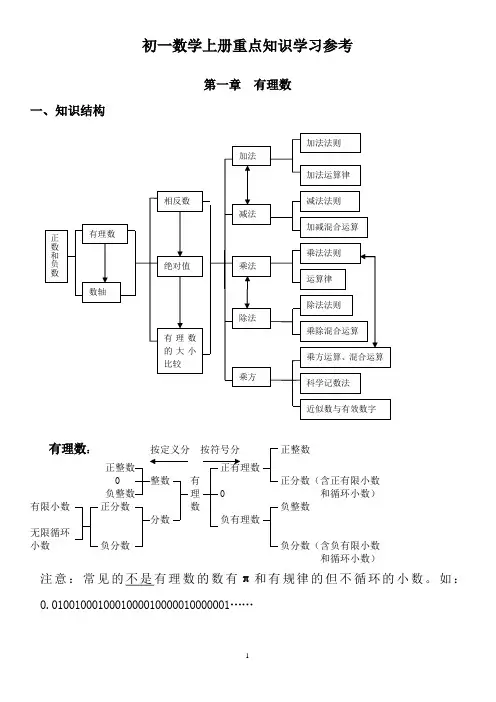
初一数学上册重点知识学习参考第一章 有理数一、知识结构有理数： 按定义分 按符号分正整数 正整数 正有理数0 整数 有 正分数（含正有限小数负整数 理 0 和循环小数）有限小数 正分数 数 负整数分数 负有理数无限循环小数 负分数 负分数（含负有限小数和循环小数）注意：常见的不是有理数的数有π和有规律的但不循环的小数。

如：0.0100100010001000010000010000001……二、掌握要点1、了解有理数的概念（什么是有理数、有理数包含的范围有哪些、有理数之间的大小比较）。

（1）大于0的数叫做正数，如3、1.8、5%等。

（2）在正数前面加上负号“—”的数叫负数，即小于0的数，如-3、-2.5、-5%等。

（3）数0既不是正数，也不是负数。

0除了表示一个也没有以外，是正数和负数的分界，是基准。

（4）在同一个问题中，分别用正数与负数表示的量具有相反的意义。

强调：用正数、负数表示实际问题中具有相反意义的量，而相反意义的量包含两个要素：一是他们的意义相反，如向东与向西、收入与支出；二是他们都是数量，而且是同类的量。

（5）正整数、0、负整数统称整数。

整数可以看作分母为1的分数。

（6）正整数、0、负整数、正分数、负分数都可以写成分数的形式，这样的数称为有理数。

（7）把一些数放在一起，就组成了一个数的集合，简称“数集”。

所有有理数组成的数集叫“有理数集”，所有整数组成的数集叫“整数集”，所有负数组成的数集叫“负数集”……数集一般用圆圈或大括号表示，因为集合中的数是无限的。

（8）有理数可以按不同的标准进行分类，标准不同，分类结果也不同。

问：有理数可分为正数和负数两大类，对吗？为什么？有理数可分为整数和分数两大类，对吗？为什么？2、有理数与数轴上的点一一对应（数轴的三要素、怎样看数轴、掌握应用数轴来进行去绝对值符号的简单运算）。

（1）通常用一条直线上的点表示数，这条直线叫数轴。

数轴三要素：原点、正方向、单位长度原点——在直线上任取一点表示数0，这个点叫原点。

知识点总结知识点1：有理数除法法则(1) 除以一个数等于乘以这个数的倒数。

即a÷b=a×1/b(b≠0)。

(2) 两数相除，同号得正，异号得负，并把绝对值相除。

0除以任何一个不等于0的数，都得0。

知识点2：有理数的乘除混合运算除转乘，确定符号。

知识点3：有理数的四则混合运算先乘除，后加减，如果有括号，就先算括号里面的。

同级运算中，要按照从左到右的顺序。

知识点4.有理数的除法考点精讲1.4.2有理数的除法1、有理数除法法则1（课本P34）除以一个不等于0的数，等于乘这个数的倒数。

a÷b=a·1/b（b≠0）2、有理数除法法则2（课本P34）两数相除，同号得正，异号得负，并把绝对值相除。

0除以任何一个不等于0的数，都得0。

3、化简分数（课本P35）-45/-12=（-45）÷（-12）=45÷12=15/44、有理数的加减乘除混合运算先乘除，后加减5、用计算器计算计算器的符号键（-）可以用来表示负数的符号。

用计算器计算：（-1.7）×4-（-2.6）÷（-4）-7.45（如图1.4-1）有理数的除法（习题）1.4.2有理数的除法（-6.5）÷0.13（7/4-7/8-7/12）÷（-7）（-7）÷（7/4-7/8-7/12）（-9）×（-11）÷8÷（-125）42×（-2/7）+（-5/4）÷（-0.25）（2）化简下列分数：-42/7，4/-16，-54/-8，-60/25（3）小商店一周的利润是1400元，平均每天的利润是元；小商店一周共亏损840元，平均每天的利润是元。

（4）用“>”“<”或“=”填空：如果a<0，b>0，那么a/b 0，如果a>0，b<0，那么a/b 0，如果a<0，b<0，那么a/b 0，如果a=0，b≠0，那么a/b 0。

第七讲 有理数的除法运算【知识要点】1.有理数除法法则① 法则一：除以一个数等于乘以这个数的倒数② 法则二：两数相除，同号得正，异号得负，并把绝对值相除。

③ 0除以任何一个非零数，等于0；0不能作除数！2. 1和1-的倒数等于它本身，即倒数等于它本身的有两个，是1±。

3. 1除以非零数，得到它的倒数。

【经典例题】【例1】求下列各数的倒数和负倒数。

①2 ② 431- ③ 20% ④ )0,0(21><-b a ba【例2】计算：① )5()25(-÷- ② )611(431-÷③ )4(4115.2-⨯÷- ④ )85()145()712(-⨯-÷-⑤3)522()213()53(÷-÷-⨯- ⑥3482773⎛⎫⎛⎫÷-⨯÷- ⎪ ⎪⎝⎭⎝⎭⑦ )241()1258343(-÷-- ⑧ )1312()173()1312(1715-÷-+-÷【例3】计算 ① .,14)31415161(m m 求=÷-+- ②11112134---【例4】数学老师布置了一道思考题“计算：⎪⎭⎫ ⎝⎛-+-÷⎪⎭⎫ ⎝⎛-526110132301 ”，小明和小红两位同学经过仔细思考，用不同的方法解答了这个问题： 小明的解法：原式=⎥⎦⎤⎢⎣⎡⎪⎭⎫⎝⎛+-⎪⎭⎫ ⎝⎛+÷⎪⎭⎫ ⎝⎛-521016132301=⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛-2165301 =3301⨯-=101- 小红的解法：原式的倒数=⎪⎭⎫ ⎝⎛-÷⎪⎭⎫ ⎝⎛-+-301526110132=()30526110132-⨯⎪⎭⎫⎝⎛-+- =-20+3-5+12=-10 故原式=101-①你觉得 的解法更好．②请你用自己喜欢的方法解答下面的问题：计算：⎪⎭⎫⎝⎛-+-÷⎪⎭⎫ ⎝⎛-723214361421。

初一上册数学青岛版第三章有理数的运算知识点归纳（史上最全面的总结）一、有理数的加法1.加法法则（1）同号两数相加，取相同的符号，并把绝对值相加。

（2）绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大绝对值减较小绝对值。

（3）互为相反数的两个数相加得零。

（4）一个数与0相加仍得这个数。

2 . 加法运算律（1）加法交换律两个数相加，交换加数的位置，和不变。

a+b=b+a注意事项：对于三个或三个以上的数相加，加法交换律仍使用。

（2）加法结合律三个数相加，先把前两个数相加，或先把后两个数相加，和不变。

(a+b)+c=a+(b+c)注意事项：对于三个以上的数相加，加法结合律仍使用。

（3）常见结合方法a 把正数和负数分别结合。

b 把同分母分数或易通分的分数相结合。

C 把相加得零的几个数相结合。

d 把相加得整数的几个小数相结合。

e几个整数和分数相加，通常整数与分数分别结合。

3.重要结论（1）在有理数范围内，和不一定大于每一个加数。

（2）ba+≠a+b二、有理数的减法1.减法法则减去一个数等于加上它的相反数。

2.数轴上两点间的距离公式设点A表示有理数a,点B表示有理数b,则AB=ba-3.重要结论（1）在有理数范围内，差不一定小于被减数。

（2）任何数减去0仍得这个数。

（3）0减去一个数得这个数的相反数。

（4）ba-≠a-b（5）设a,b为任意有理数a>b ⟺ a-b>0a=b⟺ a-b=0a<b⟺a-b<0三、有理数的乘法1.乘法法则两数相乘，同号得正，异号得负。

并把绝对值相乘。

2.多个数相乘的乘法法则（1）几个不为0的数相乘，积的符号是由负因数的个数决定的，当负因数为偶数个时，积为正。

当负因数的个数为奇数时，积为负，并把绝对值相乘。

（2）几个数相乘，有一个因数为0，积为0.3.乘法运算律（1）乘法交换律两数相乘，交换因数的位置，积不变。

（2）乘法结合律三个数相乘，先把前两个数相乘，或先把后两个数相乘，积不变。

有理数1． 掌握有理数有关分类、数轴、相反数、近似数、有效数字和科学计数法等有关概念 2． 熟练去括号法则，以及有理数的有关运算模块一 正负数与有理数的分类1. 对于正负数的理解不能简单理解为带“+”号的数就是正数，带“-”号的数就是负数。

2. 相反意义的两个量是相互的，也是相对的。

3. 掌握有理数的两种分类：按“定义”分类与按“性质符号”分类☞有理数的分类【例1】 下列说法：①0是整数；②负分数一定是负有理数；③一个数不是整数就是负数；④π-为有理数；⑤最大的负有理数是1-，正确的序号是【难度】2星【解析】考察有理数的分类 【答案】①②【巩固】下列说法：①存在最小的自然数；②存在最小的正有理数；③不存在最大的正有理数；④存在最大的负有理数；⑤不是正整数就不是整数，错误的序号是【难度】2星【解析】考察有理数的分类 【答案】②④⑤模块二 数轴、相反数、倒数1. 数形结合思想是一种重要的数学思想。

数轴就是数形结合的工具。

2. 数轴是条直线，可以向两方无限延伸。

3. 数轴的三要素：原点、正方向、单位长度、三者缺一不可。

4. 所有有理数都可以用数轴上点表示，反过来，不能说数轴上所有的点都表示有理数5. 相反数是成对出现的，不能单独存在。

相反数和为零。

☞数轴例题精讲重难点【例2】 如图所示，小明在写作业时，不慎将两滴墨水滴在数轴上，根据图中的数值，试定墨迹盖住的整数共有几个【难度】1星【解析】考察数轴的有关概念【答案】如图，盖住数中的整数有4-、3-、2-、2、3、4，共有6个【巩固】 数轴上表示整数的点称为整点，某条数轴的单位长度为1cm ，若在数轴上任意画出一条长2006cm 的线段，则线段盖住的整数点共有 个【难度】2星【解析】考察数轴的有关概念 【答案】2006或2007☞相反数与倒数【例3】 已知a 、b 互为相反数，c 、d 互为倒数，1x =±，求2a b x cdx ++-的值 【难度】3星【解析】考察相反数与倒数的有关概念 【答案】解：由相反数、倒数的定义可得 0a b +=，1cd =则当1x =时，原式=01110+-⨯= 当1x =-时，原式=20(1)1(1)2+--⨯-=【巩固】已知a 和b 互为相反数，m 和n 互为倒数，(2)c =-+，求22mna b c++的值 【难度】3星【解析】考察相反数与倒数有关概念 【答案】解：由相反数和倒数的定义可得 0a b +=，1mn =∵(2)c =-+ ∴原式112()022mn a b c =++=+=--【巩固】已知数轴上点A 和点B 分别表示互为相反数的两个数，a 和b ()a b <并且A 、B 两点间的距离是144,求a 、b 【难度】3星【解析】考察相反数有关概念【答案】解：∵a 、b 两数互为相反数 ∴0a b += ∴a b =-∵A 、B 两点间距离有144b a -= ∴1()44b b --=∴178b =，178a =-模块三 有理数的运算1. 在进行有理数加法运算时，优先确定符号，然后在计算绝对值，这样就不容易出错。

有理数及其运算专题知识点一：正数与负数正数：负数：一、怎样区分正数和负数？例1. 读下列各数，并指出其中哪些是正数，哪些是负数：-2，3，0，+3，1.5，-3.14，100，-1.732.正数有：____ _____________. 负数有：__________ ______.二、如何用正数和负数表示的量具有相反意义的量？例2.在下列横线上填上适当的词，使前后构成意义相反的量：（1）收入3500元，______6500元；（2）_______800米，下降240米；（3）向北前进200米，_______300米。

练习：如果某球队一个赛季胜12场,记作+12场,那么该队这个赛季负6场,可记作_______。

如果存入3万元记作+3万元，那么支取2万元应记作，不存不支应记作，-4万元表示。

三、正数、负数的实际生活中的应用例3.某种面粉袋上对面粉的重量这样描述：重量（+50±0.2）kg，下面的理解正确的是（） A.一袋面粉的重量是50kg B.一袋面粉的最大重量是50.2kgC.一袋面粉的最小重量是50.2kgD. -0.2kg表示的是比最大重量少0.2kg例 4.小明小学毕业了，他发现自己小学12个学期的数学成绩如下：91,89,88,93,94,90,97,94,87,94,85,86；那么他小学数学的平均成绩是多少？通过我们今天学习了正负数，你觉得有没有更简便的计算方法？知识点二：有理数的概念及分类有理数包含五种数：正整数、0、负整数、正分数、负分数，若将这五种数归类，可有两种方法。

（1） 按整数分数分类 （2）按正负分：那么，你知道有理数是什么了吗？【注意】分数包括所有有限小数，无限循环小数，假分数、带分数和百分数；正整数、0、负整数、正分数、负分数都是有理数。

1.判断，并说明理由。

（1）分数都是有理数。

（ ） （2）小数都可以写成分数。

（ ） （3）任何有理数不是整数就是分数。

人教版七年级数学上册第一章《有理数》总复习教案第一章《有理数》总复习一、内容分析小结与复习分作两个部分。

第一部分概述了正数与负数、有理数、相反数、绝对值等概念，以及有理数的加、减、乘、除、乘方的运算方法与运算律，从而给出全章内容的大致轮廓，第二部分针对这一章新出现的内容、方法等提出了5个问题；通过这5个问题引发学生的思考，主动进行新的知识的建构。

二、课时安排：小节与复习的要求是要把这一章内容系统化，从而进一步巩固和加深理解学习内容。

本章的主要内容可以概括为有理数的概念与有理数的运算两部分。

因此，本章总复习的二课时这样安排（测验课除外）：第一课时复习有理数的意义及其有关概念；第二课时复习有理数的运算。

三、教学方法的确定：设计典型例题，检测学生知识，科学地进行小结与归纳。

四、教学安排：第一课时：本节课将复习有理数的意义及其有关概念。

其内容包括正负数、有理数、数轴、有理数大小的比较、相反数与绝对值等。

在教学过程中，应利用数轴来认识、理解有理数的有关概念，借助数轴，把这些概念串在一起形成一个用以描述有理数特征的系统。

另外，在运用有理数概念的同时，还应注意纠正可能出现的错误认识。

一、教学目标；1.理解五个重要概念:有理数、数轴、倒数、绝对值、倒数。

2.使学生提高区分概念的能力，正确运用概念解决问题。

3、能正确比较两个有理数的大小。

二、教学重点：有理数五个概念的理解与应用:有理数、数轴、倒数、绝对值、倒数。

三、教学难点：对绝对值概念的理解与应用。

四、教学过程：（一）知识梳理：1.正数和负数:(给出四个问题，帮助学生理解负数的必要性及其在生产生活中的应用。

)回答下列问题（1）温度为－4℃是什么意思？（2）如果向正北规定为正，那么走－70米是什么意思？（3）21世纪的第一年，日本的服务出口额比上一年增长了-7.3%,这里的“服务出口额比上一年增长了-7.3%”是什么意思？（4）请同学们谈一谈，为什么要引入负数？你还能举出生活中有关负数的例子吗？2.有理数的分类:(通过两个问题让学生掌握有理数的两种分类方法，理解有理数的含义。

新人教版七年级数学上册有理数的加减法（复习）【学习目标】1．掌握有理数加法的意义，法则及运算律，并会使用运算律简算；2．掌握有理数减法的法则和运算技巧，认识减法与加法的内在联系，体会其中蕴含的转化的思想；3．熟练地将加减混合运算统一成加法运算，理解运算符号和性质符号的意义，运用加法运算律合理简算，并且会解决简单的实际问题.【要点梳理】 要点一、有理数的加法1.定义：把两个有理数合成一个有理数的运算叫作有理数的加法．2.法则：（1）同号两数相加，取相同的符号，并把绝对值相加；（2）绝对值不相等的异号两数相加，取绝对值较大的加数的符号，并用较大的绝对值减去较小的绝对值．互为相反数的两个数相加得0；（3）一个数同0相加，仍得这个数．要点诠释：利用法则进行加法运算的步骤：(1)判断两个加数的符号是同号、异号，还是有一个加数为零，以此来选择用哪条法则．(2)确定和的符号(是“+”还是“－”)．(3)求各加数的绝对值，并确定和的绝对值(加数的绝对值是相加还是相减)．3.语言要点二、有理数的减法1.定义： 已知两个数的和与其中一个加数，求另一个加数的运算，叫做减法，例如：(-5)+?＝7，求？，减法是加法的逆运算．要点诠释：（1）任意两个数都可以进行减法运算．（2） 几个有理数相减，差仍为有理数，差由两部分组成：①性质符号；②数字即数的绝对值．2.法则：减去一个数，等于加这个数的相反数，即有：()a b a b -=+-．要点诠释： 将减法转化为加法时，注意同时进行的两变，一变是减法变加法；二变是把减数变为它的相反数”．如：要点三、有理数加减混合运算将加减法统一成加法运算，适当应用加法运算律简化计算.过程：堂上小测,看谁又准又快化简-（+9）=___；②、化简-（-8）=__。

③、（-3）+（-4）=____；④、8+（-2）=____。

⑤、（-7）+ 2 = ___；⑥、(-1)-(-5)=____。

⑦、（-1）- 2 = ___；⑧、1-(-1) =_____。

有理数总复习【知识点一】正数与负数1.正数：像+1.8，+420、+30、+10%等带有“+”号的数叫做正数。

为了强调正数，前面加上“+”号，也可以省略不写。

2.负数：像－3、－4754、－50、－0.6、－15%等带有“－”号的数叫做负数。

而负数前面的“－”号不能省略。

3.零：既不是正数也不是负数，它是正数与负数的分界点。

归纳：正数与负数概念：大于0的叫正数，小于0的叫负数，0既不是正数也不是负数非负数：正实数与零的统称。

（表示为：x≥0）几个特殊的数：最小的自然数是0;绝对值最小的数是0；同时0也最小的非负整数是0；最小的正整数是1；最大的负整数是-1。

注意：对于正数与负数，不能简单地理解为：带“+”号的数是正数，带“－”号的数是负数。

例如－a不一定是负数，因为字母a代表任何一个有理数，当a是0时，－a是0，当a是负数时，－a是正数；能用正数与负数表示相反意义的量，习惯上把增加、盈利等规定为正，它们相反意义的量规定为负，正、负是相对而言有理数。

【典例精析】例1 把下列各数填在相应额大括号内：－0.1，-789，25，0，-20，-3.14，-590，6/7 ，π，-5/3, +3.65, π/2正数集｛｝负数集｛｝自然数集｛｝非负数集｛｝例2 下列说法正确的是：（）A．正数都带有“+”号，不带“+”号的数都是负数。

B.带“－”号的数不一定是负数.C．一个数不是正数就是负数.D.０℃表示没有温度.【知识点二】有理数及其分类：有理数：整数与分数统称为有理数。

整数包括三类：正整数、零、负整数。

分数包括两类：正分数和负分数。

按整数、分数的关系分类：按正数、负数、零的关系分类：注意：小学学过的零表示没有，而引入负数后，就不能把“零”完全当作没有了，如0℃就是一个特定的温度；现在我们学过的数，不是有理数，除和与有关的数外，其他的数都是有理数；引入负数后，数的范围扩大为有理数，奇数和偶数的外延也由自然数扩大到整数。