猴子拿香蕉 逻辑谓词复习过程

猴子摘香蕉实验报告记录(含代码)————————————————————————————————作者：————————————————————————————————日期：华中科技大学《人工智能与模式识别》实验报告院系：电子与信息工程系班级：姓名：同组人：指导老师：电话：邮箱：日期：2013年12月24日一、实验内容利用一阶谓词逻辑求解猴子摘香蕉问题：房内有一个猴子，一个箱子，天花板上挂了一串香蕉，其位置如图所示，猴子为了拿到香蕉，它必须把箱子搬到香蕉下面，然后再爬到箱子上。

请定义必要的谓词，列出问题的初始化状态（即下图所示状态），目标状态（猴子拿到了香蕉，站在箱子上，箱子位于位置b）。

（附加：从初始状态到目标状态的谓词演算过程。

）二、实验平台VC6.0三、实验分析1. 定义描述环境状态的谓词。

AT(x,w)：x在t处，个体域：xϵ{monkey}，wϵ{a,b,c,box}；HOLD(x,t)：x手中拿着t，个体域：tϵ{box,banana}；EMPTY(x)：x手中是空的；ON(t,y)：t在y处，个体域：yϵ{b,c,ceiling}；CLEAR(y)：y上是空的；BOX(u)：u是箱子，个体域：uϵ{box}；BANANA(v)：v是香蕉，个体域：vϵ{banana}；2. 使用谓词、连结词、量词来表示环境状态。

问题的初始状态可表示为：S o：AT(monkey,a)˄EMPTY(monkey)˄ON(box,c)˄ON(banana,ceiling)˄CLEAR(b)˄BOX(box)˄BANANA(banana)要达到的目标状态为：S g：AT(monkey,box)˄HOLD(monkey,banana)˄ON(box,b)˄CLEAR(ceiling)˄CLEAR(c)˄BOX(box)˄BANANA(banana)3. 从初始状态到目标状态的转化, 猴子需要完成一系列操作, 定义操作类谓词表示其动作。

实验1：猴子摘香蕉问题的VC编程实现一、实验目的利用一阶谓词逻辑求解猴子摘香蕉问题并通过编程来实现二、编程环境本文主要编译环境是Windows 10 Visual Studio 2015 在Ubuntu 12.0 用gcc编译来演示问题的另外几种状态的解法三、问题描述房内有一个猴子，一个箱子，天花板上挂了一串香蕉，其位置如图所示，猴子为了拿到香蕉，它必须把箱子搬到香蕉下面，然后再爬到箱子上。

请定义必要的谓词，列出问题的初始化状态（即下图所示状态），目标状态（猴子拿到了香蕉，站在箱子上，箱子位于位置b）。

四、解决方案1.定义描述环境状态的谓词。

AT(x,y)：x在y处，个体域：xϵ{monkey, box,banana }，yϵ{a,b,c}；HAND(s)：猴子手中拿着s，个体域：sϵ{box,banana}；ONBOX(monkey)：猴子在箱子上；2.使用谓词、连结词、量词来表示环境状态。

问题的初始状态可表示为：S o：A T(monkey,a)˄ ~HAND(s)˄AT(box,c) ˄ ~ONBOX(monkey) ˄AT(banana,b)要达到的目标状态为：S g：AT(box,b) ˄ ONBOX(monkey) ˄ HAND(banana)˄AT(monkey,b) ˄AT(banana,b)3.从初始状态到目标状态的转化, 猴子需要完成一系列操作, 定义操作类谓词表示其动作。

go(m,n)：猴子从m走到n处，个体域：m,nϵ{a,b,c}；movebox(m,n)：猴子把箱子从m 处移动到n 处，个体域：m,n ϵ{a,b,c}；onbox(m)：猴子在m 处爬上箱子，个体域：m ϵ{a,b,c}；catch(banana):猴子摘到香蕉；这3个操作也可分别用条件和动作来表示。

条件直接用谓词公式表示，是为完成相应操作所必须具备的条件；当条件中的事实使其均为真时，则可激活操作规则，于是可执行该规则中的动作部分。

习题1. 猴子摘香蕉问题，给出它的产生式系统表示：
一个房间里，天花板上挂有一串香蕉，有一只猴子可在房间里任意活动（到处走动，推移箱子，攀登箱子等）。

设房间里还有一只可被猴子移动的箱子，且猴子登上箱子时才能摘到香蕉，问猴子在某一状态下（设猴子位置为A，箱子位置为B，香蕉位置在C），如何行动可摘取到香蕉。

习题. 对三枚钱币问题给出产生式系统表示及状态空间图：
设有三枚钱币，其排列处在“正、正、反”状态，现允许每次翻动其中任意一个钱币，问只许操作三次的情况下，如何翻动钱币使其变成“正、正、正”或“反、反、反”状态。

房内有一只猴子、一个箱子，天花板上挂了一串香蕉，其位置关系如图所示，猴子为了拿到香蕉，它必须把箱子推到香蕉下面，然后再爬到箱子上。

请定义必要的谓词，写出问题的初始状态（即图示的状态）、目标状态（猴子拿到了香蕉，站在箱子上，箱子位于位置b）。

定义谓词AT(x,y)：x在y位置上BOX(y)：箱子在y的位置。

OVER（x）：x被挂在天花板上EMPTY(x)：x手中是空的HOLD(x, z)：x拿着zON(x,w)：x在w的上面NOT_on(x,w) ：x在w的上面BAN(y)：香蕉在y的位置猴子的位置为:a香蕉位置为：b箱子的位置为：c问题的初始状态：AT(monkey, a)∧BOX(c)∧BAN(b)∧OVER（b）∧EMPTY(monkey)∧NOT_on(monkey, box)问题的目标状态是：AT(monkey, b)∧BOX(b)∧BAN(b)∧HOLD(monkey, banana)∧ONmonkey, box)操作：GOTO(x, y)：从x处走到y处。

PUSH(x, y)：把箱子从x处推倒y处。

CLIMB(x)：在x处爬上箱子。

GET(x)：在x处得到香蕉。

操作对应的条件与动作如下：GOTO(x, y)条件：AT(monkey, x)∧NOT_on(monkey, box)动作：删除：AT(monkey, x)添加：AT(monkey, y)PUSH(x, y)条件：AT(monkey, x)∧BOX(x)∧NOT_on(monkey, box)动作：删除：AT(monkey, x)∧BOX(x)添加：AT(monkey, y)∧BOX(y)CLIMB(x)条件：AT(monkey, x)∧BOX(x) ∧NOT_on(monkey, box) 动作：删除：NOT_on(monkey, box)添加：ON(monkey, box)GET(x)条件：AT(monkey, x)∧BOX(x)∧ON(monkey, box)动作：删除：EMPTY(monkey)添加：HOLD(monkey, banana)。

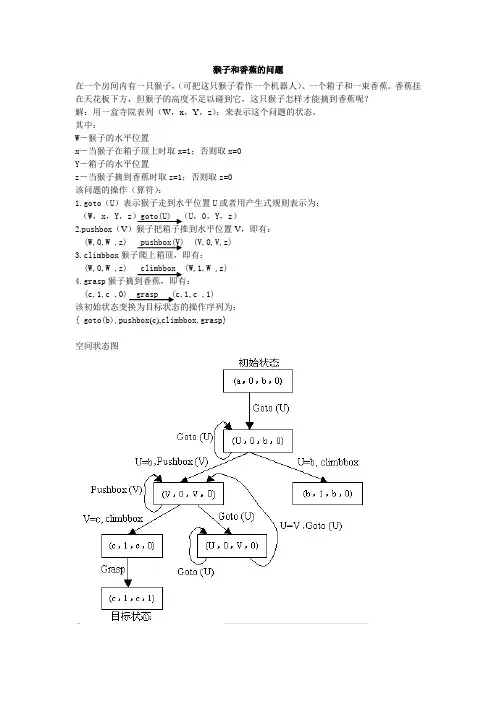
猴子和香蕉的问题在一个房间内有一只猴子，（可把这只猴子看作一个机器人）、一个箱子和一束香蕉。

香蕉挂在天花板下方，但猴子的高度不足以碰到它，这只猴子怎样才能摘到香蕉呢？解：用一盒寺院表列（W，x，Y，z）；来表示这个问题的状态，其中：W－猴子的水平位置x－当猴子在箱子顶上时取x=1；否则取x=0Y－箱子的水平位置z－当猴子摘到香蕉时取z=1；否则取z=0该问题的操作（算符）：1.goto（U）表示猴子走到水平位置U或者用产生式规则表示为：（W，x，Y，z）goto(U) （U，0，Y，z）2.pushbox（V）猴子把箱子推到水平位置V，即有：(W,0,W ,z) pushbox(V) (V,0,V,z)3.climbbox猴子爬上箱顶，即有：(W,0,W ,z) climbbox (W,1,W ,z)4.grasp猴子摘到香蕉，即有：(c,1,c ,0) grasp (c,1,c ,1)该初始状态变换为目标状态的操作序列为：{ goto(b),pushbox(c),climbbox,grasp}空间状态图问题归约法有3个柱子(1，2和3)和3个不同尺寸的圆盘（A，B和C）。

在每个圆盘的中心有一个孔，所以圆盘可以堆叠在柱子上。

最初，3个圆盘都堆在柱子1上：最大的圆盘C在底部，最小的圆盘A在顶部。

要求把所有圆盘都移到柱子3上，每次只许移动一个，而且只能先搬动柱子顶部的圆盘。

还不许把尺寸较大的圆盘堆放在尺寸较小的圆盘上。

解将上面的分析理一下顺序：就把原问题归约为3个子问题：移动A、B至柱2的双圆盘问题；（1，1，1）→（1，2，2）移动C至柱3的单元盘问题；（本原问题）（1，2，2）→（3，2，2）移动A、B至柱3的双圆盘问题。

（3，2，2）→（3，3，3）将梵塔问题归约为本原问题的问题空间2.4语义网络法用语义网络法表示下列知识：（1）更知鸟是一只鸟，（2）鸟是会飞的，（3）CLYDE是一只更知鸟；(4)CLYDE从春天到秋天只占有一个巢。

房内有一只猴子、一个箱子，天花板上挂了一串香蕉，其位置关系如图所示，猴子为了拿到香蕉，它必须把箱子推到香蕉下面，然后再爬到箱子上。

请定义必要的谓词，写出问题的初始状态（即图示的状态）、目标状态（猴子拿到了香蕉，站在箱子上，箱子位于位置b）。

定义谓词AT(x,y)：x在y位置上BOX(y)：箱子在y的位置。

OVER（x）：x被挂在天花板上EMPTY(x)：x手中是空的HOLD(x, z)：x拿着zON (x,w)：x在w的上面NOT_on (x,w) ：x在w的上面BAN(y)：香蕉在y的位置猴子的位置为: a香蕉位置为：b箱子的位置为：c问题的初始状态：AT(monkey, a)∧BOX(c)∧BAN(b)∧OVER（b）∧EMPTY(monkey)∧NOT_on (monkey, box)问题的目标状态是：AT(monkey, b)∧BOX(b)∧BAN(b)∧HOLD(monkey, banana)∧ONmonkey, box)操作：GOTO(x, y)：从x处走到y处。

PUSH(x, y)：把箱子从x处推倒y处。

CLIMB(x)：在x处爬上箱子。

GET(x)：在x处得到香蕉。

操作对应的条件与动作如下：GOTO(x, y)条件：AT(monkey, x)∧NOT_on (monkey, box)动作：删除：AT(monkey, x)添加：AT(monkey, y)PUSH(x, y)条件：AT(monkey, x)∧BOX(x)∧NOT_on (monkey, box)动作：删除：AT(monkey, x)∧BOX(x)添加：AT(monkey, y)∧BOX(y)CLIMB(x)条件：AT(monkey, x)∧BOX(x) ∧NOT_on (monkey, box) 动作：删除：NOT_on (monkey, box)添加：ON (monkey, box)GET(x)条件：AT(monkey, x)∧BOX(x)∧ON (monkey, box)动作：删除：EMPTY(monkey)添加：HOLD(monkey, banana)。

猴子吃香蕉的算法题一、基础计算类。

1. 题目。

- 一只猴子每天吃5根香蕉，现在有30根香蕉，猴子可以吃几天？- 解析。

- 这是一个简单的除法运算问题。

我们用香蕉的总数除以猴子每天吃的香蕉数，即30÷5 = 6天。

2. 题目。

- 猴子第一天吃3根香蕉，以后每天比前一天多吃2根香蕉，第5天吃多少根香蕉？- 解析。

- 这是一个等差数列的问题。

首项a_1 = 3，公差d=2。

根据等差数列通项公式a_n=a_1+(n - 1)d，当n = 5时，a_5=3+(5 - 1)×2=3 + 8 = 11根。

3. 题目。

- 有一群猴子，每只猴子吃4根香蕉，总共吃了48根香蕉，问有多少只猴子？- 解析。

- 同样是简单除法运算，用香蕉总数除以每只猴子吃的香蕉数，48÷4 = 12只猴子。

二、逻辑判断类。

4. 题目。

- 猴子吃香蕉，有大香蕉和小香蕉两种。

大香蕉一根顶2根小香蕉，猴子一天吃10根小香蕉或者5根大香蕉就饱了。

现在有3根大香蕉和8根小香蕉，问猴子能不能吃饱？- 解析。

- 首先把大香蕉换算成小香蕉，3根大香蕉相当于3×2 = 6根小香蕉，加上原有的8根小香蕉，总共是6 + 8 = 14根小香蕉。

因为猴子吃10根小香蕉就饱了，14>10，所以猴子能吃饱。

5. 题目。

- 有两种猴子，A种猴子每天吃3根香蕉，B种猴子每天吃4根香蕉。

现在有10只猴子，共吃了34根香蕉，问A种猴子和B种猴子各有几只？- 解析。

- 设A种猴子有x只，B种猴子有y只。

可以得到方程组x + y=10 3x + 4y = 34。

由第一个方程x = 10 - y，代入第二个方程得3(10 - y)+4y = 34，即30 - 3y+4y = 34，解得y = 4。

把y = 4代入x = 10 - y得x = 6。

所以A种猴子有6只，B种猴子有4只。

三、与时间相关类。

6. 题目。

- 猴子每2小时吃1根香蕉，从早上8点到晚上8点，猴子能吃多少根香蕉？- 解析。

第二章知识表示习题参考解答2.3 练习题2.1 什么是知识?它有哪些特性?有哪几种分类方法?2.2 何谓知识表示? 陈述性知识表示法与过程性知识表示法的区别是什么?2.3 在选择知识的表示方法时，应该考虑哪些主要因素?2.4 一阶谓词逻辑表示法适合于表示哪种类型的知识?它有哪些特点?2.5 请写出用一阶谓词逻辑表示法表示知识的步骤。

2.6 设有下列语句，请用相应的谓词公式把它们表示出来：（1）有的人喜欢梅花，有的人喜欢菊花，有的人既喜欢梅花又喜欢菊花。

（2）他每天下午都去玩足球。

（3）太原市的夏天既干燥又炎热。

（4）所有人都有饭吃。

（5）喜欢玩篮球的人必喜欢玩排球。

（6）要想出国留学，必须通过外语考试。

2.7 房内有一只猴子、一个箱子，天花板上挂了一串香蕉，其位置关系如图2. 11所示，猴子为了拿到香蕉，它必须把箱子推到香蕉下面，然后再爬到箱子上。

请定义必要的谓词，写出问题的初始状态（即图2.16所示的状态）、目标状态（猴子拿到了香蕉，站在箱子上，箱子位于位置b）。

图2.11 猴子摘香蕉问题2.8 对习题2.7中的猴子摘香蕉问题，利用一阶谓词逻辑表述一个行动规划，使问题从初始状态变化到目标状态。

2.9 产生式的基本形式是什么？它与谓词逻辑中的蕴含式有什么共同处及不同处？2.10 何谓产生式系统？它由哪几部分组成？2.11 产生式系统中，推理机的推理方式有哪几种？在产生式推理过程中，如果发生策略冲突，如何解决？2.12 设有下列八数码难题：在一个3×3的方框内放有8个编号的小方块，紧邻空位的小方块可以移入到空位上，通过平移小方块可将某一布局变换为另一布局（如图2.12所示）。

请用产生式规则表示移动小方块的操作。

2831231684754765S0S g图2.12 习题2.12的图图2.13 习题2.13的图2.13 推销员旅行问题：设有五个相互可直达且距离已知的城市A、B、C、D、E，如图2.13所示，推销员从城市A出发，去其它四城市各旅行一次，最后再回到城市A，请找出一条最短的旅行路线。