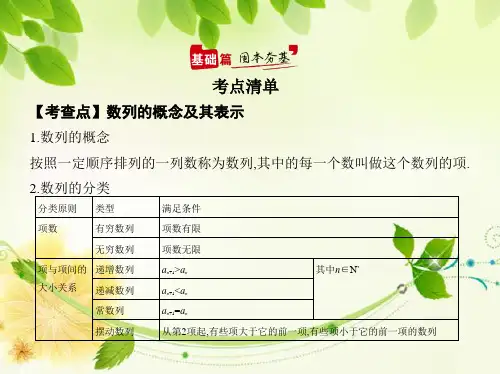
3月21日数列的基本概念修改
- 格式:ppt
- 大小:2.80 MB
- 文档页数:32

数列的概念与运算数学中,数列是由一系列按特定规律排列的数字组成的序列。
数列在数学理论与实际应用中都有着重要的地位,它常用于描述数值或事物的递增或递减规律。
本文将介绍数列的概念、分类以及常见的数列运算。
一、数列的基本概念数列是指按照一定的规律排列的一系列数字。
通常,我们用字母"a" 表示数列中的一个通项,而使用下标 "n" 来表示通项所在的位置。
例如,数列 a₁, a₂, a₃, ..., aₙ 表示数列中的第一项、第二项、第三项,依此类推。
数列可以是有限的,也可以是无限的。
有限数列是只含有有限个数字的数列,而无限数列则是包含无穷多个数字的数列。
常见的无限数列有等差数列、等比数列等。
二、常见的数列分类1. 等差数列等差数列是指数列中的每一项与其前一项之差恒定的数列。
设首项为 a₁,公差为 d,则等差数列 a₁, a₂, a₃, ..., aₙ 满足 aₙ = a₁ + (n-1)d。
其中,n 表示通项所在的位置。
等差数列可以用以下的公式来表示通项:aₙ = a₁ + (n-1)d。
例如,对于等差数列 3, 7, 11, 15, ...,其中首项 a₁ = 3,公差 d = 4,第 n 项 aₙ 可以表示为 aₙ = 3 + (n-1)4。
2. 等比数列等比数列是指数列中的每一项与其前一项之比恒定的数列。
设首项为 a₁,公比为 r,则等比数列 a₁, a₂, a₃, ..., aₙ 满足 aₙ = a₁ * r^(n-1)。
其中,n 表示通项所在的位置。
等比数列可以用以下的公式来表示通项:aₙ = a₁ * r^(n-1)。
例如,对于等比数列 2, 6, 18, 54, ...,其中首项 a₁ = 2,公比 r = 3,第 n 项 aₙ可以表示为 aₙ = 2 * 3^(n-1)。
3. 斐波那契数列斐波那契数列是一种特殊的数列,其前两项为 1,从第三项开始,每一项都是前两项之和。

数列的概念与特征数列是数学中的一个重要概念,它在各个领域中都有广泛的应用。
本文将介绍数列的概念及其特征,以帮助读者更好地理解和应用数列。
1. 数列的定义数列是一组按照一定规律排列的数字,这些数字可以是整数、实数或复数。
一般用字母a₁, a₂, a₃,..., aₙ表示数列的元素,其中a₁称为首项,aₙ称为第n项,n为数列的项数。
数列也可以用通项公式表示,即aₙ=f(n),其中f(n)是关于n的函数。
2. 数列的分类根据数列的规律和性质,可以将数列分为等差数列和等比数列两种常见类型。
2.1 等差数列等差数列是指数列中相邻两项之间的差值恒定的数列。
差值常数称为公差,用d表示。
等差数列的通项公式可以表示为aₙ=a₁+(n-1)d。
等差数列具有以下特征:- 相邻两项之间的差值恒定,即任意相邻两项之差都等于公差d。
- 每一项都可以表示为前一项与公差的和。
- 等差数列的前n项和可以通过求和公式Sn=n(a₁+aₙ)/2来计算。
2.2 等比数列等比数列是指数列中相邻两项之间的比值恒定的数列。
比值常数称为公比,用q表示。
等比数列的通项公式可以表示为aₙ=a₁q^(n-1)。
等比数列具有以下特征:- 相邻两项之间的比值恒定,即任意相邻两项之比都等于公比q。
- 每一项都可以表示为前一项与公比的乘积。
- 等比数列的前n项和可以通过求和公式Sn=a₁(q^n-1)/(q-1)来计算,其中q≠1。
3. 数列的性质除了等差数列和等比数列的特征外,数列还具有以下常见的性质:3.1 有界性如果数列的所有项都有上界M和下界m,即对于任意n,都有m≤aₙ≤M,那么称该数列是有界的。
有界的数列在数值上不会无限增大或无限减小。
3.2 单调性数列的单调性描述了数列中项的排列规律,可以分为递增和递减两种单调性。
3.2.1 递增数列当数列中的每一项都大于前一项时,则称该数列是递增的。
即对于任意n,都有a₁<a₂<...<aₙ。

数列的基本概念在数学的广袤领域中,数列如同璀璨星辰中的一串明珠,散发着独特的魅力。
对于初学者来说,理解数列的基本概念是打开这扇神奇数学之门的钥匙。
那么,究竟什么是数列呢?简单来说,数列就是按照一定顺序排列的一列数。
例如,1,3,5,7,9 就是一个数列,我们可以记作{aₙ},其中 a₁= 1,a₂= 3,a₃= 5 等等。
再比如,2,4,8,16,32 也是一个数列。
数列中的每一个数都被称为这个数列的项。
其中,排在第一位的数称为第 1 项,也叫做首项;排在第二位的数称为第 2 项,以此类推。
我们通常用下标来表示项的序号,比如第 n 项就记作 aₙ。
数列的项数可以是有限的,也可以是无限的。
项数有限的数列称为有穷数列,像 3,5,7,9 这样只有 4 个数的就是有穷数列;项数无限的数列称为无穷数列,比如自然数列 1,2,3,4,5……就是无穷数列。
数列中的数可以是整数、分数、小数,甚至可以是无理数。
比如数列√2,2√2,3√2,4√2……就是由无理数构成的。
那么数列是怎么产生的呢?在现实生活中,数列的应用无处不在。
比如银行存款的利息计算,如果每年的利率固定,那么每年的本息和就会构成一个数列;再比如,堆放的钢管数量,从上到下每层的钢管数也能构成一个数列。
数列有着不同的分类方式。
按照数列中项与项之间的大小关系,可以分为递增数列、递减数列和常数列。
递增数列就是从第 2 项起,每一项都大于它前面的一项,比如 1,2,3,4,5……;递减数列则是从第 2 项起,每一项都小于它前面的一项,例如 5,4,3,2,1;而常数列就是所有的项都相等的数列,像 3,3,3,3,3 就是一个常数列。
还有一种分类方式是按照数列的项数是奇数还是偶数来分,可以分为奇数项数列和偶数项数列。
比如数列 1,2,3,4,5 中,1,3,5 就是奇数项,2,4 就是偶数项。
理解数列,我们还需要掌握数列的通项公式。
通项公式就像是数列的“密码”,它能够让我们通过一个式子直接求出数列的任意一项。

数列的概念与性质数列,是指按照一定规律排列的一组数。
数列的概念与性质是数学中非常重要的内容之一,对于我们深入了解数学的本质和应用具有重要意义。
本文将重点介绍数列的概念以及数列的常见性质。
一、数列的概念数列是指按照一定的规律排列的一组数,数列中的每一个数称为该数列的项。
通常用字母 a,b,c,... 表示数列的项,a₁表示数列的第一项,a₂表示数列的第二项,以此类推。
数列可以是有限的,也可以是无限的。
数列的规律可以通过给出递推公式或者直接给出数列的项来表示。
递推公式是指通过前一项或前几项计算得到下一项的公式,例如斐波那契数列的规律可以表示为 aₙ=aₙ₋₁+aₙ₋₂。
直接给出数列的项可以是通过某种规律或者特征得到的,例如等差数列的项可以通过一个常数 d 与前一项的和得到。
二、数列的性质1. 通项公式:数列中的每一项都可以通过一个公式来表示,该公式称为数列的通项公式。
通项公式可以通过数列的规律或者特性来推导得到,能够用通项公式表示的数列称为解析数列。
2. 公差和公比:对于等差数列和等比数列,分别有公差和公比的概念。
等差数列是指数列的相邻两项之差都相等,该公差称为等差数列的公差。
等比数列是指数列的相邻两项之比都相等,该比值称为等比数列的公比。
3. 首项和末项:数列的第一项称为首项,最后一项称为末项。
根据数列的规律,我们可以求得数列的首项和末项。
4. 有界性:数列可以是有界的,也可以是无界的。
有界的数列是指数列的项存在上界和下界,即数列的项的取值范围是有限的;无界的数列是指数列的项没有上界或下界,即数列的项的取值范围是无限的。
5. 单调性:数列可以是单调递增的,也可以是单调递减的。
单调递增的数列是指数列的项随着项的增加而增加;单调递减的数列是指数列的项随着项的增加而减小。
6. 求和公式:对于一些特殊的数列,我们可以求得其所有项的和。
例如等差数列和等比数列都存在求和公式,可以直接计算数列的和。
7. 排列组合:数列的性质可以与排列组合问题结合,解决一些问题。

数列的概念与性质数学作为一门精确的科学,涉及到各种各样的概念与性质。
其中,数列是数学中一个重要的概念,它在许多数学问题的研究中起着重要的作用。
本文将探讨数列的概念与性质,以及与数列相关的一些定理和推论。
一、数列的概念和表示方法数列是由一系列按照一定规律排列的数所组成的集合。
数列通常用{an}表示,其中an表示数列中的第n个数。
例如,数列{1,2,3,4,5,……}是一个从1开始的自然数数列。
数列可以分为有限数列和无限数列。
有限数列是指在数列中存在最后一个数,而无限数列则没有最后一个数。
二、数列的常见性质1. 数列的有界性数列可以是有界的,也可以是无界的。
如果一个数列存在上界和下界,我们称它是有界的;如果一个数列没有上界或下界,我们称它是无界的。
例如,数列{1,2,3,4,5,……}是无界的,而数列{1,1/2,1/3,1/4,……}是有界的,因为它的上界是1,下界是0。
2. 等差数列等差数列是指数列中的相邻两项之差都相等。
我们用an = a1 + (n-1)d来表示等差数列的一般项公式,其中a1是首项,d是公差,n是项数。
例如,数列{1,3,5,7,9,……}就是一个公差为2的等差数列。
3. 等比数列等比数列是指数列中的相邻两项之比都相等。
我们用an = a1 * r^(n-1)来表示等比数列的一般项公式,其中a1是首项,r是公比,n是项数。
例如,数列{2,4,8,16,32,……}就是一个公比为2的等比数列。
三、数列的定理和推论1. 首项和公差确定等差数列如果一个数列的首项和公差确定了,那么这个数列就确定了。
换句话说,如果两个等差数列的首项和公差相同,那么它们的所有项都相等。
2. 等差数列的前n项和对于等差数列{an},它的前n项和Sn可以表示为Sn = (n/2) * (a1 + an)。
这个公式可以帮助我们快速计算等差数列的和。
3. 等比数列的前n项和对于等比数列{an},如果公比r不等于1,那么它的前n项和Sn可以表示为Sn = a1 * (1 - r^n) / (1 - r)。

数列的概念与性质数列作为数学中重要的概念之一,被广泛应用于各个领域,是数学研究和实际问题分析的基础。
在本文中,我们将介绍数列的概念与性质,并探讨其应用。
一、数列的概念数列是由一串有序的数按照一定规律排列而成的序列。
数列中的每个数称为该数列的项,用字母表示。
数列常用的表示方法有一般表示法和递推表示法。
1. 一般表示法数列的一般表示法是通过给出项的位置与对应项的数值之间的关系来定义数列。
例如,数列{1, 3, 5, 7, 9}可以表示为a1=1, a2=3, a3=5,a4=7, a5=9。
2. 递推表示法数列的递推表示法是通过给出某一项与前一项之间的关系来定义数列。
例如,数列{1, 3, 5, 7, 9}可以表示为a1=1, an=an-1+2(n≥2)。
二、数列的性质数列具有多种性质,其中包括等差数列、等比数列和斐波那契数列等。
下面我们将依次介绍这些性质。
1. 等差数列等差数列是指数列中相邻两项之间的差值都相等的数列。
设数列的首项为a1,公差为d,第n项为an,那么有如下性质:①公差:d=an-an-1;②第n项:an=a1+(n-1)d;③前n项和:Sn=n/2[2a1+(n-1)d]。
2. 等比数列等比数列是指数列中相邻两项之间的比值都相等的数列。
设数列的首项为a1,公比为q,第n项为an,那么有如下性质:①公比:q=an/an-1;②第n项:an=a1q^(n-1);③前n项和:Sn=a1(1-q^n)/(1-q)。
3. 斐波那契数列斐波那契数列是一个非常著名的数列,其定义如下:①首两项为1,1;②从第3项开始,每一项都是前两项的和。
斐波那契数列具有许多有趣的性质,如黄金分割、菲波那契数列的逼近等,在数学、自然科学等领域中有广泛的应用。
三、数列的应用数列的应用广泛,几乎涵盖了数学的各个领域。
以下是数列应用的几个典型例子。
1. 几何和几何和是数列前n项和的一种特殊情况。
当公比q不等于1时,几何和的求和公式为Sn=a1(1-q^n)/(1-q)。

数列的概念和常见数列的性质数列是数学中的一个重要概念,它是按照一定规律排列的一系列数值的集合。
本文将介绍数列的基本概念、数列的分类以及常见数列的性质。
一、数列的基本概念数列是将一系列数按照一定的次序排列而成的序列,其中每一个数称为数列的项。
数列可以用一对花括号表示,例如{a₁, a₂, a₃, ..., aₙ},其中a₁、a₂等分别为数列的前n项。
数列中每一项的下标称为项号,用n表示。
例如,a₃表示数列的第三项。
数列中的项可以是实数、整数或其他类型的数。
每一项都有确定的值,但数列本身可以是有限的,也可以是无限的。
二、数列的分类根据数列中的项与项之间的关系,常见的数列可以分为等差数列、等比数列和斐波那契数列等。
1. 等差数列等差数列是指数列中的任意两项之间的差值都相等的数列。
记作{a₁, a₂, a₃, ..., aₙ},其中每一项与前一项之间的差值都相等,差值称为公差,常用字母d表示。
即aₙ - aₙ₋₁ = d。
等差数列的通项公式为an = a₁ + (n-1)d,其中a₁为首项,n为项号。
等差数列的性质包括:公差d确定了等差数列的增减趋势;任意三项可以确定一个等差数列;等差数列的前n项和可用求和公式Sn =(n/2)(a₁ + aₙ)表示等。
2. 等比数列等比数列是指数列中的任意两项之间的比值都相等的数列。
记作{a₁, a₂, a₃, ..., aₙ},其中每一项与前一项之间的比值都相等,比值称为公比,常用字母q表示。
即aₙ / aₙ₋₁ = q。
等比数列的通项公式为an = a₁ * q^(n-1),其中a₁为首项,n为项号。
等比数列的性质包括:公比q确定了等比数列的增减趋势;任意三项可以确定一个等比数列;等比数列的前n项和可用求和公式Sn = a₁* (q^n - 1) / (q - 1)表示。
3. 斐波那契数列斐波那契数列是指从第3项开始,每一项都等于前两项之和的数列。
记作{a₁, a₂, a₃, ..., aₙ},其中a₃ = a₁ + a₂。

数列的概念与运算知识点总结数列是数学中常见的概念,它是由一系列按照特定规律排列的数所组成。
在数列的运算中,我们常常会涉及到一些重要的知识点和技巧。
本文将对数列的概念和运算知识点进行总结,并介绍一些应用技巧。
以下是数列的概念和运算知识点总结。
一、等差数列等差数列是指数列中相邻两项之间的差数值相等的数列。
其中,公差是指等差数列中相邻两项的差值。
对于等差数列,我们常涉及以下知识点:1.1 等差数列的通项公式等差数列的通项公式可以用来计算等差数列中任意一项的数值。
通项公式为an = a1 + (n - 1)d,其中an表示第n项的数值,a1表示首项的数值,d表示公差。
1.2 等差数列的前n项和公式等差数列的前n项和公式可以用来计算等差数列前n项数值的总和。
前n项和公式为Sn = n/2 * (a1 + an),其中Sn表示前n项数值的总和。
二、等比数列等比数列是指数列中相邻两项之间的比值相等的数列。
其中,公比是指等比数列中相邻两项的比值。
对于等比数列,我们常涉及以下知识点:2.1 等比数列的通项公式等比数列的通项公式可以用来计算等比数列中任意一项的数值。
通项公式为an = a1 * r^(n - 1),其中an表示第n项的数值,a1表示首项的数值,r表示公比。
2.2 等比数列的前n项和公式等比数列的前n项和公式可以用来计算等比数列前n项数值的总和。
前n项和公式为Sn = a1 * (r^n - 1) / (r - 1),其中Sn表示前n项数值的总和。
三、递推数列递推数列是一种特殊的数列,它的每一项都是通过前一项经过特定的运算得出的。
对于递推数列,我们常涉及以下知识点:3.1 递推数列的递推公式递推数列的递推公式描述了数列中每一项与前一项之间的关系。
通过递推公式,我们可以计算数列中从第2项开始的每一项数值。
四、数列的求和运算在数列的运算中,求和是一种常见的操作。
对于等差数列和等比数列,我们已经介绍了前n项和的公式。

1、计算19+199+1999+19999+1999992、四根长都是8厘米的绳子,把它们打结连在一起,成为一根长绳,打结处每根绳用去1厘米,绳结长度不计,现在这根长绳长多少厘米?解答:1、19+199+1999+19999+199999=(20+200+2000+20000+200000)-(1+1+1+1+1)=222220-5=2222152、分析:因为第一根和第四根只有一头打结,第二根和第三根有两头打结,所以一共要用去6个1厘米。
4x8-6=26(厘米)答:现在这根长绳长26厘米.三年级奥数3月22日一题(差倍问题)1.两堆煤重量相等,现从甲堆运走24吨煤,乙堆又运入8吨,这时乙堆煤的重量是甲堆的3倍,问两堆煤原来各有多少吨煤?解析:原来两堆重量相等,甲运走24吨煤,乙堆又运入8吨,可以得出现在乙堆比甲堆多了24+8=32(吨);这时乙堆煤的重量是甲堆的3倍,可以得出乙堆比甲堆多出2份,也就是说多出2份就多了32吨,因此一份就是32÷2=16(吨),现在的甲堆就有16吨,原来的甲堆有16+24=40(吨),乙堆就有40吨。
三年级奥数3月23日二题(重叠问题)1、张老师出了两道题,做对第一题的有13人,做对第二题的有22人,两道题都做对的有8人,每人至少都做对一题,这个班一共有多少人?2、有两块一样长的木板,钉在一起,如果每块木板长25厘米,中间钉在一起的长5厘米,现在长木板有多长?解析:1、两道题都做对的有8人,说明这8人既做对了第一题也做对了第二题,每人至少都做对一题,因此全班有13+22-8=27(人)。
2、中间钉在一起的长5厘米,因此两块木板的分别有5厘米重叠,最终重叠部分是5厘米,所以现在的木板长度是25+25-5=45(厘米)。
三年级奥数3月24日一题(和倍问题)1、甲、乙一共有144本书,如果乙再给甲50本,那么甲是乙的3倍,那么甲原有多少本?解析:1、已知两个数的和,又知道乙给了甲50本就有倍数关系,分析得出这道题是和倍关系的应用题,乙给甲以后,甲是3份数,乙是1份数,和起来是4份数,4份的和是144本,所以求1份就要用144÷4=36(本),现在乙就是36本,原来乙有36+50=86(本),原来甲有144-86=58(本)。

高三数学数列基本知识点数列是高中数学中的重要概念之一,对于数学的学习和应用有着重要的意义。
本文将介绍高三数学数列的基本知识点,包括数列的定义、等差数列、等比数列以及数列的通项公式和求和公式等内容。
一、数列的定义数列是按照一定顺序排列的一组数。
数列中的每一个数称为数列的项,用a1, a2, a3, ...表示。
数列可以是有限的,也可以是无限的。
有限数列是指数列中的项是有限个数,而无限数列是指数列中的项是无穷个数。
二、等差数列等差数列是指数列中的相邻两项之差都相等的数列。
设等差数列的首项为a1,公差为d,则等差数列的通项公式为:an = a1 + (n-1)d,其中n表示项数。
等差数列的前n项和公式为:Sn = (a1 + an) * n / 2。
三、等比数列等比数列是指数列中的相邻两项之比都相等的数列。
设等比数列的首项为a1,公比为q,则等比数列的通项公式为:an = a1 *q^(n-1),其中n表示项数。
等比数列的前n项和公式为:Sn = a1 * (1 - q^n) / (1 - q)。
四、数列的变形与思维拓展数列的变形是数学中常见的一个方法。
通过对数列的变形,可以获得更多有用的信息,用于解决各种数学问题。
在高三数学中,数列的变形与思维拓展是培养学生数学思维能力的重要环节,也是高考中常见的考查点。
五、应用题数列在现实生活和数学领域有着广泛的应用。
应用题是数列知识的重要应用形式,涵盖了等差数列和等比数列的基本知识点,同时融入了其他数学知识和解题思路。
通过解答应用题,可以巩固数列的基本知识,并且培养学生的问题解决能力。
六、综合题综合题是数列知识运用的综合性考察形式。
综合题通常结合了多个数列知识点,并且需要学生根据题目的要求进行综合分析和计算。
综合题在高考数学试卷中常见,要求学生善于运用数列知识解答综合性问题。
七、总结数列作为高中数学中的重要知识点,掌握数列的基本概念和运算法则,对于学生的学习和应用数学都有着重要的意义。
数列概念知识点归纳总结数列是数学中常见的一个概念,它在许多领域中都有广泛的应用。
本文将对数列的概念进行归纳总结,并探讨一些相关的知识点。
一、数列的定义及表示法数列是一系列有序的数按一定规律排列而成的集合。
通常用大写字母A、B、C等表示数列,用小写字母a1、a2、a3等表示数列中的元素。
数列可以分为等差数列和等比数列两类。
等差数列中的每个相邻元素之差相等,而等比数列中的每个相邻元素之比相等。
以等差数列为例,其通项公式为an=a1+(n-1)d,其中a1表示首项,d表示公差。
二、数列的求和公式在数列中,我们有时需要计算其中一段连续元素的和。
此时可以使用数列的求和公式来计算,具体公式如下:1. 等差数列的求和公式对于等差数列an=a1+(n-1)d的前n项和Sn,其求和公式为Sn=n/2[a1+an]。
2. 等比数列的求和公式对于等比数列an=a1*r^(n-1)的前n项和Sn(其中r为公比),其求和公式为Sn=a1*(1-r^n)/(1-r)。
三、常见数列的性质和特点1. 斐波那契数列斐波那契数列是一个非常特殊的数列,其前两个元素为1,从第三项开始,每一项都等于前两项之和。
斐波那契数列的通项公式为an=F(n-1)+F(n-2),其中F(n)表示第n个斐波那契数。
2. 等差数列的性质等差数列具有以下性质:- 任意两项的平均数等于它们的中项。
- 等差数列的倒数也是等差数列。
- 等差数列的前n项和与后n项和相等。
3. 等比数列的性质等比数列具有以下性质:- 等比数列的任意一项都不为零。
- 等比数列的倒数也是等比数列。
- 等比数列的前n项和与后n项和之比为公比的n次方减1除以公比减1。
四、数列的应用数列在数学中有广泛的应用,以下列举几个常见的应用场景:1. 财务管理利润、收入、支出等财务数据可以构成数列。
通过对数列的研究,可以分析财务情况的变化趋势,对财务决策提供参考。
2. 自然科学自然界中的很多现象都可以用数列来描述,比如物种数量的增长、天体运动的规律等。
数列的概念与性质数学中,数列是指按照一定规律排列的数字的序列。
在数学中,数列有着重要的应用,它不仅在代数学中有广泛的应用,还在分析学、概率论以及其他许多领域中起着重要的作用。
本文将介绍数列的概念、性质以及数列的应用。
一、数列的概念数列是由一组数字按照一定的规律排列形成的序列。
通常用字母表示数列,如a,b,c...或者用希腊字母表示,如α,β,γ...数列的每一项用a₁,a₂,a₃...表示,其中a₁表示第一项,a₂表示第二项,以此类推。
二、数列的性质1. 数列的通项公式:数列中的每一项都可以通过一个公式来表示,这个公式被称为数列的通项公式。
通项公式可以帮助我们计算数列中任意一项的值。
2. 等差数列:如果一个数列中任意两项之间的差值都相等,那么这个数列就是等差数列。
等差数列的通项公式为aₙ = a₁ + (n - 1)d,其中aₙ表示第n项,a₁表示第一项,d表示公差。
3. 等比数列:如果一个数列中任意两项之间的比值都相等,那么这个数列就是等比数列。
等比数列的通项公式为aₙ = a₁ * r^(n - 1),其中aₙ表示第n项,a₁表示第一项,r表示公比。
4. 递推关系:数列中后一项的值与前一项的值之间的关系被称为递推关系。
递推关系可以帮助我们根据前一项的值计算出后一项的值。
5. 数列的极限:数列中的项随着索引的增加,可能会趋向于一个固定的值,这个固定的值被称为数列的极限。
极限的概念在数学中有着重要的应用,比如在微积分中。
三、数列的应用1. 数列在代数学中广泛应用。
例如,等差数列和等比数列的性质可以用于解决各种代数问题,如求和、计算某一项的值等等。
2. 数列在几何学中也有重要的应用。
例如,斐波那契数列是一个非常经典的数列,在几何问题中也有广泛的应用。
3. 数列也有着重要的物理应用。
例如,匀速直线运动物体的位移和时间之间就可以用等差数列来描述,其他许多物理问题也可以通过数列的概念和性质来解决。
总结:数列是数学中重要的概念之一,它有着广泛的应用。
新高考数列知识点归纳总结数列是高中数学中非常重要的一个概念,它在新高考中也是必考的内容之一。
掌握数列的相关知识,对于学生的数学成绩提升有着重要的作用。
本文将对新高考数列的知识点进行归纳总结,以帮助学生更好地复习和应对考试。
一、数列的基本概念1. 数列的定义:数列是由一串按照一定规律排列的数所组成的有序集合。
2. 通项公式:数列中的每一项都可以用一个公式来表示,这个公式称为通项公式。
3. 首项和公差:数列中的第一项称为首项,相邻两项之间的差称为公差。
二、等差数列1. 等差数列的概念:如果一个数列从第二项开始,每一项与前一项的差都相等,那么这个数列就是等差数列。
2. 等差数列的通项公式:设等差数列的首项为a₁,公差为d,则第n项的通项公式为an=a₁+(n-1)d。
3. 等差数列的前n项和:设等差数列的首项为a₁,末项为an,共有n项,前n项和的公式为Sn=(a₁+an)n/2。
三、等比数列1. 等比数列的概念:如果一个数列从第二项开始,每一项与前一项的比值都相等,那么这个数列就是等比数列。
2. 等比数列的通项公式:设等比数列的首项为a₁,公比为q,则第n项的通项公式为an=a₁q^(n-1)。
3. 等比数列的前n项和:设等比数列的首项为a₁,公比为q,共有n项,前n项和的公式为Sn=a₁(q^n-1)/(q-1)。
四、特殊数列1. 斐波那契数列:斐波那契数列是一个特殊的数列,它的前两项是1,从第三项开始,每一项都等于前两项之和。
2. 等差-等差数列:等差-等差数列是指每一个项都是一个等差数列的首项,同时这些等差数列的公差也构成一个等差数列。
例如:2, 5, 8, 11, 14, ...五、数列的应用1. 数列在数学中的应用非常广泛,特别是在数学建模和数学推理方面有着重要作用。
2. 数列可以用来描述各种数量的变化规律,如人口增长、销售额增加等等。
3. 通过数列的求和公式,可以计算出各种数量的累加值,如等差数列前n项和、等比数列前n项和等。
数列的概念和性质数列是数学中一个重要的概念,它是由一系列按照一定规律排列的数字所组成的。
数列可以用来描述自然界中的很多现象,比如光的干涉、声音的频率等等。
在数学中,数列有着丰富的性质和应用,下面我们来探讨一下数列的概念和性质。
首先,我们来了解一下数列的基本概念。
数列是由一系列按照一定规律排列的数字所组成的。
这些数字可以是整数、小数或者分数,它们之间的关系可以用一个通项公式来表示。
通项公式是数列中的每一项与项号之间的关系式,通过它我们可以求出数列中的任意一项。
数列的性质包括有界性、单调性和收敛性等等。
首先,有界性指的是数列中的所有项都在一定的范围内。
数列可以是有上界和下界的,也可以是有上界或下界的。
例如,数列{1, 2, 3, 4, ...}就是一个没有上界的数列,而数列{1, 1/2, 1/3, 1/4, ...}则是一个有下界但没有上界的数列。
其次,单调性是指数列中的项按照一定的规律递增或递减。
数列可以是递增的,也可以是递减的。
递增数列是指数列中的每一项都比前一项大,而递减数列则是指数列中的每一项都比前一项小。
例如,数列{1, 2, 3, 4, ...}就是一个递增数列,而数列{3, 2, 1, 0, ...}则是一个递减数列。
最后,收敛性是指数列中的项随着项号的增加趋于一个固定的值。
数列可以是收敛的,也可以是发散的。
收敛数列是指数列中的项随着项号的增加逐渐趋于某个数,而发散数列则是指数列中的项随着项号的增加趋于无穷大或无穷小。
例如,数列{1, 1/2, 1/3, 1/4, ...}就是一个收敛数列,它的项随着项号的增加趋于0,而数列{1, 2, 3, 4, ...}则是一个发散数列,它的项随着项号的增加趋于无穷大。
除了上述性质外,数列还有许多其他的性质和应用。
例如,数列可以用来求和,即将数列中的所有项相加得到一个和。
这在计算中经常用到。
另外,数列还可以用来表示函数的图像,通过观察数列的性质可以得到函数的一些特征。
数列的基本定义数列是一系列按照特定规律排列的数的集合。
它由一串数字组成,其中每个数字称为序列的项。
数列的基本定义如下:1.项 (Term):数列中的每个数字称为项。
通常使用字母 a、b、c 等表示数列的项。
第 n 项表示数列中的第 n 个数字,通常表示为aₙ。
2.通项公式 (General Term Formula):数列中每一项与它的位置之间的关系由通项公式来表示。
通项公式描述了数列中任意项与其位置之间的对应关系。
通项公式通常使用 n 表示项的位置,例如aₙ = f(n) 表示数列中第 n 项的值由函数 f(n) 决定。
3.项数 (Number of Terms):数列中的项数指的是数列中的项的总个数。
项数通常使用字母 n 表示。
4.公差 (Common Difference):在等差数列中,项与项之间的差值保持恒定,这个差值称为公差。
公差通常用字母 d 表示。
5.公比 (Common Ratio):在等比数列中,相邻项之间的比例保持恒定,这个比例称为公比。
公比通常用字母 r 表示。
6.有界数列 (Bounded Sequence):如果数列的项有一个上界或下界,即存在一个常数 M,使得对于所有的 n,aₙ≤ M 或 aₙ≥M,则称该数列是有界数列。
7.递增数列 (Increasing Sequence):如果数列的每一项都大于前一项,即对于所有的 n,aₙ < aₙₙₙ,则称该数列是递增数列。
8.递减数列 (Decreasing Sequence):如果数列的每一项都小于前一项,即对于所有的 n,aₙ > aₙₙₙ,则称该数列是递减数列。
这些基本定义提供了描述和理解数列的基础概念,数列的规律和特性可以通过这些定义来进行研究和分析。
理解数列的基本概念与性质数列是数学中一种重要的数学概念,广泛应用于数学、物理、工程等领域。
对于数列的概念和性质的理解,不仅有助于我们解决实际问题,还可以提高我们的思维能力和逻辑推理能力。
本文将从数列的定义、常见数列的性质以及数列应用等方面来深入理解数列的基本概念与性质。
一、数列的定义数列是一组按照一定规律排列的数的集合。
数列通常用大写字母表示,如{a1, a2, a3, ...},其中ai表示数列中的第i项。
数列可以是有限的,也可以是无限的。
其中有限数列是指数列中的项数有限,无限数列是指数列中的项数无限。
例如,{1, 2, 3, 4, 5}是一个有限数列;{1, 4, 9, 16, ...}是一个无限数列,其中的每一项都是前一项的平方。
二、常见数列的性质1. 等差数列等差数列是指数列中的相邻两项之差保持不变的数列。
设等差数列的首项为a1,公差为d,第n项为an,则等差数列的通项公式为an = a1 + (n-1)d。
例如,{1, 3, 5, 7, 9}就是一个等差数列,首项为1,公差为2。
等差数列的性质有:相邻两项之差是一个常数,任意三项成等差数列,等差数列的和等于首项与末项的和乘以项数的一半。
2. 等比数列等比数列是指数列中的相邻两项之比保持不变的数列。
设等比数列的首项为a1,公比为q,第n项为an,则等比数列的通项公式为an = a1 * q^(n-1)。
例如,{2, 6, 18, 54, ...}就是一个等比数列,首项为2,公比为3。
等比数列的性质有:相邻两项之比是一个常数,任意三项成等比数列,等比数列的和等于首项与末项的差除以公比减一。
3. 斐波那契数列斐波那契数列是指数列中的每一项都是前两项之和的数列。
斐波那契数列的前两项通常定义为1,1或0,1,后续项依次为前两项之和。
例如,{1, 1, 2, 3, 5, 8, ...}就是一个斐波那契数列。
斐波那契数列的性质有:相邻两项之比趋近于黄金分割比例,即约为1.618,相邻两项之商趋近于黄金分割比例的平方。