旋转综合题

则∠ AFG=90°. ∵ ∠ ABH=∠ G=60°，AB=a，AG=2a，
∴ AH=AB×sin60°= 3 a，AF=AG×sin60°= 3 a. 2
∴ 点 F 到 BC 的最大距离为 3 a+ 3 a= 3 3 a. 22
∴ S△ BCF= 1 ×2a× 3 3 a= 3 3 a2.
2
22
PC=
=6．
考点：1.扇形面积的计算；2.正方形的性质；3.旋转的性质．
3．如图 1， ABCD 和 AEFG 是两个能完全重合的平行四边形，现从 AB 与 AE 重合时开 始，将 ABCD 固定不动， AEFG 绕点 A 逆时针旋转，旋转角为 α（0°＜α＜360°）， AB=a,BC=2a；并发现：如图 2，当 AEFG 旋转到点 E 落在 AD 上时，FE 的延长线恰好通过 点 C．
（2）根据面积公式得出 S△ GHK=S 四边形 CKGH-S△ CKH= 1 x2-3x+9，根据△ GKH 的面积恰好等于 2
△
ABC 面积的
5
，代入得出方程 1
x2-3x+9=
5
1
×
×6×6，求出即可．
12
2
12 2
解：（1）BH 与 CK 的数量关系：BH=CK，理由是：
连接 OC，
由直角三角形斜边上中线性质得出 OC=BG， ∵ AC=BC，O 为 AB 中点，∠ ACB=90°， ∴ ∠ B=∠ ACG=45°，CO⊥AB， ∴ ∠ CGB=90°=∠ KGH， ∴ 都减去∠ CGH 得：∠ BGH=∠ CGK， 在△ CGK 和△ BGH 中
∴
1
x2﹣3x+9=
5
1
×

图形的旋转练习题一、选择题1. 一个图形绕某点旋转90度后，其形状和大小：A. 发生变化B. 不发生变化C. 无法确定D. 形状不变，大小变小2. 如果一个图形绕其对称中心旋转180度，其位置：A. 不变B. 改变C. 无法确定D. 形状改变3. 一个正方形绕其中心点旋转45度后，其：A. 形状和位置都不变B. 形状不变，位置改变C. 形状改变，位置不变D. 形状和位置都改变4. 一个等边三角形绕其一个顶点旋转120度后，其：A. 形状和位置都不变B. 形状不变，位置改变C. 形状改变，位置不变D. 形状和位置都改变5. 一个圆绕其圆心旋转任意角度后，其：A. 形状和位置都不变B. 形状不变，位置改变C. 形状改变，位置不变D. 形状和位置都改变二、填空题6. 一个图形绕某点旋转______度后，其形状和位置都不变。

7. 如果一个图形绕其对称中心旋转______度，其位置不变。

8. 一个图形绕某点旋转180度后，其形状______，位置______。

9. 一个图形绕某点旋转90度后，其形状______，位置______。

10. 一个图形绕其对称中心旋转任意角度后，其形状______，位置______。

三、简答题11. 描述一个正方形绕其中心点顺时针旋转90度后，其四个顶点的新位置。

12. 解释为什么一个圆在绕其圆心旋转任意角度后，其形状和位置都不变。

13. 如果一个正六边形绕其中心点旋转60度，描述其顶点的新位置。

14. 一个矩形绕其对角线中点旋转180度后，其四个顶点的新位置是什么？15. 解释为什么一个图形绕其对称中心旋转180度后，其位置不变。

四、应用题16. 一个时钟的时针在12小时内绕钟面中心点旋转了多少度？17. 如果一个图形被设计为可以围绕其对称中心旋转，那么在旋转过程中，它的对称性如何保持？18. 一个图形绕其一个顶点旋转，如果旋转角度是360度的整数倍，图形的最终位置是什么？19. 在一个平面直角坐标系中，一个点绕原点旋转θ度后，其新的坐标如何计算？20. 如果一个图形绕其对称中心旋转了θ度，那么它的对称轴会如何变化？五、综合题21. 给出一个图形的旋转矩阵，并说明如何使用它来计算图形绕某点旋转后的新位置。

人教版九年级数学上册第二十三章《旋转》综合测试卷（含答案）班级 座号 姓名 成绩一、选择题（每小题4分，共40分）1. 在平面内，将一个图形绕一个定点沿某个方向转动一个角度，这样的图形运动称为旋转．下列图形中不能由一个图形通过旋转而构成的是( )A. B . C. D.2.将左图按顺时针方向旋转90°后得到的是( )3.在平面直角坐标系中，点.(4,3)A -关于原点对称点的坐标为（ ） A. .(4,3)A --B. .(4,3)A -C. .(4,3)A -D. .(4,3)A4.将△AOB 绕点O 旋转180°得到△DOE ，则下列作图正确的是（ ）A. B. C. D.5.如图，将三角尺ABC （其中∠ABC=60°，∠C=90°）绕B 点按顺时针方向转动一个角度到A 1BC 1的位置，使得点A ，B ，C 1在同一条直线上，那么这个角度等于（ ） A 、120° B 、90° C 、60° D 、30°6.将如图所示的正五角星绕其中心旋转，要使旋转后与它自身重合，则至少应旋转（ ）．A ．36°B ．60°C ．72°D ．180°7.若点A 的坐标为（6，3），O 为坐标原点，将OA 绕点O 按顺时针方向旋转90°得到OA′，则点A′的坐标是（ ）A 、（3，﹣6）B 、（﹣3，6）C 、（﹣3，﹣6）D 、（3，6） 8. 如图，将△ABC 绕点C 顺时针旋转90°得到△EDC ．若点A ，D ，E 在同一条直线上，∠ACB=20°，则∠ADC 的度数是（ ） A ．55° B ．60° C ．65° D ．70°9.如图，在正方形ABCD 中有一点P ，把⊿ABP 绕点B 旋转到⊿CQB ，连接PQ ，则⊿PBQ 的形状是（ ）A. 等边三角形B. 等腰三角形C.直角三角形D.等腰直角三角形10. 如图，设P 到等边三角形ABC 两顶点A 、B 的距离分别 为2、3，则PC 所能达到的最大值为（ ）A ．5B ．13C ．5D ．6 二、填空题(每题4分，共24分）11.如图，将ABC △绕点A 顺时针旋转60︒得到AED △， 若线段3AB =，则BE = .12.如图，将Rt △ABC 绕直角顶点C 顺时针旋转90°，得到△A ′B ′C ， 连接BB'，若∠A′B′B =20°，则∠A 的度数是 ．13将点A （-3，2）绕原点O 逆时针旋转90°到点B ，则点B 的坐标为 . 14.若点(2,2)M a -与(2,)N a -关于原点对称，则______．15.在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形，涂黑的小正方形的序号是_________16.如图，在平面直角坐标系中，已知点A （-3，0），B （0，4），对△AOB 连续作旋转变换，依次得到三角形①，②，③，…，那么第⑤个三角形离原点O 最远距离的坐标是(21,0),第2020个三角形离原点O 最远距离的坐标是 .•第5题图第6题图第8题图第9题图第16题图第15题图第12题图第10题图第11题图三、解答题（共86）17.在平面直角坐标系中，已知点A（4，1），B（2，0），C（3，1）．请在如图的坐标系上上画出△ABC，并画出与△ABC关于原点O对称的图形.18.如图，已知△ABC的顶点A、B、C的坐标分别是A（-1，-1），B（-4，-3），C（-4，-1）．C1；（1）作出△ABC关于原点O的中心对称图形△A1B1（2）将△ABC绕原点O按顺时针方向旋转90°后得到△A2B2C2，画出△A2B2C2；19.如图，在等边△ABC中，点D是AB边上一点，连接CD，将线段CD绕点C按顺时针方向旋转60°后得到CE，连接AE．求证：AE∥BC．20.如图，△ABC中，AD是中线．（1）画出将△ACD关于点D成中心对称的△EBD（2）如果AB=7，AC=5，若中线AD长为整数，求AD的最大值21.如图甲，在Rt△ACB中，四边形DECF是正方形．（1）将△AED绕点按逆时针方向旋转°，可变换成图乙，此时∠A1DB的度数是°．（2）若AD=3，BD=4，求△ADE与△BDF的面积之和．22.如图，点O是等腰直角三角形ABC内一点，∠ACB=90°，∠AOB=140°，∠AOC=α．将△AOC绕直角顶点C按顺时针方向旋转90°得△BDC，连接OD．（1）试说明△COD是等腰直角三角形；（2）当α=95°时，试判断△BOD的形状，并说明理由．23.已知△ABC中，△ACB=135°，将△ABC绕点A顺时针旋转90°，得到△AED，连接CD，CE．（1）求证：△ACD为等腰直角三角形；（2）若BC=1，AC=2，求四边形ACED的面积．24.建立模型：(1)如图 1,已知△ABC,AC=BC,△C=90△,顶点C 在直线 l 上。

图形的旋转综合练习题图形的旋转是数学几何中的一个基本概念，也是应用广泛的技巧。

在解决旋转相关问题时，我们需要运用一定的技巧和方法，同时结合形象的思维和逻辑推理，让我们一起来看几个有趣的综合练习题，锻炼我们的观察能力和解决问题的能力。

练习题1：将一个正方形沿顺时针方向旋转90度，得到一个新的图形。

问：这个新图形和原始图形有什么不同？解析：旋转正方形90度后，得到的新图形仍然是一个正方形。

不同之处在于，新图形的边和原图形的边相比，方向发生了改变。

例如，原图形中的顶边变为新图形中的右边，右边变为底边，底边变为左边，左边变为顶边。

由此可见，旋转会改变图形边的位置和方向，但不会改变图形的形状。

练习题2：将一个长方形沿逆时针方向旋转180度，得到一个新的图形。

问：这个新图形和原始图形有什么相同之处？解析：旋转长方形180度后，得到的新图形仍然是一个长方形。

相同之处在于，新图形的边和原图形的边长度相同。

长方形的性质决定了旋转不会改变边的长度，只会改变边的位置和方向。

因此，旋转180度后得到的新图形依然保持长方形的长宽比。

练习题3：将一个菱形沿顺时针方向旋转270度，得到一个新的图形。

问：这个新图形与原始图形有什么关系？解析：旋转菱形270度后，得到的新图形依然是一个菱形。

关系之处在于，新图形与原图形的四个顶点仍然在一条直线上，只是位置和方向发生了改变。

旋转后，原本位于菱形内部的顶点变为新图形外部的顶点，而原来的外部顶点变为内部顶点。

这个变化过程中，菱形的形状保持不变，只是位置和方向发生了变化。

练习题4：将一个正三角形沿逆时针方向旋转120度，得到一个新的图形。

问：这个新图形与原始图形有什么共同之处？解析：旋转正三角形120度后，得到的新图形仍然是一个正三角形。

共同之处在于，新图形的三个角度和原图形的三个角度相等。

正三角形的性质决定了旋转不会改变角度的大小，旋转只会改变角度的位置和方向。

因此，旋转后得到的新图形依然保持正三角形的每个内角都为60度。

初三旋转测试题卷子及答案一、选择题（每题3分，共15分）1. 一个点绕原点旋转90度后，其坐标变为原来的什么？A. 相反数B. 倒数C. 两倍D. 四倍2. 一个图形绕某点旋转180度后，与原图形的关系是？A. 完全重合B. 完全相反C. 部分重合D. 没有关系3. 一个图形绕某点旋转60度后，其面积和周长会如何变化？A. 面积不变，周长不变B. 面积变小，周长变小C. 面积不变，周长变长D. 面积变小，周长变大4. 一个图形绕其对称轴旋转180度后，图形的位置会如何变化？A. 完全重合B. 完全相反C. 部分重合D. 没有变化5. 如果一个图形绕某点旋转了θ度，那么它的旋转矩阵是什么？A. [cosθ -sinθ; sinθ cosθ]B. [cosθ sinθ; -sinθ cosθ]C. [sinθ cosθ; cosθ -sinθ]D. [sinθ -sinθ; cosθ cosθ]二、填空题（每题2分，共10分）6. 一个点P(x, y)绕原点旋转θ度后，其新坐标为_________。

7. 若一个图形绕点(a, b)旋转θ度，其旋转后的图形与原图形的对应点坐标变化关系为_________。

8. 一个正方形绕其中心点旋转45度后，其四个顶点的坐标变化情况是_________。

9. 一个圆绕其圆心旋转任意角度，其形状和大小_________。

10. 旋转矩阵可以表示为_________，其中θ为旋转角度。

三、解答题（每题5分，共20分）11. 给定一个点P(1, 2)，求该点绕原点旋转120度后的坐标。

12. 一个矩形ABCD，其中A(-1, 1)，B(1, 1)，C(1, -1)，D(-1, -1)，求该矩形绕点A旋转90度后的顶点坐标。

13. 描述一个正方形绕其对称轴旋转90度后，四个顶点的坐标变化情况。

14. 解释旋转矩阵在图形旋转变换中的作用。

四、综合题（每题5分，共10分）15. 一个正六边形绕其中心点旋转60度后，求其顶点坐标的变化。

初三旋转考试题及答案初三数学旋转考试题及答案一、选择题（每题3分，共15分）1. 在平面直角坐标系中，点P(3,4)绕原点O逆时针旋转90°后，新坐标为：A. (4,3)B. (-3,4)C. (3,-4)D. (4,-3)2. 一个正方形绕其中心点旋转45°后，其边长不变，面积不变，以下说法正确的是：A. 形状不变B. 形状改变C. 面积改变D. 形状和面积都改变3. 一个圆心在原点的圆，半径为r，绕原点旋转任意角度后，其半径：A. 变大B. 不变C. 变小D. 无法确定4. 若点A(1,2)绕点B(2,3)旋转30°，旋转后的点A'坐标为：A. (1.5, 3.5)B. (1.5, 2.5)C. (2.5, 3.5)D. 无法确定5. 一个等腰直角三角形绕其直角顶点旋转90°后，其形状：A. 不变B. 变为等边三角形C. 变为等腰三角形D. 变为直角三角形二、填空题（每题2分，共10分）6. 一个矩形绕其中心点旋转180°后，其形状________。

7. 点P(2,-1)绕原点O逆时针旋转45°后，新坐标的横坐标为________。

8. 若一个圆绕其圆心旋转任意角度，其周长________。

9. 一个平行四边形绕其对角线交点旋转90°后，其形状变为________。

10. 一个等边三角形绕其一边的中点旋转60°，旋转后的图形与原图形________。

三、解答题（共25分）11. （5分）若点M(-1,1)绕点N(1,1)旋转60°，求点M'的坐标。

12. （10分）一个边长为4的正方形ABCD，以点A为旋转中心，逆时针旋转30°，求旋转后正方形A'B'C'D'的顶点坐标。

13. （10分）一个圆心在原点，半径为5的圆，绕原点旋转60°，求旋转后圆上任意一点P(x,y)的新坐标。

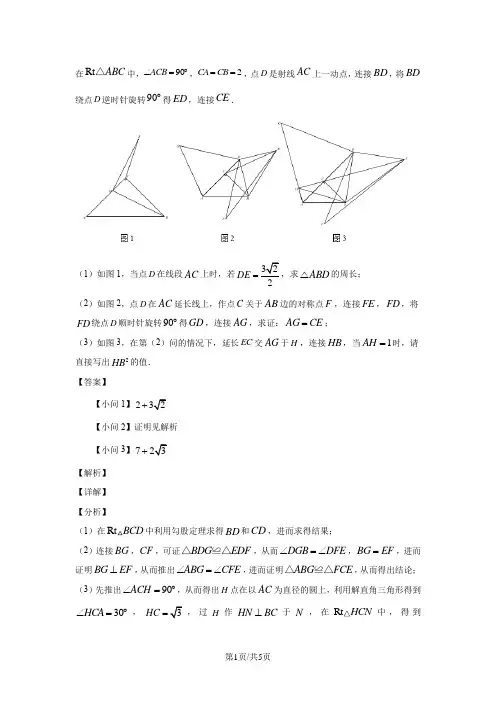
在Rt ABC △中，90ACB ∠=︒，2CA CB ==，点D 是射线AC 上一动点，连接BD ，将BD 绕点D 逆时针旋转90︒得ED ，连接CE ．（1）如图1，当点D 在线段AC 上时，若DE =ABD △的周长； （2）如图2，点D 在AC 延长线上，作点C 关于AB 边的对称点F ，连接FE ，FD ，将FD 绕点D 顺时针旋转90︒得GD ，连接AG ，求证：AG CE =；（3）如图3，在第（2）问的情况下，延长EC 交AG 于H ，连接HB ，当1AH =时，请直接写出2HB 的值．【答案】【小问1】2+【小问2】证明见解析【小问3】7+【解析】【详解】【分析】（1）在Rt BCD 中利用勾股定理求得BD 和CD ，进而求得结果；（2）连接BG ，CF ，可证BDG EDF △≌△，从而DGB DFE ∠=∠，BG EF =，进而证明BG EF ⊥，从而推出ABG CFE ∠=∠，进而证明ABG FCE △≌△，从而得出结论； （3）先推出90ACH ∠=︒，从而得出H 点在以AC 为直径的圆上，利用解直角三角形得到30HCA ∠=︒，HC =，过H 作HN BC ⊥于N ，在Rt HCN 中，得到32CN HN ==，进而2BN BC CN =+=+，在Rt HCN 中，利用勾股定理得到2227H B N N H B =+=+【小问1详解】解：如图1所示：在Rt BCD 中，2BC =，BD DE ==，2CD ∴==，22AD AC CD ∴=-=-， 2CA CB ==，90ACB ∠=︒，AB ∴==，2222ABD C AB BD AD ∴=++=+-=+△ 【小问2详解】证明：连接BG 交EF 于N ，连接CF 交AB 于M ，AB 与EF 交于点P ，DF 与BG 交于O ，如图2所示：BDE GDF∠=∠=︒，90∠=∠，∴∠+∠=∠+∠，即BDG EDF BDE BDF GDF BDF=，=，DG DFDE BDBDG EDF∴△≌△，(SAS)∴=，BG EF∴∠=∠，BGD DFE∠=∠，DOG FOB∴∠=∠=∠=︒，BNP ONF GDO90∠=∠，BPN MPFCFE ABG∴∠=∠，===，CF CM AM AB22∴△≌△，GAB ECF(SAS)∴=；AG CE【小问3详解】解：如图3所示：由（2）知(SAS)GAB ECF △≌△，GAB ECF ∴∠=∠，GAB CAB ECF BCM ∴∠-∠=∠-∠，45CAB BCM ∠=∠=︒，GAC ECB ∴∠=∠，90ACB ∠=︒，90ACH ECB ∴∠+∠=︒，90ACH GAC ∴∠+∠=︒，90AHC ∴∠=︒，∴令AC 中点为I ，则点H 在以AC 为直径的I 运动，连接HB ，当1AH =时，过H 作HN BC ⊥于N ，如图4所示：在Rt AHC 中，1AH =，2AC =，30HCA ∴∠=︒，HC =，在Rt HCN 中，60HCN ∠=︒，HC =，∴322CN HN ==，2BN BC CN ∴=+=在Rt HCN 中，90HNB ∠=︒，2BN =，32HN =，2227H B N H BN ∴=+=+【点睛】本题属于几何变换综合题，考查了等腰直角三角形性质，勾股定理，解直角三角形，全等三角形判定和性质，与圆有关的概念，图形的旋转性质等知识，解决问题的关键是熟悉常见的“手拉手”等模型证明出三角形全等．。

.解答题〔共14小题〕1.阅读与理解:图1是边长分别为a 和b 〔a>b 〕的两个等边三角形纸片 ABC 和C' DE 放在一 起〔C 与C'重合〕的图形.操作与证明：〔1〕操作：固定^ABG 将'C DE 点C 按顺时针方向旋转30°,连接AD, BE, 如图2;在图2中，线段BE 与AD 之间具有怎样的大小关系？证明你的结论；〔2〕操作：假如将图1中的* D,E 绕点C 按顺时针方向任意旋转一个角度 a, 连接AD, BE,如图3;在图3中，线段BE 与AD 之间具有怎样的大小关系？证 明你的结论； 猜测与发现: 根据上面的操作过程，请你猜测当 a 为多少度时，线段AD 的长度最大是多少? 当a 为多少度时，线段AD 的长度最小是多少？2.如图1、2是两个相似比为1:庭的等腰直角三角形，将两个三角形如图 3 放置，小直角三角形的斜边与大直角三角形的一直角边重合.〔1〕在图3中，绕点D 旋转小直角三角形，使两直角边分别与AC BC 交丁点E, F,如图 4.求证:AE 2+BF 2=EF 2;〔2〕假如在图3中，绕点C 旋转小直角三角形，使它的斜边和 CD 延长线分别 与AB 交丁点E 、F,如图5,此时结论AE ?+BF 2=EF 2是否仍然成立？假如成立，请 给出证明；假如不成立，请说明理由.旋转综合题匿1〔3〕如图6,在正方形ABCD中，E、F分别是边BC、CD上的点，满足△ CEF的周长等丁正方形ABCD的周长的一半,AE、AF分别与对角线BD交丁M、N,试问线段BM、MN、DN能否构成三角形的三边长？假如能，指出三角形的形状，并给出证明；假如不能，请说明理由.3 .某校九年级学习小组在探究学习过程中，用两块完全一样的且含60。

角的直角三角板ABC与AFE按如图〔1〕所示位置放置放置，现将R^A AEF绕A点按逆时针方向旋转角a〔0°<a<90°〕，如图〔2〕，AE与BC交丁点M , AC与EF交丁点N, BC与EF交丁点P.〔1〕求证：AM=AN;〔2〕当旋转角a =3CW，四边形ABPF是什么样的特殊四边形？并说明理由.4. 如图1,在z\ABC中，ZA=36°, AB=AC Z ABC的平分线BE交AC丁E. 〔1〕求证：AE=BC〔2〕如图〔2〕，过点E作EF// BC交AB 丁F,将△ AEF绕点A逆时针旋转角a 〔0°<a< 144°〕得到z\AE' F'连结CE, BF',求证：CE =BF〔3〕在〔2〕的旋转过程中是否存在CE'// AB?假如存在，求出相应的旋转角a;假如不存在，请说明理由.5. 在R^AABC中，ZC=90°, AC=1, BC瑚，点O 为RtAABC内一点，连接A0、B。

旋转综合题一．解答题（共14小题）1．阅读与理解：图1是边长分别为a和b（a＞b）的两个等边三角形纸片ABC和C′DE叠放在一起（C与C′重合）的图形．操作与证明：（1）操作：固定△ABC，将△C′DE绕点C按顺时针方向旋转30°，连接AD，BE，如图2；在图2中，线段BE与AD之间具有怎样的大小关系？证明你的结论；（2）操作：若将图1中的△C′DE，绕点C按顺时针方向任意旋转一个角度α，连接AD，BE，如图3；在图3中，线段BE与AD之间具有怎样的大小关系？证明你的结论；猜想与发现：根据上面的操作过程，请你猜想当α为多少度时，线段AD的长度最大是多少？当α为多少度时，线段AD的长度最小是多少？2．如图1、2是两个相似比为1：的等腰直角三角形，将两个三角形如图3放置，小直角三角形的斜边与大直角三角形的一直角边重合．（1）在图3中，绕点D旋转小直角三角形，使两直角边分别与AC、BC交于点E，F，如图4．求证：AE2+BF2=EF2；（2）若在图3中，绕点C旋转小直角三角形，使它的斜边和CD延长线分别与AB交于点E、F，如图5，此时结论AE2+BF2=EF2是否仍然成立？若成立，请给出证明；若不成立，请说明理由．（3）如图6，在正方形ABCD中，E、F分别是边BC、CD上的点，满足△CEF的周长等于正方形ABCD的周长的一半，AE、AF分别与对角线BD交于M、N，试问线段BM、MN、DN能否构成三角形的三边长？若能，指出三角形的形状，并给出证明；若不能，请说明理由．3．某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．（1）求证：AM=AN；（2）当旋转角α=30°时，四边形ABPF是什么样的特殊四边形？并说明理由．4．如图1，在△ABC中，∠A=36°，AB=AC，∠ABC的平分线BE交AC于E．（1）求证：AE=BC；（2）如图（2），过点E作EF∥BC交AB于F，将△AEF绕点A逆时针旋转角α（0°＜α＜144°）得到△AE′F′，连结CE′，BF′，求证：CE′=BF′；（3）在（2）的旋转过程中是否存在CE′∥AB？若存在，求出相应的旋转角α；若不存在，请说明理由．5．在Rt△ABC中，∠C=90°，AC=1，BC=，点O为Rt△ABC内一点，连接A0、BO、CO，且∠AOC=∠COB=BOA=120°，按下列要求画图（保留画图痕迹）：以点B为旋转中心，将△AOB绕点B顺时针方向旋转60°，得到△A′O′B（得到A、O的对应点分别为点A′、O′），并回答下列问题：∠ABC=，∠A′BC=，OA+OB+OC=．6．在△ABC中，BA=BC，∠BAC=α，M是AC的中点，P是线段BM上的动点，将线段PA绕点P顺时针旋转2α得到线段PQ．（1）若α=60°且点P与点M重合（如图1），线段CQ的延长线交射线BM于点D，请补全图形，并写出∠CDB的度数；（2）在图2中，点P不与点B，M重合，线段CQ的延长线于射线BM交于点D，猜想∠CDB的大小（用含α的代数式表示），并加以证明；（3）对于适当大小的α，当点P在线段BM上运动到某一位置（不与点B，M重合）时，能使得线段CQ的延长线与射线BM交于点D，且PQ=QD，请直接写出α的范围．7．已知，在△ABC中，AB=AC．过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ，直线a交BC边于点P（点P不与点B、点C重合），△BMN的边MN始终在直线a上（点M在点N的上方），且BM=BN，连接CN．（1）当∠BAC=∠MBN=90°时，①如图a，当θ=45°时，∠ANC的度数为；②如图b，当θ≠45°时，①中的结论是否发生变化？说明理由；（2）如图c，当∠BAC=∠MBN≠90°时，请直接写出∠ANC与∠BAC之间的数量关系，不必证明．8．如图，四边形ABCD是边长为3的正方形，长方形AEFG的宽AE=，长EF=．将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH（如图），这时BD与MN相交于点O．（1）求∠DOM的度数；（2）在图中，求D、N两点间的距离；（3）若把长方形AMNH绕点A再顺时针旋转15°得到长方形ARTZ，请问此时点B在矩形ARTZ的内部、外部、还是边上？并说明理由．9．某数学兴趣小组开展了一次活动，过程如下：如图1，在等腰直角△ABC中，AB=AC，∠BAC=90°，小敏将一块三角板中含45°角的顶点放在A上，从AB边开始绕点A逆时针旋转一个角α，其中三角板斜边所在的直线交直线BC于点D，直角边所在的直线交直线BC于点E．（1）小敏在线段BC上取一点M，连接AM，旋转中发现：若AD平分∠BAM，则AE也平分∠MAC．请你证明小敏发现的结论；（2）当0°＜α≤45°时，小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系：BD2+CE2=DE2．同组的小颖和小亮随后想出了两种不同的方法进行解决；小颖的想法：将△ABD沿AD所在的直线对折得到△ADF，连接EF（如图2）小亮的想法：将△ABD绕点A逆时针旋转90°得到△ACG，连接EG（如图3）；请你从中任选一种方法进行证明；（3）小敏继续旋转三角板，在探究中得出当45°＜α＜135°且α≠90°时，等量关系BD2+CE2=DE2仍然成立，先请你继续研究：当135°＜α＜180°时（如图4）等量关系BD2+CE2=DE2是否仍然成立？若成立，给出证明；若不成立，说明理由．10．如图，将边长为a的正方形OABC绕顶点O按顺时针方向旋转角α（0°＜α＜45°），得到正方形OA1B1C1．设边B1C1与OC的延长线交于点M，边B1A1与OB 交于点N，边B1A1与OA的延长线交于点E，连接MN．（1）求证：△OC1M≌△OA1E；（2）试说明：△OMN的边MN上的高为定值；（3）△MNB1的周长p是否发生变化？若发生变化，试说明理由；若不发生变化，请给予证明，并求出p的值．11．在正方形ABCD的边AB上任取一点E，作EF⊥AB交BD于点F，取FD的中点G，连接EG、CG，如图（1），易证EG=CG且EG⊥CG．（1）将△BEF绕点B逆时针旋转90°，如图（2），则线段EG和CG有怎样的数量关系和位置关系？请直接写出你的猜想．（2）将△BEF绕点B逆时针旋转180°，如图（3），则线段EG和CG又有怎样的数量关系和位置关系？请写出你的猜想，并加以证明．12．己知：正方形ABCD．（1）如图1，点E、点F分别在边AB和AD上，且AE=AF．此时，线段BE、DF 的数量关系和位置关系分别是什么？请直接写出结论．（2）如图2，等腰直角三角形FAE绕直角顶点A顺时针旋转∠α，当0°＜α＜90°时，连接BE、DF，此时（1）中的结论是否成立，如果成立，请证明；如果不成立，请说明理由．（3）如图3，等腰直角三角形FAE绕直角顶点A顺时针旋转∠α，当a=90°时，连接BE、DF，猜想沟AE与AD满足什么数量关系时，直线DF垂直平分BE．请直接写出结论．（4）如图4，等腰直角三角形FAE绕直角顶点A顺时针旋转∠α，当90°＜α＜180°时，连接BD、DE、EF、FB得到四边形BDEF，则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形？请直接写出结论．13．如图，点O是等边△ABC内一点，∠AOB=β，∠BOC=α．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．（1）当β=110°，α=150°时，试判断△AOD的形状，并说明理由．（2）探究：若β=110°，那么α为多少度，△AOD是等腰三角形？（只要写出探究结果）α=．（3）请写出△AOD是等边三角形时α、β的度数．α=度；β=度．14．已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．（1）求证：EG=CG；（2）将图①中△BEF绕B点逆时针旋转45°，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论（均不要求证明）．旋转综合题参考答案与试题解析一．解答题（共14小题）1．（2017•连云港四模）阅读与理解：图1是边长分别为a和b（a＞b）的两个等边三角形纸片ABC和C′DE叠放在一起（C与C′重合）的图形．操作与证明：（1）操作：固定△ABC，将△C′DE绕点C按顺时针方向旋转30°，连接AD，BE，如图2；在图2中，线段BE与AD之间具有怎样的大小关系？证明你的结论；（2）操作：若将图1中的△C′DE，绕点C按顺时针方向任意旋转一个角度α，连接AD，BE，如图3；在图3中，线段BE与AD之间具有怎样的大小关系？证明你的结论；猜想与发现：根据上面的操作过程，请你猜想当α为多少度时，线段AD的长度最大是多少？当α为多少度时，线段AD的长度最小是多少？【解答】解：操作与证明：（1）BE=AD．∵△C′DE绕点C按顺时针方向旋转30°，∴∠BCE=∠ACD=30度，∵△ABC与△C′DE是等边三角形，∴CA=CB，CE=CD，∴△BCE≌△ACD，∴BE=AD．（2）BE=AD．∵△C′DE绕点C按顺时针方向旋转的角度为α，∴∠BCE=∠ACD=α，∵△ABC与△C′DE是等边三角形，∴CA=CB，CE=CD，∴△BCE≌△ACD，∴BE=AD．猜想与发现：当α为180°时，线段AD的长度最大，等于a+b；当α为0°（或360°）时，线段AD的长度最小，等于a﹣b．2．（2014•长沙校级自主招生）如图1、2是两个相似比为1：的等腰直角三角形，将两个三角形如图3放置，小直角三角形的斜边与大直角三角形的一直角边重合．（1）在图3中，绕点D旋转小直角三角形，使两直角边分别与AC、BC交于点E，F，如图4．求证：AE2+BF2=EF2；（2）若在图3中，绕点C旋转小直角三角形，使它的斜边和CD延长线分别与AB交于点E、F，如图5，此时结论AE2+BF2=EF2是否仍然成立？若成立，请给出证明；若不成立，请说明理由．（3）如图6，在正方形ABCD中，E、F分别是边BC、CD上的点，满足△CEF的周长等于正方形ABCD的周长的一半，AE、AF分别与对角线BD交于M、N，试问线段BM、MN、DN能否构成三角形的三边长？若能，指出三角形的形状，并给出证明；若不能，请说明理由．【解答】证明：（1）连CD，如图4，∵两个等腰直角三角形的相似比为1：，而小直角三角形的斜边等于大直角三角形的直角边，∴点D为AB的中点，∴CD=AD，∠4=∠A=45°，又∵∠1+∠2=∠2+∠3=90°，∴∠3=∠1，∴△CDF≌△ADE，∴CF=AE，同理可得△CED≌△BFD，∴CE=BF，而CE2+CF2=EF2，∴AE2+BF2=EF2；（2）结论AE2+BF2=EF2仍然成立．理由如下：把△CFB绕点C顺时针旋转90°，得到△CGA，如图5∴CF=CG，AG=BF，∠4=∠1，∠B=∠GAC=45°，∴∠GAE=90°，而∠3=45°，∴∠2+∠4=90°﹣45°=45°，∴∠1+∠2=45°，∴△CGE≌△CFE，∴GE=EF，在Rt△AGE中，AE2+AG2=GE2，∴AE2+BF2=EF2；（3）线段BM、MN、DN能构成直角三角形的三边长．理由如下：把△ADF绕点A顺时针旋转90°得到△ABP，点N的对应点为Q，如图∴∠4=∠2，∠1+∠3+∠4=90°，BP=DF，BQ=DN，AF=AP，∵△CEF的周长等于正方形ABCD的周长的一半，∴EF=BE+DF，∴EF=EP，∴△AEF≌△AEP，∴∠1=∠3+∠4，而AQ=AN，∴△AMQ≌△AMN，∴MN=QM，而∠ADN=∠QBA=45°，∠ABD=45°，∴∠QBN=90°，∴BQ2+BM2=QM2，∴BM2+DN2=MN2．3．（2013•娄底）某校九年级学习小组在探究学习过程中，用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），如图（2），AE与BC交于点M，AC与EF交于点N，BC与EF交于点P．（1）求证：AM=AN；（2）当旋转角α=30°时，四边形ABPF是什么样的特殊四边形？并说明理由．【解答】（1）证明：∵用两块完全相同的且含60°角的直角三角板ABC与AFE按如图（1）所示位置放置放置，现将Rt△AEF绕A点按逆时针方向旋转角α（0°＜α＜90°），∴AB=AF，∠BAM=∠FAN，在△ABM和△AFN中，，∴△ABM≌△AFN（ASA），∴AM=AN；（2）解：当旋转角α=30°时，四边形ABPF是菱形．理由：连接AP，∵∠α=30°，∴∠FAN=30°，∴∠FAB=120°，∵∠B=60°，∴∠B+∠FAB=180°，∴AF∥BP，∴∠F=∠FPC=60°，∴AB∥FP，∴四边形ABPF是平行四边形，∵AB=AF，∴平行四边形ABPF是菱形．4．（2013•益阳）如图1，在△ABC中，∠A=36°，AB=AC，∠ABC的平分线BE交AC于E．（1）求证：AE=BC；（2）如图（2），过点E作EF∥BC交AB于F，将△AEF绕点A逆时针旋转角α（0°＜α＜144°）得到△AE′F′，连结CE′，BF′，求证：CE′=BF′；（3）在（2）的旋转过程中是否存在CE′∥AB？若存在，求出相应的旋转角α；若不存在，请说明理由．【解答】（1）证明：∵AB=BC，∠A=36°，∴∠ABC=∠C=72°，又∵BE平分∠ABC，∴∠BEC=180°﹣∠C﹣∠CBE=72°，∴∠ABE=∠A，∠BEC=∠C，∴AE=BE，BE=BC，∴AE=BC．（2）证明：∵AC=AB且EF∥BC，∴AE=AF；由旋转的性质可知：∠E′AC=∠F′AB，AE′=AF′，∵在△CAE′和△BAF′中，∴△CAE′≌△BAF′，∴CE′=BF′．（3）存在CE′∥AB，理由：由（1）可知AE=BC，所以，在△AEF绕点A逆时针旋转过程中，E点经过的路径（圆弧）与过点C且与AB平行的直线l交于M、N两点，如图：①当点E的像E′与点M重合时，则四边形ABCM为等腰梯形，∴∠BAM=∠ABC=72°，又∠BAC=36°，∴α=∠CAM=36°．②当点E的像E′与点N重合时，由AB∥l得，∠AMN=∠BAM=72°，∵AM=AN，∴∠ANM=∠AMN=72°，∴∠MAN=180°﹣2×72°=36°，∴α=∠CAN=∠CAM+∠MAN=72°．所以，当旋转角为36°或72°时，CE′∥AB．5．（2013•常州）在Rt△ABC中，∠C=90°，AC=1，BC=，点O为Rt△ABC内一点，连接A0、BO、CO，且∠AOC=∠COB=BOA=120°，按下列要求画图（保留画图痕迹）：以点B为旋转中心，将△AOB绕点B顺时针方向旋转60°，得到△A′O′B（得到A、O的对应点分别为点A′、O′），并回答下列问题：∠ABC=30°，∠A′BC=90°，OA+OB+OC=．【解答】解：∵∠C=90°，AC=1，BC=，∴tan∠ABC===，∴∠ABC=30°，∵△AOB绕点B顺时针方向旋转60°，∴△A′O′B如图所示；∠A′BC=∠ABC+60°=30°+60°=90°，∵∠C=90°，AC=1，∠ABC=30°，∴AB=2AC=2，∵△AOB绕点B顺时针方向旋转60°，得到△A′O′B，∴A′B=AB=2，BO=BO′，A′O′=AO，∴△BOO′是等边三角形，∴BO=OO′，∠BOO′=∠BO′O=60°，∵∠AOC=∠COB=∠BOA=120°，∴∠COB+∠BOO′=∠BO′A′+∠BO′O=120°+60°=180°，∴C、O、A′、O′四点共线，在Rt△A′BC中，A′C===，∴OA+OB+OC=A′O′+OO′+OC=A′C=．故答案为：30°；90°；．6．（2012•北京）在△ABC中，BA=BC，∠BAC=α，M是AC的中点，P是线段BM 上的动点，将线段PA绕点P顺时针旋转2α得到线段PQ．（1）若α=60°且点P与点M重合（如图1），线段CQ的延长线交射线BM于点D，请补全图形，并写出∠CDB的度数；（2）在图2中，点P不与点B，M重合，线段CQ的延长线于射线BM交于点D，猜想∠CDB的大小（用含α的代数式表示），并加以证明；（3）对于适当大小的α，当点P在线段BM上运动到某一位置（不与点B，M重合）时，能使得线段CQ的延长线与射线BM交于点D，且PQ=QD，请直接写出α的范围．【解答】解：（1）∵BA=BC，∠BAC=60°，M是AC的中点，∴BM⊥AC，AM=MC，∵将线段PA绕点P顺时针旋转2α得到线段PQ，∴AM=MQ，∠AMQ=120°，∴CM=MQ，∠CMQ=60°，∴△CMQ是等边三角形，∴∠ACQ=60°，∴∠CDB=30°；（2）如图2，连接PC，AD，∵AB=BC，M是AC的中点，∴BM⊥AC，即BD为AC的垂直平分线，∴AD=CD，AP=PC，PD=PD，在△APD与△CPD中，∵，∴△APD≌△CPD（SSS），∴∠ADB=∠CDB，∠PAD=∠PCD，又∵PQ=PA，∴PQ=PC，∠ADC=2∠1，∠4=∠PCQ=∠PAD，∴∠PAD+∠PQD=∠4+∠PQD=180°，∴∠APQ+∠ADC=360°﹣（∠PAD+∠PQD）=180°，∴∠ADC=180°﹣∠APQ=180°﹣2α，∴2∠CDB=180°﹣2α，∴∠CDB=90°﹣α；（3）如图1，延长BM，CQ交于点D，连接AD，∵∠CDB=90°﹣α，且PQ=QD，∴∠PAD=∠PCQ=∠PQC=2∠CDB=180°﹣2α，∵点P不与点B，M重合，∴∠BAD＞∠PAD＞∠MAD，∵点P在线段BM上运动，∠PAD最大为2α，∠PAD最小等于α，∴2α＞180°﹣2α＞α，∴45°＜α＜60°．7．（2012•本溪）已知，在△ABC中，AB=AC．过A点的直线a从与边AC重合的位置开始绕点A按顺时针方向旋转角θ，直线a交BC边于点P（点P不与点B、点C重合），△BMN的边MN始终在直线a上（点M在点N的上方），且BM=BN，连接CN．（1）当∠BAC=∠MBN=90°时，①如图a，当θ=45°时，∠ANC的度数为45°；②如图b，当θ≠45°时，①中的结论是否发生变化？说明理由；（2）如图c，当∠BAC=∠MBN≠90°时，请直接写出∠ANC与∠BAC之间的数量关系，不必证明．【解答】解：（1）①∵∠BAC=90°，θ=45°，∴AP⊥BC，BP=CP（等腰三角形三线合一），∴AP=BP（直角三角形斜边上的中线等于斜边的一半），又∵∠MBN=90°，BM=BN，∴AP=PN（等腰三角形三线合一），∴AP=PN=BP=PC，且AN⊥BC，∴四边形ABNC是正方形，∴∠ANC=45°；②连接CN，当θ≠45°时，①中的结论不发生变化．理由如下：∵∠BAC=∠MBN=90°，AB=AC，BM=BN，∴∠ABC=∠ACB=∠BNP=45°，又∵∠BPN=∠APC，∴△BNP∽△ACP，∴=，又∵∠APB=∠CPN，∴△ABP∽△CNP，∴∠ANC=∠ABC=45°；（2）∠ANC=90°﹣∠BAC．理由如下：∵∠BAC=∠MBN≠90°，AB=AC，BM=BN，∴∠ABC=∠ACB=∠BNP=（180°﹣∠BAC），又∵∠BPN=∠APC，∴△BNP∽△ACP，∴=，又∵∠APB=∠CPN，∴△ABP∽△CNP，∴∠ANC=∠ABC，在△ABC中，∠ABC=（180°﹣∠BAC）=90°﹣∠BAC．8．（2012•怀化）如图，四边形ABCD是边长为3的正方形，长方形AEFG的宽AE=，长EF=．将长方形AEFG绕点A顺时针旋转15°得到长方形AMNH（如图），这时BD与MN相交于点O．（1）求∠DOM的度数；（2）在图中，求D、N两点间的距离；（3）若把长方形AMNH绕点A再顺时针旋转15°得到长方形ARTZ，请问此时点B在矩形ARTZ的内部、外部、还是边上？并说明理由．【解答】解：（1）根据题意得：∠BAM=15°，∵四边形AMNH是矩形，∴∠M=90°，∴∠AKM=90°﹣∠BAM=75°，∴∠BKO=∠AKM=75°，∵四边形ABCD是正方形，∴∠ABD=45°，∴∠DOM=∠BKO+∠ABD=75°+45°=120°；（2）连接AN，交BD于I，连接DN，∵NH=，AH=，∠H=90°，∴tan∠HAN==，∴∠HAN=30°，∴AN=2NH=7，由旋转的性质：∠DAH=15°，∴∠DAN=45°，∵∠DAC=45°，∴A，C，N共线，∵四边形ABCD是正方形，∴BD⊥AC，∵AD=CD=3，∴DI=AI=AC==3，∴NI=AN﹣AI=7﹣3=4，在Rt△DIN中，DN==5；（3）点B在矩形ARTZ的外部．理由：如图，根据题意得：∠BAR=15°+15°=30°，∵∠R=90°，AR=，∴AK===，∵AB=3＞，∴点B在矩形ARTZ的外部．9．（2012•宁德）某数学兴趣小组开展了一次活动，过程如下：如图1，在等腰直角△ABC中，AB=AC，∠BAC=90°，小敏将一块三角板中含45°角的顶点放在A上，从AB边开始绕点A逆时针旋转一个角α，其中三角板斜边所在的直线交直线BC于点D，直角边所在的直线交直线BC于点E．（1）小敏在线段BC上取一点M，连接AM，旋转中发现：若AD平分∠BAM，则AE也平分∠MAC．请你证明小敏发现的结论；（2）当0°＜α≤45°时，小敏在旋转中还发现线段BD、CE、DE之间存在如下等量关系：BD2+CE2=DE2．同组的小颖和小亮随后想出了两种不同的方法进行解决；小颖的想法：将△ABD沿AD所在的直线对折得到△ADF，连接EF（如图2）小亮的想法：将△ABD绕点A逆时针旋转90°得到△ACG，连接EG（如图3）；请你从中任选一种方法进行证明；（3）小敏继续旋转三角板，在探究中得出当45°＜α＜135°且α≠90°时，等量关系BD2+CE2=DE2仍然成立，先请你继续研究：当135°＜α＜180°时（如图4）等量关系BD2+CE2=DE2是否仍然成立？若成立，给出证明；若不成立，说明理由．【解答】（1）证明：如图1，∵∠BAC=90°，∴∠BAD+∠DAM+∠MAE+∠EAC=90°．∵∠DAE=45°，∴∠BAD+∠EAC=45°．∵∠BAD=∠DAM，∴∠BAD+∠EAC=∠DAM+∠EAC=45°，∴∠DAM+∠MAE=∠DAM+∠EAC，∴∠MAE=∠EAC，即AE平分∠MAC；（2）选择小颖的方法．证明：如图2，连接EF．由折叠可知，∠BAD=∠FAD，AB=AF，BD=DF，∵∠BAD=∠FAD，∴由（1）可知，∠CAE=∠FAE．在△AEF和△AEC中，，∴△AEF≌△AEC（SAS），∴CE=FE，∠AFE=∠C=45°．∴∠DFE=∠AFD+∠AFE=90°．在Rt△DFE中，DF2+FE2=DE2，∴BD2+CE2=DE2．（3）当135°＜α＜180°时，等量关系BD2+CE2=DE2仍然成立．证明如下：如图4，按小颖的方法作图，设AB与EF相交于点G．∵将△ABD沿AD所在的直线对折得到△ADF，∴AF=AB，∠AFD=∠ABD=135°，∠BAD=∠FAD．又∵AC=AB，∴AF=AC．又∵∠CAE=90°﹣∠BAE=90°﹣（45°﹣∠BAD）=45°+∠BAD=45°+∠FAD=∠FAE．∴∠CAE=∠FAE．在△AEF和△AEC中，∵，∴△AEF≌△AEC（SAS），∴CE=FE，∠AFE=∠C=45°．∴∠DFE=∠AFD﹣∠AFE=∠135°﹣∠C=135°﹣45°=90°．∴∠DFE=90°．在Rt△DFE中，DF2+FE2=DE2，∴BD2+CE2=DE2．10．（2012•高淳县一模）如图，将边长为a的正方形OABC绕顶点O按顺时针方向旋转角α（0°＜α＜45°），得到正方形OA1B1C1．设边B1C1与OC的延长线交于点M，边B1A1与OB交于点N，边B1A1与OA的延长线交于点E，连接MN．（1）求证：△OC1M≌△OA1E；（2）试说明：△OMN的边MN上的高为定值；（3）△MNB1的周长p是否发生变化？若发生变化，试说明理由；若不发生变化，请给予证明，并求出p的值．【解答】（1）证明：∵正方形OABC，∴∠A1OE+∠A1OM=∠C1OM+∠A1OM=90°，∴∠A1OE=∠C1OM，在△OC1M和△OA1E中，，∴△OC1M≌△OA1E（ASA）；（2）解：∵△OC1M≌△OA1E（已证），∴OE=OM，在△EON和△MON中，，∴△EON≌△MON（SAS），∴EN=MN，∴△OMN的边MN上的高等于△OEN边EN上的高，即OA1的长a，为定值；（3）p不会发生变化，是定值2a．理由如下：根据（1）（2），△OC1M≌△OA1E，△EON≌△MON，∴MN=EN，A1E=C1M，∴△MNB1的周长p=MN+NB1+MB1，=EN+NB1+MB1，=EB1+MB1，=A1E+A1B1+MB1，=C1M+A1B1+MB1，=A1B1+B1C1，∵正方形OABC的边长为a，∴A1B1=B1C1=a，∴p=2a，是定值．11．（2011•齐齐哈尔）在正方形ABCD的边AB上任取一点E，作EF⊥AB交BD 于点F，取FD的中点G，连接EG、CG，如图（1），易证EG=CG且EG⊥CG．（1）将△BEF绕点B逆时针旋转90°，如图（2），则线段EG和CG有怎样的数量关系和位置关系？请直接写出你的猜想．（2）将△BEF绕点B逆时针旋转180°，如图（3），则线段EG和CG又有怎样的数量关系和位置关系？请写出你的猜想，并加以证明．【解答】解：（1）EG=CG，EG⊥CG．（2）EG=CG，EG⊥CG．证明：延长FE交DC延长线于M，连MG．∵∠AEM=90°，∠EBC=90°，∠BCM=90°，∴四边形BEMC是矩形．∴BE=CM，∠EMC=90°，由图（3）可知，∵BD平分∠ABC，∠ABC=90°，∴∠EBF=45°，又∵EF⊥AB，∴△BEF为等腰直角三角形∴BE=EF，∠F=45°．∴EF=CM．∵∠EMC=90°，FG=DG，∴MG=FD=FG．∵BC=EM，BC=CD，∴EM=CD．∵EF=CM，∴FM=DM，又∵FG=DG，∠CMG=∠EMC=45°，∴∠F=∠GMC．∵在△GFE与△GMC中，，∴△GFE≌△GMC（SAS）．∴EG=CG，∠FGE=∠MGC．∵∠FMC=90°，MF=MD，FG=DG，∴MG⊥FD，∴∠FGE+∠EGM=90°，∴∠MGC+∠EGM=90°，即∠EGC=90°，∴EG⊥CG．12．（2011•丹东）己知：正方形ABCD．（1）如图1，点E、点F分别在边AB和AD上，且AE=AF．此时，线段BE、DF 的数量关系和位置关系分别是什么？请直接写出结论．（2）如图2，等腰直角三角形FAE绕直角顶点A顺时针旋转∠α，当0°＜α＜90°时，连接BE、DF，此时（1）中的结论是否成立，如果成立，请证明；如果不成立，请说明理由．（3）如图3，等腰直角三角形FAE绕直角顶点A顺时针旋转∠α，当a=90°时，连接BE、DF，猜想沟AE与AD满足什么数量关系时，直线DF垂直平分BE．请直接写出结论．（4）如图4，等腰直角三角形FAE绕直角顶点A顺时针旋转∠α，当90°＜α＜180°时，连接BD、DE、EF、FB得到四边形BDEF，则顺次连接四边形BDEF各边中点所组成的四边形是什么特殊四边形？请直接写出结论．【解答】解：（1）BE=DF且BE⊥DF；（2）在△DFA和△BEA中，∵∠DAF=90°﹣∠FAB，∠BAE=90°﹣∠FAB，∴∠DAF=∠BAE，又AB=AD，AE=AF，∴△DFA≌△BEA，∴BE=DF；∠ADF=∠ABE，∴BE⊥DF；（3）AE=（﹣1）AD；（4）正方形．13．（2011•郑州校级一模）如图，点O是等边△ABC内一点，∠AOB=β，∠BOC=α．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．（1）当β=110°，α=150°时，试判断△AOD的形状，并说明理由．（2）探究：若β=110°，那么α为多少度，△AOD是等腰三角形？（只要写出探究结果）α=125°或110°或140°．（3）请写出△AOD是等边三角形时α、β的度数．α=120度；β=120度．【解答】解：（1）△AOD是直角三角形，理由如下：∵将△BOC绕点C按顺时针方向旋转∴190°﹣α=α﹣60°得△ADC∴△BOC≌△ADC，∠DCO=190°﹣α=α﹣60°∴CO=CD，∠ADC=∠BOC=α=150°∴△COD是等边三角形∴∠CDO=∴190°﹣α=α﹣60°∴∠ADO=∠ADC﹣∠CDO=150°﹣60°=90°∴△AOD是直角三角形，（2）当α=125°或110°或140°，△AOD是等腰三角形，（3）当α=120°且β=120°，△AOD是等边三角形．故答案为125°或110°或140°，120，120．14．（2009•莱芜）已知正方形ABCD中，E为对角线BD上一点，过E点作EF⊥BD交BC于F，连接DF，G为DF中点，连接EG，CG．（1）求证：EG=CG；（2）将图①中△BEF绕B点逆时针旋转45°，如图②所示，取DF中点G，连接EG，CG．问（1）中的结论是否仍然成立？若成立，请给出证明；若不成立，请说明理由；（3）将图①中△BEF绕B点旋转任意角度，如图③所示，再连接相应的线段，问（1）中的结论是否仍然成立？通过观察你还能得出什么结论（均不要求证明）．【解答】（1）证明：∵四边形ABCD是正方形，∴∠DCF=90°，在Rt△FCD中，∵G为DF的中点，∴CG=FD，同理，在Rt△DEF中，EG=FD，∴CG=EG．（2）解：（1）中结论仍然成立，即EG=CG．证法一：连接AG，过G点作MN⊥AD于M，与EF的延长线交于N点．在△DAG与△DCG中，∵AD=CD，∠ADG=∠CDG，DG=DG，∴△DAG≌△DCG（SAS），∴AG=CG；在△DMG与△FNG中，∵∠DGM=∠FGN，FG=DG，∠MDG=∠NFG，∴△DMG≌△FNG（ASA），∴MG=NG；∵∠EAM=∠AEN=∠AMN=90°，∴四边形AENM是矩形，在矩形AENM中，AM=EN，在△AMG与△ENG中，∵AM=EN，∠AMG=∠ENG，MG=NG，∴△AMG≌△ENG（SAS），∴AG=EG，∴EG=CG．证法二：延长CG至M，使MG=CG，连接MF，ME，EC，在△DCG与△FMG中，∵FG=DG，∠MGF=∠CGD，MG=CG，∴△DCG≌△FMG．∴MF=CD，∠FMG=∠DCG，∴MF∥CD∥AB，∴EF⊥MF．在Rt△MFE与Rt△CBE中，∵MF=CB，∠MFE=∠EBC，EF=BE，∴△MFE≌△CBE∴∠MEF=∠CEB．∴∠MEC=∠MEF+∠FEC=∠CEB+∠CEF=90°，∴△MEC为直角三角形．∵MG=CG，∴EG=MC，∴EG=CG．（3）解：（1）中的结论仍然成立．理由如下：过F作CD的平行线并延长CG交于M点，连接EM、EC，过F作FN垂直于AB 于N．由于G为FD中点，易证△CDG≌△MFG，得到CD=FM，又因为BE=EF，易证∠EFM=∠EBC，则△EFM≌△EBC，∠FEM=∠BEC，EM=EC ∵∠FEC+∠BEC=90°，∴∠FEC+∠FEM=90°，即∠MEC=90°，∴△MEC是等腰直角三角形，∵G为CM中点，∴EG=CG，EG⊥CG．。

【答案】（1）证明见解析；（2）45°或 135°；（3） . 【解析】 试题分析：（1）根据正方形的性质可得 AB=AD，AE=AG，∠ BAD=∠ EAG=90°，再求出 ∠ BAE=∠ DAG，然后利用“边角边”证明△ ABE 和△ ADG 全等，根据全等三角形对应边相等 证明即可. （2）当点 C 在直线 BE 上时，可知点 E 与 C 重合或 G 点 C 与重合，据此求解即可.
∵ PE2+AE2=AP2， ∴ △ PEA 是直角三角形 ∴ ∠ PEA=90°， ∴ ∠ CEA=135°， 又∵ △ CPB≌ △ CEA ∴ ∠ BPC=∠ CEA=135°． 【点睛】 考点：几何变换综合题；平行线平行线分线段成比例.
6．如图，在 Rt△ ABC 中，∠ ACB=90°，∠ A=30°，点 O 为 AB 中点，点 P 为直线 BC 上的动 点（不与点 B、点 C 重合），连接 OC、OP，将线段 OP 绕点 P 顺时针旋转 60°，得到线段 PQ，连接 BQ． （1）如图 1，当点 P 在线段 BC 上时，请直接写出线段 BQ 与 CP 的数量关系． （2）如图 2，当点 P 在 CB 延长线上时，（1）中结论是否成立？若成立，请加以证明；若 不成立，请说明理由； （3）如图 3，当点 P 在 BC 延长线上时，若∠ BPO=15°，BP=4，请求出 BQ 的长．
【答案】（1）详见解析；（2）FE·sin( －90°) 【解析】 【分析】 (1)由四边形 ABCD 是平行四边形得 AF∥ BE，所以∠ FAE=∠ BEA，由折叠的性质得 ∠ BAE=∠ FAE，∠ BEA=∠ FEA,所以∠ BAE=∠ FEA，故有 AB∥ FE，因此四边形 ABEF 是平行四 边形，又 BE=EF,因此可得结论； (2)根据点 M 在线段 BE 上和 EC 上两种情况证明∠ ENG＝90°－ ，利用菱形的性质得到

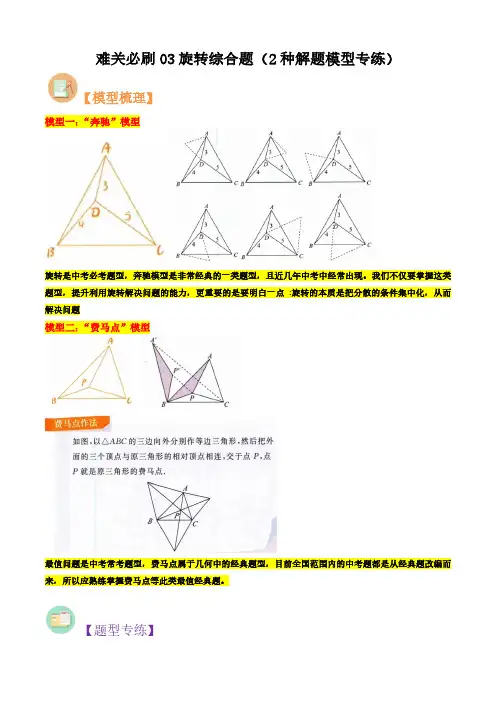
难关必刷03旋转综合题（2种解题模型专练）【模型梳理】模型一：“奔驰”模型旋转是中考必考题型，奔驰模型是非常经典的一类题型，且近几年中考中经常出现。

我们不仅要掌握这类题型，提升利用旋转解决问题的能力，更重要的是要明白一点:旋转的本质是把分散的条件集中化，从而解决问题模型二：“费马点”模型最值问题是中考常考题型，费马点属于几何中的经典题型，目前全国范围内的中考题都是从经典题改编而来，所以应熟练掌握费马点等此类最值经典题。

【题型专练】模型一：“奔驰”模型一．选择题（共2小题）1．（2023•中原区校级三模）小星利用平面直角坐标系绘制了如下风车图形，他先将△OBA固定在坐标系中，其中A（2，4），B（2，0），接着他将△OBA绕原点O逆时针转动90°至△OB1A1，称为第一次转动，然后将△OB1A1绕原点O逆时针转动90°至△OB2A2，称为第二次转动，…那么按照这种转动方式，转动2023次后，点A的坐标为（ ）A．（4，﹣2）B．C．D．（2，4）2．（2020秋•顺平县期中）如图，P是等边三角形ABC内的一点，且PA＝3，PB＝4，PC＝5，将△ABP绕点B顺时针旋转60°到△CBQ位置．连接PQ，则以下结论错误的是（ ）A．∠QPB＝60°B．∠PQC＝90°C．∠APB＝150°D．∠APC＝135°二．填空题（共1小题）3．（2022秋•新抚区期中）如图，正方形ABCD中，将边AB绕着点A旋转，当点B落在边CD的垂直平分线上的点E处时，∠BED的度数为 ．三．解答题（共5小题）4．（2021秋•长乐区期中）在Rt△ABC中，∠ACB＝90°，∠ABC＝30°，AC＝4，将△ABC绕点B顺时针旋转一定的角度得到△DBE，点A，C的对应点分别是D，E，连接AD．（1）如图1，当点E恰好在边AB上时，求∠ADE的大小；（2）如图2，若F为AD中点，求CF的最大值．5．（2021春•高州市期中）如图，P是正三角形ABC内的一点，且PA＝6，PB＝8，PC＝10．若将△PAC 绕点A逆时针旋转后，得到△P′AB．（1）求点P与点P′之间的距离；（2）求∠APB的度数．6．（2023•崂山区模拟）阅读下面材料：小伟遇到这样一个问题：如图1，在正三角形ABC内有一点P，且PA＝3，PB＝4，PC＝5，求∠APB的度数．小伟是这样思考的：如图2，利用旋转和全等的知识构造△AP′C，连接PP′，得到两个特殊的三角形，从而将问题解决．请你回答：图1中∠APB的度数等于 ．参考小伟同学思考问题的方法，解决下列问题：（1）如图3，在正方形ABCD内有一点P，且PA＝，PB＝1，PD＝，则∠APB的度数等于 ，正方形的边长为　；（2）如图4，在正六边形ABCDEF内有一点P，且PA＝2，PB＝1，PF＝，则∠APB的度数等于 ，正六边形的边长为 ．7．（2023•青岛二模）（1）探究发现下面是一道例题及其解答过程，请补充完整．如图1，在等边三角形ABC内部有一点P，PA＝3，PB＝4，PC＝5．求∠APB的度数．解：将△APC绕点A逆时针旋转60°，得到△AP′B，连接PP'，则△APP'为等边三角形．∵P′P＝PA＝3，PB＝4，P'B＝PC＝5，∴P'P2+PB2＝P′B2△BPP'为 三角形∴∠APB的度数为 ．（2）类比延伸如图2，在正方形ABCD内部有一点P，若∠APD＝135°，试判断线段PA、PB、PD之间的数量关系，并说明理由．（3）联想拓展如图3，在△ABC中，∠BAC＝120°，AB＝AC．点P在直线AB上方且∠APB＝60°，试判断是否存在常数k，满足（kPA）2+PB2＝PC2．若存在，求出k的值；若不存在，请说明理由．8．（2020秋•田家庵区校级月考）（原题初探）（1）小明在数学作业本中看到有这样一道作业题：如图1，P 是正方形ABCD内一点，连结PA，PB，PC现将△PAB绕点B顺时针旋转90°得到的△P′CB，连接PP′．若PA＝，PB＝3，∠APB＝135°，则PC的长为 ，正方形ABCD的边长为 ．（变式猜想）（2）如图2，若点P是等边△ABC内的一点，且PA＝3，PB＝4，PC＝5，请猜想∠APB的度数，并说明理由．（拓展应用）（3）聪明的小明经过上述两小题的训练后，善于反思的他又提出了如下的问题：如图3，在四边形ABCD中，AD＝3，CD＝2，∠ABC＝∠ACB＝∠ADC＝45°，则BD的长度为 ．模型二：“费马点”模型一．填空题1．（2022秋•大冶市期末）如图，D是等边三角形ABC外一点，连接AD，BD，CD，已知BD＝8，CD＝3，则当线段AD的长度最小时，①∠BDC＝ ；②AD的最小值是 ．2．（2020•荷塘区模拟）在△ABC中，若其内部的点P满足∠APB＝∠BPC＝∠CPA＝120°，则称P为△ABC的费马点．如图所示，在△ABC中，已知∠BAC＝45°，设P为△ABC的费马点，且满足∠PBA＝45°，PA＝4，则△PAC的面积为 ．二．解答题3．（2021•山西模拟）阅读下列材料，完成后面相应的任务：费马（Ferrmat，1601年8月17日﹣1665年1月12日），生于法国南部图卢兹（Toulouse）附近的波蒙•德•罗曼，被誉为业余数学家之王．1643年，费马曾提出了一个著名的几何问题：给定不在一条直线上的三个点A，B，C，求平面上到这三个点的距离之和最小的点的位置．另一位数学家托里拆利成功地解决了这个问题：如图1，△ABC（三个内角均小于120°）的三条边的张角都等于120°，即满足∠APB＝∠BPC＝∠APC＝120°的点P，就是到点A，B，C的距离之和最小的点，后来人们把这个点P称为“费马点”．下面是“费马点”的证明过程：如图2，将△APB绕着点B逆时针旋转60°得到△A′P′B，使得A′P′落在△ABC外，则△A′AB为等边三角形，∴P′B＝PB＝PP′，于是PA+PB+PC＝P′A′+PP′+PC≥A′C，…．任务：（1）材料中，判定△A′AB为等边三角形的依据是 ．（2）请你完成剩余的部分．（3）如图，△ABC为锐角三角形，以AC为一边作等边△ACD，⊙O是△ACD的外接圆，连接BD交⊙O于点M，求证：M是△ABC的费马点．4．（2023•桐城市校级开学）定义：在一个等腰三角形底边的高线上所有点中，到三角形三个顶点距离之和最小的点叫做这个等腰三角形的“近点”，“近点”到三个顶点距离之和叫做这个等腰三角形的“最近值”．【基础巩固】（1）如图1，在等腰Rt△ABC中，∠BAC＝90°，AD为BC边上的高，已知AD上一点E满足∠DEC＝60°，AC＝，求AE+BE+CE＝　；【尝试应用】（2）如图2，等边三角形ABC边长为，E为高线AD上的点，将三角形AEC绕点A逆时针旋转60°得到三角形AFG，连接EF，请你在此基础上继续探究求出等边三角形ABC的“最近值”；【拓展提高】（3）如图3，在菱形ABCD中，过AB的中点E作AB垂线交CD的延长线于点F，连接AC、DB，已知∠BDA＝75°，AB＝6，求三角形AFB“最近值”的平方．5．（2019秋•台州期中）（1）知识储备①如图1，已知点P为等边△ABC外接圆的BC上任意一点．求证：PB+PC＝PA．②定义：在△ABC所在平面上存在一点P，使它到三角形三顶点的距离之和最小，则称点P为△ABC的费马点，此时PA+PB+PC的值为△ABC的费马距离．（2）知识迁移①我们有如下探寻△ABC（其中∠A，∠B，∠C均小于120°）的费马点和费马距离的方法：如图2，在△ABC的外部以BC为边长作等边△BCD及其外接圆，根据（1）的结论，易知线段 的长度即为△ABC的费马距离．②在图3中，用不同于图2的方法作出△ABC的费马点P（要求尺规作图）．（3）知识应用①判断题（正确的打√，错误的打×）：ⅰ．任意三角形的费马点有且只有一个 ；ⅱ．任意三角形的费马点一定在三角形的内部 ．②已知正方形ABCD，P是正方形内部一点，且PA+PB+PC的最小值为，求正方形ABCD的边长．。

中考数学总复习之图形的旋转综合训练（30题）1．如图，点A在射线OX上，OA＝a．如果OA绕点O按逆时针方向旋转n°（0＜n≤360）到OA′，那么点A′的位置可以用（a，n°）表示．（1）按上述表示方法，若a＝3，n＝37，则点A′的位置可以表示为；（2）在（1）的条件下，已知点B的位置用（3，74°）表示，连接A′A、A′B．求证：A′A＝A′B．2．如图1，D为等边△ABC内一点，将线段AD绕点A逆时针旋转60°得到AE，连接CE，BD的延长线与AC交于点G，与CE交于点F．（1）求证：BD＝CE；（2）如图2，连接F A，小颖对该图形进行探究，得出结论：∠BFC＝∠AFB＝∠AFE．小颖的结论是否正确？若正确，请给出证明；若不正确，请说明理由．3．如图，点M是∠ABC的边BA上的动点，BC＝6，连接MC，并将线段MC绕点M逆时针旋转90°得到线段MN．（1）作MH⊥BC，垂足H在线段BC上，当∠CMH＝∠B时，判断点N是否在直线AB上，并说明理由；（2）若∠ABC＝30°，NC∥AB，求以MC、MN为邻边的正方形的面积S．4．如图，点E是矩形ABCD的边BC上一点，将△ABE绕点A逆时针旋转至△AB1E1的位置，此时E、B1、E1三点恰好共线．点M、N分别是AE和AE1的中点，连接MN、NB1．（1）求证：四边形MEB1N是平行四边形；（2）延长EE1交AD于点F，若EB1＝E1F，，判断△AE1F与△CB1E 是否全等，并说明理由．5．如图1，在Rt△ABC中，∠BAC＝90°，AB＝AC，D为△ABC内一点，将线段AD绕点A逆时针旋转90°得到AE，连接CE，BD的延长线与CE交于点F．（1）求证：BD＝CE，BD⊥CE；（2）如图2，连接AF，DC，已知∠BDC＝135°，判断AF与DC的位置关系，并说明理由．6．下面是小明关于“对称与旋转的关系”的探究过程，请你补充完整．（1）三角形在平面直角坐标系中的位置如图1所示，简称G，G关于y轴的对称图形为G1，关于x轴的对称图形为G2．则将图形G1绕点顺时针旋转度，可以得到图形G2．（2）在图2中分别画出G关于y轴和直线y＝x+1的对称图形G1，G2．将图形G1绕点（用坐标表示）顺时针旋转度，可以得到图形G2．（3）综上，如图3，直线l1：y＝﹣2x+2和l2：y＝x所夹锐角为α，如果图形G关于直线l1的对称图形为G1，关于直线l2的对称图形为G2，那么将图形G1绕点（用坐标表示）顺时针旋转度（用α表示），可以得到图形G2．7．如图，在由边长为1个单位长度的小正方形组成的网格中，△ABC的顶点均为格点（网格线的交点）．（1）将△ABC向上平移6个单位，再向右平移2个单位，得到△A1B1C1，请画出△A1B1C1；（2）以边AC的中点O为旋转中心，将△ABC按逆时针方向旋转180°，得到△A2B2C2，请画出△A2B2C2．8．如图，是边长为1的小正方形组成的8×8方格，线段AB的端点在格点上．建立平面直角坐标系，使点A、B的坐标分别为（2，1）和（﹣1，3）．（1）画出该平面直角坐标系xOy；（2）画出线段AB关于原点O成中心对称的线段A1B1；（3）画出以点A、B、O为其中三个顶点的平行四边形．（画出一个即可）9．如图，在2×6的方格纸中，已知格点P，请按要求画格点图形（顶点均在格点上）．（1）在图1中画一个锐角三角形，使P为其中一边的中点，再画出该三角形向右平移2个单位后的图形．（2）在图2中画一个以P为一个顶点的钝角三角形，使三边长都不相等，再画出该三角形绕点P旋转180°后的图形．10．如图所示的方格纸（1格长为一个单位长度）中，△AOB的顶点坐标分别为A（3，0），O（0，0），B（3，4）．（1）将△AOB沿x轴向左平移5个单位，画出平移后的△A1O1B1（不写作法，但要标出顶点字母）；（2）将△AOB绕点O顺时针旋转90°，画出旋转后的△A2O2B2（不写作法，但要标出顶点字母）；（3）在（2）的条件下，求点B绕点O旋转到点B2所经过的路径长（结果保留π）．11．如图是由小正方形组成的9×6网格，每个小正方形的顶点叫做格点．△ABC的三个顶点都是格点．仅用无刻度的直尺在给定网格中完成画图，画图过程用虚线表示．（1）在图（1）中，D，E分别是边AB，AC与网格线的交点．先将点B绕点E旋转180°得到点F，画出点F，再在AC上画点G，使DG∥BC；（2）在图（2）中，P是边AB上一点，∠BAC＝α．先将AB绕点A逆时针旋转2α，得到线段AH，画出线段AH，再画点Q，使P，Q两点关于直线AC对称．12．如图，在边长为1个单位长度的小正方形组成的网格中，△ABC与△DEF关于点O成中心对称，△ABC与△DEF的顶点均在格点上，请按要求完成下列各题．（1）在图中画出点O的位置．（2）将△ABC先向右平移4个单位长度，再向下平移2个单位长度，得到△A1B1C1，请画出△A1B1C1；（3）在网格中画出格点M，使A1M平分∠B1A1C1．13．如图，方格纸上每个小正方形的边长均为1个单位长度，△ABC的顶点A、B、C都在格点上（两条网格线的交点叫格点）．请仅用无刻度的直尺按下列要求画图，并保留画图痕迹（不要求写画法）．（1）将△ABC绕点A按顺时针方向旋转90°，点B的对应点为B1，点C的对应点为C1，画出△AB1C1；（2）连接CC1，△ACC1的面积为；（3）在线段CC1上画一点D，使得△ACD的面积是△ACC1面积的．14．如图，在平面直角坐标系中，线段AB的两个端点的坐标分别是A（﹣1，4），B（﹣3，1）．（1）画出线段AB向右平移4个单位后的线段A1B1；（2）画出线段AB绕原点O旋转180°后的线段A2B2．15．数学活动课上，张老师组织同学们设计多姿多彩的几何图形，如图都是由边长为1的小等边三角形构成的网格，每个网格图中有3个小等边三角形已涂上阴影，请同学们在余下的空白小等边三角形中选取一个涂上阴影，使得4个阴影小等边三角形组成一个轴对称图形或中心对称图形，请画出4种不同的设计图形．（规定：凡通过旋转能重合的图形视为同一种图形）16．如图，在△ABC中，，D，E，F分别为AC，AB，BC的中点，连接DE，DF．（1）如图1，求证：；（2）如图2，将∠EDF绕点D顺时针旋转一定角度，得到∠PDQ，当射线DP交AB于点G，射线DQ交BC于点N时，连接FE并延长交射线DP于点M，判断FN与EM的数量关系，并说明理由；（3）如图3，在（2）的条件下，当DP⊥AB时，求DN的长．17．在△ABC中，∠BAC＝90°，AB＝AC，线段AB绕点A逆时针旋转至AD（AD不与AC 重合），旋转角记为α，∠DAC的平分线AE与射线BD相交于点E，连接EC．（1）如图①，当α＝20°时，∠AEB的度数是；（2）如图②，当0°＜α＜90°时，求证：BD+2CE＝AE；（3）当0°＜α＜180°，AE＝2CE时，请直接写出的值．18．在△ABC中，点D，E分别是AB，AC边上的点，DE∥BC．基础理解：（1）如图1，若AD＝4，BD＝3，求的值；证明与拓展：（2）如图2，将△ADE绕点A逆时针旋转度，得到△AD1E1，连接BD1，CE1．①求证：＝；②如图3，若∠BAC＝90°，AB＜AC，AD＝6，△ADE在旋转过程中，点D1恰好落在DE上时，连接EE1，＝，则△E1D1E的面积为．19．【特例感知】（1）如图1，△AOB和△COD是等腰直角三角形，∠AOB＝∠COD＝90°，点C在OA 上，点D在BO的延长线上，连接AD，BC，线段AD与BC的数量关系是；【类比迁移】（2）如图2，将图1中的△COD绕着点O顺时针旋转α（0°＜α＜90°），那么第（1）问的结论是否仍然成立？如果成立，证明你的结论；如果不成立，说明理由．【方法运用】（3）如图3，若AB＝8，点C是线段AB外一动点，AC＝3，连接BC．①若将CB绕点C逆时针旋转90°得到CD，连接AD，则AD的最大值是；②若以BC为斜边作Rt△BCD（B，C，D三点按顺时针排列），∠CDB＝90°，连接AD，当∠CBD＝∠DAB＝30°时，直接写出AD的值．20．在Rt△ABC中，AC＝BC，将线段CA绕点C旋转α（0°＜α＜90°），得到线段CD，连接AD、BD．（1）如图1，将线段CA绕点C逆时针旋转α，则∠ADB的度数为；（2）将线段CA绕点C顺时针旋转α时①在图2中依题意补全图形，并求∠ADB的度数；②若∠BCD的平分线CE交BD于点F，交DA的延长线于点E，连结BE．用等式表示线段AD、CE、BE之间的数量关系，并证明．21．【问题情境】在一次数学兴趣小组活动中，小昕同学将一大一小两个三角板按照如图1所示的方式摆放．其中∠ACB＝∠DEB＝90°，∠B＝30°，BE＝AC＝3．【问题探究】小昕同学将三角板DEB绕点B按顺时针方向旋转．（1）如图2，当点E落在边AB上时，延长DE交BC于点F，求BF的长．（2）若点C、E、D在同一条直线上，求点D到直线BC的距离．（3）连接DC，取DC的中点G，三角板DEB由初始位置（图1），旋转到点C、B、D 首次在同一条直线上（如图3），求点G所经过的路径长．（4）如图4，G为DC的中点，则在旋转过程中，点G到直线AB的距离的最大值是．22．在△ABC中，∠BAC＝90°，AB＝AC＝2，D为BC的中点，E，F分别为AC，AD 上任意一点，连接EF，将线段EF绕点E顺时针旋转90°得到线段EG，连接FG，AG．（1）如图1，点E与点C重合，且GF的延长线过点B，若点P为FG的中点，连接PD，求PD的长；（2）如图2，EF的延长线交AB于点M，点N在AC上，∠AGN＝∠AEG且GN＝MF，求证：AM+AF＝AE；（3）如图3，F为线段AD上一动点，E为AC的中点，连接BE，H为直线BC上一动点，连接EH，将△BEH沿EH翻折至△ABC所在平面内，得到△B′EH，连接B′G，直接写出线段B′G的长度的最小值．23．如图，在Rt△ABC中，AC＝BC，∠ACB＝90°，点O在线段AB上（点O不与点A，B重合），且OB＝kOA，点M是AC延长线上的一点，作射线OM，将射线OM绕点O 逆时针旋转90°，交射线CB于点N．（1）如图1，当k＝1时，判断线段OM与ON的数量关系，并说明理由；（2）如图2，当k＞1时，判断线段OM与ON的数量关系（用含k的式子表示），并证明；（3）点P在射线BC上，若∠BON＝15°，PN＝kAM（k≠1），且＜，请直接写出的值（用含k的式子表示）．24．如图，在△ABC中，AB＝AC，∠BAC＝120°，点D在直线AC上，连接BD，将DB 绕点D逆时针旋转120°，得到线段DE，连接BE，CE．（1）求证：BC＝AB；（2）当点D在线段AC上（点D不与点A，C重合）时，求的值；（3）过点A作AN∥DE交BD于点N，若AD＝2CD，请直接写出的值．25．如图1，△ABC是等边三角形，点D在△ABC的内部，连接AD，将线段AD绕点A按逆时针方向旋转60°，得到线段AE，连接BD，DE，CE．（1）判断线段BD与CE的数量关系并给出证明；（2）延长ED交直线BC于点F．①如图2，当点F与点B重合时，直接用等式表示线段AE，BE和CE的数量关系为；②如图3，当点F为线段BC中点，且ED＝EC时，猜想∠BAD的度数并说明理由．26．如图，在矩形ABCD中，AD＝nAB（n＞1），点E是AD边上一动点（点E不与A，D 重合），连接BE，以BE为边在直线BE的右侧作矩形EBFG，使得矩形EBFG∽矩形ABCD，EG交直线CD于点H．【尝试初探】（1）在点E的运动过程中，△ABE与△DEH始终保持相似关系，请说明理由．【深入探究】（2）若n＝2，随着E点位置的变化，H点的位置随之发生变化，当H是线段CD中点时，求tan∠ABE的值．【拓展延伸】（3）连接BH，FH，当△BFH是以FH为腰的等腰三角形时，求tan∠ABE的值（用含n 的代数式表示）．27．如图，在锐角△ABC中，∠A＝60°，点D，E分别是边AB，AC上一动点，连接BE 交直线CD于点F．（1）如图1，若AB＞AC，且BD＝CE，∠BCD＝∠CBE，求∠CFE的度数；（2）如图2，若AB＝AC，且BD＝AE，在平面内将线段AC绕点C顺时针方向旋转60°得到线段CM，连接MF，点N是MF的中点，连接CN．在点D，E运动过程中，猜想线段BF，CF，CN之间存在的数量关系，并证明你的猜想；（3）若AB＝AC，且BD＝AE，将△ABC沿直线AB翻折至△ABC所在平面内得到△ABP，点H是AP的中点，点K是线段PF上一点，将△PHK沿直线HK翻折至△PHK所在平面内得到△QHK，连接PQ．在点D，E运动过程中，当线段PF取得最小值，且QK⊥PF时，请直接写出的值．28．在△ABC中，AB＝AC，D是边BC上一动点，连接AD，将AD绕点A逆时针旋转至AE的位置，使得∠DAE+∠BAC＝180°．（1）如图1，当∠BAC＝90°时，连接BE，交AC于点F．若BE平分∠ABC，BD＝2，求AF的长；（2）如图2，连接BE，取BE的中点G，连接AG．猜想AG与CD存在的数量关系，并证明你的猜想；（3）如图3，在（2）的条件下，连接DG，CE．若∠BAC＝120°，当BD＞CD，∠AEC ＝150°时，请直接写出的值．29．在△ABC中，AB＝AC，△CDE中，CE＝CD（CE≥CA），BC＝CD，∠D＝α，∠ACB+∠ECD＝180°，点B，C，E不共线，点P为直线DE上一点，且PB＝PD．（1）如图1，点D在线段BC延长线上，则∠ECD＝，∠ABP＝（用含α的代数式表示）；（2）如图2，点A，E在直线BC同侧，求证：BP平分∠ABC；（3）若∠ABC＝60°，BC＝+1，将图3中的△CDE绕点C按顺时针方向旋转，当BP⊥DE时，直线PC交BD于点G，点M是PD中点，请直接写出GM的长．30．如图，在△ABC中，AB＝AC，∠BAC＝α（0°＜α＜180°），过点A作射线AM交射线BC于点D，将AM绕点A逆时针旋转α得到AN，过点C作CF∥AM交直线AN于点F，在AM上取点E，使∠AEB＝∠ACB．（1）当AM与线段BC相交时，①如图1，当α＝60°时，线段AE，CE和CF之间的数量关系为．②如图2，当α＝90°时，写出线段AE，CE和CF之间的数量关系，并说明理由．（2）当tanα＝，AB＝5时，若△CDE是直角三角形，直接写出AF的长．。

第23章旋转习题精选（含答案）一．解答题（共16小题）1．（2014•龙东地区）如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点A（﹣2，2），B（0，5），C（0，2）．（1）将△ABC以点C为旋转中心旋转180°，得到△A1B1C，请画出△A1B1C的图形．（2）平移△ABC，使点A的对应点A2坐标为（﹣2，﹣6），请画出平移后对应的△A2B2C2的图形．（3）若将△A1B1C绕某一点旋转可得到△A2B2C2，请直接写出旋转中心的坐标．2．（2014•抚顺）如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC 和△DEF的顶点都在格点上，结合所给的平面直角坐标系解答下列问题：（1）画出△ABC向上平移4个单位长度后所得到的△A1B1C1；（2）画出△DEF绕点O按顺时针方向旋转90°后所得到的△D1E1F1；（3）△A1B1C1和△D1E1F1组成的图形是轴对称图形吗？如果是，请直接写出对称轴所在直线的解析式．3．（2014•眉山）如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别是A（﹣3，2），B（﹣1，4），C（0，2）．（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C；（2）平移△ABC，若A的对应点A2的坐标为（﹣5，﹣2），画出平移后的△A2B2C2；（3）若将△A2B2C2绕某一点旋转可以得到△A1B1C，请直接写出旋转中心的坐标．4．（2014•新泰市模拟）把边长为1的正方形纸片沿对角线剪开，得△ABC和△DEF．然后，将△DEF的顶点D置于△ABC 斜边中点处，使△DEF绕点D沿顺时针旋转．（1）当△DEF旋转到DF过直角顶点C时（如图1）此时DF与AC的交点H与点C重合，试判断∠DGB与∠DGH 的关系，并给以证明；（2）当△DEF继续旋转的角度为α（0＜α＜45°）（如图2）时，（1）中的结论是否成立？若成立，请给以证明；若不成立，请说明理由．5．（2014•江西模拟）（1）如图1，点P是正方形ABCD内的一点，把△ABP绕点B顺时针方向旋转，使点A与点C重合，点P的对应点是Q．若PA=3，PB=2，PC=5，求∠BQC的度数．（2）点P是等边三角形ABC内的一点，若PA=12，PB=5，PC=13，求∠BPA的度数．6．（2014•营口模拟）已知，Rt△ABC和Rt△BDE，AC=BC，BD=DE，F是AE的中点，连结CF、DF．（1）当点E在AB上时，如图①，线段CF和DF有怎样的关系？并证明你的结论．（2）将图①中△BDE绕点B逆时针旋转90°，如图②，那么（1）中的结论是否成立？如果成立，请写出证明；如果不成立，请说明理由．（3）将图①中△BDE绕点B逆时针旋转180°，如图③，那么线段CF和DF又有怎样的关系？请直接写出你的猜想．7．（2014•葫芦岛一模）如图，在方格纸中，每个小方格都是边长为1cm的正方形，△ABC的三个顶点都在格点上，将△ABC绕点O逆时针旋转90°后得到△A′B′C′（其中A、B、C的对应点分别为A′，B′，C′）（1）画出△A′B′C′．（2）求点B在旋转过程中所经过的路线的长（结果保留π）．8．（2014•石家庄一模）如图，在平面直角坐标系中，△AOB的顶点坐标分别为O（0，0），A（4，2），B（3，0）．将△AOB绕点O逆时针旋转90°，得到△A1O1B1．（1）在平面直角坐标系中，画出△A1B1O1，并填写A1的坐标为（_________，_________），B1的坐标为（_________，_________）；（2）将△AOB绕AO的中点C（2，1）逆时针旋转90°得到△A′O′B′，O′B′交OA于D，．O′A′交x轴于E，此时A′（1，3），O′（3，﹣1），B′（3，2），且O′B′经过B点，在刚才的旋转过程中，我们发现旋转中的三角形与△AOB 重叠部分面积不断变小，旋转到90°时重叠部分的面积（即四边形CEBD的面积）最小，则四边形CEBD的面积是_________．9．（2012•黑河）如图1，在正方形ABCD中，点M、N分别在AD、CD上，若∠MBN=45°，易证MN=AM+CN（1）如图2，在梯形ABCD中，BC∥AD，AB=BC=CD，点M、N分别在AD、CD上，若∠MBN=∠ABC，试探究线段MN、AM、CN有怎样的数量关系？请写出猜想，并给予证明．（2）如图3，在四边形ABCD中，AB=BC，∠ABC+∠ADC=180°，点M、N分别在DA、CD的延长线上，若∠MBN=∠ABC，试探究线段MN、AM、CN又有怎样的数量关系？请直接写出猜想，不需证明．10．（2012•铁岭）已知△ABC是等边三角形．（1）将△ABC绕点A逆时针旋转角θ（0°＜θ＜180°），得到△ADE，BD和EC所在直线相交于点O．①如图a，当θ=20°时，△ABD与△ACE是否全等？_________（填“是”或“否”），∠BOE=_________度；②当△ABC旋转到如图b所在位置时，求∠BOE的度数；（2）如图c，在AB和AC上分别截取点B′和C′，使AB=AB′，AC=AC′，连接B′C′，将△AB′C′绕点A 逆时针旋转角（0°＜θ＜180°），得到△ADE，BD和EC所在直线相交于点O，请利用图c探索∠BOE的度数，直接写出结果，不必说明理由．11．（2012•宿迁）（1）如图1，在△ABC中，BA=BC，D，E是AC边上的两点，且满足∠DBE=∠ABC（0°＜∠CBE＜∠ABC）．以点B为旋转中心，将△BEC按逆时针旋转∠ABC，得到△BE′A（点C与点A重合，点E到点E′处）连接DE′，求证：DE′=DE．（2）如图2，在△ABC中，BA=BC，∠ABC=90°，D，E是AC边上的两点，且满足∠DBE=∠ABC（0°＜∠CBE＜45°）．求证：DE2=AD2+EC2．12．（2012•绍兴模拟）阅读理解：课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC中，若AB=5，AC=3，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使得DE=AD，再连接BE（或将△ACD绕点D 逆时针旋转180°得到△EBD），把AB、AC、2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，则1＜AD＜4．感悟：解题时，条件中若出现“中点”“中线”字样，可以考虑构造以中点为对称中心的中心对称图形，把分散的已知条件和所求证的结论集中到同一个三角形中．（1）问题解决：受到（1）的启发，请你证明下面命题：如图2，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．①求证：BE+CF＞EF；②若∠A=90°，探索线段BE、CF、EF之间的等量关系，并加以证明；（2）问题拓展：如图3，在四边形ABDC中，∠B+∠C=180°，DB=DC，∠BDC=120°，以D为顶点作一个60°角，角的两边分别交AB、AC于E、F两点，连接EF，探索线段BE、CF、EF之间的数量关系，并加以证明．13．（2012•包河区二模）如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=a．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．（1）求证：△COD是等边三角形；（2）当a=150°时，试判断△AOD的形状，并说明理由；（3）探究：当a为多少度时，△AOD是等腰三角形？14．（2012•高淳县一模）如图，将边长为a的正方形OABC绕顶点O按顺时针方向旋转角α（0°＜α＜45°），得到正方形OA1B1C1．设边B1C1与OC的延长线交于点M，边B1A1与OB交于点N，边B1A1与OA的延长线交于点E，连接MN．（1）求证：△OC1M≌△OA1E；（2）试说明：△OMN的边MN上的高为定值；（3）△MNB1的周长p是否发生变化？若发生变化，试说明理由；若不发生变化，请给予证明，并求出p的值．15．（2012•崇安区二模）已知：点P是三角形ABC内任意一点，连接PA、PB、PC．（1）如图1，当△ABC是等边三角形时，将△PBC绕点B顺时针旋转60°到△P′BC′的位置．若AB的长为a，BP的长为b（b＜a），求△PBC旋转到△P′BC′的过程中边PC所扫过区域（图1中阴影部分）的面积．（用a、b表示）（2）如图2，若△ABC为任意锐角三角形，问：当∠APC、∠APB和∠BPC满足什么大小关系时，AP+BP+CP的和最小，并说明理由．16．（2012•延庆县一模）如图1，已知：已知：等边△ABC，点D是边BC上一点（点D不与点B、点C重合），求证：BD+DC＞AD．下面的证法供你参考：把△ACD绕点A顺时针旋转60°得到△ABE，连接ED，则有△ACD≌△ABE，DC=EB，∵AD=AE，∠DAE=60°，∴△ADE是等边三角形，∴AD=DE．在△DBE中，BD+EB＞DE，即：BD+DC＞AD实践探索：（1）请你仿照上面的思路，探索解决下面的问题：如图3，点D是等腰直角三角形△ABC边上的点（点D不与B、C重合）．求证：BD+DC＞AD．（2）如果点D运动到等腰直角三角形△ABC外或内时，BD、DC和AD之间又存在怎样的数量关系？直接写出结论．创新应用：（3）已知：如图4，等腰△ABC中，AB=AC，且∠BAC=α（α为钝角），D是等腰△ABC外一点，且∠BDC+∠BAC=180°，BD、DC与AD之间存在怎样的数量关系？写出你的猜想，并证明．第23章旋转习题精选（含答案）参考答案与试题解析一．解答题（共16小题）1．（2014•龙东地区）如图，方格纸中每个小正方形的边长都是1个单位长度，Rt△ABC的三个顶点A（﹣2，2），B（0，5），C（0，2）．（1）将△ABC以点C为旋转中心旋转180°，得到△A1B1C，请画出△A1B1C的图形．（2）平移△ABC，使点A的对应点A2坐标为（﹣2，﹣6），请画出平移后对应的△A2B2C2的图形．（3）若将△A1B1C绕某一点旋转可得到△A2B2C2，请直接写出旋转中心的坐标．2．（2014•抚顺）如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC 和△DEF的顶点都在格点上，结合所给的平面直角坐标系解答下列问题：（1）画出△ABC向上平移4个单位长度后所得到的△A1B1C1；（2）画出△DEF绕点O按顺时针方向旋转90°后所得到的△D1E1F1；（3）△A1B1C1和△D1E1F1组成的图形是轴对称图形吗？如果是，请直接写出对称轴所在直线的解析式．3．（2014•眉山）如图，在平面直角坐标系中，△ABC的三个顶点的坐标分别是A（﹣3，2），B（﹣1，4），C（0，2）．（1）将△ABC以点C为旋转中心旋转180°，画出旋转后对应的△A1B1C；（2）平移△ABC，若A的对应点A2的坐标为（﹣5，﹣2），画出平移后的△A2B2C2；（3）若将△A2B2C2绕某一点旋转可以得到△A1B1C，请直接写出旋转中心的坐标．4．（2014•新泰市模拟）把边长为1的正方形纸片沿对角线剪开，得△ABC和△DEF．然后，将△DEF的顶点D置于△ABC 斜边中点处，使△DEF绕点D沿顺时针旋转．（1）当△DEF旋转到DF过直角顶点C时（如图1）此时DF与AC的交点H与点C重合，试判断∠DGB与∠DGH 的关系，并给以证明；（2）当△DEF继续旋转的角度为α（0＜α＜45°）（如图2）时，（1）中的结论是否成立？若成立，请给以证明；若不成立，请说明理由．DH=AB=DB5．（2014•江西模拟）（1）如图1，点P是正方形ABCD内的一点，把△ABP绕点B顺时针方向旋转，使点A与点C重合，点P的对应点是Q．若PA=3，PB=2，PC=5，求∠BQC的度数．（2）点P是等边三角形ABC内的一点，若PA=12，PB=5，PC=13，求∠BPA的度数．6．（2014•营口模拟）已知，Rt△ABC和Rt△BDE，AC=BC，BD=DE，F是AE的中点，连结CF、DF．（1）当点E在AB上时，如图①，线段CF和DF有怎样的关系？并证明你的结论．（2）将图①中△BDE绕点B逆时针旋转90°，如图②，那么（1）中的结论是否成立？如果成立，请写出证明；如果不成立，请说明理由．（3）将图①中△BDE绕点B逆时针旋转180°，如图③，那么线段CF和DF又有怎样的关系？请直接写出你的猜想．FG=7．（2014•葫芦岛一模）如图，在方格纸中，每个小方格都是边长为1cm的正方形，△ABC的三个顶点都在格点上，将△ABC绕点O逆时针旋转90°后得到△A′B′C′（其中A、B、C的对应点分别为A′，B′，C′）（1）画出△A′B′C′．（2）求点B在旋转过程中所经过的路线的长（结果保留π）．=8．（2014•石家庄一模）如图，在平面直角坐标系中，△AOB的顶点坐标分别为O（0，0），A（4，2），B（3，0）．将△AOB绕点O逆时针旋转90°，得到△A1O1B1．（1）在平面直角坐标系中，画出△A1B1O1，并填写A1的坐标为（﹣2，4），B1的坐标为（0，3）；（2）将△AOB绕AO的中点C（2，1）逆时针旋转90°得到△A′O′B′，O′B′交OA于D，．O′A′交x轴于E，此时A′（1，3），O′（3，﹣1），B′（3，2），且O′B′经过B点，在刚才的旋转过程中，我们发现旋转中的三角形与△AOB 重叠部分面积不断变小，旋转到90°时重叠部分的面积（即四边形CEBD的面积）最小，则四边形CEBD的面积是1．× 1.5=×1=﹣=19．（2012•黑河）如图1，在正方形ABCD中，点M、N分别在AD、CD上，若∠MBN=45°，易证MN=AM+CN （1）如图2，在梯形ABCD中，BC∥AD，AB=BC=CD，点M、N分别在AD、CD上，若∠MBN=∠ABC，试探究线段MN、AM、CN有怎样的数量关系？请写出猜想，并给予证明．（2）如图3，在四边形ABCD中，AB=BC，∠ABC+∠ADC=180°，点M、N分别在DA、CD的延长线上，若∠MBN=∠ABC，试探究线段MN、AM、CN又有怎样的数量关系？请直接写出猜想，不需证明．MBN=∠MBN=∵中，MBN=∠∠∵10．（2012•铁岭）已知△ABC是等边三角形．（1）将△ABC绕点A逆时针旋转角θ（0°＜θ＜180°），得到△ADE，BD和EC所在直线相交于点O．①如图a，当θ=20°时，△ABD与△ACE是否全等？是（填“是”或“否”），∠BOE=120度；②当△ABC旋转到如图b所在位置时，求∠BOE的度数；（2）如图c，在AB和AC上分别截取点B′和C′，使AB=AB′，AC=AC′，连接B′C′，将△AB′C′绕点A 逆时针旋转角（0°＜θ＜180°），得到△ADE，BD和EC所在直线相交于点O，请利用图c探索∠BOE的度数，直接写出结果，不必说明理由．中，（AB AC ∴=，中，11．（2012•宿迁）（1）如图1，在△ABC中，BA=BC，D，E是AC边上的两点，且满足∠DBE=∠ABC（0°＜∠CBE ＜∠ABC）．以点B为旋转中心，将△BEC按逆时针旋转∠ABC，得到△BE′A（点C与点A重合，点E到点E′处）连接DE′，求证：DE′=DE．（2）如图2，在△ABC中，BA=BC，∠ABC=90°，D，E是AC边上的两点，且满足∠DBE=∠ABC（0°＜∠CBE＜45°）．求证：DE2=AD2+EC2．DBE=DBE=DBE=DBE=∵12．（2012•绍兴模拟）阅读理解：课外兴趣小组活动时，老师提出了如下问题：如图1，△ABC中，若AB=5，AC=3，求BC边上的中线AD的取值范围．小明在组内经过合作交流，得到了如下的解决方法：延长AD到E，使得DE=AD，再连接BE（或将△ACD绕点D 逆时针旋转180°得到△EBD），把AB、AC、2AD集中在△ABE中，利用三角形的三边关系可得2＜AE＜8，则1＜AD＜4．感悟：解题时，条件中若出现“中点”“中线”字样，可以考虑构造以中点为对称中心的中心对称图形，把分散的已知条件和所求证的结论集中到同一个三角形中．（1）问题解决：受到（1）的启发，请你证明下面命题：如图2，在△ABC中，D是BC边上的中点，DE⊥DF，DE交AB于点E，DF交AC于点F，连接EF．①求证：BE+CF＞EF；②若∠A=90°，探索线段BE、CF、EF之间的等量关系，并加以证明；（2）问题拓展：如图3，在四边形ABDC中，∠B+∠C=180°，DB=DC，∠BDC=120°，以D为顶点作一个60°角，角的两边分别交AB、AC于E、F两点，连接EF，探索线段BE、CF、EF之间的数量关系，并加以证明．13．（2012•包河区二模）如图，点O是等边△ABC内一点，∠AOB=110°，∠BOC=a．将△BOC绕点C按顺时针方向旋转60°得△ADC，连接OD．（1）求证：△COD是等边三角形；（2）当a=150°时，试判断△AOD的形状，并说明理由；（3）探究：当a为多少度时，△AOD是等腰三角形？AOD=﹣，14．（2012•高淳县一模）如图，将边长为a的正方形OABC绕顶点O按顺时针方向旋转角α（0°＜α＜45°），得到正方形OA1B1C1．设边B1C1与OC的延长线交于点M，边B1A1与OB交于点N，边B1A1与OA的延长线交于点E，连接MN．（1）求证：△OC1M≌△OA1E；（2）试说明：△OMN的边MN上的高为定值；（3）△MNB1的周长p是否发生变化？若发生变化，试说明理由；若不发生变化，请给予证明，并求出p的值．中，中，15．（2012•崇安区二模）已知：点P是三角形ABC内任意一点，连接PA、PB、PC．（1）如图1，当△ABC是等边三角形时，将△PBC绕点B顺时针旋转60°到△P′BC′的位置．若AB的长为a，BP的长为b（b＜a），求△PBC旋转到△P′BC′的过程中边PC所扫过区域（图1中阴影部分）的面积．（用a、b表示）（2）如图2，若△ABC为任意锐角三角形，问：当∠APC、∠APB和∠BPC满足什么大小关系时，AP+BP+CP的和最小，并说明理由．﹣π16．（2012•延庆县一模）如图1，已知：已知：等边△ABC，点D是边BC上一点（点D不与点B、点C重合），求证：BD+DC＞AD．下面的证法供你参考：把△ACD绕点A顺时针旋转60°得到△ABE，连接ED，则有△ACD≌△ABE，DC=EB，∵AD=AE，∠DAE=60°，∴△ADE是等边三角形，∴AD=DE．在△DBE中，BD+EB＞DE，即：BD+DC＞AD实践探索：（1）请你仿照上面的思路，探索解决下面的问题：如图3，点D是等腰直角三角形△ABC边上的点（点D不与B、C重合）．求证：BD+DC＞AD．（2）如果点D运动到等腰直角三角形△ABC外或内时，BD、DC和AD之间又存在怎样的数量关系？直接写出结论．创新应用：（3）已知：如图4，等腰△ABC中，AB=AC，且∠BAC=α（α为钝角），D是等腰△ABC外一点，且∠BDC+∠BAC=180°，BD、DC与AD之间存在怎样的数量关系？写出你的猜想，并证明．ADDE=＞=BC=AD。

2023年九年级中考数学复习：旋转综合题（角度问题）1．综合与实践如图1所示，将一个长为6宽为4的长方形ABEF ，裁成一个边长为4的正方形ABCD 和一个长为4、宽为2的长方形CEFD 如图2．现将小长方形CEFD 绕点C 顺时针旋转至CE F D '''，旋转角为α．(1)当点D '恰好落在EF 边上时，求旋转角α（0°＜α＜90）的值；(2)如图3，G 为BC 中点，且0°＜α＜90°，求证：GD E D ''=；(3)小军是一个爱动手研究数学问题的孩子，他发现在小长方形CEFD 绕点C 顺时针旋转一周的过程中，DCD '△与CBD '△存在两次全等，请你帮助小军直接写出当DCD '△与CBD '△全等时，旋转角α的值．2．如图1，已知ABC 是等边三角形，点E 在线段AB 上，点D 在直线BC 上，且ED ＝EC ，将BCE △绕点C 顺时针旋转60°至ACF △，连接EF ．(1)证明：AB ＝DB ＋AF ．(2)如图2，如果点E 在线段AB 的延长线上，其它条件不变，线段AB ，DB ，AF 之间又有怎样的数量关系？请说明理由．3．已知∠ABC =90°，BA =BC ，在同一平面内将等腰直角∠ABC 绕顶点A 逆时针旋转（旋转角小于180°）得∠ADE ．(1)若AE //BD 如图（1），求旋转角∠BAD 度数；(2)当旋转角为60°时，延长ED 与BC 交于点F ，如图（2）．求证：AC 平分∠DAF(3)点P 是边BC 上动点，将AP 绕点A 逆时针旋转15°到AG ，如图（3）示例，设AB =BC =α，求CG 长度最小值（用含α式子表示）4．如图∠，ABC 和ADE 是有公共顶点的等腰直角三角形，90BAC DAE ∠=∠=︒，点P 为射线,BD CE 的交点．(1)如图∠，将ADE 绕点A 旋转，当C 、D 、E 在同一条直线上时，连接BD 、BE ，求证：BD CE =且BD CE ⊥．(2)若8,4AB AD ==，把ADE 绕点A 旋转，∠当90EAC ∠=︒时，求PB 的长；∠旋转过程中线段BP 长的最小值是_______．5．如图，等腰Rt∠ABC 中，AB ＝AC ，D 为线段BC 上的一个动点，E 为线段AB 上的一个动点，使得CD =．连接DE ，以D 点为中心，将线段DE 顺时针旋转90°得到线段DF ，连接线段EF ，过点D 作射线DR ∠BC 交射线BA 于点R ，连接DR ，RF ．（1）依题意补全图形；（2）求证：∠BDE ∠∠RDF ；（3）若AB ＝AC ＝2，P 为射线BA 上一点，连接PF ，请写出一个BP 的值，使得对于任意的点D ，总有∠BPF 为定值，并证明．6．定义：如果一个三角形一条边上的高与这条边的比值叫做这条边所对角的准对（记作qad ）．如图1，在∠ABC 中，AH ∠BC 于点H ，则qad ∠BAC ＝AH BC ．当qad ∠BAC ＝35时，则称∠BAC 为这个三角形的“金角”．已知在矩形ABCD 中，AB ＝3，BC ＝6，∠ACE 的“金角”∠EAC 所对的边CE 在BC 边上，将∠ACE 绕点C 按顺时针方向旋转α（0°＜α＜90°）得到∠A 'CE '，A 'C 交AD 边于点F ．（1）如图2，当α＝45°时，求证：∠ACF 是“金角”．（2）如图3，当点E '落在AD 边上时，求qad ∠AFC 的值．7．“数学建模”是中学数学的核心素养，平时学习过程中能归纳一些几何模型，解决几何问题就能起到事半功倍的作用．（1）如图1，正方形ABCD 中，45EAF ∠=︒，且DE BF =，求证：EG AG =； （2）如图2，正方形ABCD 中，45EAF ∠=︒，延长EF 交AB 的延长线于点G ，（1）中的结论还成立吗？请说明理由；（3）如图3在（2）的条件下，作GQ AE ⊥，垂足为点Q ，交AF 于点N ，连结DN ，求证：45NDC ∠=︒．8．在学习利用旋转解决图形问题时，老师提出如下问题：（1）如图1，点P 是正方形ABCD 内一点，1PA =，2PB =，3PC =，你能求出APB ∠的度数吗？小明通过观察、分析、思考，形成了如下思路：思路一：将PBC 绕点B 逆时针旋转90︒，得到P BA '△，连接PP '，可求出APB ∠的度数；思路二：将PAB 绕点B 顺时针旋转90︒，得到P CB '△，连接PP '，可求出APB ∠的度数；请参照小明的思路，任选一种写出完整的解答过程；（2）如图2，若点P 是等边三角形ABC 内一点，若150APB ∠=︒，则线段PA ，PB ，PC 满足怎样的等量关系？请参考小明上述解决问题的方法进行探究，直接写出线段PA ，PB ，PC 满足的等量关系．9．已知∠ABC 和∠ADE 都是等腰三角形，AB ＝AC ，AD ＝AE ，∠DAE ＝∠BAC ．【初步感知】（1）特殊情形：如图∠，若点D ，E 分别在边AB ，AC 上，则DB EC ．（填＞、＜或＝）（2）发现证明：如图∠，将图∠中∠ADE 的绕点A 旋转，当点D 在∠ABC 外部，点E 在∠ABC 内部时，求证：DB ＝EC ．【深入研究】（3）如图∠，∠ABC 和∠ADE 都是等边三角形，点C ，E ，D 在同一条直线上，则∠CDB 的度数为 ；线段CE ，BD 之间的数量关系为 ．（4）如图∠，∠ABC 和∠ADE 都是等腰直角三角形，∠BAC ＝∠DAE ＝90°，点C 、D 、E 在同一直线上，AM 为∠ADE 中DE 边上的高，则∠CDB 的度数为 ；线段AM ，BD ，CD 之间的数量关系为 ．10．如图，等边三角形ABC的边长为4，直线l经过点A并与AC垂直．点P从点A开始沿射线AM运动，连接PC，并将△ACP绕点C按逆时针方向旋转60°得到△BCQ，记点P的对应点为Q，线段P A的长为m(m≥0)，当点Q恰好落在直线l上时，点P停止运动．(1)在图∠中，当∠ACP＝20°时，求∠BQC的大小；(2)在图∠中，已知BD∠l于点D，QE∠l于点E，QF∠BD于点F，试问：∠BQF的大小是否会随着点P的运动而改变？若不会，求出∠BQF的大小；若会，请说明理由．(3)在图∠中，连接PQ，记△P AQ的面积为S，请求出S与m的函数关系式(注明m的取值范围)，并求出当m为何值时，S有最大值？最大值为多少？11．把边长分别为4和6的矩形ABCO如图放在平面直角坐标系中，将它绕点C顺时针旋转a角，旋转后的矩形记为矩形EDCF．在旋转过程中，（1）如图∠，当点E在射线CB上时，E点坐标为；（2）当△CBD是等边三角形时，旋转角a的度数是（a为锐角时）；（3）如图∠，设EF与BC交于点G，当EG=CG时，求点G的坐标；（4）如图∠，当旋转角a=90°时，请判断矩形EDCF的对称中心H是否在以C为顶点，且经过点A的抛物线上．12．如图1，在Rt∠ABC中，∠ACB＝90°，AB＝10，BC＝6．D、E分别是AB、AC边的中点，连接DE．现将∠ADE绕A点逆时针旋转，连接BD，CE并延长交于点F．(1)如图2，点E正好落在AB边上，CF与AD交于点P．∠求证：AE•AB＝AD•AC；∠求BF的长；(2)如图3，若AF恰好平分∠DAE，直接写出CE的长．13．如图∠，在ABC中，∠ACB＝90°，∠ABC＝30°，AC＝1，D为ABC内部的一动点（不在边上），连接BD，将线段BD绕点D逆时针旋转60°，使点B到达点F的位置；将线段AB绕点B顺时针旋转60°，使点A到达点E的位置，连接AD，CD，AE，AF，BF，EF．(1)求证：BDA ∠BFE ；(2)当CD +DF +FE 取得最小值时，求证：AD ∥BF ．(3)如图∠，M ，N ，P 分别是DF ，AF ，AE 的中点，连接MP ，NP ，在点D 运动的过程中，请判断∠MPN 的大小是否为定值．若是，求出其度数；若不是，请说明理由． 14．图1是边长分别为a 和()b a b >的两个等边三角形纸片ABC 和CDE 叠放在一起（C 与C '重合）的图形．(1)操作：固定ABC ，将CDE 绕点C 按顺时针方向旋转20°，连结AD ，BE ，如图2，则ECA ∠=______度，并直接写出线段BE 与AD 的数量关系____．(2)操作：若将图1中的CDE ，绕点C 按顺时针方向旋转120°，使点B 、C 、D 在同一条直线上，连结AD 、BE ，如图3．∠线段BE 与AD 之间是否仍存在（1）中的结论？若是，请证明；若不是，请直接写出BE 与AD 之间的数量关系；∠求APB ∠的度数．(3)若将图1中的CDE ，绕点C 按逆时针方向旋转一个角()0360αα<<︒，当α等于多少度时，BCD △的面积最大？请直接写出答案．15．如图1所示，将一个边长为2的正方形ABCD 和一个长为2、宽为1的长方形CEFD 拼在一起，构成一个大的长方形ABEF ．现将小长方形CEFD 绕点C 顺时针旋转至''CE FD ，旋转角为α．(1)当点D 恰好落在边EF 上时，点D 到边DC 的距离为____________，旋转角α=____________︒；(2)如图2，G 为BC 的中点，且090α︒<<︒，求证：GD E D ''=；(3)小长方形CEFD 绕点C 顺时针旋转一周的过程中，DCD '与CBD '△能否全等？若能，直接写出旋转角α的值；若不能，说明理由．16．将两块完全相同的且含60°角的直角三角板ABC 和AFE 按如图1所示位置放置，现将Rt AEF 绕A 点按逆时针方向旋转()090αα︒<<︒．如图2，AE 与BC 交于点M ，AC 与EF 交于点N ，BC 与EF 交于点P ．(1)若AMC 是等腰三角形，则旋转角α的度数为______．(2)在旋转过程中，连接AP ，CE ，求证：AP 所在的直线是线段CE 的垂直平分线．(3)在旋转过程中，CPN △是否能成为直角三角形？若能，直接写出旋转角α的度数；若不能，说明理由．17．旋转是一种重要的图形变换，当图形中有一组邻边相等时，往往可以通过旋转解决问题．如图∠，在四边形ABCD 中，AD CD =，120ABC ∠=︒，60ADC ∠=︒，2AB =，1BC =．【问题提出】(1)如图∠，在图∠的基础上连接BD ，由于AD CD =，所以可将DCB 绕点D 顺时针方向旋转60°，得到DAB '，则BDB '的形状是_______；【尝试解决】(2)在（1）的条件下，求四边形ABCD 的面积；【类比应用】(3)如图∠，等边ABC 的边长为2，BDC 是顶角120BDC ∠=︒的等腰三角形，以D 为顶点作一个60°的角，角的两边分别交AB 于点M ，交AC 于点N ，连接MN ，求AMN 的周长．18．如图1，在等腰三角形ABC 中，∠A ＝120°，AB ＝AC ，点D 、E 分别在边AB 、AC 上，AD ＝AE ，连接BE ，点M 、N 、P 分别为DE 、BE 、BC 的中点．(1)观察猜想：图1中，线段NM 、NP 的数量关系是 ，∠MNP 的大小为 ；(2)探究证明：把∠ADE 绕点A 顺时针方向旋转到如图2所示的位置，连接MP 、BD 、CE ，判断∠MNP 的形状，并说明理由；(3)拓展延伸：当∠BAC ＝90°，AB ＝AC ＝10，AD ＝AE ＝6时，把∠ADE 绕点A 在平面内自由旋转，如图3，请求出∠MNP 面积的最大值．19．【发现奥秘】(1)如图1，在等边三角形ABC 中，2AB =，点E 是ABC 内一点，连接,,AE EC BE ，分别将,AC EC 绕点C 顺时针旋转60°得到,DC FC ，连接,,AD DF EF ．当B ，E ，F ，D 四个点满足______时，BE AE CE ++的值最小，最小值为_______．【解法探索】(2)如图2，在ABC 中，90,ACB AC BC ∠=︒=，点P 是ABC 内一点，连接,,PA PB PC ，请求出当PA PB PC ++的值最小时BCP ∠的度数，并直接写出此时::PA PB PC 的值．（提示：分别将,PC AC 绕点C 顺时针旋转60°得到,DC EC ，连接,,PD DE AE ）【拓展应用】(3)在ABC 中，90,30,2ACB BAC BC ︒︒∠=∠==，点P 是ABC 内一点，连接,,PA PB PC ，直接写出当PA PB PC ++的值最小时，::PA PB PC 的值．20．【问题背景】如图1，点E 、F 分别在正方形ABCD 的边BC 、CD 上，45EAF ∠=︒，连接EF ，我们可以通过把ABE △绕点A 逆时针旋转90°到ADG △，容易证得：EF BE DF =+．(1)【迁移应用】如图2，四边形ABCD 中，AB AD =，90BAD ∠=︒，点E 、F 分别在边BC 、CD 上，45EAF ∠=︒，若B ∠、D ∠都不是直角，且180B D ∠+∠=︒，试探究EF 、BE 、DF 之间的数量关系，并说明理由．(2)【联系拓展】如图3，在ABC 中，90BAC ∠=︒，AB AC =，点D 、E 均在边BC 上，且45DAE ∠=︒．猜想BD 、DE 、EC 满足的等量关系（直接写出结论，不需要证明）．参考答案：1．(1)30°(3)135°；315°2．(2)AB＝BD－AF；3．(1)90︒62a a-4．(2)∠855PB=2455；∠4345．（3）当4BP=，使得对于任意的点D，总有∠BPF为定值6．（2）237．（2）结论依然成立，8．（2）222PC PA PB=+，9．（1）=；；（3）60︒，DB CE=；（4）90︒，2AM BD CD+=10．（1）∠BQC＝70°．（2）∠BQF的大小不会随点P的运动而改变，始终为一定值，此定值为60°．（3）当m 23S311．（1）E（4，13；（2）60°；（3）13(4,)3G；（4）点H不在此抛物线上．12．(1)；52102310+13．(3)∠MPN的值为定值，30°．14．(1)40，BE＝AD(2)∠存在∠60°(3)当α＝150°或330°时，BCD△的面积最大15．(1)1，30(3)能，α为135︒或315︒16．(1)60°或15°(3)能，30α∠=︒或60︒17．(1)等边三角形(3)418．(1)MN ＝NP ，∠MNP ＝60°；(2)△MNP 是等边三角形，(3)△MNP 面积的最大值是32．19．(1)四点共线，(2)PA PB PC ++的值最小时45BCP ∠=，此时)::2:2:1PA PB PC = (3)::4:2:1PA PB PC =20．(1)EF BE DF =+，(2)222DE BD EC =+。

2024年中考数学高频考点专题复习——旋转综合题1．如图，△ABC 和△DEF 关于某点对称（1）在图中画出对称中心O ；（2）连结AF 、CD ，判断四边形ACDF 的形状，并说明理由．2．在平面直角坐标系中的位置如图所示，其中每个小正方形的边长为1个单位．（1）画出关于原点O 的中心对称图形；（2）在（1）的条件下，请分别写出点A 、B 、C 的对应点、、的坐标．ABC ABC 111A B C 1A 1B 1C3．如图1，图2，△ABC 是等边三角形，D 、E 分别是AB 、BC 边上的两个动点（与点A 、B 、C 不重合），始终保持BD=CE.（1）当点D 、E 运动到如图1所示的位置时,求证：CD=AE.（2）把图1中的△ACE 绕着A 点顺时针旋转60°到△ABF 的位置（如图2），分别连结DF 、EF.①找出图中所有的等边三角形(△ABC 除外)，并对其中一个给予证明；②试判断四边形CDFE 的形状,并说明理由.4．如图，矩形 中， ，将矩形 绕点C 顺时针旋转得到矩形 .设旋转角为 ，此时点 恰好落在边 上，连接 .（1）当 恰好是 中点时，此时 ；（2）若 ，求旋转角 及 的长.5．将线段AB 绕点A 逆时针旋转60°得到线段AC ，继续旋转α（0°＜α＜120°）得到线段AD ，连接CD 、BD ．（1）如图，若α=80°，则∠BDC 的度数为 ；（2）请探究∠BDC 的大小是否与角α的大小有关，并说明理由．ABCD 4BC =ABCD A B C D ''''αB 'AD B B 'B 'AD α=75AB B ︒∠='αAB6．在平面直角坐标系中，小方格都是边长为1的正方形，△ABC ≌△DEF ，其中点A 、B 、C 、都在格点上，请你解答下列问题：（1）如图（a ）在方格纸中，选择标有序号①②③④中的一个小正方形涂黑，与图中阴影部分构成中心对称图形，涂黑的小正方形的序号为 ．（2）画出△ABC 关于y 轴对称的△A 1B 1C 1；画出△ABC 绕点P （1，﹣1）顺时针旋转90°后的△A 2B 2C 2；（3）△A 1B 1C 1与△A 2B 2C 2成中心对称吗？若成中心对称请你求出对称中心的坐标；若不成，则说明理由．7．图1是某小型汽车的侧面示意图，其中矩形 表示该车的后备箱，在打开后备箱的过程中，箱盖 可以绕点A 逆时针方向旋转，当旋转角为 时，箱盖 落在 的位置（将后备箱放大后如图2所示）．已知 厘米， 厘米， 厘米．在图2中求： （1）点 到 的距离（结果保留根号）；（2）E 、 两点的距离（结果保留根号）．ABCD ADE 60︒ADE AD E ''90AD =30DE =40EC =D 'BC E '8．如图， 是等腰直角三角形， 是直角三角形， ，点 为边 中点将 绕点 顺时针旋转，旋转角记为 ，点 为边 的中点．（1）如图，求初始状态时 的大小；（2）如图，在旋转过程中，若点 构成平行四边形，请直接写出此时 的值；（3）在旋转过程中，若点 和点 重合，请在图中画出 并连接 ，判断此时是否有 ?如果成立，请证明；如果不成立，请说明理由．ABC 90,ABC BDE ∠=︒ 30E ∠=︒D BC BDE D (0360)αα<<︒F BE AEC ∠,,,B D F B 'a F B ,B DE ' AE AE ED ⊥9．如图，在菱形 中， ，将边 绕点 逆时针旋转至 ，记旋转角为 ．过点 作 于点 ，过点 作 直线 于点 ，连接 ．（1）（探索发现）填空：当 时， = ．的值是 （2）（验证猜想）当 时，（1）中的结论是否仍然成立?若成立，请仅就图2的情形进行证明；若不成立，请说明理由；（3）（拓展应用）在（2）的条件下，若 ，当 是等腰直角三角形时，请直接写出线段 的长．ABCD 120BAD ∠= AB A 'AB αD DF BC ⊥F B BE ⊥'B D E EF 60α= 'EBB ∠ 'EF DB 0360α<< AB =BDE ∆EF10．如图(1),在△ABC中,AB=BC,P为AB边上一点,连接CP,以PA、PC为邻边作APCD，AC与PD 相交于点E，已知∠ABC=∠AEP= (0°< <90°).（1）求证: ∠EAP=∠EPA;（2）APCD是否为矩形?请说明理由;（3）如图(2),F为BC中点,连接FP,将∠AEP绕点E顺时针旋转适当的角度,得到∠MEN(点M、N分别是∠MEN的两边与BA、FP延长线的交点).猜想线段EM与EN之间的数量关系，并证明你的结论.αα11．定义：有一组邻边相等，且它们的夹角为60°的四边形叫做半等边四边形．（1）已知在半等边四边形ABCD 中，AB=AD ，∠BAD=60°，∠BCD=120°．①如图1，若∠B=∠D ，求证：BC=CD ；②如图2，连结AC ，探索线段AC 、BC 、CD 之间的数量关系，并说明理由；（2）如图3，已知∠MAC=30°，AC=10+10，点D 是射线AM 上的一个动点，记∠DCA=a ，点B 在直线AC 的下方，若四边形ABCD 是半等边四边形，且CB=CD ．问：当点D 在15°≤a≤45°的变化过程中运动时，点B 也随之运动，请直接写出点B 所经过的路径长．12．已知，把45°的直三角板的直角顶点E 放在边长为6的正方形ABCD 的一边BC 上，直三角板的一条直角边经过点D ，以DE 为一边作矩形DEFG ，且GF 过点A ，得到图1.（1）求矩形DEFG 的面积；（2）若把正方形ABCD 沿着对角线AC 剪掉一半得到等腰直角三角形ABC ，把45°的直三角板的一个45°角的顶点与等腰直角三角形ABC 的直角顶点B 重合，直三角板夹这个45°角的两边分别交CA 和CA 的延长线于点H 、P ，得到图2.猜想：CH 、PA 、HP 之间的数量关系，并说明理由；（3）若把边长为6的正方形ABCD 沿着对角线AC 剪掉一半得到等腰直角三角形ABC ，点M 是Rt △ABC 内一个动点，连接MA 、MB 、MC ，设MA+MB+MC ＝y ，直接写出 的最小值.2y13．（1）观察猜想：如图①，在Rt △ABC 和Rt △BDE 中，∠ABC ＝∠EBD ＝90°，AB ＝BC ，BE ＝BD ，连接AE ，点F 是AE 的中点，连接CD 、BF ，当点D 、B 、C 三点共线时，线段CD 与线段BF 的数量关系是 ，位置关系是 .（2）探究证明：在（1）的条件下，将Rt △BDE 绕点B 顺时针旋转至图②位置时，（1）中的结论是否仍然成立？如果成立，请你就图②的情形进行证明；如果不成立，请说明理由；（3）拓展延伸：如图③，在Rt △ABC 和Rt △BDE 中，∠ABC ＝∠EBD ＝90°，BC ＝2AB ＝8，BD ＝2BE ＝4，连接AE ，点F 是AE 的中点，连结CD 、BF ，将△BDE 绕点B 在平面内自由旋转，请直接写出BF 的取值范围，14．请认真阅读下面的数学小探究系列，完成所提出的问题：（1）探究1，如图1，在等腰直角三角形ABC 中， ， ，将边AB 绕点B 顺时针旋转90°得到线段BD ，连接CD ，过点D 作BC 边上的高DE ，则DE 与BC 的数量关系是 ， 的面积为 ；（2）探究2，如图2，在一般的 中， ，（ ， ），将边AB 绕点B 顺时针旋转90°得到线段BD ，连接CD ，请用含m ，n 的式子表示 的面积，并说明理由.（3）探究3：如图3，在等腰三角形ABC 中， ， （ ，， ），将边AB 绕点B 顺时针旋转90°得到线段BD ，连接CD ，试探究用含a ，b ，c 的式子表示 的面积，要有探究过程.90ACB ∠=︒5BC =BCD Rt ABC 90ACB ∠=︒22()()BC m n m n =+--0m >0n >BCD AB AC =BC a b c =++0a >0b >0c >BCD15．如图1，在△ABC中，∠A＝120°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接BE，点M，N，P分别为DE，BE，BC的中点，连接NM，NP.（1）图1中，线段NM，NP的数量关系是 ，∠MNP的度数为 ；（2）把△ADE绕点A顺时针旋转到如图2所示的位置，连接MP.求证：△MNP是等边三角形；（3）把△ADE绕点A在平面内旋转，若AD＝2，AB＝5，请直接写出△MNP面积的最大值.16．（1）问题发现：如图①，正方形ABCD的边长为4，对角线AC、BD相交于点O，E是AB上点（点E不与A、B重合），将射线OE绕点O逆时针旋转90°，所得射线与BC交于点F，则四边形OEBF的面积为 .（2）问题探究：如图②，线段BQ＝10，C为BQ上点，在BQ上方作四边形ABCD，使∠ABC＝∠ADC＝90°，且AD ＝CD，连接DQ，求DQ的最小值；（3）问题解决：“绿水青山就是金山银山”，某市在生态治理活动中新建了一处南山植物园，图③为南山植物园花卉展示区的部分平面示意图，在四边形ABCD中，∠ABC＝∠ADC＝90°，AD＝CD，AC＝600米.其中AB、BD、BC为观赏小路，设计人员考虑到为分散人流和便观赏，提出三条小路的长度和要取得最大，试求AB+BD+BC的最大值.17．如图14-1，在平面直角坐标系xOy 中，直线l 2：y=与x 轴交于点B ，与直线l 1交于点c ，c点到x 轴的距离CD 为2 ，直线1交x 轴于点A(-3，0) ．（1）求直线l 1的函数表达式；（2）如图14-2，y 轴上的两个动点E 、F(E 点在F 点上方)满足线段EF 的长为 ，连接CE 、AF ，当线段CE+EF+AF 有最小值时，求出此时点F 的坐标，以及CE+EF+AF 的最小值；（3）如图14-3，将△ACB 绕点B 逆时针方向旋转60°，得到△BGH ，使点A 与点H 重合，点C 与点G 重合(C 、G 两点恰好关于x 轴对称)，将ABGH 沿直线BC 平移，记平移中的△BGH 为△B'G'H'，在平移过程中，设直线B'H'与x 轴交于点M ，是否存在这样的点M ，使得△B'MG'为等腰三角形？若存在，请直接写出此时点M 的坐标；若不存在，说明理由．18．如图（1）问题发现：如图1，已知点C 为线段 上一点，分别以线段 为直角边作两个等腰直角三角形， ，连接 ，线段 之间的数量关系为 ；位置关系为 .（2）拓展研究：如图2，把 绕点C 逆时针旋转，线段 交于点F ，则 之间的关系是否仍然成立，说明理由；x AB ,AC BC 90,,ACD CA CD CB CE ︒∠===,AE BD ,AE BD Rt ACD ∆,AF BD ,AE BD（3）解决问题：如图3，已知 ，连接 ，把线段AB 绕点A 旋转，若 ，请直接写出线段 的取值范围.19．如图1，在 中， , ，点 分别是 的中点，连接 .（1）探索发现：图1中，的值为 ； 的值为 ；（2）拓展探究若将 绕点 逆时针方向旋转一周，在旋转过程中的大小有无变化，请仅就图2的情形给出证明；（3）问题解决当 旋转至 三点在同一直线时，直接写出线段 的长.,,90AC CD BC CE ACD BCE ︒==∠=∠=,,AB AE AD 7,5AB AC ==AE ABC 2AB AC ==120BAC ∠=︒,D E ,AC BC DE AB BC AD BE CDE C AD BECDE ,,A D E BE20．有两个形状、大小完全相同的直角三角板ABC 和CDE ，其中∠ACB ＝∠DCE ＝90°．将两个直角三角板ABC 和CDE 如图①放置，点A ，C ，E 在直线MN 上．（1）三角板CDE 位置不动，将三角板ABC 绕点C 顺时针旋转一周，①在旋转过程中，若∠BCD ＝35°，则∠ACE ＝ ▲ °；②在旋转过程中，∠BCD 与∠ACE 有怎样的数量关系？请依据图②说明理由．（2）在图①基础上，三角板ABC 和CDE 同时绕点C 顺时针旋转，若三角板ABC 的边AC 从CM 处开始绕点C 顺时针旋转，转速为12°/秒，同时三角板CDE 的边CE 从CN 处开始绕点C 顺时针旋转，转速为2°/秒，当AC 旋转一周再落到CM 上时，两三角板都停止转动．如果设旋转时间为t 秒，则在旋转过程中，当∠ACE ＝2∠BCD 时，t 为多少秒？21．我们做如下的规定：如果一个三角形在运动变化时保持形状和大小不变，则把这样的三角形称为三角形板.把两块边长为4的等边三角形板 和 叠放在一起，使三角形板 的顶点 与三角形板 的AC 边中点 重合，把三角形板 固定不动，让三角形板 绕点 旋转，设射线 与射线 相交于点M ，射线 与线段 相交于点N.ABC DEF DEF D ABC O ABC DEF O DE AB DF BC（1）如图1，当射线 经过点 ，即点N 与点 重合时，易证△ADM ∽△CND.此时，AM·CN= .（2）将三角形板 由图1所示的位置绕点 沿逆时针方向旋转，设旋转角为 .其中 ，问AM·CN 的值是否改变？说明你的理由.（3）在（2）的条件下，设AM= x ，两块三角形板重叠面积为 ，求 与 的函数关系式.（图2，图3供解题用）22．已知抛物线（，，是常数，）的顶点为，与轴相交于，两点（点在点的左侧），与轴相交于点．（1）若点，求点和点的坐标；（2）将点绕点逆时针方向旋转，点的对应点为，若，两点关于点中心对称，求点的坐标和抛物线解析式：（3）在（1）的条件下，点为直线下方抛物线上的一个动点，过点作轴，与相交于点，过点作轴，与轴相交于点，求的最大值及此时点的坐标．DF B B DEF O α090α<< y y x 2y ax bx c =++a b c 0a ≠()14M -，x A B A B y C ()03C -，A B A B 90︒A 1A A 1A M 1A P BC P PD x BC D P PE y x E PD PE +P答案解析部分1．【答案】（1）解：对称中心O 如图所示；（2）解：∵A 与F ，C 与D 是对应点，∴AO=DO ，CO ＝FO ，∴四边形ACDF 是平行四边形．2．【答案】（1）解：如图所示：（2）解：由图可知：，，．3．【答案】（1）证明：∵△ABC 是正三角形，∴BC=CA ，∠B=∠ECA=60°.又∵BD=CE ，∴△BCD ≌△CAE.∴CD=AE.（2）解：① 图中有2个正三角形，分别是△BDF ，△AFE.由题设，有△ACE ≌△ABF ，∴CE=BF ，∠ECA=∠ABF=60°又∵BD=CE ，∴BD=CE=BF ，∴△BDF 是正三角形，∵AF=AE ，∠FAE=60°，∴△AFE 是正三角形.1(12)A -，1(33)B -，1(40)C ，② 四边形CDFE 是平行四边形.∵∠FDB=∠ABC =60°∴FD ∥EC.又∵FD=FB=EC ，∴四边形CDFE 是平行四边形.4．【答案】（1）60°（2）解：∵四边形 是矩形，∴ ，∴ .由旋转的性质得 ，∴ ，∴ ，即旋转角 为30°.作 于点E.则 .5．【答案】（1）30°（2）解：无关．理由如下：由旋转变换可知：∠BAC=60°，∠CAD=α， = ， AB=AC=AD ，∴ ，，ABCD //AD BC 75CBB AB B ︒'∠=∠='CB CB ='75CB B CBB ︒∠'=∠='180757530BCB ︒︒︒︒∠--='=αB E BC '⊥122AB B E CB '='==()1180602ADB α∠=︒-+︒⎡⎤⎣⎦1202α︒-()11802ADC α∠=︒-()11202ADB α︒∠=-∴∠BDC=∠ADC-∠ADB= - =30° ，∴∠BDC 的大小与ɑ的度数无关．6．【答案】（1）②（2）解：如图（3）解：如图所示：△A 1B 1C 1与△A 2B 2C 2成中心对称图形，对称中心的坐标为：（1，0）．7．【答案】（1）解：过点 作 ，垂足为点H ，交 于点F ．由题意得 （厘米）， ．∵四边形 是矩形，∴ ， ．在 中， 又∵ ， ，∴ ．∴ （厘米）答：点 到 的距离是 （厘米）．（2）解：连结 、 、 ．()11802α︒-()11202α︒-D 'D H BC '⊥AD 90AD AD =='60DAD ∠='︒ABCD AD BC 90AFD BHD ∠'=∠='︒Rt AD F ∆'sin 90sin 60D F AD DAD ︒=⋅∠=⋅='''40CE =30DE =70FH=70)D H D F FH ='++'=D 'BC ()70+AE AE 'EE '由题意得 ， ．∴ 是等边三角形．∴ ．∵四边形 是矩形，∴ ．在 中， ， ，∴（厘米）答：E 、 两点的距离是厘米．8．【答案】（1）解：∵∠BED ＝30°，△BDE 是直角三角形，∴∠EBD ＝90°－∠BED ＝60°．又∵D 是BC 的中点，∴DE 是BC 的垂直平分线．∵BE ＝CE ，∠BEC ＝60°，∴△BCE 是等边三角形．∴BC ＝BE ．∵△ABC 是等腰三角形，∠ABC ＝90°，∴AB ＝BC ．∴BE ＝AB ．∵AB ⊥BC ，DE ⊥BC ，∴AB ∥DE ，∴∠ABE ＝∠BED ＝30°．∴∠BAE ＝∠BEA ＝ (180°－∠ABE)＝75°．∴∠AEC ＝∠BAE ＋∠BEC ＝135°．（2）解：∵四边形BDFB ＇是平行四边形，∠FB ＇D ＝60°∴B ＇F ∥BD ，∴∠B D B ＇＝∠FB ＇D ＝60°AE AE ='60EAE ∠='︒AEE ∆'EE AE '=ABCD 90ADE ∠=︒Rt ADE ∆90AD =30DE =AE ===E '12即 ＝60°．（3）解：△B ＇DE 如图所示，AE ⊥DE 不成立，理由如下：DE 与AB 相交于点G ，假设AE ⊥DE ，则△AEG ∽△DBG ，设BG ＝a ，∠BDG ＝30°，∴DG ＝2a ，BD ＝ a ，AB ＝2 BD ＝ a ．∴AG ＝AB －BG ＝（－1）a ，B ＇D ＝BD ＝a ．∴DE ＝ ＝3a．∴GE ＝DE －DG＝3a －2a ＝a ．∴ ， ．∴ 与假设矛盾．∴AE ⊥DE 不成立．9．【答案】（1）30（2）解：当 时， （1）中的结论仍然成立．证明：如图1，连接 ．a tan 30B D＇AG DG ==1GE a GB a ==AG GE DG GB≠0360α<< BD，， ． ， ． ． ．，即 ． ，， ． ．，（3）解：线段 的长为 或 ．连接 ， 交于点 ．，， ，，∵DE=BE ，∠DEB=90°，∴∠EDB=∠EBD=45°，． ，∠B′EB=90°，， ． ， ． ．'AB AD AB == 1'(180)9022AB B αα∴∠=︒-=︒-1'[180(120)]3022AB D αα∠=︒-︒-=︒+'180''180(90)(306022EB B AB D AB B αα∴∠=︒-∠-∠=︒-︒--︒+=︒'30EBB ∴∠=︒11(180)3022CBD ABC BAD∠=∠=︒-∠=︒ 'EBB CBD ∴∠=∠'''EBB FBB CBD FBB ∴∠+∠=∠+∠'DBB EBF ∠=∠cos BF DBF BD ∠== cos ''BE EBB BB ∠=='BF BE BD BB ∴='DBB FBE ∆∆∽''EF BE DB BB ∴==EF 3+3-AC BD O AC DB ⊥ 1602BAO BAD ∠=∠=︒sin OB AB BAO ∴=⋅∠=2BD OB ∴==sin DE BE BD DBE ∴==⋅∠=='AB AD AB == 1'(180)9022AB B αα∴∠=︒-=︒-1'[180(120)]3022AB D αα∠=︒-︒-=︒+'180''180(90)(306022EB B AB D AB B αα∴∠=︒-∠-∠=︒-︒--︒+=︒'30EBB ∴∠=︒'tan '2EB BE EBB ∴=⋅∠==分两种情况： 如图，，∵∠B′BE=∠DBF=30°，∴cos ∠B′BE=cos ∠DBF=，又∵∠B′BE+∠EBD=∠EBD+∠DBF ，∴∠B′BD=∠EBF ，∴△B′BD ∽△EBF ，∴ ， ． 如图，．①''2B D DE BE =+=+EB FB B B DB ='=EB FB EF B B DB B D '='2)3EF D '∴==+=②''2B D DE B E =-=∵∠B′BE=∠DBF=30°，∴cos ∠B′BE=cos ∠DBF=，又∵∠B′BE-∠FBB′=∠DBF-∠FBB′，∴∠B′BD=∠EBF ，∴△B′BD ∽△EBF ，∴ ，．综上所述，线段 的长为或 ．10．【答案】（1）证明：(1)在△ABC 和△AEP 中,∠ABC=∠AEP,∠BAC=∠EAP, ∠ACB=∠APE,在△ABC 中,AB=BC. ∠ACB=∠BAC,∠EPA=∠EAP,（2）解： APCD 是矩形.四边形APCD 是平行四边形,AC=2EA,PD=2EP.由(1)知, ∠EPA=∠EAP.EA=EP ，进而AC=PDAPCD 是矩形.（3）解：EM=ENEA=EP, ∠EPA=90° - ∠EAM=180°-∠EAP =180°-∠EPA= 180°-(90°-)=90°+ 由(2)知, ∠CPB=90°,F 是BC 的中点, FP=FB,∠FPB=∠ABC= ，∠EPN=∠EPA+∠APN=∠EPA+∠FPB=90° -+ =90°+ ∠EAM=∠EPN∠AEP 绕点E 顺时针旋转适当的角度，得到∠MEN ，EB FB B B DB ='=EB FB EF B B DB B D '='2)3EF B D ∴===-'EF 33 ∴∴∴ ∴∴∴ ∴12α∴12α12α∴∴α∴12αα12α∴∠AEP-∠AEN =∠MEN-∠AEN,即∠MEA=∠NEP.△EAM ≌△EPN,EM=EN.11．【答案】（1）解：①证明：连结AC ，∵∠A+∠B+∠C+∠D=360°，且∠A=60°，∠C=120°，∴∠B+∠D=180°，且∠B=∠D ，∴∠B=∠D=90°，∵AB=AD ，AC=AC ，∴△ABC ≌△ADC （HL ），∴BC=DC ；②解：延长CB ，使得CD=BE ，∵∠BAD=60°，∠BCD=120°，∴∠ABC+∠D=180°，且∠ABC+∠ABE=180°，∴∠D=∠ABE ，又∵AB=AD∴△ABE ≌△ADC ，∴AE=AC，∴∴∴∠BAE=∠DAC ，∴∠EAC=∠BAE+∠BAC=∠DAC+∠BAC=∠BAD=60°，∴△ACE 是等边三角形，∴AC=CE=CB+BE=CB+CD（2）解：如图，设∠ACD=15°，∠DCD‘=30°，作CM ⊥AD ，D‘H ⊥AC ，由旋转图形的特点可知，CB=CD ，CB‘=CD’，∠BCB'=DCD‘=30°，∴△∠BCB'≌△DCD‘，BB'=DD’，设D'H=x ，由勾股定理得：， HC=x，则，解得x=10， 即D'H=10，得，AD’=20，在Rt △AMC 中，∵，∠DAC=30°，∴，AM=（，-5，，∴DD’为D 点的运动路程，则BB‘的运动路程也为10 .12．【答案】（1）解：∵四边形ABCD 是正方形，∴∠ADC ＝∠DCE ＝90°，∵四边形DEFG 是矩形，∴∠AGD ＝∠GDE ＝90°，∴∠DCE ＝∠AGD ＝90°，∠ADC ＝∠GDE ＝90°，∴∠ADC ﹣∠ADE ＝∠GDE ﹣∠ADE ，∴∠EDC ＝∠ADG ，∵∠EDC ＝∠ADG ，∠DCE ＝∠AGD ＝90°，∴△ECD ∽△AGD ，∴ ，∴DG•DE ＝DC•DA ＝6×6＝36，∴矩形DEFG 的面积＝DG•DE ＝36；（2）解： ，证明：把△BAP 绕着点B 顺时针旋转90°得到△BCK ，连接KH ，由旋转得△BAP ≌△BCK ，∴BK ＝BP ，∠PBA ＝∠KBC ，∠BCK ＝∠BAP ＝ ，∴∠HCK ＝ ＝ ，∴由勾股定理得， ，∵∠PBE ＝45°，∴∠PBA+∠ABE ＝45°，∵∠PBA ＝∠KBC ，∴∠KBC+∠ABE ＝45°，∵∠ABC ＝90°，∴∠HBK ＝45°，∵∠PBE ＝45°，∴∠HBK ＝∠PBE ＝45°，∵BK ＝BP ，∠HBK ＝∠PBE ，BH ＝BH ，∴△BHP ≌△BHK （SAS ），CD DE DG DA=222CH PA HP +＝18045135︒-︒=︒BCK BCA ∠-∠1354590︒-︒=︒222CH PA KH +＝∴HK ＝HP ，∵ ，∴ ；（3）解：把△BMC 绕着点B 顺时针旋转60°得到△BKN ，连接MK ，BN ，NC ，由旋转得，△BMC ≌△BKN ，∴MC ＝KN ，BM ＝BK ，∵BM ＝BK ，∠MBK ＝60°，∴△BKM 是等边三角形，∴MK ＝BM ，∴MA+MB+MC ＝AM+MK+KN ，当A ，M ，K ，N 四点共线时，AN 就是所求的MA+MB+MC 的最小值，过N 作NQ ⊥AB 交AB 的延长线于Q ，∵ ，∠BQN ＝90°，∴QN ＝BN•sin30°＝6× ＝3，BQ ＝BN•cos30°＝ ，∴AQ ＝AB+BQ ＝，在Rt △AQN 中，由勾股定理得，，∴ 的最小值为 .13．【答案】（1）CD=2BF ；BF ⊥CD（2）解：BF ⊥CD ，CD=2BF 成立，证明：∵△ABC 与△DBE 都是等腰直角三角形，∴AB=BC ，DB=EB ，∠ABC=∠DBE=90°，222CH PA KH +＝222CH PA HP +＝180906030NBQ ∠︒-︒-︒=︒＝126=6+(222226372AN AQ QN +=++=+＝2y 72+如图②，将△ABE 绕点B 顺时针旋转90°得到△CBG ，点E 、F 的对应点分别是G 、H ，连BH ， 则△ABE ≌△CBG ，BE=BG ，AE=CG ，BF=BH ，∠FBH=∠EBG=90°，AF=CH ，EF=GH ， ∴BF ⊥BH ，∵AF=EF ，∴CH=GH ，∵∠DBE=90°，∴∠DBE+∠EBG=180°，∴D 、B 、G 三点共线，∴BH ∥CD ，，∴BF ⊥CD ，，即CD=2BF ，∴BF ⊥CD ，CD=2BF 成立；（3）14．【答案】（1）DE=BC ；12.5（2）解：过点D 作BC 边上的高DE ，如图，∵∠ABC+∠A=90°，∠ABC+∠DBE=90°，∴∠A=∠DBE ，又∵∠ACB=∠E=90°，AB=BD ，∴ ，∴，12BH CD =12BF CD =13BF ≤≤ACB BED ≌BC DE =又 .∴ 的面积为：.（3）解：作 于G ，过点D 作BC 边上的高DE ，如图，由（2）同理，可证 ，∴ ，又 ，∵AB=AC ， ，∴ .∴ 的面积为： .15．【答案】（1）NM=NP ；60°（2）证明：由旋转得：∠BAD=∠CAE ，又∵AB=AC ，AD=AE ，∴△ABD ≌△ACE （SAS ），∴BD=CE ，∠ABD=∠ACE ，∵点M ，N ，P 分别为DE ，BE ，BC 的中点，∴MN= BD ，PN= CE ，MN ∥BD ，PN ∥CE ，∴MN=PN ，∠ENM=∠EBD ，∠BPN=∠BCE ，∴∠ENP=∠NBP+∠NPB=∠NBP+∠ECB ，∵∠EBD=∠ABD+∠ABE=∠ACE+∠ABE ，∴∠MNP=∠MNE+∠ENP=∠ACE+∠ABE+∠EBC+∠EBC+∠ECB=180°-∠BAC=60°，∴△MNP 是等边三角形；（322()()4mn BC m n m n =+--=BCD 221448m n 2mn mn ⨯⨯=AGB BED ≌BG DE =BC a b c =++BC a b c =++11()22BG BC a b c ==++BCD 2111()()()224a b c a b c a b c ⨯++⨯++=++121216．【答案】（1）4（2）解：如图②中，连接BD ，取AC 的中点O ，连接OB ，OD.∵∠ABD ＝∠ADC ＝90°，AO ＝OC ，∴OA ＝OC ＝OB ＝OD ，∴A ，B ，C ，D 四点共圆，∴∠DBC ＝∠DAC ，∵DA ＝DC ，∠ADC ＝90°，∴∠DAC ＝∠DCA ＝45°，∴∠DBQ ＝45°，根据垂线段最短可知，当QD ⊥BD 时，QD 的值最短，DQ 的最小值＝BQ ＝5 .（3）解：如图③中，将△BDC 绕点D 顺时针旋转90°得到△EDA ， ∵∠ABC+∠ADC ＝180°，∴∠BCD+∠BAD ＝∠EAD+BAD ＝180°，∴B ，A ，E 三点共线，∵DE ＝DB ，∠EDB ＝90°，∴BE ＝ BD ，∴AB+BC ＝AB+AE ＝BE ＝BD，∴BC+BC+BD ＝（ +1）BD ，∴当BD 最大时，AB+BC+BD 的值最大，∵A ，B ，C ，D 四点共圆，∴当BD 为直径时，BD 的值最大，∵∠ADC ＝90°，∴AC 是直径，∴BD ＝AC 时，AB+BC+BD 的值最大，最大值＝600（ +1）.17．【答案】（1）解：∵点C 的纵坐标为2 ，点c 在直线l 2：y= ∴点C(-1，2 )设l 1的表达式为y= kx+ b将A(-3，0)、C(-1，2)代入， 解得故直线l 1的表达式为：y=x+3 （2）解：作点a关于y 轴的对称点A(3，0)，将点a4向上平移个单位长度得E (3，)连接E'C 交y 轴于点E ，在E下方取EF= ，则点F是所求点，将点C 、E' 的坐标代入一次函数表达式，同理可得： CE' 的函数表达式为：y= 故点E(0，)，点F(0，)CE+EF+4F 的最小值=FE+CE'= +．（3）M(5+8，0)或(5-8，0)或(-3，0)或(-19，0) x +03k bk b=-+⎧⎪⎨=-+⎪⎩k b ⎧=⎪⎨=⎪⎩x +18．【答案】（1）AE=BD ；AE ⊥BD（2）解： 仍然成立.由题意得，∵△ACD 和△BCE 是等腰直角三角形即 ，∴∴ .∴∴ .（3）解： 连接BD.由（2）可知，AE=BD ，在△ABD 中，且 ，所以 即 在AB 绕点A 旋转过程中，当A ，B ，D 三点在一条直线上时， 或者,AE BD AE BD =⊥90ACD DCE ECB DCE DCE ︒∴∠+∠=∠+∠=+∠,,ACE DCB AC CD EC CB ∠=∠==ACE DCB∆≅∆,12AE DB =∠=∠180(4512)90EFB ︒︒︒∠=--∠+∠=AE BD⊥77AE -≤≤7AD AB ===77BD <<+77AE -<<+7AE =7AE =∴ ≤AE≤ 19．【答案】（1（2）解：无变化,理由: 由(1)知,CD=1, ,∴,∴ ,由(1)知,∠ACB=∠DCE=30°,∴∠ACD=∠BCE,∴△ACD ∽△BCE,∴,（3）解：线段BE 的长为或 ，理由如下： 当点D 在线段AE 上时,如图2,过点C 作CF ⊥AE 于F,∠CDF=180°﹣∠CDE=60°,∴∠DCF=30°,∴ ,∴,7-7+CE BE ==CD CE =AC BC =CD AC CE BC ==AD AC BE BC ==1122DF CD ==CF ==在Rt △AFC 中,AC=2,根据勾股定理得, ,∴AD=AF+DF=,由(2)知, ,∴当点D在线段AE 的延长线上时,如图3,过点C 作CG ⊥AD 交AD 的延长线于G,∵∠CDG=60°,∴∠DCG=30°,∴ ,∴ ,在Rt △ACG 中,根据勾股定理得,,∴ ,由(2)知,,∴即:线段BE 的长为或.AF ==AD BE =BE ==1122DG CD ==CG ==AG =AD AG DG =-=AD BE =BE ==20．【答案】（1）①145；②∠BCD+∠ACE ＝180°，理由如下：∵∠ACE ＝∠ACB+∠BCE ，∴∠BCD+∠ACE ＝∠BCD+∠ACB+∠BCE ＝∠ACB+∠DCE ＝90°+90°＝180°；（2）解：三角板ABC 和CDE 重合之前，∠ACE ＝180°-10°t ，∠BCD ＝10°t ，依题意有180°-10°t ＝2×10°t ，解得t ＝6；三角板ABC 和CDE 重合之后，∠ACE ＝10°t-180°，∠BCD ＝360°-10°t ，依题意有10°t-180°＝2×（360°-10°t ），解得t ＝30．故当t ＝6或30秒时，有∠ACE ＝2∠BCD ．故答案为：6或30．21．【答案】（1）4（2）解：AM•CN 的值不会改变.连接BD ，在△ADM 与△CND 中，∵∠A=∠C=60°，∠DNC=∠DBN+∠BDN=30°+α，∠ADM=30°+α，∴∠ADM=∠CND ，∴△ADM ∽△CND∴ ，∴AM•CN=AD•CD=2×2=4，∴AM•CN 的值不会改变；（3）解：情形1，当0°＜α＜60°时，1＜AM ＜4，即1＜x ＜4，此时两三角形板重叠部分为四边形AD AM CN CD如图2，过D 作DQ ⊥AB 于Q ，DG ⊥BC 于G ，∴DQ=DG= ，由（2）知，AM•CN=4，得CN=，于是y=（1＜x ＜4）； 情形2，当60°≤α＜90°时，AM≥4时，即x≥4，此时两三角形板重叠部分为△DPN ，如图3，过点D 作DH ∥BC 交AM 于H ，易证△MBP ∽△MHD ，∴ ，又∵MB=x-4，MH=x-2，DH=2,∴BP=，∴PN=4－ ，于是y= ，综上所述，1＜x ＜4时，y=；x≥4时，y= 22．【答案】（1）解：设抛物线解析式为，将点代入得，4x 21122AB AM DQ CN DG x -⋅-⋅=BP MB DH MH=282x x --4282x x x ---114284222x PN DG x x -⎛⎫⋅=--= ⎪-⎝⎭x ()214y a x =--()03C -，解得：∴抛物线解析式为当时，解得：，∵点在点的左侧，∴，；（2）解：∵，抛物线，与轴相交于，两点∴，对称轴为直线，设，则，∴∵点绕点逆时针方向旋转得到，则点一定在第四象限，如图所示，则，，∵，两点关于点中心对称，∴解得：，则∴，1a =()214y x =--0y =()2140x --=1213x x =-=，A B ()10A -，()30B ，()14M -，2y ax bx c =++x A B 0a >1x =()0A m ，()20B m -，222AB m m m=--=-A B 90︒A 'A '22BA BA m ='=-()222A m m '--，A 1A M 228m -=-3m =-()58A '-，()30A -，()50B ，将点代入得，解得：∴抛物线解析式为；（3）解：如图所示，设交于点，由（1）可得，，设直线的解析式为，将点代入得，解得所以直线的解析式为，∵抛物线解析式为，设，则，∴，∵轴，轴，由∵则是等腰直角三角形，∴()30A -，()214y a x =--1640a -=14a =()21144y x =--PE BC F ()30B ，()03C -，BC 3y kx =-()30B ，330k -=1k =BC 3y x =-()221423y x x x =--=--()223P t t t --，()0E t ，()3F t t -，223233FP t t t t t =--++=-+223PE t t =-++PD x PE y OC OB=OCB 45FDP OBC ∠=∠=︒∴也是等腰直角三角形，∴∴∴当时，取得最大值此时，即．PDF PD PF=PD PE+22323t t t t =-+-++2253t t =-++252525232168t t ⎛⎫=--+++ ⎪⎝⎭2549248t ⎛⎫=--+ ⎪⎝⎭54t =PD PE +498225632314416t t ⎛⎫--=--=- ⎪⎝⎭563416P ⎛⎫- ⎪⎝⎭。

图形变换—旋转综合题1.如图，在△ABC中，∠C=90º，∠A=30º，BC=2，D是AB中点，等腰直角三角板的直角顶点落在点D上，使三角板绕点D旋转。

（1）如图1，当三角板两边分别交边AC、BC于F、E时，线段EF与AF、BE有怎样的关系并加以证明。

（2）如图1,设AF=x，四边形CEDF的面积为y.求y关于x的函数关系式，写出自变量x的取值范围.（3）在旋转过程中，当三角板一边DM经过点C时，另一边DN交CB延长线于点E,连结AE与CD延长线交于H,如图2，求DH的长。

2.如图，已知正方形ABCD，将一块等腰直角三角尺的锐角顶点与A重合，并将三角尺绕点旋转，如图1，使它的斜边与BC交于点E，一条直角边与CD交于点F（E、F不与B、D重合），AE、AF分别与BD 交于P、Q两点.（1）求证：△ABP∽△ACF，且相似比为1∶2；（2）请再在图1中（不再添线和加注字母）找出两对相似比为1∶2的非直角三角形的相似三角形；（直接写出）（3），如图2当M点旋转到BC的垂直平分线PQ上时，连结ON,若ON=8,求MQ的长。

3.如图，操作：将一把三角尺放在边长为1的正方形ABCD上，并使它的直角顶点P在对角线AC上滑动，直角的一边始终经过点B，另一边与边DC或射线DC相交于点Q。

①当点Q在边CD上时，线段PQ与线段PB之间有怎样的大小关系？试证明你观察得到的结论；②当点Q在边CD运动上时，设四边形PBCQ的面积为S时，试用含有x的代数式表示S：③当点P在线段AC上滑动时，△PCQ是否可能成为等腰三角形？如果可能，指出所有能使△PCQ成为等腰三角形的点Q的位置，并求出相应的x的值；如果不可能，试说明理由。

4. 在梯形ABCD 中，AB ∥CD,∠BCD=90,且AB=1,BC=2，tan ∠ADC=2;对角线相交于O 点，等腰直角三角板的直角顶点落在梯形的顶点C 上，使三角板绕点C 旋转。