新课标人教版高中生物必修三第四章第二节《种群数量
- 格式:ppt
- 大小:2.28 MB
- 文档页数:30
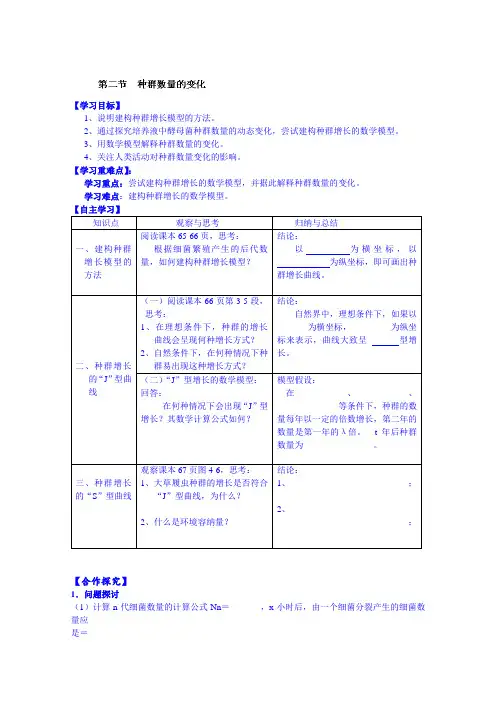
【学习目标】1、说明建构种群增长模型的方法。
2、通过探究培养液中酵母菌种群数量的动态变化,尝试建构种群增长的数学模型。
3、用数学模型解释种群数量的变化。
4、关注人类活动对种群数量变化的影响。
【学习重难点】:学习重点:尝试建构种群增长的数学模型,并据此解释种群数量的变化。
学习难点:建构种群增长的数学模型。
知识点观察与思考归纳与总结一、建构种群增长模型的方法阅读课本65-66页,思考:根据细菌繁殖产生的后代数量,如何建构种群增长模型?结论:以为横坐标,以____________为纵坐标,即可画出种群增长曲线。
二、种群增长的“J”型曲线(一)阅读课本66页第3-5段,思考:1、在理想条件下,种群的增长曲线会呈现何种增长方式?2、自然条件下,在何种情况下种群易出现这种增长方式?结论:自然界中,理想条件下,如果以_______为横坐标,_________为纵坐标来表示,曲线大致呈型增长。
(二)“J”型增长的数学模型:回答:在何种情况下会出现“J”型增长?其数学计算公式如何?模型假设:在____________、____________、______________等条件下,种群的数量每年以一定的倍数增长,第二年的数量是第一年的λ倍。
t年后种群数量为________________。
三、种群增长的“S”型曲线观察课本67页图4-6,思考:1、大草履虫种群的增长是否符合“J”型曲线,为什么?2、什么是环境容纳量?结论:1、___________________________;2、_______________________________________________________;【合作探究】1.问题探讨(1)计算n代细菌数量的计算公式Nn=_______,x小时后,由一个细菌分裂产生的细菌数量应是=_________(2)细菌种群数量按此速度繁殖的条件是_________________________________,试分析如果在一个培养基中,细菌的数量将如何变化?______________________________。

《种群的数量变动》说课稿尊敬的各位评委老师:大家好!今天我说课的题目是《种群的数量变动》。
下面我将从教材分析、学情分析、教学目标、教学重难点、教学方法、教学过程以及教学反思这几个方面来展开我的说课。
一、教材分析“种群的数量变动”是人教版高中生物必修 3《稳态与环境》第四章第二节的内容。
在此之前,学生已经学习了种群的特征,了解了种群的基本概念和一些基本的数量特征。
本节课则在此基础上,进一步探讨种群数量的变化规律,为后续学习群落的结构和演替等内容奠定基础。
本节课的内容主要包括两个方面:一是种群增长的“J”型曲线和“S”型曲线;二是种群数量的波动和下降。
通过对这两部分内容的学习,学生能够深入理解种群数量变化的本质和规律,认识到生物与环境之间的相互关系,培养学生的科学思维和环保意识。
二、学情分析授课对象为高二年级的学生,他们已经具备了一定的生物学知识和思维能力。
在之前的学习中,学生已经掌握了细胞增殖、生态系统的结构等相关知识,为理解种群数量的变动奠定了基础。
然而,种群数量的变化涉及到数学模型的构建和分析,对于学生的抽象思维和逻辑推理能力有一定的要求。
此外,学生对于实际生活中的种群数量变化现象可能缺乏系统的观察和思考。
三、教学目标1、知识目标(1)理解种群增长的“J”型曲线和“S”型曲线的含义、产生条件和特点。
(2)理解种群数量的波动和下降的原因。
2、能力目标(1)尝试构建种群增长的数学模型,培养学生的数学思维和分析问题的能力。
(2)通过分析种群数量的变化规律,培养学生运用所学知识解释和解决实际问题的能力。
3、情感态度与价值观目标(1)通过对种群数量变化的学习,使学生认识到生命的神奇和大自然的规律,培养学生热爱生命、尊重自然的情感。
(2)关注人类活动对种群数量变化的影响,增强学生的环保意识和社会责任感。
四、教学重难点1、教学重点(1)种群增长的“J”型曲线和“S”型曲线的含义和特点。
(2)“S”型曲线中 K 值的含义和应用。




第2节种群数量的变化知识点一构建种群增长模型的方法1.数学模型概念,数学模型是用来描述一个系统或它的性质的数学形式,是为了某种目的用字母、数字及其他数学符号建立起来的方程式以及图表、图像等数学表达式。
2.意义,数学模型是联系实际问题与数学规律的桥梁,具有解释、判断、预测等重要作用。
知识点二种群数量的增长,1.种群的“J”型增长(1)“J”型曲线:自然界确有类似细菌在理想条件下种群数量增长的形式,如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线则大致呈“J”型。
(2)“J”型增长的原因:食物充足、没有天敌、气候适宜等,这一理想条件只有在实验室或某物种最初进入一条件非常适宜的环境时才会出现。
(3)“J”型增长的数学模型,模型假设:在食物和空间条件充裕、气候适宜、没有敌害等条件下,种群的数量以一定的倍数增长,第二年是第一年的λ倍。
增长速率不随种群密度的变化而变化。
,建立模型:,一年后该种群的数量应为:N1=N0λ,两年后该种群的数量应为:N2=N1×λ=N0λ2,t年后该种群的数量应为:N t=N0λt,N0:该种群的起始数量;t:时间;N t:t年后种群数量;λ:增长的倍数。
注:当时,种群数量上升;当λ=1时,种群数量不变;当时,种群数量下降。
2.种群增长的“S”型曲线,(1)“S”型曲线出现的原因,自然资源是有限的,当种群密度增大时,使生存斗争加剧,种群的增长速率下降。
(2)实例:高斯的实验。
(3)“S”型曲线:种群经过一定时间的增长后,数量趋于稳定的增长曲线,呈“S”型。
①K值:在环境条件不受破坏的情况下,一定空间中所能维持的种群最大数量称为环境容纳量。
a.不同物种在同一环境中K值不同。
b.当环境改变时生物的K值改变。
②K/2值:K值的一半,是种群数量增长最快点。
③增长速率:可以看出种群的增长速率在K/2时最大,K/2之前不断增加,在K/2之后逐渐减小,当达到K值时增长速率为0。

第2节种群数量的变化知识点一构建种群增长模型的方法1.数学模型概念,数学模型是用来描述一个系统或它的性质的数学形式,是为了某种目的用字母、数字及其他数学符号建立起来的方程式以及图表、图像等数学表达式。
2.意义,数学模型是联系实际问题与数学规律的桥梁,具有解释、判断、预测等重要作用。
知识点二种群数量的增长,1.种群的“J”型增长(1)“J”型曲线:自然界确有类似细菌在理想条件下种群数量增长的形式,如果以时间为横坐标,种群数量为纵坐标画出曲线来表示,曲线则大致呈“J”型。
(2)“J”型增长的原因:食物充足、没有天敌、气候适宜等,这一理想条件只有在实验室或某物种最初进入一条件非常适宜的环境时才会出现。
(3)“J”型增长的数学模型,模型假设:在食物和空间条件充裕、气候适宜、没有敌害等条件下,种群的数量以一定的倍数增长,第二年是第一年的λ倍。
增长速率不随种群密度的变化而变化。
,建立模型:,一年后该种群的数量应为:N1=N0λ,两年后该种群的数量应为:N2=N1×λ=N0λ2,t年后该种群的数量应为:N t=N0λt,N0:该种群的起始数量;t:时间;N t:t年后种群数量;λ:增长的倍数。
注:当时,种群数量上升;当λ=1时,种群数量不变;当时,种群数量下降。
2.种群增长的“S”型曲线,(1)“S”型曲线出现的原因,自然资源是有限的,当种群密度增大时,使生存斗争加剧,种群的增长速率下降。
(2)实例:高斯的实验。
(3)“S”型曲线:种群经过一定时间的增长后,数量趋于稳定的增长曲线,呈“S”型。
①K值:在环境条件不受破坏的情况下,一定空间中所能维持的种群最大数量称为环境容纳量。
a.不同物种在同一环境中K值不同。
b.当环境改变时生物的K值改变。
②K/2值:K值的一半,是种群数量增长最快点。
③增长速率:可以看出种群的增长速率在K/2时最大,K/2之前不断增加,在K/2之后逐渐减小,当达到K值时增长速率为0。

