纠缠突然死亡
- 格式:doc
- 大小:31.00 KB
- 文档页数:2

量子纠缠对命运的解释量子纠缠是一种奇特的量子现象,其涉及两个或多个量子系统之间的关系,使得它们之间的相互作用不受空间距离的影响。
这意味着,当一个系统发生改变时,另一个系统也会感受到相应的改变,即使它们之间相隔很远,甚至是在不同的宇宙中。
这种微妙的纠缠关系引起了科学家们的极大兴趣,也在一定程度上解释了一些命运的问题。
科学家们认为,一旦两个或多个量子粒子之间建立了纠缠关系,它们就会成为不可分割的整体。
这意味着,在一个系统内发生的任何变化都会影响到与其纠缠的另一个系统。
这种量子纠缠看起来非常神奇和令人费解,但它的实际应用已经达到了前所未有的高度。
科学家们使用这种现象建造了最先进的计算机和加密系统,因此也被称为“未来技术”的核心之一。
在命运的角度来看,量子纠缠解释了人们对世界的看法。
我们经常认为我们所做的一切都是在独立的情境下发生的,但事实上,我们所做的任何事情都会影响到周围的人和环境,即使我们可能不知道或不关心我们所做的事情实际上在影响着其他人和事物。
更重要的是,量子纠缠还可以解释为什么会发生一些看似无法解释的巧合和灵验的事情。
根据量子纠缠的理论,当两个量子系统纠缠在一起时,它们之间的关系就像是一对“某种形式的爱情”,它们“彼此依存”并相互影响。
因此,当我们通过自己的思想和行动改变自己的命运时,我们实际上也会影响到周围的人和世界。
这种理论解释了我们如何独特地与周围世界互动,并为我们带来象征性的因果关系。
这种因果关系看起来与传统认识有所不同,但它解释了为什么某些人的命运似乎总是相似或陷入相似的生活路线中,而为什么另一些人在生活轨迹上走得更顺畅。
虽然这种理论很难证明,但它为人们提供了一种全新的思考方式,来解释和理解我们和周围世界之间的关系。
无论这种理论是否真实,我们可以从中得到一些启示,即我们的行为和思想确实有影响力,可以对我们的命运产生深远的影响。
因此,我们应该认真思考我们的行为和思想,以更好地掌控我们的命运,以及对周围的环境和人做出积极的贡献。

第1篇一、案情简介2019年6月,张某某(男,28岁)与李某某(女,26岁)因感情纠纷,在一家餐厅内发生激烈争吵。
在争吵过程中,双方情绪激动,互相拉扯,导致张某某倒地。
李某某见状,情绪失控,继续对张某某进行拉扯,致使张某某因心脏骤停死亡。
李某某随后被警方控制,并因涉嫌故意杀人罪被提起公诉。
二、案件经过1. 争吵起因张某某与李某某原本是一对恋人,但由于性格不合、价值观差异等问题,两人感情逐渐恶化。
2019年6月某日,两人因琐事发生争吵,矛盾升级。
2. 争吵过程争吵过程中,双方情绪激动,互相指责。
张某某指责李某某不关心自己,而李某某则认为张某某自私自利。
在争吵过程中,双方情绪愈发激动,张某某突然情绪失控,用力推了李某某一把。
3. 互相拉扯李某某被推后,情绪更加激动,她抓住张某某的衣服,两人开始互相拉扯。
张某某试图挣脱,但李某某力气较大,两人纠缠在一起。
在拉扯过程中,张某某突然倒地,李某某见状,情绪失控,继续对倒地的张某某进行拉扯。
4. 张某某死亡张某某倒地后,李某某继续对其进行拉扯,导致张某某心脏骤停。
周围群众发现后,立即拨打了急救电话。
但在医护人员赶到现场前,张某某已无生命体征。
5. 李某某被控制事发后,警方迅速赶到现场,将李某某控制。
经初步调查,李某某因涉嫌故意杀人罪被依法刑事拘留。
三、案件审理1. 公诉机关指控公诉机关认为,李某某在与张某某争吵过程中,情绪失控,故意对张某某进行拉扯,致使张某某心脏骤停死亡。
李某某的行为已构成故意杀人罪,应当依法追究其刑事责任。
2. 被告人辩解李某某在庭审中辩称,自己并非故意要杀害张某某,只是在与张某某争吵过程中情绪失控,拉扯张某某是出于自卫。
但公诉机关提供的证据显示,李某某在拉扯张某某的过程中,并未采取任何停止拉扯的行为,而是继续对其进行攻击。
3. 法院判决法院经审理认为,李某某在与张某某争吵过程中,情绪失控,故意对张某某进行拉扯,导致张某某心脏骤停死亡。
李某某的行为已构成故意杀人罪,依法应予严惩。
海森堡XYZ自旋链系统的热纠缠与局域量子不确定性研究张延亮;陈迪
【期刊名称】《原子与分子物理学报》
【年(卷),期】2024(41)2
【摘要】研究了热平衡温度,自旋交换相互作用,Dzyaloshinskii-Moriya(DM)相互作用及外加非一致性磁场对两比特海森堡XYZ自旋链量子系统的热纠缠与局域量子不确定度的影响,对比分析了并发度量子纠缠与局域量子不确定度描述自旋链系统量子关联的差别.结果表明自旋链系统的量子纠缠在热平衡温度,DM相互作用及外加磁场的非一致性参数的变化情况下均会出现纠缠突然死亡的再生现象,而自旋链系统的局域量子不确定度随着这些参数呈连续变化现象.并且,自旋交换相互作用,DM相互作用及外加横向磁场作用强度较小时,他们的变化对自旋链系统的量子纠缠与局域量子不确定度的影响有着明显的差别.
【总页数】7页(P117-123)
【作者】张延亮;陈迪
【作者单位】吉首大学计算机科学与工程学院
【正文语种】中文
【中图分类】O65
【相关文献】
1.一维自旋1的键交替海森堡模型中的量子纠缠和非局域序
2.两个二量子位海森堡XX链中热纠缠态的隐形传递(英文)
3.非均匀磁场作用下四量子比特海森堡自旋链
中的热纠缠4.二量子比特海森堡XYZ链中的热纠缠5.基于一个三量子比特海森堡链的热纠缠研究
因版权原因,仅展示原文概要,查看原文内容请购买。
量子失谐及其应用这篇文章中,简单介绍了一种新的非经典关联形式,量子失谐。
不同于传统的非经典关联,其存在于可分离态中。
对于量子失谐的度量方法,将介绍两种形式,一是采用互信息所定义的度量方式,另一种是经常使用的几何度量。
量子失谐具有某些独特的性质,如在非马尔科夫环境下,衰减的量子失谐可以从环境中恢复。
由于量子失谐优于纠缠的抗环境干扰能力,所以被用来取代纠缠应用于许多方面。
例如,在单量子位确定性计算中具有良好的稳定性;在远程量子态制备中表现出较高的保真度;以及在指示量子相变临界点时,展现出其他物理量所无法企及的准确性。
关键词:量子失谐;非经典关联;马尔科夫环境;非马尔科夫环境;量子信息绪论自20世纪初由爱因斯坦(Einstein)和玻尔(Bohr)等人发展而来的量子力学,以薛定谔(Schrödinger)建立的波动力学和海森堡(Heisenberg)建立的的矩阵力学作为工具,揭示并描述了微观世界物质的运动规律。
量子力学所描述的不同于经典物理的奇特的现象与规律也被一一呈现出来。
与人们从直接的感官所认识到的由波和粒子的运动模式构建的经典的世界不同,物质在微观世界中的运动具有波粒二相性,呈现出了态的叠加,不确定性以及量子相干性等特点。
之后,物理学家提出将这种性质应用于信息领域,从而诞生了量子信息这一新学科。
不同于经典信息,量子信息因其独特的性质天然地具有经典所无法达到的多种性质。
其中一个方面是应用在通信中,因其独特的量子性,使得在量子保密通信的协议中,信息的就收者可以察觉到通信是否被第三人窃听。
另外一个方面是在量子计算中。
传统的经典计算机在模拟量子系统时或者在处理某些算法时会遇到指数墙的问题,即计算量会随对象数量的增加而呈指数增长的现象。
但是利用量子态的叠加的性质,可以得到解决,从而提高计算速度,使得短期无法解决的问题在短时间内得到解决。
对于量子信息的实现方式,一直以来被认为是其核心的量子纠缠(entanglement),但是其在技术实现上存在很多问题,例如在环境噪声的干扰下因退相干而使其量子相干性消失而造成纠缠态的消失。
惊吓过度死亡的原理有哪些惊吓过度死亡,也被称为“惊吓死”,是指某个人在经历极度的惊吓或恐怖情境后突然死亡。
虽然这种情况非常罕见,但它确实存在,并且已经在一些案例中得到确认。
惊吓过度死亡的原理尚不完全清楚,但研究人员提出了几种可能的解释。
下面将探讨其中的几种主要原理。
1. 心脏问题:惊吓过度会导致心跳加速、心律不齐、心肌缺血等心脏问题,这可能是导致惊吓过度死亡的主要原因之一。
心脏受到惊吓刺激后,受到交感神经的激活,引发心脏异常搏动,甚至可能导致心脏骤停。
2. 血管收缩:当人体遭受惊吓时,肾上腺素和去甲肾上腺素等应激激素会被释放出来,这些物质可以引起血管收缩和血压升高。
连续或剧烈的血管收缩有可能导致脑部缺血或心脏供血不足,从而导致死亡。
3. 呼吸困难:在恐怖或惊吓的情况下,人体呼吸过快或恍惚,这可能导致低氧血症和二氧化碳激增,从而产生呼吸窘迫。
严重的呼吸窘迫可能导致意识丧失、休克和死亡。
4. 突发性脑血管意外:极度的惊吓可能引发突发性脑血管意外,如脑出血或脑梗塞。
这是因为惊吓引发的身体应激反应会导致体内肾上腺素水平升高,血管痉挛和血液凝固功能异常,从而增加脑血管意外发生的风险。
5. 恐慌障碍:有些个体在面临恐怖或惊吓的情况下可能会出现恐慌障碍。
恐慌障碍可能导致心跳加速、呼吸困难、出汗、胸闷等症状,严重的恐慌障碍被认为可能导致心律失常和心脏骤停。
6. 基础健康问题:某些情况下,个体的基础健康问题可能是导致惊吓过度死亡的触发因素。
例如,如果个体本身存在心脏疾病、呼吸系统疾病或其他潜在风险因素,那么遭受大惊小怪可能会导致这些隐患得到激活。
总结起来,惊吓过度死亡的原理涉及心脏问题、血管收缩、呼吸困难、突发性脑血管意外、恐慌障碍以及个体的基础健康问题。
然而,由于惊吓过度死亡案例相对罕见且复杂,目前还需要更多的科学研究来深入了解其机理。
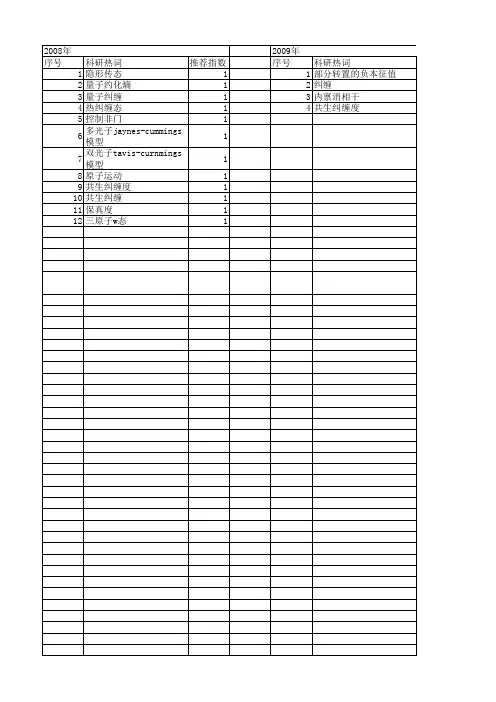
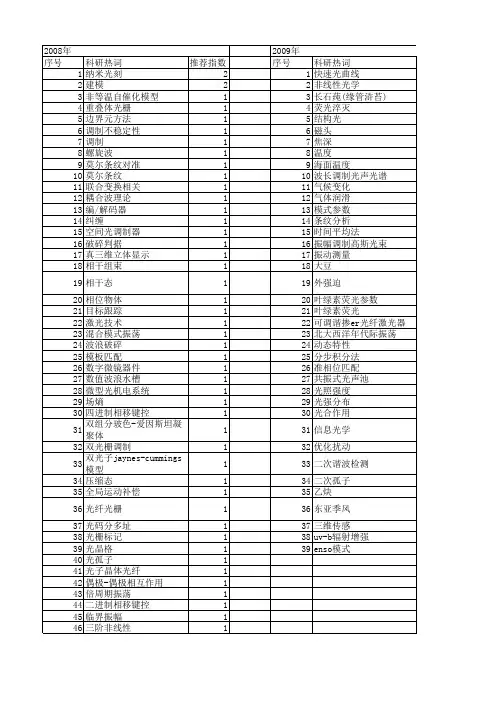
偶极相互作用对T-C模型中原子纠缠突然死亡的影响来源:《量子电子学报》2009年第06期作者:王忠纯;
1引言纠缠是量子力学最显著的特征之一,是量子物理与经典物理的根本区别川.在量子信息处理中纠缠是一个极其重要的资源,量子通信、量子密码和量子计算都依赖于量子纠缠[a]。
因此需要建立可靠的强纠缠源.近年来人们提出了多种纠缠态的制备方案,其中腔量子电动力学的方法最为成熟15].由于与背景噪声或其它系统的相互作用,所研究的量子系统会出现消相干,纠缠度减小.在一定条件下一对量子比特间的纠缠在一段时间内会突然衰变为0,称为纠缠突然死亡(Entanglement sudden death,EsD)I’].最近不少文献研究了ESD 现象[5一‘01.文献【l]研究了分别处于两个独立谐振腔中的两个原子间纠缠的演化,发现会出现ESD.文献[v]研究了二态下谐振腔中两个无相互作用的原子纠缠的演化,以及产生ESD的条件.文献[s1研究了双J一C模型中的纠缠不变量.文献田,10]分析了纠缠的演化与系统能量跃迁间的关系.最近已有人利用光学装置和原子系综的方法实验验证了EsD现象[l‘].本文将研究:态下丁hvis一cummings(T一C)模型中两个有偶极相互作用的原子间的纠缠,求出原子间的共生纠缠度(Concur(本文共计8页)......[继续阅读本文]
多光子T-C模型中二项式光场与两纠缠原子相互作用
的原子纠缠演化
来源:《内蒙古师范大学学报(自然科学汉文版)》2010年第01期
作者:包丽;萨楚尔夫;吴淑梅;
量子纠缠现象是量子力学特有的一种现象,是量子力学不同于经典物理最奇特、最不可思议的特征之一,它在量子信息处理过程中,扮演着极为重要的角色.人们对量子纠缠态的度量进行了广泛研究,相继提出了描述纠缠度的物理量,如Von Neumann熵[1]、密度算符之间的距离[2]、共生纠缠度[3]、部分转置矩阵负本征值[4]等.近几十年来,量子光学的重大进展之一就是构造出许多光场的非经典态,二项式光场就是其中之一.二项式态定义如下[5]:|ηM〉=∑Mn=0βMn|n〉(0<η<1,M>0),βMn=M!n!(M-n)!ηn(1-η)M-n12,(1)其中M为正整数.二项式态光子数的分布〈n|ηM〉2=βMn2对应概率论中的二项式分布,表现为亚泊松分布,当η=0,1时,|ηM〉分别约化为真空态和数态,而当η→0,M→∞,但ηM=α2(α为实数)时,|ηM〉为相干态.因此二项式态是介于相干态和Fock态的一种量子态,故有文献称其为中间态[6].目前,人们对Jaynes-Cummings模型中原子与光场的纠缠特性[7-8]和Tavis-Cummings模型中两原子的纠缠特性[9-13]有了较多的了解,但大(本文共计5页)......[继续阅读本文]。