数学空间几何专题

小学数学空间与图形专题(试题+答案) 图形与几何试题一、填空题（19分）1.从直线外一点到这条直线可以画无数条线段，其中最短的是与这条直线垂直的线段。

2.半圆的直径是10厘米，它的周长是π×10厘米。

3、圆柱的体积比与它等底等高的圆锥的体积大π:3.4.一个三角形中，最小的角是46°，按角分类，这个三角形是锐角三角形。

5.用百分数表示以下阴影部分是整个图形面积的百分之几。

6.把一个底面直径2分米的圆柱体截去一个高1分米的圆柱体，原来的圆柱体表面积减少π平方分米。

7.“∠ABC=60°”和“∠DEF=120°”的周长之比是2:1，面积之比是1:4.8.画一个周长25.12厘米的圆，圆规两脚间的距离是12.56厘米，画成的圆的面积是100π平方厘米。

9.一个梯形，上底长a厘米，下底长b厘米，高h厘米。

它的面积是(a+b)h/2平方厘米。

如果a=b，那么这个图形就是一个菱形。

10.在一块边长是20厘米的正方形木板上锯下一个最大的圆，这个圆的面积是100π平方厘米，剩下的边料是(400-100π)平方厘米。

11.5个棱长为30厘米的正方体木箱堆放在墙角（如下图），露在外面的表面积是1500平方厘米。

12、如图所示，把底面周长18.84厘米、高1分米的圆柱切成若干等分，拼成一个近似的长方体。

这个长方体的右侧面积是π平方厘米。

二、判断题（7分）1.小于18°的角是锐角。

（错）2.用一副三角板可以拼成105°的角。

（对）3.只要有一个角是直角的平行四边形，就是长方形或正方形。

（错）4.如果圆柱的底面周长和高相等，则它的侧面展开一定是个长方形。

（错）5.把一个长方形拉成一个平行四边形后，保持不变的是面积。

（对）6.一个正方形的边长与一个圆的直径相等，那么这个正方形的周长一定大于圆的周长。

（错）7.长6厘米的正方体，表面积和体积相等。

（错）三、选择题（每题1.5分共18分）1.有2cm,3cm，4cm,6cm长的小棒各1根，选其中的3根小棒围成三角形，最多可以围成4个。

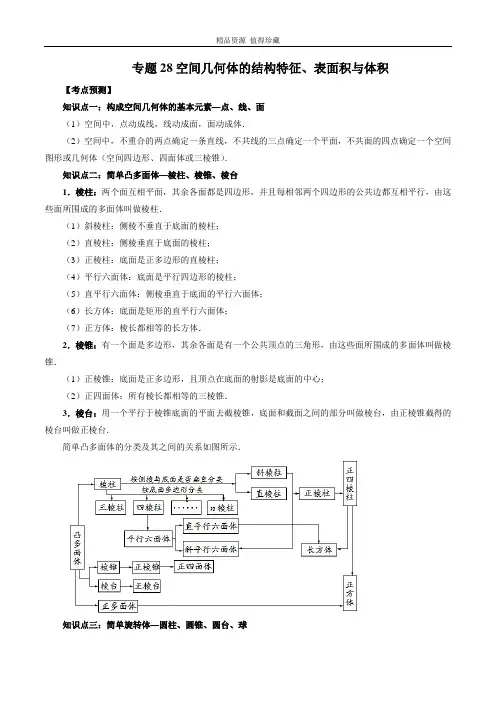
专题28空间几何体的结构特征、表面积与体积【考点预测】知识点一：构成空间几何体的基本元素—点、线、面（1）空间中，点动成线，线动成面，面动成体．（2）空间中，不重合的两点确定一条直线，不共线的三点确定一个平面，不共面的四点确定一个空间图形或几何体（空间四边形、四面体或三棱锥）．知识点二：简单凸多面体—棱柱、棱锥、棱台1．棱柱：两个面互相平面，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱．（1）斜棱柱：侧棱不垂直于底面的棱柱；（2）直棱柱：侧棱垂直于底面的棱柱；（3）正棱柱：底面是正多边形的直棱柱；（4）平行六面体：底面是平行四边形的棱柱；（5）直平行六面体：侧棱垂直于底面的平行六面体；（6）长方体：底面是矩形的直平行六面体；（7）正方体：棱长都相等的长方体．2．棱锥：有一个面是多边形，其余各面是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥．（1）正棱锥：底面是正多边形，且顶点在底面的射影是底面的中心；（2）正四面体：所有棱长都相等的三棱锥．3．棱台：用一个平行于棱锥底面的平面去截棱锥，底面和截面之间的部分叫做棱台，由正棱锥截得的棱台叫做正棱台．简单凸多面体的分类及其之间的关系如图所示．知识点三：简单旋转体—圆柱、圆锥、圆台、球1．圆柱：以矩形的一边所在的直线为旋转轴，其余三边旋转形成的面所围成的几何体叫做圆柱．2．圆柱：以直角三角形的一条直角边所在的直线为旋转轴，将其旋转一周形成的面所围成的几何体叫做圆锥．3．圆台：用平行于圆锥底面的平面去截圆锥，底面和截面之间的部分叫做圆台．4．球：以半圆的直径所在的直线为旋转轴，半圆面旋转一周形成的旋转体叫做球体，简称为球（球面距离：经过两点的大圆在这两点间的劣弧长度）．知识点四：组合体由柱体、锥体、台体、球等几何体组成的复杂的几何体叫做组合体．知识点五：表面积与体积计算公式表面积公式体积公式1．斜二测画法斜二测画法的主要步骤如下：（1）建立直角坐标系．在已知水平放置的平面图形中取互相垂直的Ox ，Oy ，建立直角坐标系． （2）画出斜坐标系．在画直观图的纸上（平面上）画出对应图形．在已知图形平行于x 轴的线段，在直观图中画成平行于''O x ，''O y ，使45'''∠=x O y （或135），它们确定的平面表示水平平面．（3）画出对应图形．在已知图形平行于x 轴的线段，在直观图中画成平行于'x 轴的线段，且长度保持不变；在已知图形平行于y 轴的线段，在直观图中画成平行于'y 轴，且长度变为原来的一般．可简化为“横不变，纵减半”．（4）擦去辅助线．图画好后，要擦去'x 轴、'y 轴及为画图添加的辅助线（虚线）．被挡住的棱画虚线． 注：4． 2．平行投影与中心投影平行投影的投影线是互相平行的，中心投影的投影线相交于一点．【题型归纳目录】题型一：空间几何体的结构特征 题型二：空间几何体的表面积与体积 题型三：直观图 题型四：最短路径问题 【典例例题】题型一：空间几何体的结构特征例1．（2022·全国·模拟预测）以下结论中错误的是（ ） A ．经过不共面的四点的球有且仅有一个 B ．平行六面体的每个面都是平行四边形 C ．正棱柱的每条侧棱均与上下底面垂直 D ．棱台的每条侧棱均与上下底面不垂直例2．（2022·全国·高三专题练习（文））下列说法正确的是（ ） A ．经过三点确定一个平面B ．各个面都是三角形的多面体一定是三棱锥C ．各侧面都是正方形的棱柱一定是正棱柱D ．一个三棱锥的四个面可以都为直角三角形例3．（2022·海南·模拟预测）“三棱锥P ABC -是正三棱锥”的一个必要不充分条件是（ ） A ．三棱锥P ABC -是正四面体 B ．三棱锥P ABC -不是正四面体 C ．有一个面是正三角形 D ．ABC 是正三角形且PA PB PC ==例4．（2022·全国·高三专题练习）给出下列命题:①在圆柱的上、下底面的圆周上各取一点,则这两点的连线是圆柱的母线; ②有一个面是多边形,其余各面都是三角形的几何体是棱锥;③直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥; ④棱台的上、下底面可以不相似,但侧棱长一定相等. 其中正确命题的个数是（ ） A ．0 B ．1C ．2D ．3例5．（2022·山东省东明县第一中学高三阶段练习）下列说法正确的是（ ） A ．有两个面平行，其余各面都是平行四边形的几何体叫棱柱 B ．过空间内不同的三点，有且只有一个平面 C ．棱锥的所有侧面都是三角形D ．用一个平面去截棱锥，底面与截面之间的部分组成的几何体叫棱台例6．（2022·全国·高三专题练习）给出下列命题：①在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线； ②直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥； ③棱台的上、下底面可以不相似，但侧棱长一定相等. 其中正确命题的个数是（ ） A ．0 B ．1C ．2D ．3例7．（2022·全国·高三专题练习）莱昂哈德·欧拉，瑞士数学家和物理学家，近代数学先驱之一，他的研究论著几乎涉及到所有数学分支，有许多公式､定理､解法､函数､方程､常数等是以欧拉名字命名的.欧拉发现，不论什么形状的凸多面体，其顶点数V ､棱数E ､面数F 之间总满足数量关系2,V F E +-=，此式称为欧拉公式，已知某凸32面体，12个面是五边形，20个面是六边形，则该32面体的棱数为___________；顶点的个数为___________.例8．（2022·安徽·合肥一六八中学模拟预测（理））如图，正方体1AC 上、下底面中心分别为1O ，2O ，将正方体绕直线12O O 旋转360︒，下列四个选项中为线段1AB 旋转所得图形是（ ）A ．B ．C ．D ．例9．（多选题）（2022·全国·高三专题练习）如图所示，观察四个几何体，其中判断正确的是（ ）（多选）A ．①是棱台B ．②是圆台C ．③是棱锥D ．④是棱柱例10．（2022·陕西·西北工业大学附属中学高三阶段练习（理））碳60（60C ）是一种非金属单质，它是由60个碳原子构成的分子，形似足球，又称为足球烯，其结构是由五元环（正五边形面）和六元环（正六边形面）组成的封闭的凸多面体，共32个面，且满足：顶点数－棱数＋面数＝2．则其六元环的个数为__________.【方法技巧与总结】 熟悉几何体的基本概念.题型二：空间几何体的表面积与体积例11．（多选题）（2022·湖北·高三阶段练习）折扇是我国古老文化的延续，在我国已有四千年左右的历史，“扇”与“善”谐音，折扇也寓意“善良”“善行”．它常以字画的形式体现我国的传统文化，也是运筹帷幄､决胜千里､大智大勇的象征（如图1）．图2是一个圆台的侧面展开图（扇形的一部分），若两个圆弧,DE AC 所在圆的半径分别是3和9，且120ABC ∠=，则该圆台的（ ）A ．高为BC ．表面积为34πD ．上底面积､下底面积和侧面积之比为1:9:22例12．（2022·青海·海东市第一中学模拟预测（理））设一圆锥的侧面积是其底面积的3倍，则该圆锥的高与母线长的比值为（ ）A ．89B C D ．23例13．（2022·云南·二模（文））已知长方体1111ABCD A B C D -的表面积为62，所有棱长之和为40，则线段1AC 的长为（ ）A B C D例14．（2022·福建省福州第一中学三模）已知AB ，CD 分别是圆柱上､下底面圆的直径，且AB CD ⊥，.1O ，O 分别为上､下底面的圆心，若圆柱的底面圆半径与母线长相等，且三棱锥A BCD -的体积为18，则该圆柱的侧面积为（ ） A ．9π B ．12π C ．16π D ．18π例15．（2022·河南·模拟预测（文））在正四棱锥P ABCD -中，AB =P ABCD -的体积是8，则该四棱锥的侧面积是（ ）AB ．C ．D ．例16．（2022·全国·高三专题练习）《九章算术》中将正四棱台体（棱台的上下底面均为正方形）称为方亭.如图，现有一方亭ABCD EFHG -，其中上底面与下底面的面积之比为1:4，方亭的高h EF =，BF =，方亭的四个侧面均为全等的等腰梯形，已知方亭四个侧面的面积之和 ）A ．24B ．643C ．563D ．16例17．（2022·湖南·高三阶段练习）如图，一种棱台形状的无盖容器（无上底面1111D C B A ）模型其上、下底面均为正方形，面积分别为24cm ，29cm ，且1111A A B B C C D D ===，若该容器模型的体积为319cm 3，则该容器模型的表面积为（ ）A ．()29cmB ．219cmC ．()29cmD ．()29cm例18．（2022·海南海口·二模）如图是一个圆台的侧面展开图，其面积为3π，两个圆弧所在的圆半径分别为2和4，则该圆台的体积为（ ）A B C D例19．（2022·全国·高三专题练习）圆台上、下底面的圆周都在一个直径为10的球面上，其上、下底面的半径分别为4和5，则该圆台的侧面积为（ ）A ．B ．C ．D ．例20．（2022·河南安阳·模拟预测（文））已知圆柱12O O 的底面半径为1，高为2，AB ，CD 分别为上、下底面圆的直径，AB CD ⊥，则四面体ABCD 的体积为（ ） A ．13B ．23C ．1D ．43例21．（2022·山东·烟台市教育科学研究院二模）鲁班锁是我国传统的智力玩具，起源于中国古代建筑中的榫卯结构，其内部的凹凸部分啮合十分精巧．图1是一种鲁班锁玩具，图2是其直观图．它的表面由八个正三角形和六个正八边形构成，其中每条棱长均为2．若该玩具可以在一个正方体内任意转动（忽略摩擦），则此正方体表面积的最小值为________．例22．（2022·湖北省天门中学模拟预测）已知一个圆柱的体积为2 ，底面直径与母线长相等，圆柱内有一个三棱柱，与圆柱等高，底面是顶点在圆周上的正三角形，则三棱柱的侧面积为__________.例23．（2022·上海闵行·二模）已知一个圆柱的高不变，它的体积扩大为原来的4倍，则它的侧面积扩大为原来的___________倍.例24．（2022·浙江绍兴·模拟预测）有书记载等角半正多面体是以边数不全相同的正多边形为面的多面体，如图，将正四面体沿相交于同一个顶点的三条梭上的3个点截去一个正三棱锥，如此共截去4个正三棱锥，若得到的几何体是一个由正三角形与正六边形围成的等角半正多面体，且正六边形的面积为2，则原正四面体的表面积为_________．例25．（2022·上海徐汇·三模）设圆锥底面圆周上两点A、B间的距离为2，圆锥顶点到直线ABAB和圆锥的轴的距离为1，则该圆锥的侧面积为___________.例26．（2022·全国·高三专题练习）中国古代的“牟合方盖”可以看作是两个圆柱垂直相交的公共部分，计算其体积所用的“幂势即同，则积不容异”是中国古代数学的研究成果，根据此原理，取牟合方盖的一半，其体积等于与其同底等高的正四棱柱中，去掉一个同底等高的正四棱锥之后剩余部分的体积（如图1所示）．现将三个直径为4的圆柱放于同一水平面上，三个圆柱的轴所在的直线两两成角都相等，三个圆柱的公共部分为如图2，则该几何体的体积为___________．【方法技巧与总结】熟悉几何体的表面积、体积的基本公式，注意直角等特殊角. 题型三：直观图例27．（2022·全国·高三专题练习）如图，已知用斜二测画法画出的ABC 的直观图是边长为a 的正三角形，原ABC 的面积为 __．例28．（2022·浙江·镇海中学模拟预测）如图，梯形ABCD 是水平放置的一个平面图形的直观图，其中45ABC ∠=︒，1AB AD ==，DC BC ⊥，则原图形的面积为（ ）A ．1B ．2C ．2D ．1例29．（2022·全国·高三专题练习）如图，△ABC 是水平放置的△ABC 的斜二测直观图，其中2O C O A O B ''''''==，则以下说法正确的是（ ）A ．△ABC 是钝角三角形B ．△ABC 是等边三角形C ．△ABC 是等腰直角三角形D ．△ABC 是等腰三角形，但不是直角三角形例30．（2022·全国·高三专题练习）如图，水平放置的四边形ABCD 的斜二测直观图为矩形A B C D ''''，已知2,2A O O B B C =='''''='，则四边形ABCD 的周长为（ ）A ．20B ．12C ．8+D ．8+例31．（2022·全国·高三专题练习（文））如图，已知等腰直角三角形O A B '''△，O A A B ''''=是一个平面图形的直观图，斜边2O B ''=，则这个平面图形的面积是（ ）A B ．1 C D ．例32．（2022·全国·高三专题练习）一个三角形的水平直观图在x O y '''是等腰三角形，底角为30，腰长为2，如图，那么它在原平面图形中，顶点B 到x 轴距离是（ ）A ．1B ．2CD ．【方法技巧与总结】斜二测法下的直观图与原图面积之间存在固定的比值关系：S 直原． 题型四：最短路径问题例33．（多选题）（2022·广东广州·三模）某班级到一工厂参加社会实践劳动，加工出如图所示的圆台12O O ，在轴截面ABCD 中，2cm AB AD BC ===，且2CD AB =，则（ ）A ．该圆台的高为1cmB ．该圆台轴截面面积为2C 3D ．一只小虫从点C 沿着该圆台的侧面爬行到AD 的中点，所经过的最短路程为5cm例34．（2022·河南洛阳·三模（理））在棱长为1的正方体1111ABCD A B C D -中，点E 为1CC 上的动点，则1D E EB +的最小值为___________.例35．（2022·黑龙江齐齐哈尔·二模（文））如图，在直三棱柱111ABC A B C -中，12,1,90AA AB BC ABC ===∠=︒，点E 是侧棱1BB 上的一个动点，则下列判断正确的有___________.（填序号）②存在点E ，使得1A EA ∠为钝角③截面1AEC 周长的最小值为例36．（2022·河南·二模（理））在正方体1111ABCD A B C D -中，2AB =，P 是线段1BC 上的一动点，则1A P PC +的最小值为________.例37．（2022·陕西宝鸡·二模（文））如图，在正三棱锥P ABC -中，30APB BPC CPA ∠=∠=∠=，4PA PB PC ===，一只虫子从A 点出发，绕三棱锥的三个侧面爬行一周后，又回到A 点，则虫子爬行的最短距离是___________.例38．（2022·安徽宣城·二模（理））已知正四面体ABCD 的棱长为2，P 为AC 的中点，E 为AB 中点，M 是DP 的动点，N 是平面ECD 内的动点，则||||AM MN +的最小值是_____________.例39．（2022·新疆阿勒泰·三模（理））如图，圆柱的轴截面ABCD 是一个边长为4的正方形.一只蚂蚁从点A 出发绕圆柱表面爬到BC 的中点E ，则蚂蚁爬行的最短距离为（ ）A ．B ．C ．D例40．（2022·云南·昆明一中高三阶段练习（文））一竖立在水平地面上的圆锥形物体，一只蚂蚁从圆锥底面圆周上一点P 出发，绕圆锥表面爬行一周后回到P 点，已知圆锥底面半径为1，母线长为3，则蚂蚁爬行的最短路径长为（ ）A ．3B ．C ．πD ．2π【方法技巧与总结】此类最大路径问题：大胆展开，把问题变为平面两点间线段最短问题． 【过关测试】一、单选题1．（2022·河北·高三阶段练习）已知圆锥的高为1，则过此圆锥顶点的截面面积的最大值为（ ）A ．2B ．52C D ．32．（2022·全国·模拟预测（文））若过圆锥的轴SO 的截面为边长为4的等边三角形，正方体1111ABCD A B C D -的顶点A ，B ，C ，D 在圆锥底面上，1A ，1B ，1C ，1D 在圆锥侧面上，则该正方体的棱长为（ ）A ．B ．C ．(2D ．(23．（2022·全国·高三专题练习）已知圆锥的轴截面是等腰直角三角形，且面积为4，则圆锥的体积为（ ） A ．43 B ．43πC ．83D ．83π4．（2022·广东深圳·高三阶段练习）通用技术老师指导学生制作统一规格的圆台形容器，用如图所示的圆环沿虚线剪开得到的一个半圆环（其中小圆和大圆的半径分别是1cm 和4cm ）制作该容器的侧面，则该圆台形容器的高为（ ）AB ．1cmCD 5．（2022·全国·高三专题练习）已知一个直三棱柱的高为2，如图，其底面ABC 水平放置的直观图（斜二测画法）为A B C '''，其中1O A O B O C ''''''===，则此三棱柱的表面积为（ ）A．4+B ．8+C ．8+D ．8+6．（2022·湖北·天门市教育科学研究院模拟预测）已知某圆锥的侧面积为的半径为（ ） A ．2B ．3C ．4D ．67．（2022·山西大同·高三阶段练习）正四棱台的上､下底面的边长分别为2､4，侧棱长为2，则其体积为（ ）A ．56B C ．D ．5638．（2022·江西九江·三模（理））如图，一个四分之一球形状的玩具储物盒，若放入一个玩具小球，合上盒盖，可放小球的最大半径为r .若是放入一个正方体，合上盒盖，可放正方体的最大棱长为a ，则ra=（ ）A B ．34C ．2D ．)3129．（2022·浙江湖州·模拟预测）如图，已知四边形ABCD ，BCD △是以BD 为斜边的等腰直角三角形，ABD △为等边三角形，2BD =，将ABD △沿对角线BD 翻折到PBD △在翻折的过程中，下列结论中不正确．．．的是（ ）A ．BD PC ⊥B ．DP 与BC 可能垂直C ．直线DP 与平面BCD 所成角的最大值是45︒D ．四面体PBCD 10．（2022·全国·高三专题练习）南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔1485m ．时，相应水面的面积为21400km ．；水位为海拔1575m ．时，相应水面的面积为21800km ．，将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔1485m ．上升到1575m ．2.65≈）（ ） A ．931.010m ⨯ B ．931.210m ⨯C ．931.410m ⨯D ．931.610m ⨯二、多选题11．（2022·河北·高三阶段练习）如图，正方体1111ABCD A B C D -棱长为1，P 是1A D 上的一个动点，下列结论中正确的是（ ）A ．BPB ．PA PC +C ．当P 在直线1AD 上运动时，三棱锥1B ACP -的体积不变D ．以点B 1AB C 12．（2022·全国·高三专题练习）如图，四边形ABCD 为正方形，ED ⊥平面ABCD ，,2FB ED AB ED FB ==∥，记三棱锥E ACD -，F ABC -，F ACE -的体积分别为123,,V V V ，则（ ）A ．322V V =B ．31V V =C ．312V V V =+D ．3123V V =13．（2022·江苏·常州高级中学模拟预测）棱长为1的正方体1111ABCD A B C D -中，点P 为线段1A C 上的动点，点M ，N 分别为线段11A C ，1CC 的中点，则下列说法正确的是（ ） A ．11A P AB ⊥ B ．三棱锥1M B NP -的体积为定值 C ．[]160,120APD ∠∈︒︒D ．1AP D P +的最小值为2314．（2022·湖北·高三阶段练习）折扇是我国古老文化的延续，在我国已有四千年左右的历史，“扇”与“善”谐音，折扇也寓意“善良”“善行”．它常以字画的形式体现我国的传统文化，也是运筹帷幄､决胜千里､大智大勇的象征（如图1）．图2是一个圆台的侧面展开图（扇形的一部分），若两个圆弧,DE AC 所在圆的半径分别是3和9，且120ABC ∠=，则该圆台的（ ）A ．高为B ．体积为3C ．表面积为34πD ．上底面积､下底面积和侧面积之比为1:9:22三、填空题15．（2022·全国·高三专题练习）已知一三角形ABCA B C '''(如图)，则三角形ABC 中边长与正三角形A B C '''的边长相等的边上的高为______．16．（2022·上海·模拟预测）已知圆柱的高为4，底面积为9π，则圆柱的侧面积为___________；17．（2022·新疆·三模（理））已知一个棱长为a 的正方体木块可以在一个圆锥形容器内任意转动，若圆锥的底面半径为1，母线长为2，则a 的最大值为______.18．（2022·吉林长春·高三阶段练习（理））中国古代数学家刘徽在《九章算术注》中，称一个正方体内两个互相垂直的内切圆柱所围成的立体为“牟合方盖”，如图（1）（2）.刘徽未能求得牟合方盖的体积，直言“欲陋形措意，惧失正理”，不得不说“敢不阙疑，以俟能言者”.约200年后，祖冲之的儿子祖暅提出“幂势既同，则积不容异”，后世称为祖暅原理，即：两等高立体，若在每一等高处的截面积都相等，则两立体体积相等，如图（3）（4）.已知八分之一的正方体去掉八分之一的牟合方盖后的剩余几何体与长宽高皆为八分之一正方体棱长的倒四棱锥“等幂等积”，祖暅由此推算出牟合方盖的体积.据此可知，若正方体的棱长为1，则其牟合方盖的体积为______. 四、解答题19．（2022·吉林·长春市第二实验中学高三阶段练习）如图，已知四棱锥P ABCD -中，PD ⊥平面ABCD ，且1,4,5AB DC AB DC PM PC ==∥.(1)求证：PA 平面MDB ；(2)当直线,PC PA 与底面ABCD 所成的角都为4π，且4,DC DA AB =⊥时，求出多面体MPABD 的体积.20．（2022·全国·南宁二中高三期末（文））图1是由矩形ABGF ，Rt ADE △和菱形ABCD 组成的一个平面图形，其中2AB =，1==AE AF ，60BAD ∠=︒，将该图形沿AB ，AD 折起使得AE 与AF 重合，连接CG ，如图2.(1)证明：图2中的C ，D ，E ，G 四点共面； (2)求图2中三棱锥C BDG -的体积.21．（2022·全国·高三专题练习）如图，三棱柱ABC －A 1B 1C 1中，已知AB ⊥侧面BB 1C 1C ，AB ＝BC ＝1，BB 1＝2，∠BCC 1＝60°．(1)求证：BC 1⊥平面ABC ；(2)E 是棱CC 1上的一点，若三棱锥E －ABC CE 的长．22．（2022·青海·海东市第一中学模拟预测（文））如图，在三棱柱111ABC A B C -中，112224AC AA AB AC BC =====，160BAA ∠=︒．(1)证明：平面ABC ⊥平面11AA B B ．(2)设P 是棱1CC 上一点，且12CP PC =，求三棱锥111A PB C -体积．。

高考数学二轮复习考点知识与题型专题讲解第31讲 空间几何体[考情分析] 空间几何体的结构特征是立体几何的基础，空间几何体的表面积和体积是高考的重点与热点，多以选择题、填空题的形式考查，难度中等或偏上．考点一 空间几何体的折展问题核心提炼空间几何体的侧面展开图 1．圆柱的侧面展开图是矩形． 2．圆锥的侧面展开图是扇形． 3．圆台的侧面展开图是扇环．例1 (1)“莫言下岭便无难，赚得行人空喜欢．”出自南宋诗人杨万里的作品《过松源晨炊漆公店》．如图是一座山的示意图，山大致呈圆锥形，山脚呈圆形，半径为40 km ，山高为4015 km ，B 是山坡SA 上一点，且AB ＝40 km.为了发展旅游业，要建设一条从A 到B 的环山观光公路，这条公路从A 出发后先上坡，后下坡，当公路长度最短时，下坡路段长为( )A ．60 kmB ．12 6 kmC ．72 kmD ．1215 km 答案 C解析 该圆锥的母线长为(4015)2＋402＝160， 所以圆锥的侧面展开图是圆心角为2×π×40160＝π2的扇形，如图，展开圆锥的侧面，连接A ′B ，由两点之间线段最短，知观光公路为图中的A ′B ，A ′B ＝SA ′2＋SB 2＝1602＋1202＝200， 过点S 作A ′B 的垂线，垂足为H ，记点P 为A ′B 上任意一点，连接PS ，当上坡时，P 到山顶S 的距离PS 越来越小，当下坡时，P 到山顶S 的距离PS 越来越大， 则下坡段的公路为图中的HB ， 由Rt △SA ′B ∽Rt △HSB ， 得HB ＝SB 2A ′B ＝1202200＝72(km)．(2)(2022·深圳检测)如图，在三棱锥P －ABC 的平面展开图中，AC ＝3，AB ＝1，AD ＝1，AB ⊥AC ，AB ⊥AD ，∠CAE ＝30°，则cos ∠FCB 等于( )A.12B.13C.35D.34 答案 D解析 由题意知，AE ＝AD ＝AB ＝1，BC ＝2， 在△ACE 中，由余弦定理知， CE 2＝AE 2＋AC 2－2AE ·AC ·cos ∠CAE ＝1＋3－2×1×3×32＝1， ∴CE ＝CF ＝1，而BF ＝BD ＝2，BC ＝2，∴在△BCF 中，由余弦定理知，cos ∠FCB ＝BC 2＋CF 2－BF 22BC ·CF ＝4＋1－22×2×1＝34.规律方法 空间几何体最短距离问题，一般是将空间几何体展开成平面图形，转化成求平面中两点间的最短距离问题，注意展开后对应的顶点和边．跟踪演练1 (1)(多选)如图是一个正方体的展开图，如果将它还原为正方体，则下列说法中正确的是( )A ．C ∈GHB ．CD 与EF 是共面直线C ．AB ∥EFD ．GH 与EF 是异面直线 答案 ABD解析 由图可知，还原正方体后，点C 与G 重合， 即C ∈GH ，又可知CD 与EF 是平行直线，即CD 与EF 是共面直线，AB 与EF 是相交直线(点B 与点F 重合)，GH 与EF 是异面直线，故A ，B ，D 正确，C 错误．(2)如图，在正三棱锥P －ABC 中，∠APB ＝∠BPC ＝∠CP A ＝30°，P A ＝PB ＝PC ＝2，一只虫子从A 点出发，绕三棱锥的三个侧面爬行一周后，又回到A 点，则虫子爬行的最短距离是( )A ．32B ．3 3C ．23D ．2 2 答案 D解析 将三棱锥由P A 展开，如图所示，则∠AP A 1＝90°，所求最短距离为AA 1的长度，∵P A ＝2， ∴由勾股定理可得 AA 1＝22＋22＝2 2.∴虫子爬行的最短距离为2 2.考点二 表面积与体积核心提炼1．旋转体的侧面积和表面积(1)S 圆柱侧＝2πrl ，S 圆柱表＝2πr (r ＋l )(r 为底面半径，l 为母线长)． (2)S 圆锥侧＝πrl ，S 圆锥表＝πr (r ＋l )(r 为底面半径，l 为母线长)． (3)S 球表＝4πR 2(R 为球的半径)． 2．空间几何体的体积公式(1)V 柱＝Sh (S 为底面面积，h 为高)． (2)V 锥＝13Sh (S 为底面面积，h 为高)．(3)V 台＝13(S 上＋S 上·S 下＋S 下)h (S 上，S 下为底面面积，h 为高)．(4)V 球＝43πR 3(R 为球的半径)．例2 (1)(2022·全国甲卷)甲、乙两个圆锥的母线长相等，侧面展开图的圆心角之和为2π，侧面积分别为S 甲和S 乙，体积分别为V 甲和V 乙．若S 甲S 乙＝2，则V 甲V 乙等于( )A. 5 B ．2 2 C.10 D.5104答案 C解析 方法一因为甲、乙两个圆锥的母线长相等，所以结合S 甲S 乙＝2，可知甲、乙两个圆锥侧面展开图的圆心角之比是2∶1.不妨设两个圆锥的母线长为l ＝3，甲、乙两个圆锥的底面半径分别为r 1，r 2，高分别为h 1，h 2， 则由题意知，两个圆锥的侧面展开图刚好可以拼成一个周长为6π的圆， 所以2πr 1＝4π，2πr 2＝2π，得r 1＝2，r 2＝1. 由勾股定理得，h 1＝l 2－r 21＝5，h 2＝l 2－r 22＝22，所以V 甲V 乙＝13πr 21h113πr 22h 2＝4522＝10.方法二 设两圆锥的母线长为l ，甲、乙两圆锥的底面半径分别为r 1，r 2，高分别为h 1，h 2，侧面展开图的圆心角分别为n 1，n 2， 则由S 甲S 乙＝πr 1l πr 2l ＝n 1πl 22πn 2πl22π＝2，得r 1r 2＝n 1n 2＝2. 由题意知n 1＋n 2＝2π， 所以n 1＝4π3，n 2＝2π3，所以2πr 1＝4π3l ，2πr 2＝2π3l ，得r 1＝23l ，r 2＝13l .由勾股定理得，h 1＝l 2－r 21＝53l ， h 2＝l 2－r 22＝223l ， 所以V 甲V 乙＝13πr 21h113πr 22h 2＝4522＝10.(2)(多选)(2022·新高考全国Ⅱ)如图，四边形ABCD 为正方形，ED ⊥平面ABCD ，FB ∥ED ，AB ＝ED ＝2FB .记三棱锥E －ACD ，F －ABC ，F －ACE 的体积分别为V 1，V 2，V 3，则( )A ．V 3＝2V 2B ．V 3＝V 1C ．V 3＝V 1＋V 2D ．2V 3＝3V 1 答案 CD解析 如图，连接BD交AC 于O ，连接OE ，OF .设AB ＝ED ＝2FB ＝2， 则AB ＝BC ＝CD ＝AD ＝2， FB ＝1.因为ED ⊥平面ABCD ，FB ∥ED ， 所以FB ⊥平面ABCD ，所以V 1＝V E －ACD ＝13S △ACD ·ED ＝13×12AD ·CD ·ED ＝13×12×2×2×2＝43，V 2＝V F －ABC ＝13S △ABC ·FB ＝13×12AB ·BC ·FB ＝13×12×2×2×1＝23.因为ED ⊥平面ABCD ，AC ⊂平面ABCD ， 所以ED ⊥AC ， 又AC ⊥BD ，且ED ∩BD ＝D ，ED ，BD ⊂平面BDEF ，所以AC ⊥平面BDEF . 因为OE ，OF ⊂平面BDEF ， 所以AC ⊥OE ，AC ⊥OF . 易知AC ＝BD ＝2AB ＝22， OB ＝OD ＝12BD ＝2，OF ＝OB 2＋FB 2＝3， OE ＝OD 2＋ED 2＝6， EF ＝BD 2＋(ED －FB )2 ＝(22)2＋(2－1)2＝3，所以EF 2＝OE 2＋OF 2，所以OF ⊥OE . 又OE ∩AC ＝O ，OE ，AC ⊂平面ACE ， 所以OF ⊥平面ACE ， 所以V 3＝V F －ACE ＝13S △ACE ·OF＝13×12AC ·OE ·OF ＝13×12×22×6×3＝2， 所以V 3≠2V 2，V 1≠V 3，V 3＝V 1＋V 2,2V 3＝3V 1， 所以选项A ，B 不正确，选项C ，D 正确． 规律方法 空间几何体的表面积与体积的求法(1)公式法：对于规则的几何体直接利用公式进行求解．(2)割补法：把不规则的图形分割成规则的图形，或把不规则的几何体补成规则的几何体，不熟悉的几何体补成熟悉的几何体．(3)等体积法：选择合适的底面来求体积．跟踪演练2 (1)已知圆锥的顶点为S ，母线SA ，SB 所成角的余弦值为78，SA 与圆锥底面所成角为45°，若△SAB 的面积为515，则该圆锥的侧面积为( ) A ．802π B ．40 C ．402π D ．405π 答案 C解析 由圆锥的顶点为S ，母线SA ，SB 所成角的余弦值为78，可得sin ∠ASB ＝1－⎝⎛⎭⎫782＝158， 又△SAB 的面积为515， 可得12SA 2sin ∠ASB ＝515，即12SA 2×158＝515，可得SA ＝45， 由SA 与圆锥底面所成角为45°， 可得圆锥的底面半径为22×45＝210， 则该圆锥的侧面积为π×210×45＝402π.(2)(2022·连云港模拟)如图是一个圆台的侧面展开图，若两个半圆的半径分别是1和2，则该圆台的体积是( )A.72π24B.73π24C.72π12D.73π12 答案 B解析 如图，设上底面的半径为r ，下底面的半径为R ，高为h ，母线长为l ，则2πr ＝π·1,2πR ＝π·2， 解得r ＝12，R ＝1，l ＝2－1＝1， h ＝l 2－(R －r )2＝12－⎝⎛⎭⎫122＝32，上底面面积S ′＝π·⎝⎛⎭⎫122＝π4， 下底面面积S ＝π·12＝π，则该圆台的体积为13(S ＋S ′＋SS ′)h ＝13×⎝⎛⎭⎫π＋π4＋π2×32＝73π24. 考点三 多面体与球核心提炼求空间多面体的外接球半径的常用方法(1)补形法：侧面为直角三角形，或正四面体，或对棱均相等的模型，可以还原到正方体或长方体中去求解；(2)定义法：到各个顶点距离均相等的点为外接球的球心，借助有特殊性底面的外接圆圆心，找其垂线，则球心一定在垂线上，再根据到其他顶点距离也是半径，列关系式求解即可．例3 (1)(2022·烟台模拟)如图，三棱锥V －ABC 中，VA ⊥底面ABC ，∠BAC ＝90°，AB ＝AC ＝VA ＝2，则该三棱锥的内切球和外接球的半径之比为( )A ．(2－3)∶1B ．(23－3)∶1C ．(3－1)∶3D ．(3－1)∶2 答案 C解析 因为VA ⊥底面ABC ，AB ，AC ⊂底面ABC ， 所以VA ⊥AB ，VA ⊥AC ， 又因为∠BAC ＝90°，所以AB ⊥AC ，而AB ＝AC ＝VA ＝2，所以三条互相垂直且共顶点的棱，可以看成正方体中共顶点的长、宽、高，因此该三棱锥外接球的半径R ＝12×22＋22＋22＝3，设该三棱锥的内切球的半径为r ， 因为∠BAC ＝90°，所以BC ＝AB 2＋AC 2＝22＋22＝22， 因为VA ⊥AB ，VA ⊥AC ，AB ＝AC ＝VA ＝2， 所以VB ＝VC ＝VA 2＋AB 2＝22＋22＝22， 由三棱锥的体积公式可得，3×13×12×2×2·r ＋13×12×22×22×32·r ＝13×12×2×2×2⇒r ＝3－33， 所以r ∶R ＝3－33∶3＝(3－1)∶3.(2)(2022·新高考全国Ⅱ)已知正三棱台的高为1，上、下底面边长分别为33和43，其顶点都在同一球面上，则该球的表面积为( ) A ．100π B ．128π C ．144π D ．192π 答案 A解析 由题意，得正三棱台上、下底面的外接圆的半径分别为23×32×33＝3，23×32×43＝4.设该棱台上、下底面的外接圆的圆心分别为O 1，O 2，连接O 1O 2(图略)，则O 1O 2＝1，其外接球的球心O 在直线O 1O 2上．设球O 的半径为R ，当球心O 在线段O 1O 2上时，R 2＝32＋OO 21＝42＋(1－OO 1)2，解得OO 1＝4(舍去)；当球心O 不在线段O 1O 2上时，R 2＝42＋OO 22＝32＋(1＋OO 2)2，解得OO 2＝3，所以R 2＝25，所以该球的表面积为4πR 2＝100π. 综上，该球的表面积为100π.规律方法 (1)求锥体的外接球问题的一般方法是补形法，把锥体补成正方体、长方体等求解． (2)求锥体的内切球问题的一般方法是利用等体积法求半径．跟踪演练3 (1)(2022·全国乙卷)已知球O 的半径为1，四棱锥的顶点为O ，底面的四个顶点均在球O 的球面上，则当该四棱锥的体积最大时，其高为( ) A.13B.12 C.33D.22答案 C解析 该四棱锥的体积最大即以底面截球的圆面和顶点O 组成的圆锥体积最大． 设圆锥的高为h (0<h <1)，底面半径为r ， 则圆锥的体积V ＝13πr 2h ＝13π(1－h 2)h ，则V ′＝13π(1－3h 2)，令V ′＝13π(1－3h 2)＝0，得h ＝33，所以V ＝13π(1－h 2)h 在⎝⎛⎭⎫0，33上单调递增，在⎝⎛⎭⎫33，1上单调递减，所以当h ＝33时，四棱锥的体积最大． (2)(2022·衡水中学调研)将两个一模一样的正三棱锥共底面倒扣在一起，已知正三棱锥的侧棱长为2，若该组合体有外接球，则正三棱锥的底面边长为________，该组合体的外接球的体积为________． 答案6823π解析 如图，连接P A 交底面BCD 于点O ，则点O 就是该组合体的外接球的球心．设三棱锥的底面边长为a ， 则CO ＝PO ＝R ＝33a ， 得2×33a ＝2， 所以a ＝6，R ＝2， 所以V ＝43π·(2)3＝823π.专题强化练一、单项选择题1．(2022·唐山模拟)圆柱的底面直径与高都等于球的直径，则球的表面积与圆柱的侧面积的比值为()A．1∶1 B．1∶2C．2∶1 D．2∶3答案 A解析设球的半径为r，依题意知圆柱的底面半径也是r，高是2r，圆柱的侧面积为2πr·2r＝4πr2，球的表面积为4πr2，其比例为1∶1.2．(2021·新高考全国Ⅰ)已知圆锥的底面半径为2，其侧面展开图为一个半圆，则该圆锥的母线长为()A．2 B．2 2 C．4 D．4 2答案 B解析设圆锥的母线长为l，因为该圆锥的底面半径为2，所以2π×2＝πl，解得l＝2 2.3.某同学为表达对“新冠疫情”抗疫一线医护人员的感激之情，亲手为他们制作了一份礼物，用正方体纸盒包装，并在正方体六个面上分别写了“致敬最美逆行”六个字．该正方体纸盒水平放置的六个面分别用“前面、后面、上面、下面、左面、右面”表示．如图是该正方体的展开图．若图中“致”在正方体的后面，那么在正方体前面的字是()A．最B．美C．逆D．行答案 B解析把正方体的表面展开图再折成正方体，如图，面“致”与面“美”相对，若“致”在正方体的后面，那么在正方体前面的字是“美”．4．已知正方体ABCD －A 1B 1C 1D 1的棱长为2，则三棱锥A －B 1CD 1的体积为( ) A.43 B.83 C ．4 D ．6 答案 B解析 如图，三棱锥A －B 1CD 1是由正方体ABCD －A 1B 1C 1D 1截去四个小三棱锥A －A 1B 1D 1，C －B 1C 1D 1，B 1－ABC ，D 1－ACD 形成的，又1111ABCD A B C D V －＝23＝8，11111111A A B D C B C D B ABC D ACD V V V V －－－－＝＝＝＝13×12×23＝43， 所以11A B CD V －＝8－4×43＝83.5．(2022·河南联考)小李在课间玩耍时不慎将一个篮球投掷到一个圆台状垃圾篓中，恰好被上底口(半径较大的圆)卡住，球心到垃圾篓底部的距离为510a ，垃圾篓上底面直径为24a ，下底面直径为18a ，母线长为13a ，则该篮球的表面积为( ) A ．154πa 2B.6163πa 2C ．308πa 2D ．616πa 2 答案 D解析 球与垃圾篓组合体的轴截面图如图所示．根据题意，设垃圾篓的高为h ，则h ＝(13a )2－(12a －9a )2＝410a . 所以球心到上底面的距离为10a . 设篮球的半径为r ， 则r 2＝10a 2＋(12a )2＝154a 2. 故篮球的表面积为4πr 2＝616πa 2.6.(2022·湖北联考)定义：24小时内降水在平地上积水厚度(mm)来判断降雨程度．其中小雨(<10 mm)，中雨(10 mm ～25 mm)，大雨(25 mm ～50 mm)，暴雨(50 mm ～100 mm)，小明用一个圆锥形容器接了24小时的雨水，如图，则这天降雨属于哪个等级()A ．小雨B ．中雨C ．大雨D ．暴雨 答案 B解析 由题意知，一个半径为2002＝100(mm)的圆面内的降雨充满一个底面半径为2002×150300＝50(mm)，高为150(mm)的圆锥，所以积水厚度d ＝13π×502×150π×1002＝12.5(mm)，属于中雨．7.(2022·八省八校联考)如图，已知正四面体ABCD 的棱长为1，过点B 作截面α分别交侧棱AC ，AD 于E ，F 两点，且四面体ABEF 的体积为四面体ABCD 体积的13，则EF 的最小值为( )A.22 B.32 C.13 D.33答案 D解析 由题知V B －AEF ＝13V B －ACD ，所以S △AEF ＝13S △ACD ＝13×12×1×1×32＝312，记EF ＝a ，AE ＝b ，AF ＝c ， 则12bc sin 60°＝312，即bc ＝13. 则a 2＝b 2＋c 2－2bc cos 60°≥2bc －bc ＝bc ＝13，当且仅当b ＝c ＝33时取等号， 所以a 即EF 的最小值为33. 8．(2022·新高考全国Ⅰ)已知正四棱锥的侧棱长为l ，其各顶点都在同一球面上．若该球的体积为36π，且3≤l ≤33，则该正四棱锥体积的取值范围是( ) A.⎣⎡⎦⎤18，814 B.⎣⎡⎦⎤274，814 C.⎣⎡⎦⎤274，643D ．[18,27] 答案 C解析 方法一 如图，设该球的球心为O ，半径为R ，正四棱锥的底面边长为a ，高为h ，依题意，得36π＝43πR 3，解得R ＝3.由题意及图可得⎩⎨⎧l 2＝h 2＋⎝⎛⎭⎫22a 2，R 2＝(h －R )2＋⎝⎛⎭⎫22a 2，解得⎩⎨⎧h ＝l 22R ＝l 26，a 2＝2l 2－l418，所以正四棱锥的体积V ＝13a 2h＝13⎝⎛⎭⎫2l 2－l 418·l 26＝l 418⎝⎛⎭⎫2－l 218(3≤l ≤33)， 所以V ′＝49l 3－l 554＝19l 3⎝⎛⎭⎫4－l 26(3≤l ≤33)．令V ′＝0，得l ＝26， 所以当3≤l <26时，V ′>0； 当26<l ≤33时，V ′<0，所以函数V ＝l 418⎝⎛⎭⎫2－l 218(3≤l ≤33)在[3，26)上单调递增，在(26，33]上单调递减，又当l ＝3时，V ＝274；当l ＝26时，V ＝643；当l ＝33时，V ＝814，所以该正四棱锥的体积的取值范围是⎣⎡⎦⎤274，643.方法二 如图，设该球的球心为O ，半径为R ，正四棱锥的底面边长为a ，高为h ，依题意，得36π＝43πR 3，解得R ＝3.由题意及图可得⎩⎨⎧l 2＝h 2＋⎝⎛⎭⎫22a 2，R 2＝(h －R )2＋⎝⎛⎭⎫22a 2，解得⎩⎨⎧h ＝l 22R ＝l 26，a 2＝2l 2－l418，又3≤l ≤33，所以该正四棱锥的体积V ＝13a 2h＝13⎝⎛⎭⎫2l 2－l 418·l 26＝l 418⎝⎛⎭⎫2－l 218 ＝72×l 236·l 236·⎝⎛⎭⎫2－l 218 ≤72×⎣⎢⎡⎦⎥⎤l 236＋l 236＋⎝⎛⎭⎫2－l 21833＝643⎝⎛⎭⎫当且仅当l 236＝2－l 218，即l ＝26时取等号， 所以正四棱锥的体积的最大值为643，排除A ，B ，D.方法三 如图，设该球的半径为R ，球心为O ，正四棱锥的底面边长为a ，高为h ，正四棱锥的侧棱与高所成的角为θ，依题意，得36π＝43πR 3，解得R ＝3，所以正四棱锥的底面边长a ＝2l sin θ，高h ＝l cos θ. 在△OPC 中，作OE ⊥PC ，垂足为E ， 则可得cos θ＝l 2R ＝l 6∈⎣⎡⎦⎤12，32，所以l ＝6cos θ， 所以正四棱锥的体积 V ＝13a 2h ＝13(2l sin θ)2·l cos θ＝23(6cos θ)3sin 2θcos θ＝144(sin θcos 2θ)2. 设sin θ＝t ，易得t ∈⎣⎡⎦⎤12，32，则y ＝sin θcos 2θ＝t (1－t 2)＝t －t 3， 则y ′＝1－3t 2.令y ′＝0，得t ＝33， 所以当12<t <33时，y ′>0；当33<t <32时，y ′<0， 所以函数y ＝t －t 3在⎝⎛⎭⎫12，33上单调递增，在⎝⎛⎭⎫33，32上单调递减．又当t ＝33时，y ＝239；当t ＝12时，y ＝38；当t ＝32时，y ＝38， 所以38≤y ≤239，所以274≤V ≤643. 所以该正四棱锥的体积的取值范围是⎣⎡⎦⎤274，643. 二、多项选择题9．(2022·武汉模拟)一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R 相等，下列结论正确的是( ) A ．圆柱的侧面积为4πR 2 B ．圆锥的侧面积为2πR 2C ．圆柱的侧面积与球的表面积相等D ．球的体积是圆锥体积的两倍 答案 ACD解析 对于A ，∵圆柱的底面直径和高都等于2R ， ∴圆柱的侧面积S 1＝2πR ·2R ＝4πR 2，故A 正确； 对于B ，∵圆锥的底面直径和高等于2R ， ∴圆锥的侧面积为S 2＝πR ·R 2＋4R 2＝5πR 2，故B 错误； 对于C ，圆柱的侧面积为S 1＝4πR 2，球的表面积S 3＝4πR 2，即圆柱的侧面积与球的表面积相等，故C 正确； 对于D ，球的体积为V 1＝43πR 3，圆锥的体积为V 2＝13πR 2·2R ＝23πR 3，即球的体积是圆锥体积的两倍，故D 正确．10．设一空心球是在一个大球(称为外球)的内部挖去一个有相同球心的小球(称为内球)，已知内球面上的点与外球面上的点的最短距离为1，若某正方体的所有顶点均在外球面上且所有面均与内球相切，则( )A ．该正方体的棱长为2B ．该正方体的体对角线长为3＋ 3C ．空心球的内球半径为3－1D ．空心球的外球表面积为(12＋63)π 答案 BD解析 设内、外球半径分别为r ，R ，则正方体的棱长为2r ，体对角线长为2R ，∴R ＝3r ， 又由题知R －r ＝1， ∴r ＝3＋12，R ＝3＋32， ∴正方体棱长为3＋1，体对角线长为3＋3， ∴外接球表面积为4πR 2＝(12＋63)π.11.如图，已知四棱台ABCD －A 1B 1C 1D 1的上、下底面均为正方形，其中AB ＝22，A 1B 1＝2，AA 1＝BB 1＝CC 1＝DD 1＝2，则下列叙述正确的是( )A ．该四棱台的高为 3B ．AA 1⊥CC 1C ．该四棱台的表面积为26D ．该四棱台外接球的体积为32π3答案 AD解析 将四棱台补为如图所示的四棱锥P －ABCD ，分别取BC ，B 1C 1的中点E ，E 1，记四棱台ABCD －A 1B 1C 1D 1的上、下底面中心分别为O 1，O ，连接AC ，A 1C 1，BD 1，B 1D 1，A 1O ，OE ，OP ，PE ，由条件知A 1，B 1，C 1，D 1分别为四棱锥的侧棱P A ，PB ，PC ，PD 的中点， 则P A ＝2AA 1＝4，OA ＝22AB ＝2A 1B 1＝2， 所以OO 1＝12PO ＝12P A 2－OA 2＝3，故该四棱台的高为3，故A 正确；由P A ＝PC ＝4，AC ＝4，得△P AC 为正三角形， 则AA 1与CC 1所成角为60°，故B 错误； 四棱台的斜高h ′＝12PE ＝12PO 2＋OE 2＝12(23)2＋(2)2＝142， 所以该四棱台的表面积为 (22)2＋(2)2＋4×2＋222×142＝10＋67，故C 错误；由△P AC 为正三角形，易知OA 1＝OA ＝OC ＝OC 1，OB 1＝OD 1＝OB ＝OD ，所以O 为四棱台外接球的球心，且外接球的半径为2，所以该四棱台外接球的体积为4π3×23＝32π3，故D 正确．12．(2022·聊城模拟)用与母线不垂直的两个平行平面截一个圆柱，若两个截面都是椭圆形状，则称夹在这两个平行平面之间的几何体为斜圆柱．这两个截面称为斜圆柱的底面，两底面之间的距离称为斜圆柱的高，斜圆柱的体积等于底面积乘以高．椭圆的面积等于长半轴长与短半轴长乘积的π倍，已知某圆柱的底面半径为2，用与母线成45°角的两个平行平面去截该圆柱，得到一个高为6的斜圆柱，对于这个斜圆柱，下列选项正确的是( ) A ．底面椭圆的离心率为22B ．侧面积为242πC ．在该斜圆柱内半径最大的球的表面积为36πD ．底面积为42π 答案 ABD解析 不妨过斜圆柱的最高点D 和最低点B 作平行于圆柱底面的截面圆，夹在它们之间的几何体是圆柱，如图，矩形ABCD 是圆柱的轴截面，平行四边形BFDE 是斜圆柱的过底面椭圆的长轴的截面，由圆柱的性质知∠ABF ＝45°， 则BF ＝2AB ，设椭圆的长轴长为2a ，短轴长为2b ， 则2a ＝2·2b ，即a ＝2b ， c ＝a 2－b 2＝a 2－⎝⎛⎭⎫22a 2＝22a ， 所以离心率为e ＝c a ＝22，A 正确；作EG ⊥BF ，垂足为G ，则EG ＝6， 易知∠EBG ＝45°，则BE ＝62， 又CE ＝AF ＝AB ＝4，所以斜圆柱侧面积为S ＝2π×2×(4＋62)－2π×2×4＝242π，B 正确；由于斜圆柱的两个底面的距离为6，而圆柱的底面直径为4，所以斜圆柱内半径最大的球的半径为2，球的表面积为4π×22＝16π，C 错误；易知2b ＝4，则b ＝2，a ＝22， 所以椭圆面积为πab ＝42π，D 正确．三、填空题13.(2022·湘潭模拟)陀螺是中国民间的娱乐工具之一，也叫做陀罗．陀螺的形状结构如图所示，由一个同底的圆锥体和圆柱体组合而成，若圆锥体和圆柱体的高以及底面圆的半径长分别为h 1，h 2，r ，且h 1＝h 2＝r ，设圆锥体的侧面积和圆柱体的侧面积分别为S 1和S 2，则S 1S 2＝________.答案22解析 由题意知，圆锥的母线长为l ＝h 21＋r 2＝2r ，则圆锥的侧面积为S 1＝πrl ＝2πr 2，根据圆柱的侧面积公式，可得圆柱的侧面积为 S 2＝2πrh 2＝2πr 2，所以S 1S 2＝22.14．(2022·福州质检)在正三棱柱ABC －A 1B 1C 1中，AB ＝AA 1＝2，F 是线段A 1B 1上的动点，则AF ＋FC 1的最小值为________． 答案6＋ 2解析 依题意，把正三棱柱ABC －A 1B 1C 1的上底面△A 1B 1C 1与侧面矩形ABB 1A 1放在同一平面内，连接AC 1，设AC 1交A 1B 1于点F ，如图，此时点F 可使AF ＋FC 1取最小值，大小为AC 1，而∠AA 1C 1＝150°，则AC 1＝AA 21＋A 1C 21－2AA 1·A 1C 1cos ∠AA 1C 1 ＝22＋22－23cos 150° ＝8＋43＝6＋2，所以AF ＋FC 1的最小值为6＋ 2.15.某同学在参加《通用技术》实践课时，制作了一个实心工艺品(如图所示)．该工艺品可以看成是一个球体被一个棱长为4的正方体的6个面所截后剩余的部分(球心与正方体的中心重合)，其中一个截面圆的周长为3π，则该球的半径为________；现给出定义：球面被平面所截得的一部分叫做球冠．截得的圆叫做球冠的底，垂直于截面的直径被截得的一段叫做球冠的高．如果球面的半径是R ，球冠的高是h ，那么球冠的表面积计算公式是S ＝2πRh .由此可知，该实心工艺品的表面积是________．答案5247π2解析 设截面圆半径为r ，则球心到某一截面的距离为正方体棱长的一半，即此距离为2，根据截面圆的周长可得3π＝2πr ，得r ＝32，故R 2＝r 2＋22＝254，得R ＝52，所以球的表面积S 1＝25π. 如图，OA ＝OB ＝52，且OO 1＝2，则球冠的高h ＝R －OO 1＝12，得所截的一个球冠表面积S ＝2πRh ＝2π×52×12＝5π2，且截面圆的面积为π×⎝⎛⎭⎫322＝9π4， 所以工艺品的表面积为4πR 2－6⎝⎛⎭⎫S －9π4＝25π－3π2＝47π2.16.(2022·开封模拟)如图，将一块直径为23的半球形石材切割成一个正四棱柱，则正四棱柱的体积取最大值时，切割掉的废弃石材的体积为________．答案 23π－4解析 设正四棱柱的底面正方形边长为a ，高为h ，则底面正方形的外接圆半径r ＝22a ， ∴h 2＋r 2＝h 2＋12a 2＝3，∴a 2＝6－2h 2，∴正四棱柱的体积V ＝a 2h ＝(6－2h 2)h ＝－2h 3＋6h (0<h <3)， ∴V ′＝－6h 2＋6＝－6(h ＋1)(h －1)，∴当0<h <1时，V ′>0；当1<h <3时，V ′<0；∴V ＝－2h 3＋6h 在(0,1)上单调递增，在(1，3)上单调递减， ∴V max ＝V (1)＝4，又半球的体积为23π×()33＝23π，∴切割掉的废弃石材的体积为23π－4.。

2．如图， 是水平放置的 的直观图，则 的面积为（）
A．6B．32C．12D．62
【答案】C
【分析】
结合斜二测法的画法原理求出 ， ，再结合面积公式求解即可.
【详解】
由斜二测画法特点得 ，
为直角三角形，
，
故选：C.
【点睛】
本题考查由直观图求平面图的面积，属于容易题.
3．如图所示的几何体是（）
A．圆锥B．棱锥C．圆台D．棱柱
三视图中反应的长、宽、高的特点：“长对正”，“高平齐”，“宽相等”
二.空间几何体的直观图
斜二测画法的基本步骤：①建立适当直角坐标系 （尽可能使更多的点在坐标轴上）
②建立斜坐标系 ，使 =450（或1350）
③画对应图形
在已知图形平行于X轴的线段，在直观图中画成平行于X‘轴，且长度保持不变；
在已知图形平行于Y轴的线段，在直观图中画成平行于Y‘轴，且长度变为原来的一半；
(1)绳子的最短长度的平方f(x).
(2)绳子最短时，顶点到绳子的最短距离.
(3)f(x)的最大值.
【答案】(1) f(x)=AM2=x2+16(0≤x≤4). (2) SR= = (0≤x≤4)，(3) f(4)=32.
【解析】试题分析：将圆锥的侧面沿SA展开在平面上，如图，则该展开图为扇形，且弧AA′的长度L就是⊙O的周长，
∴L＝2πr＝2π.∴∠ASA′＝ ×360°＝ ×360°＝90°，
(1)由题意知，绳长的最小值为展开图中的AM，其值为AM＝ (0≤x≤4)，
∴f(x)＝AM2＝x2＋16(0≤x≤4)．
故选：A
【点睛】
已知三棱锥的三条侧棱两两相互垂直，即可将三棱锥的外接球扩展为长方体的外接球是解题的关键.

专题33：空间几何体精讲温故知新一．空间几何体的结构1.多面体一般地，由若干个平面多边形围成的几何体叫做多面体。

围成多面体的各个多边形叫做多面体的面；两个面的公共边叫做多面体的棱；棱与棱的公共点叫做多面体的顶点。

2.旋转体一条平面曲线，包括直线，绕它所在平面内的一条定直线旋转所成的曲面叫做旋转面。

封闭的旋转面围成的几何体叫做旋转体。

这条定直线叫做旋转体的轴。

3.棱柱一般地，有两个面互相平行，其余各面都是四边形，并且相邻两个四边形的公共边都互相平行，由这些面所围成的多面体叫做棱柱。

在棱柱中，两个互相平行的面叫做棱柱的底面，它们是全等的多边形，其余各面叫做棱柱的侧面，它们都是平行四边形，相邻两边的公共边叫做棱柱的侧棱，侧面和底面的公共顶点叫做棱柱的顶点。

棱柱的底面可以是三角形、四边形、五边形，我们把这样的棱柱分别叫做三棱柱、四棱柱、五棱柱。

一般地，我们把侧面垂直于底面的棱柱叫做直棱柱，侧面不垂直于底面的棱柱叫做斜棱柱，底面是正多边形的，直棱柱叫做正棱柱，底面是平行四边形的四棱柱，也叫做平行六面体。

4.棱锥一般地，有一个面是多边形，其余各面都是有一个公共顶点的三角形，由这些面所围成的多面体叫做棱锥。

这个多边形面叫做棱锥的底面，有公共顶点的各个三角形面叫做棱锥的侧面，相邻两边的公共边叫做棱锥的侧棱，这侧面的公共顶点叫做棱锥的顶点。

棱锥，用表示顶点和各面各顶点的字母来表示，其中三棱锥又叫四面体，底面是正多边形并且顶点与底面中心的连线垂直于底面的棱锥叫做正棱锥。

5.棱台用一个平行于圆锥底面的平面去截棱锥，我们把底面和截面之间那部分多面体叫做棱台。

在棱台中，原棱锥的底面和截面分别叫做棱台的下底面和上底面面，类似于棱柱、棱锥，棱台也有侧面、侧棱和顶点。

6.圆柱与矩形的一边所在直线为旋转轴，其余三边旋转一周形成的面所围成的旋转体叫做圆柱。

旋转轴叫做圆柱的轴，垂直于轴的边旋转而成的圆面，叫做圆柱的底面，平行的边旋转而成的曲面叫做圆柱的侧面，无论旋转到什么位置，平行于轴的边叫做圆柱侧面的母线。

专专8.3空间几何中的平行、垂直一、单选题1. 设,l m 表示两条不同的直线，,αβ表示两个不同的平面，Q 表示一个点，给出下列四个命题，其中正确的命题是( )①,Q l Q l αα∈⊂⇒∈②,l m Q m l ββ⋂=⊂⇒⊂③//,,,l m l Q m Q m ααα⊂∈∈⇒⊂④,αβ⊥且,,,m Q Q l l l αββαβ⋂=∈∈⊥⇒⊂A. ①②B. ①③C. ②④D. ③④ 2. 如图已知正方体1111ABCD A B C D -，M ，N 分别是1A D ，1D B 的中点，则（ ）A. 直线1A D 与直线1D B 垂直，直线//MN 平面ABCDB. 直线1A D 与直线1D B 平行，直线MN ⊥平面11BDD BC. 直线1A D 与直线1D B 相交，直线//MN 平面ABCDD. 直线1A D 与直线1D B 异面，直线MN ⊥平面11BDD B3. 如图A ，B ，C ，D 为空间四点，在ABC 中，2AB =，2AC BC ==，等边三角形ADB 以AB 为轴旋转，当平面ADB ⊥平面ABC 时，CD =( )A. 3B. 2C. 5D. 14. 如图，四边形ABCD 中，//AD BC ，AD AB =，45BCD ︒∠=，90BAD ︒∠=，将ABD 沿BD 折起，使平面ABD ⊥平面BCD ，构成三棱锥A BCD -，则在三棱锥A BCD -中，下列命题正确的是( )A. 平面ABD ⊥平面ABCB. 平面ADC ⊥平面BDCC. 平面ABC ⊥平面BDCD. 平面ADC ⊥平面ABC二、多选题 5. 如图，在正方体1111ABCD A B C D -中，点P 为线段1B C 上一动点，则( )A. 直线1BD ⊥平面11AC DB. 异面直线1B C 与11A C 所成角为45︒C. 三棱锥11P A DC -的体积为定值D. 平面11AC D 与底面ABCD 的交线平行于11A C6. 如图所示，矩形ABCD 中，E 为边AB 的中点，将ADE 沿直线DE 翻转成1A DE ，若M 为线段1A C 的中点，则在ADE 翻转过程中，下列命题正确的是( )A. ||BM 是定值B. 点M 在球面上运动C. 一定存在某个位置，使1DE A C ⊥D. 一定存在某个位置，使//MB 平面1A DE7. 如图1，在正方形ABCD 中，点E 为线段BC 上的动点(不含端点)，将ABE 沿AE 翻折，使得二面角B AE D --为直二面角，得到图2所示的四棱锥B AECD -，点F 为线段BD 上的动点(不含端点)，则在四棱锥B AECD -中，下列说法正确的有( )A. B 、E 、C 、F 四点不共面B. 存在点F ，使得//CF 平面BAEC. 三棱锥B ADC -的体积为定值D. 存在点E 使得直线BE 与直线CD 垂直三、填空题 8. 《九章算术》中将底面是长方形且有一条侧棱与底面垂直的四棱锥称为阳马，将四个面都为直角三角形的四面体称为鳖臑．在如图所示的阳马P ABCD -中，PA ⊥底面ABCD ，且22BC DC PA ==，AM PD ⊥于M ，MN PD ⊥，MN 与PC 交于点.N 则(1)AM 与CD 的关系__________(填“垂直”或“平行”)；(2)PN PC=__________. 9. 如图，在正方形ABCD 中，,E F 分别是,BC CD 的中点，G 是EF 的中点.现在沿,AE AF 及EF 把这个正方形折成一个空间图形，使,,B C D 三点重合，重合后的点记为.H 下列说法错误的是__________(将符合题意的选项序号填到横线上).①AG EFH ⊥所在平面；②AH EFH ⊥所在平面；③HF AEF ⊥所在平面；④HG AEF ⊥所在平面.10. 如图，在Rt ABC 中，1AC =，BC x =，D 为斜边AB 的中点．将BCD 沿直线CD 翻折．若在翻折过程中存在某个位置，使得CB AD ⊥，则x 的取值范围是__________.11. 如图所示，正方体1111ABCD A B C D -的棱长为1，BD AC O ⋂=，M 是线段1D O 上的动点，过点M 作平面1ACD 的垂线交平面1111A B C D 于点N ，则点N 到点A 距离的最小值为__________.四、解答题12. 在三棱柱111ABC A B C -中，AB AC ⊥，1B C ⊥平面ABC ，E ，F 分别是AC ，1B C 的中点．(1)求证：//EF 平面11AB C ；(2)求证：平面1AB C ⊥平面1.ABB13. 在平行六面体1111ABCD A B C D -中，1AA AB =，111.AB B C ⊥求证：(1)//AB 平面11A B C ；(2)平面11ABB A ⊥平面1.A BC14. 如图所示，四棱锥P ABCD -的底面ABCD 为矩形，PA 是四棱锥P ABCD -的高，,,E F M 分别为,,AB CD PD 的中点．(1)求证：平面//AMF 平面PEC ；(2)若24PA AB BC ===，求多面体PECFMA 的体积.15. 如图，四边形ABCD 为菱形，60.ABC PA ︒∠=⊥平面ABCD ，E 为PC 中点． ()Ⅰ求证：平面BED ⊥平面ABCD ；()Ⅱ求平面PBA 与平面EBD 所成二面角(锐角)的余弦值．16. 如图，已知三棱柱111ABC A B C -，平面11AC A C ⊥平面ABC ，ABC=90︒∠，BAC=30︒∠，11==AC A A AC ，E ，F 分别是AC ，11A B 的中点．()Ⅰ证明：EF BC ⊥；()Ⅱ求直线EF 与平面1BC A 所成角的余弦值．17. 如图，已知三棱柱111ABC A B C -的底面是正三角形，侧面11BB C C 是矩形，,M N 分别为11,BC B C 的中点，P 为AM 上一点．过11B C 和P 的平面交AB 于E ，交AC 于.F(1)证明：1//AA MN ，且平面1A AMN ⊥平面11EB C F ；(2)设O 为111A B C 的中心，若6AO AB ==，//AO 平面11EB C F ，且3MPN π∠=，求四棱锥11B EB C F -的体积．18. 如图，在直三棱柱111ABC A B C -中，2AB AC ==，12BC AA ==，O ，M 分别为BC ，1AA 的中点．(1)求证：//OM 平面11CB A ；(2)求点M 到平面11CB A 的距离．19. 如图，在正三棱柱111ABC A B C -中，2AB =，13AA =，M 为BC 的中点，N 在线段1AA 上.(1)设1=AN NA λ，当λ为何值时，11//?MN ACB 平面 (2)若1AN =，求直线MN 与直线11A C 所成角的正弦值.20. 如图，在四棱锥P ABCD -，底面ABCD 为平行四边形，PCD 为等边三角形，平面PAC ⊥平面PCD ，PA CD ⊥，2CD =，3AD =，(1)设G ，H 分别为PB ，AC 的中点，求证：//GH 平面PAD ；(2)求证：PA ⊥平面PCD ；(3)求直线AD 与平面PAC 所成角的正弦值．答案和解析1.【答案】D解：①Q α∈，l α⊂，点Q 可以不在直线l 上，故A 错误； ②直线l 可以只有一点在面内，故B 错误；③因为//l m ，l α⊂，若m 不在平面α内，//m α，由Q m ∈， 可得Q 在平面α外，这与可点Q α∈相矛盾，故C 正确； ④αβ⊥且m αβ⋂=，Q β∈，Q l ∈，l l αβ⊥⇒⊂， 由面面垂直的性质定理知D 正确.故选.D2.【答案】A解：连1AD ，在正方体1111ABCD A B C D -中，M 是1A D 的中点，所以M 为1AD 中点，又N 是1D B 的中点，所以//MN AB ，MN ⊂/平面,ABCD AB ⊂平面ABCD ，所以//MN 平面.ABCD因为AB 不垂直BD ，所以MN 不垂直BD ，则MN 不垂直平面11BDD B ，所以选项B ，D 不正确；在正方体1111ABCD A B C D -中，11AD A D ⊥，AB ⊥平面11AA D D ，所以1AB A D ⊥， 1AD AB A ⋂=，所以1A D ⊥平面1ABD ，1D B ⊂平面1ABD ，所以11A D D B ⊥， 且直线11,A D D B 是异面直线，所以选项C 错误，选项A 正确. 故选.A3.【答案】B解：由题意，取AB 的中点E ，连接DE ，CE ，因为三角形ADB 为等边三角形，所以DE AB ⊥，当平面ADB ⊥平面ABC 时，且平面ADB ⋂平面ABC AB =，又DE ⊂平面ADB ，所以DE ⊥平面ABC ，又CE ⊂平面ABC ，所以DE EC ⊥，又2AB =，2AC BC ==， 所以222AC BC AB +=，所以AC BC ⊥，又BE AE =，所以112CE AB ==， 又332322DE BD ==⨯=， 所以此时2231 2.CD DE CE =+=+=故选.B4.【答案】D解：在四边形ABCD 中，//AD BC ，AD AB =，45BCD ︒∠=，90BAD ︒∠=， BD CD ∴⊥，又平面ABD ⊥平面BCD ，且平面ABD ⋂平面BCD BD =，CD ⊂平面BCD ， 故CD ⊥平面ABD ，则CD AB ⊥，又AD AB ⊥，AD CD D ⋂=，AD ，CD ⊂平面ADC ，AB ∴⊥平面ADC ，又AB ⊂平面ABC ，∴平面ABC ⊥平面.ADC故选.D5.【答案】ACD解：在A 中，1111A C B D ⊥，111AC BB ⊥，1111B D BB B ⋂=，11B D ，1BB ⊂平面11BB D ， 11A C ∴⊥平面11BB D ，1BD ⊂平面11BB D ，111AC BD ∴⊥，同理，11DC BD ⊥，1111A C DC C ⋂=，11A C ，1DC ⊂平面11AC D ，∴直线1BD ⊥平面11AC D ，故A 正确;对于B ，易知11//A D B C ，在11A DC 中，1111A D DC AC ==，可得11A DC 为正三角形，异面直线1BC 与11A C 所成角为60︒，故B 错误;对于C ，11//A D B C ，1A D ⊂平面11AC D ，1B C ⊂/平面11AC D ，1//B C ∴平面11AC D ， 点P 在线段1B C 上运动，P ∴到平面11AC D 的距离为定值，又11AC D 的面积是定值，∴三棱锥11P A C D -的体积为定值，故C 正确；对于D ，设平面11AC D 与底面ABCD 的交线为m ，11A C 是平面11AC D 和平面1111A B C D 的交线，平面//ABCD 平面1111A B C D ，所以11//A C m ，故D 选项正确.故选.ACD6.【答案】ABD解：A 对，取CD 中点N ，连接MN 、NB ，则1//MN A D 、//NB DE ，1A DE MNB ∠=∠，112MN A D ==定值，NB DE ==定值，根据余弦定理得，2222cos MB MN NB MN NB MNB =+-⋅⋅∠，||BM ∴是定值，B 对，B 是定点，M ∴是在以B 为球心，MB 为半径的球面上，C 错，当矩形ABCD 满足AC DE ⊥时存在，其他情况不存在，D 对，取CD 中点N ，连接MN 、NB ，则1//MN A D 、//NB DE ，因为MN ⊂/平面1A DE ，1A D ⊂平面1A DE ，所以//MN 平面1A DE ，同理//BN 平面1A DE ，又MN NB N ⋂=，∴平面//MNB 平面1A DE ，MB ⊂平面MNB ，//MB ∴平面1.A DE故选.ABD7.【答案】AB解：对于A ：假设直线BE 与直线CF 在同一平面上，所以：点E 在平面BCF 上，又点E 在线段BC 上，BC ⋂平面BCF C =，所以点E 与点C 重合，与点E 异于C 矛盾，所以直线BE 与CF 必不在同一平面上，即B 、E 、C 、F 四点不共面，故A 正确； 对于B ：当点F 为线段BD 的中点时，12EC AD =，再取AB 的中点G ， 则//FG AD 且12FG AD =， 则//EC FG ，且EC FG =，所以：四边形ECFG 为平行四边形，所以//FC EG ，又因为,EG ABE FC ABE ⊂⊄平面平面，则：直线//CF 平面BAE ，故B 正确；对于C ：由题B ADC V -，底面ACD 的面积不变，但E 的移动会导致点B 到平面ACD 的距离在变化，所以B ADC V -的体积不是定值，故C 错误；对于D ：过点B 作BO AE ⊥于O ，由于平面BAE ⊥平面AECD ，平面BAE ⋂平面AECD AE =，所以BO ⊥平面AECD ，过点D 作DH AE ⊥于H ，因为平面BAE ⊥平面AECD ，平面BAE ⋂平面AECD AE =，所以DH ⊥平面BAE ，又因为BE ABE ⊂平面，所以DH BE ⊥，若存在点E 使得直线BE 与直线CD 垂直，DH ⊂平面AECD ，DC ⊂平面AECD ，DH DC D ⋂=，所以BE ⊥平面AECD ，所以E 和O 重合，与ABE 是以点B 为直角的三角形矛盾，所以不存在点E ，使得直线BE 与直线CD 垂直，故D 错误．故选：.AB8.【答案】垂直23解：(1)由题意易得CD ⊥平面PAD ，所以CD AM ⊥，又AM PD ⊥于M ，CD PD D ⋂=，进而得AM ⊥平面PCD ，得.AM CD ⊥(2)设BC DC PA a ===，则PD ==，Rt PAD中，PM PA PA PD ==，则PM =， 易得CD ⊥平面PAD ，因为MN PD ⊥，所以//MN CD ，得2.3PN PM PC PD === 故答案为(1)垂直；2(2).39.【答案】①③④解：折之前AG EF ⊥，CG EF ⊥，折之后也垂直，所以EF ⊥平面AHG ，折之前B ∠，D ∠，C ∠均为直角，折之后三点重合， 所以折之后AH ，EH ，FH 三条直线两两垂直，所以AH EFH ⊥所在平面，②对；同时可知AH HG ⊥，又HF AEH ⊥所在平面，过AE 不可能做两个平面与直线HF 垂直，③错； 如果HG AEF ⊥所在平面，则有HG AG ⊥，与②中AH HG ⊥矛盾，④错；若AG EFH ⊥所在平面，则有AG HG ⊥，与②中AH HG ⊥矛盾，所以①也错．故答案为①③④.10.【答案】(0,3] 解：由题意得，212x AD CD BD +===，BC x =， 取BC 中点E ，翻折前，在图1中，连接DE ，CD ，则12DE =，1AC =， 翻折后，在图2中，此时 .CB AD ⊥BC DE ⊥，BC AD ⊥，DE AD D ⋂=，,DE AD ADE ⊂平面，BC ∴⊥平面ADE ，AE ADE ⊂平面，BC AE ∴⊥，DE BC ⊥，又BC AE ⊥，E 为BC 中点，1AB AC ∴==，2114AE x ∴=-，212x AD +=， 在ADE 中：①221111224x x ++>-，②221111224x x +<+-，③0x >， 由①②③，得0 3.x <<如图3，翻折后，当1B CD 与ACD 在一个平面上，AD 与1B C 交于M ，且1AD B C ⊥，1AD B D CD BD ===，1CBD BCD B CD ∠=∠=∠， 又190CBD BCD B CD ︒∠+∠+∠=，130CBD BCD B CD ︒∴∠=∠=∠=，60A ︒∴∠=，tan 60BC AC ︒=，此时1x ==综上，x 的取值范围为故答案为：11.【答案】2解：由题易知，DO AC ⊥，1D O AC ⊥，1DO D O O ⋂=，DO ，1D O ⊂平面11BDD B ， AC ∴⊥平面11BDD B ，又AC ⊂平面1ACD ，∴平面1ACD ⊥平面11BDD B ， 又MN ⊥平面1ACD ，平面1ACD ⋂平面111BDD B D O =，MN ∴⊂平面11BDD B ，且N 在平面1111A B C D 内，11N B D ∴∈，过N 作11NG A B ⊥，交11A B 于G ，将平面1111A B C D 展开，如图：设NG x =，(01)x ，11NG A B ⊥，1111A D A B ⊥，11//NG A D ∴，又11A D ⊥平面11ABB A ，NG ∴⊥平面11ABB A ，且AG ⊂平面11ABB A ，NG AG ∴⊥， 22221(1)222AN x x x x ∴=+-+=-+21362()222x =-+， 当12x =时，AN 取最小值6.2 故答案为：6.212.【答案】证明：(1)E ，F 分别是AC ，1B C 的中点．所以1//EF AB ，因为EF ⊂/平面11AB C ，1AB ⊂平面11AB C ，所以//EF 平面11AB C ；(2)因为1B C ⊥平面ABC ，AB ⊂平面ABC ，所以1B C AB ⊥，又因为AB AC ⊥，1AC B C C ⋂=，AC ⊂平面1AB C ，1B C ⊂平面1AB C ， 所以AB ⊥平面1AB C ，因为AB ⊂平面1ABB ，所以平面1AB C ⊥平面1.ABB13.【答案】证明：(1)平行六面体1111ABCD A B C D -中，11//AB A B ，又AB ⊂平面1111,A B C A B ⊂/平面11A B C ；得//AB 平面11A B C ；(2)在平行六面体1111ABCD A B C D -中，1AA AB =，得四边形11ABB A 是菱形，11.AB A B ⊥在平行六面体1111ABCD A B C D -中，1AA AB =，1111.AB B C AB BC ⊥⇒⊥ 又1A B BC C ⋂=，1A B ⊂平面1A BC ，BC ⊂平面1A BC得1AB ⊥面1A BC ，且1AB ⊂平面11ABB A∴平面11ABB A ⊥平面1.A BC14.【答案】(1)证明：矩形ABCD ，且E ，F 是AB 、CD 中点，//AE CF ∴且AE CF =，∴四边形AECF 是平行四边形，//CE AF ∴，又CE ⊂/面AMF ，AF ⊂面AMF ，//CE ∴平面AMF ；又M 是PD 中点，则//MF PC ，同理可得//PC 平面AMF ，又CE ⊂平面PEC ，PC ⊂平面PEC ，CE PC C ⋂=，∴平面//AMF 平面PEC ；(2)解：棱锥M AFD -的高等于PA 的一半，则多面体PECFMA 的体积 111120(12)44142.32323P AECD M AFD V V V --=-=⨯+⨯⨯-⨯⨯⨯⨯=15.【答案】()Ⅰ证明：连接AC 交BD 于点O ，连接OE ， 则O 是AC 的中点．又知E 是PC 中点，//EO PA ∴，PA ⊥平面ABCD ，OE ∴⊥平面.ABCD又知OE ⊂平面BED ，∴平面BED ⊥平面.ABCD()Ⅱ解：过B 作BM ⊥平面ABCD ，连接PM ，ME ，如图，由()Ⅰ可知，////PA EO MB ，则MB 是平面PBA 与平面EBD 的交线，由BM ⊥平面ABCD ，AB ，BO ⊂平面ABCD ，可得MB AB ⊥，MB BO ⊥，则ABO ∠即平面PBA 与平面EBD 所成二面角的平面角，四边形ABCD 为菱形，60.ABC ︒∠=可知30ABO ︒∠=，3cos cos30.2ABO ︒∠== 所以，平面PBA 与平面EBD 所成二面角(锐角)的余弦值为3.216.【答案】证明：()Ⅰ连结1A E ，11A A A C =，E 是AC 的中点，1A E AC ∴⊥，又平面11A ACC ⊥平面ABC ，1A E ⊂平面11A ACC ，平面11A ACC ⋂平面ABC AC =，1A E ∴⊥平面ABC ，又BC ⊂平面ABC ，1A E BC ∴⊥，1//A F AB ，90ABC ︒∠=，1BC A F ∴⊥，111A E A F A ⋂=，1A E 、1A F ⊂平面1A EF ，BC ∴⊥平面1A EF ，又EF ⊂平面1A EF ，EF BC ∴⊥；解：()Ⅱ取BC 中点G ，连结EG 、GF ，则1EGFA 是平行四边形，由于1A E ⊥平面ABC ，故1A E EG ⊥，∴平行四边形1EGFA 是矩形，由()Ⅰ得BC ⊥平面1EGFA ，则平面1A BC ⊥平面1EGFA ，EF ∴在平面1A BC 上的射影在直线1A G 上，连结1A G ，交EF 于O ，则EOG ∠是直线EF 与平面1A BC 所成角(或其补角)，不妨设4AC =，则在1Rt A EG 中，123A E =，3EG =，O 是1A G 的中点，故11522A G EO OG ===， 2223cos 25EO OG EG EOG EO OG +-∴∠==⨯⨯，∴直线EF 与平面1A BC 所成角的余弦值为3.517.【答案】(1)证明：由题意知111////AA BB CC ，又因为侧面11BB C C 是矩形且M ，N 分别是BC ，11B C 的中点，所以1//MN BB ，1BB BC ⊥，所以1//AA MN ，11MN B C ⊥，又底面为正三角形，所以AM BC ⊥，111A N B C ⊥，又因为1MN A N N ⋂=，1,MN A N ⊂平面1A AMN ，所以11B C ⊥平面1A AMN ，又11B C ⊂平面11EB C F ，所以平面11EB C F ⊥平面1.A AMN(2)解：因为//AO 平面11EB C F ，AO ⊂平面1A NMA ，平面1A NMA ⋂平面11EB C F NP =， 所以//AO NP ，又因为//NO AP ，所以6AO NP ==，3ON AP ==， 过M 作MH NP ⊥，垂足为H ，因为平面11EB C F ⊥平面1A AMN ，平面11EB C F ⋂平面1A AMN NP =，MH ⊂平面1A AMN ，所以MH ⊥平面11EB C F ，因为3MPN π∠=，所以sin33MH PM π=⋅=， 在ABC 中，EF AP BC AM = 可得2AP BC EF AM⋅== ， 11111()242EB C F S B C EF NP =+⋅=四边形， 又//BC 平面11EB C F ，所以1111B EB C F M EB C F V V --=11124.3EB C F S MH =⋅⋅=18.【答案】(1)证明：如图，连接1BC ，交1CB 于点N ，连接1A N ，.ON 则N 为1CB 的中点，又O 为BC 的中点，1//ON BB ∴，且112ON BB =， 又M 为1AA 的中点，11//MA BB ∴，且1112MA BB =， 1//ON MA ∴且1ON MA =，∴四边形1ONA M 为平行四边形，1//OM NA ∴，又1NA ⊂平面11CB A ，OM ⊂/平面11CB A ，//OM ∴平面11.CB A(2)解：如图，连接AO ，1OB ，1.ABAB AC =，O 为BC 的中点，AO BC ∴⊥， 又直三棱柱111ABC A B C -中，平面11CBB C ⊥平面ABC ，平面11CBB C ⋂平面ABC BC =，AO ⊂平面.ABCAO ∴⊥平面11.CBB C由(1)可知//OM 平面11CB A ，∴点M 到平面11CB A 的距离等于点O 到平面11CB A 的距离，设其为d ， 在直三棱柱111ABC A B C -中，由AB AC ==12BC AA ==可得，1AO =，11A B =1AC =1BC=，11CB A ∴是直角三角形，且1112CB A S = 由11111_{_}O CB A A A COB V V COB V --=-=得：111111213332COB d S AO =⨯⨯=⨯⨯⨯⨯，故d =即点M 到平面11CB A19.【答案】解：(1)连接1BC ，交1CB 于点O ，则O 为1CB 的中点，连接1A O ，MO因为M 为BC 的中点，所以1//MO BB ，所以1//MO NA ，从而M ，O ，1A ，N 四点共面.因为//MN 平面11A CB ，MN ⊂平面1MOA N ，平面1MOA N ⋂平面111=ACB AO ， 所以1//.MN AO又1//MO NA ，所以四边形1MOA N 为平行四边形， 所以1111122NA MO BB AA ===， 所以1=1.AN NA (2)因为11//A C AC ，所以直线MN 与直线11A C 所成角即为直线MN 与直线AC 所成角或者其补角. 取AB 的中点G ，连接,MG NG ，M 为BC 的中点，易得//AC GM ，则所求角为GMN ∠或者其补角GMN 中，112GM AC ==， 222GN AG AN =+=，222MN AM AN =+=由余弦定理可得1423cos 2124GMN +-∠==⨯⨯， 则7sin 4GMN ∠=， 所以，直线MN 与直线11A C 所成角的正弦值为7.420.【答案】证明：(1)如图：证明：连接BD ，由题意得AC BD H ⋂=，BH DH =，又由BG PG =，得//GH PD ，GH ⊂/平面PAD ，PD ⊂平面PAD ，//GH ∴平面PAD ；(2)证明：取棱PC 中点N ，连接DN ，依题意得DN PC ⊥， 又平面PAC ⊥平面PCD ，平面PAC ⋂平面PCD PC =，DN ⊂平面PCD ， DN ∴⊥平面PAC ，又PA ⊂平面PAC ，DN PA ∴⊥，又PA CD ⊥，CD DN D ⋂=，CD ⊂平面PCD ，DN ⊂平面PCD ，PA ∴⊥平面PCD ；(3)解：连接AN ，由(2)中DN ⊥平面PAC ，知DAN ∠是直线AD 与平面PAC 所成角， PCD 是等边三角形，2CD =，且N 为PC 中点， 3DN ∴=，又DN ⊥平面PAC ，AN PAC ⊂平面，DN AN ⊥，在Rt AND 中，3sin .3DN DAN DA ∠== ∴直线AD 与平面PAC 所成角的正弦值为3.3。

（ 7）球体：定义： 以半圆的直径所在直线为旋转轴，半圆面旋转一周形成的几何体
几何特征： ①球的截面是圆；②球面上任意一点到球心的距离等于半径。
2、空间几何体的三视图 定义三视图：正视图（光线从几何体的前面向后面正投影） 俯视图（从上向下）
；侧视图（从左向右） 、
注：正视图反映了物体上下、左右的位置关系，即反映了物体的高度和长度；
B．
C． D．
29．如图是某几何体的三视图，则该几何体的体积为（
）
A． 1 B． C． D． 30．某几何体的三视图如图所示，且该几何体的体积是 是（ ）
，则正视图中的 x 的值
A． 2 B． C． D．3
31．将边长为 a 的正方形 ABCD 沿对角线 AC 折起，使得 BD=a，则三棱锥 D﹣ ABC 的体积为（ ）
设三棱锥 F﹣ADE 的体积为 V 1，三棱柱 A 1B1C1﹣ ABC 的体积为 V 2，则 V 1：
V2=
．
39．如图，在圆柱 O1O2 内有一个球 O，该球与圆柱的上、下底面及母线均相切，
记圆柱 O1O2 的体积为 V 1，球 O 的体积为 V 2，则 的值是
．
40．若某几何体的三视图（单位： cm3．
（ 1）要使倾斜后容器内的溶液不会溢出，角 α的最大值是多少； （ 2）现需要倒出不少于 3000cm3 的溶液，当 α=60°时，能实现要求吗？请说明 理由． 47．如图，水平放置的正四棱柱形玻璃容器Ⅰ和正四棱台形玻璃容器Ⅱ的高均为 32cm，容器Ⅰ的底面对角线 AC 的长为 10 cm，容器Ⅱ的两底面对角线 EG， E1G1 的长分别为 14cm 和 62cm．分别在容器Ⅰ和容器Ⅱ中注入水，水深均为 12cm．现有一根玻璃棒 l，其长度为 40cm．（容器厚度、 玻璃棒粗细均忽略不计） （ 1）将 l 放在容器Ⅰ中， l 的一端置于点 A 处，另一端置于侧棱 CC1 上，求 l

例1。

若棱长为3的正方体的顶点都在同一球面上，求该球的表面积和体积。

分析：①334R V π=球（R 为球半径） ②24R S π=球 （R 为球半径) 需要求出半径。

正方体的棱长为a ，则:正方体的内切球、棱切球、外接球半径分别为:a 21，a 22，a 23。

变式：一个长方体的各顶点均在同一球面上，且一个顶点上的三条棱长分别为1,2,3,则此球的表面积为。

【解析】关键是求出球的半径,因为长方体内接于球，所以它的体对角线正好为球的直径。

长方体体对角线长为14,故球的表面积为14π。

变式：（已知各顶点都在一个球面上的正四棱柱高为4，体积为16，则这个球的表面积为( ）.A 。

16π B 。

20π C 。

24π D 。

32π解题关键：通过多面体的一条侧棱和球心，或接点作出截面图。

棱锥与球例题：求棱长为1的正四面体ABCD 的外接球体积. 分析:作出合适的球的轴截面图，找准球心位置，构造三角形求解半径。

常用结论：正四面体外接球的球心在高线上，半径是正四面体高的43解法一、 解法二、如何求正四面体的外接球半径法1.补成正方体法2.勾股定理法例题：求棱长为a 的正四面体的内切球半径。

分析：并非所有多面体都有内切球，正多面体存在内切球，且正多面体的中心为内切球球心。

常用结论：正多面体内切球半径是高的41；31⋅⋅=内切表多R S V 1、正三棱锥的高为1，底面边长为62，内有一个球与它的四个面都相切．求：（1）外接球的表面积和体积;(2）内切球的表面积与体积．设正四面体的棱长为a ，则：正四面体的内切球、棱切球、外接球半径分别为: a 126、a 42、a 46. 构造长方体变式 P 、A 、B 、C 是球O 面上的四个点,PA 、PB 、PC 两两垂直，PA=PB=PC=a,求这个球的体积。

例 已知点A 、B 、C 、D 在同一个球面上,B BCD A ⊥平面,BC DC ⊥,若6,AC=213,AD=8AB =，则B 、C 两点间的球面距离是____。

空间几何体[考情分析] 几何体的结构特征是立体几何的基础，空间几何体的表面积与体积是高考题的重点与热点，多以小题的形式进行考查，属于中等难度． 考点一 表面积与体积 核心提炼1．旋转体的侧面积和表面积(1)S 圆柱侧＝2πrl ，S 圆柱表＝2πr (r ＋l )(r 为底面半径，l 为母线长)． (2)S 圆锥侧＝πrl ，S 圆锥表＝πr (r ＋l )(r 为底面半径，l 为母线长)． (3)S 球表＝4πR 2(R 为球的半径)． 2．空间几何体的体积公式 V 柱＝Sh (S 为底面面积，h 为高)； V 锥＝13Sh (S 为底面面积，h 为高)；V 球＝43πR 3(R 为球的半径)．例1 (1)已知圆锥的顶点为S ，母线SA ，SB 所成角的余弦值为78，SA 与圆锥底面所成角为45°.若△SAB 的面积为515，则该圆锥的侧面积为________． 答案 402π解析 因为母线SA 与圆锥底面所成的角为45°， 所以圆锥的轴截面为等腰直角三角形． 设底面圆的半径为r ，则母线长l ＝2r .在△SAB 中，cos ∠ASB ＝78，所以sin ∠ASB ＝158.因为△SAB 的面积为515，即12SA ·SB sin ∠ASB＝12×2r ×2r ×158＝515， 所以r 2＝40，故圆锥的侧面积为πrl ＝2πr 2＝402π.(2)如图，已知正三棱柱ABC －A 1B 1C 1的各棱长均为2，点D 在棱AA 1上，则三棱锥D －BB 1C 1的体积为________．答案 233解析 如图，取BC 的中点O ，连接AO .∵正三棱柱ABC －A 1B 1C 1的各棱长均为2， ∴AC ＝2，OC ＝1，则AO ＝ 3. ∵AA 1∥平面BCC 1B 1，∴点D 到平面BCC 1B 1的距离为 3. 又11BB C S＝12×2×2＝2， ∴11D BB C V ＝13×2×3＝233.易错提醒 (1)计算表面积时，有些面的面积没有计算到(或重复计算)． (2)一些不规则几何体的体积不会采用分割法或补形思想转化求解． (3)求几何体体积的最值时，不注意使用基本不等式或求导等确定最值．跟踪演练1 (1)已知圆柱的上、下底面的中心分别为O 1，O 2，过直线O 1O 2的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为( ) A ．122π B ．12π C ．82π D ．10π答案 B解析 设圆柱的底面半径为r ，高为h ，由题意可知2r ＝h ＝22，∴圆柱的表面积S ＝2πr 2＋2πr ·h ＝4π＋8π＝12π.故选B.(2)如图，在Rt △ABC 中，AB ＝BC ＝1，D 和E 分别是边BC 和AC 上异于端点的点，DE ⊥BC ，将△CDE 沿DE 折起，使点C 到点P 的位置，得到四棱锥P －ABDE ，则四棱锥P －ABDE 的体积的最大值为________．答案327解析 设CD ＝DE ＝x (0<x <1)，则四边形ABDE 的面积S ＝12(1＋x )(1－x )＝12(1－x 2)，当平面PDE ⊥平面ABDE 时，四棱锥P －ABDE 的体积最大，此时PD ⊥平面ABDE ，且PD ＝CD ＝x ，故四棱锥P －ABDE 的体积V ＝13S ·PD ＝16(x －x 3)，则V ′＝16(1－3x 2)．当x ∈⎝⎛⎭⎫0，33时，V ′>0；当x ∈⎝⎛⎭⎫33，1时，V ′<0.∴当x ＝33时，V max ＝327. 考点二 多面体与球 核心提炼解决多面体与球问题的两种思路(1)利用构造长方体、正四面体等确定直径．(2)利用球心O 与截面圆的圆心O 1的连线垂直于截面圆的性质确定球心．例2 (1)已知三棱锥P －ABC 满足平面P AB ⊥平面ABC ，AC ⊥BC ，AB ＝4，∠APB ＝30°，则该三棱锥的外接球的表面积为__________． 答案 64π解析 因为AC ⊥BC ，所以△ABC 的外心为斜边AB 的中点，因为平面P AB ⊥平面ABC ，所以三棱锥P －ABC 的外接球球心在平面P AB 上， 即球心就是△P AB 的外心，根据正弦定理ABsin ∠APB ＝2R ，解得R ＝4，所以外接球的表面积为4πR 2＝64π.(2)(2020·全国Ⅲ)已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为________． 答案23π 解析 圆锥内半径最大的球即为圆锥的内切球，设其半径为r .作出圆锥的轴截面P AB ，如图所示，则△P AB 的内切圆为圆锥的内切球的大圆．在△P AB 中，P A ＝PB ＝3，D 为AB 的中点，AB ＝2，E 为切点，则PD ＝22，△PEO ∽△PDB ， 故PO PB ＝OE DB ，即22－r 3＝r 1，解得r ＝22， 故内切球的体积为43π⎝⎛⎭⎫223＝23π.规律方法 (1)长方体的外接球直径等于长方体的体对角线长．(2)三棱锥S －ABC 的外接球球心O 的确定方法：先找到△ABC 的外心O 1，然后找到过O 1的平面ABC 的垂线l ，在l 上找点O ，使OS ＝OA ，点O 即为三棱锥S －ABC 的外接球的球心． (3)多面体的内切球可利用等积法求半径．跟踪演练2 (1)已知A ，B 是球O 的球面上两点，∠AOB ＝90°，C 为该球面上的动点．若三棱锥O －ABC 体积的最大值为36，则球O 的表面积为( ) A ．36π B ．64π C ．144π D ．256π 答案 C解析 如图所示，设球O 的半径为R ，因为∠AOB ＝90°， 所以S △AOB ＝12R 2，因为V O －ABC ＝V C －AOB ， 而△AOB 的面积为定值，当点C 位于垂直于平面AOB 的直径端点时，三棱锥O －ABC 的体积最大， 此时V O －ABC ＝V C －AOB ＝13×12R 2×R ＝16R 3＝36，故R ＝6，则球O 的表面积为S ＝4πR 2＝144π.(2)中国古代数学经典《九章算术》系统地总结了战国、秦、汉时期的数学成就，书中将底面为长方形且有一条侧棱与底面垂直的四棱锥称之为阳马，将四个面都为直角三角形的三棱锥称之为鳖臑，如图为一个阳马与一个鳖臑的组合体，已知P A ⊥平面ABCE ，四边形ABCD 为正方形，AD ＝5，ED ＝3，若鳖臑P －ADE 的外接球的体积为92π，则阳马P －ABCD 的外接球的表面积为________．答案 20π解析 ∵四边形ABCD 是正方形，∴AD ⊥CD ，即AD ⊥CE ，且AD ＝5，ED ＝3， ∴△ADE 的外接圆半径为r 1＝AE2＝AD 2＋ED 22＝2， 设鳖臑P －ADE 的外接球的半径为R 1， 则43πR 31＝92π，解得R 1＝322. ∵P A ⊥平面ADE ，∴R 1＝⎝⎛⎭⎫P A 22＋r 21， 可得P A 2＝R 21－r 21＝102，∴P A ＝10. 正方形ABCD 的外接圆直径为2r 2＝AC ＝2AD ＝10， ∴r 2＝102， ∵P A ⊥平面ABCD ，∴阳马P －ABCD 的外接球半径R 2＝⎝⎛⎭⎫P A 22＋r 22＝5， ∴阳马P －ABCD 的外接球的表面积为4πR 22＝20π. 专题强化练一、单项选择题1.水平放置的△ABC 的直观图如图，其中B ′O ′＝C ′O ′＝1，A ′O ′＝32，那么原△ABC 是一个( )A ．等边三角形B ．直角三角形C ．三边中只有两边相等的等腰三角形D ．三边互不相等的三角形 答案 A解析 AO ＝2A ′O ′＝2×32＝3，BC ＝B ′O ′＋C ′O ′＝1＋1＝2.在Rt △AOB 中，AB ＝12＋(3)2＝2，同理AC ＝2，所以原△ABC 是等边三角形．2．(2020·全国Ⅰ)埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥．以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为( )A.5－14 B.5－12 C.5＋14 D.5＋12答案 C解析 设正四棱锥的底面正方形的边长为a ，高为h ， 侧面三角形底边上的高(斜高)为h ′， 则由已知得h 2＝12ah ′.如图，设O 为正四棱锥S －ABCD 底面的中心，E 为BC 的中点，则在Rt △SOE 中，h ′2＝h 2＋⎝⎛⎭⎫a 22， ∴h ′2＝12ah ′＋14a 2，∴⎝⎛⎭⎫h ′a 2－12·h ′a －14＝0，解得h ′a ＝5＋14(负值舍去)．3．已知一个圆锥的侧面积是底面积的2倍，记该圆锥的内切球的表面积为S 1，外接球的表面积为S 2，则S 1S 2等于( )A.12B.13C.14D.18 答案 C 解析 如图，由已知圆锥侧面积是底面积的2倍，不妨设底面圆半径为r ，l 为底面圆周长，R 为母线长， 则12lR ＝2πr 2， 即12·2π·r ·R ＝2πr 2， 解得R ＝2r ，故∠ADC ＝30°，则△DEF 为等边三角形， 设B 为△DEF 的重心，过B 作BC ⊥DF ，则DB 为圆锥的外接球半径，BC 为圆锥的内切球半径，则BC BD ＝12，∴r 内r 外＝12，故S 1S 2＝14. 4．(2020·大连模拟)一件刚出土的珍贵文物要在博物馆大厅中央展出，如图，需要设计各面是玻璃平面的无底正四棱柱将其罩住，罩内充满保护文物的无色气体．已知文物近似于塔形，高1.8米，体积0.5立方米，其底部是直径为0.9米的圆形，要求文物底部与玻璃罩底边至少间隔0.3米，文物顶部与玻璃罩上底面至少间隔0.2米，气体每立方米1 000元，则气体的费用最少为( )A ．4 500元B ．4 000元C ．2 880元D ．2 380元 答案 B解析 因为文物底部是直径为0.9米的圆形，文物底部与玻璃罩底边至少间隔0.3米，所以由正方形与圆的位置关系可知，底面正方形的边长为0.9＋2×0.3＝1.5米，又文物高1.8米，文物顶部与玻璃罩上底面至少间隔0.2(米)，所以正四棱柱的高为1.8＋0.2＝2(米)，则正四棱柱的体积V ＝1.52×2＝4.5(立方米)．因为文物的体积为0.5立方米，所以罩内空气的体积为4.5－0.5＝4(立方米)，因为气体每立方米1 000元，所以气体的费用最少为4×1 000＝4 000(元)，故选B.5.如图所示，在正方体ABCD －A 1B 1C 1D 1中，动点E 在BB 1上，动点F 在A 1C 1上，O 为底面ABCD 的中心，若BE ＝x ，A 1F ＝y ，则三棱锥O －AEF 的体积( )A ．与x ，y 都有关B ．与x ，y 都无关C ．与x 有关，与y 无关D ．与y 有关，与x 无关 答案 B解析 由已知得V 三棱锥O －AEF ＝V 三棱锥E －OAF ＝13S △AOF ·h (h 为点E 到平面AOF 的距离)．连接OC ，因为BB 1∥平面ACC 1A 1，所以点E 到平面AOF 的距离为定值．又AO ∥A 1C 1，OA 为定值，点F 到直线AO 的距离也为定值，所以△AOF 的面积是定值，所以三棱锥O －AEF 的体积与x ，y 都无关．6．在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2.将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的体积为( ) A.2π3 B.4π3 C.5π3 D ．2π 答案 C解析 如图，过点C 作CE 垂直AD 所在直线于点E ，梯形ABCD 绕AD 所在直线旋转一周而形成的旋转体是由以线段AB 的长为底面圆半径，线段BC 为母线的圆柱挖去以线段CE 的长为底面圆半径，ED 为高的圆锥，该几何体的体积为V ＝V 圆柱－V 圆锥＝π·AB2·BC －13·π·CE 2·DE ＝π×12×2－13π×12×1＝5π3.7．(2020·全国Ⅰ)已知A ，B ，C 为球O 的球面上的三个点，⊙O 1为△ABC 的外接圆．若⊙O 1的面积为4π，AB ＝BC ＝AC ＝OO 1，则球O 的表面积为( ) A ．64π B ．48π C ．36π D ．32π 答案 A解析 如图，设圆O 1的半径为r ，球的半径为R ，正三角形ABC 的边长为a .由πr 2＝4π，得r ＝2， 则33a ＝2，a ＝23， OO 1＝a ＝2 3.在Rt △OO 1A 中，由勾股定理得R 2＝r 2＋OO 21＝22＋(23)2＝16，所以S 球＝4πR 2＝4π×16＝64π.8．(2020·武汉调研)已知直三棱柱ABC －A 1B 1C 1的6个顶点都在球O 的表面上，若AB ＝AC ＝1，AA 1＝23，∠BAC ＝2π3，则球O 的体积为( )A.32π3 B ．3π C.4π3 D ．8π 答案 A解析 设△ABC 外接圆圆心为O 1，半径为r ，连接O 1O ，如图，易得O 1O ⊥平面ABC ，∵AB ＝AC ＝1，AA 1＝23，∠BAC ＝2π3，∴2r ＝AB sin ∠ACB ＝112＝2，即O 1A ＝1，O 1O ＝12AA 1＝3，∴OA ＝O 1O 2＋O 1A 2＝3＋1＝2，∴球O 的体积V ＝43π·OA 3＝32π3.故选A.9.如图所示，某几何体由底面半径和高均为5的圆柱与半径为5的半球对接而成，在该封闭的几何体内部放入一个小圆柱体，且小圆柱体的上、下底面均与外层圆柱的底面平行，则小圆柱体积的最大值为( )A.2 000π9B.4 000π27C ．81πD ．128π答案 B解析 小圆柱的高分为上、下两部分，上部分的高同大圆柱的高相等，为5，下部分深入底部半球内．设小圆柱下部分的高为h (0<h <5)，底面半径为r (0<r <5)．由于r ，h 和球的半径构成直角三角形，即r 2＋h 2＝52，所以小圆柱的体积V ＝πr 2(h ＋5)＝π(25－h 2)(h ＋5)(0<h <5)，把V 看成是关于h 的函数，求导得V ′＝－π(3h －5)(h ＋5)．当0<h <53时，V ′>0，V 单调递增；当53<h <5时，V ′<0，V 单调递减．所以当h ＝53时，小圆柱的体积取得最大值．即V max ＝π⎝⎛⎭⎫25－259×⎝⎛⎭⎫53＋5＝4 000π27，故选B. 10．已知在三棱锥P －ABC 中，P A ，PB ，PC 两两垂直，且长度相等．若点P ，A ，B ，C 都在半径为1的球面上，则球心到平面ABC 的距离为( ) A.36 B.12 C.13 D.32答案 C解析 ∵在三棱锥P －ABC 中，P A ，PB ，PC 两两垂直，且长度相等， ∴此三棱锥的外接球即以P A ，PB ，PC 为三边的正方体的外接球O ， ∵球O 的半径为1，∴正方体的边长为233，即P A ＝PB ＝PC ＝233，球心到截面ABC 的距离即正方体中心到截面ABC 的距离，设P 到截面ABC 的距离为h ，则正三棱锥P －ABC 的体积V ＝13S △ABC ×h ＝13 S △P AB ×PC ＝13×12×⎝⎛⎭⎫2333， ∵△ABC 为边长为263的正三角形，S △ABC ＝233，∴h ＝23， ∴球心(即正方体中心)O 到截面ABC 的距离为13.二、多项选择题11．(2020·枣庄模拟)如图，透明塑料制成的长方体容器ABCD －A 1B 1C 1D 1内灌进一些水，固定容器一边AB 于地面上，再将容器倾斜，随着倾斜度的不同，有下面几个结论，其中正确的是( )A ．没有水的部分始终呈棱柱形B ．水面EFGH 所在四边形的面积为定值C ．随着容器倾斜度的不同，A 1C 1始终与水面所在平面平行D ．当容器倾斜如图③所示时，AE ·AH 为定值 答案 AD解析 由于AB 固定，所以在倾斜的过程中，始终有CD ∥HG ∥EF ∥AB ，且平面AEHD ∥平面BFGC ，故水的部分始终呈棱柱形(三棱柱或四棱柱)，且AB 为棱柱的一条侧棱，没有水的部分也始终呈棱柱形，故A 正确；因为水面EFGH 所在四边形，从图②，图③可以看出，EF ，GH 长度不变，而EH ，FG 的长度随倾斜度变化而变化，所以水面EFGH 所在四边形的面积是变化的，故B 错；假设A 1C 1与水面所在的平面始终平行，又A 1B 1与水面所在的平面始终平行，则长方体上底面A 1B 1C 1D 1与水面所在的平面始终平行，这就与倾斜时两个平面不平行矛盾，故C 错；水量不变时，棱柱AEH －BFG 的体积是定值，又该棱柱的高AB 不变，且V AEH －BFG ＝12·AE ·AH ·AB ，所以AE ·AH ＝2V AEH －BFG AB ，即AE ·AH 是定值，故D 正确．12. (2020·青岛检测)已知四棱台ABCD －A 1B 1C 1D 1的上、下底面均为正方形，其中AB ＝22，A 1B 1＝2，AA 1＝BB 1＝CC 1＝DD 1＝2，则下列叙述正确的是( )A ．该四棱台的高为 3B ．AA 1⊥CC 1C ．该四棱台的表面积为26D ．该四棱台外接球的表面积为16π 答案 AD解析 将四棱台补为如图所示的四棱锥P －ABCD ，并取E ，E 1分别为BC ，B 1C 1的中点，记四棱台上、下底面中心分别为O 1，O ，连接AC ，BD ，A 1C 1，B 1D 1，A 1O ，OE ，OP ，PE .由条件知A 1，B 1，C 1，D 1分别为四棱锥的侧棱P A ，PB ，PC ，PD 的中点，则P A ＝2AA 1＝4，OA ＝2，所以OO 1＝12PO ＝12P A 2－OA 2＝3，故该四棱台的高为3，故A 正确；由P A ＝PC＝4，AC ＝4，得△P AC 为正三角形，则AA 1与CC 1所成角为60°，故B 不正确；四棱台的斜高h ′＝12PE ＝12PO 2＋OE 2＝12×(23)2＋(2)2＝142，所以该四棱台的表面积为(22)2＋(2)2＋4×2＋222×142＝10＋67，故C 不正确；易知OA 1＝OB 1＝OC 1＝OD 1＝O 1A 21＋O 1O 2＝2＝OA ＝OB ＝OC ＝OD ，所以O 为四棱台外接球的球心，所以外接球的半径为2，外接球表面积为4π×22＝16π，故D 正确．三、填空题13．(2020·浙江)已知圆锥的侧面积(单位：cm 2)为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径(单位：cm)是________． 答案 1解析 如图，设圆锥的母线长为l ，底面半径为r ，则圆锥的侧面积S 侧＝πrl ＝2π，即r·l＝2.由于侧面展开图为半圆，可知12πl2＝2π，可得l＝2，因此r＝1.14.在如图所示的斜截圆柱中，已知圆柱的底面直径为40 cm，母线长最短50 cm，最长80 cm，则斜截圆柱的侧面面积S＝________cm2.答案 2 600π解析将题图所示的相同的两个几何体对接为圆柱，则圆柱的侧面展开图为矩形．由题意得所求侧面展开图的面积S＝12×(π×40)×(50＋80)＝2 600π(cm2)．15．已知球O与棱长为4的正四面体的各棱相切，则球O的体积为________．答案82 3π解析将正四面体补成正方体，则正四面体的棱为正方体面上的对角线，因为正四面体的棱长为4，所以正方体的棱长为2 2.因为球O与正四面体的各棱都相切，所以球O为正方体的内切球，即球O的直径2R＝22，则球O的体积V＝43πR3＝823π.16．(2020·新高考全国Ⅰ)已知直四棱柱ABCD－A1B1C1D1的棱长均为2，∠BAD＝60°.以D1为球心，5为半径的球面与侧面BCC1B1的交线长为________．答案2π2解析如图，设B1C1的中点为E，球面与棱BB1，CC1的交点分别为P，Q，连接DB，D1B1，D1P，D1E，EP，EQ，由∠BAD ＝60°，AB ＝AD ，知△ABD 为等边三角形， ∴D 1B 1＝DB ＝2，∴△D 1B 1C 1为等边三角形， 则D 1E ＝3且D 1E ⊥平面BCC 1B 1，∴E 为球面截侧面BCC 1B 1所得截面圆的圆心， 设截面圆的半径为r ， 则r ＝R 2球－D 1E 2＝5－3＝ 2.又由题意可得EP ＝EQ ＝2，∴球面与侧面BCC 1B 1的交线为以E 为圆心的圆弧PQ . 又D 1P ＝5， ∴B 1P ＝D 1P 2－D 1B 21＝1， 同理C 1Q ＝1，∴P ，Q 分别为BB 1，CC 1的中点， ∴∠PEQ ＝π2，知PQ 的长为π2×2＝2π2，即交线长为2π2.。

高考数学复习考点题型专题讲解专题13 空间几何体的结构、表面积和体积高考定位空间几何体的结构特征是高考重点考查的内容.近几年主要考查空间几何体的表面积与体积，常以选择题与填空题为主，也涉及空间几何体的结构特征等内容，要求考生要有较强的空间想象能力和计算能力，难度为中低档.1.(2021·新高考Ⅰ卷)已知圆锥的底面半径为2，其侧面展开图为一个半圆，则该圆锥的母线长为( )A.2B.2 2C.4D.4 2答案 B解析设圆锥的母线长为l，因为该圆锥的底面半径为2，侧面展开图为一个半圆，所以2π×2＝πl，解得l＝22，故选B.2.(2022·新高考Ⅰ卷)南水北调工程缓解了北方一些地区水资源短缺问题，其中一部分水蓄入某水库.已知该水库水位为海拔148.5 m时，相应水面的面积为140.0 km2；水位为海拔157.5 m时，相应水面的面积为180.0 km2.将该水库在这两个水位间的形状看作一个棱台，则该水库水位从海拔148.5 m上升到157.5 m时，增加的水量约为(7≈2.65)()A.1.0×109 m3B.1.2×109 m3C.1.4×109 m3D.1.6×109 m3答案 C解析如图，由已知得该棱台的高为157.5－148.5＝9(m)，所以该棱台的体积V＝13×9×(140＋140×180＋180)×106＝60×(16＋37)×106≈60×(16＋3×2.65)×106＝1.437×109≈1.4×109(m3).故选C.3.(2022·新高考Ⅱ卷)已知正三棱台的高为1，上、下底面边长分别为33和43，其顶点都在同一球面上，则该球的表面积为( )A.100πB.128πC.144πD.192π答案 A解析由题意得，正三棱台上、下底面的外接圆的半径分别为23×32×33＝3，23×32×43＝4.设该棱台上、下底面的外接圆的圆心分别为O1，O2，连接O1O2，则O1O2＝1，其外接球的球心O在直线O1O2上.设球O的半径为R，当球心O在线段O1O2上时，R2＝32＋OO21＝42＋(1－OO1)2，解得OO1＝4(舍去)；当球心O不在线段O1O2上时，R2＝42＋OO22＝32＋(1＋OO2)2，解得OO2＝3，所以R2＝25，所以该球的表面积为4πR2＝100π.综上，该球的表面积为100π.4.(2022·全国甲卷)甲、乙两个圆锥的母线长相等，侧面展开图的圆心角之和为2π，侧面积分别为S甲和S乙，体积分别为V甲和V乙.若S甲S乙＝2，则V甲V乙＝( )A.5B.2 2C.10D.510 4答案 C解析法一因为甲、乙两个圆锥的母线长相等，所以结合S甲S乙＝2，可知甲、乙两个圆锥侧面展开图的圆心角之比是2∶1.不妨设两个圆锥的母线长为l＝3，甲、乙两个圆锥的底面半径分别为r1，r2，高分别为h1，h2，则由题意知，两个圆锥的侧面展开图刚好可以拼成一个周长为6π的圆，所以2πr1＝4π，2πr2＝2π，得r1＝2，r2＝1.由勾股定理得，h1＝l2－r21＝5，h2＝l2－r22＝22，所以V甲V乙＝13πr21h113πr22h2＝4522＝10.故选C.法二设两圆锥的母线长为l，甲、乙两圆锥的底面半径分别为r1，r2，高分别为h1，h2，侧面展开图的圆心角分别为n1，n2，则由S甲S乙＝πr1lπr2l＝n1πl22πn2πl22π＝2，得r1r2＝n1n2＝2.由题意知n1＋n2＝2π，所以n1＝4π3，n2＝2π3，所以2πr 1＝4π3l ，2πr 2＝2π3l ，得r 1＝23l ，r 2＝13l .由勾股定理得，h 1＝l 2－r 21＝53l ，h 2＝l 2－r 22＝223l ， 所以V 甲V 乙＝13πr 21h 113πr 22h 2＝4522＝10.故选C.热点一 空间几何体的结构特征关于空间几何体的结构特征辨析关键是紧扣各种几何体的概念. 例1 (1)以下四个命题中，真命题为( ) A.侧面都是等腰三角形的棱锥是正棱锥 B.底面是矩形的平行六面体是长方体 C.直四棱柱是直平行六面体 D.棱台的侧棱延长后必交于一点 (2)给出下列命题：①在圆柱的上、下底面的圆周上各取一点，则这两点的连线是圆柱的母线； ②直角三角形绕其任一边所在直线旋转一周所形成的几何体都是圆锥； ③棱台的上、下底面可以不相似，但侧棱长一定相等. 其中正确命题的个数是( )A.0B.1C.2D.3答案(1)D (2)A解析(1)A中等腰三角形的腰不一定是侧棱，A是假命题；B中，侧棱与底面矩形不一定垂直，B是假命题；C中，直四棱柱的底面不一定是平行四边形，C是假命题；根据棱台的定义，选项D是真命题.(2)①不一定，只有当这两点的连线平行于轴时才是母线；②不一定，当以斜边所在直线为旋转轴时，其余两边旋转一周形成的面所围成的几何体不是圆锥，如图所示，它是由两个同底圆锥组成的几何体；③错误，棱台的上、下底面相似且是对应边平行的多边形，各侧棱延长线交于一点，但是侧棱长不一定相等.规律方法 1.圆柱、圆锥、圆台的有关元素都集中在轴截面上，解题时要注意用好轴截面中各元素的关系.2.既然棱(圆)台是由棱(圆)锥定义的，所以在解决棱(圆)台问题时，要注意“还台为锥”的解题策略.训练1(多选)(2022·潍坊调研)下面关于空间几何体的叙述正确的是( )A.底面是正多边形的棱锥是正棱锥B.用平面截圆柱得到的截面只能是圆和矩形C.长方体是直平行六面体D.存在每个面都是直角三角形的四面体答案CD解析A中当顶点在底面的投影是正多边形的中心时才是正棱锥，A不正确；B中当平面与圆柱的母线平行或垂直时，截得的截面才为矩形或圆，否则为椭圆或椭圆的一部分，B不正确；C正确；D正确，如图，正方体ABCD－A1B1C1D1中的三棱锥C1－ABC，四个面都是直角三角形.热点二空间几何体的侧面积、表面积柱体、锥体、台体和球的表面积公式：(1)若圆柱的底面半径为r，母线长为l，则S侧＝2πrl，S表＝2πr(r＋l).(2)若圆锥的底面半径为r，母线长为l，则S侧＝πrl，S表＝πr(r＋l).(3)若圆台的上、下底面半径分别为r′，r，则S侧＝π(r＋r′)l，S表＝π(r2＋r′2＋r′l＋rl).(4)若球的半径为R，则它的表面积S＝4πR2.例2 (1)如图，四面体各个面都是边长为1的正三角形，其三个顶点在一个圆柱的下底面圆周上，另一个顶点是上底面圆心，则圆柱的侧面积是( )A.23π B.324π C.223π D.22π(2)(多选)等腰直角三角形的直角边长为1，现将该三角形绕其某一边旋转一周，则所形成的几何体的表面积可以为( )A.2πB.(1＋2)πC.22πD.(2＋2)π 答案 (1)C (2)AB解析 (1)如图所示，过点P 作PE ⊥平面ABC ，E 为垂足，点E 为等边三角形ABC 的中心，连接AE 并延长，交BC 于点D .AE ＝23AD ，AD ＝32，∴AE ＝23×32＝33，∴PE ＝PA 2－AE 2＝63. 设圆柱底面半径为r ，则r ＝AE ＝33，∴圆柱的侧面积S ＝2πr ·PE ＝2π×33×63＝22π3. (2)如果绕直角边旋转，则形成圆锥，圆锥底面半径为1，高为1，母线就是直角三角形的斜边，长为2，所以所形成的几何体的表面积S ＝π×1×2＋π×12＝(2＋1)π.如果绕斜边旋转，则形成的是上、下两个共底面的圆锥，圆锥的底面半径是直角三角形斜边上的高22，两个圆锥的母线都是直角三角形的直角边，长是1，所以形成的几何体的表面积S′＝2×π×22×1＝2π.综上可知，形成几何体的表面积是(2＋1)π或2π.故选AB.易错提醒 1.旋转体的表面积问题注意其侧面展开图的应用.2.多面体的表面积是各个面的面积之和；组合体的表面积注意衔接部分的处理.训练2 (1)已知圆锥的侧面积(单位：cm2)为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径(单位：cm)是__________.(2)(多选)(2022·青岛质检)已知四棱台ABCD－A1B1C1D1的上、下底面均为正方形，其中AB＝22，A1B1＝2，AA1＝BB1＝CC1＝2，则下列结论正确的是( )A.该四棱台的高为3B.AA1⊥CC1C.该四棱台的表面积为26D.该四棱台外接球的表面积为16π答案(1)1 (2)AD解析(1)如图，设圆锥的母线长为l，底面半径为r，则圆锥的侧面积S侧＝πrl＝2π，即r·l＝2.由于侧面展开图为半圆，可知12πl2＝2π，可得l＝2(cm)，因此r ＝1(cm).(2)由棱台的性质，把四棱台还原为四棱锥如图所示.由题易知点S 在平面A 1B 1C 1D 1和平面ABCD 的射影分别为点O 1，O ，连接OS ，OA ，则O 1在OS 上，由AB ＝22，A 1B 1＝2，可知△SA 1B 1与△SAB 的相似比为1∶2， 则SA ＝2AA 1＝4，AO ＝2， 则SO ＝23，OO 1＝3，即该四棱台的高为3，故A 正确； 因为SA ＝SC ＝AC ＝4，所以AA 1与CC 1的夹角为60°，不垂直，故B 错误；该四棱台的表面积S ＝S 上底＋S 下底＋S 侧＝(2)2＋(22)2＋4×（2＋22）2×22－⎝ ⎛⎭⎪⎫222＝10＋67，故C 错误；由于上、下底面都是正方形，则外接球的球心在OO 1上，在平面B 1BOO 1中， 由于OO 1＝3，B 1O 1＝1， 则OB 1＝2＝OB ，即点O 到点B与点B 1的距离相等，所以该四棱台的外接球的球心为O ，半径r ＝2，所以该四棱台外接球的表面积为16π，故D正确.故选AD.热点三空间几何体的体积柱体、锥体、台体和球的体积公式：(1)V柱体＝Sh(S为底面面积，h为高)；(2)V锥体＝13Sh(S为底面面积，h为高)；(3)V台体＝13(S上＋S下＋S上S下)h(S上、S下分别为上、下底面面积，h为高)；(4)V球＝43πR3.考向1 直接利用公式求体积例3 正四棱台的上、下底面的边长分别为2，4，侧棱长为2，则其体积为( ) A.20＋123B.28 2C.563D.2823答案 D解析如图，设上、下底面的中心分别为O1，O，过点B1作B1M⊥OB于点M，则O1B1＝2，OB＝22，BM＝2，所以该棱台的高h＝B1M＝4－2＝2，所以该四棱台的体积为h3(S上＋S下＋S上S下)＝23(22＋42＋22×42)＝2823，故选D.考向2 割补法求体积例4 如图，在多面体ABCDEF 中，已知四边形ABCD 是边长为1的正方形，且△ADE ，△BCF 均为正三角形，EF ∥AB ，EF ＝2，则该多面体的体积为________.答案23解析 过AD 做与底面ABCD 垂直的平面交EF 于点G ，过BC 做与底面ABCD 垂直的平面交EF 于点H ，则多面体ABCDEF 被分为三棱锥E －ADG ，三棱柱ADG －BCH ，三棱锥F －HBC 三部分.依题意，三棱锥E －ADG 的高EG ＝12，直三棱柱AGD －BHC 的高AB ＝1.则AG ＝AE 2－EG 2＝12－⎝ ⎛⎭⎪⎫122＝32.取AD 的中点M ，并连接MG ，则MG ＝⎝ ⎛⎭⎪⎫322－⎝ ⎛⎭⎪⎫122＝22，所以S △AGD ＝12×1×22＝24，∴V 多面体＝V E －ADG ＋V F －BCH ＋V ADG －BCH ＝2V E －ADG ＋V ADG －BCH ＝13×24×12×2＋24×1＝23.考向3 等体积法求体积例5(2022·台州调研)如图，已知四棱锥P－ABCD中，四边形ABCD为正方形，平面ABCD⊥平面APB，G为PC上一点，且BG⊥平面APC，AB＝2，则三棱锥P－ABC体积的最大值为( )A.23B.223C.43D.2答案 A解析由题意知，平面ABCD⊥平面APB，则BC⊥AP.又由BG⊥平面APC，得BG⊥AP.因为BC∩BG＝B，所以AP⊥平面PBC，所以AP⊥BP，所以V P－ABC＝V C－APB＝13×12PA·PB·BC＝13PA·PB.令PA＝m，PB＝n，则m2＋n2＝4，所以V P－ABC＝13mn≤13·m2＋n22＝23，当且仅当m＝n＝2时取等号，所以三棱锥P－ABC体积的最大值为23 .规律方法 1.规则的几何体可以直接利用相应的公式求解，这就需要熟记柱体、锥体的体积公式；2.不规则的几何体往往可以通过“间接法”——割补法求得，即把不规则的几何体通过“割补”手段，转化为规则几何体体积的和或差.训练3 (1)(2022·广州模拟)在五面体EF－ABCD中，正方形CDEF所在平面与平面ABCD垂直，四边形ABCD为等腰梯形，AB∥CD，AD＝DC＝BC＝12AB.若三棱锥A－BCE的体积为433，则线段AB的长为________.(2)学生到工厂劳动实践，利用3D打印技术制作模型.如图，该模型为长方体ABCD－A 1B1C1D1挖去四棱锥O－EFGH后所得的几何体.其中O为长方体的中心，E，F，G，H分别为所在棱的中点，AB＝BC＝6 cm，AA1＝4 cm.3D打印所用原料密度为0.9 g/cm3，不考虑打印损耗，制作该模型所需原料的质量为______g.答案(1)4 (2)118.8解析(1)取AB的中点O，连接CO.因为AD ＝DC ＝BC ＝12AB ，AB ∥CD ，所以四边形AOCD 为菱形， 所以CO ＝OA ＝OB ， 所以△ACB 为直角三角形， 所以AC ⊥BC .因为正方形CDEF 所在平面与平面ABCD 垂直，CD 为交线，ED ⊥CD ， 所以ED ⊥平面ABCD . 设BC ＝x ，则ED ＝x ，AB ＝2x . 由勾股定理得AC ＝3x ， 故V A －BCE ＝V E －ABC ＝13S △ABC ·ED ，S △ABC ＝12·x ·3x ＝32x 2， 所以V A －BCE ＝13·32x 2·x ＝36x 3＝433.解得x ＝2.所以AB ＝4.(2)由题知挖去的四棱锥的底面是一个菱形，其对角线长分别为6 cm 和4 cm ， 故V 挖去的四棱锥＝13×12×4×6×3＝12(cm 3).又V 长方体＝6×6×4＝144(cm 3)，所以模型的体积为V－V挖去的四棱锥＝144－12＝132(cm3)，长方体所以制作该模型所需原料的质量为132×0.9＝118.8(g).一、基本技能练1.下列说法中，正确的是( )A.棱柱的侧面可以是三角形B.若棱柱有两个侧面是矩形，则该棱柱的其他侧面也是矩形C.正方体的所有棱长都相等D.棱柱的所有棱长都相等答案 C解析棱柱的侧面都是平行四边形，选项A错误；其他侧面可能是平行四边形，选项B错误；棱柱的侧棱与底面边长并不一定相等，选项D错误；易知选项C正确.2.如图所示的等腰梯形是一个几何图形的斜二测直观图，其底角为45°，上底和腰均为1，下底为2＋1，则此直观图对应的平面图形的面积为( )A.1＋2B.2＋ 2C.2＋22D.4＋2 2答案 B解析 ∵平面图形的直观图是一个底角为45°，腰和上底长均为1的等腰梯形， ∴平面图形为直角梯形，且直角腰长为2，上底边长为1，下底边长为2＋1， ∴平面图形的面积S ＝1＋1＋22×2＝2＋ 2.故选B. 3.如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为( )A.4B.43C.23D.3 答案 B解析 易知该几何体是由上、下两个全等的正四棱锥组成的，其中正四棱锥底面边长为2，棱锥的高为1，所以该多面体的体积V ＝2×13×(2)2×1＝43.4.已知在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2，则将梯形ABCD 绕AD 所在的直线旋转一周而形成的曲面所围成的几何体的表面积为( ) A.(5＋2)π B.(4＋2)π C.(5＋22)π D.(3＋2)π 答案 A解析 因为在梯形ABCD 中，∠ABC ＝π2，AD ∥BC ，BC ＝2AD ＝2AB ＝2，所以将梯形ABCD绕AD所在的直线旋转一周得到的几何体是一个底面半径为1，高为2的圆柱挖去一个底面半径为1，高为1的圆锥后剩余的部分，如图所示.所以该几何体的表面积S＝π×12＋2π×1×2＋π×1×12＋12＝(5＋2)π.5.如图，位于西安大慈恩寺的大雁塔，是唐代玄奘法师为保存经卷、佛像而主持修建的，是我国现存最早的四方楼阁式砖塔.塔顶可以看成一个正四棱锥，其侧棱与底面所成的角为45°，则该正四棱锥的一个侧面与底面的面积之比为( )A.3∶2B.2∶2C.3∶3D.3∶4答案 D解析设塔顶是正四棱锥P－ABCD(如图)，PO是正四棱锥的高.设正四棱锥底面边长为a，则底面面积S1＝a2，因为AO＝22a，∠PAO＝45°，所以PA＝2×22a＝a，所以△PAB是正三角形，其面积为S 2＝34a2，所以S2∶S1＝34a2∶a2＝3∶4.6.过圆锥的轴作截面，如果截面为正三角形，则称该圆锥为等边圆锥.已知在一等边圆锥中，过顶点P的截面与底面交于CD，若∠COD＝90°(O为底面圆心)，且S△PCD＝7 2，则这个等边圆锥的表面积为( )A.2π＋2πB.3πC.2π＋3πD.π＋3π答案 B解析如图，连接PO，设圆锥的母线长为2a，则圆锥的底面圆的半径为a，高为PO＝3 a.由已知得CD＝2a，PC＝PD＝2a，则S△PCD＝12×2a×（3a）2＋⎝⎛⎭⎪⎫22a2＝72，从而可得a＝1，圆锥的表面积为πa×2a＋πa2＝3πa2＝3π.7.如图，四边形ABCD 是边长为2的正方形，ED ⊥平面ABCD ，FC ⊥平面ABCD ，ED ＝2FC ＝2，则四面体ABEF 的体积为( )A.13B.23C.1D.43答案 B解析∵ED ⊥平面ABCD 且AD ⊂平面ABCD ， ∴ED ⊥AD .∵在正方形ABCD 中，AD ⊥DC ， 又DC ∩ED ＝D ，DC ，ED ⊂平面CDEF ， ∴AD ⊥平面CDEF .易知FC ＝ED2＝1，V A －BEF ＝V ABCDEF －V F －ABCD －V A －DEF .∵V E －ABCD ＝13·ED ·S 正方形ABCD ＝13×2×2×2＝83，V B －EFC ＝13·BC ·S △EFC ＝13×2×2×1×12＝23， ∴V ABCDEF ＝V E －ABCD ＋V B －EFC ＝83＋23＝103.又V F －ABCD ＝13·FC ·S 正方形ABCD ＝13×1×2×2＝43，V A －DEF ＝13·AD ·S △DEF ＝13×2×2×2×12＝43，∴V A －BEF ＝V ABCDEF －V F －ABCD －V A －DEF ＝103－43－43＝23.故选B.8.黄金分割是指将整体一分为二，较大部分与整体部分的比值等于较小部分与较大部分的比值，其比值为5－12，约为0.618.这个比例被公认为是最能引起美感的比例，因此被称为黄金比.在几何世界中有很多黄金图形，在三角形中，如果相邻两边之比等于黄金比，且它们夹角的余弦值为黄金比值，那么这个三角形一定是直角三角形，且这个三角形称为黄金分割直角三角形.在正四棱锥中，以黄金分割直角三角形的长直角边作为正四棱锥的高，黄金分割直角三角形的短直角边的边长作为底面正方形的边心距(正多边形的边心距是正多边形的外接圆圆心到正多边形某一边的距离)，斜边作为正四棱锥的斜高，这样得到的正四棱锥称为黄金分割正四棱锥.在黄金分割正四棱锥中，以该正四棱锥的高为边长的正方形的面积与该正四棱锥的侧面积之比为( ) A.5－12 B.5＋12C.1D.14答案 D解析 如图，在黄金分割正四棱锥P －ABCD 中，O 是正方形ABCD 的中心，PE 是正四棱锥的斜高，设OE ＝a ，则CD ＝2a ， ∴Rt△POE 为黄金分割直角三角形，则OE PE ＝5－12， ∴PE ＝5＋12a ， 则PO ＝PE 2－OE 2＝1＋52a ， ∴以该正四棱锥的高为边长的正方形的面积S ＝PO 2＝1＋52a 2， 又正四棱锥的四个侧面是全等的，∴S 侧＝4S △PCD ＝4×12×CD ×PE ＝2(1＋5)a 2，∴该正四棱锥的高为边长的正方形的面积与该正四棱锥的侧面积之比为14.9.(2022·潍坊二模)如图，在棱长为2的正方体ABCD －A ′B ′C ′D ′中，点E ，F ，G 分别是棱A ′B ′，B ′C ′，CD 的中点，则由点E ，F ，G 确定的平面截正方体所得的截面多边形的面积等于________.答案332解析 分别取AD ，CC ′和AA ′的中点为P ，M ，N ，可得出过E ，F ，G 三点的平面截正方体所得截面为正六边形EFMGPN ，则正六边形的边长MG ＝CG 2＋CM 2＝⎝ ⎛⎭⎪⎫222＋⎝ ⎛⎭⎪⎫222＝1，故截面多边形的面积等于S＝6×34×12＝33 2.10.(2022·佛山质检)已知圆锥的顶点为S，底面圆周上的两点A，B满足△SAB为等边三角形，且面积为43，又知圆锥轴截面的面积为8，则圆锥的侧面积为________. 答案82π解析设圆锥的母线长为l，由△SAB为等边三角形，且面积为43，所以12l2sinπ3＝43，解得l＝4；又设圆锥底面半径为r，高为h，则由轴截面的面积为8，得rh＝8；又r2＋h2＝l2＝16，解得r＝h＝22，所以圆锥的侧面积S＝πrl＝π·22·4＝82π.11.如图，已知正三棱柱ABC－A1B1C1的各棱长均为2，点D在棱AA1上，则三棱锥D－BB1C1的体积为________.答案23 3解析如图，取BC的中点O，连接AO.∵正三棱柱ABC－A1B1C1的各棱长均为2，∴AC＝2，OC＝1，则AO＝ 3.∵AA1∥平面BCC1B1，∴点D到平面BCC1B1的距离为 3.又S△BB1C1＝12×2×2＝2，∴V D－BB1C1＝13×2×3＝233.12.已知三棱锥S－ABC中，∠SAB＝∠ABC＝π2，SB＝4，SC＝213，AB＝2，BC＝6，则三棱锥S－ABC的体积为________. 答案4 3解析∵∠ABC＝π2，AB＝2，BC＝6，∴AC＝AB2＋BC2＝22＋62＝210.∵∠SAB＝π2，AB＝2，SB＝4，∴AS＝SB2－AB2＝42－22＝2 3.由SC＝213，得AC2＋AS2＝SC2，∴AC⊥AS.又∵SA⊥AB，AC∩AB＝A，AC，AB⊂平面ABC，∴AS⊥平面ABC.∴AS为三棱锥S－ABC的高，∴V三棱锥S－ABC＝13×12×2×6×23＝4 3.二、创新拓展练13.(多选)(2022·无锡模拟)一个圆柱和一个圆锥的底面直径和它们的高都与一个球的直径2R相等，下列结论正确的是( )A.圆柱的侧面积为4πR2B.圆锥的侧面积为2πR2C.圆柱的侧面积与球的表面积相等D.球的体积是圆锥体积的两倍答案ACD解析对于A，∵圆柱的底面直径和高都等于2R，∴圆柱的侧面积S1＝2πR·2R＝4πR2，故A正确；对于B，∵圆锥的底面直径和高都等于2R，∴圆锥的侧面积为S2＝πR·R2＋4R2＝5πR2，故B错误；对于C，∵圆柱的侧面积为S1＝4πR2，球的表面积S3＝4πR2，即圆柱的侧面积与球的表面积相等，故C正确；对于D，球的体积为V1＝43πR3，圆锥的体积为V2＝13πR2·2R＝23πR3，即球的体积是圆锥体积的两倍，故D正确.14.(多选)(2022·邯郸模拟)攒尖是我国古代建筑中屋顶的一种结构形式，宋代称为撮尖，清代称攒尖，通常有圆形攒尖、三角攒尖、四角攒尖、八角攒尖，也有单檐和重檐之分，多见于亭阁式建筑、园林建筑.下面以四角攒尖为例，如图，它的屋顶部分的轮廓可近似看作一个正四棱锥.已知此正四棱锥的侧面与底面所成的锐二面角为θ，这个角接近30°.若取θ＝30°，侧棱长为21米，则( )A.正四棱锥的底面边长为6米B.正四棱锥的底面边长为3米C.正四棱锥的侧面积为243平方米D.正四棱锥的侧面积为123平方米答案AC解析如图，在正四棱锥S－ABCD中，O为正方形ABCD的中心，H为AB的中点，则∠SHO为侧面SAB与底面ABCD所成的锐二面角，且SH⊥AB，∠SHO＝30°，设底面边长为2a ， 所以OH ＝AH ＝a ，OS ＝33a ，SH ＝233a . 在Rt△SAH 中，a 2＋⎝ ⎛⎭⎪⎫233a 2＝21，解得a ＝3，所以正四棱锥的底面边长为6米，侧面积为S ＝12×6×23×4＝243(平方米).15.(多选)(2022·福州调研)如图，正方体ABCD －A 1B 1C 1D 1的棱长为1，线段B 1D 1上有两个动点E ，F ，且EF ＝12，则下列结论中正确的是( )A.AC ⊥AFB.EF ∥平面ABCDC.三棱锥A －BEF 的体积为定值D.△AEF 的面积与△BEF 的面积相等 答案 BC解析 由题意及图形知，当点F 与点B 1重合时，∠CAF ＝60°，故A 错误；由正方体ABCD －A 1B 1C 1D 1的两个底面平行，EF ⊂平面A 1B 1C 1D 1，知EF ∥平面ABCD ，故B 正确；由几何体的性质及图形知，三角形BEF 的面积是定值，点A 到平面DD 1B 1B 的距离是定值，故可得三棱锥A －BEF 的体积为定值，故C 正确；由图形可以看出，B到直线EF的距离与A到直线EF的距离不相等，故△AEF的面积与△BEF的面积不相等，故D错误.故选BC.16.(多选)《九章算术》是《算经十书》中最重要的一部，其中将有三条棱互相平行且有一个面为梯形的五面体称为“羡除”，则( )A.“羡除”有且仅有两个面为三角形B.“羡除”一定不是台体C.不存在有两个面为平行四边形的“羡除”D.“羡除”至多有两个面为梯形答案ABC解析由题意知AE∥BF∥CD，四边形ACDE为梯形，如图所示.选项A，由题意知“羡除”有且仅有两个面为三角形，故A正确；选项B，因为AE∥BF∥CD，所以“羡除”一定不是台体，故B正确；选项C，假设四边形ABFE和四边形BCDF为平行四边形，则AE∥BF∥CD，且AE＝BF＝CD，即四边形ACDE为平行四边形，与已知四边形ACDE为梯形矛盾，故不存在，故C正确；选项D，若AE≠BF≠CD，则“羡除”有三个面为梯形，故D错误.故选ABC.17.(多选)(2022·新高考Ⅱ卷)如图，四边形ABCD为正方形，ED⊥平面ABCD，FB∥ED，AB＝ED＝2FB.记三棱锥E－ACD，F－ABC，F－ACE的体积分别为V，V2，V3，则( )1A.V3＝2V2B.V3＝V1C.V3＝V1＋V2D.2V3＝3V1答案CD解析如图，连接BD交AC于O，连接OE，OF.设AB＝ED＝2FB＝2，则AB＝BC＝CD＝AD＝2，FB＝1.因为ED⊥平面ABCD，FB∥ED，所以FB⊥平面ABCD，所以V1＝V E－ACD＝13S△ACD·ED＝13×12AD·CD·ED＝13×12×2×2×2＝43，V 2＝V F－ABC＝13S△ABC·FB＝13×12AB·BC·FB＝13×12×2×2×1＝23.因为ED⊥平面ABCD，AC⊂平面ABCD，所以ED⊥AC，又AC⊥BD，且ED∩BD＝D，ED，BD⊂平面BDEF，所以AC⊥平面BDEF. 因为OE，OF⊂平面BDEF，所以AC⊥OE，AC⊥OF.易知AC ＝BD ＝2AB ＝22，OB ＝OD ＝12BD ＝2，OF ＝OB 2＋FB 2＝3，OE ＝OD 2＋ED 2＝6， EF ＝BD 2＋（ED －FB ）2 ＝（22）2＋（2－1）2＝3， 所以EF 2＝OE 2＋OF 2，所以OF ⊥OE . 又OE ∩AC ＝O ，OE ，AC ⊂平面ACE ， 所以OF ⊥平面ACE ，所以V 3＝V F －ACE ＝13S △ACE ·OF ＝13×12AC ·OE ·OF＝13×12×22×6×3＝2， 所以V 3≠2V 2，V 1≠V 3，V 3＝V 1＋V 2，2V 3＝3V 1，所以选项A ，B 不正确，选项C ，D 正确.故选CD.18.(2022·丽水质检)已知三棱柱ABC －A 1B 1C 1中，AB ＝AC ＝1，AA 1＝2，∠A 1AC ＝∠A 1AB ＝60°，∠BAC ＝90°，则四面体A 1BB 1C 1的体积为________. 答案26解析 法一 如图，连接A 1C ，在三角形A 1AB 中，AB ＝1，AA 1＝2，∠A 1AB ＝60°， 由余弦定理得A 1B 2＝22＋12－2×1×2×cos 60°＝3，即A 1B ＝3， 同理A 1C ＝3，则AB 2＋A 1B 2＝A 1A 2， 所以A 1B ⊥AB ，同理A 1C ⊥AC ， 所以△A 1AB ≌△A 1AC .过点B 作BD ⊥A 1A ，垂足为D ，连接CD ，则CD ⊥A 1A ，又BD ∩CD ＝D ，所以A 1A ⊥平面BCD ， 所以BD ＝CD ＝1×32＝32， 又AB ＝AC ＝1，∠BAC ＝90°， 所以BC ＝ 2.取BC 的中点E ，连接DE ，则DE ⊥BC ，且DE ＝⎝ ⎛⎭⎪⎫322－⎝ ⎛⎭⎪⎫222＝12， 所以S △BCD ＝12×BC ×DE ＝12×2×12＝24，则V A 1－BB 1C 1＝V B －A 1B 1C 1＝V A 1－ABC ＝V A 1－BCD ＋V A －BCD ＝13·S △BCD ·A 1A ＝13×24×2＝26. 法二 如图，连接A 1C ，在三角形A 1AB 中，AB ＝1，AA 1＝2，∠A 1AB ＝60°， 由余弦定理得A 1B 2＝22＋12－2×1×2×cos 60°＝3， 即A 1B ＝3，同理A 1C ＝3， 则AB 2＋A 1B 2＝A 1A 2， 所以A 1B ⊥AB ，同理A 1C ⊥AC .设A 1在平面ABC 内的射影为O ，连接A 1O ，AO ，OB ，OC ， 则A 1O ⊥平面ABC ，又AB ⊂平面ABC ，所以A 1O ⊥AB ，31 / 31 又A 1B ∩A 1O ＝A 1，所以AB ⊥平面A 1OB ，又OB ⊂平面A 1OB ，所以AB ⊥OB ，同理OC ⊥AC ，且△A 1OB ≌△A 1OC ， 所以OB ＝OC ，则点O 在∠BAC 的平分线上. 设AO 交BC 于点E ，连接A 1E ，则AE ＝22，A 1E ＝（3）2－⎝ ⎛⎭⎪⎫222＝102， 在△A 1AE 中，cos∠A 1AE ＝A 1A 2＋AE 2－A 1E 22×A 1A ×AE ＝22， 则∠A 1AE ＝45°，则A 1O ＝A 1A sin 45°＝2，V A 1－BB 1C 1＝V B －A 1B 1C 1＝V A 1－ABC ＝13·S △ABC ·A 1O ＝13×12×1×1×2＝26.。

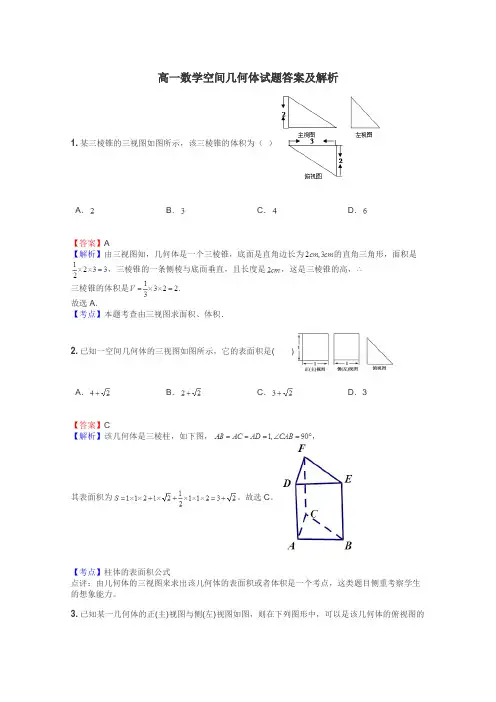
高一数学空间几何体试题答案及解析1.某三棱锥的三视图如图所示，该三棱锥的体积为（）A．B．C．D．【答案】A【解析】由三视图知，几何体是一个三棱锥，底面是直角边长为的直角三角形，面积是，三棱锥的一条侧棱与底面垂直，且长度是，这是三棱锥的高，三棱锥的体积是.故选A．【考点】本题考查由三视图求面积、体积．2.已知一空间几何体的三视图如图所示，它的表面积是()A．B．C．D．3【答案】C【解析】该几何体是三棱柱，如下图，，其表面积为。

故选C。

【考点】柱体的表面积公式点评：由几何体的三视图来求出该几何体的表面积或者体积是一个考点，这类题目侧重考察学生的想象能力。

3.已知某一几何体的正(主)视图与侧(左)视图如图，则在下列图形中，可以是该几何体的俯视图的图形有()A．①②③⑤B．②③④⑤C．①③④⑤D．①②③④【答案】D【解析】俯视图为⑤的几何体的侧视图如下，这与题目不相符，而①②③④符合题意。

故选D。

【考点】三视图点评：本题考查简单空间图形的三视图，考查空间想象能力，是基础题．4.如图是某直三棱柱(侧棱与底面垂直)被削去上底后的直观图与三视图中的侧(左)视图、俯视图，在直观图中，是的中点，侧(左)视图是直角梯形，俯视图是等腰直角三角形，有关数据如图所示．(1)求出该几何体的体积；(2)若是的中点，求证：∥平面；(3)求证：平面⊥平面.【答案】(1)4 (2)主要证明∥ (3)主要证明平面【解析】解:(1)由题意可知，四棱锥中，平面平面，，所以，平面，又，，则四棱锥的体积为.(2)连接，则∥，∥，又，所以四边形为平行四边形，∴∥，∵平面，平面，所以，∥平面.(3)∵，是的中点，∴⊥，又在直三棱柱中可知，平面平面，∴平面，由(2)知，∥，∴平面，又平面，所以，平面平面.【考点】平面与平面垂直的判定；棱柱、棱锥、棱台的体积；直线与平面平行的判定．点评：本题考查的知识点是直线与平面平行的判定，棱锥的体积，平面与平面垂直的判定，其中（1）的关键是由面面垂直的性质定理可得AB⊥平面ACDE，（2）的关键是分析出四边形ANME为平行四边形，即AN∥EM，（3）的关键是熟练掌握空间线线垂直，线面垂直与面面垂直之间的相互转化．5.如图是长方体被一平面所截得到的几何体，四边形为截面，长方形为底面，则四边形的形状为( )A．梯形B．平行四边形C．可能是梯形也可能是平行四边形D．不确定【答案】B【解析】因为，长方体中相对的平面互相平行，所以，被平面截后，EF,GH平行且相等，GF,EH 平行且相等，故四边形的形状为平行四边形，选B。

高中数学空间几何专题练习------------------------------------------作者xxxx------------------------------------------日期xxxx一、选择题1、下图(1)所示的圆锥的俯视图为 ( )2、直线30l y ++=的倾斜角α为 （ )A 、30；B 、60;C 、120；D 、150。

3、边长为a 正四面体的表面积是 ( )A3； B3； C、2; D2。

４、对于直线:360l x y -+=的截距,下列说法正确的是 ( )A 、在y 轴上的截距是6; B 、在x 轴上的截距是６;C 、在x 轴上的截距是３;D 、在y 轴上的截距是3-.5、已知,a b αα⊂//,则直线a 与直线b 的位置关系是 （ ）A 、平行;B 、相交或异面;C 、异面；D 、平行或异面．图（ABCD６、已知两条直线12:210,:40l x ay l x y +-=-=，且12l l //,则满足条件a的值为A 、12-; B 、12； C 、2-；D 、2。

7、在空间四边形ABCD 中,,,,E F G H 分别是,,,AB BC CD DA 的中点。

若AC BD a ==，且AC 与BD 所成的角为60,则四边形EFGH 的面积为( )A、28a ; B、24; C、22a ； D2。

８、在右图的正方体中,M 、Ｎ分别为棱B Ｃ和棱CC １则异面直线AC 和M Ｎ所成的角为（ )A ．30°Ｂ．４5° Ｃ.９０°Ｄ．9、下列叙述中错误的是 ( )A 、若P αβ∈且l αβ=,则P l ∈; B 、三点,,A B C 确定一个平面;C 、若直线a b A =,则直线a 与b 能够确定一个平面;D 、若,A l B l ∈∈且,A B αα∈∈,则l α⊂。

10、两条不平行的直线，其平行投影不可能是 ( )A 、两条平行直线；B 、一点和一条直线;C 、两条相交直线;D 、两个点。

小升初数学考前押题——空间几何篇1.一个圆柱形容器内放有一个长方形铁块.现打开水龙头往容器中灌水.3分钟时水面恰好没过长方体的顶面.再过18分钟水已灌满容器.已知容器的高为50厘米，长方体的高为20厘米，求长方体的底面面积和容器底面面积之比.2.有高度相等的A，B两个圆柱形容器，内口半径分别为6厘米和8厘米.容器A 中装满水，容器B是空的，把容器A中的水全部倒入容器B中，测得容器B中的水深比容器高的7/8还低2厘米.容器的高度是多少厘米？3. 一个长方形的周长是130厘米，如果它的宽增加1/5，长减少1/8，就得到一个相同周长的新长方形.求原长方形的面积.4.有一长方形，它的长与宽的比是5：2，对角线长29厘米，求这个长方形的面积.5. 一个容器中已注满水，有大、中、小三个球.第一次把小球沉入水中，第二次把小球取出，把中球沉入水中，第三次把中球取出，把小球和大球一起沉入水中，现知道每次从容器中溢出水量的情况是：第一次是第二次的1/2，第三次是第二次的1.5倍.求三个球的体积之比.6. 用10块长7厘米、宽5厘米、高3厘米的长方体积木，拼成一个长方体，这个长方体的表面积最小是多少？7. 甲、乙两个圆柱形容器，底面积比为4：3，甲容器水深7厘米，乙容器水深3厘米.再往两个容器各注入同样多的水，直到水深相等，这时水深几厘米？8. 一个正方形，如果一边减少25%，另一边增加3米，所得到的长方形与原来正方形面积正好相等，那么正方形面积是多少？9. 一个长方体木块，从下部和上部分别截去高为3厘米和2厘米的长方体后，便成为一个正方体，表面积减少了120平方厘米，原来长方体的体积是多少立方厘米？10. 在底面边长为60厘米的正方形的一个长方体的容器里，直立着一个长1米，底面为正方形，边长15厘米的四棱柱铁棍.这时容器里的水半米深.现在把铁棍轻轻地向正上方提起24厘米，露出水面的四棱柱切棍浸湿部分长多少厘米？11. 甲、乙两个圆柱体容器，底面积比为5：3，甲容器水深20厘米，乙容器水深10厘米.再往两个容器中注入同样多的水，使得两个容器中的水深相等.这时水深多少厘米？小升初数学考前押题——空间几何篇1.一个圆柱形容器内放有一个长方形铁块.现打开水龙头往容器中灌水.3分钟时水面恰好没过长方体的顶面.再过18分钟水已灌满容器.已知容器的高为50厘米，长方体的高为20厘米，求长方体的底面面积和容器底面面积之比.解法一：把这个容器分成上下两部分，根据时间关系可以发现，上面部分水的体积是下面部分的18÷3＝6倍，上面部分和下面部分的高度之比是（50－20）：20＝3：2，上面部分的底面积是下面部分装水的底面积的6÷3×2＝4倍，长方体的底面积和容器底面积之比是（4－1）：4＝3：4解法二：（50＝20）：20=3：2，当没有长方体时，灌满20厘米就需要时间18×2/3=12分，长方体的体积就是12－3=9分钟的水量，高度相同，体积比就等于底面积之比9：12=3：42.有高度相等的A，B两个圆柱形容器，内口半径分别为6厘米和8厘米.容器A 中装满水，容器B是空的，把容器A中的水全部倒入容器B中，测得容器B中的水深比容器高的7/8还低2厘米.容器的高度是多少厘米？解答：容器A中的水全部倒入容器B，容器B的水深就应该占容器高的（6×6）÷（8×8）＝9/16，容器高2÷（7/8－9/16）＝6.4厘米3. 一个长方形的周长是130厘米，如果它的宽增加1/5，长减少1/8，就得到一个相同周长的新长方形.求原长方形的面积.解答：说明长的1/8和宽的1/5相等，长和宽的比是8：5，长是130÷2÷（8＋5）×8＝40厘米，宽是40÷8×5＝25厘米，原长方形的面积是40×25＝1000平方厘米4.有一长方形，它的长与宽的比是5：2，对角线长29厘米，求这个长方形的面积.解答：算出黄色部分和中间空心部分的面积比，然后从29的平方里面来分配，面积比5×2×2：3×3＝20：9，黄色部分的面积是29×29÷（20＋9）×20＝580平方厘米，长方形的面积相当于2个三角形，所以，580÷4×2＝2905. 一个容器中已注满水，有大、中、小三个球.第一次把小球沉入水中，第二次把小球取出，把中球沉入水中，第三次把中球取出，把小球和大球一起沉入水中，现知道每次从容器中溢出水量的情况是：第一次是第二次的1/2，第三次是第二次的1.5倍.求三个球的体积之比.解答：第一次是第二次的1/2，说明第一次溢出1份，第二次溢出2份，那么中球就是小球的2＋1＝3倍，第三次是第二次的1.5倍。

A ．B ．223．若直线的方向向量为，平面l bA ．()(1,0,0,2,0,0b n ==-()(0,2,1,1,0,1b n ==--A ．B ．5136．如图，在平行六面体ABCDA．1122a b c -++C．1122a b c --+7．如图，在四面体OABC中，1-16．已知四棱锥P ABCDPC棱上运动，当平面1．C【分析】根据已知结合向量的坐标运算可得出，且.然后根据向量的数量积a b a +=- 14a = 运算求解，即可得出答案.【详解】由已知可得，且.()1,2,3a b a+=---=-14a =又，()7a b c +⋅= 所以，即有，7a c -⋅= cos ,14cos ,7a c a c a c -⋅=-=所以，.1cos ,2a c =-又，所以.0,180a c ≤≤ ,120a c =︒ 故选：C.2．C【分析】利用中点坐标公式求出中点的坐标，根据空间两点间的距离公式即可得出中线BC 长.【详解】由图可知：，，，(0,0,1)A (2,0,0)B (0,2,0)C 由中点坐标公式可得的中点坐标为，BC (1,1,0)根据空间两点间距离公式得边上的中线的长为.BC 22211(1)3++-=故选：C 3．D【分析】若直线与平面平行，则直线的方向向量与平面的法向量垂直，利用向量数量积检验.【详解】直线的方向向量为，平面的法向量为，l bαn 若可能，则，即.//l αb n ⊥r r 0b n ⋅=r r A 选项，；()1220b n =⨯-⋅=-≠B 选项，；11305160b n =⨯⨯⋅+⨯+=≠C 选项，；()()01201110b n =⨯-+⨯+⨯-⋅=-≠D 选项，；()1013310b n =⨯+-⨯=⋅+⨯因为，，3AB =4BC =2PA =所以()()(0,0,2,3,0,0,0,0,1P B Q 设平面的法向量为BQD (m x =()(),,3,0,1m BQ x y z ⎧设，2AB AD AS ===则()()()0,0,0,0,0,2,2,2,0,A S C P 设，()0,,2M t t -(1,1,2OM t =--所以1120OM AP t t ⊥=-+-+-=点到平面与平面的距离和为为定值，D 选项正确.M ABCD SAB 22t t -+=，，()2,0,0B ()()2,0,2,0,2,0SB BC =-=设平面的法向量为，SBC (),,n x y z =则，故可设，22020n SB x z n BC y ⎧⋅=-=⎪⎨⋅==⎪⎩()1,0,1n = 要使平面，又平面，//OM SBC OM ⊄SBC 则，()()1,1,21,0,11210OM n t t t t ⋅=---⋅=-+-=-=解得，所以存在点，使平面，B 选项正确.1t =M //OM SBC 若直线与直线所成角为，又，OM AB 30︒()2,0,0AB =则，()()222213cos3022661122OM ABOM ABt t t t ⋅-︒====⋅-++-+-⨯ 整理得，无解，所以C 选项错误.23970,8143730t t -+=∆=-⨯⨯=-<故选：ABD.10．BCD【分析】根据向量的多边形法则可知A 正确；根据向量的三角不等式等号成立条件可知，B 错误；根据共线向量的定义可知，C 错误；根据空间向量基本定理的推论可知，D 错误．【详解】对A ，四点恰好围成一封闭图形，根据向量的多边形法则可知，正确；对B ，根据向量的三角不等式等号成立条件可知，同向时，应有，即必要,a b a b a b+=+ 性不成立，错误；对C ，根据共线向量的定义可知，所在直线可能重合，错误；,a b对D ，根据空间向量基本定理的推论可知，需满足x +y +z =1，才有P 、A 、B 、C 四点共面，错误．故选：BCD ．11．AB【分析】以，，作为空间的一组基底，利用空间向量判断A ，C ，利用空间向量法ABAD AA 可得面，再用向量法表示，即可判断B ，利用割补法判断D ；1AC ⊥PMN AH【详解】依题意以，，作为空间的一组基底，ABAD AA 则，，11AC AB AD AA =++ ()1122MN BD AD AB ==-因为棱长均为2，，11π3A AD A AB ∠=∠=所以，，224AB AD == 11π22cos 23AA AD AA AB ⋅=⋅=⨯⨯= 所以()()1112D A A C MN AD A A B AA B++⋅⋅=- ，()2211102AB AD AB AD AB AD AA AD AA AB ⋅-+-⋅+==⋅+⋅故，即，故A 正确；1AC MN ⊥1AC MN ⊥同理可证，，面，面，PN AC ⊥MN PN N ⋂=MN ⊂PMN PN ⊂PMN 所以面，即面，即为正三棱锥的高，1AC ⊥PMN AH ⊥PMN AH A PMN -所以()()1133AH AN NH AN NP NM AN AP AN AM AN=+=++=+-+- ，()13AP AM AN =++又，，分别是，，的中点，，P M N 1AA AB AD π3PAM PAN MAN ∠=∠=∠=所以，则三棱锥是正四面体，1PA AM AN PM MN PN ======P AMN -所以()11111133222AH AP AM AN AA AB AD ⎛⎫=++=⨯++ ⎪⎝⎭ ，()111166AA AB AD AC =++=所以，故B 正确；116AH AC =因为()211AC AB AD AA =++ ()()()222111222AB ADAA AB AD AB AA AD AA =+++⋅+⋅+⋅ ，2426==()21111111=AC AA AB AD AA AA AB AA AD AA AA ⋅=++⋅⋅+⋅+ ，11222222=822=⨯⨯+⨯⨯+⨯设直线和直线所成的角为，1AC 1BB θ则，故C 错误；1111111186cos cos ,cos ,3262AC AA AC BB AC AA AC AA θ⋅=====⨯ ，11111111111111A B D C ABCD A B C D A B D A C B D A B ABC D ADCV V V V V V ------=----其中，1111111111116ABCD A B C D A B D A C B D C B ABC D ADC V V V V V -----====所以，故D 错误.1111113A B D C ABCD A B C D V V --=故选：AB.关键点睛：本题解决的关键点是利用空间向量的基底法表示出所需向量，利用空间向量的数量积运算即可得解.12．AC【分析】对于A ，根据即可算出的值；对于B ，根据计算；对于C ，根据||2a = m a b ⊥ m 计算即可；对于D ，根据求出，从而可计算出.a b λ= 1a b ⋅=- m a b + 【详解】对于A ，因为，所以，解得，故A 正确；||2a = 2221(1)2m +-+=2m =±对于B ，因为，所以，所以，故B 错误；a b ⊥ 2120m m -+-+=1m =对于C ，假设，则，a b λ= (1,1,)(2,1,2)m m λ-=--所以，该方程组无解，故C 正确；()12112m m λλλ=-⎧⎪-=-⎨⎪=⎩对于D ，因为，所以，解得，1a b ⋅=- 2121m m -+-+=-0m =所以，，所以，故D 错误.(1,1,0)a =- (2,1,2)b =-- (1,2,2)+=-- a b 故选：AC.13．15【分析】根据线面垂直，可得直线的方向向量和平面的法向量共线，由此列式计算，即得答案.【详解】∵，∴，∴，解得，l α⊥u n ∥ 3123a b ==6,9a b ==∴，15a b +=故1514．2【分析】根据垂直得到，得到方程，求出.()0a a b λ⋅-= 2λ=【详解】，()()()2,1,31,2,12,12,3a b λλλλλ-=---=--- 因为，所以，()a a b λ⊥- ()0a a b λ⋅-= 即，()()2,12,3241293702,1,134λλλλλλλ----=-++-+-=+⋅-=解得.2λ=故215．17【分析】利用向量的加法，转化为，直接求模长即可.CD CA AB BD =++ 【详解】因为.CD CA AB BD =++ 所以()22CD CA AB BD =++ 222222CA CA AB AB AB BD BD CA BD=+⋅++⋅++⋅ 222132022042342⎛⎫=+⨯++⨯++⨯⨯⨯- ⎪⎝⎭17=所以.17CD = 故答案为.1716．33【分析】首先建立空间直角坐标系，分别求平面和平面的法向量，利用法向量垂MBD PCD 直求点的位置，并利用向量法求异面直线所成角的余弦值，即可求解正弦值.M 【详解】如图，以点为原点，以向量为轴的正方向，建立空间直角坐标A ,,AB AD AP ,,x y z 系，设，2AD AP ==，，，，()2,0,0B ()0,2,0D ()002P ,,()2,2,0C 设,()()()0,2,22,2,22,22,22DM DP PM DP PC λλλλλ=+=+=-+-=-- ，，，()2,2,0BD =-u u u r ()2,0,0DC =u u u r ()0,2,2DP =- 设平面的法向量为，MBD ()111,,m x y z =r ，()()11111222220220DM m x y z DM m x y λλλ⎧⋅=+-+-=⎪⎨⋅=-+=⎪⎩33故。

专题1空间立体几何的三视图、表面积和体积【考点点击】1．以选择、填空题形式考查空间位置关系的判断，及文字语言、图形语言、符号语言的转换，难度适中；2．以熟悉的几何体为背景，考查多面体或旋转体的侧面积、表面积和体积计算，间接考查空间位置关系的判断及转化思想等，常以三视图形式给出几何体，辅以考查识图、用图能力及空间想象能力，难度中等．3.几何体的三视图与表（侧）面积、体积计算结合；【重点知识】一、空间几何体1．柱体、锥体、台体、球的结构特征名称几何特征棱柱①有两个面互相平行(底面可以是任意多边形)；②其余各面都是平行四边形，并且每相邻两个四边形的公共边互相平行棱锥①有一个面是多边形(底面)；②其余各面是有公共顶点的三角形．棱台①底面互相平行；②所有侧棱延长后交于一点(即原棱锥的顶点)圆柱①有两个互相平行的圆面(底面)；②有一个侧面是曲面(母线绕轴旋转一周形成的)，且母线与底面垂直圆台①底面互相平行；②有一个侧面是曲面，可以看成母线绕轴旋转一周形成的球①有一个曲面是球面；②有一个球心和一条半径长R，球是一个几何体(包括内部)，可以看成半圆以它的直径所在直线为旋转轴旋转一周形成的2.柱体、锥体、台体、球的表面积与体积名称体积表面积棱柱V棱柱＝Sh(S为底面积，h为高)S棱柱＝2S底面＋S侧面棱锥V棱锥＝13Sh(S为底面积，h为高)S棱锥＝S底面＋S侧面棱台V棱台＝13h(S＋SS′＋S′)S棱台＝S上底＋S下底＋S侧面圆柱V圆柱＝πr2h(r为底面半径，h为高)S圆柱＝2πrl＋2πr2(r为底面半径，l为母线长)圆锥V圆锥＝13πr2h(r为底面半径，h为高)S圆锥＝πrl＋πr2(r为底面半径，l为母线长)圆台V圆台＝13πh(r2＋rr′＋r′2)S圆台＝π(r＋r′)l＋πr2＋πr′2球V球＝43πR3(R为球的半径)S球＝4πR2(R为球的半径)3.空间几何体的三视图和直观图(1)空间几何体的三视图三视图的正视图、侧视图、俯视图分别是从物体的正前方、正左方、正上方看到的物体轮廓线的正投影围成的平面图形，三视图的画法规则为“长对正、高平齐、宽相等”．(2)空间几何体的直观图空间几何体直观图的画法常采用斜二测画法．用斜二测画法画平面图形的直观图规则为“轴夹角45°(或135°)，平行长不变，垂直长减半”．4．几何体沿表面某两点的最短距离问题一般用展开图解决；不规则几何体求体积一般用割补法和等积法求解；三视图问题要特别留意各种视图与观察者的相对位置关系.【考点分析】考点一空间几何体的结构【例1】已知正三棱锥P­ABC ，点P ，A ，B ，C 都在半径为3的球面上，若PA ，PB ，PC 两两相互垂直，则球心到截面ABC 的距离为________．【答案】33【解析】正三棱锥P­ABC 可看作由正方体PADC­BEFG 截得，如图所示，PF 为三棱锥P­ABC 的外接球的直径，且PF ⊥平面ABC.设正方体棱长为a ，则22,2,1232=====BC AC AB a a ，3223222221=⨯⨯⨯=∆ABC S ，由,PAC B ABC P V V --=得222213131⨯⨯⨯⨯=⋅∆ABC S h ，所以332=h 因此球心到平面ABC 得距离为33考点二三视图、直观图【例2】下图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的表面积为（）（A ）20π（B ）24π（C ）28π（D ）32π【答案】C【解析】由题意可知，圆柱的侧面积为12π2416πS =⋅⋅=，圆锥的侧面积为2π248πS =⋅⋅=，圆柱的底面面积为23π24πS =⋅=，故该几何体的表面积为12328πS S S S =++=，故选C.【例3】某三棱锥的三视图如图所示，则该三棱锥的表面积是()A ．2＋5B ．4＋5C ．2＋25D ．5【答案】C【解析】该三棱锥的直观图如图所示：过D 作DE ⊥BC ，交BC 于E ，连接AE ，则BC ＝2，EC ＝1，AD ＝1，ED ＝2，ABCABD ACD BCD S S S S S ∆∆∆∆+++=表5225221152115212221+=⨯⨯+⨯⨯+⨯⨯+⨯⨯=考点三几何体的表面积【例4】长方体的长、宽、高分别为3,2,1，其顶点都在球O 的球面上，则球O 的表面积为【答案】14π.【解析】球的直径是长方体的体对角线，所以222232114,4π14π.R S R =++===【例5】如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径.若该几何体的体积是328π,则它的表面积是（）（A ）17π（B ）18π（C ）20π（D ）28π【答案】A【解析】该几何体直观图如图所示：是一个球被切掉左上角的81,设球的半径为R ,则32834873ππ=⨯=R V ,解得R 2=,所以它的表面积是87的球面面积和三个扇形面积之和πππ172413248722=⨯⨯+⨯⨯=S 故选A ．考点四几何体的体积【例6．】已知圆柱的高为1，它的两个底面的圆周在直径为2的同一个球的球面上，则该圆柱的体积为（）A ．πB ．3π4C ．π2D ．π4【答案】B【解析】绘制圆柱的轴截面如图所示，由题意可得：11,2AC AB ==，结合勾股定理，底面半径2213122r ⎛⎫=-= ⎪⎝⎭，由圆柱的体积公式，可得圆柱的体积是2233ππ1π24V r h ⎛==⨯⨯= ⎝⎭，故选B.考点五与球的组合体问题纵观近几年高考对于组合体的考查，重点放在与球相关的外接与内切问题上.要求学生有较强的空间想象能力和准确的计算能力，才能顺利解答.从实际教学来看，这部分知识是学生掌握最为模糊，看到就头疼的题目.分析原因，除了这类题目的入手确实不易之外，主要是学生没有形成解题的模式和套路，以至于遇到类似的题目便产生畏惧心理.本文就高中阶段出现这类问题加以类型的总结和方法的探讨.【例7】棱长为1的正方体1111ABCD A B C D -的8个顶点都在球O 的表面上，E F ，分别是棱1AA ，1DD 的中点，则直线EF 被球O 截得的线段长为（）A ．22B ．1C ．212+D ．2解：由题意可知，球为正方体的外接球.平面11AA DD 截面所得圆面的半径12,22AD R ==11EF AA DD ⊂ 面，∴直线EF 被球O 截得的线段为球的截面圆的直径22R =.【例8】正四棱柱1111ABCD A B C D -的各顶点都在半径为R 的球面上，则正四棱柱的侧面积有最值，为.【例9】在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且AM MN ⊥,若侧棱23SA =,则正三棱锥S ABC -外接球的表面积是.解：如图，正三棱锥对棱相互垂直，即,AC SB ⊥又,,,.SB MN MN AC MN AM MN SAC ∴⊥⊥∴⊥∥又平面于是,,,SB SAC SB SA SB SC ⊥∴⊥⊥平面从而.SA SC ⊥此时正三棱锥S ABC -的三条侧棱互相垂直并且相等，故将正三棱锥补形为正方体.球的半径23,3,436.2R SA R S R ππ=∴=∴==【例10】一个几何体的三视图如图所示，其中主视图和左视图是腰长为1的两个全等的等腰直角三角形，则该几何体的外接球的表面积为()A ．12πB ．C ．3πD ．【答案】C【解析】把原来的几何体补成以DA DC DP 、、为长、宽、高的长方体，原几何体四棱锥与长方体是同一个外接球，2=R l ，=2R ，234434S R πππ==⨯=球.【例11】在三棱锥P －ABC 中，PA ＝,侧棱PA 与底面ABC 所成的角为60°，则该三棱锥外接球的体积为（）A ．πB.3π C.4πD.43π解：如图所示，过P 点作底面ABC 的垂线，垂足为O ，设H 为外接球的球心，连接,,AH AO 因60,PAO PA ∠== 故2AO =,32PO =又△AHO 为直角三角形，222,,AH PH r AH AO OH ==∴=+22233344(),1,1.2233r r r V ππ∴=+-∴=∴=⨯=【例12】矩形ABCD 中，4,3,AB BC ==沿AC 将矩形ABCD 折成一个直二面角B ACD --,则四面体ABCD 的外接球的体积是()A.π12125 B.π9125C.π6125D.π3125解：由题意分析可知，四面体ABCD 的外接球的球心落在AC 的中点，此时满足,OA OD OB OC ===522AC R ∴==,343V R π=1256π=.【总结归纳】1个特征——三视图的长度特征“长对正，宽相等，高平齐”，即正视图和侧视图一样高，正视图和俯视图一样长，侧视图和俯视图一样宽。

初中数学解空间几何练习题及答案解析题一：立体与空间几何关系已知ABCD为矩形，AE=EF，EF与CF垂直，且垂足分别为E和F，求证AE⊥CD。

解答：思路：观察题目中给出的条件，矩形ABCD和AEF之间存在着一些特殊的几何关系，我们可以根据这些关系来推导出AE⊥CD。

解法步骤：1. 连接AC和BD，由于ABCD为矩形，所以AC与BD相互垂直，且交点为O。

2. 连接EF，假设交点为H。

3. 由条件可知，EF与CF垂直，并且垂足分别为E和F，所以EH与CF垂直，且交点为G。

4. 由矩形的性质可知，AG与BC垂直。

5. 由直角三角形AGC和AHE可知，AG⊥AC，而AH⊥AC，所以AG与AH重合，即AG和AH重合，即G和H重合。

6. 设G和H重合后的点为P。

7. 由于P点为EF的垂足，所以PE⊥EF。

8. 由于P点是G和H重合后的点，即G和H重合，所以PG=GK，其中K为CD的中点。

9. 由于矩形的性质可知，AE与DK垂直。

10. 综上所述，根据步骤9，可得AE⊥CD。

解析题二：平面和空间几何关系已知P、Q、R、S为平面uvw的四个点，其中PQ⊥RS，且PR和PS的距离相等，求证QR⊥SR。

解答：思路：通过观察题目中给出的条件，我们可以利用平面几何中的性质来推导QR⊥SR的结论。

解法步骤：1. 连接PS和QR，分别交于点A。

2. 连接PR和QS，分别交于点B。

3. 由题意可知，PQ⊥RS，所以AP⊥PS，BS⊥PR。

从而可得，AP 和BS是平行线。

4. 因为AP和BS是平行线，所以APBS构成平行四边形。

5. 由平行四边形的性质可知，QR和AS平行，并且QR的长度等于AS的长度。

6. 由步骤5可知，QR和AS平行，同时QR和PS垂直。

7. 根据垂直平面的性质可知，QR⊥SR。

综上所述，根据以上步骤，可以得出QR⊥SR的结论。

答案：解析题一答案：根据推导过程，我们可以得出结论：AE⊥CD。

解析题二答案：根据推导过程，我们可以得出结论：QR⊥SR。

专专8.1空间几何体的结构特征及表面积体积一、单选题1. 给出下列命题中正确的是( )A. 棱柱被平面分成的两部分可以都是棱柱B. 底面是矩形的平行六面体是长方体C. 棱柱的底面一定是平行四边形D. 棱锥的底面一定是三角形2. 已知A ，B ，C 为球O 的球面上的三个点，1O 为ABC 的外接圆．若1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为( )A. 64πB. 48πC. 36πD. 32π3. 设A ，B ，C ，D 是同一个半径为4的球的球面上四点，ABC 为等边三角形且其面积为D ABC -体积的最大值为( )A. B. C. D.4. 已知圆锥的顶点为S ，母线SA ，SB 所成角的余弦值为78，SA 与圆锥底面所成角为45︒，若SAB 的面积为，则该圆锥的侧面积为(( )A. B. C. D.5. 埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为( )A.14B.12C.14+ D.12+ 6. 已知边长为2的等边三角形ABC ，D 为BC 的中点，以AD 为折痕，将ABC 折成直二面角B AD C --，则过A ，B ，C ，D 四点的球的表面积为( )A. 3πB. 4πC. 5πD. 6π7. 已知三棱锥P ABC -中，PA ，PB ，PC 两两垂直，且长度相等．若点P ，A ，B ，C都在半径为1的球面上，则球心到平面ABC 的距离为( )A.36B.12C.13D.328. 沙漏是古代的一种计时装置，它由两个形状完全相同的容器和一个狭窄的连接管道组成，开始时细沙全部在上部容器中，细沙通过连接管道全部流到下部容器所需要的时间称为该沙漏的一个沙时.如图，某沙漏由上下两个圆锥组成，圆锥的底面直径和高均为8cm ，细沙全部在上部，其高度为圆锥高度的2(3细管长度忽略不计).假设该沙漏每秒钟漏下30.02cm 的沙，且细沙全部漏入下部后，恰好堆成一个盖住沙漏底部的圆锥沙堆.以下结论正确的是( )A. 沙漏的侧面积是2165cm πB. 沙漏中的细沙体积为31024cm πC. 细沙全部漏入下部后此锥形沙堆的高度约为1.2cmD. 该沙漏的一个沙时大约是1985秒( 3.14)π≈9. 如图所示，在直三棱柱111ABC A B C -中，11AA =，3AB BC ==，1cos 3ABC ∠=， P 是1A B 上的一动点，则1AP PC +的最小值为( )A. 5B. 7C. 13+D. 310. 在棱长为1的正方体1111ABCD A B C D -中，E ，F ，G ，H 分别为11A B ，11C D ，AB ，CD 的中点，点P 从G 出发，沿折线GBCH 匀速运动，点Q 从H 出发，沿折线HDAG 匀速运动，且点P 与点Q 运动的速度相等，记以E ，F ，P ， Q 四点为顶点的三棱锥的体积为V ，点P 运动的路程为x ，在02x 时，V 与x 满足的函数解析式的图象应为( )A.B.C.D.二、多选题11. 将边长为2的正方形沿对角线BD 折成直二面角BD A C --，如图所示，点E ，F 分别为线段BC,AD 的中点，则( )A. EF BC ⊥B. 四面体BCD A -的表面积为4+23C. 四面体BCD A -的外接球的体积为823π D. 过EF 且与BD 平行的平面截四面体BCD A -所得截面的面积为212. 如图，在棱长为1的正方体1111ABCD A B C D -中，P 为线段11B D 上一动点(包括端点)，则以下结论正确的有( )A. 三棱锥1P A BD -的体积为定值13B. 过点P 平行于平面1A BD 的平面被正方体1111ABCD A B C D -截得的多边形的面积为32C. 直线1PA 与平面1A BD 所成角的正弦值的范围为D. 当点P 与1B 重合时，三棱锥1P A BD -的外接球的体积为32π13. 如图，在三棱锥P ABC -中，D 、E 、F 分别为棱PC 、AC 、AB 的中点，PA ⊥平面ABC ，90ABC ∠=︒，6,8,AB PA BC ===则( )A. 三棱锥D BEF -的体积为6B. 直线PB 与直线DF 垂直C. 平面DEF 截三棱锥P ABC -所得的截面面积为12D. 点P 与点A 到平面BDE 的距离相等三、填空题14. 正方体1111ABCD A B C D -的棱长为2，则平面11AC D 与平面ABCD 所成角为__________；设P 为1CC 的中点，过点A ，P ，1D 的平面截该正方体所得截面的面积为__________.15. 中国有悠久的金石文化，印信是金石文化的代表之一.印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”(图1).半正多面体是由两种或两种以上的正多边形围成的多面体.半正多面体体现了数学的对称美.图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1.则该半正多面体共有__________个面，其棱长为__________.16. 学生到工厂劳动实践，利用3D 打印技术制作模型，如图，该模型为长方体1111ABCD A B C D -挖去四棱锥O EFGH -后所得的几何体，其中O 为长方体的中心，,,,E F G H 分别为所在棱的中点，==6AB BC cm ，1=4AA cm ，3D 打印所用的材料密度为30.9/g cm ，不考虑打印损耗，制作该模型所需原料的质量为__________.g17. 如图，在平面四边形PQRS 中，2QPS π∠=，2QSR π∠=， 2.PQ PS SR ===将该平面图形沿线QS 折成一个直二面角P QS R --，三棱锥P QRS -的体积为__________ ，三棱锥P QRS -的外接球的体积为__________ .18. 如图，在一个底面边长为2，侧棱长为10的正四棱锥-P ABCD 中，大球1O 内切于该四棱锥，小球2O 与大球1O 及四棱锥的四个侧面相切，则小球2O 的体积为__________.四、解答题19. 如图，四边形ABCD 为菱形，G 为AC 与BD 的交点，BE ⊥平面.ABCD(1)证明：平面AEC ⊥平面BED ；(2)若120ABC ︒∠=，AE EC ⊥，三棱锥E ACD -，求该三棱锥的侧面积．答案和解析1.【答案】A解：平行于棱柱底面的平面可以把棱柱分成两个棱柱，故A 正确； 三棱柱的底面是三角形，故C 错误；底面是矩形的平行六面体的侧面不一定是矩形，故它也不一定是长方体，故B 错误； 四棱锥的底面是四边形，故D 错误． 故选：.A2.【答案】A解：由题意可知图形如图：1O 的面积为4π，可得12O A =，由题知ABC 是等边三角形，根据等边三角形性质， 得13sin 602AO AB ︒=，13322AO AB =， 123AB BC AC OO ∴====，外接球的半径为：22114R AO OO =+=，球O 的表面积：24464.ππ⨯⨯=故选：.A3.【答案】B解：ABC 为等边三角形且面积为2AB =6AB =， 设球心为O ，三角形ABC 的外心为O '，显然D 为O O '的延长线与球的交点时，三棱锥的体积最大.如图：2362332O C '=⨯⨯=，224(23)2OO '=-=，则三棱锥D ABC -高的最大值为：6， 则三棱锥D ABC -体积的最大值为：2136618 3.34⨯⨯⨯= 故选：.B4.【答案】A解：因为2211sin 22SAB Sl ASB l =∠==，所以l =l =，所以r =，则12.2S rl rl πππ=⨯==⋅=侧 故选：.A5.【答案】C解：设正四棱锥的高为h ，底面边长为a ，侧面三角形底边上的高为h '，则依题意有：因此有222151()4()2()10(224a h h h h ah a a a '''+'-='⇒--=⇒=负值舍去)； 故选：.C6.【答案】C解：如图所示：边长为2的等边三角形ABC ，D 为BC 的中点，以AD 为折痕， 将ABC 折成直二面角B AD C --，则AD ，BD ，DC 两两垂直， 将四面体ABCD 扩展为以D 为顶点的长方体，其中 3AD =，1BD CD ==，设过A ，B ，C ，D 四点的球的半径为r ， 故：2(2)1135r =++=， 所以：254r =， 所以254454S r πππ==⋅=， 故过A ，B ，C ，D 四点的球的表面积为5.π 故选：.C7.【答案】C解：三棱锥P ABC -中，PA ，PB ，PC 两两垂直，且长度相等，∴此三棱锥的外接球即以PA ，PB ，PC 为三边的正方体的外接球O ，且体对角线为球O 的直径，球O 的半径为1，设正方体的边长为a 2=，解得a =，∴PA PB PC ===， 球心到截面ABC 的距离即正方体中心到截面ABC 的距离， 设P 到截面ABC 的距离为h ，则正三棱锥P ABC -的体积13ABCV Sh =⨯13PABS PC =⨯31132=⨯⨯，由勾股定理易知ABC 的正三角形，2ABCS==，则3111332h =⨯⨯，23h ∴=， 由正方体的几何形状可知，直线PO 经过三菱锥P ABC -以P 为顶点的高线， 所以球心到平面ABC 的距离为113h -=， ∴球心(即正方体中心)O 到截面ABC 的距离为1.3故选：.C8.【答案】D解：对于A ，沙漏的侧面积为，故A 错误；对于B ，设细沙在上部时，细沙的底面半径为r ，则28433r cm =⨯=， 所以细沙的体积为23118161024()33381V cm ππ=⨯⨯=，故B 错误； 对于C ，设细沙流入下部后的高度为1h ，根据细沙体积不变可知：，解得1642.427h cm =≈，故C 错误； 对于D ，该沙漏的一个沙时为：10241024 3.140.025*********π⨯÷=⨯≈秒，故D 正确． 故选：.D9.【答案】B解：连接1BC ，得11A BC ，以1A B 所在直线为轴，将11A BC 所在平面旋转到平面11ABB A ，设点1C 的新位置为C '，连接AC '，则AC '即为1AP PC +的最小值， 由题意知11AA =，3AB BC ==，1cos 3ABC ∠=，得112A B BC AC ='='=，1160AA B BAC ∠=∠'=︒， 所以在1AAC '中，114212()7.2AC '=+-⨯⨯⨯-= 故选.B10.【答案】C解：(1)当102x时，点P 与点Q 运动的速度相等根据下图得出：面OEF 把几何体PEFQ 分割为相等的几何体，111122OEFS=⨯⨯=，P 到面OEF 的距离为x ， 112223263PEFQ P OEF x xV V x -==⨯⨯=⋅=四面体三棱锥，(2)当1322x <<时，P 在BC 上，Q 在AD 上， P 到平面OEF 的距离为12，111122OEFS =⨯⨯=， 1111223226PEFQ P OEF V V -==⨯⨯⨯==四面体三棱锥定值．(3)当322x 时，111122OEFS =⨯⨯=，P 到面OEF 的距离为2x -， 112122(2)3233PEFQ P OEF V V x x -==⨯⨯⨯-=-四面体三棱锥，，故选：.C11.【答案】BCD解：选项A ，如图，取BD 中点为原点，建立空间直角坐标系，坐标如下：(0,-2,0)B ，(2,0,0)C ，22(,-,0)22E ，22(0,,)22F ，(0,0,2)A ，22EF=(,2,)22∴-，BC=(2,2,0)，22EF BC=-2+22+0=1022∴⋅⨯⨯⨯≠，EF ∴与BC 不垂直，故A 错误;选项B ，22|AC |+=2+2=2AO CO =，∴四面体的表面积131131=+++=22+22+22+22=23+4222222ABC ABD ACD BCD S S S S S ∆∆∆∆⨯⨯⨯⨯⨯⨯⨯⨯⨯⨯，故B 正确;选项C ，BCD ∆外接圆半径=2r ，锥高=2h ，外接球半径R 满足222()+=R h r R -，解得=2R ，∴四面体外接球体积为3482=33R ππ⋅⋅，故C 正确;选项D ，如图，分别取AB ，CD 中点M ，N ，MF//BD ，EN//BD ，1MF=EN=BD=22，∴四边形ENFM 为平行四边形，EN//BD ，EN ⊂平面ENFM ，BD/⊂平面ENFM ，BD//∴平面ENFM ，由选项A 可知22(,,0)22N ，22(0,-,)22M ，EN=(0,2,0)，22EM=(,0,)22-，EN EM=0∴⋅，EN EM ∴⊥，ENFM ∴是矩形，面积=EN ME=21=2S ⨯⨯，故D 正确.12.【答案】BCD解：A 选项：111211213226P A BD A PBD V V --==⨯⨯⨯⨯=，A 不正确； B 选项：此平面为平面11B D C ，故三角形11B D C 的面积为233(2)42⨯=，B 选项正确； C 选项：设点P 到平面1A BD 的距离为h ， 由1116P A BD A PBD V V --==知，点P 到平面1A BD 的距离为33h =，当点P 在线段11B D 上运动时，1max ||1(PA P =为端点时)，1min 2||2PA =， 设直线1PA 与平面1A BD 所成角为θ，，则，C 正确；D 选项：11190B BD B A D ︒∠=∠=，所以三棱锥1P A BD -的外接球的球心为1B D 的中点， 故外接球半径为32，三棱锥1P A BD -的外接球的体积为32π，D 正确. 故选.BCD13.【答案】ACD解：D ，E 分别为棱PC ，AC 的中点，则//DE PA ， 又PA ⊥平面ABC ，则DE ⊥平面ABC ，即DE ⊥平面FBE ， 90ABC ︒∠=，6AB PA ==，8BC =，所以13462EFB S ∆=⨯⨯=，132DE PA ==，所以三棱锥D BEF -的体积为16363⨯⨯=，故A 正确；假设PB DF ⊥，PA ⊥平面ABC ，BC ⊂平面ABC ，BC PA ∴⊥，又BC AB ⊥，PA AB A ⋂=，PA ，AB ⊂平面PAB ，BC ∴⊥平面PAB ，E ，F 分别为AC ，AB 的中点，//EF BC ∴，EF ∴⊥平面PAB ， AB ⊂平面PAB ，EF AB ∴⊥，DE ⊥平面ABC ，AB ⊂平面ABC ，AB DE ∴⊥，EF DE E ⋂=，EF ，DE ⊂平面DEF ，AB ∴⊥平面DEF ，DF ⊂平面DEF ，AB DF ∴⊥，又假设PB DF ⊥，AB PB B ⋂=，AB ，PB ⊂平面PAB ，DF ∴⊥平面PAB ， 显然不成立，不符合题意，故假设不成立，故B 错误；取PB 的中点Q ，连DQ ，FQ ，则//DQ EF ，DQ EF =，四边形DQFE 为平行四边形，DE ⊥平面EFB ，EF ⊂平面EFB ，DE EF ⊥， 所以平行四边形DEFQ 为矩形，3DE =，4EF =，所以截面面积为12，故C 正确；因为//DE PA ，PA ⊂/平面BDE ，DE ⊂平面BDE ，所以//PA 平面.BDE 所以点P 与点A 到平面BDE 的距离相等，故D 正确； 故选.ACD14.【答案】4π 92解：连接1BC ，在正方体1111ABCD A B C D -中，易知11//AB C D 且11AB C D =，则四边形11ABC D 为平行四边形，即B ∈平面11AC D ，因为正方体中，AB BC ⊥，1AB BB ⊥，且1,BC BB ⊂平面11BB C C ， 则AB ⊥侧面11BB C C ，所以1AB BC ⊥， 又平面11AC D ⋂平面ABCD AB =，则1C BC ∠即等于平面11AC D 与平面ABCD 所成的角，所以11tan 1CC C BC BC∠==， 即14C BC π∠=；取BC 中点为Q ，连接PQ ，AQ ，因为P 为1CC 的中点，则1//PQ BC ， 又11//AD BC ，则1//PQ AD ，即A ，1D ，P ，Q 四点共面， 即梯形1AD PQ 即为过点A ，P ，1D 的平面截该正方体所得截面，因为正方体棱长为2，则11AD BC ===，11PC BQ ==，所以112PQ BC ==，AQ ==1PD == 即梯形1AD PQ 为等腰梯形，分别作1PM AD ⊥于点M ，1PN AD ⊥于点N ，则11122AD NM AD PQ D M AN --====，所以2PM ===， 因此梯形1AD PQ 的面积为故答案为：4π；9.215.【答案】261-解：该半正多面体中间层是一个正八棱柱，有8个侧面， 故该半正多面体共有888226+++=个面；设其棱长为x ，因为每个顶点都在棱长为1的正方体上，则122x x x ++=，解得 1.x =故答案为26 1.-16.【答案】118.8解：该模型为长方体1111ABCD A B C D -，挖去四棱锥O EFGH -后所得的几何体，其中O 为长方体的中心，E ，F ，G ，H ，分别为所在棱的中点，6AB BC cm ==，14AA cm =，∴该模型体积为：1111ABCD A B C D O EFGH V V ---11664(46432)332=⨯⨯-⨯⨯-⨯⨯⨯⨯314412132()cm =-=，3D 打印所用原料密度为30.9/g cm ，不考虑打印损耗，∴制作该模型所需原料的质量为：1320.9118.8().g ⨯=故答案为118.8.17.【答案】43解：如图，平面PQS ⊥平面QRS ，且平面PQS ⋂平面QRS QS =，QS SR ⊥， SR ∴⊥平面PQS ，PQ ⊂平面PQS ，从而SR PQ ⊥，PQ PS ⊥，且PS SR S ⋂=，PQ ∴⊥平面PRS ，PR ⊂平面PRS ，得PQ PR ⊥，QR ∴是三棱锥P QRS -的外接球的直径，在Rt QSR 中，2223QR QS SR =+=，则球的半径3R =，则外接球的体积为34433R ππ=； 三棱锥P QRS -的体积为1114222.3323PQSSSR ⨯=⨯⨯⨯⨯=故答案为：43；43.π18.【答案】24解：设O 为正方形ABCD 的中心，AB 的中点为M ，连接PM ，OM ，PO ， 则=1OM ，22=-=10-1=3PM PA AM ，=9-1=22PO ，如图，在截面PMO 中，设N 为球1O 与平面PAB 的切点，则N 在PM 上，且1O N PM ⊥，设球1O 的半径为R ，则1=O N R ， 因为1sin ==3OM MPO PM ∠，所以111=3NO PO ，则1=3PO R ， 11=+=4=22PO PO OO R ，所以2=2R ， 设球1O 与球2O 相切于点Q ，则=-2=2PQ PO R R ，设球2O 的半径为r ， 同理可得=4PQ r ，所以2==24R r ， 故小球2O 的体积342V=r =324ππ， 故答案为2.24π19.【答案】证明：(1)四边形ABCD 为菱形，AC BD ∴⊥，BE ⊥平面ABCD ，AC ⊂平面ABCD ，AC BE ∴⊥，BD ，BE ⊂平面BED ，BD BE B ⋂=， 则AC ⊥平面BED ，AC ⊂平面AEC ，∴平面AEC ⊥平面BED ；解：(2)设AB x =，在菱形ABCD 中，由120ABC ︒∠=， 得2AG GC x ==，2x GB GD ==，BE ⊥平面ABCD ，BG ⊂平面ABCD ，BE BG ∴⊥，则EBG 为直角三角形，1322EG AC AG x ∴===， 则2222BE EG BG x =-=， 三棱锥E ACD -的体积3116632243V AC GD BE x =⨯⋅⋅==， 解得2x =，即2AB =，120ABC ︒∠=，22212cos 44222()122AC AB BC AB BC ABC ∴=+-⋅∠=+-⨯⨯⨯-=，即1223AC ==，在三个直角三角形EBA ，EBD ，EBC 中，斜边AE EC ED ==，AE EC ⊥，EAC ∴为等腰三角形，则22212AE EC AC +==， 即2212AE =，26AE ∴=，则6AE =，∴从而得6AE EC ED ===，EAC ∴的面积1166322S EA EC =⨯⋅=⨯⨯=，在等腰三角形EAD 中，过E 作EF AD ⊥于F ， 则6AE =，112122AF AD ==⨯=， 则22(6)15EF =-=，EAD ∴的面积和ECD 的面积均为12552S =⨯⨯=，故该三棱锥的侧面积为32 5.+。