时间数列分析(精)

应用统计学时间数列分析时间数列分析是统计学中的一项重要内容，通过对时间序列数据进行分析，可以揭示数据之间的内在关联和规律。

本文将探讨时间数列分析在实际应用中的重要性和方法。

什么是时间数列分析时间数列（Time Series）指的是按时间顺序排列的一系列数据观测值。

时间数列分析是指根据时间数列数据进行的统计分析方法，旨在发现数据中存在的趋势、季节性、周期性等规律，以便进行预测和决策。

时间数列分析的重要性时间数列分析在许多领域都有广泛的应用，包括经济学、金融、医学、气象等。

通过时间数列分析，我们可以：•发现数据中的趋势和规律•预测未来数据走势•制定决策和策略•检验模型的有效性•揭示不同变量之间的关联时间数列分析方法1. 平稳性检验平稳性是时间数列分析的前提条件之一，可以通过单位根检验、ADF检验等方法来判断时间数列是否平稳。

如果时间数列不平稳，需要进行差分处理或其他转换方法使其平稳化。

2. 自相关性分析自相关性分析是检验数据是否存在自相关性（即相邻数据之间的相关性）的方法，可以通过自相关图和偏自相关图来判断数据中的自相关性程度。

3. 移动平均法移动平均法是一种基本的时间数列预测方法，通过计算一定窗口内的数据均值来平滑数据曲线，以便更好地观察数据走势和预测未来走向。

4. 季节性调整在时间数列分析中，常常需要对数据进行季节性调整，以消除季节性影响，使预测结果更为准确。

应用实例1. 股票价格预测时间数列分析在金融领域有着广泛的应用。

通过分析股票价格的时间数列数据，可以预测股价的未来走势，指导投资决策。

2. 气象预测气象数据也是时间数列数据的一种，通过对气象数据进行时间数列分析，可以预测未来的气候变化和天气情况，为灾害预警和农业生产提供依据。

3. 经济指标分析经济数据的时间数列分析可以揭示经济增长趋势、波动周期等信息，帮助政府和企业做出相应决策。

结语时间数列分析是统计学中一个重要的分析方法，通过对时间序列数据进行分析，可以揭示数据之间的规律、趋势和关联。

第十章时间数列分析一、本章重点1．时间数列的意义和种类。

时间数列是同一社会经济现象的统计指标按一定的时间顺序排列而成的数列，时间数列有绝对数时间数列、相对数时间数列和平均数时间数列。

绝对数时间数列是基础数列，相对数时间数列和平均数时间数列是派生数列。

绝对数时间数列又分时期数列和时点数列。

2．序时平均数的计算。

序时平均数是本章的重点和难点，要区分绝对数时间数列、相对数时间数列和平均数时间数列，在绝对数时间数列计算序时平均数时有间隔相等的连续时点数列、间隔不等的连续时点数列、间隔相等的间断时点数列和间隔不等的间断时点数列。

由平均数时间数列计算序时平均数时有一般平均数时间数列和序时平均数时间数列两种形势。

3．平均发展速度的计算。

平均发展速度是速度指标的基础，平均增长速度就是根据平均发展速度计算出来的。

平均发展速度的计算方法有两种：几何平均法（水平法）和方程法（累计法）。

这两种方法的应用条件要弄清楚。

4．长期趋势的测定，主要是移动平均法。

长期趋势的测定是时间数列分解的基础，有时距扩大法和移动平均法两种，同时应掌握季节变动测定的两种方法：按月（季）平均法和移动平均趋势剔除法。

二、难点释疑1.对于序时平均数的计算，关键是要掌握什么是时期指标，什么是时点指标，如果是时点指标，要分清是连续时点还是间断时点。

凡是逐日登记的，就是连续时点指标，若是每隔一段时间登记一次，则是间断时点指标。

在进行计算的时候，要一步一步来，理清头绪，问题便容易解决了。

2.对平均发展速度的计算，只要把握住各自的使用条件就可以了。

三、练习题（一）填空题1．时间数列的两个构成要素是（时间）和（指标数值）。

2．如果某种经济现象的发展变化比较稳定，则宜利用（几何平均法）来计算平均发展速度。

3．编制时间数列的基本原则是（可比性）、（时期长短要一致）、（总体范围一致）、（指标的经济内容要相同）和（指标的计算价格、计量单位和计算方法要一致）。

4．时间数列按其数列中所排列的指标性质的不同，可以分为（绝对数）时间数列、（相对数）时间数列和（平均数）时间数列三种。

第六章时间数列分析第一节时间数列分析概述一、时间数列的概念我们对现象总体的数量方面进行分析研究时，通常需要掌握和积累现象各个时期的统计资料，从时间上反映和研究现象发展变化的过程、趋势及其规律。

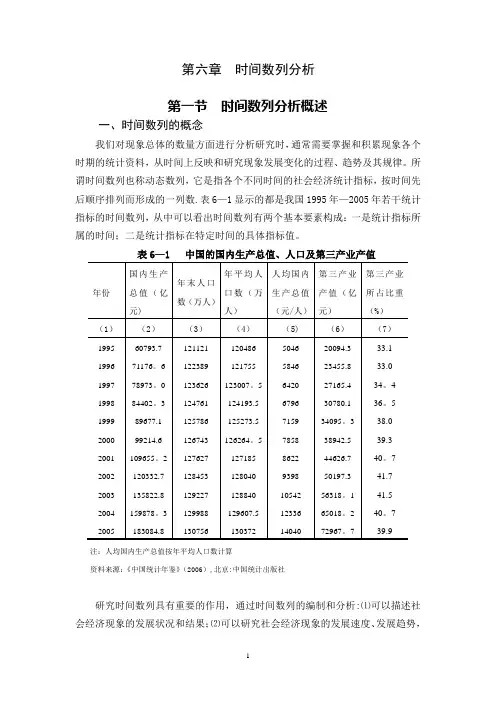
所谓时间数列也称动态数列，它是指各个不同时间的社会经济统计指标，按时间先后顺序排列而形成的一列数.表6—1显示的都是我国1995年—2005年若干统计指标的时间数列，从中可以看出时间数列有两个基本要素构成：一是统计指标所属的时间；二是统计指标在特定时间的具体指标值。

表6—1 中国的国内生产总值、人口及第三产业产值注：人均国内生产总值按年平均人口数计算资料来源：《中国统计年鉴》（2006）,北京:中国统计出版社研究时间数列具有重要的作用，通过时间数列的编制和分析:⑴可以描述社会经济现象的发展状况和结果；⑵可以研究社会经济现象的发展速度、发展趋势，探索现象发展变化的规律,并据以进行统计预测；⑶分析长期趋势、季节变动和循环变动等了解和分析社会现象发展变化的规律性。

二、时间数列的种类时间数列按照其指标的性质，可以分为总量指标、相对指标和平均指标时间数列等三大类型。

总量指标时间数列也称绝对数时间数列，是基本的时间数列，相对指标和平均指标时间数列都是在总量指标时间数列的基础上派生出来的。

㈠总量指标时间数列总量指标时间数列是指把一系列同类的总量指标按时间先后顺序排列起来形成的时间数列。

它反映社会经济现象在各个时期达到的绝对水平及其变化发展的状态。

表6—1中的国内生产总值、年末人口和第三产业产值都属于总量指标时间数列。

按照总量指标所反映的内容的不同，可以分为总体单位总量和总体标志总量两种。

年末人口数是总体单位总量指标，而国内生产总值和第三产业产值是总体标志总量指标.根据总量指标反映的社会经济现象所属的时间不同，又可将总量指标时间数列分为时期数列和时点数列。

下面来讨论时期数列和时点数列的特点.⒈时期序列各项指标都是反映某种现象在一段时期内发展过程的总量,该时间数列称为时期序列。

时间数列分析时间数列是指按时间顺序排列的一列数据。

通过对时间数列的分析，可以了解事件发展的趋势和规律，为预测未来的发展提供参考。

下面将从数列的统计特征、趋势分析和周期性分析三个方面对时间数列进行详细分析。

一、数列的统计特征统计特征是指对时间数列的基本特征进行概括和描述。

常见的数列统计特征包括最大值、最小值、平均值、中位数和标准差等。

最大值是数列中最大的一个数，它反映了事件最高点的出现时间。

最小值是数列中最小的一个数，它反映了事件最低点的出现时间。

平均值是数列中所有数的和除以总数，它反映了事件整体水平的时间变化趋势。

中位数是将数列按大小排列，位于中间位置的数，它反映了事件的中点出现时间。

标准差是用来衡量数列离散程度的指标，它反映了事件的波动程度和不确定性。

通过计算和比较这些统计特征，我们可以对事件发展的整体情况有一个大致的了解。

最大值和最小值可以帮助我们确定事件最高点和最低点的时间范围，平均值可以告诉我们事件发展的平均速度和趋势，中位数可以帮助我们确定事件的中期发展阶段，标准差可以帮助我们评估事件的波动程度和风险。

二、趋势分析趋势分析是指通过时间数列的走势和变化规律，预测事件未来的发展趋势。

常用的趋势分析方法有线性回归分析和移动平均法等。

线性回归分析是一种通过拟合直线来描述事件发展趋势的方法。

它适用于数列具有线性关系的情况，可以通过计算回归方程来预测未来的数值。

线性回归分析的关键是选取合适的变量和确定最佳的拟合直线。

移动平均法是一种通过计算某一时间段内的平均值来描述事件发展趋势的方法。

它适用于数列存在周期性变化的情况，可以抹平季节性波动，更好地反映长期趋势。

移动平均法的关键是选择合适的时间段和计算平均值的方法。

通过趋势分析，我们可以判断事件的增长趋势、下降趋势或者稳定趋势，进而预测事件未来的发展趋势。

趋势分析对于决策制定和未来规划具有重要的参考价值。

三、周期性分析周期性分析是指通过时间数列的周期性变化规律，寻找事件发展的周期性和循环特征。

时间数列分析时间数列分析时间是我们生活中不可或缺的一部分，它们组成了我们的回忆和经历。

时间数列分析是研究时间序列的变化和规律的一种方法。

通过对时间数列进行分析，我们可以了解时间的特性和变化趋势，从而为我们的生活和决策提供有益的信息。

在本文中，我们将详细分析时间数列分析的方法和应用。

时间数列分析是一种数学和统计学的工具，它通过对时间序列进行数学建模和统计分析，揭示时间变量之间的关系和规律。

常见的时间数列分析方法包括趋势分析、周期分析和季节性分析。

首先，趋势分析是指对时间序列数据的长期变化趋势进行分析和预测。

通过观察和分析时间序列的变化趋势，我们可以了解一项事物的增长或下降的速度和方向。

常见的趋势分析方法包括简单移动平均法、指数平滑法和趋势线拟合法。

简单移动平均法是将一段时间内的数据求平均值，作为该时段的预测值。

通过不断滚动窗口，我们可以得到整个时间序列的预测值。

指数平滑法则是通过对历史数据进行加权平均，得到未来的预测值。

这种方法更重视近期的数据，更能反映变化的趋势。

趋势线拟合法则是根据时间序列的变化趋势，拟合出一条线性或非线性曲线，来描述趋势的变化。

周期分析是指对时间序列中的周期性变化进行分析和预测。

周期变化是指在一定时间内重复出现的变化。

对于有明显周期性的数据，周期分析可以帮助我们预测未来的变化趋势。

常见的周期分析方法包括傅里叶分析和自回归移动平均模型（ARMA）。

傅里叶分析是将时间序列数据分解成一系列的频率分量，从而揭示数据的周期性变化。

这种方法可以将复杂的时间序列分解为多个简单的周期波动，进而进行预测和分析。

ARMA模型则是一种统计方法，它结合了自回归（AR）和移动平均（MA）模型，用于预测时间序列的未来值。

通过分析时间序列的自相关性和移动平均性，我们可以建立ARMA模型，进而进行预测。

季节性分析是指对时间序列中的季节性变化进行分析和预测。

季节性变化是指在一年内周期性出现的变化。

对于受季节因素影响较大的数据，季节性分析可以帮助我们了解季节的变化规律，并进行未来的预测。