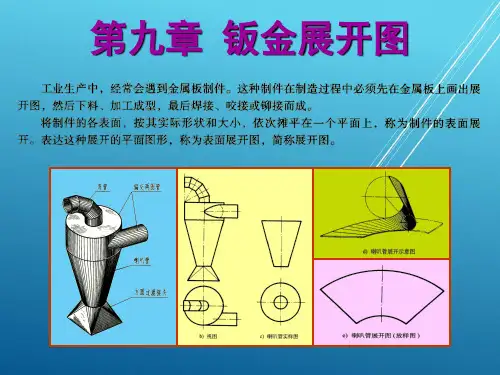
直角三角形还求实长

实长
d'
C1
Y坐标差
图a
c' X
e
c
Y坐标差
O
d
例1： 试利用Y坐标差求一般位置线段CD的实长。 在图a中作线段ED∥c' d',形成直角三角形CED，其斜边CD为线段的实长。
d'
Y坐标差
图a
c'
X
D1
e
实长 c
O
d
Y坐标差
例2 已知△ABC的两面投影，试求△ABC的实形。
B
AC边实长
b'
X
B
#39; X
b1
b'
O
a
b
逆时针旋转求实长
例2：求斜切圆锥表面上任一素线的实长。
截掉素线的实长
s'
余下素线的实长
a1' a'
b1' b'
第九章 钣金展开图
一、直角三角形法
过点A作AC∥ab,则在空间构成一个直角三角形ABC，其斜边AB是线段 的实长。
作图方法一
Z坐标差
b' Z坐标差
求线段实长的直观图。
a'
c'
X
O
b
a
实长
B1
投影图。
一、直角三角形法
过点A作AC∥ab,则在空间构成一个直角三角形ABC，其斜边AB是线段
的实长。
B1
作图方法二
Z坐标差
b' B1
Z坐标差
实长
a'
c'
A1
X
O
作
b
1）以线段某一投影（如水平投影）的长度为一直角边。

图12-3 旋转法求一般位置线段实长
线段AB为一般位置直线，过端点A作垂直于H面 直线oo为轴，将线段AB绕oo轴旋转为正平线，正面 投影a′b1′为AB的实长。由于直线上任一点的运动 轨迹为水平圆，H面投影反映圆形，V面投影为平行 OX轴的直线，其作图步骤如图12-3（b）所示。
图12-3 旋转法求一般位置线段实长
图12-6 异径直角三通管的展开
（3）用光滑曲线连接点Ⅰ、Ⅱ、Ⅲ、Ⅳ 及对称的各点，即得相贯线展开后的图形 （见图12-6（d））所示。
第3节 棱锥管和圆锥管的展开
锥管制件的表面上的棱线或素线均相交于 一点，其表面属可展表面。可借助其棱线或 素线的实长来作展开图，这种展开方法常称 为放“放射线法” 1．斜口四棱台管展开 [例12-4]求作图12-7（a）、（b）所示斜 口四棱台管的展开图。
图12-4 斜截四棱柱管的展开
分析：斜截四棱柱管的前后表面为直角 梯形，左右表面为长方形。作展开图时，分 别画出两个相等直角梯形和两个长方形的实 形。
图12-4 斜截四棱柱管的展开
作图： （1）画一水平线，依次量取ⅠⅡ = (1)(2)、 ⅡⅢ = (2)(3)、ⅢⅣ = (3)(4)、ⅣⅠ = (4)(1)。
图12-7 斜口四棱台管的展开
分析：四棱台管表面为四个梯形，展开图 依次画出这四个梯形。先按四棱锥展开，用棱 线实长作出扇形，再在扇形内作出四个等腰梯 形。
图12-7 斜口四棱台管的展开 作图： （1）将主视图棱线延长得交点s′，用旋转法或直角三 角形法求得棱线实长s′c1′或S0C0和斜口与棱线交点G0 （H0）、F0（E0）。 （2）以S为圆心，s′c1′ = S0C0为半径画圆孤。
图12-2 直有三角形法求一般位置线段实长

二、换面法
1.点的一次换面
以H1 面替代H 面
V
ax1 a’ aX a
a1 Z
作图步骤： 投影规律： 1)画OX1 轴； 1)新投影与旧投影： a1 aX1 = aaX。 2)过a’ 作OX1 轴的垂线； 2)新投影与不变投影： a‘ a1 ⊥OX1 ； 3)在垂线上截取 a1aX1 = aaX 。
线段对不变投影面的倾角。
b'
V X H
实长
a’1
α
A
a’
X
B
α
பைடு நூலகம்
a b
b’ a O a'1
实长 α
b’1
X1
b
b'1
解题完毕
§3-3 求一般位置线段的实长
二、换面法
例2 求AB 线段的实长及β。 作图要点：X1 ∥a’b’ 分析：
a1
β
实长
b1
V 面应为不 变投影面, X1
轴平行不变投 影a’b’ ，求得线 段对V 投影面的 倾角β 。
O
R30 EF
e
解题完毕
§3-3 求一般位置线段的实长
一、直角三角形法
小结
1)实长、坐标差、投影长、倾角为直角三角形的四要素。
注意：
直线的坐标差、投影长、倾角是对同一投影面而言。
TL
(实长)
α
水平投影
坐 标 差
Z
TL
(实长)
β
正面投影
坐 标 差
Y
TL
(实长)
γ
侧面投影
坐 标 差
X
§3-3 求一般位置线段的实长
§3-3 求一般位置线段的实长
一、直角三角形法

1. 已知K点在直线AB上，求出K点的侧面投影。

解答：分析：错解原因是对“直线上点分线段的长度比与对应的投影的长度比相等”这一概念不清楚。

错解中直接在侧面投影上作a"k"=a'k'，其结果a'k'/k'b'≠a"k"/k"b"。

因此，K点并不是线段AB上的点。

正确的作图步骤应是：（1）由a"任作一直线；（2）在该直线上截取a"Ⅰ=a'k'、ⅠⅡ=k'b'；（3）连接Ⅱb"；（4）过Ⅰ作直线平行于Ⅱb"交a"b"于点k"，则点k"即为所求。

2. 用直角三角形法求直线AB与H面的倾角α及与V面的倾角β。

解答：分析：错解原因是对所求的直角三角形实形的构成要素模糊不清，对直角三角形方法的作图要领理解不透。

直角三角形的作图要领归纳如下：1. 以线段投影的长度为以一直角边；2. 以线段的两端点相对于该投影面的距离差为另一直角边，该距离差可从线段的另一投影图上量得；3. 所作直角三角形的斜边即为线段的实长；4. 斜边与该投影的夹角为线段与该投影面的倾角。

所以，在求角α时，必须用线段水平投影长度与该线段两端点的高度坐标差作直角三角形；在求角β时，必须用线段正面投影长度与该线段两端点的前后坐标差作直角三角形。

作图步骤：求α角。

（1）以线段AB的水平投影ab为一条直角边，由端点b作直线垂直于ab；（2）在正面投影上求出直线AB的高度坐标差△Z AB；（3）在与ab垂直的直线上截取线段bB0=△Z AB；（4）连接aB0，则ab与aB0所夹的角度即为直线AB对H面的倾角α。

求β角的作图过程类似。

3. 已知直线AB对H面的倾角为30°，补全AB的水平投影。

解答：分析：错解误把直线AB对V面的倾角当作对H面的倾角了。

在管道安装工程中，经常遇到转弯、分支和变径所需的管配件，这些管配件中的相当一部分要在安装过程中根据实际情况现场制作，而制作这类管件必须先进行展开放样，因此，展开放样是管道工必须掌握的技能之一。

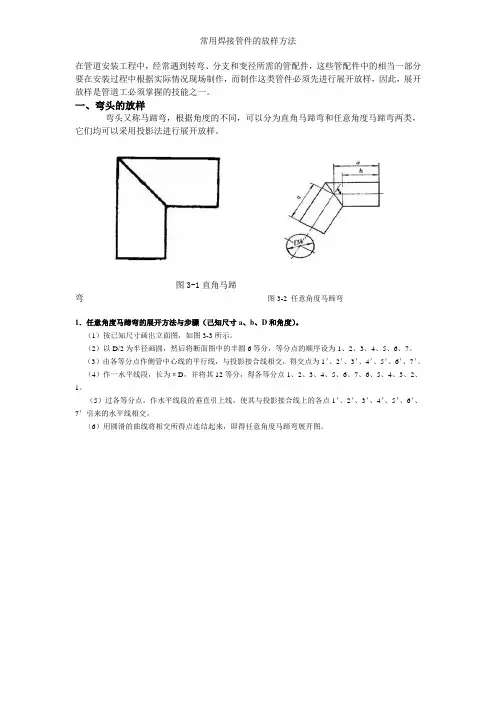
一、弯头的放样弯头又称马蹄弯，根据角度的不同，可以分为直角马蹄弯和任意角度马蹄弯两类，它们均可以采用投影法进行展开放样。

图3-1直角马蹄弯图3-2 任意角度马蹄弯1．任意角度马蹄弯的展开方法与步骤（己知尺寸a、b、D和角度）。

（1）按已知尺寸画出立面图，如图3-3所示。

（2）以D/2为半径画圆，然后将断面图中的半圆6等分，等分点的顺序设为1、2、3、4、5、6、7。

（3）由各等分点作侧管中心线的平行线，与投影接合线相交，得交点为1＇、2＇、3＇、4＇、5＇、6＇、7＇。

（4）作一水平线段，长为πD，并将其12等分，得各等分点1、2、3、4、5、6、7、6、5、4、3、2、1。

（5）过各等分点，作水平线段的垂直引上线，使其与投影接合线上的各点1＇、2＇、3＇、4＇、5＇、6＇、7＇引来的水平线相交。

（6）用圆滑的曲线将相交所得点连结起来，即得任意角度马蹄弯展开图。

图3-3 任意角度马蹄弯的展开放样图2、直角马蹄弯的展开放样（己知直径D）由于直角马蹄弯的侧管与立管垂直，因此，可以不画立面图和断面图，以D/2为半径画圆，然后将半圆6等分，其余与任意角度马蹄弯的展开放样方法相似。

图3-4 直角弯展开图二、虾壳弯的展开放样虾壳弯由若干个带斜截面的直管段组成，有两个端节及若干个中节组成，端节为中节的一半，根据中节数的多少，虾壳弯分为单节、两节、三节等；节数越多，弯头的外观越圆滑，对介质的阻力越小，但制作越困难。

1、90°单节虾壳弯展开方法、步骤：（1）作∠AOB＝90°，以O为圆心，以半径R为弯曲半径，画出虾壳弯的中心线。

（2）将∠AOB平分成两个45°，即图中∠AOC、∠COB，再将∠AOC、∠COB各平分成两个22.5°的角，即∠AOK、∠KOC、∠COD与∠DOE。

第二章
点、直线、面的投影 (3)
一、点的投影规律
Z
a ●
az
a
●
X ax a●
O
Y
ay
ay
Y
Z
V
a ●
az
X
yA A
ax
●
xA
O
a● zA
H
●a W ay
Y
① aa⊥OX轴 aa⊥OZ轴
② aax= aaz=A到V面的距离=yA
aax= aay=A到H面的距离=zA aay= aaz=A到W面的距离=xA
A a
线段实长。坐标差构 △YAB
成的直角边所对锐角
即为线段对该投影面
的倾角。
b'
△ZAB
B
.B
1
O
b
H
二、直角三角形法求实长和倾角
求AB的实长及对V面和H面的倾角。
b'
a0
b'
a' X
b 1O b
a' Xa1
a
b0 a
1. 直角三角形斜边长为实长。
O
b LAB
△YAB .
a’b'
2. 斜边与某个投影之间的夹角，即该直线与投影面的
二、两点的相对位置
Z
▲x 坐标大的在左 ▲y 坐标大的在前 ▲z 坐标大的在上
三、重影点
V
b' X bx
a'
az
A bz
a"
ax
O
W
B a
b H
ay b" by Y
重影点：是位于某一投影面的
V a●
同一条投射线上的空间两点。

(四)、复杂构件的展开
• 对于形状复杂的工件，一般采用作图法 1、开孔圆锥管的展开
展开时用放射线法，先作出圆锥管的展 开图，然后
在展开图的相应位置上开孔。
• 2、斜圆锥管的展开
• 如果圆锥的轴线与底面不垂直，则该圆锥称为斜圆
锥，其展开是采用放射线法展开。由于斜圆锥的顶点至底
圆的距离（即斜圆锥表面各素线的长度）都不相等，故展 开图时必须分别求出各素线的实长。斜圆锥管的展开，应 先画出整个圆锥面的展开，再画截去顶部即可得到展开图。
钢板的变形有弯曲、扭曲、波浪、翘曲等，对下料、 加工、装配都有影响，使工件的质量难以保证，因此，在 下料、切割、成形之前，必须对钢板的变形加以矫正。
1、矫正方法
按矫正的方式分：有手工矫正和机械矫正
按矫正时的工件温度分：冷矫正(常温)和热矫正（火焰加热）
2、手工矫正工具及设备
手工矫正用的主要工具有大锤、手锤和型锤，主要设备 是平台
交汇于一点的构件。
4、简单弯曲件的展开料长计算
• 对于形状简单的工件或型钢的弯曲，可以通过计算求得展开尺寸。由于钢材 弯曲时，内、外分别为受压和受拉影响，则一般以中间层为计算展开的依据， 但不同的断面、不同的弯曲程度，中间层的位置也就不同。我们把L×b×δ的 一块钢条弯曲成曲率为R的圆弧条时，发现上面(弧内侧)的长度变短了，下面 （弧外侧）的长度变长了。根据连续原理，其中间一定存在一个既不伸长也不缩 短的层面。这个层面我们叫它中性层.按中性层展开就是我们钣厚处理的基本
原则。因此在计算展开前首先要确定中性层的位置，然后才能进行计算展开。
计算展开的步骤为：
1）、将构件的曲线部分和直线部分在切点处分段。 2）、分别确定每段的中性层位置，并计算各段的展开长度。 3）、求各段的总和得到整个构件的展开长。 4）、根据加工要求和技术要求加放余量。

a’
c’ b’ c’
m’
n’
X m c b
0
Ｂ
ZA-ZB c n a Ｃ
a
b
判断下面形体的轮廓线的位置关系
(6) 6 4 (1)
3 (2)
5(7)
1
4 2 3 5
1(2)
6(7)
4 (3)
(5)
1A与4D 平行 AD与BC 平行 1A与CD 交叉 AB与57 交叉垂直 43与67 平行
AB与CE
交叉
两直线相交 两直线交叉（交错）—异面
相对位置
(1)两直线平行
b ´ a x´
c B´
d ´
C
b´
D
d´
a´
c´
A a
o
b
x
b c d
o
b
c
a
两直线平行的投影特性：
(1)两直线平行，则两直线的同面投影相互平行。
即AB∥CD，则：ab∥cd ；a′b′∥c′d′；a″b″∥c″d ″。 (2)平行两线段之比等于其投影之比。 AB:CD=ab:cd= a′b′:c′d′= a″b″∥c″d″
b′
60° Δ zAB
直线AB真长
a′
30°
b1
直线的H投影长
a
b2
以直线的H投影长 为半径，作圆弧
2.2.3.2
已知直线的真长和倾角求解有关的定位 和度量问题
【例题】如图所示：已知直线CD的两面投影，求CD对投影面 V、W的倾角，并在CD上取点T，T与C的真实距离为10mm ， 作点T的两面投影。
1’ 4’(3’) 2’
b′
a′ X
d′ 0
a′ a
3

量取0-1、1-2及等
分圆弧的弧长依
次画在中心线 上，
并过各
点作
垂线。
展开放样
• 圆柱面的展开
③在各垂线上量取主 视图上对应各素线的 高度，连接各点得工 件展开图。
展开放样
• 放射线展开法 • 展开时将锥面看作由汇交锥顶的一系
列素线和底线组成，素线和底线锥面分成 若干小三角形，毎个三角形作为一个平面 ，将各三角形依次画在平面上，就得所求 的展开图，该方法为放射线展开法，适用 于素线或素线延长线汇交于一点的 构件。
作图法逐步划出其他圆弧和直线，直至完成整个 划线工作； • 3 在中心线、轮廓线等部位打上样冲眼做好标记 ，按工作需要，标明零件的编号、规格、数量和 加工符号等。
展开放样
• 将构件的各个表面依次摊开在一个平面上的过 程称为展开。
• 在平面上所得的展开图形为展开图。 • 画展开图的过程称为展开放样。 • 求作展开图的方法通常有两种：一种是作图法
展开放样
• 上斜口四棱锥管的展开
②用旋转法求实长，在俯视图上
以0点为圆心，0b为半径作孤交中
心线于e点，过e点交点向主视图
投影交主视图底边延长线于2∥点，
连接O/2∥得实长。由于各棱线的
长度相等，只要过 2、3 点作
水平线，交O/2∥实长 线，即
可求得上斜截
口各棱
线的实长。
展开放样
• 上斜口四棱锥管的展开
展开放样
• 斜口正圆锥管的展开
①作出锥管的主视图和俯视图，将 俯视图圆周12等分，并向主视图底 投影，交于底边，连接交点与顶点 0，把锥体分成若干小三角形，并 与上斜口交于a/、b/、c/等各点， 因正圆锥体是回转体，所以素线o7 的长度就是实长。

（a）立体图
(b) 二直相交线垂直 (c) 二直相交线垂直
(d) 二直相交线垂直
定理一 垂直的两直线，其中有一条直线平行于投影面时，则两直线在该投 影面上的投影仍反映直角。
定理二 两直线在同一投影面上的投影反映直角，且有一条直线平行于该投 影面，则空间两直线的夹角必是直角。
2. 例题
[例题12] 求一点到水平线的距离 [例题13] 过一点作两线段的公垂线
c
b
|yA-yB|
3． 求直线的实长及对侧面投影面的夹角 角
|xA-xB|
§3-5 两直线的相对位置
一、两相交直线 二、两平行直线 三、两交叉直线 四、两相互垂直直线
一、两相交直线
1. 相交直线的投影 2. 例题
1. 相交直线的投影
[例题8] 给出平面四边形ABCD的V投影及其两条边的H投影， 试完成四边形的H投影。
[例题14] 作三角形ABC，ABC为直角，使BC在MN上， 且BCAB=23
[例题12] 求一点A到水平线BC的距离
AD
2
d'
y
d
[例题13] 过点E 作线段AB、CD 的公垂线EF。
f
f
[例题14] 作三角形ABC，ABC为直角，使BC在MN上，且
BCAB =23。
bc=BC
ab
b'
c'
AB
§3.4 直线的实长和倾角 求解一般位置线段的实长及倾角是求解画法几何综合题时经常遇到的基 本问题之一，也是工程上经常遇到的问题。而用直角三角形法求解实长、 倾角又最为方便．简捷。
一、直角三角形法的作图要领 用线段在某一投影面上的投影长作为一 条直角边，再以线段的两端点相对于该投影面的坐标差作为另一条直角边 ，所作直角三角形的斜边即为线段的实长，斜边与投影长间的夹角即为线 段与该投影面的夹角。

绪论单元测试1.本课程的学习方法有哪些？A:掌握思路和方法，勤动手、多练习。

B:从空间到平面，从平面到空间反复思考，以提高空间想象力。

C:画图时，必须养成一丝不苟、严谨细致的学习作风。

D:学习好基本理论、掌握基本方法、熟练基本技能。

答案:ABCD第一章测试1.下列直线相对位置为相交的是（）A:B:C:D:答案:B2.直线的H面投影反映实长，该直线为( )A:正平线B:侧平线C:水平线D:铅垂线答案:C3.下图立体中平面A为何种位置平面？A:正垂面B:水平面C:侧垂面D:一般位置平面答案:A4.三角形平面的三个投影均为缩小的类似形，该平面为( )A:正平面B:一般位置平面C:侧平面D:水平面答案:B5.下图中，点K在直线AB上。

这个说法是否正确？A:错B:对答案:A6.下图中，最前点和最高点分别是（）A:C点和B点B:A点和B点C:A点和C点D:B点和A点答案:C7.只凭一个投影不能唯一确定的表达物体的形状。

这个说法是否正确？A:对B:错答案:A8.立体的三视图需要满足以下的投影关系：俯、左视图长对正；主、左视图高平齐；主、俯视图宽相等。

这个说法是否正确？A:对B:错答案:B9.下图中A、B两点的相对位置为（）A:B点在A点的左方、后方和下方B:B点在A点的右方、后方和下方C:B点在A点的左方、前方和下方D:B点在A点的右方、后方和上方答案:C10.直角三角形法求实长时，直角三角形的四要素为实长、坐标差、投影长和倾角，只要已知其中两个要素就可以求得另外两个要素。

这个说法是否正确？A:对B:错答案:A11.下图中已知平面ABC以及平面外的直线MN和FG的两面投影，且f’g’//c’e’，fg//ce，m’n’//b’d’，则平面ABC是否与直线MN和直线FG分别平行？（）A:平面ABC与直线MN和直线FG都不平行B:平面ABC与直线MN和直线FG都平行C:平面ABC与直线MN不平行，与直线FG平行D:平面ABC与直线MN平行，与直线FG不平行答案:C12.试判定A、B两点是否在下列平面内。

关键词：直线实长；直角三角形法则；坐标差；夹角；圆的特性
0 引言
在建筑工程中，对于任何构件的施工都应该按照实际的尺寸进行，但由于建 筑图样通常是按照多面正投影图进行绘制，图样放置的位置与投影面的关系不同， 所以在图纸中不一定反映的均为实长。同时对于建筑工人来讲尽管实践动手能力 比较强，但整体专业理论水平还是比较欠缺的特点，这就要求我们专业技术人员 将这一部分尺寸明确标注，方便应用于工程实践。
出直线 AB 的实长及对 H 面和 V 面的倾角α和β。 对于γ的作图过程应仅仅看作是纯求解的过程，不涉及投影的问题，那么根
据图 1 可知，知道 H、V 两面投影，即可知△x、△y、△z，而所求的的 AB 实长， 可以作为下面求解其他未知量的已知条件来进行使用，在直角三角形中，已知一 条直角边和一条斜边，可以利用直角三角形法则求出其他的未知量。
参考文献 [1]宋艳，慕雪.建筑工程制图与识图[M].哈尔滨：哈尔滨工业大学出版社，2016 [2]莫章金，李瑞鸽.画法几何与建筑制图[M].重庆：重庆大学出版社，2010 [3]王宇亮，周成才.建筑工程制图与识图[M].广州：华南理工大学出版社，2015
作者简介：宋艳（1977- ），女，青岛黄海学院建筑工程学院，副教授，主要研究方向：建筑工程。
作 AB0∥ab，构成直角三角形 ABB0。该直角三角形的一条直角边 AB0 的长度等于 水平投影 ab，
另一直角边 BB0 是线段 AB 两端点高度方向的坐标差ΔZ=ZA-ZB，斜边 AB 与直 角边 AB0 的夹角为直线 AB 对 H 面的倾角α。用相同的方法也可求得直线对 V 面 的倾角β及线段的实长，直线对 W 面的倾角γ及线段的实长。
的交点，则直角三角形也构筑完成，同理可得到线段 AB 与△x 所夹的角即为γ。

直角三角形法求实长的应用摘要】直线对投影面的相对位置有一般位置和特殊位置。

处于特殊位置的直线称为特殊位置直线，特殊位置直线有两种，即投影面的垂直线和投影面的平行线。

直线与三个投影面都倾斜，称为一般位置直线，其三面投影的投影特点为：直线的三面投影相对于各投影轴而言均为斜线，直线的投影长度均小于实长且没有积聚性，直线的投影不反映直线对投影面倾角的真实大小。

特殊位置直线如投影面的垂直线和投影面的平行线可由投影图直接定出直线段的实长和对投影面的倾角。

对一般位置直线来说，其实长和倾角不能直接在投影图中定出，可根据投影用作图的方法来求得，这种方法是直角三角形法。

【关键词】直线位置；投影；实长一、直角三角形法的作图要领用线段在某一投影面上的投影长作为一条直角边，再以线段的两端点相对于该投影面的坐标差作为另一条直角边，所作直角三角形的斜边即为线段的实长，斜边与投影长间的夹角即为线段与该投影面的夹角。

二、直角三角形法的四个要素即：实长、投影长、坐标差及直线对投影面的倾角。

已知四要素中的任意两个，便可确定另外两个。

解题时，直角三角形画在任何位置，都不影响解题结果。

但用哪个长度来作直角边不能搞错。

三、直角三角形法的作图原理1.求直线的实长及对水平投影面的夹角α角2.求直线的实长及对正面投影面的夹角β角3.求直线的实长及对侧面投影面的夹角γ角从上图可以看出在哪个投影面上作直角三角形，其斜边是实长，一个直角边是该投影面所没有的坐标的坐标差，另一个直角边等于直线的水平投影长。

四、应用1.已知AB线段的正面投影和对V面的倾角β=30°，补全其水平投影。

（用直角三形法作图求解）分析：用直角三角形法在V面找到AB的Y坐标差，从而找到点B在H面的位置。

答案：2.求点A到直线CD的垂直距离。

(提示:CD直线是水平线，水平投影为CD直线实长)分析：相互垂直的两直线的投影特性，两直线同时平行于某一投影面时，在该投影面上的投影反映直角（直角定理）；两直线中有一条平行于某一投影面时，在该投影面上的投影反映直角；两直线均为一般位置直线时，在三个投影面上的投影都不反映直角。

用直角三角形法求直线的实长和倾角用直角三角形法求直线的实长和倾角1. 引言在几何学中，直角三角形是最基本的三角形之一，它的特点是其中一个角度为90度。

直角三角形的重要性在于它的应用广泛，包括测量建筑物高度、计算斜坡的倾斜度以及设计工程等。

在本文中，我们将介绍如何使用直角三角形法来求解直线的实长和倾角，帮助读者更好地理解和应用直角三角形的概念和原理。

2. 什么是直角三角形法直角三角形法是一种基于直角三角形特性的求解方法，用于计算实线长和倾角。

在直角三角形中，有三个基本要素：直角边（垂直于直角的边）、斜边（与直角不相邻的边）和另一个边。

根据直角三角形的定义，我们可以利用这些要素来求解我们关心的问题。

3. 如何使用直角三角形法求解直线的实长我们需要确认我们具有足够的已知信息以便应用直角三角形法来求解实线长。

至少需要已知两个要素，其中一个必须是直角边或斜边。

我们可以利用勾股定理来求解未知要素。

为了更好地展示直角三角形法的应用，我们假设我们要求解一个直线的实长，并已知该直线与地面的夹角为45度，距离地面50米。

根据直角三角形的定义，我们可以将这个问题转化为一个直角三角形问题。

我们可以将直角边定义为地面，斜边定义为直线，另一个边定义为垂直于地面的高度。

利用勾股定理，在已知直角边距离地面的长度为50米的情况下，我们可以计算出斜边的长度为70.71米（根号下（50^2+50^2）=70.71）。

根据直角三角形法，该直线的实长为70.71米。

4. 如何使用直角三角形法求解直线的倾角除了求解实线长外，直角三角形法还可以用于计算直线的倾角。

倾角是指直线与水平线之间的夹角。

对于确定了实线长和直角边的情况，我们可以使用反正切函数来计算倾角。

假设我们要求解一个实线长为70.71米的直线，与水平线的夹角为45度。

我们可以将直线定义为斜边，直角边定义为水平线。

通过应用反正切函数，我们可以计算出该直线与水平线之间的倾角为45度（tan^-1(1)=45度）。

直角三角形是几何学中的一个重要概念，它可以帮助我们求解直线的实长和线面夹角。

在本文中，我将从深度和广度的角度对这个主题进行全面评估，并撰写一篇有价值的文章，帮助您更深入地理解直角三角形法求直线实长及线面夹角。

1. 直角三角形的定义直角三角形是指其中一个角为90度的三角形。

根据勾股定理，直角三角形的边长关系为a²+b²=c²，其中c为斜边的长度，a和b分别为两条直角边的长度。

这个定理为我们求解直线实长提供了重要的数学工具。

2. 直线实长的求解在地理测量、建筑设计等领域，我们经常需要求解直线的实际长度。

通过利用直角三角形的性质，我们可以利用三角函数来计算直线的实长。

具体而言，我们可以利用正弦、余弦、正切函数来求解直线的实际长度，其中前两个函数分别适用于已知角度和斜边长度、已知一条直角边和斜边长度的情况，而正切函数适用于已知两条直角边长度的情况。

这些方法可以帮助我们准确地测量直线的实际长度。

3. 线面夹角的求解另一个常见的问题是求解线面夹角，即一条直线与一个平面之间的夹角。

同样地，利用直角三角形的性质，我们可以利用三角函数来计算线面夹角。

根据不同情况，我们可以利用正弦、余弦、正切函数来求解线面夹角，以及利用反三角函数来求解。

这些方法可以帮助我们准确地测量线面夹角，为工程设计和日常生活中的问题提供重要的数学支持。

4. 个人观点和理解对我来说，直角三角形法求直线实长及线面夹角是一项非常实用且重要的数学工具。

通过深入理解三角函数和直角三角形的性质，我们可以应用数学知识解决实际问题，为各种领域的工作和生活提供帮助。

在我看来，掌握这些知识不仅可以提高工作效率，还可以培养逻辑思维和解决问题的能力。

在本文中，我通过对直角三角形法求直线实长及线面夹角的深度和广度评估，希望能够帮助您更深入地理解这个重要的数学工具。

通过掌握这些知识，我们可以更准确地计算直线的实际长度和线面夹角，为工程设计和测量提供重要的支持。

直角三角形法求直线实长及线面夹角直线实长和线面夹角是在几何学中常见的概念，而直角三角形法则是一种用于求解这些问题的便捷方法。

通过这种方法，我们可以利用直角三角形的特性来确定直线的实际长度，以及线面夹角的大小。

在几何学中，直线实长指的是线段的真实长度，而线面夹角则是两条线之间的夹角。

这些概念常常在工程、建筑和地理测量等领域中得到广泛的应用。

了解如何利用直角三角形法则来求解这些问题是非常重要的。

让我们来了解一下直角三角形法则的基本原理。

直角三角形指的是具有一个90度角的三角形。

根据直角三角形的特性，我们可以利用三角函数来求解各种问题。

其中，最常用的三角函数包括正弦、余弦和正切。

假设我们需要求解一条直线的实际长度，我们可以利用直角三角形法则中的正切函数来实现。

我们需要测量线段的水平距离和竖直高度，然后利用这些数据来计算实际长度。

假设直线的水平距离为a，竖直高度为b，则直线的实际长度L可以通过以下公式来计算：L = b / tan(θ)其中，θ为直线与水平线之间的夹角。

通过以上公式，我们可以轻松求解直线的实际长度，而不需要直接测量整条直线。

除了求解直线实长，直角三角形法则还可以帮助我们求解线面夹角的大小。

假设我们需要求解两条线之间的夹角，我们同样可以利用正切函数来实现。

假设两条线之间的水平距离为c，竖直高度为d，则线面夹角的大小可以通过以下公式来计算：θ = arctan(d / c)通过以上公式，我们可以轻松求解线面夹角的大小，而不需要直接测量夹角。

直角三角形法则是一种非常实用的方法，可以帮助我们求解直线的实际长度和线面夹角的大小。

通过利用直角三角形的特性和三角函数，我们可以轻松地应用这种方法来解决各种几何学问题。

在我个人的观点和理解中，直角三角形法则是一种非常重要的工具，可以帮助我们在实际应用中更快捷、准确地求解各种几何学问题。

无论是在工程测量、建筑设计还是地理勘测中，直角三角形法则都具有非常广泛的应用前景。

一、组织教学按时带领学‎生进入教室‎，检查学生的‎考勤情况、学生佩戴标‎志牌情况，衣着安全情‎况二、课题引入：由上图可见‎，一般位置直‎线的三面投‎影都不反映‎实长,在这种情况‎下，就要运用投‎影的改造的‎方法，来求出一般‎位置直线段‎的实长,才可以进一‎步对构件的‎展开。

三、授课内容课题八；展开放样（一） §2线段实长‎求线段实长作展开图该图有（8）个顶点：分别为1；2；3；4；5；6；7；8；有（16）条线：分别为1-2；1-4；1-5；1-8；2-3；2-5；2-6；3-4； 3-6；3-7；4-7；4-8；5-6；5-8；6-7；7-8垂直线有：1-2；1-4；2-3；3-4；5-8；6-7平行线 ：没有一般位置直线有：1-5和4-8相等；2-6和3-7相等； 5-6和7-8相等；1-8；2-5；3-6；4-7（需求实长）1 2 3 4 5 6 7 8 1（4） 2（3） 5（8） 6（7） 1（2） 4（3） 5 6 7 8§2-2求线段实‎长（直角三角形‎）在构件的展‎开图上，所有图线（如轮廓线、棱线、辅助线等）都是构件表‎面上对应线‎段的实长线‎。

然而，并非构件所‎有线段在图‎样中都反映‎实长，因此，必须能够正‎确判断线段‎的投影是否‎为实长，并掌握求线‎段实长的一‎些方法。

求线段实长‎的方法：1、直角三角形‎法2、旋转法3、换面法一、直角三角形‎法下图所示为‎一般位置直‎线段AB 的‎直观图。

现在分析线‎段和它的投‎影之间的关‎系，以寻找求线‎段实长的图‎解方法。

过点A 作A ‎C ∥ab ，构成直角三‎角形ABC ‎，其斜边AB ‎是空间线段‎的实长。

两直角边的‎长度可在投‎影图上量得‎：一直角边A ‎C 的长度等‎于线段的水‎平投影 ab ；另一直角边‎B C 是线段‎两端点A 、B 距水平投‎影面的距离‎之差，其长度等于‎正面投影b ‎′c ′。

注意：根据实际需‎要，此法也可以‎在投影图外‎作图。