全等三角形压轴题精选(1)(最新整理)
- 格式:pdf
- 大小:182.28 KB
- 文档页数:6
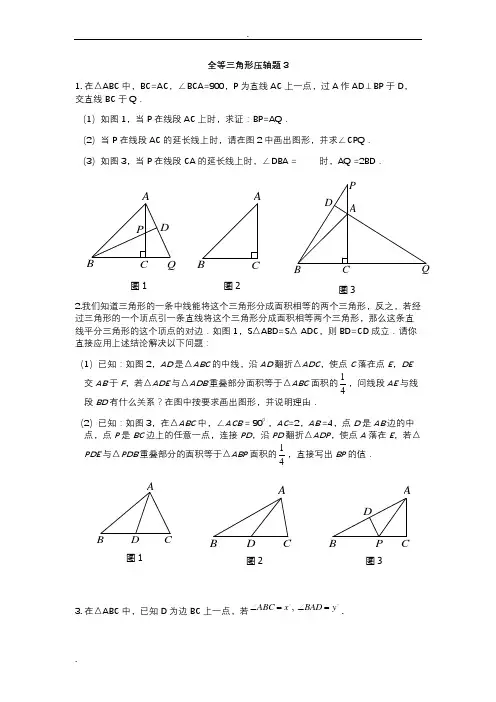
..全等三角形压轴题 31. 在△ABC 中,BC=AC ,∠BCA=900,P 为直线AC 上一点,过A 作AD ⊥BP 于D ,交直线BC 于Q .(1)如图1,当P 在线段AC 上时,求证:BP=AQ .(2)当P 在线段AC 的延长线上时,请在图2中画出图形,并求∠CPQ . (3)如图3,当P 在线段CA 的延长线上时,∠DBA = 时,AQ =2BD .2.我们知道三角形的一条中线能将这个三角形分成面积相等的两个三角形,反之,若经过三角形的一个顶点引一条直线将这个三角形分成面积相等两个三角形,那么这条直线平分三角形的这个顶点的对边.如图1,S △ABD=S △ ADC ,则BD=CD 成立.请你直接应用上述结论解决以下问题:(1)已知:如图2,AD 是△ABC 的中线,沿AD 翻折△ADC ,使点C 落在点E ,DE 交AB 于F ,若△ADE 与△ADB 重叠部分面积等于△ABC 面积的14,问线段AE 与线段BD 有什么关系?在图中按要求画出图形,并说明理由.(2)已知:如图3,在△ABC 中,∠ACB = 900 ,AC =2,AB =4,点D 是AB 边的中点,点P 是BC 边上的任意一点,连接PD ,沿PD 翻折△ADP ,使点A 落在E ,若△PDE 与△PDB 重叠部分的面积等于△ABP 面积的14,直接写出BP 的值.3. 在△ABC 中,已知D 为边BC 上一点,若,ABC x BAD y ∠=∠=.QCBPDA BAQB P DACB DAACB DAPDCBA备用图N M C AB N MC DA B 图 1B AQDC M PG图 2N F E (1)当D 为边BC 上一点,并且CD=CA ,40x =,30y =时,则AB _____ AC (填“=”或“≠”);(2)如果把(1)中的条件“CD=CA ”变为“CD=AB ”,且x,y 的取值不变,那么(1)中的结论是否仍成立?若成立请写出证明过程,若不成立请说明理由;(3)若CD= CA =AB ,请写出y 与x 的关系式及x 的取值围. (不写解答过程,直接写出结果)4. 在Rt △ABC 中,AC=BC ,P 是BC 垂直平分线MN 上一动点,直线PA 交CB 于点E ,F 是点E 关于MN 的对称点,直线PF 交AB 于点D ,连接CD 交PA 于点G. (1)如图1,若P 点在△ABC 的边BC 上时,此时点P 、E 、F 重合,线段AP 上的点Q 关于的对称点D 恰好在边AB 上,连接CQ ,求证:CQ 平分∠ACB ; (2)如图2,若点P 移到BC 上方,且∠CAP=22.5°,求∠CDP 的度数;(3)若点P 移动到△ABC 的部时,线段AE 、CD 、DF 有什么确定的数量关系,请画出图形,并直接写出结论: .5. 如图1,已知A (a ,0),B (0,b )分别为两坐标轴上的点,且a 、b 满足221212720a b a b +--+=,OC ∶OA=1∶3. (1)求A 、B 、C 三点的坐标;DCBA..ADCBEEBCGFDA(2)若D (1,0),过点D 的直线分别交AB 、BC 于E 、F 两点,设E 、F 两点的横坐标分别为E F x x 、.当BD 平分△BEF 的面积时,求E F x x +的值;(3)如图2,若M (2,4),点P 是x 轴上A 点右侧一动点,AH ⊥PM 于点H ,在HM 上取点G ,使HG=HA ,连接CG ,当点P 在点A 右侧运动时,∠CGM 的度数是否改变?若不变,请求其值;若改变,请说明理由.6. 如图,点D 、E 分别在等边△ABC 的AB 、AC 上,且CD >BD ,AE >EC ,AD 和BE 相交于点F..(1)若∠BAD=∠CBE ,则AD BE ;(填“>”、“=”、“<”) (2)若AD=BE ,求证:∠BAD=∠CBE ;(3)在(2)的条件下,以AB 为边作如图所示的等边△ABG ,连接FG ,若FG=11,BF=3,请直接写出线段AF 的长度为 .7. 如图1,已知A (a ,0),B (0,b ).(1)当a 、b 满足2288320a a b b -+-+=时,求∠BAO 的度数;(2)如图1,在(1)的条件下,点C 为线段AB 上一点(BC >CA ),以点C 为直角顶点,OC 为腰作等腰Rt △OCD ,连接BD ,求证:∠BDO=∠BCO ;A BCO yOxyx图 1图 2QF EDB A(3)如图2,△ABO 的两条角平分线AE 、BF 交于点Q ,若△ABQ 的面积为24,求四边形AFEB 的面积.8. 已知:点A 、C 分别是∠B 的两条边上的点,点D 、E 分别是直线BA 、BC 上的点,直线AE 、CD 相交于点P(1) 点D 、E 分别在线段BA 、BC 上① 若∠B =60°(如图1),且AD =BE ,BD =CE ,则∠APD 的度数为___________ ② 若∠B =90°(如图2),且AD =BE ,BD =CE ,求∠APD 的度数(2) 如图3,点D 、E 分别在线段AB 、BC 的延长线上,若∠B =90°,AD =BC ,∠APD =45°,求证:BD =CE9. 已知A(a ,0)、B(0,b),且满足2a2+b2+4a -4b =-6,以A 为直角顶点,且以AB 为腰作等腰直角△ABC (1) 求C 点的坐标(2) 如图,若点C 在第二象限,点M 在BC 的延长线上,且AM =AN ,AM ⊥AN ,则CM 与BN 存在怎样的关系?请予以证明.(3) 如图,若点C在第二象限,以AB为边在直线AB的另一侧做等边△ABD,连接CD,过A作AF⊥BC于F,AF与CD交于点E,试判断线段CE、AE、CD 之间存在何种数量关系,并证明你的结论10.如图(1),已知A(0,a),B(b,0),且a,b满足a2+2ab+b2+(b+3)2=0,D为x轴上B点左边一动点,连AD,过A作AE⊥AD交x轴于F,且AE=AD,连BE交y轴于点P.(1) 求∠ABO的度数;(2)若AO=3OP,求E点的坐标;(3)如图(2)若C为线段BF(靠近B)的一个三等分点,且∠ACO=600,试求∠AFB的度数。
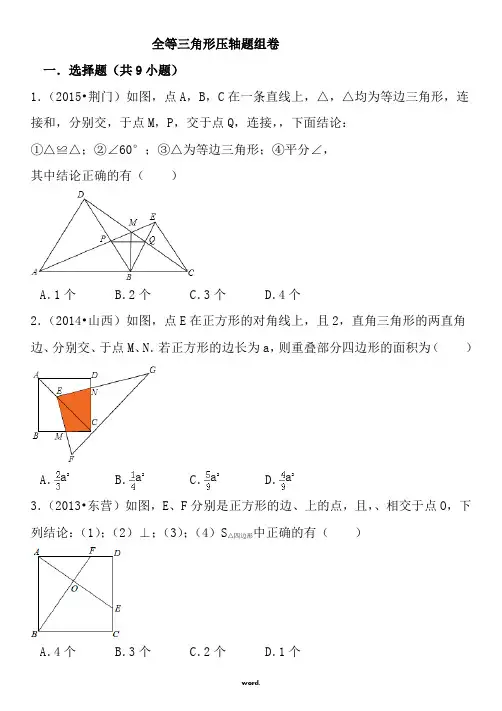
全等三角形压轴题组卷一.选择题(共9小题)1.(2015•荆门)如图,点A,B,C在一条直线上,△,△均为等边三角形,连接和,分别交,于点M,P,交于点Q,连接,,下面结论:①△≌△;②∠60°;③△为等边三角形;④平分∠,其中结论正确的有()A.1个B.2个C.3个D.4个2.(2014•山西)如图,点E在正方形的对角线上,且2,直角三角形的两直角边、分别交、于点M、N.若正方形的边长为a,则重叠部分四边形的面积为()A.a2B.a2C.a2D.a23.(2013•东营)如图,E、F分别是正方形的边、上的点,且,、相交于点O,下列结论:(1);(2)⊥;(3);(4)S△四边形中正确的有()4.(2012•长春)如图,在平面直角坐标系中,在x轴、y轴的正半轴上分别截取、,使;再分别以点A、B为圆心,以大于长为半径作弧,两弧交于点C.若点C的坐标为(m﹣1,2n),则m与n的关系为()A.21 B.m﹣21 C.2n﹣1 D.n﹣215.(2012•山西模拟)如图,点P、Q是边长为4的等边△边、上的动点,点P 从顶点A,点Q从顶点B同时出发,且它们的速度都为1,连接、交于点M,则在P、Q运动的过程中,下列结论错误的是()A.B.△≌△C.∠的度数不变,始终等于60°D.当第秒或第秒时,△为直角三角形6.(2012•镇平县校级一模)如图,在△中,∠90°,平分∠,⊥于D,如果3,那么等于()A.2B.3C.4D.57.(2011•恩施州)如图,是△的角平分线,⊥,垂足为F,,△和△的面积分别为50和39,则△的面积为()A.11 B.5.5 C.7D.3.58.(2010•武汉模拟)如图,△中,∠、∠的角平分线、交于点P,下列结论:①平分∠;②∠∠180°;③若点M、N分别为点P在、上的正投影,则;④∠2∠.其中正确的是()A.只有①②③B.只有①③④C.只有②③④D.只有①③9.(2004•内江)如图,∠30°,平分∠,∥,⊥,如果6,那么等于()二.填空题(共5小题)10.(2015•眉山)如图,以△的三边为边分别作等边△、△、△,则下列结论:①△≌△;②四边形为平行四边形;③当,∠120°时,四边形是正方形.其中正确的结论是.(请写出正确结论的番号).11.(2015•广西)如图,在△中,平分∠交于点D,⊥交于点E,⊥于点F,且4,2,则△的面积是.12.(2011•随州)如图,△的外角∠的平分线与内角∠平分线交于点P,若∠40°,则∠.13.(2011•杭州校级模拟)如图,在平面直角坐标系中,矩形的两边分别在x轴和y轴上,10,6.F是线段上的动点,从点O出发,以1的速度沿方向作匀速运动,点Q在线段上.已知A、Q两点间的距离是O、F两点间距离的a倍.若用(a,t)表示经过时间t(s)时,△、△、△中有两个三角形全等.请写出(a,14.(1999•重庆)如图,△中,,∠40°,,,则∠度.三.解答题(共12小题)15.(2015•于洪区一模)如图1,在△中,∠为锐角,点D为射线上一点,连接,以为一边且在的右侧作正方形.(1)如果,∠90°,①当点D在线段上时(与点B不重合),如图2,线段、所在直线的位置关系为,线段、的数量关系为;②当点D在线段的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;(2)如果≠,∠是锐角,点D在线段上,当∠满足什么条件时,⊥(点C、F不重合),并说明理由.16.(2014•绍兴)(1)如图1,正方形中,点E,F分别在边,上,∠45°,延长到点G,使,连结,.求证:.(2)如图,等腰直角三角形中,∠90°,,点M,N在边上,且∠45°,若1,3,求的长.17.(2013•东营)(1)如图(1),已知:在△中,∠90°,,直线m经过点A,⊥直线m,⊥直线m,垂足分别为点D、E.证明:.(2)如图(2),将(1)中的条件改为:在△中,,D、A、E三点都在直线m上,并且有∠∠∠α,其中α为任意锐角或钝角.请问结论是否成立?如成立,请你给出证明;若不成立,请说明理由.(3)拓展与应用:如图(3),D、E是D、A、E三点所在直线m上的两动点(D、A、E三点互不重合),点F为∠平分线上的一点,且△和△均为等边三角形,连接、,若∠∠∠,试判断△的形状.18.(2013•昭通)已知△为等边三角形,点D为直线上的一动点(点D不与B、C重合),以为边作菱形(A、D、E、F按逆时针排列),使∠60°,连接.(1)如图1,当点D在边上时,求证:①;②;(2)如图2,当点D在边的延长线上且其他条件不变时,结论是否成立?若不成立,请写出、、之间存在的数量关系,并说明理由;(3)如图3,当点D在边的延长线上且其他条件不变时,补全图形,并直接写出、、之间存在的数量关系.19.(2013秋•广州校级期中)在等边△的两边、所在直线上分别有两点M、N,D 为△外一点,且∠60°,∠120°,.探究:当M、N分别在直线、上移动时,、、之间的数量关系及△的周长Q与等边△的周长L的关系.(1)如图1,△是周长为9的等边三角形,则△的周长;(2)如图2,当点M、N边、上,且时,、、之间的数量关系是;此时= ;(3)点M、N在边、上,且当≠时,猜想(2)问的两个结论还成立吗?写出你的猜想并加以证明.20.(2012•昌平区模拟)(1)如图,在四边形中,,∠∠90°,E、F分别是边、上的点,且∠∠.求证:;(2)如图,在四边形中,,∠∠180°,E、F分别是边、上的点,且∠∠,(1)中的结论是否仍然成立?(3)如图,在四边形中,,∠∠180°,E、F分别是边、延长线上的点,且∠∠,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.21.(2011•绍兴)数学课上,李老师出示了如下框中的题目.小敏与同桌小聪讨论后,进行了如下解答:(1)特殊情况•探索结论当点E为的中点时,如图1,确定线段与的大小关系.请你直接写出结论:(填“>”,“<”或“=”).(2)特例启发,解答题目解:题目中,与的大小关系是:(填“>”,“<”或“=”).理由如下:如图2,过点E作∥,交于点F,(请你完成以下解答过程)(3)拓展结论,设计新题在等边三角形中,点E在直线上,点D在直线上,且.若△的边长为1,2,求的长(请你直接写出结果).22.(2010•长春)如图,△中,,延长至D,使,点E在边上,以,为邻边做▱,过点C作∥交于点G,连接,.(1)∠与∠有怎样的数量关系?请说明理由;(2)求证:△≌△.23.(2007•常州)已知,如图,延长△的各边,使得,,顺次连接D,E,F,得到△为等边三角形.求证:(1)△≌△;(2)△为等边三角形.24.(2007•牡丹江)已知四边形中,,∠120°,∠60°,∠绕B点旋转,它的两边分别交,(或它们的延长线)于E,F.当∠绕B点旋转到时(如图1),易证;当∠绕B点旋转到≠时,在图2和图3这两种情况下,上述结论是否成立?若成立,请给予证明;若不成立,线段,,又有怎样的数量关系?请写出你的猜想,不需证明.25.(2005•扬州)(本题有3小题,第(1)小题为必答题,满分5分;第(2)、(3)小题为选答题,其中,第(2)小题满分3分,第(3)小题满分6分,请从中任选1小题作答,如两题都答,以第(2)小题评分.)在△中,∠90°,,直线经过点C,且⊥于D,⊥于E.(1)当直线绕点C旋转到图1的位置时,求证:①△≌△;②;(2)当直线绕点C旋转到图2的位置时,求证:﹣;(3)当直线绕点C旋转到图3的位置时,试问、、具有怎样的等量关系?请写出这个等量关系,并加以证明.注意:第(2)、(3)小题你选答的是第2小题.最新文件仅供参考已改成word文本。


人教版数学八年级上册第十二章全等三角形压轴题训练1.已知,是等腰直角三角形,,点在轴负半轴上,直角顶点在轴上,点在轴左侧.如图,若的坐标是,点的坐标是,求点的坐标;如图,若点的坐标为,与轴交于点,求线段的长;如图,若轴恰好平分,与轴交于点,过点作轴于点,则、、间有怎样的数量关系?并说明理由.2.如图,在平面直角坐标系中,直线分别交轴、轴于、两点,且,满足,且,是常数.直线平分,交轴于点.若的中点为,连接交于,求证:;如图,过点作,垂足为,猜想与间的数量关系,并证明你的猜想;如图,在轴上有一个动点在点的右侧,连接,并作等腰,其中,连接并延长交轴于点,当点在运动时,的长是否发生改变?若改变,请求出它的变化范围;若不变,求出它的长度.3.如图,点,分别在直线,上,,顶点在点右侧的两边分别交线段于,直线于,,,交直线于点.若平分,求证:;已知的平分线与的平分线交于点请把图形补完整,并证明:.4.解答下列问题:如图,,射线在这个角的内部,点、分别在的边、上,且,于点,于点求证:如图,点、分别在的边、上,点、都在内部的射线上,、分别是、的外角已知,且求证:如图,在中,,点在边上,,点、在线段上,若的面积为,求与的面积之和.5.在平面直角坐标系中,直线与两坐标轴分别交于点与点,以为边作直角三角形,并且.如图,若点在第三象限,请构造全等,求出点的坐标;若点不在第三象限,请直接写出所有满足条件的点的坐标;在的条件下,过点作交轴于点,求证:.6.已知,点在上以的速度由点向点运动,同时点在上由点向点运动.它们运动的时间为.如图,,,若点的运动速度与点的运动速度相等,当时,与是否全等,请说明理由,并判断此时线段和线段的位置关系;如图,将图中的“,”为改“”,其他条件不变.设点的运动速度为,是否存在实数,使得与全等?若存在,求出相应的、的值;若不存在,请说明理由.7.如图,点,将一个的角尺的直角顶点放在点处,角尺的两边分别交轴、轴正半轴于,即,求证:平分;作的平分线交于点,过点作轴于,求的值;把角尺绕点旋转时,的值是否会发生变化?若发生变化请说明理由;若不变请求出这个值.8.画,并画的平分线.图图图将一块足够大的三角尺的直角顶点落在射线的任意一点上,并使三角尺的一条直角边与垂直,垂足为点,另一条直角边与交于点如图证明:;把三角尺绕点旋转,三角尺的两条直角边分别交、于点、如图,与相等吗?请直接写出结论:_____填,,;若点在的反向延长线上,其他条件不变如图,与相等吗?若相等请进行证明,若不相等请说明理由.9.如图,,点是的中点,直线于点,点在直线上,直线点以每秒个单位长度的速度,从点沿路径向终点运动,运动时间设为秒.如图,当时,作直线于点,此时与全等吗请说明理由.如图,当点在上时,作于点,于点.是否存在或与全等的时刻若存在,求出的值若不存在,请说明理由.连接,当时,求的长.10.如图,已知在四边形中,,点、分别是边、上的点,连接、、,.直接写出、、三者之间的数量关系____________________;若,猜想线段、、三者之间有怎样的数量关系?并加以证明;如图,若点、分别是、延长线上的点,且,其它条件不变时,猜想线段、、三者之间有怎样的数量关系?并加以证明.11.如图:在四边形中,,,,,分别是,上的点,且探究图中线段,,之间的数量关系。

全等三角形压轴题精选全等三角形压轴题精选全等三角形是初中数学中重要的一个概念,也是数学竞赛中常考的知识点。
全等三角形具有相等的所有对应边和对应角,它们可以完全重合,只是位置和方向可能不同。
全等三角形的性质和应用十分广泛。
本文将介绍几个全等三角形的精选题目,帮助读者加深对全等三角形的理解和应用。
题目一:相似还是全等?某个三角形ABC和三角形XYZ的三边分别相等,角度分别相等,那么这两个三角形是相似的还是全等的?解析:根据题目条件,三角形ABC和三角形XYZ既有边长相等又有角度相等,由全等三角形的性质可知,这两个三角形是全等的。
因为全等三角形除了对应边和对应角相等外,还要求对应顶点相同,位置和方向也要相同。
题目二:全等图形存在的必要条件是什么?请阐述全等图形存在的必要条件,并证明这一结论。
解析:全等图形存在的必要条件是:对于两个图形A和B,如果它们是全等的,那么它们的对应边和对应角必须相等。
证明如下:设图形A和B是全等的,记作A ≌B。
由全等三角形的定义可知,图形A的一个顶点经过平移、翻转、旋转等运动变换后能够与图形B完全重合。
因此,图形A和图形B对应的边必须相等。
同时,图形A和图形B对应的角也必须相等。
假设图形A的一个内角a对应于图形B的一个内角b,如果a ≠ b,那么通过平移、翻转、旋转等运动变换,图形A将无法与图形B完全重合。
因此,图形A和图形B对应的角必须相等。
综上所述,全等图形存在的必要条件是对应边和对应角相等。
题目三:利用全等三角形证明线段之间的比例关系已知在三角形ABC中,线段AD和线段BE是各边上的中线,且交于点O。
利用全等三角形的性质,证明线段DO与线段EO的比值为1:2。
解析:首先,我们在图形ABC上标出线段AD和线段BE的中点分别为M和N。
由线段AD是边AB的中线,可知线段AM = MD;同理,线段BN = NE。
接下来,我们观察三角形AMO和三角形BNO。
根据全等三角形的性质,如果能够证明这两个三角形全等,那么可以得出线段MO和线段NO的比值为1:1,进而推导出线段DO和线段EO的比值。

八年级上册全等三角形压轴题一、题目1. 如图,在△ABC中,∠ACB = 90°,AC = BC,E为AC边的中点,过点A作AD ⊥AB交BE的延长线于点D,CG平分∠ACB交BD于点G,F为AB边上一点,连接CF,且∠ACF =∠CBG。
(1)求证:AF = CG;(2)若AG = 6,求BD的长。
二、解析(1)证明AF = CG在△ACF和△CBG中:已知∠ACF =∠CBG(题目所给条件)。
因为AC = BC(题目中已知△ABC是等腰直角三角形,∠ACB = 90°,AC = BC)。
由于∠ACB = 90°,CG平分∠ACB,所以∠BCG=45°。
又因为△ABC是等腰直角三角形,∠CAB =∠CBA = 45°,所以∠CAF =∠BCG。
根据“角边角”(ASA)全等判定定理,可得△ACF≌△CBG。
全等三角形对应边相等,所以AF = CG。
(2)求BD的长因为E为AC中点,AC = BC,设AC = BC = 2a,则CE=a。
由∠ACB = 90°,AD⊥AB,可得∠DAB = 90°。
又因为∠AEB+∠CBE = 90°,∠D+∠DBE = 90°(直角三角形两锐角互余),且∠AEB =∠DEB(对顶角相等),所以∠D =∠CBE。
在△BCE和△ACD中:∠D =∠CBE(已证)。
∠BCE =∠ACD = 90°。
BC = AC(已知)。
根据“角角边”(AAS)全等判定定理,可得△BCE≌△ACD。
所以AD = CE=a。
由(1)知△ACF≌△CBG,所以CF = BG。
因为CG平分∠ACB,∠ACB = 90°,所以∠BCG = 45°,又∠CBA = 45°,所以△BCG是等腰直角三角形,BG = CG。
又因为AF = CG,设AF = x,则BG = CG=x,AB=公式,BF = 2\sqrt{2}a x。

全等三角形压轴题1.如图,已知BD⊥DE,CE⊥DE,垂足分别是D、E,AB=AC,∠BAC=90°,试探索DE、BD、CE长度之间的关系,并说明你的结论的正确性.2.已知四边形ABCD中,AB=AD,AB⊥AD,连接AC,过点A作AE⊥AC,且使AE=AC,连接BE,过A作AH⊥CD于H交BE于F.如图1,当E在CD的延长线上时,求证:①△ABC≌△ADE;②BF=EF;3.如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.4.已知:△ABC中,BD、CE分别是AC、AB边上的高,BQ=AC,点F在CE 的延长线上,CF=AB,求证:AF⊥AQ.5.阅读下题及证明过程:已知:如图,D是△ABC中BC边上一点,E是AD上一点,EB=EC,∠ABE=∠ACE,求证:∠BAE=∠CAE.证明:在△AEB和△AEC中,∵EB=EC,∠ABE=∠ACE,AE=AE,∴△AEB≌△AEC…第一步∴∠BAE=∠CAE…第二步问上面证明过程是否正确?若正确,请写出每一步推理的依据;若不正确,请指出错在哪一步,并写出你认为正确的证明过程.6.如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为____,线段CF、BD的数量关系为____;②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;7.一节数学课后,老师布置了一道课后练习题:如图,已知在Rt△ABC中,AB=BC,∠ABC=90°,BO⊥AC于点O,点P、D分别在AO和BC上,PB=PD,DE⊥AC于点E,求证:△BPO≌△PDE.(1)理清思路,完成解答(2)本题证明的思路可用下列框图表示:根据上述思路,请你完整地书写本题的证明过程.(2)特殊位置,证明结论若PB平分∠ABO,其余条件不变.求证:AP=CD.(3)知识迁移,探索新知若点P是一个动点,点P运动到OC的中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系.(不必写解答过程)8.探究问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为_____.拓展问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M 在三角形ABC的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.9.已知:直线a∥b,点A、B在直线a上,点C、D在直线b上,如图(1)若S△CBD=6cm2,则S△ADCcm2(2)若S△AOB=S△COD,那么△ACD≌△DBA吗?说明你的理由.10.(1)如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE =90°.①当点D在AC上时,如图1,线段BD、CE有怎样的数量关系和位置关系?直接写出你猜想的结论;②将图1中的△ADE绕点A顺时针旋转α角(0°<α<90°),如图2,线段BD、CE有怎样的数量关系和位置关系?请说明理由.(2)当△ABC和△ADE满足下面甲、乙、丙中的哪个条件时,使线段BD、CE 在(1)中的位置关系仍然成立?不必说明理由.甲:AB:AC=AD:AE=1,∠BAC=∠DAE≠90°;乙:AB:AC=AD:AE≠1,∠BAC=∠DAE=90°;丙:AB:AC=AD:AE≠1,∠BAC=∠DAE≠90°.11.(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F分别是边1∠BAD.BC、CD上的点,且∠EAF=2求证:EF=BE+FD;(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、1∠BAD,(1)中的结论是否仍然成立?CD上的点,且∠EAF=2(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边1∠BAD,(1)中的结论是否仍然成立?BC、CD延长线上的点,且∠EAF=2若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.12.【问题提出】学习了三角形全等的判定方法(即“SAS”、“ASA”、“AAS”、“SSS”)和直角三角形全等的判定方法(即“HL”)后,我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究.【初步思考】我们不妨将问题用符号语言表示为:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,然后,对∠B进行分类,可分为“∠B是直角、钝角、锐角”三种情况进行探究.【深入探究】第一种情况:当∠B是直角时,△ABC≌△DEF.(1)如图①,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E=90°,根据 _____,可以知道Rt△ABC≌Rt△DEF.第二种情况:当∠B是钝角时,△ABC≌△DEF.(2)如图②,在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是钝角,求证:△ABC≌△DEF.第三种情况:当∠B是锐角时,△ABC和△DEF不一定全等.(3)在△ABC和△DEF,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,请你用尺规在图③中作出△DEF,使△DEF和△ABC不全等.(不写作法,保留作图痕迹)(4)∠B还要满足什么条件,就可以使△ABC≌△DEF?请直接写出结论:在△ABC和△DEF中,AC=DF,BC=EF,∠B=∠E,且∠B、∠E都是锐角,若________,则△ABC≌△DEF.13.问题背景:如图1:在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E,F分别是BC,CD上的点.且∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系.小王同学探究此问题的方法是,延长FD到点G.使DG=BE.连结AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得出结论,他的结论应是______;探索延伸:如图2,若在四边形ABCD中,AB=AD,∠B+∠D=180°.E,F分别是BC,1∠BAD,上述结论是否仍然成立,并说明理由;CD上的点,且∠EAF=2实际应用:如图3,在某次军事演习中,舰艇甲在指挥中心(O处)北偏西30°的A处,舰艇乙在指挥中心南偏东70°的B处,并且两舰艇到指挥中心的距离相等,接到行动指令后,舰艇甲向正东方向以60海里/小时的速度前进,舰艇乙沿北偏东50°的方向以80海里/小时的速度前进.1.5小时后,指挥中心观测到甲、乙两舰艇分别到达E,F处,且两舰艇之间的夹角为70°,试求此时两舰艇之间的距离.14.将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.(1)求证:AF+EF=DE;(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.15.已知:如图所示,直线MA∥NB,∠MAB与∠NBA的平分线交于点C,过点C作一条直线l与两条直线MA、NB分别相交于点D、E.(1)如图1所示,当直线l与直线MA垂直时,猜想线段AD、BE、AB之间的数量关系,请直接写出结论,不用证明;(2)如图2所示,当直线l与直线MA不垂直且交点D、E都在AB的同侧时,(1)中的结论是否成立?如果成立,请证明;如果不成立,请说明理由;(3)当直线l与直线MA不垂直且交点D、E在AB的异侧时,(1)中的结论是否仍然成立?如果成立,请说明理由;如果不成立,那么线段AD、BE、AB 之间还存在某种数量关系吗?如果存在,请直接写出它们之间的数量关系.16.在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.(1)当直线MN绕点C旋转到图1的位置时,求证:①△ADC≌△CEB;②DE=AD+BE;(2)当直线MN绕点C旋转到图2的位置时,求证:DE=AD-BE;(3)当直线MN绕点C旋转到图3的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以证明.。

“全等三角形”压轴题精选11道,含详细解答以微课堂学习资料群奥数国家级教练与四名特级教师联手执教。
八上全等三角形常考压轴题汇总一、如图所示,△ABC≌△ADE,BC的延长线过点E,∠ACB=∠AED=105°,∠CAD=10°,∠B=50°,求∠DEF的度数。
解:∵△ABC≌△AED∴∠D=∠B=50°∵∠ACB=105°∴∠ACE=75°∵∠CAD=10° ∠ACE= 75°∴∠EFA=∠CAD+∠ACE=85°(三角形的一个外角等于和它不相邻的两个内角的和)同理可得∠DEF=∠EFA-∠D=85°-50°=35°二、如图,△AOB中,∠B=30°,将△AOB绕点O顺时针旋转52°,得到△A′OB′,边A′B′与边OB交于点C(A′不在OB上),则∠A′CO的度数为多少?解:∵△A′OB′是由△AOB绕点O顺时针旋转得到,∠B=30°,∴∠B′=∠B=30°,(关注公众号:初一数学语文英语)∵△AOB绕点O 顺时针旋转52°,∴∠BOB′=52°,∵∠A′CO是△B′OC的外角,∴∠A′CO=∠B′+∠BOB′=30°+52°=82°.三、如图所示,在△ABC中,∠A=90°,D、E分别是AC、BC上的点,若△ADB≌△EDB≌△EDC,则∠C的度数是多少?解:∵△ADB≌△EDB≌△EDC,∴∠A=∠DEB=∠DEC,∠ADB=∠BDE=∠EDC,∵∠DEB+∠DEC=180°,∠ADB+∠BDE+EDC=180°,∴∠DEC=90°,∠EDC=60°,∴∠C=180°-∠DEC-∠EDC,=180°-90°-60°=30°.四、如图所示,把△ABC绕点C顺时针旋转35°,得到△A′B′C,A′B′交AC于点D,若∠A′DC=90°,则∠A等于多少?解:∵三角形△ABC绕着点C时针旋转35°,(关注公众号:初一数学语文英语)得到△AB′C′∴∠ACA′=35°,∠A'DC=90°∴∠A′=55°,∵∠A的对应角是∠A′,即∠A=∠A′,∴∠A=55°;故答案为:55°.五、已知,如图所示,AB=AC,(关注公众号:初一数学语文英语)AD⊥BC于D,且AB+AC+BC=50cm,而AB+BD+AD=40cm,则AD 是多少?因为AB=AC 三角形ABC是等腰三角形所以AB+AC+BC=2AB+BC=50BC=50-2AB=2(25-AB)(关注公众号:初一数学语文英语)又因为AD垂直于BC于D,所以BC=2BD,BD=25-ABAB+BD+AD=AB+25-AB+AD=AD+25=40AD=40-25=15cm(关注公众号:初一数学语文英语)六、如图,Rt△ABC中,(关注公众号:初一数学语文英语)∠BAC=90°,AB=AC,分别过点B、C作过点A的垂线BC、CE,垂足分别为D、E,若BD=3,CE=2,则D是多少?解:∵BD⊥DE,CE⊥DE∴∠D=∠E∵∠BAD+∠BAC+∠CAE=180°又∵∠BAC=90°,∴∠BAD+∠CAE=90°∵在Rt△ABD中,∠ABD+∠BAD=90°∴∠ABD=∠CAE(关注公众号:初一数学语文英语)∵在△ABD与△CAE中∠ABD=∠CAE,∠D=∠E,AB=AC∴△ABD≌△CAE(AAS)∴BD=AE,AD=CE∵DE=AD+AE∴DE=BD+CE∵BD=3,CE=2 ∴DE=5七、如图,AD是△ABC的角平分线,DE⊥AB,DF⊥AC,垂足分别是E、F,连接EF,交AD于G,AD与EF垂直吗?证明你的结论。

初二全等三角形压轴题全等三角形可是初二数学里超有趣的部分呢,尤其是压轴题,那可真是像一场刺激的冒险。
咱先来说说全等三角形是啥。
全等啊,就好比是两个三角形双胞胎一样,长得一模一样,大小、形状都分毫不差。
这时候就会有一些特别的条件来判断它们是不是全等,像SSS(边边边),就是三条边都相等,那这两个三角形肯定全等啦。
就好像三个人比身高、体重、臂长都一样,那肯定就是同一个模子里刻出来的。
还有SAS (边角边),两条边和它们的夹角相等,这也能证明全等。
这就好比两个人胳膊长度一样,两条腿长度一样,然后中间的角度也一样,那肯定长得一样呀。
还有ASA(角边角)和AAS(角角边)呢,角和边的关系组合起来就能确定这两个三角形是不是全等啦。
那在压轴题里呢,这些条件可不会明明白白地摆在你面前。
出题的老师就像一个调皮的小精灵,把这些条件藏起来,让你去费心思找。
有时候啊,你得在一个复杂的图形里,像寻宝一样去挖掘那些隐藏的边和角的关系。
比如说,给你一个大三角形,里面又套着好几个小三角形,然后告诉你一些角的度数或者边的长度,让你证明其中哪两个三角形全等。
这时候你就得眼睛放光,把那些有用的信息都挑出来。
有很多小技巧可以用哦。
你可以先把已知的条件都标在图上,这样就一目了然啦。
然后从要求证的全等三角形入手,去想我需要什么条件才能证明它们全等呢?要是缺了哪个条件,就再去图里找。
有时候还得利用一些对顶角相等啊,或者是同角的余角相等这些隐藏的小关系。
就像玩解谜游戏一样,一步一步地解开谜题。
我还遇到过那种要做辅助线才能证明全等的题呢。
辅助线就像是给你一把神秘的钥匙,打开了解题的新大门。
比如说在一个三角形里,你觉得这两个三角形好像能全等,但是差了一条边或者一个角的关系,这时候画一条合适的辅助线,可能就把这个关系给补上了。
不过画辅助线可不容易,就像在黑暗里摸索一样,有时候得试好几次才能找到合适的那条线。
而且在做这些压轴题的时候,可不能着急。
越着急越容易出错。

专题03高分必刷题-全等三角形压轴题真题(解析版)题型一:全等三角形小压轴题考向1:多项选择题1.如图,已知AB=AC,AF=AE,∠EAF=∠BAC,点C、D、E、F共线.则下列结论,其中正确的是()①△AFB≌△AEC;②BF=CE;③∠BFC=∠EAF;④AB=BC.A.①②③B.①②④C.①②D.①②③④【解答】解:∵∠EAF=∠BAC,∴∠BAF=∠CAE,∵AF=AE,AB=AC,∴△F AB≌△EAC(SAS),故①正确,∴BF=EC,故②正确,∴∠ABF=∠ACE,∵∠BDF=∠ADC,∴∠BFC=∠DAC,∵∠DAC=∠EAF,∴∠BFC=∠EAF,故③正确,无法判断AB=BC,故④错误,故选:A.2.如图,△ABC中,∠C=90°、AD是角平分线,E为AC边上的点,DE=DB,下列结论:①∠DEA+∠B=180°;②∠CDE=∠CAB;③AC=(AB+AE);④S△ADC=S四,其中正确的结论个数为()边形ABDEA.4个B.3个C.2个D.1个【解答】解:如图,过D作DF⊥AB于F,∵∠C=90°,AD是角平分线,∴DC=DF,∠C=∠DFB,又∵DE=DB,∴Rt△CDE≌Rt△FDB,∴∠B=∠CED,∠CDE=∠FDB,CE=BF,又∵∠DEA+∠DEC=180°,∴∠DEA+∠B=180°,故①正确;∵∠C=∠DFB,∠B=∠B,∴∠BDF=∠BAC,∴∠CDE=∠CAB,故②正确;∵AD是角平分线,∴∠CAD=∠F AD,又∵∠C=∠AFD,AD=AD,∴△ACD≌△AFD,∴AC=AF,∴AB+AE=(AF+FB)+(AC ﹣CE)=AF+AC=2AC,∴AC=(AB+AE),故③正确;∵Rt△CDE≌Rt△FDB,∴S△CDE=S△FDB,∴S四边形ABDE=S四边形ACDF,又∵△ACD≌△AFD,∴S△ACD=S△ADF,∴S△ADC=S四边形ACDF=S四边形ABDE,故④正确;故选:A.3.如图,直线AC上取点B,在其同一侧作两个等边三角形△ABD和△BCE,连接AE,CD 与GF,下列结论正确的有()①AE=DC;②∠AHC=120°;③△AGB≌△DFB;④BH平分∠AHC;⑤GF∥AC.A.①②④B.①③⑤C.①③④⑤D.①②③④⑤【解答】解:∵△ABD和△BCE都是等边三角形,∴BA=BD,BE=BC,∠ABD=∠CBE =60°,∵∠DBE=180°﹣60°﹣60°=60°,∴∠ABE=∠DBC=120°,∵BA=BD,∠ABD=∠DBC,BE=BC,∴△ABE≌△DBC(SAS),∴AE=DC,所以①正确;∠BAE=∠BDC,∵∠BDC+∠BCD =∠ABD=60°,∴∠BAE+∠BCD=60°,∴∠AHC=180°﹣(∠BAH+∠BCH)=180°﹣60°=120°,所以②正确;∵∠BAG=∠BDF,BA=BD,∠ABG=∠DBF=60°,∴△AGB≌△DFB(ASA);所以③正确;∵△ABE≌△DBC,∴AE和DC边上的高相等,即B点到AE和DC的距离相等,∴BH平分∠AHC,所以④正确;∵△AGB≌△DFB,∴BG=BF,∵∠GBF=60°,∴△BGF为等边三角形,∴∠BGF=60°,∴∠ABG=∠BGF,∴GF∥AC,所以⑤正确.故选:D.考向2:动点问题4.如图,已知△ABC中,∠B=∠C,BC=8cm,BD=6cm,如果点P在线段BC上以1cm/s 的速度由B点向C点运动,同时点Q在线段CA上由C点向A点运动,当一个点停止运动时,另一个点也随之停止运动,设点Q的速度为xcm/s,则当△BPD与△CQP全等时,x=1或.【解答】解:设运动的时间为ts,则BP=t,PC=8﹣t,CQ=tx,∵∠B=∠C,∴当BD=CQ,BP=CP时,△BPD≌△CPQ(SAS),即tx=6,t=8﹣t,解得t=4,x=;当BD=CP,BP=CQ时,△BPD≌△CQP(SAS),即8﹣t=6,t=tx,解得t=2,x=1;综上所述,x的值为1或.故答案为1或.5.如图,AB=4cm,AC=BD=3cm.∠CAB=∠DBA=60°,点P在线段AB上以1cm/s 的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).设点Q的运动速度为xcm/s,若使得△ACP与△BPQ全等.x的值为1或1.5.【解答】解:要使△ACP与△BPQ全等,有两种情况:①AP=BQ,∵点P在线段AB上以1cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).设点Q的运动速度为xcm/s,∴x=1;②AC=BQ=3cm,AP=BP=AB==2cm,∴时间为=2秒,即x==1.5,所以x的值是1或1.5.题型二:全等三角形的大压轴题6.根据全等多边形的定义,我们把四个角,四条边分别相等的两个凸四边形叫做全等四边形,记作:四边形ABCD≌四边形A1B1C1D1.(1)若四边形ABCD≌四边形A1B1C1D1,已知AB=3,BC=4,AD=CD=5,∠B=90°,∠D=60°,则A1D1=5,∠B1=90°,∠A1+∠C1=210°.(直接写出答案);(2)如图1,四边形ABEF≌四边形CBED,连接AD交BE于点O,连接OF,求证:∠AOB=∠FOE;(3)如图2,若AB=A1B1,BC=B1C1,CD=C1D1,AD=A1D1,∠B=∠B1,求证:四边形ABCD≌四边形A1B1C1D1.【解答】解:(1)∵四边形ABCD≌四边形A1B1C1D1,∴A1D1=AD=5,∠B1=∠B=90°,∠D=∠D1=60°,∠A=∠A1,∠C=∠C1,∵∠A+∠C=160°﹣90°﹣60°=210°,∴∠A1+∠C1=210°,故答案为5,90°,210°.(2)如图1中,∵四边形ABEF≌四边形CBED,∴EF=ED,∠FEO=∠DEO,∵EO=EO,∴△FEO≌△DEO(SAS),∴∠EOF=∠DOE,∵∠AOB=∠DOE,∴∠AOB=∠EOF.(3)如图2中,连接AC,A1C1.∵AB=A1B1,∠B=∠B1,BC=B1C1,∴△ABC≌△A1B1C1,∴AC=A1C1,∠BAC=∠B1A1C1,∠BCA=∠B1C1A1,∵AD=A1D1,CD=C1D1,∴△ADC≌△A1D1C1(SSS),∴∠D=∠D1,∠DAC=∠D1A1C1,∠ACD=∠A1C1D1,∴∠BAD=∠B A A1D1,∠BCD =∠B1C1D1,∴四边形ABCD≌四边形A1B1C1D1.7.(1)如图1,已知∠EOF=120°,OM平分∠EOF,A是OM上一点,∠BAC=60°,且与OF、OE分别相交于点B、C,求证:AB=AC;(2)如图2,在如上的(1)中,当∠BAC绕点A逆时针旋转使得点B落在OF的反向延长线上时,(1)中的结论是否还成立?若成立,给出证明;若不成立,说明理由;(3)如图3,已知∠AOC=∠BOC=∠BAC=60°,求证:①△ABC是等边三角形;②OC=OA+OB.【解答】(1)证明:过A作AG⊥OF于G,AH⊥OE于H,则∠AHO=∠AGO=90°,∵∠EOF=120°,∴∠HAG=60°=∠BAC,∴∠HAG﹣∠BAH=∠BAC﹣∠BAH,∴∠BAG =∠CAH,∵OM平分∠EOF,AG⊥OF,AH⊥OE,∴AG=AH,在△BAG和△CAH中,∵,∴△BAG≌△CAH(ASA),∴AB=AC;(2)结论还成立,证明:过A作AG⊥OF于G,AH⊥OE于H,与(1)证法类似根据ASA 证△BAG≌△CAH(ASA),则AB=AC;(3)证明:①如图,∠FOA=180°﹣120°=60°,∠FOC=60°+60°=120°,即OM 平分∠COF,由(2)知:AC=AB,∵∠CAB=60°,∴△ABC是等边三角形;②在OC上截取BO=ON,连接BN,∵∠COB=60°,∴△BON是等边三角形,∴ON=OB,∠OBN=60°,∵△ABC是等边三角形,∴∠ABC=60°=∠NBO,∴都减去∠ABN 得:∠ABO=∠CBN,在△AOB和△CNB中∵,∴△AOB≌△CNB(SAS),∴NC=OA,∴OC=ON+CN=OB+OA,即OC=OA+OB.8.如图1,OA=2,OB=4,以A点为顶点、AB为腰在第三象限作等腰Rt△ABC.(1)求C点的坐标;(2)如图2,P为y轴负半轴上一个动点,当P点向y轴负半轴向下运动时,以P为顶点,P A为腰作等腰Rt△APD,过D作DE⊥x轴于E点,求OP﹣DE的值;(3)如图3,已知点F坐标为(﹣2,﹣2),当G在y轴的负半轴上沿负方向运动时,作Rt△FGH,始终保持∠GFH=90°,FG与y轴负半轴交于点G(0,m),FH与x轴正半轴交于点H(n,0),当G点在y轴的负半轴上沿负方向运动时,求证m+n为定值,并求出其值.【解答】解:(1)过C作CM⊥x轴于M点,如图1,∵CM⊥OA,AC⊥AB,∴∠MAC+∠OAB=90°,∠OAB+∠OBA=90°,则∠MAC=∠OBA,在△MAC和△OBA中,,∴△MAC≌△OBA(AAS)∴CM=OA=2,MA=OB=4,∴点C的坐标为(﹣6,﹣2);(2)如图2,过D作DQ⊥OP于Q点,∵DQ⊥OP,DE⊥OE,∠POE=90°∴四边形OEDQ是矩形,∴OE=QD,DE=OQ,∴OP=PQ+OQ=DE+PQ,∵∠APO+∠QPD=90°,∠APO+∠OAP=90°,∴∠QPD=∠OAP,在△AOP和△PDQ中,,∴△AOP≌△PDQ(AAS),∴QP=AO=2,∴OP﹣DE=2;(3)结论②是正确的,m+n=﹣4,理由如下:如图3,过点F分别作FS⊥x轴于S点,FT ⊥y轴于T点,∴FS=FT=2,∠FHS=∠HFT=∠FGT,在△FSH和△FTG中,,∴△FSH≌△FTG(AAS)∴GT=HS,又∵G(0,m),H(n,0),点F坐标为(﹣2,﹣2),∴OT═OS=2,OG=|m|=﹣m,OH=n,∴GT=OG﹣OT=﹣m﹣2,HS=OH+OS=n+2,∴﹣2﹣m=n+2,∴m+n=﹣4.9.在△ABC中,AB=AC,CG⊥BA交BA的延长线于点G.一等腰直角三角尺按如图1所示的位置摆放,该三角尺的直角顶点为F,一条直角边与AC边在一条直线上,另一条直角边恰好经过点B.(1)在图1中请你通过观察、测量BF与CG的长度,猜想并写出BF与CG满足的数量关系,然后证明你的猜想;(2)当三角尺沿AC方向平移到图2所示的位置时,一条直角边仍与AC边在同一直线上,另一条直角边交BC边于点D,过点D作DE⊥BA于点E.此时请你通过观察、测量DE、DF与CG的长度,猜想并写出DE+DF与CG之间满足的数量关系,然后证明你的猜想;(3)当三角尺在(2)的基础上沿AC方向继续平移到图3所示的位置(点F在线段AC 上,且点F与点C不重合)时,若AG:AB=5:13,BC=4,求DE+DF的值.【解答】解:(1)猜想:BF=CG.理由:如图1.∵BF⊥AC,CG⊥AB,∴S△ABC=AC•BF=AB•CG.∵AB=AC,∴BF=CG;(2)猜想:DE+DF=CG.理由:连接AD,如图2.∵DF⊥AC,DE⊥AB,CG⊥AB,∴S△ACD=AC•DF,S△ABD=AB•DE,S△ABC=AB•CG.∵S△ACD+S△ABD=S△ABC,∴AC•DF+AB•DE=AB•CG.∵AB=AC,∴DF+DE=CG;(3)连接AD,如图3.同(2)可得:DF+DE=CG.设AG=5x,∵AG:AB=5:13,AB =AC,∴AC=AB=13x.∴∠G=90°,∴GC==12x.在Rt△BGC中,∵BG=AB+AG=13x+5x=18x,GC=12x,BC=4,∴(18x)2+(12x)2=(4)2,解得:x=,∴DE+DF=CG=12x=8.10.如图1,在平面直角坐标系中,A(﹣2,0)、B(0,5),AB=AD,∠ABC+∠ADC=180°,BC⊥CD.(1)求证:∠ABO=∠CAD;(2)求点D坐标;(3)如图2,若OC=OB=5,E为∠BCO的邻补角的平分线上的一点,且∠BEO=45°,OE交BC于点F,求BF的长.【解答】解:(1)如图1,在四边形ABCD中,∵∠ABC+∠ADC=180°,∴∠BAD+∠BCD =180°,∵BC⊥CD,∴∠BCD=90°,∴∠BAD=90°.∴∠BAC+∠CAD=90°,又∵∠BAC+∠ABO=90°.∴∠ABO=∠CAD.(2)如图1,过点D作DG⊥AC,∴∠AGD=∠BOA=90°,又∵∠ABO=∠CAD,AB=AD,∴△ABO≌△DAG(AAS),∴DG=AO=2,AG=BO=5,∴OG=AG﹣AO=3,则点D的坐标为(3,﹣2);(3)如图2,过点E作EH⊥BC于点H,作EG⊥x轴于点G,∵E点在∠BCO的邻补角的平分线上,∴EH=EG.又∵∠BCO=∠BEO=45°,∴∠EBC=∠EOC.∴△EBH≌△EOG(AAS),∴EB=EO.又∵∠BEO=45°,∴∠EBO=∠EOB=67.5°,∵∠OBC=45°,∴∠BOE=∠BFO=67.5°.∴BF=BO=5.11.在平面直角坐标系中,点A在x轴上,点B、C在y轴上,且点B与点C关于x轴对称,点D在线段AB上,点E为该坐标平面内一点.(1)已知BD=CE.①如图1,若点E在线段AC上,求证:CD=BE;②如图2,若点E在线段BC上,且∠DEA=∠ABC,求证:∠ACO=2∠OAE.(2)如图3,已知BD=AE,点E在线段CA的延长线上,F为CD中点,且∠OAB=30°,求证:BF⊥EF.【解答】证明:(1)①∵点B和点C关于x轴对称,∴AB=AC,∴∠CBD=∠BCE,在△CBD和△BCE中,,∴△CBD≌△BCE(SAS),∴CD=BE;②∵∠DEA+∠DEB=∠ACB+∠CAE,∠DEA=∠ABC=∠ACB,∴∠DEB=∠CAE,在△BED和△CAE中,,∴△BED≌△CAE(AAS),∴BE=AC=AB,∴∠BEA=∠BAE,∵点B和点C关于x轴对称,∴AB=AC,OB=OC,∴∠BAO=∠CAO,∴∠BAE=2∠CAO﹣∠EAC=2∠OAE+∠EAC,∵∠DEB=∠CAE,∴∠DEA=2∠OAE,∵∠DEA=∠ABC=∠ACO,∴∠ACO=2∠OAE;(2)延长BF到点G,使BF=FG,连接CG、EG、BE,如图3所示:∵点B和点C关于x轴对称,∴AB=AC,OB=OC,∴∠OAB=∠OAC=30°,∴∠BAC=60°,∴△ABC是等边三角形,∴CB=AB,∠BCA=60°,∵F为DC中点,∴DF=CF,在△BDF和△GCF中,,∴△BDF≌△GCF(SAS),∴CG=BD=AE,∠CGF=∠DBF,∴BD∥CG,∴∠GCA=∠BAC=60°,∴∠BCG=∠BCA+∠GCA=60°+60°=120°,∵∠BAE=180°﹣∠OAB﹣∠EAx=180°﹣∠OAB﹣∠OAC=180°﹣30°﹣30°=120°,∴∠BCG=∠BAE,在△BCG和△BAE中,,∴△BCG≌△BAE(SAS),∴∠CBG=∠ABE,BG=BE,∵∠CBG+∠GBA=60°,∴∠ABE+∠GBA=60°,即∠GBE =60°,∴△GBE是等边三角形,∵F是BG的中点,∴EF⊥BG,∴BF⊥EF.12.如图,平面直角坐标系中,已知点A(a﹣1,a+b),B(a,0),且+(a﹣2b)2=0,C为x轴上点B右侧的动点,以AC为腰作等腰△ACD,使AD=AC,∠CAD=∠OAB,直线DB交y轴于点P.(1)求证:AO=AB;(2)求证:OC=BD;(3)当点C运动时,点P在y轴上的位置是否发生改变,为什么?【解答】证明:(1)∵+(a﹣2b)2=0,≥0,(a﹣2b)2≥0,∴=0,(a﹣2b)2=0,解得:a=2,b=1,∴A(1,3),B(2,0),∴OA==,AB==,∴OA=AB;(2)∵∠CAD=∠OAB,∴∠CAD+∠BAC=∠OAB+∠BAC,即∠OAC=∠BAD,在△OAC 和△BAD中,,∴△OAC≌△BAD(SAS),∴OC=BD;(3)点P在y轴上的位置不发生改变.理由:设∠AOB=∠ABO=α,∵由(2)知△AOC≌△ABD,∴∠ABD=∠AOB=α,∵OB =2,∠OBP=180°﹣∠ABO﹣∠ABD=180°﹣2α为定值,∵∠POB=90°,∴OP长度不变,∴点P在y轴上的位置不发生改变.13.在△ABC中,∠A<60°,以AB,AC为边分别向外作等边△ABD,△ACE,连接DC,BE交于点H.(如图1)(1)求证:△DAC≌△BAE;(2)求DC与BE相交的∠DHB的度数;(3)又以BC边向内作等边三角形△BCF,连接DF(如图2),试判断AE与DF的位置与数量关系,并证明你的结论.【解答】(1)证明:如图1中,∵△ABD、△ACE都是等边三角形,∴AD=AB,AC=AE,∠DAB=∠CAE=60°,∴∠DAC=∠BAE,在△DAC和△BAE中,,∴△DAC≌△BAE.(2)如图1中,∵△DAC≌△BAE,∴∠ADC=∠ABE,∵∠AOD=∠BOH,∠AOD+∠ADC+∠DAO=180°,∠BOH+∠OHB+∠ABE=180°,∴∠OHB=∠DAO=60°,∴∠DHB=60°.(3)结论AE=DF,AE∥FD.如图2中,连接EF,∵△ABD,△BCF,△ACE都是等边三角形,∴BD=BA=AD,BF=BC,CA=CE=AE,∠ABD=∠CBF=∠BCF=∠ACE=60°,∴∠DBF=∠CBA,∠BCA=∠ECF,在△ABC和△DBF中,,∴△ABC≌△DBF,同理△ABC≌△EFC,∴DF=AC=AE,EF=AB=AD,∴四边形ADFE是平行四边形,∴DF=AE,DF∥AE.14.已知,△ABC是等腰直角三角形,BC=AB,A点在x负半轴上,直角顶点B在y轴上,点C在x轴上方.(1)如图1所示,若A的坐标是(﹣3,0),点B的坐标是(0,1),求点C的坐标;(2)如图2,过点C作CD⊥y轴于D,请直接写出线段OA,OD,CD之间等量关系;(3)如图3,若x轴恰好平分∠BAC,BC与x轴交于点E,过点C作CF⊥x轴于F,问CF与AE有怎样的数量关系?并说明理由.【解答】解:(1)作CH⊥y轴于H,如图1,∵点A的坐标是(﹣3,0),点B的坐标是(0,1),∴OA=3,OB=1,∵△ABC是等腰直角三角形,∴BA=BC,∠ABC=90°,∴∠ABO+∠CBH=90°,∵∠ABO+∠BAO=90°,∴∠CBH=∠BAO,在△ABO和△BCH中,∴△ABO≌△BCH,∴OB=CH=1,OA=BH=3,∴OH=OB+BH=1+3=4,∴C(﹣1,4);(2)OA=CD+OD.理由如下:如图2,∵△ABC是等腰直角三角形,∴BA=BC,∠ABC =90°,∴∠ABO+∠CBD=90°,∵∠ABO+∠BAO=90°,∴∠CBD=∠BAO,在△ABO和△BCD中,∴△ABO≌△BCD,∴OB=CD,OA=BD,而BD=OB+OD=CD+OD,∴OA=CD+OD;(3)CF=AE.理由如下:如图3,CF和AB的延长线相交于点D,∴∠CBD=90°,∵CF⊥x,∴∠BCD+∠D=90°,而∠DAF+∠D=90°,∴∠BCD=∠DAF,在△ABE和△CBD中,,∴△ABE≌△CBD(ASA),∴AE=CD,∵x轴平分∠BAC,CF⊥x轴,∴CF=DF,∴CF=CD=AE.15.在△ABC中,AB=AC,D是直线BC上一点(不与点B、C重合),以AD为一边在AD 的右侧作△ADE,AD=AE,∠DAE=∠BAC,连接CE.(1)如图1,当点D在线段BC上时,写出△ABD≌△ACE的理由;(2)如图2,当点D在线段BC上,∠BAC=90°,直接写出∠BCE的度数;(3)如图3,若∠BCE=α,∠BAC=β,点D在线段CB的延长线上时,则α、β之间有怎样的数量关系?写出你的理由.【解答】(1)证明:∵∠BAC=∠DAE,∴∠BAC﹣∠DAC=∠DAE﹣∠DAC,即∠BAD=∠CAE,在△ABD和△ACE中,,∴△ABD≌△ACE(SAS);(2)解:∵AB=AC,∠BAC=90°,∴∠ABC=∠ACB=45°,同(1)的方法可得,△ABD≌△ACE(SAS),∴∠ACE=∠ABD=45°,∴∠BCE=∠ACB+∠ACE=45°+45°=90°;(3)解:α=β.理由如下:同(1)的方法可得,△ABD≌△ACE(SAS),∴∠ACE=∠ABD,∵∠BCE=α,∴∠ACE=∠ACB+∠BCE=∠ACB+α,∵∠ABD是△ABC的一个外角,∴∠ABD=∠ACB+∠BAC=∠ACB+β,∴α=β.。
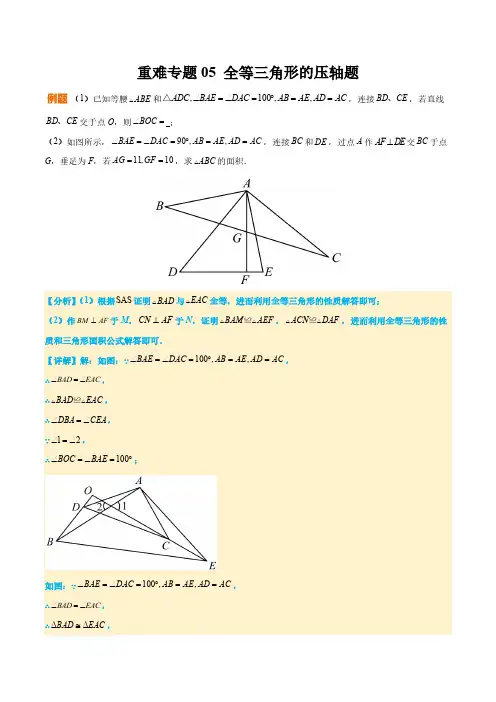
重难专题05 全等三角形的压轴题(1)已知等腰ABE V 和,100,,ADC BAE DAC AB AE AD AC Ð=Ð=°==△,连接BD CE 、,若直线BD CE 、交于点O ,则BOC Ð= ;(2)如图所示,90,,BAE DAC AB AE AD AC Ð=Ð=°==,连接BC 和DE ,过点A 作AF D E ^交BC 于点G ,垂足为F ,若11,10AG GF ==,求ABC V 的面积.【分析】(1)根据SAS 证明BAD V 与EAC V 全等,进而利用全等三角形的性质解答即可;(2)作BM AF ^于M ,CN AF ^于N ,证明BAM AEF V V ≌,ACN DAF V V ≌,进而利用全等三角形的性质和三角形面积公式解答即可.【详解】解:如图:∵100,,BAE DAC AB AE AD AC Ð=Ð=°==,∴BAD EAC Ð=Ð,∴BAD EAC V V ≌,∴DBA CEA Ð=Ð,∵12Ð=Ð,∴100BOC BAE Ð=Ð=°;如图:∵100,,BAE DAC AB AE AD AC Ð=Ð=°==,∴BAD EAC Ð=Ð,∴ΔΔBAD EAC @,(2)作BM AF ^于M ,CN AF ^于N ∵AF D E ^,∴90BMA AFE Ð=Ð=°,∵90,BAE AB AE Ð=°=,∴90BAM FAE Ð+Ð=°,E FAE Ð+Ð=∴BAF E Ð=Ð,231ABC ABG ACG S S S =+=V V V .【点拨】本题考查了全等三角形的判定与性质,解题关键是恰当作辅助线,构建全等三角形,利用全等三角形的性质解决问题.如图1,BE 是ABC V 中AC 边上的高,点D 是AB 上一点,连接CD 交BE 于点F ,EFC A Ð=Ð.(1)求证:CD AB ^;(2)若2ACB ABE Ð=Ð,求证:AC BC =;(3)如图2,在(2)的条件下,延长BE 至点G ,连接AG ,CG ,若22ABCGBC S =四边形,16ABG S =△,求线段AB 的长.(注:不能应用等腰三角形的相关性质和判定)【分析】(1)首先根据ABC V 高的意义得出,90ACD EFC Ð+Ð=°,再结合已知条件可得到90ACD A Ð+Ð=°,据此得出结论;(2)首先根据ABC V 高的意义及(1)的结论可得出ACD ABE Ð=Ð,然后再结合已知条件可得出BCD ACD ABE Ð=Ð=Ð,据此可证明BCD D 和ACD D 全等,进而可得出结论;(3)首先根据四边形ABGC 的面积ABG =V 的面积BCG +V 面积可得出BG BC =,过点G 作GH BA ^交BA 的延长线于点H ,再证GBH V 和BCD V 全等,从而得GH BD =,由(2)可知AD BD =,据此可得2AB BD =,然后根据16ABG S =V 可求出BD 的长,进而可得出AB 的长.【详解】(1)证明:BE Q 是ABC V 中AC 边上的高,BE AC \^,则90H Ð=°,由(1)知:CD AB ^,90CDB \Ð=°,H CDB \Ð=Ð,由(2)知:ABE BCD =∠∠即:GBH BCD Ð=Ð,4BD \=,28AB BD \==.【点拨】此题主要考查了全等三角形的判定和性质,三角形的面积计算公式等,解答此题的关键是熟练掌握全等三角形的判定方法与技巧,理解全等三角形的性质,难点是在解答(3)时,过点G 作GH BA ^交BA 的延长线于点H ,从而构成全等三角形.如图,Rt ACB V 中,90ACB Ð=°,AC BC =,E 点为射线CB 上一动点,连接AE ,作AF AE ^且AF AE =.(1)如图1,过F 点作FD AC ^交AC 于D 点,求证:ADF ECA V V ≌,并写出EC CD 、和DF 的数量关系;(2)如图2,连接BF 交AC 于G 点,若3AG CG=,求证:E 点为BC 中点;(3)当E 点在射线CB 上,连接BF 与直线AC 交于G 点,若73BC BE =,求AG CG .∵ADF ECA V V ≌,∴FD AC BC ==,在FDG △和BCG V 中,90FGD CGB FDG C Ð=ÐìïÐ=Ð=°íï,∵73BC BE =,BC AC CE CB ==,∴710AC CE =,由(1)(2)知:ADF ECA V V ≌∴CG GD AD CE ==,,∴710AC AD =,∴73AC CD =,∵73BC BE =,BC AC CE CB BE ==-,∴74AC CE =,由(1)(2)知:ADF ECA V V V ≌,∴CG GD AD CE ==,,如图,直线AB ,CD 交于点O ,点E 是BOC Ð平分线的一点,点M ,N 分别是射线OA ,OC 上的点,且ME NE =.(1)求证:MEN AOC Ð=Ð;(2)点F 在线段NO 上,点G 在线段NO 延长线上,连接EF ,EG ,若EF EG =,依题意补全图形,用等式表示线段NF ,OG ,OM 之间的数量关系,并证明.【分析】(1)先根据角的平分线的性质,过点E 作EH CD ^,EK AB ^,垂足分别是H ,K ,得EH EK =,再根据三角形全等的判定,证明Rt EHN Rt EKM V V ≌即可得结论.(2)作辅助线,在线段OM 上截取1OG OG =,连接EG 1,先证明1EOG EOG V V ≌,得1EG EG =,1EG O EGF Ð=Ð,再证明1ENF EMG V V ≌,得1NF MG =,再推导得出结论.【详解】(1)(1)证明:作EH CD ^,EK AB ^,垂足分别是H ,K ,如图.∵OE 是BOC Ð的平分线,∴EH EK =.∵ME NE =,∴Rt EHN Rt EKM V V ≌.∴ENH EMK ÐÐ=.记ME 与OC 的交点为P ,∴EPN OPM ÐÐ=.∴MEN AOC ÐÐ=.(2)(2)OM NF OG =+.证明:在线段OM 上截取1OG OG =,连接EG 1,如图.∵OE 是BOC Ð的平分线,∴EON EOB ÐÐ=.∵MOF DOB ÐÐ=,∴EOM EOD ÐÐ=.∵OE OE =,∴1EOG EOG V V ≌.∴1EG EG =,1EG O EGF Ð=Ð. ∵EF EG =,∴1EF EG =,EFG EGF Ð=Ð.∴1EFG EG O Ð=Ð.∴1EFN EG M Ð=Ð.∵1ENF EMG Ð=Ð.∴1ENF EMG V V ≌.∴1NF MG =.∵11OM MG OG =+,∴OM NF OG =+.【点拨】此题考查了角平分线的性质、全等三角形的判定与性质.此题难度适中,注意掌握数形结合思想与转化思想的应用.如图,四边形ABCD 和四边形AEFG 是正方形,(正方形四条边都相等,四个内角都是直角)【感知】(1)某学习小组探究如下问题:如图1,连接DG ,BE ,直线AH DG ^于点H ,交BE 于点M ,则ADG △与ABE V 面积的大小关系是:ADG S V _________ABE S V .【探究】(2)该学习小组在探究(1)中面积问题时,发现M 为BE 中点,你认为是否成立?若成立,请证明;若不成立,请说明理由.【拓展】(3)经过以上探究,该学习小组也提出问题:若正方形ABCD 和正方形AEFG 的位置如图2所示,点M 为BE 中点,连接AM 交DG 于点H ,那么AM 与DG 有怎样的关系?试探究,并说明理由【分析】(1)过点E 作EQ AB ^于点Q ,延长DA ,过点G 作GP DA ⊥于点P ,证明()AAS AEQ AGP V V ≌,得出EQ GP =,根据AD AB =,得出ADG ABE S S =V V ;(2)过点E 作EP MH ⊥于点P ,过点B 作BQ MH ⊥于点Q ,证明()AAS AGH EAP V V ≌,得出AH EP =,同理得:AHD BQA V V ≌,证明AH BQ =,求出EP BQ =,证明()AAS EMP BMQ V V ≌,得出EM BM =;(3)延长AM ,在延长线上截取MN AM =,连接EN 、BN ,证明()SAS AMB NME V V ≌,得出EN AB =,ENM BAM =∠∠,证明()SAS ADG ENA V V ≌,得出2DG AN AM ==,AGD EAN =∠∠,证明90AGD NAG +=°∠∠,得出90AHG Ð=°,即AH DG ^.【详解】解:(1)过点E 作EQ AB ^于点Q ,延长DA ,过点G 作GP DA ⊥于点P ,如图所示:则90APG AQE ==°∠∠,∵90BAD Ð=°,∴90BAP Ð=°,∵90GAE Ð=°,∴90EAQ EAP EAP GAP +=+=°∠∠∠∠,∴EAQ GAP =∠∠,∵AG AE =,∴()AAS AEQ AGP V V ≌,∴EQ GP =,∵AD AB =,∴ADG ABE S S =V V .故答案为:=.(2)成立;理由如下:过点E 作EP MH ⊥于点P ,过点B 作BQ MH ⊥于点Q ,如图所示:∵AH DG ^,∴90AHG APE ==°∠∠,∵90GAE Ð=°,∴90GAH EAP EAP AEP +=+=°∠∠∠∠,∴GAH AEP =∠∠,∵AG AE =,∴()AAS AGH EAP V V ≌,∴AH EP =,同理得:AHD BQA V V ≌,∴AH BQ =,∴EP BQ =,∵90EPM BQM ==°∠∠,EMP BMQ Ð=Ð,∴()AAS EMP BMQ V V ≌,∴EM BM =,∴M 为BE 中点.(3)2DG AM =,AM DG ^.理由如下:延长AM ,在延长线上截取MN AM =,连接EN 、BN ,如图所示:∵M 为BE 的中点,∴BM EM =,∵NME AMB =∠∠,∴()SAS AMB NME V V ≌,∴EN AB =,ENM BAM =∠∠,∵AB AD =,∴EN AD =,∵ENM BAM =∠∠,∴EN AB ∥,∴180AEN EAB +=°∠∠,∵180DAB EAG Ð=Ð=°,EAG EAB BAG =+∠∠∠,∴180DAB EAB BAG ++=°∠∠∠,即180DAG EAB Ð+Ð=°,∴AEN DAG =∠∠,∵AE AG =,∴()SAS ADG ENA V V ≌,∴2DG AN AM ==,AGD EAN =∠∠,∵90EAN GAN +=°∠∠,∴90AGD NAG +=°∠∠,∴90AHG Ð=°,∴AH DG ^.【点拨】本题主要考查了全等三角形的判定和性质,余角的性质,平行线的判定和性质,垂线定义理解,解题的关键是作出辅助线,熟练掌握三角形全等的判定方法.【初步探索】(1)如图1,在四边形ABCD 中,AB AD =,90B ADC Ð=Ð=°,E 、F 分别是BC 、CD 上的点,且EF BE FD =+,探究图中BAE Ð、FAD Ð、EAF Ð之间的数量关系.小王同学探究此问题的方法是:延长FD 到点G ,使DG BE =.连接AG ,先证明ABE ADG △≌△,再证明AEF AGF V V ≌,可得出结论,他的结论应是 ;【灵活运用】(2)如图2,若在四边形ABCD 中,AB AD =,180B D Ð+Ð=°.E 、F 分别是BC 、CD 上的点,且EF BE FD =+,上述结论是否仍然成立,并说明理由;【拓展延伸】(3)如图3,已知在四边形ABCD 中,180ABC ADC Ð+Ð=°,AB AD =,若点E 在CB 的延长线上,点F 在CD 的延长线上,如图3所示,仍然满足EF BE FD =+,请写出EAF Ð与DAB Ð的数量关系,并给出证明过程.【分析】(1)延长FD 到点G ,使DG BE =,连接AG ,可判定ABE ADG △≌△,进而得出BAE DAG Ð=Ð,AE AG =,再判定AEF AGF V V ≌,可得出EAF GAF DAG DAF BAE DAF Ð=Ð=Ð+Ð=Ð+Ð,据此得出结论;(2)延长FD 到点G ,使DG BE =,连接AG ,先判定ABE ADG △≌△,进而得出BAE DAG Ð=Ð,AE AG =,再判定AEF AGF V V ≌,可得出EAF GAF DAG DAF BAE DAF Ð=Ð=Ð+Ð=Ð+Ð;(3)在DC 延长线上取一点G ,使得DG BE =,连接AG ,先判定ABE ADG △≌△,再判定AEF AGF V V ≌,得出FAE FAG Ð=Ð,最后根据360FAE FAG GAE Ð+Ð+Ð=°,推导得到2360FAE DAB Ð+Ð=°,即可得出结论.【详解】(1)解:结论:BAE FAD EAF Ð+Ð=Ð.理由:如图1,延长FD 到点G ,使DG BE =,连接AG ,在ABE V 和ADG △中,90AB AD B ADG BE DG =ìïÐ=Ð=°íï=î,(SAS)ABE ADG \V V ≌,BAE DAG \Ð=Ð,AE AG =,EF BE DF =+Q ,EF DF DG FG \=+=,在AEF △和AGF V 中,1.阅读理解在通过构造全等三角形解决的问题中,有一种典型的方法是倍延中线法.如图1,AD 是ABC V 的中线,7AB =,5AC =,求AD 的取值范围.我们可以延长AD 到点M ,使DM AD =,连接BM ,易证ADC MDB ≌△△,所以BM AC =.接下来,在ABM V 中利用三角形的三边关系可求得AM 的取值范围,从而得到中线AD 的取值范围是______;类比应用如图2,在四边形ABCD 中,//AB DC ,点E 是BC 的中点.若AE 是BAD Ð的平分线,试判断AB ,AD ,DC 之间的等量关系,并说明理由;拓展创新如图3,在四边形ABCD 中,//AB CD ,AF 与DC 的延长线交于点F ,点E 是BC 的中点,若AE 是BAF Ð的平分线,试探究AB ,AF ,CF 之间的数量关系,请直接写出你的结论.2.如图,在ABC V 和ADE V 中,AB AC =,AD AE =,BAC DAE Ð=Ð,CE 的延长线交BD 于点F .(1)求证:CE BD =.(2)过点A 作AP DE ^于点P ,求证:AEP ADP Ð=Ð.(3)若30ACE Ð=°,15BAE Ð=°,6DAE AED Ð=Ð-°,求BDE Ð的度数.(4)过点A 作AH BD ^于点H ,试写出EF ,FH ,DH 之间的数量关系,并证明.3.问题提出,如图(1),在ABC V 和DEC V 中,60ACB DCE °Ð=Ð=,BC AC =,EC DC =,点E 在ABC V 内部,直线AD 与BE 交于点F ,线段,,AF BF CF 之间存在怎样的数量关系?问题探究(1)先将问题特殊化.如图(2),当点D ,F 重合时,直接写出一个等式,表示,,AF BF CF 之间的数量关系;(2)再探究一般情形.如图(1),当点D ,F 不重合时,证明(1)中的结论仍然成立.问题拓展(3)如图(3),在ABC V 和DEC V 中,60ACB DCE °Ð=Ð=,BC AC =,EC DC =,点E 在ABC V 内部,直线AD 与BE 交于点F ,直线AF 与BC 交于点G ,点H 为线段AB 上一点,BH CG =,BF 与CH 交于点I ,若AG m =,BF n =,则IF =___________(用含m ,n 的式子表示)4.已知O 是四边形ABCD 内一点,且OA OD =,OB OC =,E 是CD 的中点.(1)如图1,连接AC ,BD ,若AC BD =,求证:AOD BOC Ð=Ð;(2)如图2,连接OE ,若2AB OE =,求证:180AOD BOC Ð+Ð=°;(3)如图3,若90AOD BOC Ð=Ð=°,OF AB ^,垂足为F ,求证:点E ,O ,F 在同一条直线上.5.在直角三角形ABC 中,90ACB Ð=°,直线l 过点C .(1)当AC BC =时,①如图1,分别过点A 和B 作AD ^直线l 于点D ,BE ^直线l 于点E .求证:ACD CBE V V ≌;②如图2,过点A 作AD ^直线l 于点D ,点B 与点F 关于直线l 对称,连接BF 交直线l 于E ,连接CF .求证:DE AD EF =+.(2)当8AC =cm ,6BC =cm 时,如图3,点B 与点F 关于直线l 对称,连接BF 、CF .点M 从A 点出发,以每秒1cm 的速度沿A C ®路径运动,终点为C ,点N 以每秒3cm 的速度沿F C B C F ®®®®路径运动,终点为F ,分别过点M 、N 作MD ^直线l 于点D ,NE ^直线l 于点E ,点M 、N 同时开始运动,各自达到相应的终点时停止运动,设运动时间为t 秒.当MDC △与CEN V 全等时,求t 的值.6.如图①,在ABC V 中,AB =12cm ,BC =20cm ,过点C 作射线CD AB ∥.点M 从点B 出发,以4cm /s 的速度沿BC 匀速移动;点N 从点C 出发,以acm /s 的速度沿CD 匀速移动.点M 、N 同时出发,当点M 到达点C 时,点M 、N 同时停止移动,连接AM 、MN ,设移动时间为t (s ).(1)点M 、N 从移动开始到停止,所用时间为 s ;(2)当ABM V 与MCN △全等时,①若点M 、N 的移动速度相同,求t 的值;②若点M 、N 的移动速度不同,求t 的值;(3)如图②、当点M 、N 开始移动时,点P 同时从点A 出发,以3cm /s 的速度沿AB 向点B 匀速移动,到达点B 后立刻以原速度沿BA 返回.当点M 到达点C 时,点M 、N 、P 同时停止移动.在移动的过程中,是否存在PBM V 与MCN △全等的情形?若存在,求出t 的值,若不存在,说明理由.7.已知:ABC V 中,90ACB Ð=°,AC CB =,D 为直线BC 上一动点,连接AD ,在直线AC 右侧作AE AD ^,且AE AD =.(1)如图1,当点D 在线段BC 上时,过点E 作EH AC ^于H ,连接DE .求证:EH BC =;(2)如图2,当点D 在线段BC 的延长线上时,连接BE 交CA 的延长线于点M ,求证:BM EM =;(3)当点D 在直线CB 上时,连接BE 交直线AC 于M ,若27AC CM =,请求出ADB AEM S S △△的值.8.在ABC V 中,BD 平分ABC Ð,CE 平分ACB Ð,BD 和CE 交于点O ,其中令BAC x Ð=,BOC y Ð=.(1)【计算求值】如图1,①如果50x =°,则y =______;②如果130y =°,则x =______.(2)【猜想证明】如图2请你根据(1)中【计算求值】的心得猜想写出y 与x 的关系式为y =______,并请你说明你的猜想的正确性.(3)【解决问题】如图3,某校园内有一个如图2所示的三角形的小花园,花园中有两条小路,BD 和CE 为三角形的角平分线,交点为点O ,在O 处建有一个自动浇水器,需要在BC 边取一处接水口F ,经过测量得知120BAC Ð=°,12000OD OE ×=米2,170BC BE CD --=米,请你求出水管OF 至少要多长?(结果取整数)。
全等三角形压轴题复习1、如图,已知A(—2,3),B(—5,0),C(—1,0),△ABC和4A^1c l关于x轴对称,(1)作4ABC关于x轴对称的^A1B1C1,直接写出点A1坐标;(2)在y轴上有一点P使AP+A1P最小,直接写出点P的坐标;(3)请直接写出点A关于直线x=m(直线上各点的横坐标都为m)对称的点的坐标.知识点一、全等三角形的常见模型与辅助线【知识梳理】1、常见辅助线:(1)角平分线:^(2)垂直平分线:^(3)中线:^(4)等腰三角形:^(5)线段和(差):^2、常见的模型:(1)三垂直:(2)手拉手:(3)夹半角:(4)对角互补:(5)脚拉脚:【例题精讲一】最短路径1、平面直角坐标系中,已知A(4,3)、B(2,1),x轴上有一点P,要使PA-PB最大,则P点坐标为2、如图,在Rt^ABC中,N ACB=90°,AC>BC,AD平分N CAB交BC于口,点E、F分别是AD、AC上的动点,点O为AB中点,点M在AB上,且AM=AC,则CE+EF的最小值等于()A.点O到点C的距离B.点M到点C的距离C.点O到BC边上的距离D.点C到AB的距离(第2题)(第3题)(第5题)3、如图,在四边形ABCD中,DA,AB,DA=6cm,Z B+Z C=150°.CD与BA延长交于E点,点A刚好是BE的中点,P、Q分别是线段CE、BE上的动点,则BP+PQ最小值是^4、已知A(3,1),B(5,2),点P(a,0)在x轴上,当PA—PB达到最大值时,a=。
5、如图,等边△ABC中,BF是AC边上中线,点D在BF上,连接AD,在AD的右侧作等边△ADE,连接£尸,当4AEF周长最小时,N CFE的大小是^【课堂练习】1、如图,已知N MON=40°,P为^MON内一点,A为OM上的点,B为ON上的点.当△PAB的周长取最小值时,则N APB的度数为。
BA ODCE图88年级三角形综合题归类一、 双等边三角形模型1. (1)如图7,点O 是线段AD 的中点,分别以AO 和DO 为边在线段AD 的同侧作等边三角形OAB 和等边三角形OCD ,连结AC 和BD ,相交于点E ,连结BC .求∠AEB 的大小; (2)如图8,ΔOAB 固定不动,保持ΔOCD 的形状和大小不变,将ΔOCD 绕着点O 旋转(ΔOAB 和ΔOCD 不能重叠),求∠AEB 的大小.2. 已知:点C 为线段AB 上一点,△ACM,△CBN 都是等边三角形,且AN 、BM 相交于O.① 求证:AN=BM ② 求 ∠AOB 的度数。
③ 若AN 、MC 相交于点P ,BM 、NC 交于点Q ,求证:PQ ∥AB 。
(湘潭·中考题)同类变式: 如图a ,△ABC 和△CEF 是两个大小不等的等边三角形,且有一个公共顶点C ,连接AF 和BE.(1)线段AF 和BE 有怎样的大小关系?请证明你的结论;(2)将图a 中的△CEF 绕点C 旋转一定的角度,得到图b ,(1)中的结论还成立吗?作出判断并说明理由;(3)若将图a 中的△ABC 绕点C 旋转一定的角度,请你画出一个变换后的图形c(草图即可),(1)中的结论还成立吗?作出判断不必说明理由.图c3. 如图9,若△ABC 和△ADE 为等边三角形,,M N 分别为,EB CD 的中点,易证:CD BE ,△AMN 是等边三角形.CBOD图7 AEA BCMNO PQ(1)当把△ADE 绕A 点旋转到图10的位置时,CD BE =是否仍然成立?若成立,请证明;若不成立,请说明理由;(2)当△ADE 绕A 点旋转到图11的位置时,△AMN 是否还是等边三角形?若是,请给出证明,若不是,请说明理由.同类变式:已知,如图①所示,在ABC △和ADE △中,AB AC =,AD AE =,BAC DAE ∠=∠,且点B A D ,,在一条直线上,连接BE CD M N ,,,分别为BE CD,的中点.(1)求证:①BE CD =;②AN AM =;(2)在图①的基础上,将ADE △绕点A 按顺时针方向旋转180,其他条件不变,得到图②所示的图形.请直接写出(1)中的两个结论是否仍然成立.4. 如图,四边形ABCD 和四边形AEFG 均为正方形,连接BG 与DE 相交于点H .(1)证明:△ABG ≌△ADE ;(2)试猜想∠BHD 的度数,并说明理由;图9 图10 图11CENDA BM图①CAE M BDN 图②(3)将图中正方形ABCD 绕点A 逆时针旋转(0°<∠BAE <180°),设△ABE 的面积 为1S ,△ADG 的面积为2S ,判断1S 与2S 的大小关系,并给予证明.5.已知:如图,ABC △是等边三角形,过AB 边上的点D 作DG BC ∥,交AC 于点G ,在GD 的延长线上取点E ,使DE DB =,连接AE CD ,. (1)求证:AGE DAC △≌△;(2)过点E 作EF DC ∥,交BC 于点F ,请你连接AF ,并判断AEF △是怎样的三角形,试证明你的结论.CGAEDBF二、 垂直模型(该模型在基础题和综合题中均为重点考察内容)考点1:利用垂直证明角相等1. 如图,△ABC 中,∠ACB =90°,AC =BC ,AE 是BC 边上的中线,过C 作CF ⊥AE ,垂足为F ,过B 作BD ⊥BC 交CF 的延长线于D .求证:(1)AE =CD ; (2)若AC =12 cm ,求BD 的长.C FGEDAH2.(西安中考)如图(1), 已知△ABC中, ∠BAC=900, AB=AC, AE是过A的一条直线, 且B、C在A、E的异侧, BD⊥AE于D, CE⊥AE于E 。
全等三角形压轴题1.在△ABC中,AB=AC,∠BAC=α(0°<α<60°),将线段BC绕点B逆时针旋转60°得到线段BD.(1)如图1,直接写出∠ABD的大小(用含α的式子表示);(2)如图2,∠BCE=150°,∠ABE=60°,判断△ABE的形状并加以证明;(3)在(2)的条件下,连接DE,若∠DEC=45°,求α的值.【分析】(1)求出∠ABC的度数,即可求出答案;(2)连接AD,CD,ED,根据旋转性质得出BC=BD,∠DBC=60°,求出∠ABD=∠EBC=30°﹣α,且△BCD为等边三角形,证△ABD≌△ACD,推出∠BAD=∠CAD=∠BAC=α,求出∠BEC=α=∠BAD,证△ABD≌△EBC,推出AB=BE即可;(3)求出∠DCE=90°,△DEC为等腰直角三角形,推出DC=CE=BC,求出∠EBC=15°,得出方程30°﹣α=15°,求出即可.【解答】(1)解:∵AB=AC,∠A=α,∴∠ABC=∠ACB=(180°﹣∠A)=90°﹣α,∵∠ABD=∠ABC﹣∠DBC,∠DBC=60°,即∠ABD=30°﹣α;(2)△ABE是等边三角形,证明:连接AD,CD,ED,∵线段BC绕B逆时针旋转60°得到线段BD,则BC=BD,∠DBC=60°,∵∠ABE=60°,∴∠ABD=60°﹣∠DBE=∠EBC=30°﹣α,且△BCD为等边三角形,在△ABD与△ACD中∴△ABD≌△ACD(SSS),∴∠BAD=∠CAD=∠BAC=α,∵∠BCE=150°,∴∠BEC=180°﹣(30°﹣α)﹣150°=α=∠BAD,在△ABD和△EBC中∴△ABD≌△EBC(AAS),∴AB=BE,∴△ABE是等边三角形;(3)解:∵∠BCD=60°,∠BCE=150°,∴∠DCE=150°﹣60°=90°,∵∠DEC=45°,∴△DEC为等腰直角三角形,∴DC=CE=BC,∵∠BCE=150°,∴∠EBC=(180°﹣150°)=15°,∵∠EBC=30°﹣α=15°,∴α=30°.【点评】本题考查了全等三角形的性质和判定,等边三角形的性质和判定,等腰直角三角形的判定和性质的应用,注意:全等三角形的判定定理有SAS,ASA,AAS,SSS,全等三角形的性质是全等三角形的对应边相等,对应角相等.2.已知,Rt△ABC中,∠ACB=90°,∠CAB=30°.分别以AB、AC为边,向三角形外作等边△ABD和等边△ACE.(1)如图1,连接线段BE、CD.求证:BE=CD;(2)如图2,连接DE交AB于点F.求证:F为DE中点.【解答】证明:(1)∵△ABD和△ACE是等边三角形,∴AB=AD,AC=AE,∠DAB=∠EAC=60°,∴∠DAB+∠BAC=∠EAC+∠BAC,即∠DAC=∠BAE,在△DAC和△BAE中,,∴△DAC≌△BAE(SAS),∴DC=BE;(2)如图,作DG∥AE,交AB于点G,由∠EAC=60°,∠CAB=30°得:∠FAE=∠EAC+∠CAB=90°,∴∠DGF=∠FAE=90°,又∵∠ACB=90°,∠CAB=30°,∴∠ABC=60°,又∵△ABD为等边三角形,∠DBG=60°,DB=AB,∴∠DBG=∠ABC=60°,在△DGB和△ACB中,,∴△DGB≌△ACB(AAS),∴DG=AC,又∵△AEC为等边三角形,∴AE=AC,∴DG=AE,在△DGF和△EAF中,,∴△DGF≌△EAF(AAS),∴DF=EF,即F为DE中点.3.在课外小组活动时,小慧拿来一道题(原问题)和小东、小明交流.原问题:如图1,已知△ABC,∠ACB=90°,∠ABC=45°,分别以AB、BC为边向外作△ABD与△BCE,且DA=DB,EB=EC,∠ADB=∠BEC=90°,连接DE交AB于点F.探究线段DF与EF的数量关系.小慧同学的思路是:过点D作DG⊥AB于G,构造全等三角形,通过推理使问题得解.小东同学说:我做过一道类似的题目,不同的是∠ABC=30°,∠ADB=∠BEC=60度.小明同学经过合情推理,提出一个猜想,我们可以把问题推广到一般情况.请你参考小慧同学的思路,探究并解决这三位同学提出的问题:(1)写出原问题中DF与EF的数量关系;(2)如图2,若∠ABC=30°,∠ADB=∠BEC=60°,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明;(3)如图3,若∠ADB=∠BEC=2∠ABC,原问题中的其他条件不变,你在(1)中得到的结论是否发生变化?请写出你的猜想并加以证明.【分析】本题的解题思路是通过构建全等三角形来求解.先根据直角三角形的性质,等边三角形的性质得到一些隐含的条件,然后根据所得的条件来证明所构建的三角形的全等;再根据全等三角形的对应边相等得出DF=EF的猜想.【解答】解:(1)DF=EF.(2)猜想:DF=FE.证明:过点D作DG⊥AB于G,则∠DGB=90度.∵DA=DB,∠ADB=60度.∴AG=BG,△DBA是等边三角形.∴DB=BA.∵∠ACB=90°,∠ABC=30°,∴AC=AB=BG.在Rt△DBG和Rt△BAC中∴Rt△DBG≌Rt△BAC(HL).∴DG=BC.∵BE=EC,∠BEC=60°,∴△EBC是等边三角形.∴BC=BE,∠CBE=60度.∴DG=BE,∠ABE=∠ABC+∠CBE=90°.∵∠DFG=∠EFB,∠DGF=∠EBF,在△DFG和△EFB中∴△DFG≌△EFB(AAS).∴DF=EF.(3)猜想:DF=FE.证法一:过点D作DH⊥AB于H,连接HC,HE,HE交CB于K,则∠DHB=90度.∵DA=DB,∴AH=BH,∠1=∠HDB.∵∠ACB=90°,∴HC=HB.在△HBE和△HCE中∴△HBE≌△HCE(SSS).∴∠2=∠3,∠4=∠BEH.∴HK⊥BC.∴∠BKE=90°.∴∠3+∠ABC=90°∵∠ADB=∠BEC=2∠ABC,∴∠HDB=∠BEH=∠ABC.∴∠DBC=∠DBH+∠ABC=∠DBH+∠HDB=90°,∴∠3=∠DBH∠EBH=∠EBK+∠ABC=∠EBK+∠BEK=90°=∠DHB又∵HB是公共边,所以△DBH≌△EHB∴DH=BE同理可以证明△DHF≌△EBF∴DF=EF.4.已知,点P是Rt△ABC斜边AB上一动点(不与A、B重合),分别过A、B向直线CP作垂线,垂足分别为E、F,Q为斜边AB的中点.(1)如图1,当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系是QE=QF;(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.【分析】(1)根据AAS推出△AEQ≌△BFQ,推出AE=BF即可;(2)延长EQ交BF于D,求出△AEQ≌△BDQ,根据全等三角形的性质得出EQ=QD,根据直角三角形斜边上中点性质得出即可;(3)延长EQ交FB于D,求出△AEQ≌△BDQ,根据全等三角形的性质得出EQ=QD,根据直角三角形斜边上中点性质得出即可.【解答】解:(1)如图1,当点P与点Q重合时,AE与BF的位置关系是AE∥BF,QE与QF的数量关系是AE=BF,理由是:∵Q为AB的中点,∴AQ=BQ,∵AE⊥CQ,BF⊥CQ,∴AE∥BF,∠AEQ=∠BFQ=90°,在△AEQ和△BFQ中∴△AEQ≌△BFQ,∴QE=QF,故答案为:AE∥BF,QE=QF;(2)QE=QF,证明:延长EQ交BF于D,∵由(1)知:AE∥BF,∴∠AEQ=∠BDQ,在△AEQ和△BDQ中∴△AEQ≌△BDQ,∴EQ=DQ,∵∠BFE=90°,∴QE=QF;,(3)当点P在线段BA(或AB)的延长线上时,此时(2)中的结论成立,证明:延长EQ交FB于D,如图3,∵由(1)知:AE∥BF,∴∠AEQ=∠BDQ,在△AEQ和△BDQ中∴△AEQ≌△BDQ,∴EQ=DQ,∵∠BFE=90°,∴QE=QF.5.在△ABC中,AB=AC,∠BAC=60°,点E为直线AC上一点,D为直线BC上的一点,且DA=DE.当点D在线段BC上时,如图①,易证:BD+AB=AE;当点D在线段CB的延长线上时,如图②、图③,猜想线段BD,AB和AE之间又有怎样的数量关系?写出你的猜想,并选择一种情况给予证明.【分析】图②中,论:BD+AE=AB,作EM∥AB交BC于M,先证明△EMC是等边三角形得CE=CM,AE=BM,再证明△ABD≌△DEM,得DB=EM=MC由此可以对称结论.图③中,结论:BD﹣AE=AB,证明方法类似.【解答】解;如图②中,结论:BD+AE=AB.理由:作EM∥AB交BC于M,∵△ABC是等边三角形,∴∠ABC=∠C=∠BAC=60°,AB=BC=AC,∴∠CEM=∠CAB=60°,∠CME=∠CBA=60°,∴△CME是等边三角形,∴CE=CM=EM,∠EMC=60°,∴AE=BM,∵DA=DE,∴∠DAE=∠DEA,∴∠BAC+∠DAB=∠C+∠EDM,∴∠DAB=∠EDM,∵∠ABD=180°﹣∠ABC=120°,∠EMD=180°﹣∠EMC=120°,∴∠ABD=∠DME,在△ABD和△DEM中,,∴△ABD≌△DEM,∴DB=EM=CM,∴DB+AE=CM+BM=BC=AB.如图③中,结论:BD﹣AE=AB.理由:作EM∥AB交BC于M,∵△ABC是等边三角形,∴∠ABC=∠C=∠BAC=60°,AB=BC=AC,∴∠CEM=∠CAB=60°,∠CME=∠CBA=60°,∴△CME是等边三角形,∴CE=CM=EM,∠EMC=∠MEC=60°,∴AE=BM,∵DA=DE,∴∠DAE=∠DEA,∴∠C+∠ADC=∠MEC+∠EDDEM,∴∠ADB=∠DEM,∵∠ABD=180°﹣∠ABC=120°,∠EMD=180°﹣∠EMC=120°,∴∠ABD=∠DME,在△ABD和△DEM中,,∴△ABD≌△DME,∴DB=EM=CM,∴DB﹣AE=CM﹣BM=BC=AB.【点评】本题考查全等三角形的判定和性质、等边三角形的性质、等腰三角形的性质等知识,解题的关键是添加辅助线构造全等三角形,注意形变证明方法基本不变,属于中考常考题型.6.如图1,我们定义:在四边形ABCD中,若AD=BC,且∠ADB+∠BCA=180°,则把四边形ABCD叫做互补等对边四边形.(1)如图2,在等腰△ABE中,AE=BE,四边形ABCD是互补等对边四边形,求证:∠ABD=∠BAC=∠AEB.(2)如图3,在非等腰△ABE中,若四边形ABCD仍是互补等对边四边形,试问∠ABD=∠BAC=∠AEB是否仍然成立?若成立,请加以证明;若不成立,请说明理由.【分析】(1)根据等边对等角可得∠EAB=∠EBA,根据四边形ABCD是互补等对边四边形,可得AD=BC,根据SAS可证△ABD≌△BAC,根据全等三角形的性质可得∠ABD=∠BAC,再根据等腰三角形的性质即可证明;(2)仍然成立;理由如下:如图所示:过点A、B分别作BD的延长线与AC的垂线,垂足分别为G、F,证明△AGD≌△BFC,得到AG=BF,又AB=BA,所以△ABC≌△BAF,得到∠ABD=∠BAC,根据∠ADB+∠BCA=180°,得到∠EDB+∠ECA=180°,进而得到∠AEB+∠DHC=180°,由∠DHC+∠BHC=180°,所以∠AEB=∠BHC.因为∠BHC=∠BAC+∠ABD,∠ABD=∠BAC,所以∠ABD=∠BAC=∠AEB.【解答】解:(1)∵AE=BE,∴∠EAB=∠EBA,∵四边形ABCD是互补等对边四边形,∴AD=BC,在△ABD和△BAC中,,∴△ABD≌△BAC(SAS),∴∠ADB=∠BCA,又∵∠ADB+∠BCA=180°,∴∠ADB=∠BCA=90°,在△ABE中,∵∠EAB=∠EBA==90°﹣∠AEB,∴∠ABD=90°﹣∠EAB=90°﹣(90°﹣∠AEB)=∠AEB,同理:∠BAC=∠AEB,∴∠ABD=∠BAC=∠AEB;(2)仍然成立;理由如下:如图③所示:过点A、B分别作BD的延长线与AC的垂线,垂足分别为G、F,∵四边形ABCD是互补等对边四边形,∴AD=BC,∠ADB+∠BCA=180°,又∠ADB+ADG=180°,∴∠BCA=∠ADC,又∵AG⊥BD,BF⊥AC,∴∠AGD=∠BFC=90°,在△AGD和△BFC中,∴△AGD≌△BFC,∴AG=BF,在△ABG和△BAF中,∴△ABG≌△BAF,∴∠ABD=∠BAC,∵∠ADB+∠BCA=180°,∴∠EDB+∠ECA=180°,∴∠AEB+∠DHC=180°,∵∠DHC+∠BHC=180°,∴∠AEB=∠BHC.∵∠BHC=∠BAC+∠ABD,∠ABD=∠BAC,∴∠ABD=∠BAC=∠AEB.【点评】本题考查了等腰三角形的性质、全等三角形的判定与性质,解决本题的关键是根据SAS证明△ABD≌△BAC.7.已知△ABC为等边三角形,点D为直线BC上的一动点(点D不与B、C重合),以AD为边作等边△ADE(顶点A、D、E按逆时针方向排列),连接CE.(1)如图1,当点D在边BC上时,求证:①BD=CE,②AC=CE+CD;(2)如图2,当点D在边BC的延长线上且其他条件不变时,结论AC=CE+CD是否成立?若不成立,请写出AC、CE、CD之间存在的数量关系,并说明理由;(3)如图3,当点D在边BC的反向延长线上且其他条件不变时,补全图形,并直接写出AC、CE、CD之间存在的数量关系.【分析】(1)根据等边三角形的性质及等式的性质就可以得出△ABD≌△ACE,从而得出结论;(2)根据等边三角形的性质及等式的性质就可以得出△ABD≌△ACE,就可以得出BD=CE,就可以得出AC=CE﹣CD;(3)先根据条件画出图形,根据等边三角形的性质及等式的性质就可以得出△ABD≌△ACE,就可以得出BD=CE,就可以得出AC=CD﹣CE.【解答】解:(1)∵△ABC和△ADE都是等边三角形,∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°.∴∠BAC﹣∠CAD=∠DAE﹣∠CAD,即∠BAD=∠CAE.在△ABD和△ACE中,,∴△ABD≌△ACE(SAS),∴BD=CE.∵BC=BD+CD,AC=BC,∴AC=CE+CD;(2)AC=CE+CD不成立,AC、CE、CD之间存在的数量关系是:AC=CE﹣CD.理由:∵△ABC和△ADE都是等边三角形,∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°.∴∠BAC+∠CAD=∠DAE+∠CAD,∴∠BAD=∠CAE在△ABD和△ACE中,∴△ABD≌△ACE(SAS)∴BD=CE∴CE﹣CD=BD﹣CD=BC=AC,∴AC=CE﹣CD;(3)补全图形(如图)AC、CE、CD之间存在的数量关系是:AC=CD﹣CE.理由:∵△ABC和△ADE都是等边三角形,∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°.∴∠BAC﹣∠BAE=∠DAE﹣∠BAE,∴∠BAD=∠CAE在△ABD和△ACE中,∴△ABD≌△ACE(SAS)∴BD=CE.∵BC=CD﹣BD,∴BC=CD﹣CE,∴AC=CD﹣CE.【点评】本题考查了等边三角形的性质的运用,等式的性质的运用,全等三角形的判定及性质的运用,解答时证明三角形全等是关键.8.如图,已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE,∠DAB=∠CAE,连接DC与BE.G、F分别是DC与BE的中点.(1)求证:DC=BE;(2)当∠DAB=80°,求∠AFG的度数;(3)若∠DAB=α,则∠AFG与α的数量关系是.【分析】(1)根据等式的性质就可以得出∠DAC=∠BAE.就可以得出△ADC≌△ABE就可以得出DC=BE;(2)连接AG,根据条件就可以得出△ADG≌△ABF,就可以求出AG=AF,∠GAF=∠DAB,由等腰三角形的性质就可以求出∠AFG的值,(3)连接AG,根据条件就可以得出△ADG≌△ABF,就可以求出AG=AF,∠GAF=∠DAB,由等腰三角形的性质就可以表示∠AFG与a的关系.【解答】解:(1)∵∠DAB=∠CAE,∴∠DAB+∠BAC=∠CAE+∠BAC,∴∠DAC=∠BAE.在△ADC和△ABE中,∴△ADC≌△ABE(SAS),∴DC=BE;(2)连接AG.∵△ADC≌△ABE,∴∠ADC=∠ABE.AD=AB.∵G、F分别是DC与BE的中点,∴DG=DC,BF=BE,∴DG=BF.在△ADG和△ABF中,∴△ADG≌△ABF(SAS),∴AG=AF,∠DAG=∠BAF,∴∠AGF=∠AFG,∠DAG﹣∠BAG=∠BAF﹣∠BAG,∴∠DAB=∠GAF.∵∠DAB=80°,∴∠GAF=80°.∵∠GAF+∠AFG+∠AGF=180°,∴∠AFG=50°.答:∠AFG=50°;(3)∵∠DAB=α,∴∠GAF=α.∵∠GAF+∠AFG+∠AGF=180°,∴α+2∠AFG=180°,∴∠AFG=90°﹣α.故答案为:∠AFG=50°,90°﹣α.【点评】本题考查了全等三角形的判定及性质的运用,等式的性质的运用,等腰三角形的性质的运用,三角形内角和定理的运用,解答时证明三角形全等是关键.9.△ABC是等边三角形,点D、E分别在边AB、BC上,CD、AE交于点F,∠AFD=60°.(1)如图1,求证:BD=CE;(2)如图2,FG为△AFC的角平分线,点H在FG的延长线上,HG=CD,连接HA、HC,求证:∠AHC=60°;(3)在(2)的条件下,若AD=2BD,FH=9,求AF长.【分析】(1)根据等边三角形的性质得出AB=BC,∠BAC=∠C=∠ABE=60°,根据SAS推出△ABE≌△BCD,即可证得结论;(2)根据角平分线的性质定理证得CM=CN,利用∠CEM=∠ACE+∠CAE=60°+∠CAE,∠CGN=∠AFH+∠CAE=60°+∠CAE,得出∠CEM=∠CGN,然后根据AAS证得△ECM≌△GCN,得出CG=CE,EM=GN,∠ECM=∠GCN,进而证得△AMC≌△HNC,得出∠ACM=∠HCN,AC=HC,从而证得△ACH是等边三角形,证得∠AHC=60°;(3)在FH上截取FK=FC,得出△FCK是等边三角形,进一步得出FC=KC=FK,∠ACF=∠HCK,证得△AFC≌△HKC得出AF=HK,从而得到HF=AF+FC=9,由AD=2BD 可知AG=2CG,再由=,根据等高三角形面积比等于底的比得出===2,再由AF+FC=9求得.【解答】解:(1)如图1,∵△ABC是等边三角形,∴∠B=∠ACE=60°BC=AC,∵∠AFD=∠CAE+∠ACD=60°∠BCD+∠ACD=∠ACB=60°,∴∠BCD=∠CAE,在△ABE和△BCD中,∴△ABE≌△BCD(ASA),∴BD=CE;(2)如图2,作CM⊥AE交AE的延长线于M,作CN⊥HF于N,∵∠EFC=∠AFD=60°∴∠AFC=120°,∵FG为△AFC的角平分线,∴∠CFH=∠AFH=60°,∴∠CFH=∠CFE=60°,∵CM⊥AE,CN⊥HF,∴CM=CN,∵∠CEM=∠ACE+∠CAE=60°+∠CAE,∠CGN=∠AFH+∠CAE=60°+∠CAE,∴∠CEM=∠CGN,在△ECM和△GCN中∴△ECM≌△GCN(AAS),∴CE=CG,EM=GN,∠ECM=∠GCN,∴∠MCN=∠ECG=60°,∵△ABE≌△BCD,∵AE=CD,∵HG=CD,∴AE=HG,∴AE+EM=HG+GN,即AM=HN,在△AMC和△HNC中∴△AMC≌△HNC(SAS),∴∠ACM=∠HCN,AC=HC,∴∠ACM﹣∠ECM=∠HCN﹣∠GCN,即∠ACE=∠HCG=60°,∴△ACH是等边三角形,∴∠AHC=60°;(3)如图3,在FH上截取FK=FC,∵∠HFC=60°,∴△FCK是等边三角形,∴∠FKC=60°,FC=KC=FK,∵∠ACH=60°,∴∠ACF=∠HCK,在△AFC和△HKC中∴△AFC≌△HKC(SAS),∴AF=HK,∴HF=AF+FC=9,∵AD=2BD,BD=CE=CG,AB=AC,∴AG=2CG,∴==,作GW⊥AE于W,GQ⊥DC于Q,∵FG为△AFC的角平分线,∴GW=GQ,∵===,∴AF=2CF,∴AF=6.【点评】本题考查了全等三角形的判定和性质,等边三角形的判定和性质,角平分线的性质,找出辅助线根据全等三角形和等边三角形是解题的关键.10.如图1,△ABE是等腰三角形,AB=AE,∠BAE=45°,过点B作BC⊥AE于点C,在BC上截取CD=CE,连接AD、DE并延长AD交BE于点P;(1)求证:AD=BE;(2)试说明AD平分∠BAE;(3)如图2,将△CDE绕着点C旋转一定的角度,那么AD与BE的位置关系是否发生变化,说明理由.【分析】(1)利用SAS证明△BCE≌△ACD,根据全等三角形的对应边相等得到AD=BE.(2)根据△BCE≌△ACD,得到∠EBC=∠DAC,由∠BDP=∠ADC,得到∠BPD=∠DCA=90°,利用等腰三角形的三线合一,即可得到AD平分∠BAE;(3)AD⊥BE不发生变化.由△BCE≌△ACD,得到∠EBC=∠DAC,由对顶角相等得到∠BFP=∠ACF,根据三角形内角和为180°,所以∠BPF=∠ACF=90°,即AD⊥BE.【解答】解:(1)∵BC⊥AE,∠BAE=45°,∴∠CBA=∠CAB,∴BC=CA,在△BCE和△ACD中,∴△BCE≌△ACD,∴AD=BE.(2)∵△BCE≌△ACD,∴∠EBC=∠DAC,∵∠BDP=∠ADC,∴∠BPD=∠DCA=90°,∵AB=AE,∴AD平分∠BAE.(3)AD⊥BE不发生变化.如图2,∵△BCE≌△ACD,∴∠EBC=∠DAC,∵∠BFP=∠ACF,∴∠BPF=∠ACF=90°,∴AD⊥BE.【点评】本题考查了全等三角形的性质定理与判定定理,解决本题的关键是证明△BCE≌△ACD.11.情境观察:如图1,△ABC中,AB=AC,∠BAC=45°,CD⊥AB,AE⊥BC,垂足分别为D、E,CD与AE交于点F.①写出图1中所有的全等三角形△ABE≌△ACE,△ADF≌△CDB;②线段AF与线段CE问题探究:如图2,△ABC中,∠BAC=45°,BAC,AD⊥CD,垂足为D,AD与BC交于点E.求证:AE=2CD.拓展延伸:如图3,△ABC中,∠BAC=45°,AB=BC,点D在AC上,∠EDC=∠BAC,DE⊥CE,垂足为E,DE与BC交于点F.求证:DF=2CE.要求:请你写出辅助线的作法,并在图3中画出辅助线,不需要证明.【分析】情境观察:①由全等三角形的判定方法容易得出结果;②由全等三角形的性质即可得出结论;问题探究:延长AB、CD交于点G,由ASA证明△ADC≌△ADG,得出对应边相等CD=GD,即CG=2CD,证出∠BAE=∠BCG,由ASA证明△ADC≌△CBG,得出AE=CG=2CD即可.拓展延伸:作DG⊥BC交CE的延长线于G,同上证明三角形全等,得出DF=CG即可.【解答】情境观察:解:①图1中所有的全等三角形为△ABE≌△ACE,△ADF≌△CDB;故答案为:△ABE≌△ACE,△ADF≌△CDB②线段AF与线段CE的数量关系是:AF=2CE;故答案为:AF=2CE.问题探究:证明:延长AB、CD交于点G,如图2所示:∵AD平分∠BAC,∴∠CAD=∠GAD,∵AD⊥CD,∴∠ADC=∠ADG=90°,在△ADC和△ADG中,,∴△ADC≌△ADG(ASA),∴CD=GD,即CG=2CD,∵∠BAC=45°,AB=BC,∴∠ABC=90°,∴∠CBG=90°,∴∠G+∠BCG=90°,∵∠G+∠BAE=90°,∴∠BAE=∠BCG,在△ABE和△CBG中,,∴△ADC≌△CBG中(ASA),∴AE=CG=2CD.拓展延伸:解:作DG⊥BC交CE的延长线于G,如图3所示.【点评】本题考查了全等三角形的判定与性质、等腰三角形的性质等知识;熟练掌握等腰三角形的性质,证明三角形全等是解决问题的关键.12.如图1,点P、Q分别是等边△ABC边AB、BC上的动点(端点除外),点P从顶点A、点Q从顶点B同时出发,且它们的运动速度相同,连接AQ、CP交于点M.(1)求证:△ABQ≌△CAP;(2)如图1,当点P、Q分别在AB、BC边上运动时,∠QMC变化吗?若变化,请说理由;若不变,求出它的度数.(3)如图2,若点P、Q在分别运动到点B和点C后,继续在射线AB、BC上运动,直线AQ、CP交点为M,则∠QMC=120度.(直接填写度数)【分析】(1)根据等边三角形的性质,利用SAS证明△ABQ≌△CAP;(2)由△ABQ≌△CAP根据全等三角形的性质可得∠BAQ=∠ACP,从而得到∠QMC=60°;(3)由△ABQ≌△CAP根据全等三角形的性质可得∠BAQ=∠ACP,从而得到∠QMC=120°.【解答】(1)证明:∵△ABC是等边三角形∴∠ABQ=∠CAP,AB=CA,又∵点P、Q运动速度相同,∴AP=BQ,在△ABQ与△CAP中,,∴△ABQ≌△CAP(SAS);(2)解:点P、Q在运动的过程中,∠QMC不变.理由:∵△ABQ≌△CAP,∴∠BAQ=∠ACP,∵∠QMC=∠ACP+∠MAC,∴∠QMC=∠BAQ+∠MAC=∠BAC=60°;(3)解:∵△ABQ≌△CAP,∴∠BAQ=∠ACP,∵∠QMC=∠BAQ+∠APM,∴∠QMC=∠ACP+∠APM=180°﹣∠PAC=180°﹣60°=120°.故答案为:120°.【点评】本题考查了等边三角形的性质,全等三角形的判定与性质,熟练掌握全等三角形的判定是解题的关键.13.如图,在等腰Rt△ABC中,∠C=90°,D是斜边上AB上任一点,AE⊥CD于E,BF⊥CD交CD的延长线于F,CH⊥AB于H点,交AE于G.(1)试说明AH=BH(2)求证:BD=CG.(3)探索AE与EF、BF之间的数量关系.【分析】(1)根据等腰三角形的三线合一证明;(2)证明△ACG≌△CBD,根据全等三角形的性质证明;(3)证明△ACE≌△CBF即可.【解答】证明:(1)∵AC=BC,CH⊥AB,∴AH=BH;(2)∵ABC为等腰直角三角形,CH⊥AB,∴∠ACG=45°,∵∠CAG+∠ACE=90°,∠BCF+∠ACE=90°,∴∠CAG=∠BCF,在△ACG和△CBD中,,∴△ACG≌△CBD(ASA),∴BD=CG;(3)AE=EF+BF,理由如下:在△ACE和△CBF中,,∴△ACE≌△CBF,∴AE=CF,CE=BF,∴AE=CF=CE+EF=BF+EF.【点评】本题考查的是全等三角形的判定和性质,掌握全等三角形的判定定理和性质定理是解题的关键.14.在△ABC中,AB=AC,∠BAC=100°,点D在BC边上,△ABD和△AFD关于直线AD对称,∠FAC的平分线交BC于点G,连接FG.(1)求∠DFG的度数;(2)设∠BAD=θ,①当θ为何值时,△DFG为等腰三角形;②△DFG有可能是直角三角形吗?若有,请求出相应的θ值;若没有,请说明理由.【分析】(1)由轴对称可以得出△ADB≌△ADF,就可以得出∠B=∠AFD,AB=AF,在证明△AGF≌△AGC就可以得出∠AFG=∠C,就可以求出∠DFG的值;(2)①当GD=GF时,就可以得出∠GDF═80°,根据∠ADG=40+θ,就有40°+80°+40°+θ+θ=180°就可以求出结论;当DF=GF时,就可以得出∠GDF=50°,就有40°+50°+40°+2θ=180°,当DF=DG时,∠GDF=20°,就有40°+20°+40°+2θ=180°,从而求出结论;②有条件可以得出∠DFG=80°,当∠GDF=90°时,就有40°+90°+40°+2θ=180°就可以求出结论,当∠DGF=90°时,就有∠GDF=10°,得出40°+10°+40°+2θ=180°求出结论.【解答】解:(1)∵AB=AC,∠BAC=100°,∴∠B=∠C=40°.∵△ABD和△AFD关于直线AD对称,∴△ADB≌△ADF,∴∠B=∠AFD=40°,AB=AF∠BAD=∠FAD=θ,∴AF=AC.∵AG平分∠FAC,∴∠FAG=∠CAG.在△AGF和△AGC中,,∴△AGF≌△AGC(SAS),∴∠AFG=∠C.∵∠DFG=∠AFD+∠AFG,∴∠DFG=∠B+∠C=40°+40°=80°.答:∠DFG的度数为80°;(2)①当GD=GF时,∴∠GDF=∠GFD=80°.∵∠ADG=40°+θ,∴40°+80°+40°+θ+θ=180°,∴θ=10°.当DF=GF时,∴∠FDG=∠FGD.∵∠DFG=80°,∴∠FDG=∠FGD=50°.∴40°+50°+40°+2θ=180°,∴θ=25°.当DF=DG时,∴∠DFG=∠DGF=80°,∴∠GDF=20°,∴40°+20°+40°+2θ=180°,∴θ=40°.∴当θ=10°,25°或40°时,△DFG为等腰三角形;②当∠GDF=90°时,∵∠DFG=80°,∴40°+90°+40°+2θ=180°,∴θ=5°.当∠DGF=90°时,∵∠DFG=80°,∴∠GDF=10°,∴40°+10°+40°+2θ=180°,∴θ=45°∴当θ=5°或45°时,△DFG为直角三角形.【点评】本题考查了轴对称的性质的运用,全等三角形的判定及性质的运用,等腰三角形的判定及性质的运用,直角三角形的判定及性质的运用,解答时证明三角形的全等是关键.15.如图,在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过B 作BE⊥CD交CD的延长线于点E,连接AE,过A作AF⊥AE交CD于点F.(1)求证:AE=AF;(2)求证:CD=2BE+DE.【分析】(1)通过证△AEB≌△AFC(SAS),得到AE=AF;(2)如图,过点A作AG⊥EC,垂足为G,通过证△BED≌△AGD(AAS),得到ED=GD,BE=AG,易证CF=BE=AG=GF.因为CD=DG+GF+FC,所以CD=DE+BE+BE,故CD=2BE+DE.【解答】证明:(1)如图,∵∠BAC=90°,AF⊥AE,∴∠EAB+∠BAF=∠BAF+∠FAC=90°,∴∠EAB=∠FAC,∵BE⊥CD,∴∠BEC=90°,∴∠EBD+∠EDB=∠ADC+∠ACD=90°,∵∠EDB=∠ADC,∴∠EBA=∠ACF,∴在△AEB与△AFC中,,∴△AEB≌△AFC(ASA),∴AE=AF;(2)如图,过点A作AG⊥EC,垂足为G.∵AG⊥EC,BE⊥CE,∴∠BED=∠AGD=90°,∵点D是AB的中点,∴BD=AD.∴在△BED与△AGD中,,∴△BED≌△AGD(AAS),∴ED=GD,BE=AG,∵AE=AF∴∠AEF=∠AFE=45°∴∠FAG=45°∴∠GAF=∠GFA,∴GA=GF,∴CF=BE=AG=GF,∵CD=DG+GF+FC,∴CD=DE+BE+BE,∴CD=2BE+DE.【点评】本题考查了全等三角形的判定与性质.在应用全等三角形的判定时,要注意三角形间的公共边和公共角,必要时添加适当辅助线构造三角形.16.如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC,垂足是D,AE平分∠BAD,交BC于点E.在△ABC外有一点F,使FA⊥AE,FC⊥BC.(1)求证:BE=CF;(2)在AB上取一点M,使BM=2DE,连接MC,交AD于点N,连接ME.求证:①ME⊥BC;②CM平分∠ACE.【分析】(1)根据等腰直角三角形的性质求出∠B=∠ACB=45°,再求出∠ACF=45°,从而得到∠B=∠ACF,根据同角的余角相等求出∠BAE=∠CAF,然后利用“角边角”证明△ABE和△ACF全等,根据全等三角形对应边相等证明即可;(2)①过点E作EH⊥AB于H,求出△BEH是等腰直角三角形,然后求出HE=BH,再根据角平分线上的点到角的两边距离相等可得DE=HE,然后求出HE=HM,从而得到△HEM是等腰直角三角形,再根据等腰直角三角形的性质求解即可;②求出∠CAE=∠CEA=67.5°,根据等角对等边可得AC=CE,再利用“HL”证明Rt△ACM和Rt△ECM全等即可得到结论.【解答】证明:(1)∵∠BAC=90°,AB=AC,∴∠B=∠ACB=45°,∵FC⊥BC,∴∠BCF=90°,∴∠ACF=90°﹣45°=45°,∴∠B=∠ACF,∵∠BAC=90°,FA⊥AE,∴∠BAE+∠CAE=90°,∠CAF+∠CAE=90°,∴∠BAE=∠CAF,在△ABE和△ACF中,,∴△ABE≌△ACF(ASA),∴BE=CF;(2)①如图,过点E作EH⊥AB于H,则△BEH是等腰直角三角形,∴HE=BH,∠BEH=45°,∵AE平分∠BAD,AD⊥BC,∴DE=HE,∴DE=BH=HE,∵BM=2DE,∴HE=HM,∴△HEM是等腰直角三角形,∴∠MEH=45°,∴∠BEM=45°+45°=90°,∴ME⊥BC;②由题意得,∠CAE=45°+×45°=67.5°,∴∠CEA=180°﹣45°﹣67.5°=67.5°,∴∠CAE=∠CEA=67.5°,∴AC=CE,在Rt△ACM和Rt△ECM中,,∴Rt△ACM≌Rt△ECM(HL),∴∠ACM=∠ECM,∴CM平分∠ACE.【点评】本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,角平分线上的点到角的两边距离相等的性质,熟记性质并作辅助线构造出等腰直角三角形和全等三角形是解题的关键,难点在于最后一问根据角的度数得到相等的角.17.如图,在△ABC中,已知∠ABC=45°,过点C作CD⊥AB于点D,过点B作BM ⊥AC于点M,CD与BM相交于点E,且点E是CD的中点,连接MD,过点D作DN⊥MD,交BM于点N.(1)求证:△DBN≌△DCM;(2)请探究线段NE、ME、CM之间的数量关系,并证明你的结论.【分析】(1)根据两角夹边相等的两个三角形全等即可证明.(2)结论:NE﹣ME=CM.作DF⊥MN于点F,由(1)△DBN≌△DCM 可得DM=DN,由△DEF≌△CEM,推出ME=EF,CM=DF,由此即可证明.【解答】(1)证明:∵∠ABC=45°,CD⊥AB,∴∠ABC=∠DCB=45°,∴BD=DC,∵∠BDC=∠MDN=90°,∴∠BDN=∠CDM,∵CD⊥AB,BM⊥AC,∴∠ABM=90°﹣∠A=∠ACD,在△DBN和△DCM中,,∴△DBN≌△DCM.(2)结论:NE﹣ME=CM.证明:由(1)△DBN≌△DCM 可得DM=DN.作DF⊥MN于点F,又ND⊥MD,∴DF=FN,在△DEF和△CEM中,,∴△DEF≌△CEM,∴ME=EF,CM=DF,∴CM=DF=FN=NE﹣FE=NE﹣ME.【点评】本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是熟练掌握全等三角形的判定和性质,属于中考常考题型.18.问题情境:如图①,在△ABD与△CAE中,BD=AE,∠DBA=∠EAC,AB=AC,易证:△ABD≌△CAE.(不需要证明)特例探究:如图②,在等边△ABC中,点D、E分别在边BC、AB上,且BD=AE,AD与CE交于点F.求证:△ABD≌△CAE.归纳证明:如图③,在等边△ABC中,点D、E分别在边CB、BA的延长线上,且BD=AE.△ABD与△CAE是否全等?如果全等,请证明;如果不全等,请说明理由.拓展应用:如图④,在等腰三角形中,AB=AC,点O是AB边的垂直平分线与AC 的交点,点D、E分别在OB、BA的延长线上.若BD=AE,∠BAC=50°,∠AEC=32°,求∠BAD的度数.【分析】特例探究:利用等边三角形的三条边都相等、三个内角都是60°的性质推知AB=AC,∠DBA=∠EAC=60°,然后结合已知条件BD=AE,利用全等三角形的判定定理SAS证得△ABD≌△CAE.归纳证明:△ABD与△CAE全等.利用等边三角形的三条边都相等、三个内角都是60°的性质以及三角形外角定理推知AB=AC,∠DBA=∠EAC=120°,然后结合已知条件BD=AE,利用全等三角形的判定定理SAS证得△ABD≌△CAE;拓展应用:利用全等三角形(△ABD≌△CAE)的对应角∠BDA=∠AEC=32°,然后由三角形的外角定理求得∠BAD的度数.【解答】特例探究:证明:∵△ABC是等边三角形,∴AB=AC,∠DBA=∠EAC=60°,在△ABD与△CAE中,,∴△ABD≌△CAE(SAS);解:归纳证明:△ABD与△CAE全等.理由如下:∵在等边△ABC中,AB=AC,∠ABC=∠BAC=60°,∴∠DBA=∠EAC=120°.在△ABD与△CAE中,,∴△ABD≌△CAE(SAS);拓展应用:∵点O在AB的垂直平分线上,∴OA=OB,∴∠OBA=∠BAC=50°,∴∠EAC=∠DBC.在△ABD与△CAE中,,∴△ABD≌△CAE(SAS),∴∠BDA=∠AEC=32°,∴∠BAD=∠OBA﹣∠BDA=18°.【点评】本题考查了全等三角形的判定与性质,等边三角形的性质,线段垂直平分线的性质等知识点.在证明两个三角形全等时,一定要找准对应角和对应边.19.情境创设:如图1,两块全等的直角三角板,△ABC≌△DEF,且∠C=∠F=90°,现如图放置,则∠ABE=90°.问题探究:如图2,△ABC中,AH⊥BC于H,以A为直角顶点,分别以AB、AC为直角边,向△ABC形外作等腰直角△ABE和等腰直角△ACF,过点E、F作射线HA的垂线,垂足分别为M、N,试探究线段EM和FN之间的数量关系,并说明理由.拓展延伸:如图3,△ABC中,AH⊥BC于H,以A为直角顶点,分别以AB、AC为一边,向△ABC形外作正方形ABME和正方形ACNF,连接E、F交射线HA于G点,试探究线段EG和FG之间的数量关系,并说明理由.【分析】(1)求出∠A=∠EDF,∠A+∠ABC=90°,推出∠EDF+∠ADC=90°,求出∠ADE的度数即可;(2)根据全等三角形的判定得出△EAM≌△ABH,进而求出EM=AH.同理AH=FN,因而EM=FN.(3)与(2)证法类似求出EG=FG,求出△EPG≌△FQG即可.【解答】解:(1)∵△ABC≌△DEF,∴∠A=∠EDF,∵∠C=90°,∴∠A+∠ABC=90°,∴∠EDF+∠ADC=90°,∴∠ADE=180°﹣90°=90°,故答案为:90;(2)解:EM=FN,如图2,理由如下:∵Rt△ABE是等腰三角形,∴EA=BA,∠BAE=90°,∴∠BAH+∠MAE=90°,∵AH⊥BC,EM⊥AH,∴∠AME=∠AHB=90°,∴∠ABH+∠BAH=90°,∴∠ABH=∠MAE,在△EAM与△ABH中∴△EAM≌△ABH(AAS),∴EM=AH.同理AH=FN.∴EM=FN;(3)解:EG=FG,如图3,作EP⊥HG,FQ⊥HG,垂足分别为P、Q,由(2)可得EP=FQ,∵EP⊥HG,FQ⊥HG,∴∠EPG=∠FQG=90°,在△EPG和△FQG中∵,∴△EPG≌△FQG,∴EG=FG.【点评】本题考查了全等三角形的性质和判定,注意:①全等三角形的对应角相等,对应边相等,②全等三角形的判定定理有SAS,ASA,AAS,SSS.。
八年级上册数学《第十二章全等三角形》专题全等三角形压轴题训练(30题)1.(2022秋•忠县期末)在△ABC中,点D、E分别在AB、AC边上,设BE与CD相交于点F.(1)如图①,设∠A=60°,BE、CD分别平分∠ABC、∠ACB,证明:DF=EF.(2)如图②,设BE⊥AC,CD⊥AB,点G在CD的延长线上,连接AG、AF;若∠G=∠6,BD=CD,证明:GD=DF.【分析】(1)在BC上截取BM=BD,连接FM,证明△BFD≌△BFM,△ECF≌△MCF,进而可以解决问题;(2)根据已知条件证明△BDF≌△CDA,进而可以解决问题.【解答】证明:(1)如图,在BC上截取BM=BD,连接FM,∵∠A=60,∴∠BFC=90°+60°÷2=120°,∴∠BFD=60°,∵BE平分∠ABC,∴∠1=∠2,在△BFD和△BFM中,BD=BM∠1=∠2,BF=BF∴△BFD≌△BFM(SAS),∴∠BFM=∠BFD=60°,DF=MF,∴∠CFM=120°﹣60°=60°,∵∠CFE=∠BFD=60°,∴∠CFM=∠CFE,∵CD平分∠ACB,∴∠3=∠4,又CF=CF,在△ECF和△MCF中,∠CFE=∠CFMFC=FC,∠3=∠4∴△ECF≌△MCF(ASA),∴EF=MF,∴DF=EF;(2)∵BE⊥AC,CD⊥AB,∴∠BDF=∠CDA=90°,∴∠1+∠BFD=90°,∠3+∠CFE=90°,∠BFD=∠CFE,∴∠1=∠3,∵BD=CD,在△BDF和△CDA中,∠BDF=∠CDABD=CD,∠1=∠3∴△BDF≌△CDA(ASA),∴DF=DA,∵∠ADF=90°,∴∠6=45°,∵∠G=∠6,∴∠5=45°∴∠G=∠5,∴GD=DA,∴GD=DF.【点评】本题属于三角形的综合题,考查了全等三角形的判定与性质,角平分线的性质,解决本题的关键是掌握全等三角形的判定与性质.2.如图,△ABC中,AB=AC,D为AC边上一点,E为AB延长线上一点,且CD=BE,DE与BC相交于点F.(1)求证:DF=EF.=5,求EG的长.(2)过点F作FG⊥DE,交线段CE于点G,若CE⊥AC,CD=4,S△EFG【分析】(1)过点D作DH∥AB交BC于点H,根据等腰三角形的性质及平行线的性质得到∠BEF=∠HDF,∠DHC=∠DCH,则DH=CD,结合∠BFE=∠HFD,即可利用AAS判定△BEF≌△HDF,根据全等三角形的性质即可得解;(2)根据三角形的面积公式求解即可.【解答】(1)过点D作DH∥AB交BC于点H,∵AB=AC,∴∠ABC=∠ACB,∵DH∥AB,∴∠DHC=∠ABC,∴∠DHC=∠ACB=∠DCH,∴DH=CD,∵CD=BE,∴DH=BE,∵DH∥AB,∴∠BEF=∠HDF,在△BEF和△HDF中,∠BFE=∠HFD∠BEF=∠HDFBE=DH,∴△BEF≌△HDF(AAS),∴DF=EF;(2)连接DG,∵DF=EF,FG⊥DE,∴S△DFG =S△EFG=5,∴S△DEG=10,∵CE⊥AC,CD=4,∴S△DEG =12EG•CD=12EG×4,∴12EG×4=10,∴EG=5.【点评】此题考查了全等三角形的判定与性质,利用AAS判定△BEF≌△HDF是解题的关键.3.如图1,在等腰直角三角形ABC中,AB=AC,∠BAC=90°,点P为BC边上的一个动点,连接AP,以AP为直角边,A为直角顶点,在AP右侧作等腰直角三角形PAD,连接CD.(1)当点P在线段BC上时(不与点B重合),求证:△BAP≌△CAD;(2)当点P在线段BC的延长线上时(如图2),试猜想线段BP和CD的数量关系与位置关系分别是什么?请给予证明.【分析】(1)证得∠BAP=∠CAD,根据SAS可证明△BAP≌△CAD;(2)可得∠BAP=∠CAD,由SAS可证明△BAP≌△CAD,可得BP=CD,∠B=∠ACD,则结论得证.【解答】(1)证明:∵∠BAC=∠PAD=90°,∴∠BAC﹣∠PAC=∠PAD﹣∠PAC,即:∠BAP=∠CAD,在△BAP和△CAD中AB=AC∠BAP=∠CAD,PA=DA∴△BAP≌△CAD(SAS);(2)猜想:BP=CD,BP⊥CD.证明:∵∠BAC=∠PAD=90°,∴∠BAC+∠PAC=∠PAD+∠PAC,即:∠BAP=∠CAD,在△BAP和△CAD中AB=AC∠BAP=∠CAD,PA=DA∴△BAP≌△CAD(SAS),∴BP=CD(全等三角形的对应边相等),∠B=∠ACD(全等三角形的对应角相等),∵∠B+∠ACB=90°,∴∠ACD+∠ACB=90°,即:BP⊥CD.【点评】本题考查了全等三角形的判定与性质,等腰直角三角形的性质,根据同角的余角相等求出两边的夹角相等是证明三角形全等的关键.4.在△ABC中,∠ABC=90°.点G在直线BC上,点E在直线AB上,且AG与CE相交于点F,过点A 作边AB的垂线AD,且CD∥AG,EB=AD,AE=BC.(1)如图①,当点E在△ABC的边AB上时,求∠DCE的度数;(2)如图②,当点E在线段BA的延长线上时,求证:AB=BG.【分析】(1)如图①,连接ED,根据已知条件得到△ADE≌△BEC(SAS),根据全等三角形的性质得到∠AED=∠BCE,ED=CE,于是得到结论;(2)如图②,连接DE,根据已知条件得到△ADE≌△BEC(SAS),根据全等三角形的性质得到∠AED =∠BCE,ED=CE,根据等腰三角形的性质得到∠EDC=∠ECD,推出AF平分∠DAE,于是得到结论.【解答】解:(1)如图①连接ED,∵AD⊥AB,∴∠DAE=90°,∵∠ABC=90°,∵AD=EB,AE=BC,∴△ADE≌△BEC(SAS),∴∠AED=∠BCE,ED=CE,∴∠AED+∠BEC=∠BCE+∠BEC;∴∠AED+∠CEB=90°,∴∠DEC=90°,∴∠DCE=45°;(2)如图②,连接DE,∵AD⊥AB,∴∠DAE=90°,∵∠ABC=90°,∴∠DAE=∠ABC,∵AD=EB,AE=BC,∴△ADE≌△BEC(SAS),∴∠ADE=∠BEC,ED=CE,∵ED=CE,∴∠EDC=∠ECD,即∠ADE+∠ADC=∠ECD,∴∠BEC+∠DAF=∠AFC,∵∠BEC+∠EAF=∠AFC,∴∠DAF=∠EAF,∴AF平分∠DAE,∵∠DAE=90°,∴∠EAF=45°,∵∠EAF=∠BAG,∴∠BAG=45°,∵∠ABC=90°,∴∠ABG=90°,∴∠BGA=∠BAG,∴AB=BG.【点评】本题考查了平行线的性质,全等三角形的判定和性质,角平分线的定义,等腰直角三角形的判定和性质,正确的识别图形是解题的关键.5.在Rt△ABC中,∠ABC=90°,点D是CB延长线上一点,点E是线段AB上一点,连接DE.AC=DE,BC=BE.(1)求证:AB=BD;(2)BF平分∠ABC交AC于点F,点G是线段FB延长线上一点,连接DG,点H是线段DG上一点,连接AH交BD于点K,连接KG.当KB平分∠AKG时,求证:AK=DG+KG.【分析】(1)证明Rt△ACB≌Rt△DEB即可解决问题;(2)作BM平分∠ABD交AK于点M,证明△BMK≌△BGK,△ABM≌△DBG,即可解决问题.【解答】证明:(1)在Rt△ACB和Rt△DEB中,AC=DEBC=BE,∴Rt△ACB≌Rt△DEB(HL),∴AB=BD,(2)如图:作BM平分∠ABD交AK于点M,∵BM平分∠ABD,KB平分∠AKG,∴∠ABM=∠MBD=45°,∠AKB=∠BKG,∵∠ABF=∠DBG=45°∴∠MBD=∠GBD,在△BMK和△BGK中,∠MBD=∠GBDBK=BK,∠AKB=∠BKG∴△BMK≌△BGK(ASA),∴BM=BG,MK=KG,在△ABM和△DBG中,AB=BD∠ABM=∠DBG,BM=BG∴△ABM≌△DBG(SAS),∴AM=DG,∵AK=AM+MK,∴AK=DG+KG.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是得到△BMK≌△BGK.6.(2023春•市南区期末)如图,在△ABC中,AB=AC,AD⊥BC于点D,E为AC边上一点,连接BE与AD交于点F,G为△ABC外一点,满足∠ACG=∠ABE,∠FAG=∠BAC,连接EG.(1)求证:△ABF≌△ACG;(2)求证:BE=CG+EG.【分析】(1)根据已知条件可得∠BAD=∠CAG,然后利用ASA即可证明△ABF≌△ACG;(2)结合(1)的结论,再证明△AEF≌△AEG,即可解决问题.【解答】(1)证明:∵∠BAC=∠FAG,∴∠BAC﹣∠CAD=∠FAG﹣∠CAD,∴∠BAD=∠CAG,在△ABF和△ACG中,∠BAD=∠CAGAB=AC,∠ABF=∠ACG∴△ABF≌△ACG(ASA);(2)证明:∵△ABF≌△ACG,∴AF=AG,BF=CG,∵AB=AC,AD⊥BC,∴∠BAD=∠CAD,∵∠BAD=∠CAG,∴∠CAD=∠CAG,在△AEF和△AEG中,AF=AG∠FAE=∠GAE,AE=AE∴△AEF≌△AEG(SAS).∴EF=EG,∴BE=BF+FE=CG+EG.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是得到△AEF≌△AEG.7.(2022秋•新市区校级期中)已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.求证:(1)AD=AE=EC.(2)BA+BC=2BF.【分析】(1)由△BCD和△BEA为等腰三角形,∠ABD=∠EBC,得出∠BCD=∠BEA,由△ABD≌△EBC可得∠BCE=∠BDA,由∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA得出∠BCD+∠DCE=∠DAE+∠BEA,进而得出∠DCE=∠DAE,即可证明AE=EC;(2)过点E作EG⊥BC交BC的延长线于点G,由“HL”得出Rt△BFE≌Rt△BGE和Rt△BFE≌Rt△BGE,从而得出BF=BG,FA=CG,再通过等量代换即可得出结论.【解答】(1)证明:∵BD为△ABC的角平分线,∴∠ABD=∠EBC,在△ABD与△EBC中,AB=EB∠ABD=∠EBD,BD=BC∴△ABD≌△EBC(SAS),∴∠BCE=∠BDA,∵∠BCE=∠BCD+∠DCE,∠BDA=∠DAE+∠BEA,∴∠BCD+∠DCE=∠DAE+∠BEA,∵BD=BC,BE=BA,∴△BCD和△BEA为等腰三角形,∵∠ABD=∠EBC,∴∠BCD=∠BEA,∴∠DCE=∠DAE,∴AE=EC,∵△ABD≌△EBC,∴AD=EC,∴AD=EC=AE;(2)证明:如图,过点E作EG⊥BC交BC的延长线于点G,∵BE平分∠ABC,EF⊥AB,EG⊥BG,∴EF=EG,在Rt△BFE与Rt△BGE中,EF=EGBE=BE,∴Rt△BFE≌Rt△BGE(HL),∴BF=BG,在Rt△AFE与Rt△CGE中,EF=EGEA=EC,∴Rt△AFE≌Rt△CGE(HL),∴FA=CG,∴BA+BC=BF+FA+BG﹣CG=BF+BG=2BF.【点评】本题考查了全等三角形的判定与性质,掌握三角形全等的判定方法是解决问题的关键.8.(2023春•余江区期末)如图,大小不同的两块三角板△ABC和△DEC直角顶点重合在点C处,AC=BC,DC=EC,连接AE、BD,点A恰好在线段BD上.(1)找出图中的全等三角形,并说明理由;(2)当AD=AB=4cm,则AE的长度为 cm.(3)猜想AE与BD的位置关系,并说明理由.【分析】(1)根据SAS证明△CBD≌△CAE即可;(2)根据全等三角形的性质解答即可;(3)根据全等三角形的性质和垂直的定义解答即可.【解答】解:(1)△CBD≌△CAE,理由如下:∵∠ACB=∠DCE=90°,∴∠ACB+∠ACD=∠DCE+∠ACD,即∠BCD=∠ACE,在△CBD与△CAE中,BC=AC∠BCD=∠ACE,DC=EC∴△CBD≌△CAE(SAS);(2)∵△CBD≌△CAE,∴BD=AE=AD+AB=4+4=8(cm),故答案为:8;(3)AE⊥BD,理由如下:AE与CD相交于点O,在△AOD与△COE中,∵△CBD≌△CAE,∴∠ADO=∠CEO,∵∠AOD=∠COE,∴∠OAD=∠OCE=90°,∴AE⊥BD.【点评】此题考查全等三角形的判定和性质,关键是根据SAS得出△CBD与△CAE全等解答.9.已知,△ABC中,∠ACB=90°,AC=BC,点E是BC上一点,连接AE(1)如图1,当AE平分∠BAC时,EH⊥AB于H,△EHB的周长为10m,求AB的长;(2)如图2,延长BC至D,使DC=BC,将线段AE绕点A顺时针旋转90°得线段AF,连接DF,过点B作BG⊥BC,交FC的延长线于点G,求证:BG=BE.【分析】(1)根据等腰三角形的性质得到∠B=45°,根据角平分线的性质得到CE=EH=BH,根据全等三角形的性质得到AH=AC,于是得到结论;(2)先连接AD,依据AAS判定△ADF≌△ABE,得到DF=BE,再判定△BCG≌△DCF,得出DF=BG,进而得到BG=BE.【解答】解:(1)∵∠ACB=90°,AC=BC,∴∠B=45°,∵AE平分∠BAC时,EH⊥AB于H,∴CE=EH=BH,在Rt△ACE与Rt△AHE中,CE=EH AE=AE,∴Rt△ACE与Rt△AHE(HL),∴AH=AC,∴AH=BC,∵△EHB的周长为10m,∴AB=AH+BH=BC+BH=10m;(2)如图所示,连接AD,线段AE绕点A顺时针旋转90°得线段AF,则AE=AF,∠EAF=90°,∵AC⊥BD,DC=BC,∴AD=AB,∠ABE=∠ADC=45°,∴∠BAD=90°=∠EAF,∴∠BAE=∠DAF,∴△ABE≌△ADF(SAS),∴DF=BE,∠ADF=∠ABE=45°,∴∠FDC=90°,∵BG⊥BC,∴∠CBG=∠CDF=90°,又∵BC=DC,∠BCG=∠DCF,∴△BCG≌△DCF(ASA),∴DF=BG,∴BG=BE.【点评】本题主要考查了旋转的性质,等腰直角三角形的性质以及全等三角形的判定与性质的综合运用,解决问题的关键是作辅助线构造全等三角形,依据全等三角形的对应边相等得出结论.10.在△ABC中,∠ABC=45°,AM⊥MB,垂足为M,点C是BM延长线上一点,连接AC.(1)如图①,点D在线段AM上,且DM=CM.求证:△BDM≌△ACM;(2)如图②,在(1)的条件下,点E是△ABC外一点,且满足EC=AC,连接ED并延长交BC于点F,且F为线段BC的中点,求证:∠BDF=∠CEF.【分析】(1)利用SAS即可证明△BMD≌△AMC.(2)延长EF到点G,使得FG=EF,证△BMD≌△AMC得AC=BD,再证△BFG≌△CFE可得BG=CE,∠G=∠E,从而得BD=BG=CE,即可得∠BDG=∠G=∠CEF.【解答】(1)证明:∵∠ABM=45°,AM⊥BM,在△BMD和△AMC中,DM=CM∠BMD=∠AMC BM=AM,∴△BMD≌△AMC(SAS);(2)证明:延长EF到点G,使得FG=EF,连接BG.如图所示:∵△BMD≌△AMC∴BD=AC,又∵CE=AC,∴BD=CE,在△BFG和△CFE中,BF=FC∠BFG=∠EFC FG=FE,∴△BFG≌△CFE(SAS),∴BG=CE,∠G=∠CEF,∴BD=CE=BG,∴∠BDF=∠G=∠CEF.∴∠BDF=∠CEF.【点评】本题主要考查全等三角形的判定与性质,等腰直角三角形的性质等知识点,熟练掌握全等三角形的判定与性质是解题的关键.11.如图1,在△ABC中,∠A=120°,∠C=20°,BD平分∠ABC,交AC于点D.(1)求证:BD=CD.(2)如图2,若∠BAC的角平分线AE交BC于点E,求证:AB+BE=AC.(3)如图3,若∠BAC的外角平分线AE交CB的延长线于点E,则(2)中的结论是否成立?若成立,给出证明,若不成立,写出正确的结论.【分析】(1)根据∠A=120°,∠C=20°,可得∠ABC的度数,再根据BD平分∠ABC,可得∠DBC=∠C=20°,进而可得结论;(2)如图2,过点E作EF∥BD交AC于点F,证明△ABE≌△AFE,可得BE=EF=FC,进而可得AB+BE =AC;(3)如图3,过点A作AF∥BD交BE于点F,结合(1)和AE是∠BAC的外角平分线,可得FE=AF=AC,进而可得结论BE﹣AB=AC.【解答】(1)证明:∵∠A=120°,∠C=20°,∴∠ABC=180°﹣120°﹣20°=40°,∵BD平分∠ABC,∴∠ABD=∠DBC=12∠ABC=20°,∴∠DBC=∠C=20°,∴BD=CD;(2)证明:如图2,过点E作EF∥BD交AC于点F,∴∠FEC=∠DBC=20°,∴∠FEC=∠C=20°,∴∠AFE=40°,FE=FC,∴∠AFE=∠ABC,∵AE是∠BAC的平分线,∴∠BAE=∠FAE,在△ABE和△AFE中,∠BAE=∠FAE∠ABE=∠AFE,AE=AE∴△ABE≌△AFE(AAS),∴BE=EF,∴BE=EF=FC,∴AB+BE=AF+FC=AC;(3)(2)中的结论不成立,正确的结论是BE﹣AB=AC.理由如下:如图3,过点A作AF∥BD交BE于点F,∴∠AFC=∠DBC=20°,∴∠AFC=∠C=20°,∴AF=AC,∵AE是∠BAC的外角平分线,∴∠EAB=12(180°﹣∠ABC)=30°,∵∠ABC=40°,∴∠E=∠ABC﹣∠EAB=10°,∴∠E=∠FAE=10°,∴FE=AF,∴FE=AF=AC,∴BE﹣AB=BE﹣BF=EF=AC.【点评】本题考查了全等三角形的判定与性质,解决本题的关键是掌握全等三角形的判定与性质.12.(2022秋•渝北区校级期末)已在等腰Rt△ABC中,∠ABC=90°,AB=CB,D为直线AB上一点,连接CD,过点C作CE⊥CD,且CE=CD,连接DE,交AC于点F.(1)如图1,当点D在线段AB上,且∠DCB=30°时,请探究DF,EF,CF之间的数量关系,并说明理由;(2)如图2,在(1)的条件下,在FC上任取一点G,连接DG,作射线GP使∠DGP=60°,交∠DFG 的平分线于点Q,求证:FD+FG=FQ.【分析】(1)在EF上找到G点使得FG=CF,易证△CFG是等边三角形,可得CG=CF=GF,即可求得∠ECG=∠ACD,即可证明△ECG≌△CDF,可得DF=EG,即可解题;(2)在FP上找到H点,使得FH=FG,易证△FGH是等边三角形,可得∠GHF=∠FGH=60°,GH =FG=FH,即可求得∠FGD=∠QGH,即可证明△DFG≌△QHG,可得DF=QH,即可解题.【解答】(1)解:EF=DF+CF;在EF上找到G点使得FG=CF,如图2,∵∠BCD=30°,∠ACB=45°,∴∠ACD=15°,∴∠CFG=∠CDE+∠ACD=60°,∵FG=CF,∴△CFG是等边三角形,∴CG=CF=GF,∠FCG=60°,∴∠GCE=90°﹣15°﹣60°=15°,在△ECG和△CDF中,CG=CF∠ECG=∠ACD,CE=CD∴△ECG≌△CDF,(SAS)∴DF=EG,∵EF=EG+GF,∴EF=DF+CF;(2)证明:在FQ上找到H点,使得FH=FG,如图3,∵FQ平分∠DFG,∴∠QFG=60°,∵FG=FH,∴△FGH是等边三角形,∴∠GHF=∠FGH=60°,GH=FG=FH,∵∠AFD=∠CDE+∠ACD=60°,∴∠GHQ=∠DFG=120°,∵∠FGD+∠DGH=60°,∠DGH+∠QGH=60°,∠QGH=∠DGF,∴∠FGD=∠QGH,在△DFG和△QHG中,∠DFG=∠QHG=120°FG=HG,∠FGD=∠QGH∴△DFG≌△QHG,(ASA)∴DF=QH,∵FQ=FH+QH,∴FQ=FG+FD.【点评】本题考查了全等三角形的判定,考查了全等三角形对应边相等的性质,本题中求证△ECG≌△CDF和△DFG≌△QHG是解题的关键.13.(2022春•运城期末)综合与探究如图,在△ABC和△ADE中,AB=AC,AD=AE,∠BAC=∠DAE,CE的延长线交BD于点F.(1)求证:△ACE≌△ABD.(2)若∠BAC=∠DAE=50°,请直接写出∠BFC的度数.(3)过点A作AH⊥BD于点H,求证:EF+DH=HF.【分析】(1)可利用SAS证明结论;(2)由全等三角形的性质可得∠AEC=∠ADB,结合平角的定义可得∠DAE+∠DFE=180°,根据∠BFC+∠DFE=180°,可求得∠BFC=∠DAE,即可求解;(3)连接AF,过点A作AJ⊥CF于点J.结合全等三角形的性质利用HL证明Rt△AFJ≌Rt△AFH,Rt△AJE≌Rt△AHD可得FJ=FH,EJ=DH,进而可证明结论.【解答】(1)证明:∵∠BAC=∠DAE.∴∠CAE=∠BAD.在△ACE和△ABD中,AC=AB∠CAE=∠BAD,AE=AD∴△ACE ≌△ABD (SAS );(2)解:∵△ACE ≌△ABD ,∴∠AEC =∠ADB ,∴∠AEF +∠AEC =∠AEF +∠ADB =180°.∴∠DAE +∠DFE =180°,∵∠BFC +∠DFE =180°,∴∠BFC =∠DAE =∠BAC =50°;(3)证明:如图,连接AF ,过点A 作AJ ⊥CF 于点J .∵△ACE ≌△ABD ,∴S △ACE =S △ABD ,CE =BD ,∵AJ ⊥CE ,AH ⊥BD .∴12CE ⋅AJ =12BD ⋅AH ,∴AJ =AH .在Rt △AFJ 和Rt △AFH 中,AF =AF AJ =AH ,∴Rt △AFJ ≌Rt △AFH (HL ),∴FJ =FH .在Rt △AJE 和Rt △AHD 中,AE =AD AJ =AH ,∴Rt △AJE ≌Rt △AHD (HL ),∴EJ =DH ,∴EF +DH =EF +EJ =FJ =FH .【点评】本题主要考查全等三角形的判定与性质,掌握全等三角形的判定条件是解题的关键.14.(2022春•沙坪坝区校级期中)如图,在△ABC 中,∠ABC 、∠ACB 的平分线交于点D ,延长BD 交AC 于E ,G 、F 分别在BD 、BC 上,连接DF 、GF ,其中∠A =2∠BDF ,GD =DE .(1)当∠A =80°时,求∠EDC 的度数;(2)求证:CF =FG +CE .【分析】(1)方法一:先求∠ABC 和∠ACB 的和为100°,再根据角平分线求∠DBC +∠DCB =50°,再根据外角即可解决问题;方法二:在BC 上取点M ,使CM =CE ,证明△CDE ≌△CDM (SAS ),可得DE =DM ,∠DEC =∠DMC ,∠EDC =∠MDC ,证明∠BDM =180°−12∠ABC ﹣∠DMB =180°−12∠ABC ﹣∠AEB =∠A =80°,进而可以解决问题.(2)结合(1)然后证明△DGF ≌△DMF (SAS ),可得GF =MF ,进而可以解决问题.【解答】(1)解:方法一:∵∠A =80°,∴∠ABC +∠ACB =100°,∵BE 平分∠ABC 、CD 平分∠ACB ,∴∠DBC +∠DCB =50°,∴∠EDC =∠DBC +∠DCB =50°;方法二:如图,在BC 上取点M ,使CM =CE ,∵CD 平分∠ACB ,∴∠ACD=∠BCD,在△CDE和△CDM中,CE=CM∠ECD=∠MCDCD=CD,∴△CDE≌△CDM(SAS),∴DE=DM,∠DEC=∠DMC,∠EDC=∠MDC,∵GD=DE,∴GD=MD,∵∠DEC+∠AEB=180°,∠DMC+∠DMF=180°,∴∠AEB=∠DMF,∵BE平分∠ABC,∴∠ABE=∠CBE=12∠ABC,∴∠BDM=180°−12∠ABC﹣∠DMB=180°−12∠ABC﹣∠AEB=∠A=80°,∴∠EDM=100°,∴∠EDC=50°;(2)证明:∵∠A=2∠BDF,∴∠BDM=2∠BDF,∴∠FDM=∠BDF,在△DGF和△DMF中,DG=DM∠GDF=∠MDFDF=DF,∴△DGF≌△DMF(SAS),∴GF=MF,∴CF=CM+FM=CE+GF.∴CF=FG+CE.【点评】本题考查了全等三角形的判定与性质,角平分线的定义,解决本题的关键是根据题意准确作出辅助线得到△DGF≌△DMF.15.如图,在△ABC中,∠C=90°,AD是∠BAC的角平分线交BC于点D,过D作DE⊥BA于点E,点F在AC上,且BD=DF.(1)求证:AC=AE;(2)求证:∠BAC+∠FDB=180°;(3)若AB=9.5,AF=1.5,求线段BE的长.【分析】(1)证△ACD≌△AED(AAS),即可得出结论;(2)设∠DAC=∠DAE=α,在AB上截取AM=AF,连接MD,证△FAD≌△MAD(SAS),得FD=MD,∠ADF=∠ADM,再证Rt△MDE≌Rt△BDE(HL),得∠DME=∠B,然后证∠FDB=90°+90°﹣2α=180°﹣2α,即可得出结论;(3)求出MB=AB﹣AM=8,由全等三角形的性质得ME=BE,即可求解.【解答】(1)证明:∵AD平分∠BAC,∴∠DAC=∠DAE,∵DE⊥BA,∴∠DEA=∠DEB=90°,∵∠C=90°,∴∠C=∠DEA=90°,在△ACD和△AED中,∠C=∠DEA∠DAC=∠DAE,AD=AD∴△ACD≌△AED(AAS),∴AC=AE;(2)证明:设∠DAC=∠DAE=α,∵∠C=∠DEA=90°,∴∠ADC=90°﹣α,∠ADE=90°﹣α,则∠FDB=∠FCD+∠DFC=90°+∠DFC,在AB上截取AM=AF,连接MD,如图所示:在△FAD和△MAD中,AF=AM∠DAF=∠DAM,AD=AD∴△FAD≌△MAD(SAS),∴FD=MD,∠ADF=∠ADM,∵BD=DF,∴BD=MD,在Rt△MDE和Rt△BDE中,MD=BDDE=DE∴Rt△MDE≌Rt△BDE(HL),∴∠DME=∠B,∵∠DAC=∠DAE=α,∴∠DAC+∠ADF=∠ADM+∠ADM,在△FAD中,∠DAC+∠ADF=∠DFC,在△AMD中,∠DAE+∠ADM=∠DME,∴∠DFC=∠DME,∴∠DFC=∠B,∵∠C=90°,在△ABC中,∠B=90°﹣2α,∴∠DFC=90°﹣2α,∴∠FDB=90°+90°﹣2α=180°﹣2α,∵∠BAC=∠DAC+∠DAE=2α,∴∠FDB+∠BAC=180°﹣2α+2α=180°;(3)解:∵AF=AM,且AF=1.5,∴AM=1.5,∵AB=9.5,∴MB=AB﹣AM=9.5﹣1.5=8,由(2)得:Rt△MDE≌Rt△BDE,∴ME=BE,∴BE=12BM=4,即BM的长为4.【点评】本题考查了全等三角形的判定与性质、角平分线定义、直角三角形的性质、三角形的外角性质等知识;证明△FAD≌△MAD和Rt△MDE≌Rt△BDE是解题的关键.16.在△ABC中,AB=AC,D是直线BC上一点,以AD为一条边在AD的右侧作△ADE,使AE=AD,∠DAE=∠BAC,连接DE,CE.(1)如图,当点D在BC延长线上移动时,求证:BD=CE.(2)设∠BAC=α,∠DCE=β.①当点D在线段BC的延长线上移动时,α与β之间有什么数量关系?请说明理由.②当点D分别在线段BC上、线段BC的反向延长线上移动时,α与β之间有什么数量关系?请说明理由.【分析】(1)根据SAS证△BAD≌△CAE,可得结论;(2)①由△BAD≌△CAE,推出∠B=∠ACE,根据三角形外角性质求出即可;②α+β=180°或α=β,根据三角形外角性质求出即可.【解答】(1)证明:∵∠DAE=∠BAC,∴∠DAE+∠CAD=∠BAC+∠CAD,∴∠BAD=∠CAE,在△BAD和△CAE中,AB=AC∠BAD=∠CAE,AD=AE∴△BAD≌△CAE(SAS),(2)解:①当点D在线段BC的延长线上移动时,α与β之间的数量关系是α=β,理由是:由(1)知△BAD≌△CAE,∴∠B=∠ACE,∵∠ACD=∠B+∠BAC=∠ACE+∠DCE,∴∠BAC=∠DCE,∵∠BAC=α,∠DCE=β,∴α=β;②分三种情况:i)当D在线段BC上时,如图2,α+β=180°,理由是:同理可证明:△ABD≌△ACE(SAS),∴∠ADB=∠AEC,∠ABC=∠ACE,∵∠ADC+∠ADB=180°,∴∠ADC+∠AEC=180°,∴∠DAE+∠DCE=180°,∵∠BAC=∠DAE=α,∠DCE=β,∴α+β=180°,ii)当点D在线段BC反向延长线上时,如图3,α=β.如图3,同理可证明:△ABD≌△ACE(SAS),∴∠ABD=∠ACE,∵∠ACE=∠ACD+∠DCE,∠ABD=∠ACD+∠BAC,∴∠ACD+∠DCE=∠ACD+∠BAC,∴∠BAC=∠DCE,∵∠BAC=α,∠DCE=β,∴α=β;ii)当点D在线段BC的延长线上时,如图1,α=β.综上,当点D在BC上移动时,α=β或α+β=180°.【点评】本题是三角形的综合题,考查了全等三角形的性质和判定,三角形的外角性质等知识,解题的关键是正确寻找全等三角形解决问题,属于中考常考题型.17.(2022春•南海区校级月考)如图,在△ABC中,∠ACB为锐角,点D为射线BC上一动点,连接AD.以AD为直角边且在AD的上方作等腰直角三角形ADF.(1)若AB=AC,∠BAC=90°.①当点D在线段BC上时(与点B不重合),试探讨CF与BD的数量关系和位置关系;②当点D在线段BC的延长线上时,①中的结论是否仍然成立,请在图②中画出相应的图形并说明理由;(2)如图③,若AB≠AC,∠BAC≠90°,∠BCA=45°,点D在线段BC上运动,试探究CF与BD 的位置关系.【分析】(1)①根据同角的余角相等求出∠CAF=∠BAD,然后利用“边角边”证明△ACF和△ABD全等,根据全等三角形的性质及等腰直角三角形的性质求解即可;②先求出∠CAF=∠BAD,然后与①的思路相同求解即可;(2)过点A作AE⊥AC交BC于E,可得△ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE,∠AED=45°,再根据同角的余角相等求出∠CAF=∠EAD,然后利用“边角边”证明△ACF 和△AED全等,根据全等三角形对应角相等可得∠ACF=∠AED,然后求出∠BCF=90°,从而得到CF ⊥BD.【解答】解:(1)①CF=BD,CF⊥BD,理由如下:∵∠BAC=90°,△ADF是等腰直角三角形,AB=AC,∴∠CAF+∠CAD=90°,∠BAD+∠CAD=90°,∠B=∠ACB=45°,∴∠CAF=∠BAD,在△ACF和△ABD中,AC=AB∠CAF=∠BAD,AF=AD∴△ACF≌△ABD(SAS),∴CF=BD,∠ACF=∠B=45°,∵∠ACB=45°,∴∠FCB=45°+45°=90°,∴CF⊥BD;②①中的结论成立,理由如下:如图②:∵∠BAC=90°,△ADF是等腰直角三角形,AB=AC,∴∠BAC=∠DAF=90°,∠B=∠ACB=45°,∴∠BAC+∠CAD=∠DAF+∠CAD,即∠CAF=∠BAD,在△ACF和△ABD中,AC=AB∠CAF=∠BAD,AF=AD∴△ACF≌△ABD(SAS),∴CF=BD,∠ACF=∠B,∴∠BCF=∠ACF+∠ACB=45°+45°=90°,∴CF⊥BD;(3)如图③,过点A作AE⊥AC交BC于E,∵∠BCA=45°,∴△ACE是等腰直角三角形,∴AC=AE,∠AED=45°,∵∠CAF+∠CAD=90°,∠EAD+∠CAD=90°,∴∠CAF=∠EAD,在△ACF和△AED中,AC=AE∠CAF=∠EAD,AF=AD∴△ACF≌△AED(SAS),∴∠ACF=∠AED=45°,∴∠BCF=∠ACF+∠BCA=45°+45°=90°,∴CF⊥BC.【点评】此题是三角形综合题,主要考查了全等三角形的判定与性质,等腰直角三角形的性质,作出合理的辅助线根据同角的余角相等求出两边的夹角相等是证明三角形全等的关键.18.如图,∠BAD=∠CAE=90°,AB=AD,AE=AC,AF⊥CB,垂足为F.(1)△ABC≌△ADE吗?为什么?(2)求∠FAE的度数;(3)延长BF到G,使得FG=FB,试说明CD=2BF+DE.【分析】(1)由“SAS”可证△ABC≌△ADE;(2)由等腰直角三角形的性质可得∠AEC=∠ACE=45°,由全等三角形的性质可得∠ACB=∠AED=45°,即可求解;(3)由全等三角形的性质可得∠ABC=∠ADE,BC=DE,由线段垂直平分线的性质和等腰三角形的性质可得AB=AG=AD,∠ABG=∠AGB=∠ADC,由“AAS”可证△ACD≌△ACG,可得CD=CG,可得结论.【解答】证明:(1)△ABC≌△ADE,理由如下:∵∠BAD=∠CAE=90°,∴∠EAD=∠CAB,在△ABC和△ADE中,AB=AD∠BAC=∠DAE,AC=AE∴△ABC≌△ADE(SAS);(2)∵∠CAE=90°,AC=AE,∴∠AEC=∠ACE=45°,∵△ABC≌△ADE,∴∠ACB=∠AED=45°,∵AF⊥CB,∴∠FAC=45°,∴∠FAE=135°;(3)∵△ABC≌△ADE,∴∠ABC=∠ADE,BC=DE,∴∠ADC=∠ABG,∵AF⊥BF,BF=FG,∴AB=AG,∴AG=AD,∠ABG=∠AGB=∠ADC,又∵∠ACG=∠ACD=45°,∴△ACD≌△ACG(AAS),∴CD=CG,∴CD=BG+CB=2BF+DE.【点评】本题是三角形综合题,考查了全等三角形的判定和性质,等腰三角形的判定和性质,线段垂直平分线的性质等知识,证明△ACD≌△ACG是解题的关键.19.Rt△ABC中,∠C=90°,点D在直线AC上,点E在直线AB上,∠ADE=∠ABC.(1)如图1,当点D、E分别在边AC、AB上时,求证:DE⊥AB;(2)如图2,当点D在CA延长线上,点E在BA延长线上时,DE、BC延长线交于点F,作∠EAC的角平分线AG交DF于点G,求证:∠D+2∠DGA=90°;(3)如图3,在(2)的条件下,连接BG交CD于点H,若∠DGH=∠DHG,∠AGB=3∠CBH,求∠DGA的度数.【分析】(1)根据直角三角形的两锐角互余得到∠ABC+∠A=90°,等量代换得出∠ADE+∠A=90°,进而得出∠AED=90°,根据垂直的定义即可得解;(2)过点G作GN∥FB交CD于点N,根据平行线的性质及垂直的定义推出∠AEG=∠ANG=90°,根据角平分线定义得出∠EAG=∠NAG,利用AAS证明△EAG≌△NAG,根据全等三角形的性质及直角三角形的性质即可得解;(3)根据直角三角形的性质及对顶角相等得出∠DGH=90°−13∠AGB,根据等腰三角形的性质推出∠DGH=90°−12∠D,则90°−13∠AGB=90°−12∠D,进而推出∠AGB=32∠D,则∠DGA+32∠D=90°−12∠D,结合(2)求解即可.【解答】(1)证明:∵∠C=90°,∴∠ABC+∠A=90°,∵∠ADE=∠ABC,∴∠ADE+∠A=90°,∴∠AED=90°,∴DE⊥AB;(2)证明:如图2,过点G作GN∥FB交CD于点N,则∠GNC=∠ACB=90°,∴GN⊥CD,∵∠ACB=90°,∴∠ABC+∠BAC=90°,∵∠ADE=∠ABC,∠BAC=∠DAE,∴∠ADE+∠DAE=90°,∴∠DEA=90°,∴BE⊥DF,∴∠AEG=∠ANG=90°,∵AG平分∠EAC,∴∠EAG=∠NAG,在△EAG和△NAG中,∠AEG=∠ANG∠EAG=∠NAGAG=AG,∴△EAG≌△NAG(AAS),∴∠DGA=∠NGA,∴∠DGN=2∠DGA,∵∠D+∠DGN=90°,∴∠D+2∠DGA=90°;(3)解:∵∠AGB=3∠CBH,∴∠CBH=13∠AGB,∵∠DHG=∠CHB=90°﹣∠CBH,∴∠DGH=90°−13∠AGB,∵∠DGH=∠DHG,∴∠DGH=12(180°﹣∠D)=90°−12∠D,∴90°−13∠AGB=90°−12∠D,∴∠AGB=32∠D,∵∠DGH=∠DGA+∠AGB,∴∠DGA+∠AGB=90°−12∠D,∴∠DGA+32∠D=90°−12∠D,∴2∠D+∠DGA=90°,由(2)知,∠D+2∠DGA=90°,∴∠D=∠DGA,∴3∠DGA=90°,∴∠DGA=30°.【点评】此题是三角形综合题,考查了直角三角形的判定与性质、全等三角形的判定与性质、等腰三角形的性质、平行线的性质等知识,熟练掌握直角三角形的判定与性质、全等三角形的判定与性质、等腰三角形的性质并作出合理的辅助线是解题的关键.20.(2023春•新市区期末)在△ABC中,∠ACB=90°,AC=BC,D是直线AB上一点(点D不与点A、B重合),连接DC并延长到E,使得CE=CD,过点E作EF⊥直线BC,交直线BC于点F.(1)如图1,当点D为线段AB上的任意一点时,用等式表示线段EF、CF、AC的数量关系,并证明;(2)如图2,当点D为线段BA的延长线上一点时,依题意补全图2,猜想线段EF、CF、AC的数量关系是否发生改变,并证明;(3)如图3,当点D在线段AB的延长线上时,直接写出线段EF、CF、AC之间的数量关系.【分析】(1)过D作DH⊥CB于H,由“AAS”可证△FEC≌△HDC,可得CH=FC,DH=EF,可得结论;(2)过D作DH⊥CB于H,由“AAS”可证△FEC≌△HDC,可得CH=FC,DH=EF,可得结论.(3)过D作DH⊥CB交CB的延长线于H,由“AAS”可证△FEC≌△HDC,可得CH=FC,DH=EF,可得结论.【解答】解:(1)结论:AC=EF+FC.理由如下:过D作DH⊥CB于H,∴∠DHC=∠DHB=90°,∵EF⊥CF,∴∠EFC=∠DHC=90°,在△FEC和△HDC中,∠EFC=∠DHC=90°∠FCE=∠DCH,EC=DC∴△FEC≌△HDC(AAS),∴CH=FC,DH=EF,∵∠ACB=90°,AC=BC,∴∠B=45°,∵∠DHB=90°,∴∠B=∠HDB=45°,∴DH=HB=EF,∵BC=CB+HB,∴AC=FC+EF;(2)依题意补全图形,结论:AC=EF﹣CF,理由如下:过D作DH⊥CB交BC的延长线于H,∵EF⊥CF,∴∠EFC=∠DHC=90°,在△FEC和△HDC中,∠FCE=∠DCH∠EFC=∠DHC=90°,EC=DC∴△FEC≌△HDC(AAS),∴CH=FC,DH=EF,∵∠DHB=90°,∴∠B=∠HDB=45°,∴DH=HB=EF,∵BC=HB﹣CH,∴AC=EF﹣CF;(3)AC=CF﹣EF.如图3,过D作DH⊥CB交CB的延长线于H,同理可证△FEC≌△HDC(AAS),∴CH=FC,DH=EF,∵∠DHB=90°,∴∠B=∠HDB=45°,∴DH=HB=EF,∵BC=CH﹣BH,∴AC=CF﹣EF.【点评】本题是三角形综合题,考查了全等三角形的判定和性质,添加恰当辅助线构造全等三角形是本题的关键.21.如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.(1)如果AB=AC,∠BAC=90°,①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为 ,线段CF、BD的数量关系为 ;②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC(点C、F 不重合),并说明理由.【分析】(1)当点D在BC的延长线上时①的结论仍成立.由正方形ADEF的性质可推出△DAB≌△FAC,所以CF=BD,∠ACF=∠ABD.结合∠BAC=90°,AB=AC,得到∠BCF=∠ACB+∠ACF=90°.即CF⊥BD.(2)当∠ACB=45°时,过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,可推出∠ACB=∠AGC,所以AC=AG,由(1)①可知CF⊥BD.【解答】证明:(1)①正方形ADEF中,AD=AF,∵∠BAC=∠DAF=90°,∴∠BAD=∠CAF,又∵AB=AC,∴△DAB≌△FAC,∴CF=BD,∠B=∠ACF,∴∠ACB+∠ACF=90°,即CF⊥BD.②当点D在BC的延长线上时①的结论仍成立.由正方形ADEF得AD=AF,∠DAF=90度.∵∠BAC=90°,∴∠DAF=∠BAC,∴∠DAB=∠FAC,又∵AB=AC,∴△DAB≌△FAC,∴CF=BD,∠ACF=∠ABD.∵∠BAC=90°,AB=AC,∴∠ABC=45°,∴∠ACF=45°,∴∠BCF=∠ACB+∠ACF=90度.即CF⊥BD.(2)当∠ACB=45°时,CF⊥BD(如图).理由:过点A作AG⊥AC交CB的延长线于点G,则∠GAC=90°,∵∠ACB=45°,∠AGC=90°﹣∠ACB,∴∠AGC=90°﹣45°=45°,∴∠ACB=∠AGC=45°,∴AC=AG,∵∠DAG=∠FAC(同角的余角相等),AD=AF,∴△GAD≌△CAF,∴∠ACF=∠AGC=45°,∠BCF=∠ACB+∠ACF=45°+45°=90°,即CF⊥BC.【点评】本题考查三角形全等的判定和直角三角形的判定,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.判定两个三角形全等,先根据已知条件或求证的结论确定三角形,然后再根据三角形全等的判定方法,看缺什么条件,再去证什么条件.22.(1)如图1,∠B=∠D=90°,E是BD的中点,AE平分∠BAC,求证:CE平分∠ACD.(2)如图2,AM∥CN,∠BAC和∠ACD的平分线并于点E,过点E作BD⊥AM,分别交AM、CN于B、D,请猜想AB、CD、AC三者之间的数量关系,请直接写出结论,不要求证明.(3)如图3,AM∥CN,∠BAC和∠ACD的平分线交于点E,过点E作不垂直于AM的线段BD,分别交AM、CN于B、D点,且B、D两点都在AC的同侧,(2)中的结论还成立吗?若成立,请加以证明;若不成立,请说明理由.【分析】(1)过点E作EF⊥AC于F,根据角平分线上的点到角的两边的距离相等可得OB=OE,从而求出OE=OD,然后根据到角的两边距离相等的点在角的平分线上证明;(2)如图2,过E作EF⊥AC于F,根据平行线的性质得到BD⊥CD,由角平分线的性质得到BE=EF,证得Rt△AEF≌Rt△ABE,根据全等三角形到现在得到AF=AB,同理CF=CD,等量代换得到结论;(3)成立,如图3,在AC上截取AF=AB,根据角平分线的定义得到∠BAE=∠FAE,推出△ABE≌△AFE,根据全等三角形的性质得到∠AFE=∠ABE,根据角平行线的性质得到∠ABE+∠CDE=180°,求得∠CFE=∠CDE,证得△CEF≌△CDE,根据全等三角形的性质即可得到结论.【解答】解:(1)如图1,过E作EF⊥AC于F,∵∠B=90°,AE平分∠BAC,∴EF=BE,∵E是BD的中点,∴BE=DE,∴EF=DE,∵∠D=90°,∴CE平分∠ACD;(2)如图2,过E作EF⊥AC于F,∵AM∥CN,BD⊥AM,∴BD⊥CD,∵AE平分∠BAC,∴BE=EF,在Rt△AEF与Rt△ABE中,BE=EF AE=AE,∴Rt△AEF≌Rt△ABE,∴AF=AB,同理CF=CD,∵AC=AF+CF,∴AC=AB+CD;(3)成立,如图3,在AC上截取AF=AB,∵AE平分∠BAC,∴∠BAE=∠FAE,在△ABE与△AFE中,AB=AF∠BAE=∠FAEAE=AE,∴△ABE≌△AFE,∴∠AFE=∠ABE,∵AM∥CN,∴∠ABE+∠CDE=180°,∵∠AFE+∠EFC=180°,∴∠CFE=∠CDE,∵CE平分∠ACD,∴∠FCE=∠DCE,在△CEF与△CDE中,∠CFE=∠CDE ∠FCE=∠DCE CE=CE,∴△CEF≌△CDE,∴CF=CD,∵AC=AF+CF,∴AC=AB+CD.【点评】本题考查了全等三角形的判定和性质,角平分线的性质,角平分线的定义,平行线的性质,正确的作出辅助线构造全等三角形是解题的关键.23.将两个全等的直角三角形ABC和DBE按图①方式摆放,其中∠ACB=∠DEB=90°,∠A=∠D=30°,点E落在AB上,DE所在直线交AC所在直线于点F.(1)求证:AF+EF=DE;(2)若将图①中的△DBE绕点B按顺时针方向旋转角α,且0°<α<60°,其它条件不变,请在图②中画出变换后的图形,并直接写出你在(1)中猜想的结论是否仍然成立;(3)若将图①中的△DBE绕点B按顺时针方向旋转角β,且60°<β<180°,其它条件不变,如图③.你认为(1)中猜想的结论还成立吗?若成立,写出证明过程;若不成立,请写出AF、EF与DE之间的关系,并说明理由.【分析】(1)我们已知了三角形BED和CAB全等,那么DE=AF+CF,因此只要求出EF=CF就能得出本题所求的结论,可通过全等三角形来实现,连接BF,那么证明三角形BEF和BCF全等就是解题的关键,这两三角形中已知的条件有BE=BC,一条公共边,根据斜边直角边定理,这两个直角三角形就全等了,也就得出EF=CF,也就能证得本题的结论了;(2)解题思路和辅助线的作法与(1)完全一样;(3)结论不成立.结论:AF=DE+EF.同(1)得CF=EF,由△ABC≌△DBE,可得AC=DE,AF=AC+FC=DE+EF.【解答】(1)证明:连接BF(如图①),∵△ABC≌△DBE(已知),∴BC=BE,AC=DE.∵∠ACB=∠DEB=90°,∴∠BCF=∠BEF=90°.在Rt△BFC和Rt△BFE中,BF=BFBC=BE∴Rt△BFC≌Rt△BFE(HL).∴CF=EF.又∵AF+CF=AC,∴AF+EF=DE.(2)解:画出正确图形如图②∴(1)中的结论AF+EF=DE仍然成立;(3)不成立.结论:AF=DE+EF.。
图12 -3 图12 -4 图12 -2 图12 -1 1.判断与说理(1)如图11-1,△ADE 中,AE=AD 且∠AED=∠ADE,∠EAD=90°,EC 、DB 分别平分∠AED、∠ADE,交AD 、AE 于点C 、B ,连接BC .请你判断AB 、AC 是否相等,并说明理由;(2)△ADE 的位置保持不变,将△ABC 绕点A 逆时针旋转至图11-2的位置,AD 、BE 相交于O由.2.某课外学习小组在一次学习研讨中,得到如下两个命题:①如图12-1,在正三角形ABC 中,M 、N 分别是AC 、AB 上的点,BM 与CN 相交于点O ,若∠BON = 60°,则BM = CN.②如图12-2,在正方形ABCD 中,M 、N 分别是CD 、AD 上的点,BM 与CN 相交于点O ,若∠BON = 90°,则BM = CN.学习小组成员根据上述两个命题运用类比..的思想又提出了如下的命题: ③如图12-3,在正五边形ABCDE 中,M 、N 分别是CD 、DE 上的点,BM 与CN 相交于点O ,若∠BON = 108°,则BM = CN. (友情提示:正多边形的各边相等且各内角也相等)图11-1 图11-2EDDE图12 -5(1)请你从①、②、③三个命题中选择一个..说明理由; (2)请你继续完成下面的探索:①如图12-4,在正n 边形(n ≥6)中,M 、N 分别是CD 、DE 上的点,BM 与CN 相交于点O ,问当∠BON 等于多少度时,结论BM = CN 成立?(不要求证明)②如图12-5,在正五边形ABCDE 中,M 、N 分别是DE 、AE 上的点,BM 与CN 相交于点O ,当∠BON = 108°时,请问结论BM = CN 是否还成立?若成立,请给予证明;若不成立,请说明理由. 解:(1)我选 .(仅填写①、②、③中的一个) 理由如下: (2)3. 如图9所示,△ABC 是等腰直角三角形,∠ACB =90°,AD 是BC 边上的中线,过C 作AD 的垂线,交AB 于点E ,交AD 于点F 。
全等三角形压轴题精选(1)
1.(2016•常德)已知四边形ABCD中,AB=AD,AB⊥AD,连接AC,过点A作AE⊥AC,且使AE=AC,连接BE,过A作AH⊥CD于H交BE于F.
(1)如图1,当E在CD的延长线上时,求证:①△ABC≌△ADE;②BF=EF;
(2)如图2,当E不在CD的延长线上时,BF=EF还成立吗?请证明你的结论.
2.(2015•菏泽)如图,已知∠ABC=90°,D是直线AB上的点,AD=BC.
(1)如图1,过点A作AF⊥AB,并截取AF=BD,连接DC、DF、CF,判断△CDF的形状并证明;
(2)如图2,E是直线BC上一点,且CE=BD,直线AE、CD相交于点P,∠APD的度数是一个固定的值吗?若是,请求出它的度数;若不是,请说明理由.
3.(2015•于洪区一模)如图1,在△ABC中,∠ACB为锐角,点D为射线BC上一点,连接AD,以AD为一边且在AD的右侧作正方形ADEF.
(1)如果AB=AC,∠BAC=90°,
①当点D在线段BC上时(与点B不重合),如图2,线段CF、BD所在直线的位置关系为______,线段CF、BD的数量关系为______;
②当点D在线段BC的延长线上时,如图3,①中的结论是否仍然成立,并说明理由;
(2)如果AB≠AC,∠BAC是锐角,点D在线段BC上,当∠ACB满足什么条件时,CF⊥BC (点C、F不重合),并说明理由.
4.(2013•庐阳区校级模拟)如图,将两个全等的直角三角形△ABD、△ACE拼在一起(图1).△ABD不动,
(1)若将△ACE绕点A逆时针旋转,连接DE,M是DE的中点,连接MB、MC(图2),证明:MB=MC.
(2)若将图1中的CE向上平移,∠CAE不变,连接DE,M是DE的中点,连接MB、MC(图3),判断并直接写出MB、MC的数量关系.
(3)在(2)中,若∠CAE的大小改变(图4),其他条件不变,则(2)中的MB、MC
的数量关系还成立吗?说明理由.
5.(2013春•北京校级期中)探究
问题1 已知:如图1,三角形ABC中,点D是AB边的中点,AE⊥BC,BF⊥AC,垂足分别为点E,F,AE,BF交于点M,连接DE,DF.若DE=kDF,则k的值为______.
拓展
问题2 已知:如图2,三角形ABC中,CB=CA,点D是AB边的中点,点M在三角形ABC 的内部,且∠MAC=∠MBC,过点M分别作ME⊥BC,MF⊥AC,垂足分别为点E,F,连接DE,DF.求证:DE=DF.
推广
问题3 如图3,若将上面问题2中的条件“CB=CA”变为“CB≠CA”,其他条件不变,试探究DE与DF之间的数量关系,并证明你的结论.
6.(2012•昌平区模拟)(1)如图,在四边形ABCD中,AB=AD,∠B=∠D=90°,E、F
分别是边BC、CD上的点,且∠EAF=∠BAD.
求证:EF=BE+FD;
(2)如图,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是边BC、CD上的点,
且∠EAF=∠BAD,(1)中的结论是否仍然成立?
(3)如图,在四边形ABCD中,AB=AD,∠B+∠ADC=180°,E、F分别是边BC、CD延
长线上的点,且∠EAF=∠BAD,(1)中的结论是否仍然成立?若成立,请证明;若不成立,请写出它们之间的数量关系,并证明.
7.(2012•重庆模拟)如图,已知在梯形ABCD中,AD∥BC,DE⊥BC于点E,交AC于点F,∠ACB=45°,连接BF,∠FBC=∠EDC.
(1)求证:BF=CD;
(2)若AB=5,BC=7,求梯形ABCD的面积.
8.(2015•江西三模)已知△ABC,分别以AB、AC为边作△ABD和△ACE,且AD=AB,AC=AE,∠DAB=∠CAE,连接DC与BE,G、F分别是DC与BE的中点.
(1)如图1,若∠DAB=60°,则∠AFG=______;如图2,若∠DAB=90°,则∠AFG=______;
(2)如图3,若∠DAB=α,试探究∠AFG与α的数量关系,并给予证明;
(3)如果∠ACB为锐角,AB≠AC,∠BAC≠90°,点M在线段BC上运动,连接AM,以AM为一边以点A为直角顶点,且在AM的右侧作等腰直角△AMN,连接NC;试探究:若NC⊥BC(点C、M重合除外),则∠ACB等于多少度?画出相应图形,并说明理由.(画图不写作法)。