2011学年第一学期八年级数学期中检测试卷

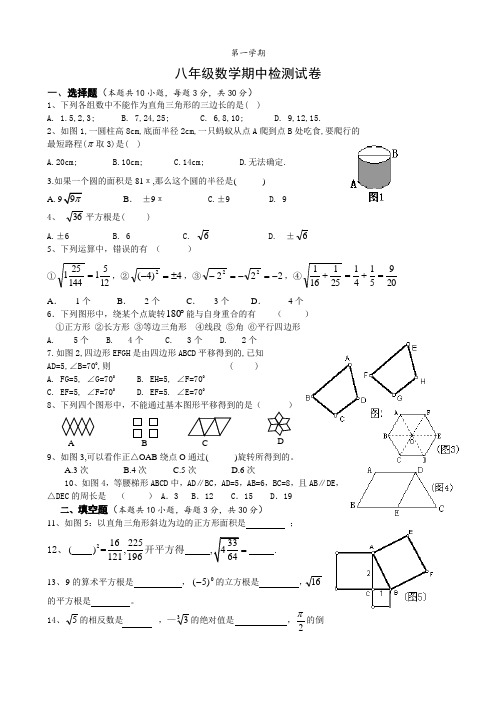
第一学期八年级数学期中检测试卷一、选择题（本题共10小题，每题3分，共30分）1、下列各组数中不能作为直角三角形的三边长的是( )A. 1.5,2,3;B. 7,24,25;C. 6,8,10;D. 9,12,15.2、如图1,一圆柱高8cm,底面半径2cm,一只蚂蚁从点A 爬到点B 处吃食,要爬行的 最短路程(π取3)是( )A.20cm;B.10cm;C.14cm;D.无法确定. 3.如果一个圆的面积是81π,那么这个圆的半径是( )B ． ±9π C.±9 D. 9 4、 36平方根是( )A.±6B. 6C. 6D. ±6 5、下列运算中，错误的有 （ ） ①1251144251=，②4)4(2±=-，③22222-=-=-，④2095141251161=+=+ A ． 1个 B ． 2个 C ． 3个 D ． 4个 6．下列图形中，绕某个点旋转︒180能与自身重合的有 （ ） ①正方形 ②长方形 ③等边三角形 ④线段 ⑤角 ⑥平行四边形 A. 5个 B. 4个 C. 3个 D. 2个 7.如图2,四边形EFGH 是由四边形ABCD 平移得到的,已知AD=5,∠B=700,则 ( )A. FG=5, ∠G=700B. EH=5, ∠F=700C. EF=5, ∠F=700D. EF=5. ∠E=7008、下列四个图形中，不能通过基本图形平移得到的是（ ）9O 通过()旋转所得到的。

A.3次B.4次C.5次D.6次10、如图4，等腰梯形ABCD 中，AD ∥BC ，AD=5，AB=6，BC=8，且AB ∥DE ，△DEC 的周长是 （ ） A ．3 B ．12 C ．15 D ．19 二、填空题（本题共10小题，每题3分，共30分） 11、如图5：以直角三角形斜边为边的正方形面积是 ；12、216225( )=,,.121196=开平方得 13、 9的算术平方根是 ， 0)5(-的立方根是 ，16的平方根是 。

2023-2024学年度第一学期山东省青岛市八年级数学期中训练与检测试卷一、、选择题（本大题共有8个小题，每小题3分，共24分）1．电影院的第3排第6座表示为（3，6）．若某同学的座位号为（4，2），那么该同学的位置是（ ）A ．第2排第4座B ．第4排第2座C ．第4座第4排D ．无法确定2．若点()1,3P 在直线2y x b =+上，则下列各点也在直线l 上的是（ ） A ．()2,1-B ．()2,5C ．()2,3−D ．()2,9−3．下列各数中：227，3.14159260.2020020002…（每两个2中间依次增加1个0），4π 无理数的个数有（ ）个．A ．1个B ．2个C ．3个D ．4个4．若ABC 的三边分别是a ，b ，c ，则下列条件能判断ABC 是直角三角形的是（ ）A ．2ABC ∠=∠=∠ B ．::3:4:5A B C ∠∠∠=C ．a b c ==D ．1,a b c ==5．点P 是第二象限内的点，且点P 到x 轴的距离为2，到y 轴的距离为3，则点P 的坐标为（ ）A ．()23−，B ．()23−，C ．()32−，D ．()32−，6．如图，AB AC =，则数轴上点C 所表示的数为（ ）A 1+B 1C ．1D ．1则函数y＝kx+b的图象大致是（）A．B．C．D．8．如图，一个圆柱形花瓶上下底面圆上有相对的A，B两点，现要用一根金色铁丝装饰花瓶，金色铁丝沿侧面缠绕花瓶一圈，并且经过A，B两点．若花瓶高16cm，底面圆的周长为24cm，则需要金色铁丝的长度最少为（）A．20cm B．C．D．40cm二、填空题（本大题共有6个小题，每小题3分，共18分）9．14的平方根是．101（“>”“<”或“=”)．11．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形E的边长为7cm，则图中五个正方形A、B、C、D、E的面积和为2cm．12.已知点()11A x y ，，()22B x y ，，()33C x y ，，()21D −，四点在直线4y kx =+的图象上， 且132x x x >>，则123y y y ，，的大小关系为_______________12．如图，折叠长方形的一边AD 使点D 落在BC 边的点F 处，已知AB = 8cm ，BC = 10 cm ，则EC 的长为 cm ．13．如图，有一圆柱，其高为12cm ，它的底面半径为3cm ，在圆柱下底面A 处有一只蚂蚁，它想得到上面B 处的食物，则蚂蚁经过的最短路程为 cm.（π取3）三、解答题（本大题共有19个小题，共78分）15．解方程：(1)()241100x −=(2)()3218x −=−16．如图，四边形ABCD 中，3AB =cm ，4AD =cm ，=13BC cm ，12CD =cm ，90A ∠°＝，求四边形ABCD 的面积．17．如图所示，ABC 的顶点坐标分别为()()()A 3,5,B 6,1,C 1,3−−−（1）作出ABC 关于x 轴对称的图形111A B C ；（2）写出111,,A B C 的坐标；（3）求ABC 的面积．18．计算与化简(1)(2)2(3(2−0(1(4)19.已知正数a的两个不同平方根分别是2x﹣2和6﹣3x，a﹣4b的算术平方根是4．（1）求这个正数a以及b的值；（2）求b2+3a﹣8的立方根．20.阅读下列解题过程：====2===请回答下列问题：(1)=___________．(2)利用上面提供的信息请化简：(+++……+)(1)的值．21.A、B两地相距3000米，甲、乙两人沿同一条路从A地到B地，l1，l2分别表示甲乙两人离开A地的距离y（m）与时间x（min）之间的关系，根据图象填空：（1）甲出发min后，乙才出发；（2）先到达终点（4）乙出发后min追上甲，这时他们距离B地m22.甲乙两商店出售同样的茶壶和茶杯，茶壶每只定价20元，茶杯每只定价5元，两家商店搞促销活动，甲店：买一只茶壶赠一只茶杯；乙店：按定价的9折优惠，某顾客需购买茶壶4只，茶杯若干只（不少于4只）．（1）设购买茶杯数为x（只），在甲店购买的付款为y甲（元），在乙店购买的付款数为y乙（元），分别写出在两家商店购物的付款数与茶杯数x之间的关系式；（2）当购买多少只茶杯时，两家商店的花费相同？（3）当购买20只茶杯时，去哪家商店购物比较合算？23.在信息技术迅猛发展的今天，很多同学都能够借助网络平台进行学习，在学习了平面直角坐标系后，小明同学在网上搜索到下面的文字材料：在x轴上有两个点，它们的坐标分别为（a，0）和（c，0），则这两点所成线段的长为|a﹣c|；同样的，若在y轴上的两点坐标分别为（0，b）和（0，d），则这两点所成线段的长为|b﹣d|．分别过这两点作两坐标轴的平行线，构成一个直角三角形，其中直角边P1Q＝|a﹣c|，PQ＝|b﹣d|，利用勾股定理可得，线段P1P2根据上面材料，回答下面的问题：（1）在平面直角坐标系中，已知A（7，﹣2），B（7，7），则线段AB的长为_____．（2）在平面直角坐标系中，已知M（﹣4，3），N（8，﹣2），则线段MN的长为______．（3）若点C在y轴上，点D的坐标是（﹣3，1），且CD=5，则点C的坐标是______．（4）如图2，在直角坐标系中，点A、B的坐标分别为（1，4）和（3，0），点C是y轴上的动点，且A、B、C三点不在同一直线上，求△ABC周长的最小值．24.如图，一次函数y=x+3的图象分别与x轴和y轴交于C，A两点，且与正比例函数y＝kx的图象交于点B（﹣1，m）．（1）求m的值；（2）求正比例函数的表达式；（3）点D是一次函数图象上的一点，且△OCD的面积是4，求点D的坐标．2023-2024学年度第一学期山东省青岛市八年级数学期中训练与检测试卷（解答卷）一、、选择题（本大题共有8个小题，每小题3分，共24分）1．电影院的第3排第6座表示为（3，6）．若某同学的座位号为（4，2），那么该同学的位置是（ ）A ．第2排第4座B ．第4排第2座C ．第4座第4排D ．无法确定【答案】B2．若点()1,3P 在直线2y x b =+上，则下列各点也在直线l 上的是（ ） A ．()2,1-B ．()2,5C ．()2,3−D ．()2,9−【答案】B3．下列各数中：227，3.14159260.2020020002…（每两个2中间依次增加1个0），4π 无理数的个数有（ ）个．A ．1个B ．2个C ．3个D ．4个【答案】C4．若ABC 的三边分别是a ，b ，c ，则下列条件能判断ABC 是直角三角形的是（ ）A ．2ABC ∠=∠=∠ B ．::3:4:5A B C ∠∠∠=C ．a b c ==D ．1,a b c ==【答案】D5．点P 是第二象限内的点，且点P 到x 轴的距离为2，到y 轴的距离为3，则点P 的坐标为（ ）A ．()23−，B ．()23−，C ．()32−，D ．()32−，=，则数轴上点C所表示的数为（）6．如图，AB ACA1+B1C．1D．1【答案】B7.已知一次函数y＝kx+b，函数值y随自变量x的增大而减小，且kb＞0，则函数y＝kx+b的图象大致是（）A．B．C．D．【答案】B8．如图，一个圆柱形花瓶上下底面圆上有相对的A，B两点，现要用一根金色铁丝装饰花瓶，金色铁丝沿侧面缠绕花瓶一圈，并且经过A，B两点．若花瓶高16cm，底面圆的周长为24cm，则需要金色铁丝的长度最少为（）A．20cm B．C．D．40cm【答案】D二、填空题（本大题共有6个小题，每小题3分，共18分）9．14的平方根是 ． 【答案】12±10 1（“>”“<”或“=”)． 【答案】＜11．如图，所有的四边形都是正方形，所有的三角形都是直角三角形，其中最大的正方形E 的边长为7cm ，则图中五个正方形A 、B 、C 、D 、E 的面积和为 2cm ．【答案】9812.已知点()11A x y ，，()22B x y ，，()33C x y ，，()21D −，四点在直线4y kx =+的图象上， 且132x x x >>，则123y y y ，，的大小关系为_______________【答案】132y y y <<12．如图，折叠长方形的一边AD 使点D 落在BC 边的点F 处，已知AB = 8cm ，BC = 10 cm ，则EC 的长为 cm ．13．如图，有一圆柱，其高为12cm ，它的底面半径为3cm ，在圆柱下底面A 处有一只蚂蚁， 它想得到上面B 处的食物，则蚂蚁经过的最短路程为 cm.（π取3）【答案】15三、解答题（本大题共有19个小题，共78分）15．解方程：(1)()241100x −=(2)()3218x −=− 解：（1）()241100x −= ∴()2125x −=， ∴15x −=±， 解得：4x =−或6；（2）解：()3218x −=− ∴212x -=-， 解得：12x =−．16．如图，四边形ABCD 中，3AB =cm ，4AD =cm ，=13BC cm ，12CD =cm ，90A ∠°＝，求四边形ABCD 的面积．解：连接BD ，∵3AB =cm ，4AD = cm ，90A ∠=°∴5BD = cm ，13462ABD S =××= cm 2 又∵5BD = cm ，13BC = cm ，12CD = cm∴222BD CD BC +=∴90BDC ∠=° ∴1512302BDC S =××= cm 2 ∴63036ABD BDC ABCD S S S =+=+= 四边形 cm 2．17．如图所示，ABC 的顶点坐标分别为()()()A 3,5,B 6,1,C 1,3−−−（1）作出ABC 关于x 轴对称的图形111A B C ；（2）写出111,,A B C 的坐标；（3）求ABC 的面积．解：（1）如图所示，△A 1B 1C 1即为所求；（2）由图象知A 1()35−−，B 1（﹣6，﹣1）C 1（﹣1，﹣3）；（3）△ABC 的面积4×5﹣12×3×4﹣12×2×2﹣12×2×5=7．18．计算与化简(1)(2)2(3(2−0(1(4)（1）解：=+=（2）解：2+−+(3(2()=+−−924310=+；(1（301==++411=；6（4）解：=×2=19.已知正数a的两个不同平方根分别是2x﹣2和6﹣3x，a﹣4b的算术平方根是4．（2）求b2+3a﹣8的立方根．解：（1）∵正数a的两个不同平方根分别是2x﹣2和6﹣3x，∴2x﹣2+6﹣3x＝0，∴x＝4，∴2x﹣2＝6，∴a＝36，∵a﹣4b的算术平方根是4，∴a﹣4b＝16，∴36-4b=16∴b＝5；（2）当a=36,b=5时，b2+3a﹣8＝25+36×3﹣8＝125，∴b2+3a﹣8=5．20.阅读下列解题过程：====2===请回答下列问题：(1)=___________．(2)利用上面提供的信息请化简：(+++……+)(1)的值．解：（1=3===，3（2）原式=)11+ )11 20081−2007=21. A 、B 两地相距3000米，甲、乙两人沿同一条路从A 地到B 地，l 1，l 2分别表示甲乙两人离开A 地的距离y （m ）与时间x （min ）之间的关系，根据图象填空：（1）甲出发 min 后，乙才出发；（2） 先到达终点（3）乙的速度是 m /min ．（4）乙出发后 min 追上甲，这时他们距离B 地 m解:（1）甲出发5min后，乙才出发；（2）乙先到达终点（3）乙的速度是3000205−=200m/min．（4）设y乙＝200x+b；把（20，3000）代入，可得：3000＝200×20+b，解得：b＝﹣1000，所以y乙＝200x﹣1000，设y甲＝kx（k≠0），把点（25，3000）代入，可得：3000＝25k，解得：k＝120，∴y甲＝120x．令y甲＝y乙，则120x＝200x﹣1000，解得：x＝12.5，12.5﹣5＝7.5乙出发后 7.5min 追上甲，这时他们距离B 地1500m ．故答案为5；乙；200；7.5；1500．22. 甲乙两商店出售同样的茶壶和茶杯，茶壶每只定价20元，茶杯每只定价5元， 两家商店搞促销活动，甲店：买一只茶壶赠一只茶杯；乙店：按定价的9折优惠， 某顾客需购买茶壶4只，茶杯若干只（不少于4只）．（1）设购买茶杯数为x （只），在甲店购买的付款为y 甲（元），在乙店购买的付款数为y 乙（元）， 分别写出在两家商店购物的付款数与茶杯数x 之间的关系式；（2）当购买多少只茶杯时，两家商店的花费相同？（3）当购买20只茶杯时，去哪家商店购物比较合算？解:（1）y 甲=2045(4)560x x ×+−，y 乙=(2045)0.94.572x x ×+×=+； （2）当y 甲=y 乙时，560 4.572x x +=+，解得x=24，∴当购买24只茶杯时，两家商店的花费相同；（3）当x=20时，y 甲=160，y 乙=90+72=162，∵y 甲<y 乙,∴应去甲商店购买比较合算.23.在信息技术迅猛发展的今天，很多同学都能够借助网络平台进行学习，在学习了平面直角坐标系后，小明同学在网上搜索到下面的文字材料：在x轴上有两个点，它们的坐标分别为（a，0）和（c，0），则这两点所成线段的长为|a﹣c|；同样的，若在y轴上的两点坐标分别为（0，b）和（0，d），则这两点所成线段的长为|b﹣d|．如图1，在直角坐标系中的任意两点P1，P2，其坐标分别是（a，b）和（c，d），分别过这两点作两坐标轴的平行线，构成一个直角三角形，其中直角边P1Q＝|a﹣c|，PQ＝|b﹣d|，利用勾股定理可得，线段P1P2根据上面材料，回答下面的问题：（1）在平面直角坐标系中，已知A（7，﹣2），B（7，7），则线段AB的长为_____．（2）在平面直角坐标系中，已知M（﹣4，3），N（8，﹣2），则线段MN的长为______．（3）若点C在y轴上，点D的坐标是（﹣3，1），且CD=5，则点C的坐标是______．（4）如图2，在直角坐标系中，点A、B的坐标分别为（1，4）和（3，0），点C是y轴上的动点，且A、B、C三点不在同一直线上，求△ABC周长的最小值．解：（1）由线段的公式得：9AB=，故答案为：9；（2）由线段的公式得：13MN=，故答案为：13；（3）设点C（0，m），则5CD==，解得m=5或-3，故点C的坐标为（0，5）或（0，-3），故答案为：（0，5）或（0，-3）；（4）作点A关于y轴的对称点D（-1，4），连接BD交y轴于点C，则此时△ABC周长最小，∵CA=CD，AB为定长，∴△ABC周长=AB+AC+BC=AB+CD+BC=AB+BD为最小，则AB同理可得：BD=，故△ABC周长的最小值=AB+AC+BC=AB+CD+BC=AB+BD=24.如图，一次函数y=x+3的图象分别与x轴和y轴交于C，A两点，且与正比例函数y＝kx的图象交于点B（﹣1，m）．（1）求m的值；（2）求正比例函数的表达式；（3）点D是一次函数图象上的一点，且△OCD的面积是4，求点D的坐标．解：（1）因为点B（-1，m）在一次函数y=x+3的图象上，所以，m=-1+3=2，故m的值为2；（2）因为正比例函数y=kx图象经过点B（-1，2），所以，-k=2，所以，k=-2，所以，y=-2x，正比例函数的表达式为y=-2x；（3）对于y=x+3，令y=0得，x=-3，所以，点C 的坐标为（-3，0），所以，OC =3，设点D 的坐标为（x ，y ）， 所以，1342y ××=， 所以，83y =，即83y =或83y =−， 当83y =时， 833x =+，解得13x =−， 所以，点D 的坐标为（13−，83）， 当83y =−时， 833x −=+，解得173x =−， 所以，点D 的坐标为（173−，83−）， 故D 的坐标为（13−，83）或（173−，83−）．。

金普新区2024-2025学年度第一学期期中质量检测试卷八年级数学2024.11（本试卷共23道题 满分120分考试时间共120分钟）注意：所有试题必须在答题卡上作答，在本试卷上作答无效。

第一部分 选择题（共30分）一、选择题（本题共10小题，每小题3分，共30分．在每小题给出的四个选项中，只有一项是符合题目要求的）1．下列长度的三条线段能组成三角形的是（ ）A ．1，3，2B ．2，5，8C ．3，4，5D ．5，5，102．下列计算正确的是（ ）A ．B ．C ．D ．3．在平面直角坐标系中，与点关于y 轴对称的点的坐标为（ ）A ．B ．C ．D ．4．中国体育代表团在2024年巴黎奥运会取得优异成绩，下列图标中，是轴对称图形的是（）A ．B ．C ．D ．5．下列各图形中，分别是四位同学所画的中BC 边上的高AE ，其中正确的是（）A ．B ．C ．D ．6．榫卯结构是我国古代建筑，家具及其他木制器械的主要结构方式．如图，将两块全等的木楔（）水平钉入长为16 cm 的长方形木条中（点B ，C ，F ，E 在同一条直线上）．若，则木楔BC 的长为（ ）（第6题）248a a a⋅=()428bb =2246a a a⋅=235a b ab +=()1,7A -A '()1,7()1,7-()1,7--()1,7-ABC △ABC DEF △△≌4cm CF =A ．4 cmB ．6 cmC ．8 cmD ．12 cm7．如图，AD ，CE 都是的中线，连接ED ，的面积足，则的面积是（）（第7题）A ．B ．C ．D ．8．如图，三座商场分别坐落在A ，B ，C 所在位置，现要规划一个地铁站，使得该地铁站到三座商场的距离相等，该地铁站应建在（）（第8题）A ．三条高所在直线的交点B ．三条中线的交点C ．三个内角的角平分线的交点D ．三条边的垂直平分线的交点9．如图，直线l 是一条河，P ，Q 是两个村庄，欲在l 上的某处修建一个水泵站，向P ，Q 两地供水，现有如下四种铺设方案，图中实线表示铺设的管道，则所需管道最短的是（）A ．B ．C ．D ．10．如图，在中，，，，沿过点B 的直线折叠这个三角形，使点C 落在AB 边上的点E 处，折痕为BD ，则的周长为（）（第10题）A ．6B ．7C ．8D ．9第二部分 非选择题（共90分）ABC △ABC △220cm CDE △22.5cm25cm27.5cm210cmABC △ABC △ABC △ABC △ABC △10AB =7BC =6AC =AED △二、填空题（本题共5小题，每小题3分，共15分）11．如图是环己烷的结构简式（正六边形），其内角和为______°．（第11题）12．若，，则______．13．已知等腰三角形的一个底角是70°，则它的顶角的度数是______°．14．如图，中，，若沿图中虚线截去∠F ，则______°．（第14题）15．如图，四边形ABCD 中，，，，，以点B 为圆心，适当长为半径作弧，分别与AB ，BC 相交于点点E ，F ，再分别以点E ，F为圆心，大于的长为半径作弧，两弧在的内部相交于点G ，作射线BG ，与AD 相交于点H ，则HD 的长为______（用含a 的代数式表示）．（第15题）三、解答题（本题共8小题，共75分．解答应写出文字说明、演算步骤或推理过程）16．（10分）．计算：（1）；（2）．17．（8分）如图，点M ，N 在线段BD 上，，，．求证：．2ma =4na =m na+=DEF △35F ∠=︒12∠+∠=AD BC ∥AD AB >AD a =8AB =12EF ABC ∠()232462a a a a +⋅-()()()3243x y x y x x y x ++-+÷BM DN =AN CM =AN CM ∥ABN CDM △△≌（第17题）18．（8分）如图，已知中，，，．（1）画出与关于x 轴对称的图形，并写出各顶点坐标；（2）的面积为______．（第18题）19．（8分）如图，在中，AD 平分∠BAC ，于D ，于C ，且，．（1）求证：；（2）求证：．（第19题）20．（8分）如图，在中，CD 平分，E 为线段CD 上一点，过E 作交BA 的延长线于点F ，若，，求的度数．ABC △()1,3A ()3,1B ()5.4C ABC △111A B C △111A B C △ABC △ABC △AD BC ⊥EC BC ⊥AB BE =CD CE =AB AC =Rt Rt ABD BEC △△≌ABC △ACB ∠EF CD ⊥115BAC ∠=︒35B ∠=︒F ∠（第20题）21．（8分）如图，已知中，，于D ，的平分线分别交AD ，AB 于P 、Q ．（1）试说明是等腰三角形；（2）若点Q 恰好在线段BC 的垂直平分线上，试说明线段AC 与线段BC 之间的数量关系．（第21题）22．（12分）阅读下列材料，解决相应问题：已知两个两位数，将它们各自的十位数字和个位数字交换位置后，得到两个与原两个两位数均不同的新数，若这两个两位数的乘积与交换位置后两个新两位数的乘积相等，则称这样的两个两位数为“倒同数对”．例如：，所以23和96与32和69都是“倒同数对”．（1）请判断43和68是否是“倒同数对”，并说明理由；（2）为探究“倒同数对”的本质，可设“倒同数对”中一个数的十位数字为m ，个位数字为n ，且；另一个数的十位数字为p ，个位数字为q ，且，请探究m ，n ，p ，q 的数量关系，并说明理由；（3）若有一个两位数，十位数字为x ，个位数字为，另一个两位数，十位数字为，个位数字为，且这两个数为“倒同数对”，则x 的值为______．23．（13分）【问题初探】（1）综合与实践数学活动课上，李老师给出了一个问题：如图1，若，，CD 平分，求证：．（第20题图1）①如图2，小明同学从结论的角度出发给出如下解题思路：在BC 上截取，连接DE ，将线段BC ，AC ，AD 之间的数量关系转化为BE 与AD的数量关系；Rt ABC △90BAC ∠=︒AD BC ⊥ACB ∠APQ △239632692208⨯=⨯=m n ≠p q ≠1x +3x +1x +60A ∠=︒90ACB ∠=︒ACB ∠BC AC AD =+CE CA =（第20题图2）②如图3，小强同学从CD 平分这个条件出发给出另一种解题思路：延长CA 至点E ，使，连接DE ，将线段BC ，AC ，AD 之间的数量关系转化为AE 与AD 的数最关系；请你选择一名同学的解题思路，写出证明过程：（第20题图3）【类比分析】（2）李老师发现两名同学都运用了转化思想，将证明三条线段的关系转化为证明两条线段的关系；为了帮助学生更好地感悟转化思想，李老师将问题进行变式，请你解答：如图4，在四边形ABCD 中，E 是BC 的中点，若AE 平分，，请你探究AB 、AD 、CD 的数量关系并证明；（第20题图4）【学以致用】（3）如图5，在中，，和的平分线交于点P ，M ，N 为AB ，AC 上的点，且P 为MN 中点，若，，，求BC 的值．（第20题图5）ACB ∠CE CB =BAD ∠90AED ∠=︒ABC △60A ∠=︒ABC ∠ABC ∠5BM =45CN =4MN =金普新区2024-2025学年度第一学期期中质量检测八年级数学参考答案及评分标准（说明：试题解法不唯一，其他方法备课组统一意见，酌情给分。

2022-2023学年八年级第一学期期中考试数学(人教版）(总分120分，考试时间120分钟)一、选择题(本大题共16个小题.1～10小题每题3分，11～16小题每题2分，共42分.在每小题给出的四个选项中，只有一项是符合题目要求的)1.钢架雪车是2022年北京冬奥会的比赛项目之一.下面这些钢架雪车运动标志是轴对称图形的是( )2.在平面直角坐标系中，点A(−1，4)关于x轴对称的点的坐标为( )A.(1，4)B.( −1，4)C.(0，−4)D.(−1，−4)3.下列正多边形中，内角和是540°的是( )4.如图，用纸板挡住部分三角形后，能用尺规画出与此三角形全等的三角形，其全等的依据是( )A.ASAB.AASC.SASD.HL5.若α为正六边形的一个外角，则α的度数为( )A.45°B.50°C.60°D.72°4题图A5题图B E F C6.如图，△ABF ≌△ACE ，点B 和点C 是对应顶点，则下列结论中不一定．．．成立的是() A.∠B=∠C B.BE=CF C.∠BAE=∠CAF D.AE=EF7.如图，物业公司计划在小区内修建一个电动车充电桩，要求到A ，B ，C 三个出口的距离都相等，则充电桩应建在( )A.△ABC 的三条高的交点处B.△ABC 的三条角平分线的交点处C.△ABC 的三条中线的交点处D.△ABC 的三条边的垂直平分线的交点处 8.如图，E 是△ABC 的边AC 的中点，CF ∥AB ，连接FE 并延长交AB 于点D ，若AB=9，CF=6，则BD 的长为( )A.1.5B.2C.3D.3.59.如图，在△ABC 中，CD 是边AB 上的高，BE 平分∠ABC ，交CD 于点E ，若BC=10，DE=3，则△BCE 的面积为( )A.14B.15C.18D.30 10.具备下列条件的△ABC ，不是．．直角三角形的是( ) A.∠A ︰∠B ︰∠C=5︰2︰3 B.∠A −∠C=∠B C.∠A=∠B=2∠C D.∠A=12∠B=13∠C11.如图，△ABC 与△A 1B 1C ，关于直线MN 对称，P 为MN 上任一点(P 不与AA 1共线)，下列结论不正确．．．的是( ) A.AP=A 1P B.△ABC 与△A 1B 1C 1的面积相等 C.MN 垂直平分线段AA 1 D.直线AB ，A 1B 1的交点不一定在MN 上 12.如图所示，已知在△ABC 中，∠C=90°，AD=AC ，DE ⊥AB 交BC 于点E ，若∠B=28°，A8题图BCEFD 7题图ABC9题图则∠AEC=( )A.28°B.59°C.60°D.62°13.如图，将三角形纸片ABC 翻折，点A 落在点A ´的位置，折痕为DE.若∠A=30°，∠BDA ´=80°，则∠CEA ´的度数为( )A.15°B.20°C.30°D.40°14.如图，小亮和小明分别用尺规作∠APB 的平分线PQ ，则关于两人的作图方法，下列判断正确的是( )A.小亮、小明均正确B.只有小明正确C.只有小亮正确D.小亮、小明均不正确15.如图，AD 为△ABC 的中线，DE 平分∠ADB ，DF 平分∠ADC ，BE ⊥DE ，CF ⊥DF ，下列结论正确的有( )①∠EDF=90°；②∠BAD=∠CAD ；③△BDE ≌△DCF ；④EF ∥BC. A.4个 B.3个 C.2个 D.1个16.有一道题目：“如图，∠AOB=60°，点M ，N 分别在OA ，OB 上运动(不与点O 重合），13题图A CBDE A ´A14题图APP B BQQ小明小亮11题图A MN CBP A 1B 1C 112题图ME 平分∠AMN ，ME 的反向延长线与∠MNO 的平分线交于点F ，在点M ，N 的运动过程中，求∠F 的度数.”甲的解答：∠F 的度数不能确定，它随着点M ，N 的运动而变化，且随∠OMN 的增大而减小；乙的解答：∠F 始终等于45°，下列判断正确的是( )A.甲说的对B.乙说的对C.乙求的结果不对，∠F 始终等于30°D.两人说的都不对，凭已知条件无法确定∠F 的值或变化趋势二、填空题(本大题共3个小题，每小题3分，共9分.其中18小题第一空2分，第二空1分；19小题每空1分)17.如图，AB=AC ，点D ，E 分别在AB ，AC 上，连接BE ，CD ，要使△ABE ≌△ACD ，则添加的条件是_______.(只需填一个即可)18.如图，在△ABC 中，AB 的垂直平分线交AC 于点D ，若△BCD 的周长为5，BC=2，则AC 的长为_______，边AB 长的取值范围是_______.19.如图，在△ABC 中，AD 平分∠BAC 交BC 于点D ，BE 平分∠ABC 交AD 于点E.17题图ACEDB18题图19题图ABCD E16题图A EBFMON 15题图(1)若∠C=50°，∠BAC=60°，则∠ADB的度数为_______.(2)若∠BED=45°，则∠C的度数为_______.(3)猜想∠BED与∠C的数量关系为_______.三、解答题(本大题共7个小题，共69分.解答应写出文字说明、证明过程或演算步骤）20.已知一个多边形的边数为n.(1)若n=7，求这个多边形的内角和.比一个四边形的外角和多90°，求n的值.(2)若这个多边形的内角和的1421.如图，在平面直角坐标系中，△ABC的顶点坐标分别为A(1，−4)，B(3，−3)，C(1，−1).(1)画出△ABC关于y轴对称的△A1B1C1.(2)写出(1)中所画的△A1B1C1的各顶点坐标.(3)连接CC1，BB1，则四边形BCC1B1的面积为_______.22.如图，在Rt△ABC中，∠ACB=90°，D为边AB上一点.将△ACB沿CD折叠，使点A恰好落在边BC上的点E处.(1)若AC=6，BC=8，AB=10，求△BDE 的周长. (2)若∠B=37°，求∠CDE 的度数.23.已知：如图，在△ABC 中，∠ABC 和∠ACB 的角平分线相交于点P ，且PE ⊥AB ，PF ⊥AC ，垂足分别为E 、F. (1)求证：PE=PF.(2)若∠BAC=60°，连接AP ，求∠EAP 的度数.24.在△ABC 中，AF 平分∠BAC ，CD ⊥AF ，垂足为F ，与AB 交于点D.(1)如图1，若∠BAC=80°，∠B=40°，求∠BCD 的度数. (2)如图2，在△ABC 内部作∠ACE=∠B ，求证：∠BCD=∠DCE.A图2图1AAD BEC25.如图，AE=AF ，AE ⊥AF ，点E ，F ，B 在同一直线上，AB=AC ，∠BAC=90°.(1)判断△AEB 与△AFC 是否全等？若全等，请给出证明；若不全等，请说明理由. (2)当EF 和BF 满足什么数量关系时，CE=CB?请给出结论并说明理由.26.【问题提出】如图1，△ABC 是直角三角形，∠BAC=90°，AB=AC ，直线l 经过点A ，分别过点B ，C 向直线l 作垂线，垂足分别为D ，E.求证：△ABD ≌△CAE.【变式探究】若图1中的点B ，C 在直线l 的两侧，其他条件不变(如图2所示），判断△ABD 与△CAE 是否依然全等，并说明理由.【深入思考】如图3，在△ABC 中，AB=AC ，直线l 经过点A ，且点B ，C 位于直线l 的两侧，若∠BDA+∠BAC=180°，∠BDA=∠AEC ，判断线段BD ，CE ，DE 之间的数量关系，并加以说明.图1l图2图3ACD E BlF2022-2023学年八年级第一学期期中考试数学(人教版）(总分120分，考试时间120分钟)一、选择题(本大题共16个小题.1～10小题每题3分，11～16小题每题2分，共42分.在每小题给出的四个选项中，只有一项是符合题目要求的)1.钢架雪车是2022年北京冬奥会的比赛项目之一.下面这些钢架雪车运动标志是轴对称图形的是( )1.解：D 是轴对称图形，关于对称轴两侧对称且能完全重合，故选D 。

2021-2022学年八年级上学期期中考试数学试卷一．选择题（共10小题，满分30分，每小题3分）1．在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中．轴对称图形是（ ）A ．B ．C ．D ．2．下列每组数分别是三根小木棒的长度，用它们能摆成三角形的是（ ） A ．3cm ，4cm ，8cm B ．8cm ，7cm ，15cmC ．13cm ，12cm ，20cmD ．5cm ，5cm ，11cm3．如图，AC ＝AD ，BC ＝BD ，则有（ ）A ．AB 与CD 互相垂直平分 B ．CD 垂直平分ABC ．AB 垂直平分CDD ．CD 平分∠ACB4．如图，AB ＝DB ，∠1＝∠2，请问添加下面哪个条件不能判断△ABC ≌△DBE 的是（ ）A ．BC ＝BEB ．AC ＝DEC ．∠A ＝∠DD ．∠ACB ＝∠DEB5．如图，AD 是△ABC 中∠BAC 的平分线，DE ⊥AB 于点E ，DF ⊥AC 于点F ．若S △ABC ＝28，DE ＝4，AB ＝8，则AC 长是（ ）A ．8B ．7C ．6D ．56．如图，在△ABC 中，AB ＝AC ，分别以点A 、点B 为圆心，以大于12AB 长为半径画弧，两弧交点的连线交AC 于点D ，交AB 于点E ，连接BD ，若∠A ＝40°，则∠DBC ＝（ ）A ．40°B ．30°C ．20°D ．10°7．若等腰三角形的一边长等于6，另一边长等于4，则它的周长等于（ ） A ．15或17B ．16C ．14D ．14或168．如图，在平面直角坐标系中，AB ＝2OB ，在坐标轴上取一点P ，使得△ABP 为等腰三角形，则符合条件的点P 共有（ ）A ．4个B ．5个C ．6个D ．7个9．如图，将长方形纸片ABCD 沿对角线AC 折叠，点B 落在点E 处，AB ＝10，AD ＝5，下列结论中正确的有（ ）个． ①△AFC 是等腰三角形 ②△ADF 的面积是758③点B 与点E 关于AC 对称④若直线AD 与直线CE 交于点G ，那么直线FG 垂直平分ACA ．1 个B ．2 个C ．3 个D ．4 个10．如图，等腰Rt△ABC中，BC＝8√5，以边AC为斜边向右做等腰Rt△ACD，点E是线段CD的中点，连接AE，作线段CE关于直线AC的对称线段CF，连接BF，并延长BF 交线段AE于点G，则线段BG长为（）A．16√5B．16√2C．12√5D．12√2二．填空题（共6小题，满分18分，每小题3分）11．在平面直角坐标系xOy中，点P（1，2）关于y轴的对称点Q的坐标是．12．一个多边形的每一个外角为30°，那么这个多边形的边数为．13．如图，△ABC内有一点D，且DA＝DB＝DC，若∠DAB＝20°，∠DAC＝30°，则∠BDC＝．14．如图，MN是正方形ABCD的一条对称轴，点P是直线MN上的一个动点，当PC+PD 最小时，∠PCD＝°．15．如图，△ABC中，∠ABC与∠ACB的平分线相交于点O，EF经过点O，分别交AB，AC于点E，F，BE＝OE，OF＝3cm，点O到BC的距离为4cm，则△OFC的面积为cm2．16．下列说法中正确的是（只填番号）①一个多边形的内角和小于其外角和，则这个多边形是四边形；②方程2x+y＝7在正整数范围内的解有3组；③关于x的不等式abx＞1的解集为x＜1ab，则a、b中至少有一个是负数；④直角三角形两锐角平分线相交，所成的钝角的度数是135°三．解答题（共8小题，满分72分）17．（8分）如图，△ABC和△EBD中，∠ABC＝∠DBE＝90°，AB＝CB，BE＝BD，连接AE，CD，AE与CD交于点M，AE与BC交于点N．（1）求证：AE＝CD；（2）求证：AE⊥CD；（3）连接BM，有以下两个结论：①BM平分∠CBE；②MB平分∠AMD．其中正确的有（请写序号，少选、错选均不得分）．18．（8分）已知等腰三角形的一边长为18，腰长是底边长的34，试求此三角形的周长．19．（8分）如图，AC ⊥BC ，DC ⊥EC ，AC ＝BC ，DC ＝EC ，AE 与BD 交于点F ． （1）求证：AE ＝BD ； （2）求∠AFD 的度数．20．（8分）在平面直角坐标系xOy中，△ABC的位置如图所示，直线l经过点（0，1），并且与x轴平行，△A1B1C1与△ABC关于直线l对称．（1）画出三角形A1B1C1；（2）若点P（m，n）在AC边上，则点P关于直线l的对称点P1的坐标为；（3）在直线l上画出点Q，使得QA+QC的值最小．21．（8分）如图，四边形ABCD中，AD∥BC，DE＝EC，连接AE并延长交BC的延长线于点F，连接BE．（1）求证：AE＝EF；（2）若BE⊥AF，求证：BC＝AB﹣AD．22．（10分）如图1，在平面直角坐标系xOy中，点A在y轴上，点B是第一象限的点，且AB⊥y轴，且AB＝OA，点C是线段OA上任意一点，连接BC，作BD⊥BC，交x轴于点D．（1）依题意补全图1；（2）用等式表示线段OA，AC与OD之间的数量关系，并证明；（3）连接CD，作∠CBD的平分线，交CD边于点H，连接AH，求∠BAH的度数．23．（10分）如图，在正方形ABCD中，M、N分别是射线CB和射线DC上的动点，且始终∠MAN＝45°．（1）如图1，当点M、N分别在线段BC、DC上时，请直接写出线段BM、MN、DN之间的数量关系；（2）如图2，当点M、N分别在CB、DC的延长线上时，（1）中的结论是否仍然成立，若成立，给予证明，若不成立，写出正确的结论，并证明；（3）如图3，当点M、N分别在CB、DC的延长线上时，若CN＝CD＝6，设BD与AM 的延长线交于点P，交AN于Q，直接写出AQ、AP的长．24．（12分）如图①所示，已知正方形ABCD和正方形AEFG，连接DG，BE．（1）发现：当正方形AEFG绕点A旋转，如图②所示．①线段DG与BE之间的数量关系是；②直线DG与直线BE之间的位置关系是；（2）探究：如图③所示，若四边形ABCD与四边形AEFG都为矩形，且AD＝2AB，AG ＝2AE时，上述结论是否成立，并说明理由．（3）应用：在（2）的情况下，连接BG、DE，若AE＝1，AB＝2，求BG2+DE2的值（直接写出结果）．2021-2022学年八年级上学期期中考试数学试卷参考答案与试题解析一．选择题（共10小题，满分30分，每小题3分）1．在“回收”、“节水”、“绿色食品”、“低碳”四个标志图案中．轴对称图形是（）A．B．C．D．【解答】解：A、不是轴对称图形，故此选项不合题意；B、不是轴对称图形，故此选项不合题意；C、是轴对称图形，故此选项符合题意；D、不是轴对称图形，故此选项不合题意．故选：C．2．下列每组数分别是三根小木棒的长度，用它们能摆成三角形的是（）A．3cm，4cm，8cm B．8cm，7cm，15cmC．13cm，12cm，20cm D．5cm，5cm，11cm【解答】解：A、3+4＜8，不能组成三角形；B、8+7＝15，不能组成三角形；C、13+12＞20，能够组成三角形；D、5+5＜11，不能组成三角形．故选：C．3．如图，AC＝AD，BC＝BD，则有（）A．AB与CD互相垂直平分B．CD垂直平分ABC．AB垂直平分CD D．CD平分∠ACB【解答】解：∵AC＝AD，BC＝BD，∴AB是线段CD的垂直平分线，故选：C．4．如图，AB ＝DB ，∠1＝∠2，请问添加下面哪个条件不能判断△ABC ≌△DBE 的是（ ）A ．BC ＝BEB ．AC ＝DE C ．∠A ＝∠D D ．∠ACB ＝∠DEB【解答】解：A 、添加BC ＝BE ，可根据SAS 判定△ABC ≌△DBE ，故正确；B 、添加AC ＝DE ，SSA 不能判定△ABC ≌△DBE ，故错误；C 、添加∠A ＝∠D ，可根据ASA 判定△ABC ≌△DBE ，故正确；D 、添加∠ACB ＝∠DEB ，可根据ASA 判定△ABC ≌△DBE ，故正确．故选：B ．5．如图，AD 是△ABC 中∠BAC 的平分线，DE ⊥AB 于点E ，DF ⊥AC 于点F ．若S △ABC ＝28，DE ＝4，AB ＝8，则AC 长是（ ）A ．8B ．7C ．6D ．5【解答】解：∵AD 是△ABC 中∠BAC 的平分线，DE ⊥AB 于点E ，DF ⊥AC 交AC 于点F ，∴DF ＝DE ＝4．又∵S △ABC ＝S △ABD +S △ACD ，AB ＝8，∴28=12×8×4+12×AC ×4， ∴AC ＝6．故选：C ．6．如图，在△ABC 中，AB ＝AC ，分别以点A 、点B 为圆心，以大于12AB 长为半径画弧，两弧交点的连线交AC 于点D ，交AB 于点E ，连接BD ，若∠A ＝40°，则∠DBC ＝（ ）A．40°B．30°C．20°D．10°【解答】解：∵AB＝AC，∠A＝40°，∴∠ABC＝∠C=12（180°﹣40°）＝70°，∵AD＝BD，∴∠ABD＝∠A＝40°，∴∠DBC＝∠ABC﹣∠ABD＝30°，故选：B．7．若等腰三角形的一边长等于6，另一边长等于4，则它的周长等于（）A．15或17B．16C．14D．14或16【解答】解：当4为底边时，腰长为6，则这个等腰三角形的周长＝4+6+6＝16；当6为底边时，腰长为4，则这个等腰三角形的周长＝4+4+6＝14；故选：D．8．如图，在平面直角坐标系中，AB＝2OB，在坐标轴上取一点P，使得△ABP为等腰三角形，则符合条件的点P共有（）A．4个B．5个C．6个D．7个【解答】解：如图，在Rt△AOB中，∵AB＝2OB，∴∠BAO＝30°，当P 在x 轴上时，AB ＝AP 时，P 点有两个，BP ＝AP 时，P 点有一个，AB ＝BP 时，P 点有一个当P 在y 轴上时，AB ＝BP 时，P 点有两个，BP ＝AP 时或AB ＝AP 时，和前面重合， 综上所述：符合条件的P 点有6个，故选：C ．9．如图，将长方形纸片ABCD 沿对角线AC 折叠，点B 落在点E 处，AB ＝10，AD ＝5，下列结论中正确的有（ ）个．①△AFC 是等腰三角形②△ADF 的面积是758③点B 与点E 关于AC 对称④若直线AD 与直线CE 交于点G ，那么直线FG 垂直平分ACA ．1 个B ．2 个C ．3 个D ．4 个【解答】解：如图所示：①∵四边形ABCD 为矩形∴DC ∥AB ，∴∠FCA ＝∠CAB ，由折叠可知：∠F AC ＝∠CAB ，∴∠FCA ＝∠F AC ，∴F A ＝FC ，∴△AFC 是等腰三角形．∴①正确；②设DF ＝x ，则FC ＝F A ＝10﹣x ，AD ＝5，∴在Rt △ADF 中，x 2+52＝（10﹣x ）2，解得x =154， ∴S △ADF =12DF •AD =12×154×5=758．∴△ADF 的面积为758．∴②正确；③∵AB ＝AE ，CB ＝CE ，∴AC 是BE 的垂直平分线，∴点B 与点E 关于AC 对称．∴③正确；④如图：延长AD 和CE 交于点G ，连接GF ，∵FD＝FE，FG＝FG，∴Rt△GDF≌Rt△GEF（HL），∴GD＝GE，又AD＝CE，∴GA＝GC，FD＝FE，∴FG是AC的垂直平分线，∴④正确．故选：D．10．如图，等腰Rt△ABC中，BC＝8√5，以边AC为斜边向右做等腰Rt△ACD，点E是线段CD的中点，连接AE，作线段CE关于直线AC的对称线段CF，连接BF，并延长BF 交线段AE于点G，则线段BG长为（）A．16√5B．16√2C．12√5D．12√2【解答】解：如图，设AC交BG于O．∵∠BCA＝∠FCE＝90°，∴∠BCF＝∠ACE，∵CB＝CA，CF＝CE，∴△BCF≌△ACE（SAS），∴∠CBF＝∠CAE，∵∠BOC＝∠AOG，∴∠AGO＝∠BCO＝90°，∵△ABC，△ACD都是等腰直角三角形，∴∠BAC＝∠CAD＝45°，∴∠BAD＝90°，∴∠ABG+∠BAG＝90°，∠BAG+∠EAD＝90°，∴∠ABG＝∠EAD，∴tan∠ABG＝tan∠EAD=DEAD=12，∴AGBG =12，设AG＝x，BG＝2x，∵AC＝BC＝8√5，∠ACB＝90°，∴AB=√2BC＝8√10在Rt△ABG中，则有x2+（2x）2＝（8√10）2，∴x＝8√2，∴BG＝16√2，故选：B．二．填空题（共6小题，满分18分，每小题3分）11．在平面直角坐标系xOy中，点P（1，2）关于y轴的对称点Q的坐标是（﹣1，2）．【解答】解：点P（1，2）关于y轴的对称点Q的坐标是：（﹣1，2）．故答案为：（﹣1，2）．12．一个多边形的每一个外角为30°，那么这个多边形的边数为12．【解答】解：多边形的边数：360°÷30°＝12，则这个多边形的边数为12．故答案为：12．13．如图，△ABC内有一点D，且DA＝DB＝DC，若∠DAB＝20°，∠DAC＝30°，则∠BDC＝100°．【解答】解：延长BD交AC于E．∵DA＝DB＝DC，∴∠ABE＝∠DAB＝20°，∠ECD＝∠DAC＝30°．又∵∠BAE＝∠BAD+∠DAC＝50°，∠BDC＝∠DEC+∠ECD，∠DEC＝∠ABE+∠BAE，∴∠BDC＝∠ABE+∠BAE+∠ECD＝20°+50°+30°＝100°．故答案为：100°．14．如图，MN是正方形ABCD的一条对称轴，点P是直线MN上的一个动点，当PC+PD 最小时，∠PCD＝45°．【解答】解：∵当PC+PD最小时，作出D点关于MN的对称点，正好是A点，连接AC，AC为正方形对角线，根据正方形的性质得出∠PCD＝45°，∴∠PCD＝45°．故答案为：45°．15．如图，△ABC中，∠ABC与∠ACB的平分线相交于点O，EF经过点O，分别交AB，AC于点E，F，BE＝OE，OF＝3cm，点O到BC的距离为4cm，则△OFC的面积为6 cm2．【解答】解：∵BE ＝OE ，∴∠EBO ＝∠EOB ，∵BO 平分∠ABC ，∴∠EBO ＝∠CBO ，∴∠EOB ＝∠CBO ，∴EF ∥BC ，∵点O 到BC 的距离为4cm ，∴△COF 中OF 边上的高为4cm ，又∵OF ＝3cm ，∴△OFC 的面积为12×3×4＝6cm 2． 故答案为：6．16．下列说法中正确的是 ②④ （只填番号）①一个多边形的内角和小于其外角和，则这个多边形是四边形；②方程2x +y ＝7在正整数范围内的解有3组；③关于x 的不等式abx ＞1的解集为x ＜1ab，则a 、b 中至少有一个是负数； ④直角三角形两锐角平分线相交，所成的钝角的度数是135°【解答】解：①一个多边形的内角和小于其外角和，则这个多边形是三角形，故这个说法错误；②方程2x +y ＝7，解得：y ＝﹣2x +7，当x ＝1时，y ＝5；当x ＝2时，y ＝3；当x ＝3时，y ＝1，则方程的正整数解有3组，故这个说法正确；③关于x 的不等式abx ＞1的解集为x ＜1ab ，则a 、b 中只能有一个是负数，故这个说法错误；④如图：∵AE 、BD 是直角三角形中两锐角平分线，∴∠OAB +∠OBA ＝90°÷2＝45°，两角平分线组成的角有两个：∠BOE 与∠EOD 这两个交互补，根据三角形外角和定理，∠BOE ＝∠OAB +∠OBA ＝45°，∴∠EOD ＝180°﹣45°＝135°，直角三角形两锐角平分线相交，所成的钝角的度数是135°是正确的．故答案为：②④．三．解答题（共8小题，满分72分）17．（8分）如图，△ABC 和△EBD 中，∠ABC ＝∠DBE ＝90°，AB ＝CB ，BE ＝BD ，连接AE ，CD ，AE 与CD 交于点M ，AE 与BC 交于点N ．（1）求证：AE ＝CD ；（2）求证：AE ⊥CD ；（3）连接BM ，有以下两个结论：①BM 平分∠CBE ；②MB 平分∠AMD ．其中正确的有 ② （请写序号，少选、错选均不得分）．【解答】（1）证明：∵∠ABC ＝∠DBE ，∴∠ABC +∠CBE ＝∠DBE +∠CBE ，即∠ABE ＝∠CBD ，在△ABE 和△CBD 中，{AB =CB ∠ABE =∠CBD BE =BD，∴△ABE ≌△CBD ，∴AE ＝CD ．（2）∵△ABE ≌△CBD ，∴∠BAE ＝∠BCD ，∵∠NMC ＝180°﹣∠BCD ﹣∠CNM ，∠ABC ＝180°﹣∠BAE ﹣∠ANB ，又∠CNM ＝∠ANB ，∵∠ABC ＝90°，∴∠NMC ＝90°，∴AE ⊥CD ．（3）结论：②理由：作BK ⊥AE 于K ，BJ ⊥CD 于J ．∵△ABE ≌△CBD ，∴AE ＝CD ，S △ABE ＝S △CDB ，∴12•AE •BK =12•CD •BJ ， ∴BK ＝BJ ，∵作BK ⊥AE 于K ，BJ ⊥CD 于J ，∴BM 平分∠AMD ．不妨设①成立，则△ABM ≌△DBM ，则AB ＝BD ，显然不可能，故①错误．故答案为②．18．（8分）已知等腰三角形的一边长为18，腰长是底边长的34，试求此三角形的周长． 【解答】解：∵等腰三角形一边长为18cm ，且腰长是底边长的34， ①如果腰长为18cm ，则底边为24cm ，等腰三角形的三边为18、18、24，能构成三角形，∴C △＝18+18+24＝60cm ；②如果底长为18cm ，则腰长为13.5cm ，等腰三角形的三边为18、13.5、13.5，能构成三角形，∴C △＝13.5+13.5+18＝45cm ．19．（8分）如图，AC ⊥BC ，DC ⊥EC ，AC ＝BC ，DC ＝EC ，AE 与BD 交于点F ．（1）求证：AE ＝BD ；（2）求∠AFD 的度数．【解答】解：（1）∵AC ⊥BC ，DC ⊥EC ，∴∠ACB ＝∠DCE ＝90°，∴∠ACE ＝∠BCD ，在△ACE 和△BCD 中，{AC =BC ∠ACE =∠BCD CE =CD，∴△ACE ≌△BCD （SAS ），∴AE ＝BD ；（2）设BC 与AE 交于点N ，∵∠ACB ＝90°，∴∠A +∠ANC ＝90°，∵△ACE ≌△BCD ，∴∠A ＝∠B ，∵∠ANC ＝∠BNF ，∴∠B +∠BNF ＝∠A +∠ANC ＝90°，∴∠AFD ＝∠B +∠BNF ＝90°．20．（8分）在平面直角坐标系xOy中，△ABC的位置如图所示，直线l经过点（0，1），并且与x轴平行，△A1B1C1与△ABC关于直线l对称．（1）画出三角形A1B1C1；（2）若点P（m，n）在AC边上，则点P关于直线l的对称点P1的坐标为（m，2﹣n）；（3）在直线l上画出点Q，使得QA+QC的值最小．【解答】解：（1）如图所示，△A1B1C1即为所求．（2）若点P（m，n）在AC边上，则点P关于直线l的对称点P1的坐标为（m，2﹣n），故答案为：（m，2﹣n）；（3）如图所示，点Q即为所求．21．（8分）如图，四边形ABCD中，AD∥BC，DE＝EC，连接AE并延长交BC的延长线于点F，连接BE．（1）求证：AE＝EF；（2）若BE⊥AF，求证：BC＝AB﹣AD．【解答】证明：（1）∵AD∥BC，∴∠DAE＝∠F，∠ADE＝∠FCE，又∵DE＝CE，∴△ADE≌△FCE（AAS），∴AE＝EF；（2）∵AE＝EF，BE⊥AF，∴AB＝BF，∵△ADE≌△FCE，∴AD＝CF，∴AB＝BC+CF＝BC+AD，∴BC＝AB﹣AD．22．（10分）如图1，在平面直角坐标系xOy中，点A在y轴上，点B是第一象限的点，且AB⊥y轴，且AB＝OA，点C是线段OA上任意一点，连接BC，作BD⊥BC，交x轴于点D．（1）依题意补全图1；（2）用等式表示线段OA，AC与OD之间的数量关系，并证明；（3）连接CD，作∠CBD的平分线，交CD边于点H，连接AH，求∠BAH的度数．【解答】解：（1）如图1所示，（2）OA +AC ＝OD ，如图1，过B 作BE ⊥x 轴于E ，则四边形AOEB 是矩形，∴BE ＝AO ，∠ABE ＝90°，∵AB ＝AO ，∴AB ＝BE ，∵BD ⊥BC ，∴∠CBD ＝90°，∴∠ABC ＝∠DBE ，在△ABC 与△BDE 中，{∠BAC =∠BED AB =BE ∠ABC =∠DBE，∴△ABC ≌△EBD （ASA ），∴AC ＝DE ，∵OE ＝AB ＝OA ，∴AO +AC ＝OD ；（3）如图2，由（1）知：△ABC ≌△EBD ，∴BC＝BD，∵BD⊥BC，∴△BCD是等腰直角三角形，∴∠BCD＝45°，∵BH平分∠CBD，∴∠BHC＝90°，∵∠BAO＝90°，过H作HN⊥OA，HM⊥AB，∴四边形ANMH是矩形，∴∠NHM＝90°，∴∠NHC＝∠MHB，∴△CNH≌△BHM（AAS），∴HN＝HM，∴AH平分∠CAB，∴∠BAH＝45°．23．（10分）如图，在正方形ABCD中，M、N分别是射线CB和射线DC上的动点，且始终∠MAN＝45°．（1）如图1，当点M、N分别在线段BC、DC上时，请直接写出线段BM、MN、DN之间的数量关系；（2）如图2，当点M、N分别在CB、DC的延长线上时，（1）中的结论是否仍然成立，若成立，给予证明，若不成立，写出正确的结论，并证明；（3）如图3，当点M、N分别在CB、DC的延长线上时，若CN＝CD＝6，设BD与AM 的延长线交于点P，交AN于Q，直接写出AQ、AP的长．【解答】解：（1）BM+DN＝MN，理由如下：如图1，在MB的延长线上，截取BE＝DN，连接AE，∵四边形ABCD是正方形，∴AB＝AD，∠BAD＝∠ABC＝∠D＝90°，∴∠ABE＝90°＝∠D，在△ABE和△ADN中，{AB=AD∠ABE=∠D BE=DN，∴△ABE≌△ADN（SAS），∴AE＝AN，∠EAB＝∠NAD，∴∠EAN＝∠BAD＝90°，∵∠MAN＝45°，∴∠EAM＝45°＝∠NAM，在△AEM和△ANM中，{AE=AN∠EAM=∠NAM AM=AM，∴△AEM≌△ANM（SAS），∴ME＝MN，又∵ME＝BE+BM＝BM+DN，∴BM+DN＝MN；故答案为：BM+DN＝MN；（2）（1）中的结论不成立，DN﹣BM＝MN．理由如下：如图2，在DC上截取DF＝BM，连接AF，则∠ABM＝90°＝∠D，在△ABM和△ADF中，{AB=AD∠ABM=∠D BM=DF，∴△ABM≌△ADF（SAS），∴AM＝AF，∠BAM＝∠DAF，∴∠BAM+∠BAF＝∠BAF+∠DAF＝∠BAD＝90°，即∠MAF＝∠BAD＝90°，∵∠MAN＝45°，∴∠MAN＝∠F AN＝45°，在△MAN和△F AN中，{AM=AF∠MAN=∠FAN AN=AN，∴△MAN≌△F AN（SAS），∴MN＝NF，∴MN＝DN﹣DF＝DN﹣BM，∴DN﹣BM＝MN．（3）∵四边形ABCD是正方形，∴AB＝BC＝AD＝CD＝6，AD∥BC，AB∥CD，∠ABC＝∠ADC＝∠BCD＝90°，∴∠ABM＝∠MCN＝90°，∵CN＝CD＝6，∴DN＝12，∴AN=√AD2+DN2=√62+122=6√5，∵AB∥CD，∴△ABQ∽△NDQ，∴BQDQ =AQNQ=ABDN=612=12，∴AQAN =13，∴AQ=13AN＝2√5；由（2）得：DN﹣BM＝MN．设BM＝x，则MN＝12﹣x，CM＝6+x，在Rt△CMN中，由勾股定理得：62+（6+x）2＝（12﹣x）2，解得：x＝2，∴BM＝2，∴AM=√AB2+BM2=√62+22=2√10，∵BC ∥AD ，∴△PBM ∽△PDA ，∴PM PA =BM DA =26=13， ∴PM =12AM =√10，∴AP ＝AM +PM ＝3√10．24．（12分）如图①所示，已知正方形ABCD 和正方形AEFG ，连接DG ，BE ．（1）发现：当正方形AEFG 绕点A 旋转，如图②所示．①线段DG 与BE 之间的数量关系是 DG ＝BE ；②直线DG 与直线BE 之间的位置关系是 DG ⊥BE ；（2）探究：如图③所示，若四边形ABCD 与四边形AEFG 都为矩形，且AD ＝2AB ，AG ＝2AE 时，上述结论是否成立，并说明理由．（3）应用：在（2）的情况下，连接BG 、DE ，若AE ＝1，AB ＝2，求BG 2+DE 2的值（直接写出结果）．【解答】解：（1）①如图②中，∵四边形ABCD 和四边形AEFG 是正方形，∴AE ＝AG ，AB ＝AD ，∠BAD ＝∠EAG ＝90°，∴∠BAE ＝∠DAG ，在△ABE 和△DAG 中，{AB =AD ∠BAE =∠DAG AE =AG，∴△ABE ≌△ADG （SAS ），∴BE ＝DG ；②如图2，延长BE 交AD 于T ，交DG 于H ．由①知，△ABE ≌△DAG ，∴∠ABE ＝∠ADG ，∵∠ATB +∠ABE ＝90°，∴∠ATB +∠ADG ＝90°，∵∠ATB ＝∠DTH ，∴∠DTH +∠ADG ＝90°，∴∠DHB ＝90°，∴BE ⊥DG ，故答案为：BE ＝DG ，BE ⊥DG ；（2）数量关系不成立，DG ＝2BE ，位置关系成立．如图③中，延长BE 交AD 于T ，交DG 于H ．∵四边形ABCD与四边形AEFG都为矩形，∴∠BAD＝∠EAG，∴∠BAE＝∠DAG，∵AD＝2AB，AG＝2AE，∴ABAD =AEAG=12，∴△ABE∽△ADG，∴∠ABE＝∠ADG，BEDG =1 2，∴DG＝2BE，∵∠ATB+∠ABE＝90°，∴∠ATB+∠ADG＝90°，∵∠ATB＝∠DTH，∴∠DTH+∠ADG＝90°，∴∠DHB＝90°，∴BE⊥DG；（3）如图④中，作ET⊥AD于T，GH⊥BA交BA的延长线于H．设ET＝x，AT＝y．∵△AHG∽△ATE，第 31 页 共 31 页∴GH ET =AH AT =AG AE =2，∴GH ＝2x ，AH ＝2y ，∴4x 2+4y 2＝4，∴x 2+y 2＝1，∴BG 2+DE 2＝（2x ）2+（2y +2）2+x 2+（4﹣y ）2＝5x 2+5y 2+20＝25．。

2011学年第一学期八年级数学期中检测试卷（本卷共三个大题，25个小题，测试时间90分钟，满分100分）★亲爱的同学，经过八年级（上）上半学期数学的学习，你的数学能力一定有了提高，展示你才能的机会来了！祝你在这次数学期中测试中取得好成绩！别忘了要沉着冷静、细心答题哟！可以使用计算器。

答案及解答过程请做在答题卷上．．．．．．．．．．．．．．一、选择题(每小题3分，共计30分)1、如图，∠1与∠2是-------------------------------------（ ◆ ） A ．同位角 B ．内错角 C ．同旁内角 D ．以上都不是2、已知等腰三角形的一个底角是50O ，则它的顶角为：-------------------（ ◆ ） A 、50O B 、80O C 、65O D 、130O3、学校开展为贫困地区捐书活动，以下是5名同学捐书的册数：2，2，3，4，9． 则这组数据的中位数．．．和众数．．分别是-------------------------------------------（ ◆ ） A ．2和2 B ．4和2 C ．2和3 D ．3和24、等腰三角形的两边长分别是2和7，则它的周长是--------------------（ ◆ ） A ．9 B ．11 C ．16 D ．11或165、直角三角形两条直角边长分别是5和12,则第三边上的中线．．长为----------( ◆ ) A 、5 B 、6.5 C 、12 D 、 136、一个印有“嫦娥二号奔月”字样的立方体纸盒表面展开图如图所示，则与印有“娥”．．．字面相对的表面上印有-------------( ◆ )字。

A ．二 B ．号 C ．奔 D ．月7、如图：直线a,b 都与直线c 相交，给出下列条件： ①∠1=∠2， ②∠3=∠6，③∠4+∠7=180°，④∠5+∠8=180°，其中能判断 a ∥b 的条件有------------------------------（ ◆ ）个。

考场班级______座位号_______班级__________姓名___________学号____________……………………………………………………………密………………封………………线…………………………………………………………… 2012学年度第一学期八年级数学期中考试卷 （满分100 分，考试时间 90 分钟） 2012.11 一、填空题：（每题2分，共20分） 1= 。

2 。

3．a -的有理化因式是 。

41的解集是 。

5．方程2x =3x 的根是 。

6关于x 的方程2(k+1)x 2x+3=0-有两个不相等的实数根，则k 的取值范围是 7．在实数范围内分解因式：222x 4xy 3y =-- 。

8． 把命题“垂直于同一直线的两直线互相平行”改写成“如果┄┄，那么┄┄”的形式： 。

9．某车间一月份生产a 个零件，月平均增长率为x ，则第一季度的产量为 。

10．如图将ΔABC 绕点B 顺时针旋转30°后，得到ΔBDE ，如果点D 恰好在边AC 上，那么∠ADE 的度数是 。

二、选择题（每题3分，共12分） 11．下列根式中，是最简根式的是（ ） B. C. 12．下列方程中是一元二次方程的是（ ） ①222x 3x=1x -+；②2y =2；③22x 3=0x 1+--；④221+x =1xy+x - A.① B.①和② C.①和④ D.②③和④ 13．下列图形中，两个三角形全等的是（ ） A. 含80°的两个锐角三角形 B. 边长为20cm 的两个等边三角形C ．腰长对应相等的两个等腰三角形 D.有一个钝角对应相等的两个等腰三角形14．下列说法正确的是（ ）A.方程22x a =0-没有实数根B.方程2x 4x 40--=有两个相等的实数根C.在方程22ax +bx+c=0b 4ac>0-中，如果，那么这个方程有两个不相等的实数根D.无论a 取何值，方程2x +4ax 1=0-总有两个不相等的实数根三、解答题：15．化简与计算：（每题5分共20分）（1÷- （2）（3- （416.用适当方法解下列关于x 的方程：（每题5分共20分）（1）2(3x+2)=(2x 5)(3x+2)- （2）21)=+（3）2(5x1)(5x1)+8=0---６（4）22x3x m+3m=0--17.（本题5分）已知x18.（本题5分）小明要在一幅长90厘米，宽40厘米的风景画的四周镶上一条宽度相同的金色纸边，制成一幅挂图，使风景画的面积是整个挂图面积的611，求金色纸边的宽度是多少厘米？19.（本题6分）在ΔABC中，∠BAC=90°，AB=AC，BD⊥AE，CE⊥AE。

2022/2023学年度第一学期期中考试八年级数学试题时间：100分钟分值：120分考试形式：闭卷命题人：审核人：一、选择题（本大题共有8小题，每小题3分，共24分．在每小题所给出的四个选项中，只有一项是符合题目要求的，请将正确选项的字母代号填写在答题卡相应位置上）1．下列四个图形中，是轴对称图形的为【▲ 】A ．B ．C ．D ．2．下列等式正确的是【▲ 】A ．±＝2B ．＝﹣2C ．＝﹣2D ．＝0.13．下列各组数中，能作为直角三角形三边长的是【▲ 】A．1，2，3 B．4，5，6 C．6，8，10 D．7，8，94．在联欢会上，有A、B、C三名选手站在一个三角形的三个顶点位置上，他们在玩“抢手绢”游戏，要求在他们中间放一个手绢，谁先抢到手绢谁获胜，为使游戏公平，则手绢应放的最适当的位置是在△ABC的【▲ 】A．三边垂直平分线的交点B．三边中线的交点C．三条角平分线的交点D．三边上高的交点5．如图，点P是∠BAC的平分线AD上一点，PE⊥AC于点E．已知PE＝10，则点P到AB的距离是【▲ 】A．15 B．12 C．5 D．10（第5题）（第6题）（第8题）（第11题）6．如图，DE是△ABC中边AC的垂直平分线，若BC＝18cm，AB＝10cm，则△ABD的周长为【▲ 】A．16cm B．28cm C．26cm D．18cm7．若等腰三角形一个外角等于100°，则它的顶角度数为【▲ 】A．20°B．80°C．20°或80°D．无法确定8．如图，在四边形ABCD中，AC平分∠BAD，BC＝CD＝10，AC＝17，AD＝9．则AB为【▲ 】A．19 B．12 C．21 D．26二、填空题（本大题共有8小题，每小题3分，共24分．不需写出解答过程，请将答案直接写在答题卡相应位置上）．9．16的算术平方根是▲ .10．已知+（n ﹣1）2＝0，则mn＝▲ .11．如图所示，是一块由花园小道围成的边长为12米的正方形绿地，在离C处5米的绿地旁边B 处有健身器材，为提醒居住在A处的居民爱护绿地，不直接穿过绿地从A到B，而是沿小道从A→C→B，请问你多走了▲ 米．12．如图，点D是BC上的一点，若△ABC≌△ADE，且∠B＝65°，则∠EAC＝▲ °．（第12题）（第14题）（第15题）（第16题）13．直角三角形的两边长为5、12，则斜边上的中线长为▲ ．14．如图，折叠长方形纸片ABCD，使点D落在边BC上的点F处，折痕为AE．已知AB＝6cm，BC＝10cm．则EC的长为▲ cm．15．如图，A、B两点在正方形网格的格点上，每个方格都是边长为1的正方形、点C也在格点上，且△ABC为等腰三角形，则符合条件的点C共有▲个．16．如图，在Rt△ABC中，∠C＝90°，点P为AC边上的一点，延长BP至点D，使得AD＝AP ＝5，当AD⊥AB时，过D作DE⊥AC于E，若DE＝4，则△BCP面积为▲ ．三、解答题（本大题共有10小题，共72分．请在答题卡指定区域内作答，解答时应写出文字说明、推理过程或演算步骤）17．（本题满分6分）求下列各式中x的值：（1）x2﹣25＝0；（2）（x﹣2）3﹣8＝0．18．（本题满分6分）已知2a﹣1的平方根为±3，3a+b﹣1的算术平方根为4．（1）求a、b的值；（2）求a+2b的算术平方根．19．（本题满分5分）如图，校园有两条路OA、OB，在交叉口附近有两块宣传牌C、D，学校准备在这里安装一盏路灯，要求灯柱的位置P离两块宣传牌一样远，并且到两条路的距离也一样远，请你用尺规作出灯柱的位置点P．（请保留作图痕迹）20．（本题满分5分）如图，B、C、D、E在同一条直线上，AB∥EF，BC＝DE，AB＝EF，求证：△ACB≌△FDE．（第19题）（第20题）21．（本题满分6分）如图，秋千OA静止的时候，踏板离地高一尺（AC＝1尺），将它往前推进两步（EB＝10尺），此时踏板升高离地五尺（BD＝5尺），求秋千绳索（OA或OB）的长度．22．（本题满分6分）如图，在长度为1个单位长度的小正方形组成的正方形中，点A、B、C在小正方形的顶点上．（1）在图中画出与△ABC关于直线l成轴对称的△AB′C′；（2）三角形ABC 的面积为▲；（3）在直线l上找一点P，使PB+PC的长最短．23．（本题满分8分）如图，已知在四边形ABCD中，点E在AD上，∠BCE＝∠ACD，∠BAC＝∠D，BC＝CE．（1）求证：AC＝CD．（2）若AC＝AE，∠ACD＝80°，求∠DEC的度数．24．（本题满分8分）如图，在△ABC中，AB、AC边的垂直平分线相交于点O，分别交BC边于点M、N，连接AM，AN．（1）若△AMN的周长为6，求BC的长；（2）若∠MON ＝30°，求∠MAN的度数；（3）若∠MON＝45°，BM＝3，BC＝12，求MN的长度．25．（本题满分10分）阅读理解：亲爱的同学们，在以后的学习中我们会学习一个定理：直角三角形斜边上的中线等于斜边的一半．即：如图1：在Rt△ABC中，∠ACB＝90°，若点D是斜边AB的中点，则CD＝AB．牛刀小试：（1）在图1中，若AC＝6，BC＝8，其他条件不变，则CD＝▲；活学活用：（2）如图2，已知∠ABC＝∠ADC＝90°，点E、F分别为AC、BD的中点，AC＝26，BD＝24．求EF的长；问题解决：（3）如图3，在Rt△ABC中，∠ACB＝90°，AB＝10，以AB为边在AB上方作等边三角形ABD，连接CD，求CD的最大值．26．（本题满分12分）阅读以下材料，完成以下两个问题．[阅读材料]已知：如图，△ABC（AB≠AC）中，D、E在BC上，且DE＝EC，过D作DF∥BA 交AE于点F，DF＝AC．求证：AE平分∠BAC．结合此题，DE＝EC，点E是DC的中点，考虑倍长，并且要考虑连接哪两点，目的是为了证明全等，从而转移边和角．有两种考虑方法：①考虑倍长FE，如图（1）所示；②考虑倍长AE，如图（2）所示以图（1）为例，证明过程如下：证明：延长FE至G，使EG＝EF，连接CG．在△DEP和△CEG中，，∴△DEF≌△CEG（SAS）．∴DF＝CG，∠DFE＝∠G．∵DF＝AC，∴CG＝AC．∴∠G＝∠CAE．∴∠DFE＝∠CAE．∵DF∥AB，∴∠DFE＝∠BAE．∴∠BAE＝∠CAE．∴AE平分∠BAC．问题1：参考上述方法，请完成图（2）的证明．问题2：根据上述材料，完成下列问题：已知，如图3，在△ABC中，AD是BC边上的中线，分别以AB，AC为直角边向外作等腰直角三角形，∠BAE＝∠CAF＝90°，AE＝AB，AC＝AF，AD＝3，求EF的长．。

2024–2025学年度第一学期期中调研测试八年级数学参考答案及评分标准一、选择题（本大题共8小题，每题3分，共24分）.1. B2.C3.D4. A5. B6. D7.C8. D二、填空题（本大题共10小题，每题3分，共30分.）.9.稳定性 10C B ∠=∠（或ADC AEB ∠=∠或BDC CEB ∠=∠或AD AE =或BD CE =等）（只要写出一种情况即可） 11. °58 12. 18 13. 4 14.13 15. 5 16. °24 或 °66 17.°45 18. ①②③④三、解答题（本大题共10小题，共96分）.（说明：解答题，若出现不同解法，请参照给分）19.（1）证明：在OAB ∆和OMN ∆中∠=∠=∠=∠（对顶角相等）MON AOB OMOA M A ∴OAB ∆≌OMN ∆（ASA ）………………………………………6分∴MN AB =.……………………………………………8分20.解：ACD ∆是等腰三角形.……………………………………………5分∵BD BC =,°=∠36B ， ∴°=°−°=∠−°=∠=∠72)36180(21)180(21B BDC BCD ；…………2分 ∴°=°−°=∠−°=∠10872180180BDC ADC .…………………………4分 ∵CB CA =,°=∠36B ，∴°=∠=∠36B A ，……………………………………………6分∴°=°−°−°=∠−∠−°=∠3610836180180ADC A ACD ；∴ACD A ∠=∠；∴DC DA =（等角对等边）；∴ACD ∆是等腰三角形.………………………………………8分21.证明：∵AC FD ⊥，∴°=∠90FDC ；∴°=∠+∠90FCD F ；∵BA CE ⊥，∴°=∠90AEC ；∴°=∠+∠90FCD A ；∴F A ∠=∠； ……………………………………………3分在ABC ∆和FCD ∆中=°=∠=∠∠=∠FC AB FDC ACB F A 90∴ABC ∆≌)(AAS FCD ∆……………………………………………8分22.解：如图所示，画出4个即可，每个2分. （答案不唯一）23.解：（1）如图1，则点P 即为所求.………5分 （2） 如图2，则点Q 即为所求．………10分24.解：∵BC AD ⊥，∴°=∠=∠90ADC ADB .在ABD Rt ∆中,222AB BD AD =+，∴22222.1=+BD ，∴m BD 6.1=.…………………………………2分∴m CD BD 5.29.06.1=+=+.…………………………………3分在ACD Rt ∆中,222AC CD AD =+，∴2229..02.1AC =+,∴m AC 5.1=.…………………………………5分∵25.65.122222=+=+AC AB ，25.65.222==BC ，∴222BC AC AB =+；……………………………………………7分∴°=∠90BAC .……………………………………………9分∴学生搭建的帐篷符合条件.……………………………………10分25.（1）证明：∵EB ∥CF ，∴FCB EBC ∠=∠,∴DCF ABE ∠=∠；……………………………………………2分∵BD AC =，∴BC DB BC AC −=−，即DC AB =.……………………………………………4分 在ABE ∆和DCF ∆中=∠=∠=DC AB DCF ABE FC EB∴ABE ∆≌)(SAS DCF ∆……………………………………………7分（2）AE ∥DF ，DF AE =……………………………………………8分∵ABE ∆≌DCF ∆∴D A ∠=∠，DF AE =；∴AE ∥DF .……………………………………………10分26.（1）证明：∵CE 平分ACB ∠，∴ACE BCE ∠=∠；………………………………2分∵EH ∥BC ，∴GEC BCE ∠=∠；………………………………3分∴GEC ACE ∠=∠；………………………………4分∴CG EG =.…………………………………5分（2）∵点G 是EH 的中点，∴GH EG =；∵CG EG =，∴GH CG =；………………………………6分∴GHC GCH ∠=∠；………………………………7分∵EH ∥BC ，∴HCD GHC ∠=∠；………………………………8分∴HCD GCH ∠=∠；………………………………9分∴CH 平分ACD ∠.…………………………………10分27.（1）证明：连接DC ，∵DG 垂直平分BC ，∴DC DB =；……………………………………………………………1分∵AD 是EAC ∠的平分线，AE DE ⊥，AC DF ⊥，垂足分别为E 、F ， ∴DF DE =，°=∠90DEB ，°=∠=∠90DFC DFA .……………………3分 在DEB Rt ∆和DFC Rt ∆中，°=∠=∠90DFC DEB ，==DC DB DF DE ∴DEB Rt ∆≌)(HL DFC Rt ∆.∴CF BE =. ……………………6分（2）∵DEB Rt ∆≌)(HL DFC Rt ∆,∴FDC EDB ∠=∠； …………7分∴BDF FDC BDF EDB ∠+∠=∠+∠；∴BDC EDF ∠=∠；…………………………………………………8分∵在四边形AEDF 中，°=∠+∠+∠+∠360DFA EDF AED EAC ，°=∠76EAC ，°=∠90DEB ，°=∠90DFA ，∴°=∠104EDF ；∴°=∠104BDC ；…………………………………………………10分∵DC DB =, ∴°=°−°=∠=∠38)108180(21DCB DBC .………………12分28.（1） 当点P 在AC 上时3118242118221×××=⋅⋅t ∴4=t …………………………………………1分当点P 在BC 上时3118242124)21824(21×××=⋅−+⋅t ∴18=t …………………………………………2分∴点P 运动4或18秒时ABP ∆的面积是ABC Rt ∆面积的31.………………3分 （2）①I 当CB CP =时，得：cm t CP )224(−=.∴18224=−t ；∴s t 3=； ………4分II 当CB CP =时，作AB CM ⊥，垂足分别为M ，∴（三线合一）BM PM = ，5721824302121=×=⋅=⋅=∆∆CM CM BC AC CM AB S S ABCABC 在CBM Rt ∆中，°=∠90CMB ,，554)572(1822222=−=−=BM CM BC BM分654315542182422⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅=×++=++=++=s t BM BC AC BP BC AC t②当BC BP =时，得：cm t t BP )422(18242−=−−=∴18422=−t ；∴s t 30=； ………7分③当PC PB =时，ABC Rt ∆中，°=∠90ACB ，∴222AB BC AC =+，∴2221824AB =+，∴cm AB 30=；得：cm t t BP )422(18242−=−−=， PCB B ∠=∠；∵°=∠90ACB ，∴°=∠+∠90A B ,°=∠+∠90PCB ACP ；∴ACP A ∠=∠；∴PC PA =； ∴cm AB PB PA 15302121=×===； ∴15422=−t ；∴s t 5.28=.综上：点P 运动s 3或s 5431或s 30或s 5.28时，BCP ∆为等腰三角形. ………9分（3）0或215或12或16或21或7192或36（写对一个得0.5，全对得3分，其中0和36写对一个也可以）………………………12分。

2024～2025学年度第一学期期中调研试题（卷）八年级数学注意事项：1．本试卷共6页，满分120分，时间120分钟，学生直接在试题上答卷；2．答卷前将装订线内的项目填写清楚．一、选择题（共8小题，每小题3分，计24分．每小题只有一个选项是符合题意的）1．下列四个实数中，是无理数的为（）A．0B．C．D．2．下列各组数据，是勾股数的是（）A．B．C．D．3．化简正确的是（）A．5B．C．D．4．将直线向上平移2个单位长度，则平移后的直线为（）A．B．C．D．5．下列说法正确的是（）A．－27的立方根是3B．C．4的算术平方根是2D．1的平方根是16．已知，则直线的图象是下列选项中的（）A．B．C．D．7．如图，分别以的三边为斜边向外作，，，且，这三个直角三角形的面积分别为，且，则（）A．25B．C．30D．358．在物理实验探究课上，小明利用滑轮组及相关器材进行实验，不计绳重和摩擦，他把得到的拉力和所悬挂重物的重力的几组数据用电脑绘制成如图所示的图象，请你根据图象判断以下结论错误的是（）A．当拉力时，物体的重力B．拉力随着重物重力的增加而增大C．拉力与重力成正比例函数关系D．当滑轮组不挂重物时，所用拉力为0.5N二、填空题（共5小题，每小题3分，计15分）9．若，写出一个满足条件的的值为_________．（写出一个即可）10．在中，，若，则的长为_________．11．若一次函数的图象经过点和点，则的大小关系为（填“”“”或“”）．12．在平面直角坐标系中，已知点和点关于轴对称，则的值是_________．13．如图，圆柱形杯子（无盖）的高为18cm，底面周长为24cm，已知蚂蚁在外壁处（距杯子上沿2cm ）发现一滴蜂蜜在杯子内壁处（距杯子下沿4cm），则蚂蚁从处爬到处的最短距离（杯子厚度忽略不计）为_________cm．三、解答题（共13小题，计81分．解答应写出过程）14．（5分）计算：．15．（5分）在平面直角坐标系中，已知点的坐标为，则点到坐标原点的距离是多少? 16．（5分）已知与成正比例，当时，．（1）求与之间的函数表达式；（2）请判断点是否在这个函数的图象上，并说明理由．17．（5分）在平面直角坐标系中，已知点，根据条件解决下列问题：（1）若点在轴上，求点的坐标；（2）若点在过点且与轴平行的直线上，求点的坐标．18．（5分）已知实数的平方根为，求实数的算术平方根和立方根．19．（5分）如图，在平面直角坐标系中，的三个顶点的坐标分别为，．（1）作出关于轴对称的，点的对应点分别为点；（2）在（1）的条件下，写出点的坐标。