信号与系统第二次作业

《信号与系统》作业参考解答第一章（P16-17）1-3 设)(1t f 和)(2t f 是基本周期分别为1T 和2T 的周期信号。

证明)()()(21t f t f t f +=是周期为T 的周期信号的条件为T nT mT ==21 （m ,n 为正整数） 解：由题知)()(111t f mT t f =+ )()(222t f mT t f =+要使)()()()()(2121t f t f T t f T t f T t f +=+++=+则必须有21nT mT T == （m ,n 为正整数） 1-5 试判断下列信号是否是周期信号。

若是，确定其周期。

（1）t t t f πsin 62sin 3)(+= （2）2)sin ()(t a t f =（8）⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛=2cos 28sin 4cos )(k k k k f πππ解：（1）因为t 2sin 的周期为π，而t πsin 的周期为2。

显然，使方程n m 2=π （m ,n 为正整数）成立的正整数m ,n 是不存在的，所以信号t t t f πsin 62sin 3)(+=是非周期信号。

（2）因为)2cos 1()sin ()(22t a t a t f -==所以信号2)sin ()(t a t f =是周期π=T 的周期信号。

（8）由于)4/cos(k π的周期为8)4//(21==ππN ，)8/sin(k π的周期为16)8//(22==ππN ，)2/cos(k π的周期为4)2//(23==ππN ，且有16412321=⨯=⨯=⨯N N N所以，该信号是周期16=N 的周期信号。

1-10 判断下列系统是否为线性时不变系统，为什么？其中)(t f 、][k f 为输入信号，)(t y 、][k y 为零状态响应。

（1）)()()(t f t g t y = （2）)()()(2t f t Kf t y += 解：（1）显然，该系统为线性系统。

信号与系统第2章习题一、选择题1、下列信号不能用复指数信号stAe t x =)(表示的是（ ）A.冲激信号B.直流信号C.指数信号D.正弦信号 2、)22(4t e t--δ等于（ ）A. te4- B. )22(t -δ C.)1(214--t e δ D. )1(214δ-e 3、积分⎰--+642)8(dt t e t δ等于（ ）A.0B.16e C.1 D.)8(+t δ 4、已知信号)(t x 如下图所示，其表达式是（ ）A.)3()2(2)(---+t u t u t uB. )3(2)2()1(---+-t u t u t uC. )3()2()(---+t u t u t uD. )3()2()1(---+-t u t u t u 5、已知信号)(t x 如下图所示，其反转右移的信号)(1t x 是（ ）A. B.C. D.6、如下图所示：)(t x 为原始信号，)(1t x 为变换信号，则)(1t x 的表达式是（ ）A. )1(+-t xB. )1(+t xC. )12(+-t xD. )121(+-t x 7、若)(t x 是已录制声音的磁带，则下列表述错误的是（ ）A.)(t x -表示将磁带倒转播放产生的信号B.)2(t x 表示将磁带以二倍速度加快播放C.)2(t x 表示原磁带放音速度降低一半播放D.2)(t x 表示将磁带的音量放大一倍播放8、设)(t x 表示你在山谷喊话的声音，则你耳朵听到的声音可表示为（ ） A.∑∞=0)(n nt x a，0>n a B. ∑∞=+0)(n n nT t x a，0,0>>n n T aC.∑∞=-0)(n n nT t x a，0,0>>n n T a D.∑∞=-0)(n nTt x ，0>n T9、如下图所示周期信号)(~t x ，其直流分量等于（ ）A.0B.2C.4D.6二、判断题1、两个奇信号的和还是奇信号（ ）2、任何信号可分解为直流分量与交流分量之和（ ）3、任何信号可分解为偶分量与奇分量之和（ ）4、)cos(t 是功率信号，)]()()[cos(T t u t u t --是能量信号（ ）5、积分1)(=⎰∞-td ττδ（ ）6、对连续周期信号进行抽样所得离散序列一定还是周期的（ ）7、设)2()(1k x k x =，则)2/()(1k x k x =（ ）三、简答题1、单位冲激信号和单位脉冲序列各有什么特性？2、正弦信号)sin(0t ω和正弦序列)sin(0k Ω有什么区别与联系？3、信号的时域分解有哪几种方法？4、连续时间信号分解为冲激信号的线性组合有何实际意义？四、计算题教材P66习题：2-9、2-10、2-12、2-14。

1试分别指出以下波形是属于哪种信号？题图1-11-2试写出题1-1图中信号的函数表达式。

1-3已知信号)(1t x 与)(2t x 波形如题图1-3中所示，试作出下列各信号的波形图，并加以标注。

题图1-3⑴)2(1-t x ⑵)1(1t x -⑶)22(1+t x⑷)3(2+t x ⑸)22(2-t x ⑹)21(2t x - ⑺)(1t x )(2t x -⑻)1(1t x -)1(2-t x ⑼)22(1t x -)4(2+t x 1-4已知信号)(1n x 与)(2n x 波形如题图1-4中所示，试作出下列各信号的波形图，并加以标注。

题图1-4⑴)12(1+n x ⑵)4(1n x -⑶)2(1n x ⑷)2(2n x -⑸)2(2+n x ⑹)1()2(22--++n x n x⑺)2(1+n x )21(2n x -⑻)1(1n x -)4(2+n x ⑼)1(1-n x )3(2-n x1-5已知信号)25(t x -的波形如题图1-5所示，试作出信号)(t x 的波形图，并加以标注。

题图1-51-6试画出下列信号的波形图：⑴)8sin()sin()(t t t x ΩΩ=⑵)8sin()]sin(211[)(t t t x ΩΩ+= ⑶)8sin()]sin(1[)(t t t x ΩΩ+=⑷)2sin(1)(t tt x = 1-7试画出下列信号的波形图：⑴)(1)(t u e t x t -+=⑵)]2()1([10cos )(---=-t u t u t e t x t π⑶)()2()(t u e t x t --=⑷)()()1(t u e t x t --=⑸)9()(2-=t u t x ⑹)4()(2-=t t x δ1-8试求出以下复变函数的模与幅角，并画出模与幅角的波形图。

⑴)1(1)(2Ω-Ω=Ωj e j X ⑵)(1)(Ω-Ω-Ω=Ωj j e e j X ⑶Ω-Ω---=Ωj j e e j X 11)(4⑷21)(+Ω=Ωj j X 1-9已知信号)]()([sin )(π--=t u t u t t x ，求出下列信号，并画出它们的波形图。

北航《信号与系统》在线作业二
试卷总分:100 得分:100
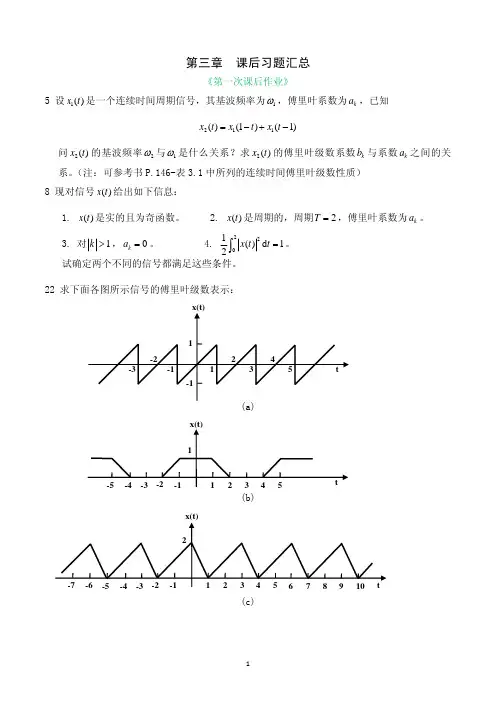
一、单选题 (共 10 道试题,共 30 分)
1. 连续周期信号的傅氏变换是 ________。

A. 连续的
B. 周期性的
C. 离散的
D. 与单周期的相同
满分：3 分
正确答案:C
2. 某系统的系统函数为 H （ s ），若同时存在频响函数 H （ j ω），则该系统必须满足条件 ________。

A. 时不变系统
B. 因果系统
C. 稳定系统
D. 线性系统
满分：3 分
正确答案:A
3. 欲使信号通过系统后只产生相位变化，则该系统一定是 ________。

A. 高通滤波网络
B. 带通滤波网络
C. 全通网络
D. 最小相移网络
满分：3 分
正确答案:C
4. 已知某连续时间系统的系统函数H（s）= 1/(s+1)，该系统属于什么类型 ________。

A. 高通滤波器
B. 低通滤波器
C. 带通滤波器
D. 带阻滤波器
满分：3 分
正确答案:B
5. 当输入信号的复频率等于系统函数的零点时，系统的强迫响应分量为 ________。

A. 无穷大
B. 不为零的常数
C. 0。

苏州大学 信号与系统 课程 第2次过程化考试参考答案 共 页一、 简算、填空与作图（每题4分，共40分）1、已知−→−F t f )()(j ωF ，则()(25)()F y t f t Y j ω=+−−→= 。

521()22j j ωF e ω 2、已知频谱)]()([)(00ωωδωωδπω-++=j F ，则原时间信号=)(t f 。

0cos()t ω3、3、已知周期信号()f t 前四分之一周期的波形如图所示，且()f t 是t 的偶函数，其傅里叶级数只有奇次谐波，画出整个周期内()f t 信号的波形。

4、计算222)(ta at f +=的傅里叶变换()F j ω= 。

2a eωπ-5、图中所示电路的频率响应)(ωj H = 。

RR j Lω+6、理想低通滤波器在物理上是否可以实现？ ，说明理由： 。

不能实现，因为违背了因果律7、画出图中)(t f 的偶分量波形。

8、简述周期信号频谱的特点： 。

离散性、谐波性、收敛性9、已知系统的幅频特性1)(=ωj H ，信号通过该系统是否会失真？ ，理由是 。

不一定失真，该系统相频特性未知，若相频特性是经过原点的直线则不会失真，否则失真。

10、已知理想高通滤波器的系统函数()()00()0 0 j tj Ke H j H j e ωϕωωωωωωω--⎧>⎪==⎨<⎪⎩，则该系统的冲激响应()h t = 。

00000000sin[()]()()[()]()K t t K K t t K t t S t t t t ωωδδαωππ---=----二、 （10分）计算如图所示波形信号)(t f 的频谱函数)(ωj F 。

解： ()()2()()f t t t t ετεετ=+-+- （2分）()'()2()()f t t t t δτδδτ=+-+- （3分）()22cos()24sin()2j j j F j e e ωτωτωτωωωτ-=-+=-=- （3分）()24sin ()2j F j ωτωω=或2cos()2j ωτω-或22()2j S ωττα （2分）三、 （10分）已知1()f t 的频谱函数为121F (),()()j f t f t ω与波形有如图所示的关系，试用1()f t 的频谱函数表示2()f t 的频谱函数)(F 2ωj 。

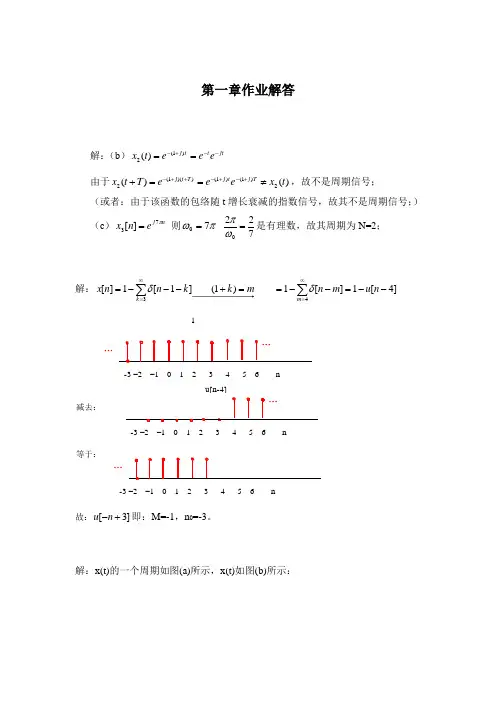
第一章作业解答解：（b ）jt t t j e e e t x --+-==)1(2)(由于)()(2)1()1())(1(2t x e e e T t x T j t j T t j ≠==++-+-++-，故不是周期信号；（或者：由于该函数的包络随t 增长衰减的指数信号，故其不是周期信号；） （c ）n j e n x π73][= 则πω70= 7220=ωπ是有理数，故其周期为N=2；解：]4[1][1)1(]1[1][43--=--==+---=∑∑∞=∞=n u m n mk k n n x m k δδ-3 –2 –1 0 1 2 3 4 5 6 n1…减去：-3 –2 –1 0 1 2 3 4 5 6 nu[n-4]等于：-3 –2 –1 0 1 2 34 5 6 n…故：]3[+-n u 即：M=-1，n 0=-3。

解：x(t)的一个周期如图(a)所示，x(t)如图(b)所示：而：g(t)如图(c)所示……dtt dx )(如图（d ）所示：……故：)1(3)(3)(--=t g t g dtt dx 则：1t ,0t 3,32121==-==；A A 1.15解：该系统如下图所示： 2[n]（1）]4[2]3[5]2[2]}4[4]3[2{21]}3[4]2[2{]3[21]2[][][1111111222-+-+-=-+-+-+-=-+-==n x n x n x n x n x n x n x n x n x n y n y即：]4[2]3[5]2[2][-+-+-=n x n x n x n y（2）若系统级联顺序改变，该系统不会改变，因为该系统是线性时不变系统。

（也可以通过改变顺序求取输入、输出关系，与前面做对比）。

解：（a ）因果性：)(sin )(t x t y =举一反例：当)0()y(,0int s x t =-=-=ππ则时输出与以后的输入有关，不是因果的；（b ）线性：按照线性的证明过程（这里略），该系统是线性的。

1. 系统的冲激响应是阶跃响应的 ________。

A. 四阶导数B. 三阶导数C. 二阶导数D. 一阶导数该题参考选项是：D 满分：3 分2. 因果系统是物理上_____________系统。

A. 不可实现的B. 可实现的C. 未定义的D. 以上都不对该题参考选项是：B 满分：3 分3. 已知一连续系统在输入f(t)的作用下的零状态响应为y=f(4t)，则该系统为 ________。

A. 线性时不变系统B. 线性时变系统C. 非线性时不变系统D. 非线性时变系统该题参考选项是：B 满分：3 分4. 信号的时宽与信号的频宽之间呈 ________。

A. 正比关系B. 反比关系C. 平方关系D. 没有关系该题参考选项是：B 满分：3 分5. 对因果系统，只要判断H(s)的极点，即A(s)=0的根（称为系统特征根）是否都在左半平面上，即可判定系统是否稳定。

下列式中对应的系统可能稳定的是？ ________A. s*s*s+2008s*s-2000s+2007B. s*s*s+2008s*s+2007sC. s*s*s-2008s*s-2007s-2000D. s*s*s+2008s*s+2007s+2000该题参考选项是：B 满分：3 分6. 计算ε(3-t)ε(t)= ________。

A. ε(t)-ε(t-3)B. ε(t)C. ε(t)- ε(3-t)D. ε(3-t)该题参考选项是：A 满分：3 分7. If f1(t) ←→F1(jω)，f2(t) ←→F2(jω)，Then ________。

A. f1(t)*f2(t) ←→F1(jω)F2(jω)B. f1(t)+f2(t) ←→F1(jω)F2(jω)C. f1(t) f2(t) ←→F1(jω)F2(jω)D. f1(t)/f2(t) ←→F1(jω)/F2(jω)该题参考选项是：A 满分：3 分8. 信号〔ε(t)－ε(t－2)〕的拉氏变换的收敛域为 ________。

福师《信号与系统》在线作业二试卷总分：100 测试时间：--一、单选题（共25 道试题，共50 分。

）1. 在变换域中解差分方程时，首先要对差分方程两端进行( )。

A. 傅立叶变换B. 拉普拉斯变换C. Z变换D. 以上答案都不正确满分：2 分2. 激励为x(n)时，响应y(n)=x(n)sin(2πn/7+π/6)的系统是( )系统。

A. 线性且时不变B. 非线性且时不变C. 线性且时变D. 非线性且时变满分：2 分3. 某系统的系统函数为H(z)=z/[(z-0.5)*(z-2)]，若该系统是稳定系统，则其收敛区为( )。

A. |z|＜0.5B. |z|＞2C. 0.5＜|z|＜2D. 以上答案都不对满分：2 分4. 单位序列响应h(n)是指离散系统的激励为( ) 时，系统的零状态响应。

A. 单位序列B. E指数序列C. 对数序列D. 以上答案都不正确满分：2 分5. f(t)的频宽是200Hz,那么f(-2t-6)的奈奎斯特频率为( )。

A. 400HzB. 200HzC. 800HzD. 100Hz满分：2 分6. 信号f(t)=Asin(500πt)cos(2000πt)的归一化功率等于( )。

A. A*A/2B. A*A/4C. 1/4D. 以上答案都不正确满分：2 分7. 离散信号f(n)是指()。

A. n的取值是连续的，而f(n)的取值是任意的信号B. n的取值是离散的，而f(n)的取值是任意的信号C. n的取值是连续的，而f(n)的取值是连续的信号D. n的取值是连续的，而f(n)的取值是离散的信号满分：2 分8. 函数f(s)=1/s+1/(s+1)逆变换的初值等于( )。

A. 0B. 1C. 2D. 3满分：2 分9. 信号f(t)=Sa(100t)+Sa(50t)的奈奎斯特间隔等于( )。

A. 100/πB. π/100C. 100D. 1/100满分：2 分10. 信号f(t)=Acos(2000πt)+Bsin(200πt)的归一化功率等于( )。

Charpt 11.21—(a),(b),(c)一连续时间信号x(t)如图original所示，请画出下列信号并给予标注：a）x(t-1)b）x(2-t)c）x(2t+1)d）x(4-t/2)e）[x(t)=x(-t)]u(t)f）x(t)[δ(t+3/2)-δ(t-3/2)](d),(e),(f)1.22一离散时间信号x[n]如图original所示，请画出下列信号并给予标注。

a)x[n-4]b)x[3-n]c)x[3n]e)x[n]u[3-n]f)x[n-2]δ[n-2]1.23确定并画出图original信号的奇部和偶部，并给予标注。

1.25判定下列连续时间信号的周期性，若是周期的，确定它的基波周期。

a)x(t)=3cos(4t+π/3)T=2π/4=π/2;b)x(t)=e )1(t j T=2π/π=2;c)x(t)=[cos(2t-π/3)]2x(t)=1/2+cos[(cos(4t-2π/3))]/2, so T=2π/4=π/2;d)x(t)=E v {cos(4πt)u(t)}定义x(0)=1/2,则T=1/2; e)E v {sin(4πt)u(t)}非周期f ）x(t)=n n t e )2(假设其周期为T 则n n t e )2(=n T n t e )22(=n T n t e ))2(2(=n n t e )2(所以T=1/2(最小正周期)；1.26判定下列离散时间信号的周期性；若是周期的，确定他们的基波周期。

(a)x[n]=sin(6π/7+1) N=7(b)x[n]=cos(n/8-π) 不是周期信号（c ）x[n]=cos(πn 2/8)假设其周期为N ，则8/8/)(22n N n ＋k 2所以易得N=8（d ）x[n]=)4cos()2cos(n n N=8(e) x[n]=)62cos(2)8sin()4cos(2n n n N=16 1.31在本题中将要说明线性时不变性质的最重要的结果之一，即一旦知道了一个线性系统或线性时不变系统对某单一输入的响应或者对若干个输入的响应，就能直接计算出对许多其他输入信号的响应。

Charpt 11.21—(a),(b),(c)一连续时间信号x(t)如图original所示，请画出下列信号并给予标注：a）x(t-1)b）x(2-t)c）x(2t+1)d）x(4-t/2)e）[x(t)=x(-t)]u(t)f）x(t)[δ(t+3/2)-δ(t-3/2)](d),(e),(f)1.22一离散时间信号x[n]如图original所示，请画出下列信号并给予标注。

a)x[n-4]b)x[3-n]c)x[3n]e)x[n]u[3-n]f)x[n-2]δ[n-2]1.23确定并画出图original信号的奇部和偶部，并给予标注。

1.25判定下列连续时间信号的周期性，若是周期的，确定它的基波周期。

a) x(t)=3cos(4t+π/3)T=2π/4=π/2;b) x(t)=e )1(-t j πT=2π/π=2;c) x(t)=[cos(2t-π/3)]2x(t)=1/2+cos[(cos(4t-2π/3))]/2, so T=2π/4=π/2;d) x(t)=E v {cos (4πt)u(t)}定义x(0)=1/2,则T=1/2;e) E v {sin(4πt)u(t)}非周期f ）x(t)=∑∞-∞=--n n t e )2(假设其周期为T 则∑∞-∞=--n n t e )2(=∑∞-∞=+--n T n t e )22(=∑∞-∞=---n T n t e ))2(2(=∑∞-∞=--n n t e )2( 所以T=1/2(最小正周期)；1.26判定下列离散时间信号的周期性；若是周期的，确定他们的基波周期。

(a) x[n]=sin(6π/7+1)N=7(b) x[n]=cos(n/8-π)不是周期信号（c ）x[n]=cos(πn 2/8)假设其周期为N ，则8/8/)(22n N n ππ=+＋πk 2 所以易得N=8（d ）x[n]=)4cos()2cos(n n ππ N=8 (e) x[n]=)62cos(2)8sin()4cos(2ππππ+-+n n n N=161.31在本题中将要说明线性时不变性质的最重要的结果之一，即一旦知道了一个线性系统或线性时不变系统对某单一输入的响应或者对若干个输入的响应，就能直接计算出对许多其他输入信号的响应。

第2章信号与系统部分课后作业解答编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（第2章信号与系统部分课后作业解答）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为第2章信号与系统部分课后作业解答的全部内容。

2—2 解：由系统的特征方程：2210λλ++=，解得1,21λ=-，为二重根， 那么零输入响应及一阶导数的形式为：12()--=+t t zi r t c e c te ， '122()---=-+-t t t zi r t c e c e c te ，将0=t 时将已知的初始的状态代入以上两式，得到方程组：12112=⎧⎨-=⎩c c c解得：1213=⎧⎨=⎩c c 代入求得零输入响应()30--=+≥t t zi r t e te t2-5解仅有1(0)1x =时产生的零输入响应为21()t t zi y t e e --=+ 0t ≥仅有2(0)1x =时产生的零输入响应为22()t t zi y t e e --=- 0t ≥设()f t 产生的零状态响应为()zs y t ，则由1(0)0x =，2(0)1x =-和()f t 共同产生的全响应为122()(1)()()t zi zi f e y t y t y t -+=+-+ 20()()t t f e e y t --=--+ 0t ≥得2()22t t f y t e e --=+- 0t ≥于是由1(0)3x =,2(0)2x =和激励2()f t 共同产生的全响应为12()3()2()2()zi zi f y t y t y t y t =++2(49)t t e e --=+- 0t ≥2-11 解：电路中的输入信号()x t 为电流源，输出信号()y t 为电感电流.由KCL 可得()()()+=L dy t y t x t R dt整理可得系统的输入输出关系为()()()+=dy t R Ry t x t dt L L可以证明为当R 、L 为常数时，该系统为LTI 系统。