逆命题与逆否命题
- 格式:doc
- 大小:327.00 KB
- 文档页数:5

四种命题及其相互关系
∙1、四种命题:
一般地,用p和q分别表示原命题的条件和结论,用或分别表示p和q的否定,四种命题的形式是:
(1)原命题:若p则q;
(2)逆命题:若q则p;
(3)否命题:若则;
(4)逆否命题:若则。
2、四种命题的真假关系:
一个命题与它的逆否命题是等价的,其逆命题与它的否命题也是等价的;
3、四种命题的相互关系:
∙注意:
1、区别“否命题”与“命题的否定”,若原命题是“若p则q”,则这个命题的否定是“若p则非q”,
而它的否命题是“若非p则非q”。
2、互为逆否命题同真假,即“等价”
真命题、假命题
∙命题的概念:
1、命题:把语言、符号或式子表达的,可以判断真假的陈述句称为命题;
2、真命题、假命题:判断为真的语句称为真命题,判断为假的语句称为假命题。
∙注意:
1、并不是所有的语句都是命题,只有能够判断真假的语句才是命题。
2、如果一个语句是命题,则它是真命题或是假命题,二者必具其一。

四种命题及其关系一、四种命题的概念1. 原命题- 定义:若用p表示条件,q表示结论,则原命题为“若p,则q”,例如“若x = 1,则x^2=1”。
2. 逆命题- 定义:将原命题的条件和结论互换得到的命题,即“若q,则p”。
对于上面的例子,其逆命题为“若x^2=1,则x = 1”。
3. 否命题- 定义:将原命题的条件和结论都进行否定得到的命题,即“若¬ p,则¬q”。
对于“若x = 1,则x^2=1”,其否命题为“若x≠1,则x^2≠1”。
4. 逆否命题- 定义:将逆命题的条件和结论都进行否定得到的命题,即“若¬ q,则¬p”。
对于“若x = 1,则x^2=1”,其逆否命题为“若x^2≠1,则x≠1”。
二、四种命题之间的关系1. 原命题与逆命题- 关系:原命题的条件和结论是逆命题的结论和条件,它们之间是互逆的关系。
原命题为真时,逆命题不一定为真。
例如原命题“若a = 0,则ab=0”是真命题,其逆命题“若ab = 0,则a = 0”是假命题(因为当b = 0时,a可以不为0)。
2. 原命题与否命题- 关系:原命题与否命题是互否的关系,原命题为真时,否命题不一定为真。
例如原命题“若x>2,则x>1”是真命题,其否命题“若x≤slant2,则x≤slant1”是假命题。
3. 原命题与逆否命题- 关系:原命题与逆否命题是同真同假的关系。
例如原命题“若a = b,则a^2=b^2”是真命题,其逆否命题“若a^2≠ b^2,则a≠ b”也是真命题;原命题“若x = 1且y = 2,则x + y=3”是真命题,其逆否命题“若x + y≠3,则x≠1或y≠2”也是真命题。
4. 逆命题与否命题- 关系:逆命题与否命题是互为逆否的关系,所以它们也是同真同假的关系。
例如对于原命题“若p,则q”,其逆命题“若q,则p”和否命题“若¬ p,则¬q”,若逆命题为真,则否命题也为真;若逆命题为假,则否命题也为假。

1.3.2命题的四种形式学习目标 1.了解四种命题的概念,会写出所给命题的逆命题、否命题和逆否命题.2.认识四种命题之间的关系以及真假性之间的联系.3.会利用命题的等价性解决问题.知识点一四种命题的概念命题“如果p,则(那么)q”是由条件p和结论q组成的,对p,q进行“换位”和“换质”,一共可以构成四种不同形式的命题.(1)原命题:如果p,则q;(2)条件和结论“换位”:如果q,则p,这称为原命题的逆命题;(3)条件和结论“换质”(分别否定):如果綈p,则綈q,这称为原命题的否命题.(4)条件和结论“换位”又“换质”:如果綈q,则綈p,这称为原命题的逆否命题.知识点二四种命题间的相互关系(1)四种命题间的关系(2)四种命题间的真假关系由上表可知四种命题的真假性之间有如下关系:①两个命题互为逆否命题,它们有相同的真假性,即两命题等价;②两个命题为互逆命题或互否命题,它们的真假性没有关系,即两个命题不等价.1.有的命题没有逆命题.(×)2.两个互逆命题的真假性相同.(×)3.对于一个命题的四种命题,可以一个真命题也没有.(√)4.一个命题的四种命题中,真命题的个数一定为偶数.(√)题型一四种命题的结构形式例1把下列命题写成“若p,则q”的形式,并写出它们的逆命题、否命题与逆否命题.(1)正数的平方根不等于0;(2)当x=2时,x2+x-6=0;(3)对顶角相等.解(1)原命题:若a是正数,则a的平方根不等于0.逆命题:若a的平方根不等于0,则a是正数.否命题:若a不是正数,则a的平方根等于0.逆否命题:若a的平方根等于0,则a不是正数.(2)原命题:若x=2,则x2+x-6=0.逆命题:若x2+x-6=0,则x=2.否命题:若x≠2,则x2+x-6≠0.逆否命题:若x2+x-6≠0,则x≠2.(3)原命题:若两个角是对顶角,则它们相等.逆命题:若两个角相等,则它们是对顶角.否命题:若两个角不是对顶角,则它们不相等.逆否命题:若两个角不相等,则它们不是对顶角.反思感悟由原命题写出其他三种命题的关键是找到原命题的条件和结论,根据其他三种命题的定义,确定所写命题的条件和结论.跟踪训练1写出下列命题的逆命题、否命题、逆否命题.(1)实数的平方是非负数;(2)等底等高的两个三角形是全等三角形.解(1)逆命题:若一个数的平方是非负数,则这个数是实数.否命题:若一个数不是实数,则它的平方不是非负数.逆否命题:若一个数的平方不是非负数,则这个数不是实数.(2)逆命题:若两个三角形全等,则这两个三角形等底等高.否命题:若两个三角形不等底或不等高,则这两个三角形不全等.逆否命题:若两个三角形不全等,则这两个三角形不等底或不等高.题型二四种命题的真假判断例2写出下列命题的逆命题、否命题、逆否命题,并判断其真假.(1)若a>b,则ac2>bc2;(2)若四边形的对角互补,则该四边形是圆的内接四边形.解(1)逆命题:若ac2>bc2,则a>b.真命题.否命题:若a≤b,则ac2≤bc2.真命题.逆否命题:若ac2≤bc2,则a≤b.假命题.(2)逆命题:若四边形是圆的内接四边形,则该四边形的对角互补.真命题.否命题:若四边形的对角不互补,则该四边形不是圆的内接四边形.真命题.逆否命题:若四边形不是圆的内接四边形,则该四边形的对角不互补.真命题.反思感悟若原命题为真命题,则它的逆命题、否命题可能为真命题,也可能为假命题.原命题与逆否命题互为逆否命题,否命题与逆命题互为逆否命题.互为逆否命题的两个命题的真假性相同.在原命题及其逆命题、否命题、逆否命题中,真命题的个数要么是0,要么是2,要么是4. 跟踪训练2下列命题中为真命题的是()①“若x2+y2≠0,则x,y不全为零”的否命题;②“正三角形都相似”的逆命题;③“若m>0,则x2+x-m=0有实根”的逆否命题;④“若x-2是有理数,则x是无理数”的逆否命题.A.①②③④B.①③④C.②③④D.①④答案 B解析 ①原命题的否命题为“若x 2+y 2=0,则x ,y 全为零”.故为真命题.②原命题的逆命题为“若两个三角形相似,则这两个三角形是正三角形”.故为假命题. ③原命题的逆否命题为“若x 2+x -m =0无实根,则m ≤0”. ∵方程无实根,∴判别式Δ=1+4m <0,∴m <-14<0.故为真命题.④原命题的逆否命题为“若x 不是无理数,则x -2不是有理数”. ∵x 不是无理数,∴x 是有理数.又2是无理数,∴x -2是无理数,不是有理数.故为真命题. 故正确的命题为①③④,故选B. 题型三 等价命题的应用例3 证明:已知函数f (x )是(-∞,+∞)上的增函数,a ,b ∈R ,若f (a )+f (b )≥f (-a )+f (-b ),则a +b ≥0.证明 原命题的逆否命题为“已知函数f (x )是(-∞,+∞)上的增函数,a ,b ∈R ,若a +b <0, 则f (a )+f (b )<f (-a )+f (-b )”. 若a +b <0,则a <-b ,b <-a . 又∵f (x )在(-∞,+∞)上是增函数, ∴f (a )<f (-b ),f (b )<f (-a ), ∴f (a )+f (b )<f (-a )+f (-b ). 即原命题的逆否命题为真命题. ∴原命题为真命题.反思感悟 因为原命题与其逆否命题是等价的,可以证明一个命题的逆否命题成立,从而证明原命题也是成立的.正确写出原命题的逆否命题是证题的关键.跟踪训练3 判断命题“已知a ,x 为实数,若关于x 的不等式x 2+(2a +1)x +a 2+2≤0的解集不是空集,则a ≥1”的逆否命题的真假. 解 先判断原命题的真假.因为a ,x 为实数,且关于x 的不等式x 2+(2a +1)x +a 2+2≤0的解集不是空集, 所以Δ=(2a +1)2-4(a 2+2)≥0,即4a -7≥0,解得a ≥74,a ≥74⇒a ≥1,所以原命题为真,又因为原命题与其逆否命题等价,所以逆否命题为真.命题的等价性典例 主人邀请张三、李四、王五三个人吃饭,时间到了,只有张三、李四准时赴约,王五打电话说:“临时有急事,不能去了.”主人听了,随口说了句:“该来的没有来.”张三听了脸色一沉,起来一声不吭地走了,主人愣了片刻,又道了句:“不该走的又走了.”李四听了大怒,拂袖而去.请你用逻辑学原理解释二人离去的原因.解 张三走的原因是:“该来的没有来”的逆否命题是“来了不该来的”,张三觉得自己是不该来的.李四走的原因是:“不该走的又走了”的逆否命题是“没走的应该走”,李四觉得自己是应该走的.[素养评析] 逻辑推理是在数学活动中进行交流的基本思维品质,本例是利用原命题与其逆否命题的等价性的逻辑原理,得出相应的合理解释.1.命题“如果a ∉A ,则b ∈B ”的否命题是( ) A .如果a ∉A ,则b ∉B B .如果a ∈A ,则b ∉B C .如果b ∈B ,则a ∉A D .如果b ∉B ,则a ∉A答案 B解析 命题“如果p ,则q ”的否命题是“如果綈p ,则綈q ”,“∈”与“∉”互为否定形式.2.命题“若綈p ,则q ”的逆否命题为( ) A .若p ,则綈q B .若綈q ,则綈p C .若綈q ,则p D .若q ,则p 答案 C3.下列命题为真命题的是( ) A .命题“若x >y ,则x >|y |”的逆命题 B .命题“若x =1,则x 2>1”的否命题C.命题“若x=1,则x2+x-2=0”的否命题D.命题“若x2>1,则x>1”的逆否命题答案 A解析对A,即判断:若x>|y|,则x>y的真假,显然是真命题.4.在原命题“若A∪B≠B,则A∩B≠A”与它的逆命题、否命题、逆否命题中,真命题的个数为________.答案 4解析逆命题为“若A∩B≠A,则A∪B≠B”;否命题为“若A∪B=B,则A∩B=A”;逆否命题为“若A∩B=A,则A∪B=B”,全为真命题.5.已知命题p:“若ac≥0,则二次不等式ax2+bx+c>0无解”.(1)写出命题p的否命题;(2)判断命题p的否命题的真假.解(1)命题p的否命题为:“若ac<0,则二次不等式ax2+bx+c>0有解”.(2)命题p的否命题是真命题.判断如下:因为ac<0,所以-ac>0⇒Δ=b2-4ac>0⇒二次方程ax2+bx+c=0有实根⇒ax2+bx+c>0有解,所以该命题是真命题.写一个命题的否命题时,要对命题的条件和结论都进行否定,避免出现不否定条件,而只否定结论的错误.若由p经逻辑推理得出q,则命题“若p,则q”为真;确定“若p,则q”为假时,则只需举一个反例说明即可.一、选择题1.“如果x>y,则x2>y2”的逆否命题是()A.如果x≤y,则x2≤y2B.如果x>y,则x2<y2C.如果x2≤y2,则x≤y D.如果x<y,则x2<y2答案 C解析由互为逆否命题的定义可知,把原命题的条件的否定作为结论,原命题的结论的否定作为条件即可得逆否命题.2.命题“如果a>-3,则a>-6”以及它的逆命题、否命题、逆否命题中,真命题的个数为() A.1 B.2 C.3 D.4答案 B解析原命题显然为真命题,故其逆否命题为真命题,而其逆命题为“如果a>-6,则a>-3”,这是假命题,从而否命题也是假命题,因此只有两个真命题.3.“△ABC中,若∠C=90°,则∠A,∠B全是锐角”的否命题为()A.△ABC中,若∠C≠90°,则∠A,∠B全不是锐角B.△ABC中,若∠C≠90°,则∠A,∠B不全是锐角C.△ABC中,若∠C≠90°,则∠A,∠B中必有一钝角D.以上都不对答案 B解析若∠C≠90°,则∠A,∠B不全是锐角,此处“全”的否定是“不全”.4.若命题p的否命题为q,命题p的逆否命题为r,则q与r的关系是()A.互逆命题B.互否命题C.互为逆否命题D.以上都不正确答案 A解析设p为“如果A,则B”,那么q为“如果綈A,则綈B”,r为“如果綈B,则綈A”.故q与r为互逆命题.5.有下列四个命题:①“如果x+y=0,则x,y互为相反数”的逆命题;②“全等三角形的面积相等”的否命题;③“如果q≤1,则x2+2x+q=0有实根”的逆命题;④“不等边三角形的三个内角相等”的逆否命题.其中真命题的序号为()A.①②B.②③C.①③D.③④答案 C解析 命题①:“如果x ,y 互为相反数,则x +y =0”是真命题;命题②:可考虑其逆命题“面积相等的三角形是全等三角形”是假命题,因此命题②是假命题;命题③:“如果x 2+2x +q =0有实根,则q ≤1”是真命题;命题④是假命题.6.原命题为“若a n +a n +12<a n ,n ∈N +,则{a n }为递减数列”,关于其逆命题、否命题、逆否命题真假性的判断依次如下,正确的是( ) A .真、真、真 B .假、假、真 C .真、真、假 D .假、假、假答案 A解析 从原命题、逆命题的真假入手,a n +a n +12<a n ⇔a n +1<a n ⇔{a n }为递减数列,即原命题、逆命题都为真命题,则其逆否命题、否命题也为真命题.7.设原命题:若a +b ≥2,则a ,b 中至少有一个不小于1,则原命题与其逆命题的真假情况是( )A .原命题为真命题,逆命题为假命题B .原命题为假命题,逆命题为真命题C .原命题与逆命题均为真命题D .原命题与逆命题均为假命题 答案 A解析 逆否命题:若a ,b 都小于1,则a +b <2,是真命题,所以原命题是真命题.逆命题:若a ,b 中至少有一个不小于1,则a +b ≥2.例如,a =3,b =-3满足条件a ,b 中至少有一个不小于1,但a +b =0,故逆命题是假命题.故选A.8.关于命题“若拋物线y =ax 2+bx +c 开口向下,则{x |ax 2+bx +c <0}⇏∅”的逆命题、否命题、逆否命题的真假性,下列结论正确的是( ) A .都是真命题 B .都是假命题 C .否命题是真命题 D .逆否命题是真命题 答案 D解析 原命题为真命题,所以其逆否命题也为真命题.逆命题“若{x |ax 2+bx +c <0}D =/∅,则拋物线y =ax 2+bx +c 开口向下”是一个假命题,因为当不等式ax 2+bx +c <0的解集非空时,可以有a >0,即拋物线的开口可以向上,因此否命题也是假命题,故选D. 二、填空题9.下列命题:①“如果xy =1,则x ,y 互为倒数”的逆命题; ②“四边相等的四边形是正方形”的否命题; ③“梯形不是平行四边形”的逆否命题; ④“如果ac 2>bc 2,则a >b ”的逆命题. 其中真命题是________.(填序号) 答案 ①②③解析 ①“如果xy =1,则x ,y 互为倒数”的逆命题是“如果x ,y 互为倒数,则xy =1”,是真命题;②“四边相等的四边形是正方形”的否命题是“四边不都相等的四边形不是正方形”,是真命题;③“梯形不是平行四边形”本身是真命题,所以其逆否命题也是真命题;④“如果ac 2>bc 2,则a >b ”的逆命题是“如果a >b ,则ac 2>bc 2”,是假命题.所以真命题是①②③.10.已知命题“若m -1<x <m +1,则1<x <2”的逆命题为真命题,则m 的取值范围是________. 答案 [1,2]解析 由已知得,若1<x <2成立,则m -1<x <m +1也成立.∴⎩⎪⎨⎪⎧m -1≤1,m +1≥2,∴1≤m ≤2. 11.下列命题中:①若一个四边形的四条边不相等,则它不是正方形; ②若一个四边形对角互补,则它内接于圆; ③正方形的四条边相等; ④圆内接四边形对角互补; ⑤对角不互补的四边形不内接于圆;⑥若一个四边形的四条边相等,则它是正方形.其中互为逆命题的有________;互为否命题的有______;互为逆否命题的有________. 答案 ②和④,③和⑥ ①和⑥,②和⑤ ①和③,④和⑤解析 命题③可改写为“若一个四边形是正方形,则它的四条边相等”;命题④可改写为“若一个四边形是圆内接四边形,则它的对角互补”;命题⑤可改写为“若一个四边形的对角不互补,则它不内接于圆”,再依据四种命题间的关系便不难判断. 三、解答题12.判断下列命题的真假.(1)对角线不相等的四边形不是等腰梯形;(2)若x∉A∩B,则x∉A且x∉B;(3)若x2+y2≠0,则xy≠0.考点四种命题间的相互关系题点利用四种命题的关系判断真假解(1)该命题的逆否命题是“若一个四边形是等腰梯形,则它的对角线相等”,它为真命题,故原命题为真.(2)该命题的逆否命题是“若x∈A或x∈B,则x∈A∩B”,它为假命题,故原命题为假.(3)该命题的逆否命题是“若xy=0,则x2+y2=0”,它为假命题,故原命题为假.13.判断命题:“若b≤-1,则关于x的方程x2-2bx+b2+b=0有实根”的逆否命题的真假.解方法一(利用原命题)因为原命题与逆否命题真假性一致,所以只需判断原命题真假即可.方程判别式为Δ=4b2-4(b2+b)=-4b,因为b≤-1,所以Δ≥4>0,故此方程有两个不相等的实根,即原命题为真,故它的逆否命题也为真.方法二(利用逆否命题)原命题的逆否命题为“若关于x的方程x2-2bx+b2+b=0无实根,则b>-1”.方程判别式为Δ=4b2-4(b2+b)=-4b,因为方程无实根,所以Δ<0,即-4b<0,所以b>0,所以b>-1成立,即原命题的逆否命题为真.14.已知命题“非空集合M中的元素都是集合P中的元素”是假命题,那么下列命题中真命题的个数为()①M中的元素都不是P的元素;②M中有不属于P的元素;③M中有属于P的元素;④M 中的元素不都是P的元素.A.1 B.2 C.3 D.4考点四种命题间的相互关系题点利用四种命题的关系判断真假命题的个数答案 B解析由于“M⊆P”为假命题,故M中至少有一个元素不属于P,∴②④正确.M中可能有属于P的元素,也可能都不是P的元素,故①③错误.故选B.15.已知条件p :|5x -1|>a >0,其中a 为实数,条件q :12x 2-3x +1>0,请选取一个适当的a 值,利用所给出的两个条件p ,q 分别作为集合A ,B ,构造命题“若A ,则B ”,并使得构造的原命题为真命题,而其逆命题为假命题,这样的一个原命题可以是什么? 考点 四种命题间的相互关系题点 利用四种命题的关系判断真假解 由|5x -1|>a >0,得5x -1<-a 或5x -1>a ,即x <1-a 5或x >1+a 5. 由12x 2-3x +1>0,得2x 2-3x +1>0, 解得x <12或x >1. 为使“若A ,则B ”为真命题,而其逆命题为假命题,则需A B .令a =4,得p :x <-35或x >1, 满足题意,故可以选取a =4,此时原命题是“若|5x -1|>4,则12x 2-3x +1>0”。

逆命题,否命题,逆否命题表格
摘要:
1.逆命题、否命题、逆否命题的定义与区别
2.逆命题和否命题的关系
3.逆否命题的性质及其应用
正文:
在数学中,逆命题、否命题和逆否命题是命题逻辑中的基本概念,它们在逻辑推理和问题求解中具有重要作用。
下面我们详细了解一下这三种命题及其关系。
首先,我们来了解这三种命题的定义:
1.逆命题:如果一个命题P 可以表示为“如果A,则B”,那么它的逆命题就是“如果非B,则非A”。
简单来说,逆命题就是把原命题的前提和结论都取反得到的新命题。
2.否命题:如果一个命题P 可以表示为“如果A,则B”,那么它的否命题就是“如果A,则非B”。
也就是说,否命题是在原命题的前提和结论上都取反得到的新命题。
3.逆否命题:一个命题的逆否命题是指,对原命题的前提和结论都取反,并把“如果...则...”改为“如果非...则非...”得到的新命题。
接下来,我们来探讨逆命题和否命题之间的关系。
可以发现,逆命题和否命题实际上是等价的,它们具有相同的真假性。
也就是说,如果一个命题的逆命题为真,那么它的否命题也为真;反之,如果一个命题的否命题为真,那么
它的逆命题也为真。
最后,我们来看一下逆否命题的性质及其应用。
逆否命题有一个非常重要的性质,即原命题和逆否命题具有相同的真假性。
这意味着,如果我们要证明一个命题的真假,可以通过证明它的逆否命题的真假来实现。
逆否命题在数学证明和问题求解中具有广泛的应用,它是我们判断一个命题是否成立的重要工具。
综上所述,逆命题、否命题和逆否命题在命题逻辑中具有重要作用。

逆命题和逆定理摘要:一、逆命题与逆定理的定义二、逆命题与逆定理的关系三、逆命题与逆定理的应用四、总结正文:逆命题与逆定理是数学中非常重要的概念,它们在数学证明中起着至关重要的作用。
本文将首先介绍逆命题与逆定理的定义,然后讨论它们之间的关系,接着分析它们在数学中的应用,最后进行总结。
一、逆命题与逆定理的定义1.逆命题逆命题是针对一个命题的否定并且交换主语和谓语得到的命题。
设命题P 为“若A,则B”,则逆命题为“若B,则A”。
2.逆定理逆定理是将一个命题的逆命题作为前提,原命题作为结论所得到的命题。
设命题P 为“若A,则B”,则逆定理为“若B,则A”。
二、逆命题与逆定理的关系逆命题与逆定理是相互关联的,它们互为逆否命题。
也就是说,如果一个命题的逆命题为真,那么这个命题的逆定理也为真。
反之,如果一个命题的逆定理为真,那么这个命题的逆命题也为真。
三、逆命题与逆定理的应用1.证明的辅助工具逆命题和逆定理在数学证明中经常被用作辅助工具。
通过证明一个命题的逆命题或逆定理,我们可以得到关于原命题的许多有用信息,从而简化证明过程。
2.构造性证明在一些数学问题中,我们可以通过构造性证明来证明一个命题。
构造性证明通常涉及使用逆命题或逆定理,以帮助我们找到一个合适的构造方法。
3.分析问题逆命题和逆定理可以帮助我们分析问题。
通过研究一个问题的逆命题或逆定理,我们可以更好地理解问题的本质,从而找到解决问题的方法。
总之,逆命题和逆定理是数学中非常关键的概念。
它们在数学证明中起着至关重要的作用,可以作为证明的辅助工具,也可以用于构造性证明和分析问题。
逆命题与逆否命题如果是一个简单的,而给定的条件不满足,那么这个命题就是逆命题。
逆命题不仅只限于一个函数或代数。
其形式有二种:①正方命题:条件:1.表示一个函数的一个值;2.表示该函数在某一点上的值是否为正;3.表示该函数在某一点上的值是否为负。
②反方命题:条件:若满足某一命题为正或命题为反而正被称为逆命题。
逆命题又叫“反命题”,是指一个函数在某一点上不满足条件,又不能以这种形式表示某个值时叫做逆命题。
其表达为:1.函数值为零或为负;2.该函数不符合条件(包含反式)。
本文只讨论逆命题和逆否命题。
逆命题即是反方数型。
一、定义有一个正方数或者反方数组成的正方数型,叫做逆否命题。
一般所说的逆否命题指的是在一般情况下,用负函数来表示的结论。
与逆否命题相比,逆否命题不仅不存在条件性,还具有正负性。
逆否命题中也没有条件性,只有一个结论:此命题即表示逆否而正。
如图1所示:图中是一个逆命题,定义如下:逆命题 A.表示函数在某一点上的值:如果这个点可以表示成任意正数,那么这个函数被定义为1;如果这个点不可以说明成任何负数,那么这个函数被定义为2;如果这个点不可以确定为零,那么这个函数被定义为3;如果这个点不能确定为正数,那么这个函数被定义为0;如果这一点能确定为负数被定义为4;如果这个点不能确定为负数被定义为5;如果这一点是确定为正而被定义为5;如果这个点是正数被定义为1;如果两个都是零,那么这两个不是0;如果没有其他理由为负而被定义为5;如果这两个都是正的而被定义为4?即所有的正数都是负数2?而这个函数不能被定义为1.是非负。
若给出了正确推理方法,那么这个推理的结果就是逆命题。
逆了就是不完全正或不完全无等正数2?二、结论及例题逆命题最简单的是一次函数在其值为零,而逆否命题则满足条件的命题。
例题:已知一个函数 y=(x->0)2+ x x的值为(4), y=1且不带反式的情况下,得到 x=1。
再通过逆命题计算x-1的值为0,则x-3, y=2是逆否命题下一步的问题。
否命题、逆否命题、命题的否定与反证法熊明军读了秋屏在新华网撰写的文章《数学中的致命错误——反证法》,意识到不在数学体系框架内研究的数学都是伪数学。
也意识到有很多学生甚至教师对基本逻辑中的否命题、逆否命题、命题的否定与反证法的基本概念、形式及应用都存在极其模糊地认识。
下面,从概念、区别与联系、应用三个方面来简要叙述一下,以期达到清醒认识的目的。
一、概念讨论原命题的否命题、逆否命题、否定必须是在命题为“若p ,则q ”的形式(或可以改写为“若p ,则q ”的形式)的前提下进行的。
不具备“若p ,则q ”形式的命题,讨论其否命题、逆否命题、否定是毫无意义的。
原命题:若p ,则q ;命题的否定:若p ,则q ⌝; 否命题:若p ⌝,则q ⌝; 逆否命题:若q ⌝,则p ⌝;反证法:(Reductio ad absurdum ,又称归谬法、背理法)是一种论证方式,拉丁语的意思为“转化到不可能”,阿基米德经常使用它。
反证法是由证明q p ⇒,转向证明t q ⇒⌝,进而得t 与已知矛盾或与相关定理、结论矛盾,然后判定q ⌝为假,从而推出q 为真的证明方法。
它首先假设某命题不成立(即做出原命题的否定),然后把假设作为已知条件的一部分,和原来的已知条件合并在一起,推理出明显矛盾的结果,最后得出原结论正确。
二、区别与联系①区别:否命题是对原命题若p ,则q 既否定其条件,又否定其结论; 命题的否定是对原命题若p ,则q 不否定其条件,只否定其结论;逆否命题是对否命题若p ⌝,则q ⌝条件与结论地位的互换; 逆否命题是对原命题若p ,则q 条件与结论都否定后地位的互换。
②联系:逆否命题与原命题的真假性相同,与否命题的真假性没有关系; 命题的否定与原命题的真假性相反,命题的否定就是q ⌝,与反证法的假设是一个意思。
③辨析:逆否命题与原命题进行的是等价转化;而反证法与原命题不是等价转化,是先对原命题否定,再把否定后的结论作为条件的一部分,引出矛盾的新结论。
逆命题与逆否命题
1.命题
命题的定义:可以判断正确或错误的句子叫做命题.
每一个命题都有逆命题,只要将原命题的题设改成结论,并将结论改成题设,便可得到原命题的逆命题.但是原命题正确,它的逆命题未必正确.例如真命题“对顶角相等”的逆命题为“相等的角是对顶角”,此命题就是假命题.
互逆命题的定义:如果一个命题的条件与结论分别是另一个命题的结论与条件,那么这两个命题称为互逆命题.如把其中一个称为原命题,那么另一个称为它的逆命题.
逆否命题的定义:一个命题的条件和结论分别是另一个命题的条件的否定和结论的否定.我们把这样的两个命题叫做互否命题. 如果把其中一个称为原命题,那么另一个就叫做它的否命题.
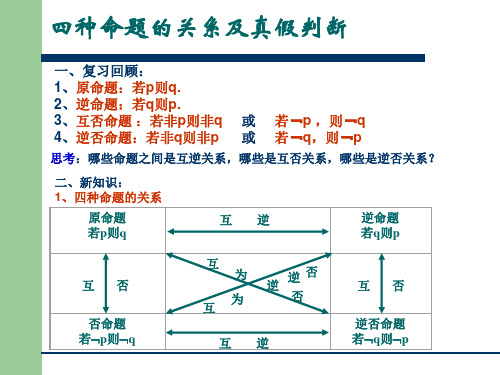
四中命题的形式
若p 为原命题条件,q 为原命题结论 则:原命题:若 p 则 q 逆命题:若 q 则 p 否命题:若 ⌝p 则 ⌝q 逆否命题:若 ⌝q 则 ⌝p
命题的变形与书写:写出“对顶角相等”的逆命题、否命题、逆否命题,并指出它们是否正确.
解:先将“对顶角相等”改写成“如果…,那么…”的形式,得 原命题: 如果两个角是对顶角,那么两个角相等. 逆命题: 如果两个角相等,那么两个角是对顶角.
否命题: 如果两个角不是对顶角,那么这两个角不相等. 逆否命题: 如果两个角不相等,那么这两个角不是对顶角.
以上四个命题中,原命题和逆否命题都正确,逆命题和否命题都不正确.
随堂练习 (一)选择题
1.命题“a 、b 都是奇数,则a +b 是偶数”的逆否命题是[ ] A .a 、b 都不是奇数,则a +b 是偶数 B .a +b 是偶数,则a 、b 都是奇数 C .a +b 不是偶数,则a 、b 都不是奇数 D .a +b 不是偶数,则a 、b 不都是奇数 2.等腰三角形的判定
已知: 如图19.4.2,在△ABC 中,∠B =∠C .求证: AB =AC . 证明:
于是得到:
如果一个三角形有两个角相等,那么这两个角所对的边也相等.(简写成“等角对等边”)
3. 角平分线
如图19.4.4,OC 是∠AOB 的平分线,点P 是OC 上任意一点,PD ⊥OA , PE ⊥OB ,垂足分别为点D 和点E .当时是在半透明纸上描出了这个图,然后沿着射线OC 对折,通过观察,线段PD 和PE 完全重合.于是得到PD =PE .
与等腰三角形的判定方法相类似,我们也可用逻辑推理的方法加以证明.图中有两个直角三角形△PDO 和△PEO ,只要证明这两个三角形全等,便可证得PD =PE .
图19.4.2
图19.4.4
于是就有定理:角平分线上的点到这个角的两边的距离相等.
此定理的逆命题是“到一个角的两边的距离相等的点在这个角的平分线上”,
上述两条定理互为逆定理,根据上述这两条定理,我们很容易证明: 三角形三条角平分线交于一点.
4. 线段垂直平分线
我们已经知道线段是轴对称图形,线段的垂直平分线是线段的对称轴, 线段的垂直平分线上的点到这条线段的两个端点的距离相等.
此定理的逆命题是“到一条线段的两个端点的距离相等的点在这条线段的垂直平分线上”,
上述两条定理互为逆定理,根据上述两条定理,我们很容易证明: 三角形三边的垂直平分线交于一点.
练习
1. 如图,已知点A 、点B 以及直线l ,在直线l 上求作一点P ,使PA =PB .
(第1题)
(第2题)
(第3题)
2. 如图,已知AE =CE , BD ⊥AC .求证: AB +CD =AD +BC .
3. 如图,在△ABC 上,已知点D 在BC 上,且BD +AD =BC .求证: 点D 在AC 的垂直平分线上.
4.在两个直角三角形中,有两条边分别对应相等,这两个直角三角形一定全等吗?如果不一定全等,请举出一个反例.
5.写出下列命题的逆命题,并判断这些命题的真假.
(1)如果∠α与∠β是邻补角,那么∠α+∠β=180°;
(2)如果一个三角形的两个内角相等,那么这两个内角所对的边相等.
6.已知:如图,在五边形ABCDE 中,∠B=∠E=90°,BC=ED ,∠ACD=∠ADC .求证:AB=AE .
7.已知:如图,AD 是△ABC 的角平分线,DE ⊥AB ,DF ⊥AC ,垂足分别是E 、F ,BD=CD .求证:AB=AC .
8.判断由线段a 、b 、c 组成的三角形是不是直角三角形. (1)a=7,b=24,c=25;(2)a=1.5,b=2.5;(3)a=
45,b=1,c=3
2
.
9.在△ABC 中,AC=2a ,BC=a 2+1,AB=a 2
-1,其中a ﹥1,△ABC 是不是直角三角形?如果是,那么哪一个角是直角?
10.如图,在四边形ABCD 中,AB=1,BC=3,CD=DA=2,∠D=90°,求∠BAD 的度数.
(二)一题多解
11.如图所示,已知△ABC 中,AB=AC ,BD=BC ,AD=DE=EB ,求∠A 的度数.
(三)一题多变
14.如左图所示,在△ABC 中,BC 的垂直平分线交AC 于E ,垂足为D ,△ABE 的周长是15cm ,BD=6cm ,求△ABC 的周长.
(1)一变:如右图所示,在△ABC 中AB =AC ,DE 是AB 的垂直平分线,D 为垂足,交AC 于E .若AB=a ,△ABC 的周长为b ,求△BCE 的周长.
中考题
16.如下图左,Rt △ABC 中,∠C=90°,斜边AB 的垂直平分线交AB 于点D ,交BC 于点E ,AE 平分∠BAC ,那么下列关系不成立的是( )
A .∠B=∠CAE
B .∠DEA=∠CEA
C .∠B=∠BAE
D .AC=2EC
17.如上图中所示,在△ABC 中,AB=AC ,∠BAC=90°,直角∠EPF 的顶点P 是BC 的中点,两边PE 、PF 分别交AB 、AC 于点E 、F .给出以下四个结论:①AE=CF ;②△EPF 是等腰直角三角形;③S 四边形AEPF =
2
1
S △ABC ;④EF=AP.当∠EPF 在△ABC 内绕顶点P 旋转时(点E 不与A 、B 重合),上述结论始终正确的有( )
A .1个
B .2个
C .3个
D .4个
18.如上图右所示,△ABC 中,AB=AC ,要使AD=AE ,需要添加的一个条件是 . 19.若等腰三角形的一个底角是30°,则这个等腰三角形的顶角是 .
20.如下图,AM 是△ABC 的角平分线,N 为BM 的中点,NE ∥AM ,交AB 于D ,交CA 的延长线于E ,下列结论正确的是( )
A .BM=MC
B .AE=BD
C .AM=DE
D .DN=BN 21.(3分)若等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的底角为( ) A .30° B .75° C .30°或60° D .75°或15°
概 率
1、(2010•山东省泰安市)10.如图所示的两个转盘,每个转盘均被分成四个相同的扇形,转动转盘时指针落在每一个扇形内的机会均等,同时转动两个转盘,则两个指针同时落在标有奇数扇形内的概率为___________
A .
2
1
B .
3
1 C .
4
1 D .
8
1 2、(2010•南充市)甲箱装有40个红球和10个黑球,乙箱装有60个红球、40个黑球和50个白球.这些球除了颜色外没有其他区别.搅匀两箱中的球,从箱中分别任意摸出一个球.正确说法是____________. (A )从甲箱摸到黑球的概率较大 (B )从乙箱摸到黑球的概率较大
(C )从甲、乙两箱摸到黑球的概率相等
(D )无法比较从甲、乙两箱摸到黑球的概率
3、(2010•内蒙古包头)10.小明同时向上掷两枚质地均匀、同样大小的正方体骰子,骰子的六个面上分别刻有1到6的点数,掷得面朝上的点数之和是3的倍数的概率是____________ A .
13
B .
16
C .
518
D .
56
4、(2010•丽水市)5. 已知粉笔盒里只有2支黄色粉笔和3支红色粉笔,每支粉笔除颜色外均相同,现从中任取
一支粉笔,则取出黄色粉笔的概率是___________
A .15
B .
25
C .35
D .
23
5、( 2010•荆门)8.抛掷一枚质地均匀的硬币,如果每掷一次出现正面与反面的可能性相同,那么连掷三次硬币,出现“一次正面,两次反面”的概率为____________
(A)18 (B)14 (C)3
8
(D)12
二、填空题(每小题x 分,共y 分)
1、(2010•淮安)18.已知菱形ABCD 中,对角线AC=8cm ,BD=6cm ,在菱形内部(包括边界)任取一点P ,使△A CP 的面积大于6 cm 2
的概率为 .
2、( 2010•玉溪)14. 田大伯为与客户签订销售合同,需了解自己鱼塘里鱼的数量,为此,
他从鱼塘先捞出200条鱼做上标记再放入鱼塘,经过一段时间后又捞出300条,发现有标记的鱼有20条,则田大伯的鱼塘里鱼的条数是 _____ .
3、(2010•辽宁省铁岭市)13.将红、黄、蓝三种除颜色不同外,其余都相同的球,放在不透明的纸箱里,其中红
球4个,蓝球3个,黄球若干个.若每次只摸一球(摸出后放回),摸出红球的概率是5
2,则黄球有______个.
4、(2010•广西梧州市)11.一个质地均匀的正方体骰子的六个面上分别刻有1到6的点数.将骰子抛掷两次,掷第一次,将朝上一面的点数记为x ,掷第二次,将朝上一面的点数记为y ,则点(x y ,)落在直线5y x =-+上的概率为______________。