下载文档原格式
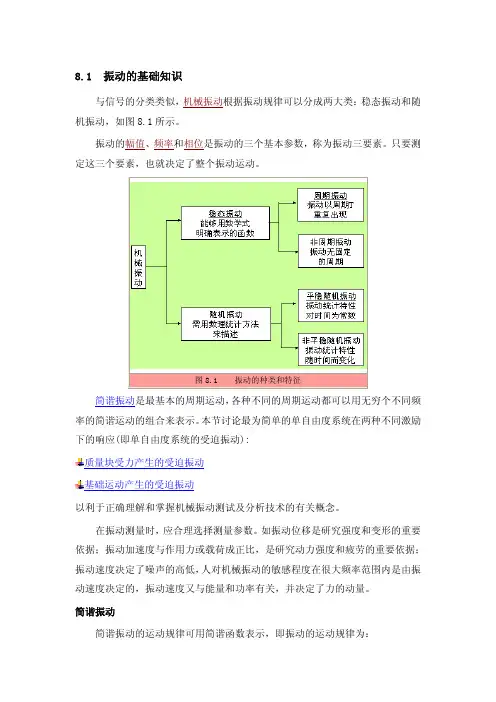
8.1 振动的基础知识与信号的分类类似，机械振动根据振动规律可以分成两大类：稳态振动和随机振动，如图8.1所示。
振动的幅值、频率和相位是振动的三个基本参数，称为振动三要素。
只要测定这三个要素，也就决定了整个振动运动。
图8.1 振动的种类和特征简谐振动是最基本的周期运动，各种不同的周期运动都可以用无穷个不同频率的简谐运动的组合来表示。
本节讨论最为简单的单自由度系统在两种不同激励下的响应(即单自由度系统的受迫振动):质量块受力产生的受迫振动基础运动产生的受迫振动以利于正确理解和掌握机械振动测试及分析技术的有关概念。
在振动测量时，应合理选择测量参数。
如振动位移是研究强度和变形的重要依据；振动加速度与作用力或载荷成正比，是研究动力强度和疲劳的重要依据；振动速度决定了噪声的高低，人对机械振动的敏感程度在很大频率范围内是由振动速度决定的，振动速度又与能量和功率有关，并决定了力的动量。
简谐振动简谐振动的运动规律可用简谐函数表示，即振动的运动规律为：(8.2)(8.3)比较式(8.1)至(8.3)可见，速度的最大值比位移的最大值导前900 ，加速度的最大值要比位移最大值导前1800 。
质量块受力产生的受迫振动如图8.2所示为单自由度系统在质量块受力所产生的受迫振动示意图。
在外力f(t)的作用下，质量块m的运动方程为：（8.4）式中c为粘性阻尼系数，k为弹簧刚度，位移y(t)为振动系统的输出。
这是一个典型的二阶系统，其系统频率响应函数H(ω)和幅频特性函数、相频特性函数ϕ(ω)分别为：（8.5a）图8.2 质量块受力所产生的受迫振动（8.5b）（8.5c）式中：ω基础运动的圆频率；ζ振动系统的阻尼比， ；。
（8.6） 由上式可见，在幅频特性图上，质量块受力产生的受迫振动其共振频率ωr总是小于系统的固有频率ωn，阻尼越小两者越靠近，因此，在小阻尼情况下可以采用ωr作为的ωn估计值；而在相频特性图上，不管系统的阻尼比为多少，在ωr/ωn=1时位移始终落后于激振力90°。
