A题_西安市经开区公共自行车服务系统设计说明

公共自行车服务系统运行规律研究-----以浙江省温州市鹿城区为例摘要：根据浙江省温州市鹿城区公共自行车使用数据，基于公共自行车服务模式和使用规则，对公共自行车服务系统的运行规律从各个站点运行规律、借车人借车规律和高峰日系统的具体运行规律三个方面进行研究。

并基于所发现的规律对目前公共自行车服务系统的设置进行了评价，同时给出了提高系统效率的建议。

首先分别统计各站点20天中每天及累计的借车频次和还车频次。

结果显示，几乎所有站点在20天中的累计借车频次排序和还车频次排序大致相同。

另外也对每次用车时长的分布情况也进行了分析，发现用车时长主要集中在30分钟之内，约占用车量的90%；而用车时长在60分钟之内的用车量占总用车量的99%。

这与鹿城区公共自行车租赁收费标准（1小时内免费，超过1小时收费）相吻合。

以上现象也间接说明了政府制定的收费机制的有效性。

然后统计了20天中各天使用公共自行车的不同借车人数量，并统计了数据中出现过的每张借车卡累计借车次数的分布情况。

结果表明，20天中借车人数呈现明显的周期性波动，并且波动周期大约为7天。

而且波动量非常大，从最高峰第20天约20000个借车人到最低峰不到5000人。

还发现每张借车卡累计借车次数的分布情况如下：20天中55%的借车人借车次数不超过10次，35%的在10-30次之间，9%的在30次以上。

最后基于用车次数最多的第20天的数据对系统进行更为详细的分析。

发现借还车站点之间最长距离为32号站到45号站的距离，最短为73号站到115号站，99号站到150号站的距离。

借还车频次最高的站点分别为42号站点（770次）和56号站点（743次）。

两个站点借还车主要时间段相同，98.6%的借车在7:00到21:00之间，99.9%的还车在7:00到21:30之间。

发现两个站点运行规律的不同点有：56号站点比42号站点在早晨上班时的用车高峰更明显。

56号站点比45号站点用车时长在30分钟之内的多3.3%，说明还车高峰期人们会较快使用完自行车。

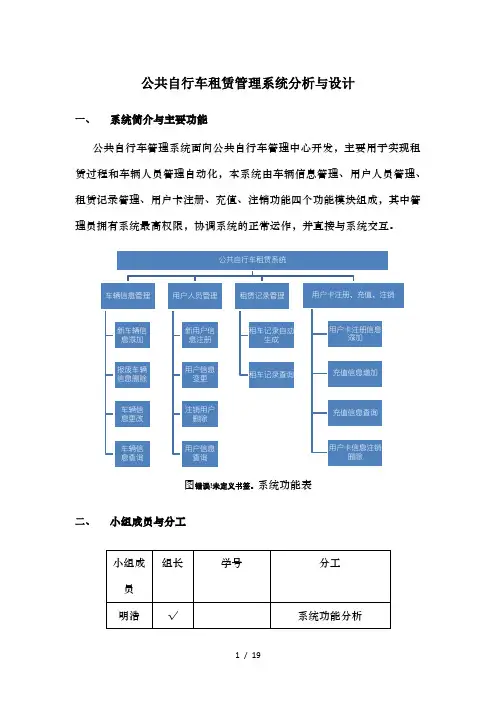
公共自行车租赁管理系统分析与设计一、系统简介与主要功能公共自行车管理系统面向公共自行车管理中心开发，主要用于实现租赁过程和车辆人员管理自动化，本系统由车辆信息管理、用户人员管理、租赁记录管理、用户卡注册、充值、注销功能四个功能模块组成，其中管理员拥有系统最高权限，协调系统的正常运作，并直接与系统交互。

图错误!未定义书签。

系统功能表二、小组成员与分工三、需求模型图错误!未定义书签。

系统用例图用例规约：四、分析模型类图：描述系统内的实体类与类之间的关系其中，参与者分为用户和管理员，每一名用户对应一张属于自己的用户卡，并通过用户卡与系统交互，用户卡可存储租车记录与充值记录，也可以与自助终端机交互完成租借与归还任务，管理员拥有较高权限，可帮助用户注册、充值、注销用户卡，也可以管理自行车信息，租车记录会出现超出时限的现象，系统将自动根据罚款细则进行记录并在用户卡中扣除金额。

图错误!未定义书签。

类图顺序图：充值顺序图：管理员通过登录到系统，完成身份验证，管理员通过刷卡向系统传输用户卡信息，并手动输入金额，保存信息并完成充值。

图错误!未定义书签。

充值顺序图租车顺序图：用户通过租车自助终端机刷卡验证身份，取得自行车，终端机会自动更改所租用自行车的租借状态，并生成租车记录存储到租车记录档案中。

: 管理员: 用户图错误!未定义书签。

租车顺序图还车顺序图：用户通过租车自助终端机刷卡验证身份，归还自行车，终端机会自动更改所租用自行车的租借状态，并生成还车车记录存储到租车记录档案中。

图错误!未定义书签。

还车顺序图五、设计模型：包括设计阶段的类图、顺序图与相关说明图错误!未定义书签。

设计阶段实体类图图错误!未定义书签。

表现层类图图错误!未定义书签。

控制层类图图错误!未定义书签。

领域类图:User图错误!未定义书签。

租车顺序图图错误!未定义书签。

还车顺序图图错误!未定义书签。

充值顺序图六、总结与感想信息系统分析与设计是利用现代信息技术没处理组织中的信息、业务、管理和决策等问题，并未组织目标服务的综合系统。

普通高中学业水平考试（真题）通用技术时间：90分钟满分：100分。

第一部分(选择题共50分)一、单项选择题(共16小題，每小題2分，计32分。

在每小题给出的四个选项中，只有一项是符合题目要求的)1．共享单车随时取用和停放给民众带来极大便利，方便了人们“最后一公里”的出行。

下列共享单车构件中属于标准件的是A．防滑脚踏B．舒适座椅C．智能车锁D．螺栓螺母2．近几年，绿色发展的理念日益深入人心，建设美丽中国的行动不断升级提速。

一个天蓝、地绿、水清的大美中国，正在重回身边、重现眼前。

关于技术与自然的关系说法最恰当的是A．改变社会生活的习惯B．提高人类生活的质量C．促进社会经济的发展D．注重人与自然的和谐3．某同学注意到冬季天冷，儿童吃饭慢，经常吃到冷饭的现象，设计了一款注水保温碗，可实现持续保温。

该同学发现问题的途径是A．收集和分析信息B．观察日常生活C．奇特性构思法D．技术研究与技术试验4．西安天坛，又名圜丘，是隋唐时期皇帝祭天的重要礼仪建筑。

圜丘共四层，整体为夯土结构高约8米，最底层直径约54米，顶层直径约20米。

圜丘的结构类型属于A．框架结构B．实体结构C．组合结构D．壳体结构5．某款概念汽车釆用球形轮胎的设计，可实现横向行驶，使超车、入库等操作不用改变车身方向即可进行。

该轮胎设计主要体现结构改变导致变化的是A．材料B．功能C．稳定性D．经济性6．台式风扇电机轴承在启动瞬间的受力分析正确的是A．受拉(力)B．受压(力)C．受扭转(力)D．受剪切(力)7．如图示为某款登高车，它配置特有的防滑锁定机构。

人站上去后，在重力作用下爬梯下降，爬梯底部橡胶垫紧压地面起到自锁的作用，减少了移动登高车后需手动固定的环节。

该设计体现了人机关系中的A．高效B．安全C．舒适D．健康8．为保证我国自主研发的全球首列智轨列车安全稳定运行，研发机构完成了24小时不间断试技术试验采用的方法是A．优选试验法B．强化试验法C．虚拟试验法D．移植试验法9．下列行为不属于侵犯他人知识产权的是A．擅自使用他人集成电路布图设计B．网络下载影视作品用于商业用途C．引用或转载他人文本资料，并标明出处D．利用计算机技术暴力破解软件贩卖牟利10．关于产品说明书的说法正确的是A．应告诉用户如何仿制或改造产品B．必须使用专业的技术用语和图表C．说清楚提醒话、关键话，不用考虑用户的阅读需要D应根据产品的特点、功能和经济价值而有所侧重11．某研发机构独创的机器人调度系统，最多可对区域内100台机器人进行统一协调、调度，解决多机器人工作时可能发生的冲突、拥堵等现象，其定位精度达到厘米级，实现机器人无固定轨道自运行。

2024-2025学年度第一学期期中检测八年级地理(中图版)考生注意:本试卷共6页,满分60分,时间60分钟。

第一部分(选择题共23分)一、选择题(本大题共23小题,每小题1分,共23分。

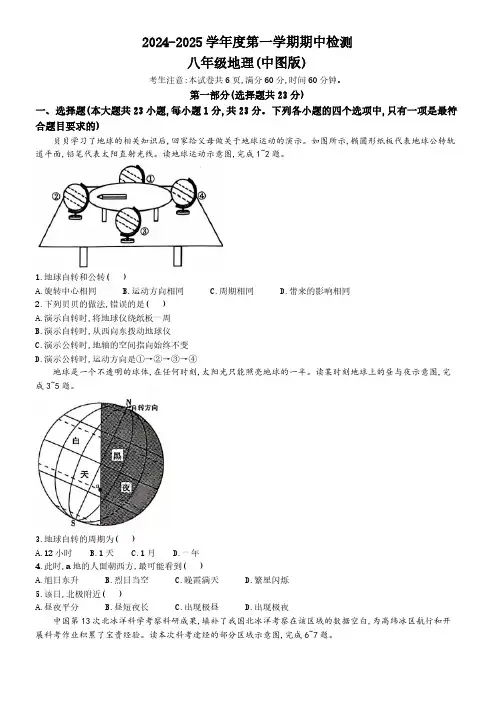
下列各小题的四个选项中,只有一项是最符合题目要求的)贝贝学习了地球的相关知识后,回家给父母做关于地球运动的演示。

如图所示,椭圆形纸板代表地球公转轨道平面,铅笔代表太阳直射光线。

读地球运动示意图,完成1~2题。

1.地球自转和公转( )A.旋转中心相同B.运动方向相同C.周期相同D.带来的影响相同2.下列贝贝的做法,错误的是( )A.演示自转时,将地球仪绕纸板一周B.演示自转时,从西向东拨动地球仪C.演示公转时,地轴的空间指向始终不变D.演示公转时,运动方向是①→②→③→④地球是一个不透明的球体,在任何时刻,太阳光只能照亮地球的一半。

读某时刻地球上的昼与夜示意图,完成3~5题。

3.地球自转的周期为( )A.12小时B.1天C.1月D.一年4.此时,a地的人面朝西方,最可能看到( )A.旭日东升B.烈日当空C.晚霞满天D.繁星闪烁5.该日,北极附近( )A.昼夜平分B.昼短夜长C.出现极昼D.出现极夜中国第13次北冰洋科学考察科研成果,填补了我国北冰洋考察在该区域的数据空白,为高纬冰区航行和开展科考作业积累了宝贵经验。

读本次科考途经的部分区域示意图,完成6~7题。

6.科考船途经的甲海峡是( )A.白令海峡B.马六甲海峡C.台湾海峡D.土耳其海峡7.甲海峡沟通的海洋是( )A.北冰洋、大西洋B.北冰洋、太平洋C.大西洋、太平洋D.印度洋、太平洋在地球内力的驱动下,印度古陆漂洋过海,经历了地质历史上漫长的漂泊,终于到达现今位置。

读2亿年以来印度古陆不同时期的经纬度位置示意图,完成8~9题。

8.图示印度古陆在漂移过程中,其主体( )A.最初位于南半球热带B.从南温带漂移至北寒带C.漂移的速度越来越快D.现今已与亚欧大陆相连9.2亿年以来,印度古陆( )A.呈逆时针旋转并向东北方向运动B.呈逆时针旋转并向西南方向运动C.呈顺时针旋转并向东北方向运动D.呈顺时针旋转并向西南方向运动世界各地的降水分布很不均衡。

2022-2023学年陕西省西安市经开一中九年级（上）期末语文试卷1. 下列各组词语中，加点字的读音全部正确的一组是（）A. 熏陶．（táo）狡黠．（xiá）侍．候（cì）伤痕累．累（lěi）B. 荣膺．（yīng）绰．号（chuō）诘难．（nàn）血．雨腥风（xuè）C. 顷．刻（qǐng）恐吓．（hè）夹．袄（jiá）一曝．十寒（pù）D. 盘桓．（huán）挣．脱（zhèng）径．自（jìng）吹毛求疵．（zī）2. 下列各组词语中，汉字书写全都正确的一组是（）A. 要决扭绞飞窜取义成仁B. 装饰苍茫坠毁不屑置辨C. 憋闷娇贵戏虐千钧之力D. 诸侯练达傅彩颓唐不安3. 经典诗文默写。

(1) 春谷持作饭，______ 。

（乐府诗集《十五从军征》）(2) 纷纷暮雪下辕门，______ 。

（岑参《白雪歌送武判官归京》）(3) ______ ，坐断东南战未休。

（辛弃疾《南乡子登京口北固亭有怀》）(4) 望西都，______ 。

（张养浩《山坡羊潼关怀古》）(5) 人生自古谁无死，______ 。

（文天祥《过零丁洋》）(6) 浊酒一杯家万里，______ 。

”（范仲淹《渔家傲秋思》）(7) 马作的卢飞快，______ 。

（辛弃疾《破阵子为陈同甫赋壮词以寄之》）(8) 陛下亦宜自谋，______ ，察纳雅言。

（诸葛亮《出师表》）(9) ______ ，读诗使人灵秀。

（培根《谈读书》）(10) 我是你额上熏黑的矿灯，______ 。

（舒婷《祖国啊，我亲爱的祖国》）4. 阅读下面语段，按照要求，完成下面的题目。

ㅤㅤ①中华民族是历经磨难、不屈不挠的伟大民族；中国人民是勤劳勇敢、自强不息的伟大人民；中国共产党是敢于斗争、敢于胜利的伟大政党。

②历史车轮滚滚向前，时代潮流浩浩荡荡。

③历史只会眷顾_______者、______者、______者，而不会等待犹豫者、懈怠者、畏难者。

西安市人民政府办公厅关于印发公共自行车运营补助暂行办法和绩效考核奖励暂行办法的通知文章属性•【制定机关】西安市人民政府办公厅•【公布日期】2017.02.27•【字号】市政办发〔2017〕15号•【施行日期】2017.01.01•【效力等级】地方规范性文件•【时效性】失效•【主题分类】交通运输其他规定正文西安市人民政府办公厅关于印发公共自行车运营补助暂行办法和绩效考核奖励暂行办法的通知市政办发〔2017〕15号各区、县人民政府，市人民政府各工作部门、各直属机构：《西安市公共自行车运营补助暂行办法》、《西安市公共自行车运营绩效考核奖励暂行办法》已经市政府研究同意，现印发给你们，请遵照执行。

西安市人民政府办公厅2017年2月27日西安市公共自行车运营补助暂行办法第一章总则第一条为加快完善城市生活功能，不断增强城市综合承载力，持续推进缓堵保畅，解决“治堵难”，促进公共自行车系统健康发展，结合我市实际，制定本办法。

第二条公共自行车运营补助按照“财政补助、统筹包干、自负盈亏、企业增效、奖惩结合”的原则进行。

第三条公共自行车运营补助分为运行经费和绩效奖励两部分，经市财政局核定后列入城建计划，由西安城市公共自行车服务管理有限责任公司统筹使用。

第二章运行经费核定第四条运行经费由人工成本、管理费用以及其他费用三部分组成。

第五条每年年终，西安城投集团应随同部门预算上报下年度公共自行车运营补助预算。

第六条人工成本。

综合考虑年社平工资增幅、同行业水平等因素，管理人员的工资、社保参照公交总公司相应级别标准核定;其他人员参照西安城投集团其他单位临聘人员工资标准核定，社保按市级部门编制外人员标准核定;其他人工费，按现行规定核定;管理人员及其他人员均享受取暖、降温费等。

人员的配备标准，应综合考虑外地同业、自行车总量等因素合理设置。

人员配备如有变动，需经西安城投集团批准同意，并向市财政局备案。

第七条管理费用。

参照同级全额事业单位标准核定。

2023年全国职业院校技能大赛“轨道车辆技术”赛项模块3竞赛任务书A卷场次_______________工位_______________场次处填写，C1，C2，C3；工位处填写“两位数工位号+已确认”，例：01已确认1 / 24注意事项：（1）任务书下发后应仔细检查，如出现任务书缺页、字迹不清等问题，请及时向裁判示意，更换任务书。

（2）参赛选手提交的答题卡与任务书上只能按要求填写场次号、工位号（“两位数的场次/工位号+已确认”）进行识别，不得填写指定内容之外的任何识别性标记。

如果出现地区、校名、姓名等其他任何与竞赛队有关的识别信息，一经发现，竞赛试卷和提交结果作废，比赛按零分处理，并且提请赛项执委会进行处罚。

（3）任务中要求提交的任何文件中都不允许出现本工位或者其他工位参赛选手图像、选手姓名、校名或者其他任何识别性的标记。

一经发现，竞赛试卷和提交结果作废，比赛按零分处理，并且提请赛项执委会进行处罚。

（4）竞赛任务书、竞赛工具、竞赛器材及竞赛材料等不得带出竞赛场地，一经发现，竞赛提交结果作废，比赛按零分处理，并且提请赛项执委会进行处罚。

（5）正式比赛前，参赛选手需对竞赛平台中的设备工具模块进行清点确认，正式比赛开始后，参赛选手如测定竞赛技术平台中的设备工具模块有故障可提出更换，但该工具/模块经现场裁判与技术支持人员测定完好，确属参赛选手误判，不予任何延时。

（6）竞赛过程中，参赛选手要遵守安全操作规程，确保人身及设备安全，并接受裁判员的监督和警示。

竞赛过程中由于参赛选手不规范操作造成的设备模块损坏，裁判员与裁判长商定后，根据赛项规程给予酌情扣分。

（7）在竞赛过程中，参赛选手如有舞弊、不服从裁判判决、扰乱赛2 / 24场秩序等行为，裁判长按照赛项规程扣减相应分数。

情节严重的取消竞赛资格，竞赛成绩记为零分。

安全注意：●项目所需的工具、电器、材料均由竞赛场地提供，参赛选手可直接选择使用，比赛前检查工具是否配套齐全，比赛过程中注意工具使用规范。

目录一、问题引入..................................................................................................................................... - 3 -二、问题分析..................................................................................................................................... - 3 -2.1第一问分析................................................................................................................... - 4 -2.2第二问分析................................................................................................................... - 4 -2.3第三问分析................................................................................................................... - 4 -三、模型假设和符号说明................................................................................................................. - 5 -3.1模型假设....................................................................................................................... - 5 -3.2符号系统....................................................................................................................... - 6 -四、模型建立..................................................................................................................................... - 6 -4.1模型分类....................................................................................................................... - 6 -4.2 租赁点分配方案建模.................................................................................................. - 7 -4.3 调度车调度方案建模.................................................................................................. - 8 -4.3.1一辆调度车调度方案....................................................................................... - 8 -4.3.2多辆调度车调度方案....................................................................................... - 9 -4.4租赁点数目和位置的确定......................................................................................... - 11 -4.5 调度时间的模型........................................................................................................ - 12 -五、模型的求解............................................................................................................................. - 13 -5.0经纬度转换为横纵坐标............................................................................................. - 13 -5.1 求解最短路径............................................................................................................ - 13 -5.2 模型一次运行后的单车重分配求解........................................................................ - 14 -5.3 求解分配方案的预估—校正算法............................................................................ - 16 -5.4 求解调度方案的启发式算法.................................................................................... - 16 -5.4.1算法简介......................................................................................................... - 16 -5.4.2算法内容......................................................................................................... - 17 -5.4.3约束条件......................................................................................................... - 18 -5.4.4算法流程图..................................................................................................... - 19 -5.5租赁点位置................................................................................................................. - 20 -5.6计算结果..................................................................................................................... - 20 -5.6.1第一问结果..................................................................................................... - 20 -5.6.2第二问结果..................................................................................................... - 21 -5.6.3第三问结果..................................................................................................... - 23 -六、模型检验................................................................................................................................... - 26 -七、模型优缺点以及改进............................................................................................................... - 26 -7.1分配方案的优点......................................................................................................... - 27 -7.2调度方案的缺优点..................................................................................................... - 27 -7.3新增节点模型的优缺点............................................................................................. - 27 -7.4模型和算法的改进..................................................................................................... - 28 -7.4.1算法的改进..................................................................................................... - 28 -7.4.2模型的改进..................................................................................................... - 28 -八、参考文献................................................................................................................................... - 30 -附录................................................................................................................................................... - 30 -一、问题引入近年来，随着经济的发展，我国各级城市的机动车保有量都进入了持续高速增长时期，但由此所引发的道路拥堵、空气污染也引起了政府以及百姓的极大关注。

西安工业大学数学建模竞赛承诺书我们仔细阅读了西安工业大学数学建模竞赛的参赛规则与竞赛纪律。

我们完全明白，在竞赛开始后参赛队员不能以任何方式（包括电话、电子邮件、网上咨询等）与队外的任何人研究、讨论与赛题有关的问题。

我们知道，抄袭别人的成果是违反竞赛纪律的, 如果引用别人的成果或其他公开的资料（包括网上查到的资料），必须按照规定的参考文献的表述方式在正文引用处和参考文献中明确列出。

我们郑重承诺，严格遵守参赛规则和竞赛纪律，以保证竞赛的公正、公平性。

如有违反竞赛纪律的行为，我们将受到严肃处理。

我们授权西安工业大学数学建模竞赛组委会，可将们的论文以任何形式进行公开展示（包括进行网上公示，在书籍、期刊和其他媒体进行正式或非正式发表等）。

西安市经开区公共自行车服务系统设计模型摘要本文主要研究了西安市经开区公共自行车服务系统设计的问题。

主要运用了蚁群算法得出了较为合理的调度车辆运行路径，并采用了离散概率模型对需要调度的公共自行车情况进行了估计。

在三期建设的规划选点问题上，我们建立了层次分析法模型（AHP），较为科学的确定了新增点的数目及其位置。

针对问题一，利用matlab把各站点位置经纬度坐标转换为更便于求解的距离矩阵，并由此通过建立离散概率模型的方式得出较为合适的各站点还车数目，最终通过蚁群算法实现了最优路径的筛选，得出合理的车辆分配方案及调度方案，求得最优的调度耗时。

针对问题二，对带筛选站点位置进行了合适的区域划分，又通过线性规划模型得到的新增租赁点数目及车辆总数。

以此为基础，建立了AHP模型，得出了各区域建租赁点合理的重要性程度，按权重确定了各点所在位置及其分配的车辆数目。

针对问题三，在前两问求解的基础上得知必须要增加调度车辆。

通过大量的计算机模拟，在尽量保证调度时间少和增加车辆数少的前提下，应用蚁群算法，反复的求解，最终得出了较为合适的新增调度车辆数目和自行车调度方案。

关键词：蚁群算法层次分析法离散概率模型最优化问题1问题的重述公共自行车租赁服务系统纳入城市公共交通体系，有助于解决公交出行“最后一公里”问题，使公共交通服务网络趋于更加完善。

公共自行车系统服务点布设的有限元估算方法董红召;章丽萍;刘冬旭;陈宁【摘要】针对城市公共自行车系统(PBS)依靠人工经验规划服务点布设导致的"租还车难"问题,根据PBS的运行特性,借鉴有限元原理,研究PBS不同空间位置区域的供需不平衡度有限元估算模型,建立PBS服务点布设的有限元估算方法.以杭州市部分区域为例,应用有限元分析软件ANSYS对估算方法进行验证.结果显示:在研究区域内未建服务点4146时,公共自行车供需不平衡度最大的位置位于120.151 275°E~120.152 55°E和30.302 04°N~30.303 774°N;建立服务点4146后,该位置的供需不平衡度明显缓解,单元供需不平衡度最大的位置与服务点4146实际位置相比,经、纬度误差分别为0.044 5%、0.047 3%.分析结果表明,该估算方法能够有效分析PBS的单元供需不平衡度,从而有助于服务点的科学布设.%The present planning method of service-stations' layout for public bicycle system (PBS) depends on human experience, which usually leads to the issue of bike-renting or bike-returning difficulty.According to the PBS running history characteristics and referring to the finite element theory, the imbalance degree between bicycle supply and demand in different spatial areas was estimated, and a finite element estimation model of the PBS supply and demand was established. An empirical study was conducted by software ANSYS to verify the estimation method in some district of urban Hangzhou. Results show that,before the service-station No.4146 was built, the location which had the maximum supply and demand imbalance degree was at the regions from 120.151 275°E to 120.152 55°E andfrom30.302 04°N to 30.303 774°N. After the service-station No.4146 wasbuilt, supply and demand imbalance degree at the location was significantly alleviated; compare the location where the supply and demand imbalance degree was the maximum and the actual location of the service-station No.4146, and the errors were about 0.044 5% at longitude and 0.047 3% at latitude. Results indicate that the proposed finite-element method can effectively analyze the imbalance degree between bicycle supply and demand, and contribute to the reasonable layout of service-stations for PBS.【期刊名称】《浙江大学学报（工学版）》【年(卷),期】2017(051)006【总页数】7页(P1097-1103)【关键词】公共自行车;服务点布设;单元供需不平衡度;有限元方法【作者】董红召;章丽萍;刘冬旭;陈宁【作者单位】浙江工业大学智能交通系统联合研究所,浙江杭州 310006;浙江工业大学智能交通系统联合研究所,浙江杭州 310006;浙江工业大学智能交通系统联合研究所,浙江杭州 310006;浙江工业大学智能交通系统联合研究所,浙江杭州310006;浙江科技学院机械与汽车工程学院,浙江杭州 310012【正文语种】中文【中图分类】TP206;U121公共自行车系统(public bike system,PBS)已成为许多城市越来越重要的公共交通方式之一[1-2].但是,PBS在实际运行过程中还存在着不少问题[3-4],其中最突出的是服务点规划不合理[5]及“租还车难”.服务点规划不合理加剧了“租还车难”,降低了PBS的使用效率.关于PBS服务点布设的研究主要包括以下内容.Lin等[6-8]综合考虑总成本和服务水平下得出PBS中服务点设置的最佳位置和数量.Garracía-Palomares等[9-10]提出了一种基于地理信息系统的方法来确定服务点的容量.Vogel等[11]通过研究高峰时段租还信息和服务点位置,进行了服务点的位置优化.Martine等[12]提出了能同时解决服务点选址和服务点规模问题的优化模型.Li等[13]提出了城市公共自行车服务点的复杂网络构建方法.Dai等[14]根据公共自行车系统规划的实践,提出了系统规划的基本原则和思路.耿雪等[15]在将公共自行车系统分区的基础上,测算各区日均出行次数,进而确定公共自行车服务点的数量和规模.李黎辉等[16]提出了“总量调控、分类分块、平衡规模、灵活调整”的布局总体思路.陈景旭等[17]提出了分层分级布设公共自行车服务点的布局方法.这些工作推动了PBS的科学布设研究,但是也比较明显地受到了经验与主观因素的限制.有限元方法是一种客观分析分布式数据的有效方法,用于解决工程中平面薄板的力学问题,根据相邻子域间的相互作用机制进行求解.有限元方法与交通流的空间分布特征不谋而合,但目前用有限元方法解决交通问题的研究比较少,主要有李福祥等[18]基于流体有限元的思想对交通流的研究.该研究证明了有限元流体分析系统ANSYS-FLOTR AN可以较好地模拟交通流状况.PBS相邻服务点的服务区域之间的区域租还平衡,具有与有限元中相邻子域间的类似相互作用机制.运用有限元思想建立PBS单元供需不平衡度的估算模型,有助于合理布设公共自行车服务点,缓解“租还车难”问题.本文借鉴有限元法原理,提出一种公共自行车系统服务点布设的有限元估算方法.根据杭州城市公共自行车系统7年来的实践经验,服务点布设需要分布密度较高且尽量均匀,这样,在PBS无车可租或者无空位可还车时,用户可以较方便地步行到相邻各服务点或者更远的服务点租还车[19],PBS租还需求量通过相互邻接的区域实现了空间的传递与扩散.PBS交通出行的实际调查发现,某区域中用户选择步行到相邻或者更远的各服务点租还车的可能性大致相等,也就是每个单元租还需求的传递扩散能力基本相同,因此公共自行车系统的微区域单元具有统计意义上的连续性、均匀性等特征,符合运用有限元方法对单元特性的要求.在PBS运营过程中,需要有各种参数描述系统运行性能及服务质量.在应用有限元估算方法分析PBS单元供需不平衡度时,用到的参数定义如下:1)单元:PBS覆盖区域通过虚拟网格划分离散出的虚拟矩形小片区,包含若干服务点.2)节点:由租还需求量拟合成的租还函数在单元上的插值点,即虚拟矩形单元上的4个顶点.3)单元需求强度:用于衡量在某时间段内,PBS覆盖的某区域采用公共自行车交通模式的租还需求差异的大小,用该区域单位面积的租车数与还车数的差值来计算,用Fui表示,正、负符号分别表示租车和还车.4)单元服务能力:用于衡量PBS覆盖的某区域内各服务点为该服务点所服务的范围可以提供随租随还公共自行车的能力,用该服务点某时刻的公共自行车数m与服务面积S的比值Focp和空锁桩数n与服务面积S的比值Femp表示.5)单元供需不平衡度:PBS单元需求强度与该单元服务能力的差值,用某时刻该区域单位面积的租车数与还车数的差值与在该区域单位面积上Focp或Femp的差值,用p表示,p<0.121e8,p位于小值区间;0.121 e8<p<0.242 e8,p所在的区间适中;0.242 e8<p,p位于大值区间.若需求强度为正,则有:当Focp-Fui<0.121e8时,p位于小值区间,且p随着Focp-Fui的减小而减小;当Focp-Fui>0.242e8时,p位于大值区间,且p随着Focp-Fui 的增大而增大;当0.121e8<Focp-Fui< 0.242e8时,p所在的区间适中,且p随着Focp-Fui的增大而增大.若需求强度为负,则有:当Femp+Fui<0.121 e8时,p位于小值区间,且p随着Femp+Fui的减小而减小;当Femp+Fui>0.242 e8时,p位于大值区间,且p随着Femp+Fui的增大而增大;当0.121 e8< Femp+Fui<0.242 e8时,p所在的区间适中,且p随着Femp+Fui的增大而增大.6)车锁比:某服务点公共自行车数量与该服务点锁桩数量的比值,用α表示.7)需求增度:PBS的单元需求强度和车锁比的比值.需求增度矩阵为单元需求增度的集合,用K表示.8)车变比:在采用PBS交通模式的一定需求量作用下,公共自行车服务点车锁比的变化系数,即需求量作用前、后的车锁比之差与作用前的车锁比之比,用于仿真实验. 将PBS覆盖区域作为研究平面,通过虚拟网格划分离散成各个虚拟矩形小片区为单元,根据区域中的租还需求量[20],求解计算出单元需求强度、服务点的车锁比、空缺数及满位数.有限元估算方法具体步骤如下.1)虚拟网格划分.考虑估算的精度,在PBS服务覆盖区域中选择一个能完全包含研究区域的最小矩形,将矩形的长宽按比例划分,形成各个小矩形,依次对这些小矩形进行虚拟网格划分,离散获得的这些虚拟矩形(设长为2a,宽为2b)小片区为一个单元,设虚拟矩形单元为i-j-m-k(逆时针顺序编号),i、j、m、k为4个节点,坐标分别为(xi,yi)、(xj,yj)、(xm,ym)、(xk,yk),x为纬度方向,y为经度方向.2)虚拟矩形单元的插值租还函数.插值租还函数是单元节点上的租还需求量拟合成的租还函数,表达式为式中:s、t分别为节点的租、还需求量.将4个节点代入式(1),解出a1、a2、a3、a4和b1、b2、b3、b4,并将单元内的需求量表示成由4个节点的需求量为待定系数的近似展开式,矩阵形式为式中:N为单元上租还基函数列阵,即其中,δ为i、j、m、k这4个节点租还量组成的列阵.3)分析求解车锁比α、单元需求强度Fui.由于相邻服务点的服务区域之间租还需求具有相互作用机制,推算可得出某一公共自行车服务点车锁比由沿纬度方向车锁比εx、经度方向车锁比εy和纬度与经度2个方向之间的车锁比γxy的列阵表示:记令单元车锁比状态矩阵:其中,相应地,需求量来自服务点附近的所有方向,单元需求强度即为由沿纬度方向单元需求强度σx、沿经度方向单元需求强度σy和垂直于纬度方向的平面上且沿经度方向的单元需求强度τxy的列阵表示.式中:E为各单元需求强度与相应车锁比的比值的平均值;μ为横向车锁比与纵向车锁比的绝对值的比值,由于公共自行车的需求只有租和还2种可能,且在同一平面上,μ=0.即:其中,Fuiω为每个单元的单元需求强度,αω为每个单元的车锁比,ω为第ω个矩形单元,n为研究区域的总单元数.令单元需求强度状态矩阵:当α<0时,表示某服务点的公共自行车在某段时间内无法满足自行车租借的需求;当α>1时,表示某服务点的锁桩设施在某段时间内无法满足自行车归还的需求.当出现以上2种情况时,短时间内不能通过PBS用户的租还自动调节到合理状态,此服务点需要上架(或下架)公共自行车.4)PBS单元需求增度矩阵K计算:5)系统综合并引入边界条件.单元节点租还需求量列阵叠加后的系统方程为式中:F为叠加后各单元节点租还需求量列阵,K'叠加后需求增度矩阵,η'为叠加后区域内所有节点的车锁比列阵.边界条件为式中:Ci(i=1,2,3,4)分别表示研究区域平面的4个边,Ca为研究区域平面4个边的车锁比约束.6)求解方程组.将式(12)边界条件代入系统方程(11),可求出区域内每个虚拟矩形节点的租还需求量.将节点的租还需求量s1、t1、s2、t2、s3、t3、…、si、ti代入式(3),即可求出各单元的近似车锁比;利用式(8),即可得到单元需求强度的近似解.7)PBS服务点布设.求解方程组得出PBS覆盖范围内所有的单元需求强度,进而求得单元需求强度与单元服务能力之差,判断单元供需不平衡度p的大小.在p位于大值区间的区域内设置新服务点或增加该区域内原服务点的锁桩数,科学布设服务点,有效解决“租还车难”的问题.3.1 服务点布设的有限元估算模型与边界条件根据数学计算步骤在ANSYS软件上实践杭州市区域PBS服务点布设的有限元估算.杭州是国内最先施行公共自行车的城市,已经拥有7年的历史运行数据,这可以为有限元估算方法的验证提供充实的数据支撑.取杭州市拱墅区30.300 0°N~ 30.306 0°N和120.150 0°E~120.157 0°E区域为研究对象,该区域内共有8个公共自行车服务点.从历史运营数据分析可以得出公共自行车系统出行时间分布特性,公共自行车“租还车难”的问题在早晚高峰开始和结束时段特别突出,以某日7:00~7:30的实际租还量历史统计数据为例进行有限元法估算,服务点相关数据如表1所示.在此需要说明的是,表中7:00~7:30时间段内租借的车辆数多于该服务点7:00的公共自行车数量和该时间段内归还的车辆数之和,这是采用人工或机动车方法对自行车进行调度产生的结果.将选取的研究区域及8个服务点在ANSYS中建模,根据“1 m=0.01”将研究区域转化为长1 m、宽1 m的矩形平面.公共自行车服务点位置如图1所示.按照ANSYS建模要求和PBS的简化运行特性建立边界条件,约束模型四边的单元服务能力,即使有租还需求,边界不提供租还服务.设置租借公共自行车为正方向,归还公共自行车为反方向,由于租还需求量来自于服务点各个方向,租还需求量为以相应服务点为圆心,100 m为半径的圆面均匀需求量.首先输入仿真的基本参数,设置有限元估算仿真的需求增度为2.06e8,车变比为0.3.在服务点香积寺路247号(编号为4146,简称“服务点4146”)建立之前,对该区域已建成的7个服务点在相应需求量作用下进行ANSYS有限元估算,得到的单元供需不平衡度分析结果如图2所示.从图2中可以看出,在有限元估算模型的有效范围内,公共自行车单元供需不平衡度最大的位置为图中白色区域,该位置位于120.151 275°E~ 120.152 55°E和30.302 04°N~30.303 774°N.未建的服务点4146位置为120.153 44°E、30.304 72 °N,纬度误差为0.000 946(0.047 3%),经度误差为0.000 89(0.044 5%).从模型分析估算值与实际设点的情况看,两者虽然不完全一致,但经、纬度平均相对误差均已小于0.05%,基本能够反映出公共自行车供需不平衡度大的区域位置及范围.3.2 服务点布设的有限元估算仿真与结果分析在建立服务点4 146之后,相同参数下对该区域8个服务点在相应需求量作用下再次进行ANSYS有限元估算,得到的单元供需不平衡度分析结果如图3所示.在有限元估算模型的有效范围内,该范围内公共自行车单元供需不平衡度适中.在服务点4 416未建之前,该位置出现了局部单元供需不平衡度较大,服务点供需不平衡的现象;而在该服务点建成之后,单元供需不平衡度适中,供需基本平衡.这与目前杭州PBS 的实际运行状况比较吻合,说明了有限元估算方法的有效性,能够评估PBS的单元供需不平衡度.若把服务点4 146布设到图2白色中间位置,相同参数下对8个服务点在相应需求量作用下再次进行ANSYS有限元估算,得到的单元供需不平衡度分析结果如图4所示.在有限元估算模型的有效范围内,该范围内大部分区域公共自行车单元供需不平衡度小.与图3相比,单元供需不平衡度明显减缓,这进一步说明了有限元估算方法用于PBS服务点的布设的有效性.需要指出的是,该方法也有局限性.在仿真实验过程中,由于PBS有限元估算的边界约束与公共自行车系统特性有差异,仿真实验发现估算模型边界20%区域的相互作用机制受到了边界约束影响,只能判断为无效区域,不作有限元估算讨论;而中间80%的范围,主要受到PBS区域租还平衡的相互作用机制影响,因此是有效区域,可以用于PBS单元供需不平衡度估算.根据PBS的运行特性,提出了PBS单元供需不平衡度的有限元估算模型,建立了PBS服务点布设的有限元估算方法.以杭州市部分区域为例,采用有限元分析软件ANSYS对方法的可行性予以验证,实验结果显示,未建服务点4 146前在120.151 275°E~ 120.152 55°E和30.302 04°N~30.303 774°N范围内出现公共自行车单元供需不平衡度位于大值区间的现象,而在建立服务点4146后,该位置的供需不平衡度明显缓解.若把服务点4 146布设到白色中间区域,有效范围内大部分区域公共自行车单元供需不平衡度位于小值区间,研究区域的公共自行车供需基本平衡.对比在该区域增加服务点4 146前、后及将4 146布设到单元供需不平衡度最大的位置的单元供需不平衡度分析结果,证明此估算方法较为可靠,能够分析PBS覆盖区域的供需不平衡度,从而指导公共自行车系统服务点的布设.PBS服务点布设的有限元估算方法还停留在小规模区域的研究阶段,关于扩大到杭州区域更大范围的方法适用性以及如何通过改进边界条件的设置增加有效区域的比例等方面还需要进行深入研究.【相关文献】[1]CHEN J X,CHEN X W,JIANG H,et al.Determining the optimal layout design for public bicycle system within the attractive scope of a metro station[J].Mathematical Problems in Engineering,2015,2015(2134):1-8. [2]VOGELA P,GREISERA T,MATTFELDA DC.Understanding bike-sharing systems using data mining: exploring activitypatterns[J].Procedia Social and Behavioral Sciences,2011,20(6):514-523.[3]CHEMLA D,MEUNIER F,CALVO W R,et al.Bike sharing systems:solving the static rebalancing problem [J].Discrete Optimiz,2013,10(2):120-146.[4]RAVIV T,TZUR M,FORMA I A.Static repositioning in a bike-sharing system:models and solution approaches[J].EURO Journal on Trans portation and Logistics,2013,2(3):187-229.[5]RAINER-HARBACH M,PAPAZEK P,RAIDL G R,et al.PILOT,GRASP,and VNS approaches for the static balancing of bicycle sharing systems[J].Journal of GlobalOptimization,2015,63(3):1-33.[6]LIN J R,YANG T H,CHANG Y C.A hub location inventory model for bicycle sharing system design:formulation and solution[J].Computers and IndustrialEngineering,2013,1(65):77-86.[7]LIN J R,YANG T H.Strategic design of public bicycle sharing systems with service level constraints[J]. Transportation Research Part E,2011,2(47):284-294.[8]王懿.小城市公共自行车选址及需求优化设计[J].交通科学与工程,2016,32(1):96-100.WANG Yi.Research on public bicycle rental sites selection and stock demand forecasting of a small city[J]. Journal of Transport Science and Engin eering,2016, 32(1):96-100. [9]GARRACÍA-PALOMARES J C,GUTIÉRREZ J, LATORRE M.Opt imizing the location of stations in bike-sharing programs:a GIS approach[J].Applied Geography,2012,1-2(35):235-246.[10]ZHOU Y L,,LU J M,XU S,et al.Research on the site selection of the public bicycle system[J].Advanced Materials Research,2014,8(1030-1032): 229-2295.[11]VOGEL P,MATTFELD D C.Modeling of repositioning activities in bike-sharing systems[C]∥12th World Conference on Transport Research.Portugal: [s.n.],2010:1-13. [12]MARTINE L M,CAETANO L,EIRO T,et al.An optimisation algorithm to establish the location of stations of a mixed fleet biking system an application to the city ofLisbon[J].Procedia-Social and Behavioral Sciences,2012,54(1):513-524.[13]LI C,WANG Z F.Method on layout optimizing of public bicycle rental stations based on complex network theory[C]∥International Conference on TransportationEngineering.Miami:[s.n.],2011:247-252.[14]DAI J F,ZHAO X L,LIN J X.Public bicycle system station deployment and scale prediction[J].Advanced Materials Research,2013,3(790):510-514.[15]耿雪,田凯,张宇,等.巴黎公共自行车租赁点规划设计[J].城市交通,2009,7(4):21-29.GENG Xue,TIAN Kai,ZHANG Yu,et al.Bike rental station planning and design inParis[J].Urban Transport of China,2009,7(4):21-29.[16]李黎辉,陈华,孙小丽.武汉市公共自行车租赁点布局规划[J].城市交通,2009,7(4):30-38.LI Li-hui,CHEN Hua,SUN Xiao-li.Bike rental station deployment planning inWuhan[J].Urban Transport of China,2009,7(4):30-38.[17]陈景旭,王炜.轨道交通站点公共自行车租赁点布局研究[J].武汉理工大学学报:交通科学与工程版,2013, 37(6):1206-1210.CHEN Jing-xu,WANG Wei.Research on the layout of bike rental station around a railway station[J].Journal of Wuhan University of Technology:Transportation Science and Engineering,2013,37(6):1206-1210.[18]李福祥,李文勇,李长军,等.基于有限元分析的交通流理论与技术研究[J].武汉理工大学学报:交通科学与工程版,2012,1(36):124-128.LI Fu-xiang,LI Wen-yong,LI Chang-jun,et al.Traffic flow theory and technology research based on finite element analysis[J].Journal of Wuhan University ofTechnology:Transportation Science and Engineering, 2012,(36):124-128.[19]董红召,史彩霞,陈宁,等.基于关联规则的公共自行车调度区域聚类划分[J].科技通报,2013,29(9): 209-216.DONG Hong-zhao,SHI Cai-xia,CHEN Ning,et al. Clustering division of public bicycle scheduling regional based on association rules[J].Bullet in of science and technology,2013,29(9):209-216.[20]董红召,吴满金,刘冬旭,等.城市公共自行车系统自然租赁需求的估算方法[J].浙江大学学报:工学版, 2016,50(2):265-270.DONG Hong-zhao,WU Man-jin,LIU Dong-xu,et al. Estimation method of natural demand of urban public bicycle system[J].Journal of Zhejiang University:EngineeringScience,2016,50(2):265-270.。

陕西省西安市2024年社会工作者新教材通关(精选题)（带答案解析）1、社工单选题（综合能力）（共80题）1. 关于地区发展模式实施特点的说法，正确的是( )。

A.提升居民解决问题的能力，实现自助互助B.界定社区问题的优先次序。

逐一加以解决C.设计可行性方案，并预估方案的收益与成效D.邀请专业人士针对社区问题，制定解决方案【答案】A【解析】本题考查地区发展模式的实施特点。

地区发展模式是社会工作者协助社区成员分析问题、发挥其自主性的工作过程，目的是提高他们及社区团体对社区的认同，鼓励他们通过自助和互助，解决社区问题。

地区发展模式的主要实施特点有：（1）较多关注社区共同性问题；（2）通过建立社区自主能力来实现社区的重新整合；（3）过程目标的重要性超过任务目标：（4）特别重视居民的参与。

2. 某儿童福利院接收了一些曾被拐卖的儿童，这些儿童健康状况差，经常表现出胆怯、惊恐。

为此，社会工作者小李决定用小组工作方法为他们提供辅导，协助其恢复和发展社会功能。

该小组较适合采取的工作模式是（）。

A.互动模式B.治疗模式C.发展模式D.社会目标模式【答案】C【解析】发展模式旨在解决和预防服务对象社会功能的衰减问题、恢复和发展服务对象的社会功能。

发展模式关注的焦点在于小组组员的社会功能而不是有关生理和病理方面的因素，重视的是组员个人潜力的发掘与发挥而不是治疗性辅导。

故答案选C。

3. 社会工作者小刘与服务对象李女士初步接触后，运用心理社会治疗模式对李女士问题的原因进行诊断，对其困扰产生的时间，重要影响时间及个人成长经历等方面进行了探索，上述小刘的工作内容属于（）。

A.心理动态诊断B.人格诊断C.分类诊断D.缘由诊断【答案】D【解析】缘由诊断是对服务对象困扰产生、变化的过程进行分析。

例如，服务对象的困扰是什么时候产生的、有什么重要的影响事件、在服务对象的成长过程中有什么样的变化等，是对服务对象个人历史的考察。

由题干可知，选项D符合题意。

基于骑行时空数据的共享单车使用特征研究——以西安市主城区为例刘清，王录仓摘要：论文对西安市主城区2017年11月2日与4日摩拜单车使用数据进行了空间可视化分析与时间统计，对比总结了工作日与休息日单车使用的时空间特征、闲置单车的空间分布与移动单车的具体使用情况。

研究发现，工作日单车使用有明显的早晚高峰与午间小高峰，休息日没有明显的早午高峰，但有晚高峰与午夜小高峰，并且平均单车骑行时耗大于工作日；空间分布上城三区单车总体使用强度低于郊三区。

研究建议未来的共享单车设施规划应利用大数据构建单车市场供需统计系统，并分区域、分时段、分频次有针对性地进行投放布局与智能调度。

关键词：共享单车，西安市主城区，时空分布，使用特征Shared bike Usage Characteristics Based on Cycling Spatio-temporal DataA Case Study of the Host City of Xi’anAbstract：The article analyzes the time statistics and spatial visualization of Maba bicycle usage data on the host city of Xi’an on November2and4,2017,comparing and summarizing the time-space characteristics of bicycles used on work days and holidays and Specific usage of idle and mobile bicycles.The study found that bicycles on working days have obvious morning and evening peaks and small midday peaks.There are no early morning rush hours on rest days,but there are obvious night peaks and midnight peaks,and the average bicycle ride time is larger than the working days;The utilization rate of bicycles is generally lower than that of the peripheral urban area。

陕西省西安市经开区经开第二中学2024-2025学年七年级上学期期中考试数学试题一、单选题1．实数5-的相反数是（）A ．5B ．5-C ．15D ．15-2．锂电池是电动汽车的关键部件，我国的锂电池正突破重围，势不可挡．规定充电时长为正，耗电时长为负，若新能源汽车快充充电0.5小时记作0.5+小时，那么新能源汽车连续性耗电7小时记作（）A ．0.5+小时B ．0.5-小时C ．7+小时D ．7-小时3．截至目前中国森林面积达到175000000公顷，森林覆盖率为18.21％，人工林面积居世界首位，其中数字175000000用科学记数法表示为（）A ．617510⨯B ．717.510⨯C ．81.7510⨯D ．90.17510⨯4．用一个平面截下列立体图形，截面不可能．．．是圆的是（）A ．B ．C ．D ．5．对于多项式256x x --，下列说法正确的是（）A ．它是三次三项式B ．它的常数项是6C ．它的一次项系数是5-D ．它的二次项系数是26．下列说法正确的是（）A ．整数和分数统称为有理数B ．一个有理数的绝对值一定大于它本身C ．x 与y 的和除以x 的商是yx x+D ．相反数等于本身的数只有0和17．某工厂计划生产n 个零件，原计划每天生产a 个零件，实际每天比原计划多生产b 个零件，则实际生产所用的天数比原计划少（）A ．n n a b ⎛⎫- ⎪⎝⎭天B ．n n b a ⎛⎫- ⎪⎝⎭天C ．nn a b a ⎛⎫-⎪+⎝⎭天D ．nn a a b ⎛⎫- ⎪+⎝⎭天8．已知,,a b c 三个数在数轴上对应的点如图所示，则下列结论中错误的是（）A ．0a b +<B ．0c b ->C ．0abc >D ．b c b c+=+二、填空题9．比较大小：85-236-．（填“>”“<”或“=”）10．如图是一个正方体的展开图，如果相对面上两个数的和为0，则x y +的值为．11．对幻方的研究体现了中国古人的智慧，如图是一个没有填写完整的幻方，它每一横行、每一竖列以及两条斜对角线上的3个数的和都相等，那么m 表示的数为．12．数轴上与点A 距离3个单位长度的点表示的数是1，则点A 表示的数是．13．按照图（1）、（2）、（3）的方式分割三角形，所得三角形总个数分别是5个、9个、13个，照此规律分割下去，第n 个图中共有个三角形．三、解答题14．计算：()()22892323-÷-++⨯-．15．计算：()()4345222--+-÷-．16．化简：()()22234321m m m m -+--+．17．在数轴上表示下列各数，并用“<”把这些数连接起来．2-， 1.5+，72，12⎛⎫-- ⎪⎝⎭，4--．18．如图是一个“数值转换机”的示意图．(1)写出输出结果______（用含x 的代数式表示）；(2)填写下表；x 2-1-012输出19．某公司上半年1月份盈利25万元，2月份亏损20万元，3月份盈利18万元，4月份亏损24万元，5月份盈利19万元，6月份亏损23万元，该公司上半年是盈利还是亏损，盈利或亏损了多少万元？20．先化简，再求值：()()22212322ab a b a ab -+---，其中1a =，2b =-．21．如图，大拇指与食指尽量张开时，两指尖的距离称为“一拃长”，某项研究表明身高与“一拃长”有如下的近似关系：一拃的长度乘10，再把结果加2cm ，就能得知对应的身高．(1)设一拃长为cm d ，对应的身高为cm h ，用代数式表示h 与d 之间的关系；(2)某同学一拃长为16.8cm ，则他的身高约是多少厘米？22．某特技飞行队在黄山湖风景区进行特技表演．其中一架飞机从起点开始起飞后的高度变化如下（记上升为正，下降为负）：5.5km +， 3.2km -，1km +， 1.5km -，0.8km-(1)此时这架飞机比起飞点高了多少千米？(2)若飞机上升1千米平均消耗4升燃油，下降1千米平均消耗2升燃油，那么这架飞机在这5次高度变化中，一共需消耗多少升燃油？23．小明房间窗户的装饰物如图所示，它是由两个相等的四分之一圆组成，阴影部分表示阳光不能透过装饰物照进房间．(1)用含a ，b 的代数式表示窗户能射进阳光部分（空白部分）的面积；(2)当8dm a =，3dm b =时，求窗户能射进阳光部分（空白部分）的面积．（π取3.14，结果精确到0.1）24．乐高侧重于培养孩子的解决问题能力，沟通表达能力，自我学习能力和创新实践能力．某线上文具店计划每天销售100套乐高，但由于种种原因，实际每天的销售量与计划量相比有出入，下表是某周的销售情况（超额记为正，不足记为负．单位：套）．星期一二三四五六日与计划量的差值+4-3-5+14-8+21-6(1)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售______套；(2)本周实际销售量是否达到了计划量？试说明理由；(3)若每套乐高按80元售卖，平均每套乐高需要线上文具店支付的运费是10元，那么该线上文具店本周销售乐高实际收入多少元？25．网约车是一种便捷的出行工具．某平台网约车计价规则如下表：计费项目里程费时长费远途费单价a 元/公里0.45元/分钟()1.4a -元/公里注：车费由里程费、时长费、远途费三部分构成，其中里程费按行车的实际里程计算，时长费按行车的实际时间计算，远途费的收取方式为：行车里程10公里以内（含10公里）不收远途费，超过10公里的，超出部分每公里收()1.4a -元．(1)当行车里程为8公里，行车时间为7分钟时，在该平台约车需付车费多少元？(2)若小明乘坐该平台网约车，行车里程为30公里，行车时间为20分钟，则小明应付车费多少元？(3)小王与小张各自乘坐该平台网约车，行车里程分别为9公里与15公里，受路况情况影响，小王比小张乘车多用了23分钟，小王的行车时间为b 分钟，小张比小王付的车费多多少元？26．如图，在单位长度为1的数轴上有A ，B ，C ，D 四个点表示4个不同的有理数，点A ，C 表示的有理数互为相反数．(1)点A 表示的有理数是______，点B 表示的有理数是______；点C 表示的有理数是______；点D 表示的有理数是______；(2)点A ，B ，C ，D 同时开始在数轴上运动，若点C 和点D 分别以每秒2个单位长度和3个单位长度的速度向右匀速运动．同时，若点A 和点B 分别以每秒6个单位长度和5个单位长度的速度向左匀速运动，运动时间为t 秒．①用含t 的代数式表示点A ，D 之间的距离；②若点A ，C 之间的距离为m ，点B ，D 之间的距离为n ，求m n -的值．。