自然循环热水锅炉水动力计算
- 格式:doc
- 大小:1.37 MB
- 文档页数:22

第18卷 第5期 ・36・1998年10月动 力 工 程POW ER EN G I N EER I N G V o l .18N o.5 O ct .1998 中低压自然循环锅炉水动力计算中的多解问题朱建宁 王妍 周玉铭 张晓鹏 朱文华(西安 西安交通大学)摘 要 通过分析证实:采用现行的水动力分析方法分析中低压自然循环锅炉的水动力特性时会遇到数学上解不唯一问题,对如何确定实际运行状态下的水动力特性提出了对策。
图2参5主题词: 中低压 自然循环锅炉 水动力计算 研究 19950425来稿,19960118收到修改稿。
1 问题的提出水动力计算是锅炉设计中确定并检验锅炉水循环特性的主要手段。
长期以来,由于计算手段的限制不少产品的设计并不进行此项计算,而只是参照已有的锅炉布置形式完成设计。
因此可以说有相当多的水循环回路的设计是凭经验完成的。
当然,这样的设计也就必然带有一定的盲目性,尤其对一些新的回路布置形式,这样做的结果则带有一定程度的冒险性。
近10年来随着计算机的普及与计算技术的发展,不少学者为解决这一问题先后尝试了利用计算机计算分析来确定锅炉的水循环工作特性。
他们编制了计算软件,提出了一些巧妙的算法[1,2,3]。
然而,不幸的是所有的这些计算均是建立在以往分析电站锅炉水动力特性方法的基础之上的。
当将其应用在参数较低的中低压自然循环锅炉时,便遇上了预想不到的麻烦。
其具体表现为求解过程的收敛性差,对初值的要求高且依赖性强,不少求解结果常常出人意料并难以解释。
经笔者多年的研究发现造成上述问题的祸根是回路方程的多解性或解的不唯一的问题。
2 不唯一解的存在性应当承认:尽管水循环计算相当繁琐,但其理论毕竟已使用了数十年之久。
为什么以往的分析计算都能经得起实践的检验?而现在提出这一问题有什么实际的意义呢?对此,笔者的回答是:过去水动力计算大多是针对参数较高的电站锅炉进行的。
由于电站锅炉水循环回路相对简单,管屏中各并联管子的结构与热负荷差异相对较小,更由于这些循环回路的设计中决不允许出现停滞与倒流,所以并不存在多解的问题。




电锅炉自然循环原理
电锅炉自然循环原理
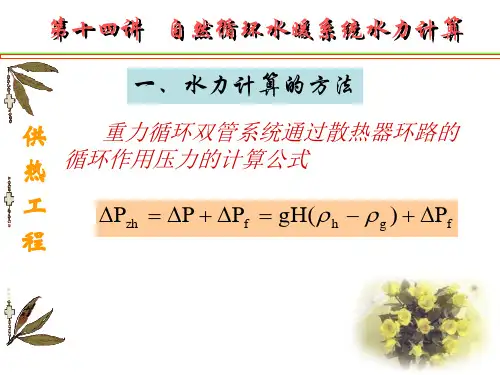
1. 运动压头:自然循环回路的循环推动力叫做循环运动压头,等于回路各部分的总压头。
计算公式: (12-1)
2. 运动压头的三要素:饱和汽和饱和水的密度、上升管中的含汽率、循环回路的高度。
3. 有效压头:运动压头减去上升管侧阻力是有效压头,在数值上等于下降管侧阻力。
计算公式: (12-3)
4. 有效压头和下降管阻力不是一个概念,有效压头是流动的动力;下降管阻力是流动阻力,两者只是在数量上相等。
汽水混合物的流型和传热
管中汽水两相流的流型分为3种:
1.管中汽水两相流的流型:单相水、汽泡状流、弹状流、环状流、环状带液滴流、液雾流、单相汽。
讲解清楚各个流型的具体形状。
2.在自然循环锅炉的水冷壁中,最多是弹状流。
3.传热区域:液体对流传热、过冷沸腾、饱和核态沸腾、强制水膜对流传热、含水不足、蒸汽对流传热。



采用水动力回路分析法进行自然循环热水锅炉水动力数值计算董芃;徐艳英;兰日华
【期刊名称】《工业锅炉》
【年(卷),期】2006(000)002
【摘要】根据流体力学原理和锅炉水动力计算的基本原则,提出了一种能够直接计算自然循环热水锅炉各循环回路中每根单管水动力特性的自然循环热水锅炉水动力数值计算新方法,即水动力回路分析法,推导得出了基于该方法的水动力计算基本方程组,给出了其数值求解方法及程序框图,并应用该方法对两台自然循环热水锅炉进行了水动力特性计算分析,将其计算结果与按照JB/T8659-1997<热水锅炉水动力计算方法>的图解法分析结果进行比较,证明了水动力回路分析法的正确性和实用性.【总页数】6页(P8-13)
【作者】董芃;徐艳英;兰日华
【作者单位】哈尔滨工业大学能源科学与工程学院,哈尔滨,150001;哈尔滨工业大学能源科学与工程学院,哈尔滨,150001;哈尔滨工业大学能源科学与工程学院,哈尔滨,150001
【正文语种】中文
【中图分类】TK229
【相关文献】
1.自然循环热水锅炉水动力不确定因素分析 [J], 毛博;范武航
2.自然循环锅炉对流管束回路水动力数值计算的水动力压差分析法 [J], 徐艳英;董
芃;兰日华;赵玉江
3.应用Excel进行自然循环热水锅炉水动力计算 [J], 袁良义;李长征;魏继永
4.自然循环锅炉水动力回路分析法 [J], 董芃;徐艳英;兰日华
5.自然循环热水锅炉水动力回路分析法的计算原理 [J], 徐艳英;董芃;兰日华
因版权原因,仅展示原文概要,查看原文内容请购买。
自然循环热水锅炉水动力计算例题A1 锅炉规范额定供热量Q sup:7.0MW额定工作压力P: 1.0MPa回水温度t bac.w:70℃供水温度t hot.w:115℃锅炉为双锅筒、横置式链条炉,回水进入锅筒后分别进入前墙、后墙、两侧墙和对流管束回路中,两侧水冷壁对称布置,前墙和后墙水冷壁在3.2m标高下覆盖有耐火涂料层,如图A -1所示。
图A-1 锅炉简图A2 锅炉结构特性计算A2.1 前墙回路上升管划分为三个区段,第Ⅰ区段为覆盖有耐火涂料层的水冷壁管,第Ⅱ区段为未覆盖有耐火涂料层的水冷壁管,第Ⅲ区段为炉顶水冷壁(图A-2)A2.2 后墙回路上升管划分为二个区段,第Ⅰ区段为覆盖有耐火涂料层的水冷壁管,剩下的受热面作为第Ⅱ区段(图A-3)。
A2.3 侧墙水冷壁回路上升管不分段(图A-4)A2.4 对流管束回路不分段,循环高度取为对流管束回路的平均循环高度,并设对流管束高温区为上升区域(共7排),低温区为下降区(共6排)。
对流管束共有347根,相应的上升管区域根数为191根,下降管区域根数为156根(图A-5)。
对流管束总的流通截面积A o 为:A o =347×0.785×0.0442 = 0.5274 m 2下降管区域流通截面积A dc 为 :A dc =156×0.785×0.0442 = 0.2371 m 2下降管区域流通截面积与对流管束总的流通截面积比A dc / A o 为:4500=5274023710=...o dc A A 其值在推荐值(0.44—0.48)的范围内。
图A-2 前墙水冷壁回路 图A-3 后墙水冷壁回路图A4 侧墙水冷壁图A5对流管束回路A2.5 结构特性数据如表A-1所示表A-1 结构特性数据A3 各循环回路局部阻力系数计算各循环回路局部阻力系数计算结果如表A-2所示。
表A-2 各循环回路局部阻力系数计算A4 各受热面吸热量分配由热力计算得,炉膛水冷壁平均热流密度q av 为107.67kW/m 2,炉膛出口温度为θout.f = 893.6℃,对流管束烟气出口温度θout.conv = 220℃, 对流管束总的受热面积为A o =250.9m 2, (其中上升管区域受热面积为A rs =138.1m 2), 对流管束总吸热量为3109.46kW(其中吸收来自炉膛的辐射吸热量为Q fr =320.5kW)。
设来自炉膛的辐射热被对流管束高温区(即上升管区域)均匀吸收。
设对流管束高温区与低温区分界处的烟气温度为θ (℃), 则θ为:rs of out conv out f out A A t t t t =)lg()lg()lg()lg(... ------θθθθ (A-1)式中: t −对流管束内工质平均温度, ℃。
t 可取为: t=0.5(t hot.w + t bac.w )= 0.5×(115+70) = 92.5 (℃) 则由式(A-1)得:11389250=59259268935922205926893..).lg()..lg().lg()..lg(-- - -- -θ求得: θ = 383.8 (℃)则对流管束下降管区域所吸收的热量Q cd 为:19678=22068932208383×5320463109==...)..(... - - - -- conv out f out conv out cd QQ θθθθ (kW)上升管区域总吸热量Q cr :Q cr = Q - Q cd =3109.46-678.19=2431.27 (kW)表A-3给出了各受热面热量分配结果。
A5 各回路水循环计算A5.1 各回路下降管入口水温的假设t in.dc= 0.5(t hot.w + t bac.w ) = (115+70)/2 = 92.5 (℃)A5.2 各回路中循环流量的假设假设四个回路中循环流量G1、G2、G3所对应的上升管中的流速约为:G1 −对应上升管水速W rs.1约为0.15 (m/s)G2 −对应上升管水速W rs.2约为0.20 (m/s)G3 −对应上升管水速约W rs.3为0.35 (m/s)则:G i = 3600fρW rs.i (i=1,2,3) (kg/h)A rs−上升管流通截面积,m2;W rs.i −假设的上升管水速,m/s;ρ−水的密度,kg/m3;G i −与W rs.i相对应的流量,kg/h。
计算ρ时,对应的温度t可取为:t= (t hot.w + t bac.w)/2 = (115+70)/2 = 92.5(℃)ρ=1008.6263-0.2811t-0.0021921t2 =1008.6263-0.2811×92.5-0.0021921×92.52= 963.87各回路中的循环流量取值如表A-4所示:A5.3 各回路水循环计算A5.3.1 各回路水循环计算结果如表A-5至A-8∆P s , ∆P x j (P a )G (kg/h)图A-6前墙水冷壁回路水循环特性曲线∆P s , ∆P x j (P a )G (kg/h)图A-7后墙水冷壁回路水循环特性曲线表A-8 对流管束水循环计算结果2000022000240002600028000300004670046800G (kg/h)图A-8 侧墙水冷壁回路水循环特性曲线3475034800348503490034950∆P r s , ∆P d c (P a )G (kg/h)图A-9 对流管束水循环特性曲线∆P s , ∆P x j (P a )G (kg/h)A5.4 计算结果由各回路水循环特性曲线, 可以得到在假设的下降管入口水温下, 回路工作点及工作点的流量,结果如表A-9所示。
计算全炉循环倍率:锅炉总的回水量G bac (kg/h)为:h)133778(kg/70)-(1157000860t Q 860G bac =×==Δ K=∑G/G bac =278900/133778=2.085由式(4-18)得,当K>1.0,t in.dc =t hot.w -(t hot.w-t bac.w )/k=115-(115-70)/2.085=93.4℃, 与假设的t in.dc =92.5℃相差在15℃以内。
因此, 计算有效。
A6 循环回路中最低、最高水速的计算以前墙循环回路为例A6.1 回路中受热最弱、最强管各段吸热量计算回路中受热最弱、最强管各段吸热量计算结果如表A-11所示。
表A -11回路中受热最弱、最强管各段吸热量计算结果A6.2 平均工况下管组两端压差确定由图A-6可知,平均工况下管组两端压差 P=44060 Pa A6.3 受热最弱管中两端压差计算管内流量(单根管,截面积为A=0.00152 m2)假设G1 =500(kg/h),G2 = 800(kg/h),G3 = 1200(kg/h),两端压差计算结果见表A-12。
A6.4 受热最强管中两端压差计算管内流量(单根管,截面积为A=0.00152 m2)假设G1 =1000(kg/h),G2 = 1400(kg/h),G3 = 1800(kg/h),两端压差计算结果见表A-13。
表A-12 受热最弱管中两端压差计算结果A6.5 受热最弱管中工作点时水速W rs, min的确定如图A-10a所示, 得到W rs, min为0.1497 (m/s) A6.6 受热最强管中工作点时水速W rs, max的确定如图A-10b所示, 得到W rs, max为0.2702 (m/s)(a)(b)图A-10 受热最弱(a)、最强管(b)中水速的确定∆P s ,m i nW(m/s)∆P s , m a xW (m/s)A7 过冷沸腾的校验以前墙回路为例工作绝对压力: 1.1(MPa)前墙水冷壁管内径: d in= 0.044(m), 管长l = 8.16 (m)上升管出口处倾角为: α=75 oA7.1 管内壁热流密度q n计算A7.1.1 平均工况管管子吸热量Q p=55.74 kW'=πd n l ) = 55.74 / (3.14×0.044×8.16) = 49.44 (kW/m2)q pQ/(n则q n = J×Cβ×q’n按第三章3.5.5节,取J= 0.9。
由第三章式(3-30)计算可得: Cβ=1.225q n = 0.9×1.225×49.44 = 54.50(kW/m2)A7.1.2 受热最弱管管子吸热量Q min = 27.87 kWq n,min=J CβQ min/(πd n l ) = 0.9×1.225×27.87/(3.14×0.044×8.16)=27.25 (kW/m2) A7.1.3 受热最强管管子吸热量Q max=72.47kWq n,max=J CβQ max/(πd n l ) = 0.9×1.225×72.47/(3.14×0.044×8.16)=70.87 (kW/m2)A7.2 管内流速A7.2.1 平均工况管由前计算得W ps=0.202 (m/s)A7.2.2 受热最弱管按第四章4.2.8.2第h规定, W s,min= 0.9×W s,min=0.9×0.1497=0.135 (m/s)A7.2.3 受热最强管按第四章 4.2.8.2第h规定, W s,max= 0.9×W s,max=0.9×0.2702 =0.243(m/s)A7.3 上升管出口水温A7.3.1平均工况管由前计算得: t"ps=133..59 ℃A7.3.2 受热最弱管管内循环流量G min可用内插法求得G min=500+(800-500)/(0.1535-0.0966)×(0.1497-0.0966) = 780(kg/h)t''min,s = t''xj+860Q min/G min = 93.4 +860×27.87/780=124.13(℃) A7.3.3 受热最强管管内循环流量G max可用内插法求得G max= 1000+(1400-1000)/(0.2702-0.1945)×(0.2702-0.1945) =1400(kg/h)t''max,s = t''xj + 860Q max/G max = 93.4 + 860×72.47/1400 = 137.92 (℃) A7.4 过冷沸腾校验按第三章第3.5节中最小安全水速公式(3-26)和(3-28)可计算出工质为除氧水或非除氧水时, 最小安全水速。