胡汉才编著《理论力学》课后习题答案第3章习题解答(精编文档).doc
- 格式:doc
- 大小:1.07 MB
- 文档页数:17

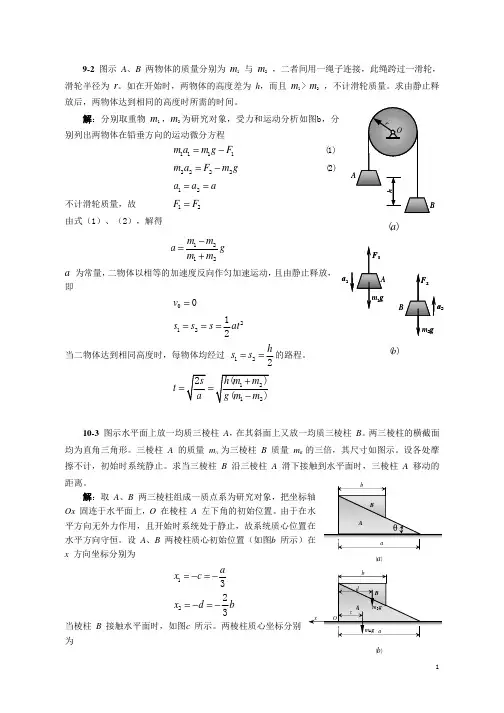

《理论力学》第三章作业参考答案习题3-9解:力F在x 、y 坐标轴上的投影分别为:)(03.169100050301010222N F x =⨯++=)(09.507100050301030222N F y =⨯++=力F作用点的坐标为1500.15x m m m =-=-,(10050)0.15y mm m =+=。
所以,0.15507.090.15169.09101.4(.)Z y x M xF yF N m =-=-⨯-⨯≈-答: 力F对z 轴的力矩为-101.4Nm .习题3-11解:力F在x 、y 、z 坐标轴上的投影分别为:00cos 60cos 304x F F F ==1cos 60sin 304y F F F=-=-FF F Z 2360sin 0-=-=力F的作用点C 的坐标为1sin 302o x r r==,cos 302o y r ==,z h =。
所以,()Fr h F h F r zF yF My z X341412323-=⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛-=-=()F r h F r F h xF zF Mz x y+=⎪⎪⎭⎫ ⎝⎛--⎪⎪⎭⎫ ⎝⎛=-=4323243rF F r F r yF xF Mxy Z214323412-=⎪⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛-=-=答:力F对x 、y 、z 轴的矩分别为:()134h r F -,)4h r F +,12rF-。
习题3-12解:以整个支架为研究对象。
由于各杆为二力杆,球铰链A 、B 、C 处的约束力A F 、B F 、C F 沿杆件连线汇交于D 端球铰链,与物块的重力P构成一空间汇交力系,其受力情况如图所示。
以O 为原点建立坐标系,列平衡方程,我们有⎪⎪⎩⎪⎪⎨⎧===∑∑∑000z y x F F F⎪⎩⎪⎨⎧=-++=++=-015sin 30sin 45sin 30sin 45sin 015cos 30cos 45sin 30cos 45sin 045cos 45cos 000000000000P F F F F F F F F C B A C B A B A 解之得:()()()cos1526.39()2sin 45sin 3015cos1526.39()2sin 45sin 3015cos 3033.46()sin 3015o A o o ooB o o ooC o o P F kN P F kN F P kN ⎧⎪==-⎪⎪⎪==⎨-⎪⎪⎪=-=-⎪-⎩答:铰链A 、B 的约束力均等于26.39kN ,方向与图示相同,即为压力,铰链C 的约束力等于-33.46 kN ,方向与图示相反,即为拉力。


理论力学教科书课后习题及解析第一章偶,大小是260Nm,转向是逆时针。
.求图示平面力系的合成结果,长度单位为m1习题4-习题4-3.求下列各图中平行分布力的合力和对于A点之矩。
A点的矩是:(1) 解:平行力系对O(1) 解:取点为简化中心,求平面力系的主矢:B取点为简化中心,平行力系的主矢是:求平面力系对点的主矩:O 点的主矩是:B 平行力系对B RB向点简化的结果是一个力,且:M和一个力偶合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力(2) B.理论力学教科书课后习题及解析A,且:M向A点简化的结果是一个力如图所示;R和一个力偶A如图所示;将,使满足:d R向下平移一段距离B的大小等于载荷分布的其几何意义是:。
R最后简化为一个力R,大小等于R B,使满足:d R将向右平移一段距离A矩形面积,作用点通过矩形的形心。
A(2) 取点为简化中心,平行力系的主矢是:的大小等于载荷分布的R。
其几何意义是:RR最后简化为一个力,大小等于A三角形面积,作用点通过三角形的形心。
点的主矩是:A平行力系对.理论力学教科书课后习题及解析列平衡方程:。
.求下列各梁和刚架的支座反力,长度单位为习题4-4m解方程组:反力的实际方向如图示。
校核:解:(1) 研究AB杆,受力分析,画受力图:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:理论力学教科书课后习题及解析(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:列平衡方程:反力的实际方向如图示。
校核:解方程组:结果正确。
.理论力学教科书课后习题及解析反力的实际方向如图示。
校核:结果正确。
的约束反力A.重物悬挂如图,已知习题4-5G=1.8kN,其他重量不计;求铰链和杆BC所受的力。
列平衡方程:解方程组:BC是二力杆),画受力图:研究整体,受力分析((1) 解:反力的实际方向如图示。
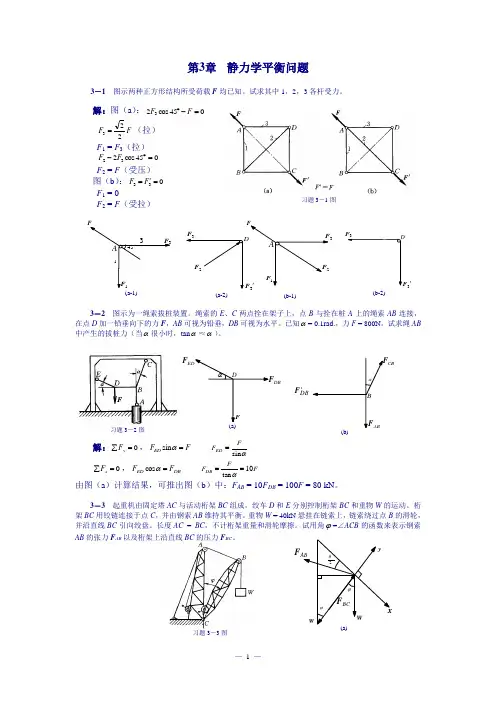
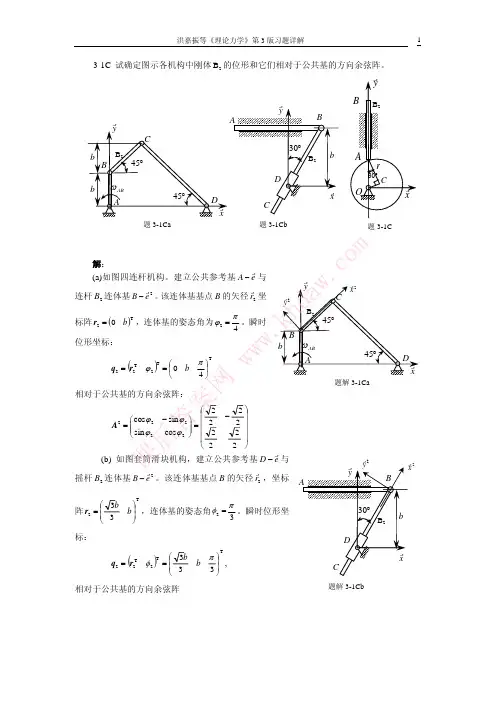
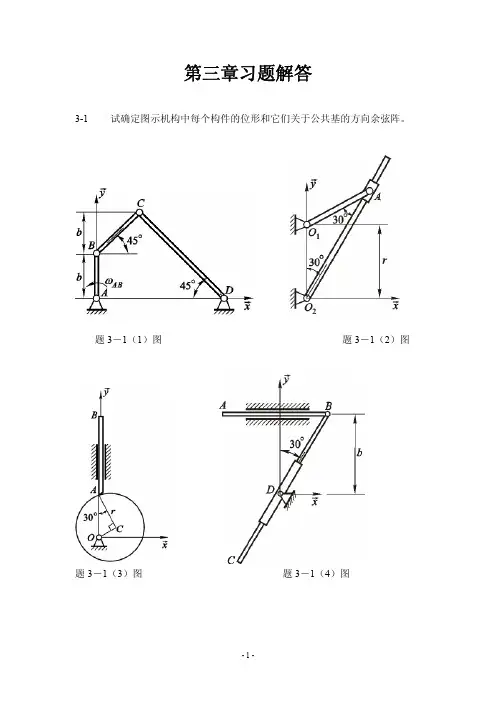
EDF DDBF Fα(a)αCBF BDBF 'ABF (b)习题3-3图第3章 静力学平衡问题3-1 图示两种正方形结构所受荷载F 均已知。
试求其中1,2,3各杆受力。
解:图(a ):045cos 23=-︒F FF F 223=(拉) F 1 = F 3(拉) 045cos 232=︒-F F F 2 = F (受压) 图(b ):033='=F F F 1 = 0F 2 = F (受拉)3-2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上,点B 与拴在桩A 上的绳索AB 连接,在点D 加一铅垂向下的力F ,AB 可视为铅垂,DB 可视为水平。
已知α= 0.1rad.,力F = 800N 。
试求绳AB 中产生的拔桩力(当α很小时,tan α≈α)。
解:0=∑y F ,F F ED =αsin αsin FF ED = 0=∑x F ,DB ED F F =αcos F FF DB 10tan ==α由图(a )计算结果,可推出图(b )中:F AB = 10F DB = 100F = 80 kN 。
3-3 起重机由固定塔AC 与活动桁架BC 组成,绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ,并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上,链索绕过点B 的滑轮,并沿直线BC 引向绞盘。
长度AC = BC ,不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
AF3F 2F 1F(b-1)习题3-1图F3F451F A 13(a-1)3F 2F D'3F(a-2)D3F '3F(b-2)习题3-2图ABF WBCF ϕW x2θyϕ习题3-5图习题3-4图 解:图(a ):0=∑x F ,0sin 2cos=-ϕϕW F AB ,2sin2ϕW F AB =0=∑y F ,02sin cos =---ϕϕAB BC F W W F即 2sin 2cos 2ϕϕW W W F BC ++=W W W W 2)cos 1(cos =-++=ϕϕ3-4 杆AB 及其两端滚子的整体重心在G 点,滚子搁置在倾斜的光滑刚性平面上,如图所示。


第一章 静力学基本概念
1-1 考虑力对物体作用的运动效应,力是( A )。
A.滑动矢量
B.自由矢量
C.定位矢量
1-2 如图1-18所示,作用在物体A 上的两个大小不等的力1F 和2F ,沿同一直线但方向相
反,则其合力可表为( C )。
A.1F –2F
B.2F - 1F
C.1F +2F
图1-18 图1-19 1-3 F =100N ,方向如图1-19所示。
若将F 沿图示x ,y 方向分解,则x 方向分力的大小 x F = C N ,y 方向分力的大小y F = ___B __ N 。
A. 86.6
B. 70.0
C. 136.6
D.25.9
1-4 力的可传性只适用于 A 。
A. 刚体
B. 变形体
1-5 加减平衡力系公理适用于 C 。
A. 刚体;
B. 变形体;
C. 刚体和变形体。
1-6 如图1-20所示,已知一正方体,各边长a ,沿对角线BH 作用一个力F ,则该力在x 1轴上的投影为 A 。
A. 0
B. F/2
C. F/6
D.-F/3
1-7如图1-20所示,已知F=100N ,则其在三个坐标轴上的投影分别为: Fx = -402N ,Fy = 302N ,Fz = 502 N 。
图1-20 图1-21。
力学第三章答案————————————————————————————————作者:————————————————————————————————日期:3.5.1 质量为2kg 的质点的运动学方程为j t t i t r ˆ)133(ˆ)16(22+++-=ρ(单位:米,秒), 求证质点受恒力而运动,并求力的方向大小。
解:∵j idt r d a ˆ6ˆ12/22+==ρρ, j i a m F ˆ12ˆ24+==ρρ为一与时间无关的恒矢量,∴质点受恒力而运动。
F=(242+122)1/2=125N ,力与x 轴之间夹角为:'34265.0/︒===arctg F arctgF x y α3.5.2 质量为m 的质点在o-xy 平面内运动,质点的运动学方程为:j t b i t a r ˆsin ˆcos ωω+=ρ,a,b,ω为正常数,证明作用于质点的合力总指向原点。
证明:∵r j t b it a dt r d a ρρρ2222)ˆsin ˆcos (/ωωωω-=+-== r m a m F ρρρ2ω-==, ∴作用于质点的合力总指向原点。
3.5.3 在脱粒机中往往装有振动鱼鳞筛,一方面由筛孔漏出谷粒,一方面逐出秸杆,筛面微微倾斜,是为了从较低的一边将秸杆逐出,因角度很小,可近似看作水平,筛面与谷粒发生相对运动才可能将谷粒筛出,若谷粒与筛面静摩擦系数为0.4,问筛沿水平方向的加速度至少多大才能使谷物和筛面发生相对运动?解:以地为参考系,设谷物的质量为m ,所受到的最大静摩擦力为 mg f oμ=,谷物能获得的最大加速度为2/92.38.94.0/s m g m f a o =⨯===μ ∴筛面水平方向的加速度至少等于3.92米/秒2,才能使谷物与筛面发生相对运动。
μ1 μ23.5.3 题图 3.5.4题图3.5.4 桌面上叠放着两块木板,质量各为m 1 ,m 2,如图所示,m 2和桌面间的摩擦系数为μ2,m 1和m 2间的摩擦系数为μ1,问沿水平方向用多大的力才能把下面的木板抽出来。
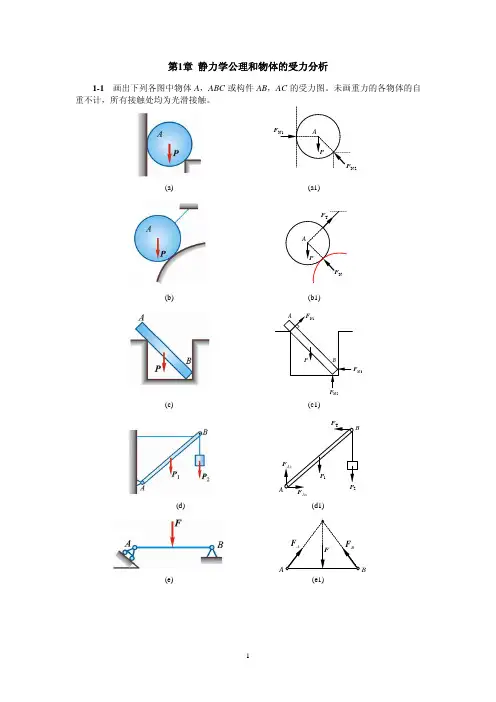
理论力学(郝桐生)第一章习题1-1.画出下列指定物体的受力图。
解:习题1-2.画出下列各物系中指定物体的受力图。
解:习题1-3.画出下列各物系中指定物体的受力图。
解:第二章习题2-1.铆接薄钢板在孔心A、B和C处受三力作用如图,已知P1=100N沿铅垂方向,P2=50N沿AB方向,P3=50N沿水平方向;求该力系的合成结果。
解:属平面汇交力系;合力大小和方向:习题2-2.图示简支梁受集中荷载P=20kN,求图示两种情况下支座A、B的约束反力。
解:(1)研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:(2) 研究AB,受力分析:画力三角形:相似关系:几何关系:约束反力:习题2-3.电机重P=5kN放在水平梁AB的中央,梁的A端以铰链固定,B端以撑杆BC支持。
求撑杆BC所受的力。
解:(1)研究整体,受力分析:(2) 画力三角形:(3) 求BC受力习题2-4.简易起重机用钢丝绳吊起重量G=2kN的重物,不计杆件自重、磨擦及滑轮大小,A、B、C三处简化为铰链连接;求杆AB和AC所受的力。
解:(1) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆受拉,BC杆受压。
(2) 研究铰A,受力分析(AC、AB是二力杆,不计滑轮大小):建立直角坐标Axy,列平衡方程:解平衡方程:AB杆实际受力方向与假设相反,为受压;BC杆受压。
习题2-5.三铰门式刚架受集中荷载P作用,不计架重;求图示两种情况下支座A、B的约束反力。
解:(1) 研究整体,受力分析(AC是二力杆);画力三角形:求约束反力:(2) 研究整体,受力分析(BC是二力杆);画力三角形:几何关系:求约束反力:习题2-6.四根绳索AC、CB、CE、ED连接如图,其中B、D两端固定在支架上,A端系在重物上,人在E点向下施力P,若P=400N,α=4o,求所能吊起的重量G。
解:(1) 研究铰E,受力分析,画力三角形:由图知:(2) 研究铰C,受力分析,画力三角形:由图知:习题2-7.夹具中所用的两种连杆增力机构如图所示,书籍推力P作用于A点,夹紧平衡时杆AB与水平线的夹角为;求对于工件的夹紧力Q和当α=10o时的增力倍数Q/P。
理论力学习题答案精编W O R D版IBM system office room 【A0816H-A0912AAAHH-GX8Q8-GNTHHJ8】静力学第一章习题答案1-3 试画出图示各结构中构件AB 的受力图1-4 试画出两结构中构件ABCD 的受力图1-5 试画出图a 和b 所示刚体系整体合格构件的受力图1-5a 1-5b1- 8在四连杆机构的ABCD 的铰链B 和C 上分别作用有力F 1和F 2,机构在图示位置平衡。
试求二力F 1和F 2之间的关系。
解:杆AB ,BC ,CD 为二力杆,受力方向分别沿着各杆端点连线的方向。
解法1(解析法)假设各杆受压,分别选取销钉B 和C 为研究对象,受力如图所示:由共点力系平衡方程,对B 点有:对C 点有:解以上二个方程可得:221362F F =F 2F BCF ABB45oyxF BCF CDC 60oF 130oxy解法2(几何法)分别选取销钉B 和C 为研究对象,根据汇交力系平衡条件,作用在B 和C 点2F =对C 点由几何关系可知: 0130cos F F BC =解以上两式可得:2163.1F F =静力学第二章习题答案2-3 在图示结构中,二曲杆重不计,曲杆AB 上作用有主动力偶M 。
试求A 和C 点处的约束力。
解:BC 为二力杆(受力如图所示),故曲杆AB 在B 点处受到约束力的方向沿BC 两点连线的方向。
曲杆AB 受到主动力偶M 的作用,A 点和B 点处的约束力必须构成一个力偶才能使曲杆AB 保持平衡。
AB 受力如图所示,由力偶系作用下刚体的平衡方程有(设力偶逆时针为正):其中:31tan =θ。
对BC 杆有:aM F F F A B C 354.0=== A ,C 两点约束力的方向如图所示。
2-4F CD F AB解:机构中AB 杆为二力杆,点A,B 出的约束力方向即可确定。
由力偶系作用下刚体的平衡条件,点O,C 处的约束力方向也可确定,各杆的受力如图所示。
第三章作业答案3-6 力系中,1F =100 N ,2F =300 N ,3F F=200 N ,各力作用线的位置如图 3-6 所示。
试将力系向原点 O 简化。
图3-63-11 水平圆盘的半径为 r ,外缘 C 处作用有已知力 F 。
力 F 位于铅垂平面内,且与 C 处圆盘切线夹角为 60°,其他尺寸如图 3-11a 所示。
求力 F 对 x ,y ,z 轴之矩。
图3-11解 (1)方法 1,如图 3-11b 所示,由已知得(2)方法23-14 图3-14a 所示空间桁架由杆1,2,3,4,5 和6 构成。
在节点A 上作用1 个力F,此力在矩形ABDC 平面内,且与铅直线成45°角。
ΔEAK =ΔFBM。
等腰三角形EAK,FBM和NDB 在顶点A,B 和D 处均为直角,又EC=CK=FD=DM。
若F=10 kN,求各杆的内力。
图3-14解(1) 节点 A 为研究对象,受力及坐标如图3-14b 所示(2)节点B 为研究对象,受力如图3-14b 所示3-19 图3-19a 所示6 杆支撑1 水平板,在板角处受铅直力F 作用。
设板和杆自重不计,求各杆的内力。
图3-19解截开6 根杆,取有板的部分为研究对象,受力如图3-19b 所示。
3-22 杆系由球铰连接,位于正方体的边和对角线上,如图3-22a 所示。
在节点D 沿对F。
在节点C 沿CH 边铅直向下作用F。
如球铰B,L 和H 是固角线LD 方向作用力D定的,杆重不计,求各杆的内力。
图3-22解(1)节点D 为研究对象,受力如图3-22b 所示(2)节点C 为研究对象,受力如图3-22b 所示3-25 工字钢截面尺寸如图3-25a 所示,求此截面的几何中心。
图3-25解把图形的对称轴作轴x,如图3-25b 所示,图形的形心C 在对称轴x 上,即第五章作业答案5-3 如图 5-3 所示,半圆形凸轮以等速o v = 0.01m/s 沿水平方向向左运动,而使活塞杆 AB 沿铅直方向运动。
【最新整理,下载后即可编辑】
3-3在图示刚架中,已知kN/m
3
=
m
q,2
6
=
F kN,m
kN
10⋅
=
M,不计刚架自重。
求固定端A处的约束力。
m
kN
12
kN
6
0⋅
=
=
=
A
Ay
Ax
M
F
F,
,
3-4杆AB及其两端滚子的整体重心在G点,滚子搁置在倾斜的光滑刚性平面上,如图所示。
对于给定的θ角,试求平衡时的β角。
A
θ
3
l
G
β
G
θ
B
B
F
A
R
F3
2l
O
解:解法一:AB为三力汇交平衡,如图所示ΔAOG中
β
sin
l
AO=,θ-︒
=
∠90
AOG,β-︒
=
∠90
OAG,β
θ+
=
∠AGO
由正弦定理:
)
90
sin(
3
)
sin(
sin
θ
β
θ
β
-
︒
=
+
l
l,
)
cos
3
1
)
sin(
sin
θ
β
θ
β
=
+
l
即β
θ
β
θ
θ
βsin
cos
cos
sin
cos
sin
3+
=
即θ
βtan
tan
2=
)
tan
2
1
arctan(θ
β=
解法二::
=
∑
x
F,0
sin
R
=
-θ
G
F A(1)
=
∑
y
F,0
cos
R
=
-θ
G
F B(2)
)(=∑F A M ,0
sin )sin(3
R =++-β
βθl F l
G B (3)
解(1)、(2)、(3)联立,得
)tan 2
1
arctan(θβ=
3-5 由AC 和CD 构成的组合梁通过铰链C 连接。
支承和受力如图所示。
已知均布载荷强度kN/m 10=q ,力偶矩m kN 40⋅=M ,不计梁重。
kN 15kN 5kN 40kN 15===-=D C B A F F F F ;;;
解:取CD 段为研究对象,受力如图所示。
0)(=∑F C M ,024=--q M F D ;kN 15=D F 取图整体为研究对象,受力如图所示。
0)(=∑F A M ,01682=--+q M F F D B ;kN 40=B F 0=∑y F ,04=+-+D B Ay F q F F ;kN 15-=Ay F 0=∑x F ,0=Ax F
3-6如图所示,组合梁由AC 和DC 两段铰接构成,起重机放在梁上。
已知起重机重P1 = 50kN ,重心在铅直线EC 上,起重载荷P2 = 10kN 。
如不计梁重,求支座A 、B 和D 三处的约束反力。
解:(1)取起重机为研究对象,受力如图。
0)(=∑F F M ,0512P R =--W F F G ,kN 50R =G F
(2)取CD 为研究对象,受力如图
0)(=∑F C M ,016'R R =-G D F F ,kN 33.8R =D F
(3)整体作研究对象,受力图(c ) 0)(=∑F A M ,0361012R P R =+--B D F F W F ,kN 100R =B F
0=∑x F ,0=Ax F
0=∑y F ,kN 33.48-=Ay F
3-7 构架由杆AB,AC和DF铰接而成,如图所示。
在DEF杆上作用一矩为M的力偶。
不计各杆的重量,求AB杆上铰链A,D 和B所受的力。
3-8 图示构架中,物体P 重1200N ,由细绳跨过滑轮E 而水平系于墙上,尺寸如图。
不计杆和滑轮的重量,求支承A 和B 处的约束力,以及杆BC 的内力F BC 。
解:(1)整体为研究对象,受力图(a ),W F =T 0=∑A M ,0)5.1()2(4T R =--+-⋅r F r W F B ,N 1050R =B F 0=∑x F ,N 1200T ===W F F Ax 0=∑y F ,N 501=Ay F
(2)研究对象CDE (BC 为二力杆),受力图(b ) 0=∑D M ,0)5.1(5.1sin T =-+⋅+⨯r F r W F BC θ
N 15005
41200
sin -=-=-=
θ
W F BC (压力)
3-9 图示结构中,A 处为固定端约束,C 处为光滑接触,D 处为铰链连接。
已知
N
40021==F F ,m N 300⋅=M ,mm 400==BC AB ,
mm 300==CE CD ,︒=45α,不计各构件自重,求固定端A 处与铰链
D 处 的约束
力。
3-10 图示结构由直角弯杆DAB与直杆BC、CD铰接而成,并在A 处与B处用固定铰支座和可动铰支座固定。
杆DC受均布载荷q 的作用,杆BC受矩为2qa
M 的力偶作用。
不计各构件的自重。
求铰链D受的力。
3-11 图示构架,由直杆BC,CD及直角弯杆AB组成,各杆自重
不计,载荷分布及尺寸如图。
在销钉B上作用载荷P。
已知q、a、
M、且2qa
M 。
求固定端A的约束力及销钉B对BC杆、AB杆的作用力。
3-12无重曲杆ABCD有两个直角,且平面ABC与平面BCD垂直。
杆的D端为球铰支座,A端为轴承约束,如图所示。
在曲杆的AB、BC和CD上作用三个力偶,力偶所在平面分别垂直于AB、BC和CD三线段。
已知力偶矩M
2
和M3 ,求使曲杆处于平衡的力偶矩
M
1和D
A、处的约束力。
解:如图所示:ΣF x = 0,F Dx = 0
ΣM y = 0,012=⋅-d F M Az ,1
2d M F
Az
=
ΣF z = 0,1
2d M F
Dz
-
=
ΣM z = 0,013=⋅+d F M Ay ,1
3
d
M F Ay -= ΣF y = 0,1
3
d M F
Dy
=
ΣM x = 0,0231=⋅+⋅--d F d F M Az Ay ,21
231
3
1M d
d M d d M += 3-13在图示转轴中,已知:Q=4KN ,r=0.5m ,轮C 与水平轴AB 垂直,自重均不计。
试求平衡时力偶矩M 的大小及轴承A 、B 的约束反力。
解:Σm Y =0, M -Qr=0, M=2KN ·m
ΣY=0, N AY =0
Σmx=0, N Bz ·6-Q ·2=0, N BZ =4/3KN
Σmz=0, N BX =0 ΣX=0, N AX =0
ΣZ=0, N AZ +N Bz -Q=0,N AZ =8/3KN
3-14匀质杆AB 重Q 长L ,AB 两端分别支于光滑的墙面及水平地板上,位置如图所示,并以二水平索AC 及BD 维持其平衡。
试求(1)墙及地板的反力;(2)两索的拉力。
解:ΣZ=0 N B =Q
Σmx=0
N B ·BDsin30°-Q ·2
1BDsin30°-Sc ·BDtg60°=0
Sc=0.144Q Σm Y =0
-N B ·BDsin60°+Q ·2
1BDsin60°+N A ·BDtg60°=0
N A =0.039Q
ΣY=0 -S B cos60°+Sc=0 S B =0.288Q
3-15 平面悬臂桁架所受的载荷如图所示。
求杆1,2和3的内力。
3-16 平面桁架的支座和载荷如图所示。
ABC为等边三角形,E,
F为两腰中点,又AD=DB。
求杆CD的内力
F。
CD
解:ED 为零杆,取BDF 研究,F CD =-0.866F
3-17 桁架受力如图所示,已知kN 101=F ,kN 2032==F F 。
试求桁
架4,5,7,10各杆的内力。
3-18 平面桁架的支座和载荷如图所示,求杆1,2和3的内力。
3-19 均质圆柱重P、半径为r,搁在不计自重的水平杆和固定斜面之间。
杆端A为光滑铰链,D端受一铅垂向上的力F,圆柱上作用一力偶。
如图所示。
已知P
F=,圆柱与杆和斜面间的静滑动摩擦系数皆为f S=0.3,不计滚动摩阻,当︒
α时,AB=BD。
求
=45
此时能保持系统静止的力偶矩M的最小值。
3-20 如图所示,A块重500N,轮轴B重1000N,A块与轮轴的轴以水平绳连接。
在轮轴外绕以细绳,此绳跨过一光滑的滑轮D,在绳的端点系一重物C。
如A块与平面间的摩擦系数为0.5,轮轴与平面间的摩擦系数为0.2,不计滚动摩阻,试求使系统平衡时物体C的重量P的最大值。