奥数-整式加减-第二讲教师版
- 格式:docx
- 大小:634.00 KB
- 文档页数:6

第二讲整式的加减代数式的概念1.代数式由数和表示数的字母经过有限次加、减、乘、除、乘方和开方等代数运算所得的数学表达式,称为代数式。
单独的一个数或一个字母也是代数式。
例如:22, 0,,,323a ab -+等等都是代数式2.单项式像262100,6,, 2.5,,t a a b c x vt n -,这些式子都是数或字母乘积的形式,我们把这样的代数式叫做单项式单项式中的数字因数叫做这个单项式的系数。
判断单项式的系数时,应将单项式拆成数字与字母的乘积。
例如:100100t t =⨯,系数是;1vt vt =⨯,系数;是1n n -=-⨯,系数是单项式中不同字母的个数叫做这个单项式的元数。
例如:3abc 的元数是,6a 2的元数是一个单项式中,所有字母的指数的和叫做这个单项式的次数。
例如,在单项式100t 中,字母t 的指数是,100t 是次单项式;在单项式v 2t 中,字母v 与t 的指数之和是,v 2t 是次单项式注意:(1)单项式表示数字与字母,字母与字母相乘时,一般把乘号“×”写作“·”或干脆不写。
单项式表示数字与字母相乘时,我们通常把数字写在最前面,字母则根据情况依次排在后面(2)相同的字母必须写成指数的形式,例如:6a 2b 不能写成6aab 的样子(3)单独的一个常数或一个字母都是单项式,但我们一般不讨论常数的系数和次数(4)单项式的系数包括前面的符号,例如:-5ab 2的系数是-5,而不是5(5)单项式系数为分数时,不能写成带分数,例如:113x应写成43x,也可写成43x(6)单项式的系数是1或-1时,应该省略1不写。
例如:1x2y3的系数是1,应写为x2y3;-1abc的系数是-1,应写为-abc(7)圆周率不是字母,而是一个数(8)从概念来说,单项式的系数不可能是0(9)除以一个常数可以看成乘以它的倒数,但是除数中不能有字母。
例如x÷3可以写为13 x,仍然是单项式,但是3x不是单项式3.同类项像100t与-2t,3x2与2x2,3ab2与-4ab2这样,如果两个单项式所含字母相同,并且相同字母的次数也相同,我们就称这两个单项式为就称这两个单项式为同类单项式,简称同类项。




第二讲 代数式化简与求值代数式是用基本运算符号,将数和表示数的字母连接而成的式子。
代数式的变形、推导、求值是整个初中数学代数部分的基本功。
它综合了数学中的各种常见方法和技巧,既要求我们对基本的公式及其变形要熟记,同时也要灵活掌握各种解题方法,学会分析代数式条件,建立已知和求解之间的关系,为将来进一步的数学思维的培养打下基础。
当然,这部分内容也是初中竞赛常考的内容之一。
一、 基础知识●代数式定义1 用基本运算符号(加、减、乘、除、乘方、开方)把数或表示数的字母连结而成的式子叫做代数式。
单独一个数或字母也是代数式。
● 代数式的值定义2 用数值代替代数式里的字母,计算后所得的结果叫做代数式的值。
● 列代数式列代数式的关键是正确地分析数量关系,要掌握和、差、积、商、幂、倍、分、大、小、多、少、增加、增加到等数学概念和有关知识。
列代数式实质上是把“文字语言”翻译成“符号语言”。
● 求代数式的值代数式的值由它所含字母的取值决定,并随字母取值的改变而改变,字母取不同的值,代数式的值可能同也可能不同。
代数式中所含字母取值时,不能使代数式无意义。
求代数式的值的一般步骤是(1)代入,(2)计算。
二、 例题第一部分 列代数式 例1. 轮船在静水中的速度是每小时a 千米,水流速度为每小时b 千米(b<a),甲乙两码头间相距S 千米,则轮船在甲乙两码头间往返一趟的平均速度为每小时 千米。
分析:轮船在甲乙两码头间往返一趟的平均速度应为往返一趟的总路程除以总时间。
解 因为轮船在静水中的速度是每小时a 千米,水流速度为每小时b 千米(b<a)则轮船的顺流速度为(a+b)千米,逆流速度为(a-b)千米,所以顺流所用时间是b a +S逆流所用时间是b a -S,轮船在甲乙两码头间往返一趟的平均速度为往返路程的和除以往返所用时间的和,即ab a ba Sb a S 222S-=-++评注:顺流速度=静水中的速度+水流速度;逆流速度=静水中的速度-水流速度。

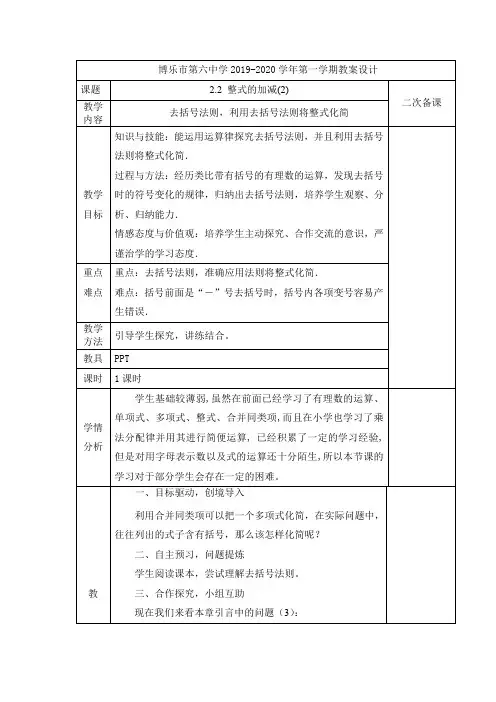

课题 2.2整式的加减(2)主备人符亚兵课型新授课教学目标知识与技能:掌握去括号法则,运用法则,能按要求正确去括号.过程与方法:通过去括号法则的推导,培养学生观察能力和归纳能力;通过去括号法则的应用,培养学生全方位考虑问题的能力.情感态度价值观:让学生体验在数学学习活动中充满了探索与创造,在探索中学会与人合作、交流,在探索中体验成功的快乐.教学资源多媒体重点难点去括号法则及其应用;括号前面是“—”号,去括号时括号内各项要变号的理解及应用.教学过程环节时间教师活动学生活动设计意图动态修改复习提问创设情境讲授新课1.同类项2.合并同类项法则3.你记得乘法分配律吗?用字母怎样表示?4.小黑板练习:计算(1)12×(16-23)(2)-12×(14-13)注意项数和各项的符号,为什么会出现这种情况呢?这个就是我们这节课要来研究的问题归纳:(1)、以上练习中的括号怎么了?(2)、去括号后,括号内的符号和数字有何变化?A层学生回答B层学生回答用字母表示为:a(b+c)=ab+ac学生小组讨论牢固基础为本节课打基础问题引入本节课知识点培养小组合作意识,分层教学4.用“+”,“-”号填空,使等式成立。
⑴13+(7-5)= 13 7 5⑵13-(7-5)=137 5⑶9a+(6a-b)=9a 6a b(4 9a-(6a+b)= 9a6a b环节时间教师活动学生活动设计意图动态修改例题讲解巩固练习小结作业如果括号外的因数是正数,去括号后原括号内的各项的符号与原来的符号相同。
如果括号外的因数是负数,去括号后原括号内的各项的符号与原来的符号相反。
教材66页例4例5-5a+(3a-2)-(3a-7)a-(2a+b)+2(a-2b)练习册相应习题通过本节课学习有何收获?P67 练习第1 、2题学生理解性记忆学会应用去括号法则A层学生回答B层学生回答A,B层学生共同总结培养学生应用意识巩固学生学习新知培养学生总结归纳问题(1)8a+2b+(5a-b)(2)(5a-3b)-3(a2-2b)()()x y z x y z x y z+-+-+---222(2)(2)a ab b a ab b++--+2223(2)2(32)x y y x---板书设计2.2整式的加减(2)1.探究2.去括号法则3. 例题4.练习教学后记去括号这节内容,看似容易,实际上是学生最易出错的地方。

【知识提要】⎧⎧⎪⎪⎪⎪⎪⎪⎧⎪⎪⎨⎨⎪⎩⎨⎪⎪⎪⎧⎪⎪⎨⎪⎪⎩⎩⎪⎪⎩代数式单项式定义、次数、系数单项式整式同类项整式加减多项式定义多项式项、常数项、次数整式运算--取(添)括号、合并同类项【例题精讲】一、整式Ⅰ:代数式代数式的定义:用基本的运算符号(加、减、乘、除、乘方等)把数或表示数的字母连结而成的式子叫做代数式.单独的一个数或字母也是代数式.【例 1】 指出下列各式,哪些是代数式,哪些不是代数式?(1)21x + (2)23ab (3)0 (4)10n a ⨯ (5)a b b a +=+ (6)32> (7)2S R π= (8)347+= (9)π【解析】 (1)、(2)、(3)、(4)、(9)是代数式,其它的不是代数式.首先根据代数式定义可知,代数式是用基本的运算符号连接而成的式子,单独的数字或字母也是代数式;其次代数式当中不含有等号或不等号.Ⅱ:单项式单项式: 像2a -,2r π,213x y -,abc -,237x yz ,……这些代数式中,都是数字与字母的积,这样的代数式称为单项式.也就是说单项式中不存在数字与字母或字母与字母的加、减、除关系,特别的单项式的分母中不含未知数.单独的一个字母或数也叫做单项式,例:a 、3-.单项式的次数:是指单项式中所有字母的指数和.例如:单项式212ab c -,它的指数为1214++=,是四次单项式.单独的一个数(零除外),它们的次数规定为零,叫做零次单项式.单项式的系数:单项式中的数字因数叫做单项数的系数.例如:我们把47叫做单项式247x y 的系数.同类项: 所含字母相同,并且相同字母的指数也分别相同的项叫做同类项.【例 2】 写出下列单项式的系数和次数:第二讲有 整 式【解析】 答案如下表【例 3】 单项式113a b a x y +--与23x y 是同类项,求a b -的值.【解析】 根据题意可知2a b +=,11a -=,所以2a =,0b =,2a b -= 【例 4】 若3m m ma b -与n nab 是同类项,求2003()n m -的值.【解析】 根据题意可知1m =,3m n -=,2n =,所以20032003()(21)1n m -=-=【例 5】 若0.11a b a b x y +--与1359a x y -是同类项,求a ,b 的值.【解析】 根据题意有:1a b a +=-,3a b -=,可得2a =,1b =- Ⅲ:多项式多项式: 几个单项式的和叫做多项式.例如:27319x x -+是多项式.多项式的项: 其中每个单项式都是该多项式的一个项.多项式中的各项包括它前面的符号.多项式中不含字母的项叫做常数项.多项数的次数:多项式里,次数最高项的次数就是这个多项式的次数. 整式: 单项式和多项式统称为整式.【例 6】 下列各式中,哪些是多项式?并指出它是几次几项式.(1)424215x x +-; (2)2a ab b +; (3)33332a ab b a b ++-; (4)x y x +.【解析】 (1)424215x x +-,是多项式,是四次三项式;(3)33332a ab b a b ++-是多项式,是四次四项式. (2)、(4)有字母在分母上,故不是多项式.【例 7】 将多项式223421x y xy x y -+-按x 的降幂排列,并指出是几次,几项式,并指出系数最小的项. 【解析】 223421x y xy x y -+-按x 的降幂排列为:322241x y x y xy +--,是四次四项式,系数最小项为24xy -.【例 8】 334220.010.13xy x y x y x y ---+是____次_____项式,把它按字母x 的降幂排列成__________________,排列后的第二项系数是____,系数最小的项是_________.【解析】 六,四;342320.10.013xy x y x y x y --+-;0.01-;33xy -【例 9】 把多项式321325x x x --+按x 的降幂排列,并指出是几次,几项式,并指出系数最小的项. 【解析】 原式322531x x x =-+-+,是三次四项式;系数最小的项为:3x - 【例 10】 把下列多项式按x 降幂排列,并指出是几次,几项式,并指出系数最小的项:(1)322132187y xy x y x y ---; (2)2233521xy x y x y y ---+-【解析】 (1)原式322187213x y x y xy y =---+,是四次四项式;系数最小的项为:318x y -;(2)原式3225321x y x y xy y =---+-,是四次五项式;系数最小的项为:25x y -.单项式 325x y - 23a b - 0.9mn - 22r π 2x yz - 3x系数次数单项式 325x y - 23a b - 0.9mn - 22r π 2x yz -3x系数 15- 3-0.9- 2π 1- 1次数 5 3 2 2 43二、整式运算合并同类项: 把多项式中同类项合并成一项,叫做合并同类项.合并同类项时,只需把系数相加,所含字母和字母指数不变.【例 1】 下面各式正确的是( )A . 321a a -=B . 6612x x x +=C . 222523x x x -=D . 235325x x x +=【解析】 只有同类项才可以合并,选择C 【例 2】 化简:(1)22228123x y xy x y xy --+(2)3()2()()x y x y y x ----- 【解析】 (1)原式222222812342x y x y xy xy x y xy =--+=-+(2)原式3()2()()2()x y x y x y x y =---+-=-【例 3】 化简下列各式:(1)2222x x x x ----(2)3223225115225363363a b a b ab a b ab ba --+-+++(3)1110.50.20.3n n n n n x x x x x +++--+-【解析】 (1)原式22(1111)4x x =----=-(2)原式322322512513511(5)()(23)63363632a b a b ab a b a b ab =++-++-++-=+++(3)原式11(10.2)(0.510.3)0.80.2n n n n x x x x ++=-+-+-=+ 【例 4】 (1)2235()()2()3()()x y y x y x x y x y +-+-+++-+(2)222()()6()11()a b b a b a a b ---+---【解析】 (1)原式223325()()2()3()()()3()2()x y x y x y x y x y x y x y x y =+-+-+++-+=-+++++ (2)原式2222()()6()11()8()10()a b a b a b a b a b a b =-+-+---=---注意运用整体思想,并注意其中的等价转化,互为相反数的两个数的偶数次幂相等【例 5】 化简:222()3()2()a b a b b a -----【解析】 原式2222()3()2()4()a b a b a b a b =-----=--注意其中的等价转化,互为相反数的两个数的偶数次幂相等【例 6】 化简:2222222243{3[24(2)]}xy x y x y xy xy x y x y xy --+--+- 【解析】 (法1):(由内向外逐层去括号)原式2222222243[3(242)]xy x y x y xy xy x y x y xy =--+--+-2222222222243(33)43639xy x y x y xy x y xy x y x y xy xy x y =--++=--+=- (法2):(由外向内进行)原式22222222433[24(2)]xy x y x y xy xy x y x y xy =---+-+-2222222222223624(2)510239xy x y xy x y x y xy xy x y x y xy xy x y =-+-+-=-+-=- 【例 7】 若323951A a b b =--,233782B a b b =-++.求:(1)2A B +;(2)3B A - 【解析】 (1)32323322(951)(782)A B a b b a b b +=--+-++322331872a b a b b =--(2)23332333(782)(951)B A a b b a b b -=-++---23323219297a b a b b =--++【例 8】 一个多项式加上234253x x x ---得43353x x --,求这个多项式. 【解析】 设这个多项式为A ,则有:23443(253)353A x x x x x +---=--,所以有:43234432353(253)6422A x x x x x x x x =------=--+三、代数式求值【例1】 ⑴若283()034a b -++=,求代数式[]232()ab a ab a -+-的值; ⑵化简求值:1323(1)2(21)4x x x x ⎡⎤--+--+-⎢⎥⎣⎦,其中12x =-;⑶求代数式22532(23)7x x x x ⎡⎤---+⎣⎦的值,其中12x =-; ⑷化简求值:222972(3)a a a a a ⎡⎤+---⎣⎦,其中23a =-. 【解析】 ⑴由283()034ab -++=可知,803a -=且304b +=,从而可知,83a =,34b =-[]232()236()236634ab a ab a ab a ab a ab a ab a a ab -+-=---=--+=-88334()16334=⨯-⨯⨯-=⑵111323(1)2(21)323(1)2(21)53342444x x x x x x x x x x x ⎡⎤--+--+-=----++-=--+++-⎢⎥⎣⎦1924x =-,又12x =-,故原式19119192322()142444x =-=⨯--=--=-⑶2222222532(23)7532(23)75346726x x x x x x x x x x x x x x ⎡⎤---+=-+--=-+--=-+-⎣⎦ 又12x =-,故原式221111262()6672222x x =-+-=-⨯---=---=-⑷222222222972(3)972(3)162315a a a a a a a a a a a a a a a a ⎡⎤+---=+---=--+=+⎣⎦ 又23a =-,故原式22222021515()63333a a =+=⨯--=-=【点评】 以上主要介绍代数式的化简求值.【例2】 ⑴已知代数式235x x ++的值是7时,代数式2392x x +-的值是多少?⑵若2310x x --=,求代数式3223118x x x --+的值;⑶若230x x ++=,求代数式543232210x x x x x +++-的值;⑷已知32c a b =-,求代数式22523c a b a b c ----的值.【解析】 ⑴当2357x x ++=时,232x x +=,所以223923(3)24x x x x +-=+-=.⑵3222231182(31)3(31)1111x x x x x x x x --+=--+--+=;⑶54323222323232210(3)2(3)34103410x x x x x x x x x x x x x x x x x +++-=+++++---=--- 22223(3)33(3)33x x x x x x x x x =-++--=---+=-+++=另外,也可通过230x x ++=得出,23x x +=-,故543232424332210()22()102316x x x x x x x x x x x x x x x x +++-=++++-=--22222222()5()5166155163x x x x x x x x x x x x x x =+-++-=-++-=--=⑷22515236242333c a b a b c ---=⨯--=-=- 【点评】 本例主要介绍整体代入求代数式的值.【例3】 如果a 、b 、c 、d 满足1a bc +=-,25b a -=,22a b d +=, 35a bc +=,求abcd 的值. 【解析】 由1a bc +=-,35a bc +=可知,263a a =⇒=,又25b a -=,故23584b b =+=⇒= 又22a b d +=,35a bc +=,故1c =-,5d =,从而34(1)560abcd =⨯⨯-⨯=-.【例4】 如果1111n na a +=+(1n =,2,…,1996),则11a =时,122320072008...a a a a a a +++的值是多少?【解析】 运用裂项相消的思想即可,由1111n na a +=+及11a =可知,212a =,313a =,…,200812008a =原式=111111111120071(1)()()22320072008223200720082008⨯+⨯+⋯+⨯=-+-+⋯-=. 【例5】 ⑴已知代数式235x x ++的值是7时,代数式2392x x +-的值是多少?⑵若2310x x --=,求代数式3223118x x x --+的值.⑶已知237,4323a b c a b c -+=+-=,求代数式51213a b c +-的值.【解析】 ⑴当2357x x ++=时,232x x +=,所以223923(3)24x x x x +-=+-=.⑵3222231182(31)3(31)1111x x x x x x x x --+=--+--+=.⑶51213(432)2(23)362115a b c a b c a b c +-=+-⨯--+⨯=-=-.【例6】 如果210x x +-=,求代数式3227x x +-的值.【解析】322227(1)(1)66x x x x x x x +-=+-++--=-. 【例7】 如果225a ab +=,222ab b +=-,则224a b -= ,22252a ab b ++= .【解析】 利用整体思想,我们不需要求出a ,b 的值,而只需用已知的代数式将结论表示出来()()22224222a b a ab ab b -=+-+()5229=-⨯-=;22252a ab b ++()()22222a ab ab b =+++()252=⨯+-8=.对于简单的此种类型题目,我们可以靠观察发现变形得出结果,以后的学习中我们将会接触到如何从理论上求得变形过程.【变式1】 已知3a ba b-=+,求代数式2()4()3()a b a b a b a b +---+的值. 【解析】 2()4()1410233()333a b a b a b a b +--=⨯-⨯=--+.【例8】 设1114x y -=,求2322y xy x y x xy +---的值.【解析】 (法1)将原式分子、分母同时除以xy 可得:1112323232421112224y xy x x y y x xy x y ⨯-+⨯++-===------()()(法2)由1114x y -=,知4()xy y x =-,则23232()12()2()22()2()8()y xy x xy y x y x y x y x xy y x xy y x y x +-+--+-===--------.这两种方法都很重要,下面两个巩固再次展现两个方法的妙处.【变式1】 已知3a b =,23a c =,求代数式ab ca b c +++-的值.【解析】 (法1)注意将未知数划归统一,2,33a abc ==,123331233a a aa b c a b c a a a ++++==+-+- (法2)3a b =,223233a c b b ==⨯=,32332a b c b b ba b c b b b++++==+-+-.【例9】 (第15届江苏省竞赛题)已知0a b +=,a b ≠,求b a (1)a ++ab(1)b +的值.【解析】 由0,a b a b +=≠可得,a b 互为相反数,(1)(1)(1)(1)()22b aa b a b a b a b+++=-+-+=-+-=-.【变式2】 如果235x y y x +=-,求2222410623x xy y x y +++的值. 【解析】 2222410623x xy y x y +++461023x yy xx y y x++=+2321023x y y x x y y x⎛⎫++ ⎪⎝⎭=+()251005⋅-+==-.【变式3】 设210020001200(337)2x x a a x a x +-=+++,求b0021982002()S a a a a =++++的值.【解析】 在方程中设1x =,得:0120012a a a =+++ ①令1x =-,得:10001219920072a a a a a =-+--+② ①+②得:1000220017422a a a +=+++③又令0x =,得100072a = ④③-④得:0022002()1S a a a =+++=.【变式】 (无锡市竞赛题)已知()5234501234521x a a x a x a x a x a x -=+++++, ⑴求012345a a a a a a -+-+-的值. ⑵求12345a a a a a ++++的值. ⑶求024a a a ++的值.【解析】 ⑴ 将1x =-代入式子可以得到:50123453243a a a a a a -+-+-=-=-,⑵ 将0x =代入式子可以得到01a =-,将1x =代入式子可以得到:0123451a a a a a a =+++++, 所以123452a a a a a ++++=.⑶ 50123453243a a a a a a -+-+-=-=-,0123451a a a a a a +++++=,两式相加得024121a a a ++=-.。