当前位置：文档之家 › 关于指数函数图象的平移课件

关于指数函数图象的平移课件

  • 格式：ppt
  • 大小：714.50 KB
  • 文档页数：18

下载文档原格式

  / 18

合集下载

2025届高中数学一轮复习课件《指数函数》PPT

2025届高中数学一轮复习课件《指数函数》PPT

第29页
求解与指数函数有关的复合函数问题时，首先要熟知指数函数的定义域、值域、单调性 等相关性质，其次要明确复合函数的构成，当涉及单调性问题时，要借助“同增异减”这一 性质分析判断．
高考一轮总复习•数学
第30页
对点练 4(1)(2024·山东莱芜模拟)已知函数 f(x)＝|－2x－x＋15|，，xx≤>22，， 若函数 g(x)＝f(x)－
解析：∵y＝35x 是 R 上的减函数，∴35－13 >35－14 >350，即 a>b>1，又 c＝32－34 <320 ＝1，∴c<b<a.
高考一轮总复习•数学
第11页
4．(2024·四川成都模拟)若函数 f(x)＝13－x2＋4ax 在区间(1,2)上单调递增，则 a 的取值范 围为___－__∞__，__12_ _．
在(4，＋∞)上单调递增．令12x≤4，得 x≥－2，令12x>4，得 x<－2， 代入外层函数的单调递减区间，得到自变量 x 的取值范围，这才是复合函数的单调递增 区间． 而函数 t＝12x 在 R 上单调递减，所以函数 y＝122x－8·12x＋17 的单调递增区间为[－2， ＋∞)．
高考一轮总复习•数学
所谓“底大图高”，反映指数函数的排列规律．
高考一轮总复习•数学
第8页
1．判断下列结论是否正确． (1)函数 y＝a－x(a>0，且 a≠1)是 R 上的增函数．( ) (2)函数 y＝ax(a>0，且 a≠1)与 x 轴有且只有一个交点．( ) (3)若 am>an，则 m>n.( ) (4)函数 y＝ax 与 y＝a－x(a>0，且 a≠1)的图象关于 y 轴对称．( √ )

人教A版高中数学必修一 《指数函数》指数函数与对数函数PPT(第1课时指数函数的概念、图象及性质)

人教A版高中数学必修一 《指数函数》指数函数与对数函数PPT(第1课时指数函数的概念、图象及性质)
解析：选 C.函数 y＝ax－a(a>0，且 a≠1)的图象恒过点(1，0)， 故可排除选项 A，B，D.
5．求下列函数的定义域和值域： (1)y＝2x－1 4；(2)y＝23 －|x|.
解：(1)要使函数有意义，则 x－4≠0，解得 x≠4.
1
所以函数 y＝2x－4的定义域为{x|x≠4}． 因为x－1 4≠0，所以 2x－1 4≠1，即函数 y＝2x－1 4的值域为{y|y>0，且 y≠1}．
(2)要使函数有意义，则－|x|≥0，解得 x＝0. 所以函数 y＝23 －|x|的定义域为{x|x＝0}． 因为 x＝0，所以23 －|x|＝230＝1，即函数 y＝23 －|x|的值域为{y|y＝ 1}．
本部分内容讲解结束
问题导学 预习教材 P111－P118，并思考以下问题： 1．指数函数的概念是什么？ 2．结合指数函数的图象，分别指出指数函数 y＝ax(a>1)和 y＝ ax(0<a<1)的定义域、值域和单调性各是什么？
1．指数函数的概念 一般地，函数 y＝__a_x__ (a>0，且 a≠1)叫做指数函数，其中 x 是____自_变__量___．
指数函数的图象
根据函数 f(x)＝12x的图象，画出函数 g(x)＝12|x|的图象， 并借助图象，写出这个函数的一些重要性质．
【解】
g(x)＝12|x
|＝12x（x≥0），其图象如图． 2x（x<0），
由图象可知，函数 g(x)的定义域为 R，值域是(0，1]， 图象关于 y 轴对称，单调递增区间是(－∞，0]， 单调递减区间是(0，＋∞)．
■名师点拨 指数函数解析式的 3 个特征
(1)底数 a 为大于 0 且不等于 1 的常数． (2)自变量 x 的位置在指数上，且 x 的系数是 1. (3)ax 的系数是 1.

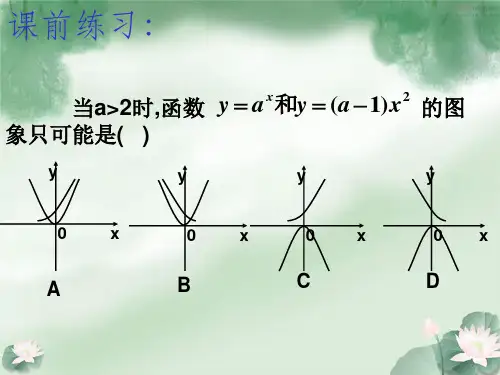
高一必修1-函数图象的变换ppt课件.ppt

高一必修1-函数图象的变换ppt课件.ppt
如:y=f(x)±h的图象可由y=f(x)的图象 _向__上__（__下__）__平__移__h_个__单__位__而得到.
练习： 将直线y=2x+1向左平移5个单位，
得到的函数为__y_=_2_x+_1_1_______
左右平移时，发生变化的仅是x本身，如果x的系 数不是1时，需要把系数提出来，再进行变换.
(6)y=f(|x|)的图象:可先作出y=f(x)当x≥0 时的图象,再利用_偶__函__数__的__图__象__关__于__y_轴__对__称, 作出y=f(x)(x≤0)的图象.
函数y=|log2x|的图象是( A )
解析
f
(x)
|
lo g2
x
|
lo g2
lo
g1
2
x, x x,0
1, x
课前练习：
当a>2时,函数 y ax和y (a 1)x2 的图 象只可能是( )
y
y
y
y
0
x
A
0
x
B
0x
C
0x
D
知识回顾：基本初等函数及图象（大致图象）
函数 一次函数 y=kx+b
图象
二次函数
y=ax2+bx+ c
指数函数 y=ax
对数函数 y=logax
知识回顾：
下列二次函数的图象，是由 抛物线y=x2通过怎样的平移变换得 到的？
y f 1(x) 与y=f(x)的图象关于直线y=x对称.
设奇函数 f(x) 的定义域为[-5, 5], 若当x∈[0, 5]时, f(x)的图象如右图所
示. 则不等式 f(x)<0 的解集
是 (-2, 0)∪(2, 5]

高一数学指数函数ppt课件

高一数学指数函数ppt课件

与对数式的转换、对数运算的性质等。
拓展延伸：挑战更高难度题目
复杂指数函数的性质研究
引入更复杂的指数函数形式，如复合指数函 数、分段指数函数等，探讨它们的性质和应 用。
指数函数在实际问题中的应 用
结合实际问题，如复利计算、人口增长等，展示指 数函数的应用价值，并引导学生运用所学知识解决 实际问题。
指数函数与其他数学知识 的综合应用
指数函数图像特征
当a>1时，图像在x轴上方，且随着x 的增大，y值迅速增大；当0<a<1时， 图像在x轴上方，但随着
当a>1时，指数函数在R上是增函数；当0<a<1时，指数函数在R 上是减函数。
指数函数的值域
指数函数的值域为(0, +∞)。
在解题时，要注意判断题目所给 条件是否满足对称性，以便更好
地应用这一性质。
05 复杂问题解决方 法与策略
分段讨论法在处理复杂问题时应用
分段讨论法概念
将复杂问题按照一定条件分成若 干段，每一段内问题相对简单，
易于解决。
分段讨论法应用
在处理指数函数问题时，当自变量 在不同区间内取值时，函数性质可 能发生变化，此时可以采用分段讨 论法。
数形结合思想概念
将数学中的“数”与“形”结合起来，通过图形 直观展示数量关系，帮助理解问题本质。
数形结合思想应用
在处理指数函数问题时，可以通过绘制函数图像 来观察函数性质，如单调性、周期性等。
数形结合思想优势
通过数形结合可以更加直观地理解问题，提高解 题准确性。
06 总结回顾与拓展 延伸
关键知识点总结回顾
幂的乘方规则
$(a^m)^n = a^{m times n}$，幂的乘方，底 数不变，指数相乘。

3. 指数函数图像

3. 指数函数图像
x x 1 x 1 2 x 0 ,即x 1 ,或x 0 ，
当0 x 1 时，y 0 ;当x 1 时，y 0 , 故选B
4.翻折变化：
1 y f x 去掉y 轴左边图，保 留y 轴右 边图 y f x 将y 轴右边的图像翻折到左边去
① f x ex f x = e x
② f x = e x f x 2 = e x-2
指数函数的图象
知识点
1.当 当0a

1 a
时， 底数a 越大，图象在x 1 时，底数a 越小，图象在x
0
时越接近y 轴，在x 0 0 时越接近x 轴，在x
时越接近x 轴 0 时越接近y 轴
2.平移变换：左加右减
1 f x 向左平移a 个单位 f x a 2 f x 向上平移 a个单位 f x a 3 f x 向右平 移 a个单位 f x a 4 f x 向下平移a个单位 f x a

解析：① 有界性：由函数的定义域得x 0 , A错； 当x 0 时，y 0 ,B错;
② 指数爆炸，当x , y 0 ,D错
例7 函数y x3 x 2 x 的图象大致是

解析：① 奇偶性：f x x3 x 2 x f x ,故函数为奇函数，C错； ② 有界性：令y 0 ,则 x3 x 2 x 0
D. a b 1 d c
例2 已知1 n m 0 ,则指数函数① y mx ,
② y nx 的图象为
例3 已知函数y ax b a 0且 a 1 的图象经过
第二、三、四象限，则有

A. 0 a 1 ,b 1

指数函数图像的变换(采用)ppt课件

指数函数图像的变换(采用)ppt课件
x x ( 2 ) 当 x 0 时，总有 a b 1 ;
x x ( 3 ) 当 x 0 时，总有 0 a b 1 ;
以上时a>1时的情况，那0<a<1是什么样的呢？ x x x 0 . 2,y 0 . 3 与 y 0 . 5 图像， 画出 y 并比较0<a<1 时a对函数图象变化的影响.
特别当x<0时，指数函数的底数越小，函数值减少越快 即0<a<1时，a越小，图像越 “陡”.
综上总结， ya中 ,指数 x 与底数 a 满足以下
x
即a>1时，a越大，图像越“陡”. 即0<a<1时，a越小，图像越 “陡”.
x x
同一 x 下，比较 y a与 y b的大小方法
x
x 正半轴（即 x 0 ），同一 x 下， a 越大， y a 的值
f( x m ) )与 y 推广:比较函数 y f (x 的关系
向左平行移动m个单位长度 y f ( x ) 当m>0时,
yf( x m )
) 向右平行移动|m|个单位长度 yf( x m ) 当m<0时, y fቤተ መጻሕፍቲ ባይዱ(x
作业：
P A 组第 3 题， B 组第 2 题 77
ya中 ,指数 x 与底数 a 满足以下规律
x
即a>1时，a越大，图像越“陡”. 即0<a<1时，a越小，图像越 “陡”.
x x
同一 x 下，比较 y a与 y b的大小方法
x
x 正半轴（即 x 0 ），同一 x 下， a 越大， y a 的值
x x 负半轴（即 x 0 ），同一 x 下， a 越大， y a 的值 .

课件人教A版高中数学必修一《指数函数及其性质》实用PPT课件_优秀版

课件人教A版高中数学必修一《指数函数及其性质》实用PPT课件_优秀版

②利用指数函数y＝au的单调性求得此函数的值域.
2.求形如y＝A·a2x＋B·ax＋C类函数的值域一般用换元法，设ax＝t(t>0)再转
化为二次函数求值域.
反思与感悟
解析答案
跟踪训练 4 (1)函数 f(x)＝ 1－2x＋ x1＋3的定义域为( A )
A.(－3,0]
B.(－3,1]
C.(－∞，－3)∪(－3,0] D.(－∞，－3)∪(－3,1]
(2)对称变换：函数y＝a－x的图象与函数y＝ax的图象关于y轴对称；
函数y＝－a－x的图象与函数y＝ax的图象关于原点对称；
当x＜0时，_________
反思与感悟
解析答案
跟踪训练3 (1)函数y＝|2x－2|的图象是( B )
解析 y＝2x－2的图象是由y＝2x的图象向下平移2个单位长度得到的， 故y＝|2x－2|的图象是由y＝2x－2的图象在x轴上方的部分不变，下方部分 对折到x轴的上方得到的.
过点_(_0_，__1_)_，即x＝_0_时，y＝_1_ 若下向列下 各平函移数φ中(φ，>是0)个指单数位函，数则的得是到( y＝)ax－φ的图象. 性质 跟一踪般训 地练，3函数(1y)＝函a数x y＝|2x－2|的图叫象做是指(数函数) ，其中x是自变量，函数的定义域是R.
当x＞0时，y＞1； 纠(3)错ax心的得系数凡是换1. 元时应立刻写出新元范围，这样才能避免失误.
解析 ∵x2－1≥－1，
解 ∵y＝2－x与y＝2x的图象关于y轴对称，
④中，y＝x3的底为自变量，指数为常数，故④不是指数函数.
其中，指数函数第的个二数章是( 2.1) .2 指数函数及其性质
(3)ax的系数是1.
例2 如图是指数函数①y＝ax，②y＝bx，③y＝cx，④y＝dx的图象，则a，b，c，d与1的大小关系是( )

高中数学指数运算与指数函数课件

高中数学指数运算与指数函数课件

(2)f (x)＝2x2＋x＋1－1 2＝1－2x＋2 1， 因为 2x＋1>1，所以 0<2x＋2 1<2， 即－2<－2x＋2 1<0， 所以－1<1－2x＋2 1<1。 所以 f (x)的值域为(－1,1)。
(3)g(x)为偶函数。 由题意知 g(x)＝f xx＝22xx＋ －11·x， 易知函数 g(x)的定义域为(－∞，0)∪(0，＋∞)， g(－x)＝(－x)·22－ －xx＋ －11＝(－x)·11－＋22xx＝x·22xx－＋11＝g(x)， 所以函数 g(x)为偶函数。
(2)若 f (x)为奇函数，则 f (0)＝0，即 a－20＋2 1＝0，解得 a＝1。 此时 f (－x)＝1－2－x2＋1＝1－12＋·22xx＝－1－2x＋2 1＝－f (x)，故当 a＝1 时，函数 f (x) 为奇函数。 (3)由(2)知 f (x)＝1－2x＋2 1，因为 2x＋1>1，所以 0<2x＋1 1<1， 所以 0<2x＋2 1<2，所以－2<－2x＋2 1<0，所以－1<1－2x＋2 1<1，即－1<f (x)<1，所以 f (x)的值域为(－1,1)。
【解析】 因为 2x>0，所以 2x＋1>1，即|y|>1，又因为曲线|y|＝2x＋1 与 直线 y＝b 没有公共点，所以－1≤b≤1。
【答案】 [－1,1]
方法小结 (1)处理函数图象问题的策略 ①抓住特殊点：指数函数的图象过定点(0,1)。 ②巧用图象变换：函数图象的平移变换(左右平移、上下平移)。 ③利用函数的性质：奇偶性与单调性。
23－x 的图象。
答案 A
[解析] (2)
由题意得[f(x)－2]·[f(x)－a]＝0，所以 f(x)＝2 或 f(x)＝a， 所以|3x－1|＋1＝2 或|3x－1|＋1＝a，所以|3x－1|＝1 或|3x－1|＝a－1， |3x－1|＝1 有一个根，所以方程|3x－1|＝a－1 有两个不同的实根， 函数 y＝|3x－1|的图象如图所示，所以 0<a－1<1，所以 1<a<2.

指数函数及图像.ppt

指数函数及图像.ppt

[规律方法] 1.求含有指数型的函数定义域时，要注意考 虑偶次根式的被开方数大于等于0，分母不为0等限制条件．
2．求含有指数式的复合函数的值域时，要结合指数函数的 单调性和定义域来考虑，不要遗漏了指数函数的值域大于0.
【活学活用 3】 求下列函数的定义域与值域：
(1)y＝
；(2)y＝ 1－3x.
解 (1)由 x－2≥0，得 x≥2.
R.因为5－x>0，所以5－x－1>－1，
所以函数的值域为(－1，＋∞)
课堂小结
1．指数函数的定义域为(－∞，＋∞)，值域为(0，＋∞)，
且f(0)＝1.
2． 当a>1时，a的 值 越 大，图 象 越 靠 近y轴 ，递增速度越 快．当0<a<1时，a的值越小，图象越靠近y轴，递减的速
度越快．
历史ⅱ岳麓版第13课交通与通讯 的变化资料
”；此后十年间，航空事业获得较快发展。
筹办航空事宜
处
三、从驿传到邮政 1．邮政 (1)初办邮政： 1896年成立“大清邮政局”，此后又设 ， 邮传邮正传式部脱离海关。 (2)进一步发展：1913年，北洋政府宣布裁撤全部驿站； 1920年，中国首次参加 万国。邮联大会
2．电讯 (1)开端：1877年，福建巡抚在 架台设湾第一条电报线，成为中国自 办电报的开端。
二、水运与航空
1．水运 (1)1872年,
轮船正招式成商立局，标志着中国新式航运业的诞生。
(2)1900年前后，民间兴办的各种轮船航运公司近百家，几乎都是
在列强排挤中艰难求生。
2．航空
(1)起步：1918年，附设在福建马尾造船厂的海军飞机工程处开始
研制 。
(2)发展水：上1飞918机年，北洋政府在交通部下设“

人教B版(2019)数学必修(第二册)：4.1.2 指数函数的性质与图像 课件(共104张PPT)

人教B版(2019)数学必修(第二册)：4.1.2 指数函数的性质与图像 课件(共104张PPT)

c=0.22.1，则a，b，c的大小关系是( )
A.a<c<b
B.b>a>c
C.b<a<c
D.c>a>b
【解析】选B.a=0.52.1∈(0，1)，b=20.5>1，c=0.22.1， 0.52.1>0.22.1，所以a>c，所以b>a>c.
【加练·固】
已知
a

(
3
)
1 3
,
b

(
3 )
1 4
类型一 指数函数的概念 【典例】1.函数y=(a2-3a+3)·ax是指数函数，则a的值 为________. 2.指数函数y=f(x)的图像经过点(π，e)，则f(-π) =________.
【思维·引】1.根据指数函数的解析式的特征列方程 求解. 2.设出指数函数的解析式，代入点的坐标求f(-π).
A.[3，9] C. [ 1，3]
3
B.[ 1，9]
3
D. [ 1，1]
93
3.已知函数f(x)=ax(a>0，a≠1)在区间[-1，1]上的最 大值与最小值的差是1，则实数a的值为________.
【思维·引】1.根据被开方数大于等于0求定义域. 2.先确定函数的单调性，再求最值. 3.分情况表示出最大值、最小值，列方程求a的值.
【加练·固】
函数y= 1－(1)x 的定义域为________.
3
【解析】因为函数有意义的充要条件是1- (1)x ≥0，则
3
(1)x ≤1，即x≥0，
3
所以函数的定义域为[0，+∞).
第2课时 指数函数的性质与图像的应用

高中数学人教A版必修1《函数的图象变换》PPT

高中数学人教A版必修1《函数的图象变换》PPT

例：作出下列函数的图象． (1)y＝12|x|；(2)y＝|log2(x＋1)|；(3)y＝2xx－－11.
分析：作函数图象的方法有：列表描点法（列表， 描点，连线）和图象变换法(平移变换、对称变换、 翻折变换）
解析：(1)作出 y＝12x 的图象，保留 y＝12x 图象中 x≥0 部分，加上 y＝12x 的图象中 x＞0 部分关于 y 轴的对称部分，
答案：A
课堂总结：
本节课从特殊到一般的思路学习函数图 象的三种变换（平移变换、对称变换、翻 折变换）及其应用。利用图象变换解题， 关键是理清图象变换的过程，掌握好基本 初等函数的图象及变换的实质（要通过具 体的实例作为载体来理解掌握三种变换）。 在后续的学习中我们将进一步学习它的应 用。
谢谢！！！
翻折到y轴左侧，便得到g(x) x2 2 | x | f (| x |)的图象，
（2）画函数h(x) | x2 2x |的图象，并说由函数
f (x) x2 2x的图象怎样变换而得到？
解析：h(
x)
x2
x
2
2x (x 2x (0
0或x x
2) 2)
保留f (x) x2 2x图象在x轴上方部分，把位于x轴下
5
f (x) x2
4
3
2
h(x) x2 - 2
1
又h(x) f (x) 2
-4 -3 -2 -1 o 1 2 3 4 x
g (x) x2 2的图象是由f (x) x2的图象向上平移2个单位得到， h(x) x2 - 2的图象是由f (x) x2的图象向下平移2个单位得到。
平移变换—竖直平移
A．向右平行移动 2 个单位长度 B．向右平行移动 1 个单位长度 C．向左平行移动 2 个单位长度 D．向左平行移动 1 个单位长度

指数函数_优秀课件

指数函数_优秀课件

[巧练模拟]—————(课堂突破保分题，分分必保！)
5．(2012·温州调研)设函数f(x)＝a－|x|(a＞0，且a≠1)，
f(2)＝4，则
()
A．f(－2)＞f(－1)
B．f(－1)＞f(－2)
C．f(1)＞f(2)
D．f(－2)＞f(2)
解析：由a－2＝4，a＞0得a＝12， ∴f(x)＝12－|x|＝2|x|. 又∵|－2|＞|－1|，∴2|－2|＞2|－1|， 即f(－2)＞f(－1)．
答案： (0,1)
[冲关锦囊] 1．与指数函数有关的函数的图象的研究，往往利用相应
指数函数的图象，通过平移、对称变换得到其图象． 2．一些指数方程、不等式问题的求解，往往利用相应的
指数型函数图象数形结合求解.
[精析考题] [例 3] (2011·宁波三校联考)若函数 f(x)＝a|x－2|(a>0，a≠1)满足 f(1)＝13，则 f(x)的单调递减区间是________．
答案：A
[高手点拨] 本题给出三种比较指数幂大小的方法，法一是构造函 数法，利用指数函数性质比较大小，利用这种方法应注意 底数是否大于1；法二与法三两种方法相类似，都是对a、 b、c进行简单变形，转化为同次根式的形式，由被开方数 的大小可得出a、b、c的大小．
答案： [－1，－∞)
5．函数y＝121－x的值域是________． 解析：函数的定义域为R，令u＝1－x∈R，
∴y＝12u>0.
答案：(0，＋∞)
1．分数指数幂与根式的关系 分数指数幂与根式可以相互转化，通常利用分数指数 幂的意义把根式的运算转化为幂的运算，从而简化计 算过程．
2．函数y＝ax、y＝|ax|、y＝a|x|(a>0，a≠1)三者之间的关系 函数y＝ax与y＝|ax|是同一个函数的不同表现形式， 函数y＝a|x|与y＝ax不同，前者是一个偶函数，其图象 关于y轴对称，当x≥0时两函数图象相同．

北师大版高中数学课件第三章 §3 第1课时 指数函数的概念、图象与性质

北师大版高中数学课件第三章 §3 第1课时 指数函数的概念、图象与性质

无意义;
二、指数函数的图象和性质
1.指数函数的图象和性质
a>1
图象
0<a<1
(1)定义域:R
(2)值域:(0,+∞)
(3)过定点(0,1),即x=0时,y=1
(4)当x<0时,0<y<1;
当x>0时,y>1
性质
(5)在R上是增函数
当x值趋近于正无穷大时,函数值
趋近于正无穷大;
当x值趋近于负无穷大时,函数值
方部分,并保留y=f(x)的图象在x轴上及其上方部分即可得到函数y=|f(x)|的
图象.
②将函数y=f(x)的图象在y轴右侧的部分沿y轴翻折到y轴左侧,替代原y轴左
侧部分,并保留y=f(x)的图象在y轴上及其右侧的部分即可得到函数y=f(|x|)
的图象.
(3)利用变换作图法作图要注意以下两点:
①选择哪个指数函数作为起始函数;
数函数既不是奇函数,也不是偶函数.
2.指数函数的图象永远在x轴的上方.底数越大,图象越高,简称“底大图高”.
微判断
判断下列说法是否正确,正确的在后面的括号内画“ ”,错误的画“×”.
(1)指数函数y=mx(m>0,且m≠1)是R上的增函数.(
)
(2)指数函数y=ax(a>0,且a≠1)既不是奇函数,也不是偶函数.(
是
.
解析∵当x+1=0,即x=-1时,f(-1)=a0+3=4恒成立,故函数f(x)=ax+1+3的图象
恒过点(-1,4).
答案(-1,4)
反思感悟 指数型函数图象过定点问题的解法
因为函数y=ax(a>0,且a≠1)的图象恒过点(0,1),所以对于函数

高考数学复习知识点讲义课件25---指数函数的概念及其图象和性质

高考数学复习知识点讲义课件25---指数函数的概念及其图象和性质

答案：(－1，－1) (2)y＝13x＋1＋2＝3－(x＋1)＋2.作函数 y＝3x 的图象关于 y 轴的对称图象得函数 y＝3－x 的图象，再向左平移 1 个单位长度就得到函数 y＝3－(x＋1)的图象，最后再 向上平移 2 个单位长度就得到函数 y＝3－(x＋1)＋2＝13x＋1＋2 的图象，如图所示．
x0 1
2
3
…
y 200 210 220.5 231.525 …
作直线y＝300与函数y＝200(1＋5%)x的图象交于A点，则A(x0,300)，A点的横 坐标x0的值就是函数值y＝300时(木材蓄积量为300万立方米时)所经过的时间x年 的值．
∵8<x0<9，则取x＝9(计划留有余地，取过剩近似值)，即经过9年后，林区的 木材蓄积量能达到300万立方米．
[解析] (1)函数 y＝13x 是指数函数，且 y＝4x 也是指数函数，其它函数不 符合指数函数的三个特征．
(2)设指数函数 fx＝ax，由 f2－f1＝6 得 a2－a＝6，解得 a＝－2(舍去)或 a＝3，则 f3＝33＝27.
[答案](1)①④ (2)27
[方法技巧] (1)判断一个函数是否为指数函数，只需判断其解析式是否符合y＝ax(a＞0， 且a≠1)这一形式，其具备的特点为：
2.底数与指数函数图象的关系 (1)由指数函数 y＝ax 的图象与直线 x＝1 相交于点(1，a)可知，在 y 轴右侧， 图象从下到上相应的底数由小变大． (2)由指数函数 y＝ax 的图象与直线 x＝－1 相交于点－1，1a 可知，在 y 轴左侧，图象从下到上相应的底数由大变小． 如图所示，指数函数底数的大小关系为 0＜a4＜a3＜1＜a2＜a1.
(一)指数函数的概念 一般地，函数 y＝ax(a>0，且a≠1) 叫做指数函数，其中指数x是自变量，定义 域是 R .

指数函数的图像和性质(教学课件)高一数学(人教A版2019必修第一册)

指数函数的图像和性质(教学课件)高一数学(人教A版2019必修第一册)

3．函数 y＝121－x 的单调增区间为(
)
A．R
B．(0，＋∞)
C．(1，＋∞)
D．(0,1)
【答案】A [令 u(x)＝1－x，则 u(x)在 R 上是减函数，又 y＝12u(x)是减函数，故
y＝121－x 在 R 上单调递增，故选 A.]
4．已知 a＝ 52－1，函数 f(x)＝ax，若实数 m，n 满足 f(m)>f(n)，则 m，n 的大 小关系为________.
课堂小结 1、指数函数y ax与y ( 1 )x的图象关于y轴对称
a
a>1
0<a<1
指 数
图
y
y
函
象
1
1
数
o
x
o
x
图 象 与
(1)定义域:
性 (2)值域:
R (0,+∞)
性
(3)过定点:
(0,1)
质
(4)单调性：增函数 (4)单调性： 减函数
质 (5)奇偶性： 非奇非偶 (5)奇偶性：非奇非偶
(6)当x>0时，y>1. (6)当x>o时，0<y<1,
则下列结论正确的是( )
A．a＞1，b＜0 C．0＜a＜1，b＞0
B．a＞1，b＞0 D. 0＜a＜1，b＜0
解析：从曲线的变化趋势，可以得到函数 f(x)为减函数，从而有 0 ＜a＜1；从曲线位置看，是由函数 y＝ax(0＜a＜1)的图象向左平移 |－b|个单位长度得到，所以－b＞0，即 b＜0.
(2)因为y=0.6x是单调递减函数，且-1.2>-1.5, 所以0.6-1.2<0.6-1.5
(3)因为1.70.2>1.70=1，0.92.1<0.90=1， 所以1.70.2>0.92.1

指数函数图像平移PPT

指数函数图像平移PPT
x - m的图像.
y
y=a x
y=ax+m
1
O
y=ax-m x
(3)平移后产生新函数——复合函数，它已 不再是指数函数了.
(4)本题分析时使用了归纳法，它是分析问 题时常用的方法.
三.函数图像一般平移规律
（1）沿x 轴左右平移(m>0) y y=f(x)
右移m
y=f(x+m)
左移m
y=f(x-m) x
y( )
（1） y
1 x的图像的关系，并画出示意图 3

1
3
x2
1 （2） y x 1 3
2. 说明函数 y=4x-3的图像与函数 y=4x
的关系，并画出示意图.
课堂小结
(1) 本节学习了指数函数图像的平移，并拓展到 一般函数图像平移的情形；
(2) 掌握平移方法，利用平移画出相关函数图像，
x
4 A. 3 3 3 1 B. 5 10 1 3 C. 10 5 4 D. 3 3
1 10
3 5
c3
c4
1
O Y
3 1 5 10
4 3 3 4 3 3
c2 c1
X
二.指数函数图像的平移
1. 实例 说明下列函数图像与指数函数y=2x
图像的关系, 并画出它们的示意图：
(1) y 2
x 1
(2) y 2
指数函数图像平移ppt指数函数的图像ppt二次函数图像平移三角函数图像平移函数图像平移函数图像的平移一次函数图像平移二次函数图像的平移函数图像的平移变换二次函数图像平移规律
指数函数
y = ax
1 y ( )x 10 y 1 y ( )x 2
一般性质：

指数函数图像的变换

指数函数图像的变换

y
y 1 x 2
底 大 图 低
y 1 x 3
在第一象限沿 箭头方向底增
大
y 3x y 2x
底 大 图 高
1
y 1 x
2
0 y 1 x
x
3
函数图象的变换
本节课主要研究函数图象的变换，得出y=f(x)与 y=f(-x), y=-f(x), y=f(|x|), y=|f(x)|的图象关系；并能 够通过y=f(x)图象的对称和翻折得出其余四个函数 图象。
（1）作出函数的图象； （2）指出函数 的单调区间； （3）指出x取何值时，函数有最值。
y
y=2x
y=2x-2
y=|2x-2|
1
y=|2x-2|
O 1 23 x -1
x
y=a(a=0) 有两个交点
-4
课堂训练
f ( x) x2 4x 3 函数的单调增区间 为
问题1：如何由f(x)=x2的图象得到下列各函
数的图象？
y y=f(x)+1
（1）f(x-1)=(x-1)2 （2）f(x+1)=(x+1)2
（3）f(x)+1=x2+1 （4）f(x) -1=x2-1
y=f(|x|) y=|f(x)|
f
(|
x
|)


f (x),(x 0) f (x),(x 0)
y
f (x)

f
(x), f (x) f (x), f (x)
0； 0.
y f 1(x) 与y=f(x)的图象关于直线y=x对称.
翻折变换
小结：
1、y=f(x)y=f(|x|)，将y=f(x)图象 在y轴右侧部分沿y轴翻折到y轴左 侧，并保留y轴右侧部分。 2、 y=f(x)y=|f(x)|，将y=f(x)图象 在x轴下侧部分沿x轴翻折到x轴上 侧，并保留x轴上侧部分。

高中数学 2.1.2.1指数函数的定义与简单性质课件 新人教A版必修1

高中数学 2.1.2.1指数函数的定义与简单性质课件 新人教A版必修1

1
32
[走出误区] 易错点⊳忽略分类讨论致求指数型函数值域出错 [典例] [2013·赤壁高一检测]若函数f(x)＝ax－1(a>0且a≠1)的定义域和值域都是[0,2]，求实数a的值．
a0－1＝0， [错解档案] 由题意可知a2－1＝2， 解得a＝ 3.
[误区警示] 虽然结果正确，但解题过程缺少步骤，没有分类讨论的意识．实际上在不知底数a的取 值的情况下，要对a的取值分a>1和0<a<1两种情况讨论．
由指数函数的性质知，y＝(13) x－2≤(13)0＝1， 且y>0，故此函数的值域为(0,1]．
1
31
[规律小结] 1.指数函数的定义 理解指数函数的定义，需注意的几个问题：
(1)因为a>0，x是任意一个实数时，ax是一个确定的实数，所以函数的定义域为实数集R；且ax>0，所 以函数的值域是(0，＋∞)．
1．底数a与1的大小关系决定了指数函数图象的“升降”；当a>1时，指数函数的图象“上升”；当 0<a<1时，指数函数的图象“下降”．
2．底数的大小决定了图象相对位置的高低：不论是a>1，还是0<a<1，在第一象限内底数越大，函数 图象越靠近y轴．
当a>b>1时， (1)若x>0，则ax>bx>1； (2)若x<0，则1>bx>ax>0. 当1>a>b>0时， (1)若x>0，则1>ax>bx>0； (2)若x<0，则bx>ax>1.
1
16
【跟踪训练1】 函数f(x)＝(a2－3a＋3)ax是指数函数，则有( )
A．a＝1或a＝2

指数函数的图象及性质--优质获奖精品课件 (22)

指数函数的图象及性质--优质获奖精品课件 (22)

2．求函数 y (1)x (1)x (1 x 2) 的值域.
42
【解析】1.因为1≤x≤2,所以2≤2x≤4,1≤2x-1≤3,
函数的值域为［ 1,1］.
3
答案：［ 1,1］
3
2.令( 1)x=t,因为1≤x≤2,所以 1 ，t 1
2
42
y t2 t(1 ,对t 称 1轴) 为 ， t 1
42
2
∵函数y=t2-t在［ 1 ］, 1 上单调递减,
42
∴函数最小值为 (1)2 1, 1
224
最大值为(1)2 1 , 3
4 4 16
故函数的值域为［ 1 ,］3.
4 16
【规范解答】分类讨论求指数型函数的值域 【典例】(12分)(2012·赤壁高一检测)若函数f(x)=ax-1 (a＞0，且a≠1)的定义域和值域都是［0,2］，求实数a的值.
2.要作出形如y=a|x+m|(a＞0且a≠1,m∈R)的图象，有两种方 法: (1)先去掉绝对值，化简函数解析式，转化为分段函数，然后 再画出图象； (2)借助指数函数的图象，利用平移变换来作图.
指数型函数的定义域与值域 【技法点拨】
1.指数型函数的定义域和值域的求法的关注点 (1)分类讨论：底数为字母时要注意讨论，如求函数 y ax 1 的定义域，解ax-1≥0时，要讨论a＞1与0＜a＜1两种情况. (2)图象：求值域与定义域时能画图则画图，通过图象上点的 横、纵坐标看函数的定义域与值域.
第1课时 指数函数的图象及性质
1.理解指数函数的概念和意义. 2.探索并理解指数函数的单调性. 3.掌握指数函数图象通过的特殊点.
1.本课重点是指数函数的概念及指数函数的图象与性质. 2.本课难点是指数函数的有关性质及应用.
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
思考：为了得到y=2x-3-1的图像，只需把 y=2x的图像 向右平移3个单位，再向下平移1个单位
三.函数图像一般平移规律 （1）沿x 轴左右平移(m>0)
y y=f(x)
y=f(x+m) 左移m 右移m y=f(x-m)
O
x
注意: 数与形变化的变化规律
（2） 沿y 轴上下平移 (n>0)
y
上移n O 下移n
思路：通过分析函数解析式的数量关系，分 析出该函数图像与指数函数图像上的点的 坐标关系，再归纳出函数图像间的关系.
分析:（1）比较函数 y=2x+1与y=2x数量关系：
y=2-2+1与y=2-1的值相等， y=2-1+1与 y=20的值相等，
y y=2x+1 y 2x
y=22+1与 y=23的值相等， (t-1, 2t)
y 2x
向左平行移动1个单位长度 y 2 x1
y 2x
向左平行移动2个单位长度
y 2x2
y
8
● ● y＝2x
7
6 y＝2x＋1
5
y＝ 2x +2
4 3
●●
2● ●
1● ●
●●
-5 -4 -3 -2-1O 1 2 3 4 5 x
图像平移练习
1. 说明下列函数的图像与指数函数.
y (13)x的图像的关系，并画出示意图
图象的解析式为 y 2x .
3. 指数函数的性质
1
O
x
(1) 定义域: R
性 (2) 值域:（0，+ ∞） 质 (3) 过点(0, 1)，即x = 0 时，y=1
(4)在R上是增函数
(4)在R上是减函数
二.指数函数图像的平移
1. 实例 说明下列函数图像与指数函数y=2x
图像的关系, 并画出它们的示意图：
(1)y2x1 (2)y2x2
y=f(x)+n y=f(x)
y=f(x)-n
x
（3）函数f (x) 平移的一般规律 y= f(x- m)
左右移
y=f(x)
上下移
y = f(x)+n
规律小结：左加右减，上加下减
练：函数y=2-x-1+1的图象可由函数y=2-x的图象
(B)
A.向右平移一个单位,再向上平移一个单位得到 B.向左平移一个单位,再向上平移一个单位得到 C.向右平移一个单位,再向下平移一个单位得到 D.向左平移一个单位,再向下平移一个单位得到
关于指数函数图象 的平移
一. 指数函数的定义、图像与性质
1. 指数函数定义
一般地，函数 y= a x ( a > 0, a 1) 叫做
指数函数，其中x是自变量，函数定义域是R
2. 叙述指数函数y= a x ( a > 0, a 1)图像特征
y=ax y
(a>1)
y y=ax
(0<a<1)
1
Ox
y y=a x
(1) 函数y=ax的图像左移m (m>0) 个单位，得y=a x + m的图像.
(2)函数y=ax图像右移m 个单位，得y=a x - m的图像.
y=ax+m
1
y=ax-m
O
x
(3)平移后产生新函数——复合函数，它已
不再是指数函数了.
比较函数y 2x、y 2x1与 y 2x2 的关系
（1） y
1 3x2
（2） y
1 3 x1
2. 说明函数 y=4x-3的图像与函数 y=4x
的关系，并画出示意图.
练习
1. f (x) 图像向右平移2个单位后为
则 f (x) = y 2. x
2. y x的图象怎样平移y得 到x3
y 2x的图象怎样平移y得 到 2x3
练习
• 由y=2x 的图像怎样得到y=2x+2 ， y=2x+3， y=2x-4， y=2x-5的图像？
……
2
y=2(t-1)+1与y=2t 的值相等.
1
-1
所以,两函数图像上点的坐标存在关系：
O
1
(t, 2t) x
点(t-1, 2t) 左移1 点(t, 2t)
结论： 指数函数y=2x的图像向左平移1个 单位，可得到函数y=2x+1的图像.
2 21
（2）类似可比较函数y=2x-2与y=2x的关系：
∵y=2-1-2与y=2-3 相等 y=20-2与y=2-2 相等
比较函数y 2x、y 2x1与 y 2x2 的关系
y 2x
向左平行移动1个单位长度 y 2 x1y 2x向左平行移动2个单位长度
y 2x2
y
8
● ● y＝2x
7
6 y＝2x＋1
5
y＝ 2x +2
4 3
●●
2● ●
1● ●
●●
-5 -4 -3 -2-1O 1 2 3 4 5 x
练习
1.y 5x1 的图象向右平移2个单位得到的
y y 2x
y=2…3-2 与…y=21 相等
∴y=2(t+2)-2与y=2t 相等
两个函数图像上纵坐标相等
1
的点的横坐标恰好相差 2
O
点(t, 2t) 右移2 点(t+2, 2t)
y=2x-2
x
结论：将指数函数y=2x的图像向右平移2个单位 就得到函数y=2x-2的图像 (如图)
2. 方法小结: