下载文档原格式
第17章 动量定理和 动量矩定理工程力学学习指导第17章 动量定理和动量矩定理17.1 教学要求与学习目标1. 正确理解动量的概念，能够熟练计算质点系、刚体以及刚体系的动量。
2. 认真理解有关动量定理、动量守恒定理以及质心运动定理，掌握这些定理的相互关系。
3. 正确而熟练地应用动量定理、动量守恒定理以及质心运动定理解决质点系动力学两类问题，特别是已知运动求未知约束力的问题。
4. 学习动量矩定理时，首先需要认识到，在动力学普遍定理中，动量定理和动量矩定理属于同一类型的方程，即均为矢量方程。
而质点系的动量和动量矩，可以理解为动量组成的系统（即动量系）的基本特征量——动量系的主矢和主矩。
两者对时间的变化率等于外力系的基本特征量——力系的主矢和主矩。
5. 认真理解质点系动量矩概念，正确计算系统对任一点的动量矩。
6. 熟悉动量矩定理的建立过程，正确应用动量矩定理求解质点系的两类动力学问题。
7. 于作平面运动的刚体，能够正确建立系统运动微分方程和补充的运动学方程，并应用以上方程求解刚体平面运动的两类动力学问题。
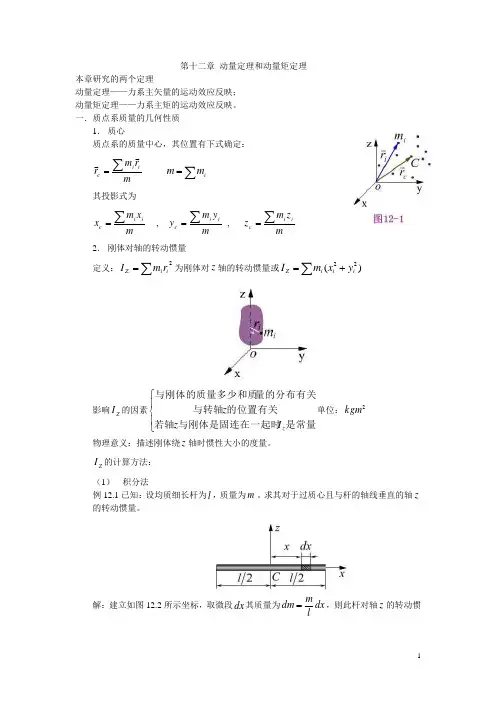
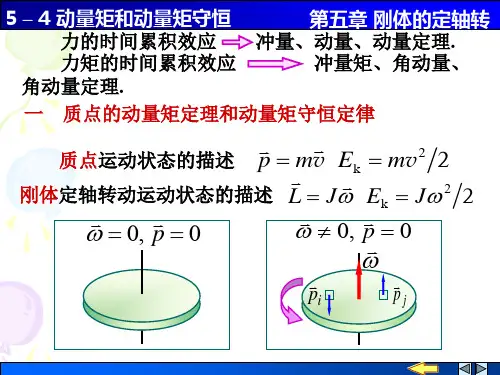
17.2 理 论 要 点17.2.1 质点系的动量质点系中所有质点动量的矢量和（即质点系动量的主矢）称为质点系的动量。
即i ii m v p ∑=质点系的动量是自由矢，是度量质点系整体运动的基本特征量之一。
具体计算时可采用其在直角坐标系的投影形式，即⎪⎪⎪⎭⎪⎪⎪⎬⎫===∑∑∑i iz i z i iy i y iix i x v m p v m p v m p质点系的动量还可用质心的速度直接表示：质点系的动量等于质点系的总质量与质心速度的乘积，即C m v p =这相当于将质点系的总质量集中于质心一点的动量，所以说质点系的动量描述了其质心的运动。
上述动量表达式对于刚体系也是正确的。
17.2.2 质点系动量定理质点系动量定理建立了质点系动量的变化率与外力主矢量之间的关系。
其微分形式为(e)(e)R d d i it ==∑pF F 质点系的动量对时间的变化率等于质点系所受外力系的矢量和。
动量和动量矩定理
如果不考虑鱼雷运动过程中的弹性变形，以及由于然料消耗引起的鱼雷重量和重心位置的变化，可以把鱼雷看成一个常质量的刚体。
刚体的空间运动由重心的运动和绕中心的转动两部分组成。
描述重心运动规律的是动量定理。
描速重心转动规律的是动量矩定理。
所以动量和动量矩定理是建立鱼雷运动方程组的出发点。
一、动量定理
用矢量表示鱼雷的动量，用矢量表示作用在鱼雷上的所有外力之和，在静止坐标系中的动量矩定理是：
(2-88
) 在建立鱼雷重心运动方程时，选用原点在鱼雷重心的半速度坐标系为参考系，因为在半速度系中重心运动方程形式最简。
半速度系的轴指向重心速度方向，轴垂直于轴OX并处于包含OX的铅垂面内指向上方，轴垂直于平面，从雷尾往前看指向右侧。
鱼雷运动过程中半速度系是运动的，以矢量表示半速度系的旋转角速度，表示动量的矢量端点在半速度系中的相对速度，则以半速度坐标系为参考系的动量定理是。
(2-89
) 式中叉乘可写为矩阵形式：
式中是沿半速度系三个轴的单位矢量。
显然，矢量在半速度系三个轴上的分量是
式中m是鱼雷质量，v是鱼雷速度，即重心速度。
将上式代入式(2-89)得到
(2-90
) 参阅图1-4，矢量在半速度系三个轴上的分量是
(2-91
) 将式(2-91)代入式(2-90)得到
(2-92
)
式中是m鱼雷质量，v是鱼雷速度；是弹道倾角；
是弹道偏角；分别是外力矢量F在半速度系三个轴上的分量。
式(2-92)就是以半速度系为参考写出的动量定理，是建立鱼雷重心运动方程组的出发点。
一、概述可压缩流体是指密度随着压强和温度的变化而变化的流体。
在空气动力学和航天动力学中，可压缩流体动力学是一个重要的研究领域。
在研究可压缩流体运动时，动量方程和动量矩方程是非常重要的方程。
本文将从动量方程和动量矩方程入手，系统地阐述可压缩流体的动力学原理。
二、可压缩流体的动量方程动量方程描述了流体内部的动量变化。
对于可压缩流体，其动量方程可以通过Navier-Stokes方程推导得到。
Navier-Stokes方程是描述了流体运动的基本方程之一，其形式如下：∂(ρv)/∂t + ∇•(ρv⃗v⃗ ) = -∇p+ ∇•τ+ ρf⃗其中，ρ表示流体密度，v表示流体速度，t表示时间，p表示压强，τ表示应力张量，f⃗表示外力。
对于可压缩流体，动量方程还需要考虑压力和密度对流体速度的影响。
可以通过状态方程将压力和密度通联起来，从而得到包含压力-密度项的动量方程。
在一维情况下，动量方程可以表达为：∂(ρv)/∂t + ∂(ρv^2)/∂x = -∂p/∂x+ ρf在三维情况下，动量方程会更加复杂，需要同时考虑各个方向上的动量变化。
通过动量方程，我们可以清晰地了解流体内部的动量传递和转化过程，以及外力对流体动量的影响。
三、可压缩流体的动量矩方程动量矩方程描述了流体内部动量矩的变化。
对于可压缩流体，动量矩方程可以被用来分析流体内部旋转运动的特性。
动量矩方程可以通过Euler方程推导得到。
Euler方程是Navier-Stokes方程在无粘性流体情况下的特殊形式，其表达式如下：∂(ρv)/∂t + ∇•(ρv⃗v⃗ ) = -∇p+ ∇•τ+ ρf⃗在此基础上，再根据流体内部动量矩的性质，可以得到动量矩方程的表达式。
动量矩方程不仅包含了流体速度的变化，还考虑了流体内部的角动量变化。
对于可压缩流体，动量矩方程可以表达为：∂(ρv)/∂t + v•∇(ρv) +∇•(τ) = ρf⃗通过动量矩方程，我们可以研究流体内部旋转运动的特性，分析流体内部动量矩的传递和转化情况，为深入理解可压缩流体的运动提供重要的理论基础。
在现行的普通物理教材中，力学中的三大守恒定律，即动量守恒定律、动量矩守恒定律和机械能守恒定律。
现代物理学业已证明这些守恒定律是和时空对称性相联系的：动量守恒定律与空间平移对称性相联系；动量矩守恒定律与空间转动对称性相联系；能量守恒定律与时间平移对称性相联系。
由上述对称性可导出相应的守恒定律,进一步导出牛顿运动定律。
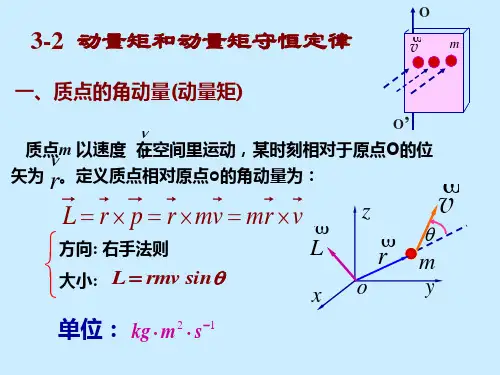
动量矩守恒定律，又称角动量守恒定律。
指的是根据动量矩定理推论，当合外力矩为0时，其动量矩保持不变。
表述动量矩守恒条件的定律。
质点不受力或作用力对某固定点(或轴)之矩始终等于零时，该质点对该点(或轴)的动量矩保持不变。
质点系所受外力对某固定点(或轴)之矩的和始终等于零时，该质点系对该点(或轴)的动量矩保持不变。
例如行星所受太阳引力始终指向太阳中心，故如不计其他星体的引力，行星对太阳中心的动量矩守恒
一个系统不受外力或所受外力之和为零，这个系统的总动量保持不变，这个结论叫做动量守恒定律。
1.动量守恒定律是自然界中最重要最普遍的守恒定律之一，是一个实验规律，也可用牛顿第三定律结合动量定理推导出来。
2.相互间有作用力的物体系称为系统，系统内的物体可以是两个、三个或者更多，解决实际问题时要根据需要和求解问题的方便程度，合理地选择系统。
角动量和动量矩角动量和动量矩都是物理学中描述物体运动状态的重要概念，它们在运动学和动力学中有着关键的作用。
一、动量（Linear Momentum）：动量是描述物体运动状态的物理量，它是物体质量乘以其速度的乘积。
动量（p）的数学表示为：p=m⋅v其中，m是物体的质量，v是物体的速度。
动量是守恒的，即在封闭系统中，总动量保持不变。
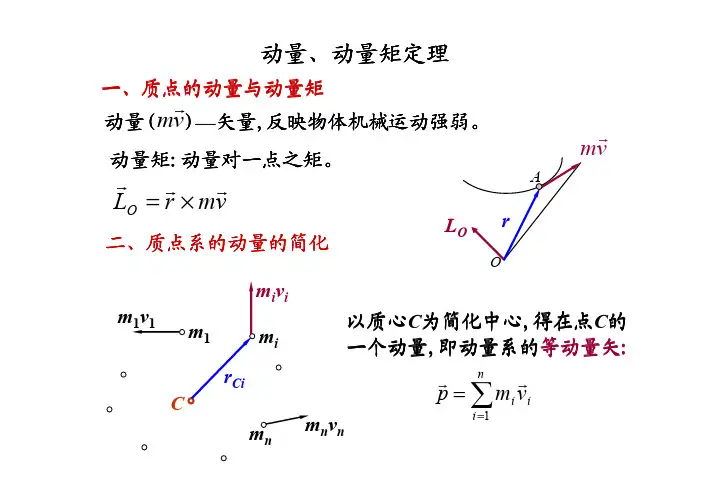
二、角动量（Angular Momentum）：角动量是描述物体绕某一轴旋转的运动状态的物理量，它是物体的惯性矩乘以其角速度的乘积。
角动量（L）的数学表示为：L=I⋅ω其中，I是物体绕旋转轴的惯性矩（或称转动惯量），ω是物体的角速度。
类似于动量，角动量也是守恒的，即在没有外力矩作用的封闭系统中，总角动量保持不变。
三、动量矩（Torque）：动量矩是描述力对物体产生旋转运动影响的物理量，它是力对物体的作用点到旋转轴的距离与力的乘积。
动量矩（或力矩，τ）的数学表示为：τ=r⋅F其中，r是力的作用点到旋转轴的距离，F是力的大小。
动量矩的单位是牛顿·米（N·m）。
四、动量矩和角动量的应用：动量矩的作用：动量矩是引起物体绕轴旋转的原因，类似于力引起物体直线运动的原因。
例如，当你用力拉门时，产生的动量矩将导致门绕铰链旋转。
角动量的应用：角动量在自然界中有广泛的应用，例如行星绕太阳的运动、自行车轮的旋转等。
在工程学和物理学中，理解和控制角动量对设计和操作旋转系统非常重要。
这些概念的理解对于解释和预测物体的运动和旋转行为至关重要。
在物理学和工程学领域，动量和角动量的概念广泛用于解决各种问题，包括机械系统的运动、天体运动、核物理等。
动量矩守恒定律动量守恒定律动能动量矩守恒定律是物理学中的重要定律之一，它告诉我们在一个封闭系统中，如果外部力矩为零，则系统的角动量将守恒不变。
而动量守恒定律则告诉我们在一个封闭系统中，如果外部力为零，则系统的动量将守恒不变。
这两个定律在物理学中有着广泛的应用，可以帮助我们理解许多物理现象。
首先，让我们来看一下动量守恒定律。
动量是物体的运动状态的量度，它是质量和速度的乘积。
当一个物体受到外部力的作用时，它的动量会发生改变。
然而，如果一个系统是封闭的，即没有外部力的作用，那么系统的总动量将守恒不变。
这就意味着，系统中任何一个物体的动量的改变都会以相等的方式被其他物体所吸收，从而确保系统总动量守恒。
举一个简单的例子来说明动量守恒定律：假设有两个物体A和B 在一条直线上以相同的速度相向而行，它们的质量分别为m1和m2。
当它们发生碰撞时，根据动量守恒定律，它们的总动量在碰撞前后都将保持不变。
假设碰撞后物体A的速度为v1’，物体B的速度为v2’，那么根据动量守恒定律有m1v1 + m2v2 = m1v1’ + m2v2’。
这个简单的例子清楚地展示了动量守恒定律的应用。
接下来，让我们来看一下动量矩守恒定律。
角动量是物体围绕某一轴旋转时的运动状态的量度，它是质量、速度和与轴的距离的乘积。
当一个物体受到外部力矩的作用时，它的角动量会发生改变。
然而，如果一个系统是封闭的，即外部力矩为零，那么系统的总角动量将守恒不变。
举一个简单的例子来说明角动量守恒定律：假设有一个转动的物体在没有外力矩的情况下保持着一定的角速度，当它改变形状或者重新分布质量分布时，它的角动量将保持不变。
这个例子清楚地展示了角动量守恒定律的应用。
总的来说，动量守恒定律和角动量守恒定律是非常重要的物理定律，它们可以帮助我们理解并解释许多物理现象。
在实际应用中，我们可以利用这些定律来计算碰撞、旋转等各种物理过程中的动量和角动量的变化，从而更好地理解系统的运动状态。
三）动量矩定理
下面研究质点相对于某一根指定的直线的运动，这根直线称为“轴线”．这时着重的是力矩而不是力．
1．力对于轴线的力矩
图3－1
力F对轴线AB的力矩等于力F在垂直于轴线的平面S中的投影F⊥再乘以其与轴线AB的垂直距离d（一般称之为力臂）．如果力F本身就在与AB垂直的平面内，力矩就等于F乘以F与AB的垂直距离d。
力F对轴线AB的力矩记为
M，
AB
AB M F =⊥ d
（3．15）
通常按右手法则来规定力矩的指向，将右手的四指捏成拳状以表示力矩驱使物体转动的趋势，伸直的大拇指的指向即力矩的指向
2．对于轴线的动量矩和动量矩定理 （1）质点与轴连结．
如果质点与轴AB 相连结，则质点必在垂直于AB 的平面内作圆周运动．质点所受外力对AB 轴的力矩为
（3．16）
mv 是质点的动量，R 是动量与轴AB 间的垂直距离．仿照力矩，我们将 mv 与R 的乘积称为质点对于AB 轴的动量矩（角动量） AB J ，
即
AB AB M J =
（3. 17） 这就是动量矩定理． （2）转动惯量．
将上式中的 AB J 以质点绕轴转动的角速度 ω表示
2
AB J mR ω= （3. 18）
2mR 称为质点对AB 轴的转动惯量，记为I AB ，则
AB AB J I ω= 动量矩定理（3．17）即
（3．19）
式中 α是质点绕轴转动的角加速度，这与牛顿第二定律 F ma =多么相似！从这类比中还可以看出， I 与 m 相对应， I 反映绕轴转动的惯性，所以称为转动惯量．
（3）质点并不与轴连结．
图3－2
所讨论的质点并不与轴AB 连结，也不一定是绕轴转圈，只是相对于轴来研究质点的运动情况．为了方便，取AB 为直角坐标系的Z 轴．如质点的动量 m v 在 xy 平面内，它相对于z 轴的动量矩为
sin z J mvr θ= （3．20）
若动量 m v 不在 xy 平面内，我们可以将它分解为与 xy 平面垂直和与
xy 平面平行的分量，其中与 xy 平面垂直的动量分量对Z 轴的动量矩为零．所以
只要考虑在 xy 平面内的动量分量．
动量矩的正负和力矩一样，也用右手法则决定，和Z 轴正指向相同者取正值，反之为负值．
由牛顿第二定律可以导出一般情况下的动量矩定理
（3．21）
这是它的微分形式．
注意在一般情况下，此定理不宜表为 M Ia =，除非质点的转动惯量I 是常数．一般说来，质点运动时，它与转轴的距离不是常数，所以I 也不是常数．
我们还可以考察力矩的时间累积效果，将上式积分一次,得
2
1
21t z
z
z
t M dz J
J =-⎰ （3．22）
式中 1z J 与 2z J 分别表示质点在时刻 1t 及 2t 的动量矩，力矩对时间的积分称为冲量矩．这就是对z 轴动量矩定理的积分形式，适宜用来研究冲击作用．
3．动量矩守恒原理
如果质点所受的力对于Z 轴的力矩为零，这时冲量矩自然也为零，由动量矩定理可得出
0z J =
或 1z J = 2z J （3．23）
上面两式的意义相同，它们指出如果质点所受的力对Z 轴的力矩为零，则质点对该轴的动量矩守恒．
如果质点与轴线连结而绕轴转动，则动量矩守恒原理为
2J mvR mR ω===常数 （3．24）
式中R 为质点与轴线间的垂直距离， ω为质点绕轴转动的角速度，上式意味着质点绕轴转动的角速度不变．
如果质点并非固定连结于轴上，则动量矩守恒原理为
2
J m ρϕ
== 常数 （3．25） 例如在舞蹈或滑冰表演中，演员常绕自身的轴旋转．略去摩擦，他所受的重力对转轴的力矩为零，动量矩守恒．当演员将两手合抱于胸前，旋转就加快起来；演员将两臂伸展出去，旋转就减慢。
（四）质点组的动量矩定理 1．对于轴线的动量矩定理
质点组包含N 个质点．考察各质点对于Z 轴的动量矩，由各质点的动量矩定理得
1112131,11,2221222,12,123,1
N N
N N N N N N N N N J M M M M M J M M M M M J M M M M M ---⎧=+++⋅⋅⋅++⎪
=+++⋅⋅⋅++⎪⎨
⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⋅⎪⎪=++++⋅⋅⋅+⎩
（3. 26）
这里 i J 为第 i 个质点对Z 轴的动量矩， i M 为作用于 i 质点的外力对Z 轴的力矩， ik M 为质点k 作用于质点i 的内力对Z 轴的力矩．将上式累加起来．注意内力 ik F 与 ki F 大小相等，指向相反，沿着同一条直线，它们在 xy 平面中的投
影必然也是大小相等，指向相反，沿着同一条直线，因而它们对Z 轴的力矩之和为零．这样，在累加的结果中只出现外力的力矩，不出现内力的力矩．
1212N N J J J M M M ++⋅⋅⋅+=++⋅⋅⋅
（3．27）
将质点组各质点对Z 轴的动量矩之和定义为质点组对Z 轴的动量矩J
121
2
N N
J J J J J
M M M =++⋅⋅⋅+=++⋅⋅⋅+ （3. 28）
这就是质点组对轴线的动量矩定理的微分形式。
将上式积分一次，就得到质点组对轴线的动量矩定理的积分形式。
2
2
2
21121
1
1
t t t N t t t J J M dt M dt M dt
-=++⋅⋅⋅+⎰⎰⎰ （3. 29）
质点组对Z 轴的动量矩的改变，等于组内各质点在这段时间内所受外力对Z 轴的冲量矩之和．
2．质点组的动量矩与质心的动量矩
前文已指出，质点组的动量就等于质心的动量，那么质点组的动量矩是否也等于质心的动量矩呢？这却未必，通过下面的例子很容易说明这一点．
一物体绕通过其质心的Z 轴转动，Z 轴是固定不动的．质心既然不动，它对Z 轴的动量矩必定为零．而物体的动量矩 I ω却不等于零．可见物体的动量矩一般不等于质心的动量矩．
通过计算可以证明，质点组对某轴线的动量矩，等于质心对该轴线的动量矩 c J 再加上质点组对于通过质心和该轴平行的轴的动量矩 'J 之和，即
'c J J J =+ （3．30）
3．动量矩守恒
如果质点组所受的外力对Z 轴的力矩之和等于零， 即
120N M M M ++⋅⋅⋅+=
那么，质点组的动量矩守恒，即
0z J =
或 1z J = 2z J （3. 31）。
