龙格现象

拉格朗日插值法在实践中的应 用
在数值分析中的应用
单击此处添加标题
插值法：拉格朗日插值法是数值分析中常用的插值方法之一，具有简单易 行、计算量小等优点。
单击此处添加标题
数据拟合：拉格朗日插值法可以用于数据拟合，通过对已知数据进行插值， 得到未知数据的近似值。
单击此处添加标题
数值微积分：拉格朗日插值法在数值微积分中也有广泛应用，例如在求解 函数的导数、积分等运算时，可以利用拉格朗日插值法进行近似计算。
龙格现象
龙格现象的定义
定义：当插值多项式的阶数过高时， 插值结果可能变得不可预测或出现 剧烈振荡
解决方法：在实际应用中，应避免 使用过高的插值多项式阶数，而应 选择合适的阶数以保证插值结果的 稳定性和准确性
添加标题
添加标题
添加标题
添加标题
原因：由于高阶插值多项式对数据 点的敏感性增强，导致插值结果不 稳定
拉格朗日插值龙格现象的 Matlab实现
汇报人：XX
单击输入目录标题 拉格朗日插值法 龙格现象 拉格朗日插值法在Matlab中的实现 拉格朗日插值法的龙格现象分析 拉格朗日插值法在实践中的应用
添加章节标题
拉格朗日插值法
插值法的定义
插值法是一种数学方法，通过已知的离散数据点，构造一个多项式函数，使得该函数在 数据点处的取值等于已知的数据点值。
算法收敛性：在某些情况下，龙格现象可能导致算法收敛速度减慢，增加计算时间和计算成本。
实际应用限制：由于龙格现象的存在，某些数值方法在实际应用中可能受到限制，无法处理某些 复杂问题。
算法改进需求：为了克服龙格现象的影响，需要研究和发展新的数值方法和算法，提高数值计算 的稳定性和精度。
拉格朗日插值法在Matlab中的 实现

幂激励矩阵 V 和插值输出列向量 y 分别为：
[ ] =a a0 , a1,, an T ∈ Rn+1
1

=V
1
x0 x1

x0n x1n

∈
R ( n +1)×( n +1)
1
xn

xnn

[ ] =y y0 , y1,, yn T ∈ Rn+1
DOI: 10.12677/aam.2019.88175
Received: August 6th, 2019; accepted: August 21st, 2019; published: August 28th, 2019
Abstract
Firstly, this paper explains the Runge phenomenon generated by high-order polynomial interpolation, and proves that the interpolation polynomial divergence is obtained by calculating the systematic error. Secondly, taking the Runge function, inverse trigonometric function and fractional function as examples, the interpolation polynomial of the function is obtained by using the equally spaced Newton interpolation, and then the interpolation residual function expression is obtained, and then the midpoint of adjacent two nodes is calculated. The error at the location determines that the above three functions have generated the Runge phenomenon. Thirdly, the three algorithms of Chebyshev node, piecewise linear interpolation and cubic spline interpolation are introduced and verified, which can avoid the Runge phenomenon. Finally, the approximation performance index is proposed, and based on the optimal polynomial construction coefficient and order double determination method, the algorithm has excellent function approximation effect while avoiding the Runge phenomenon.

插值MATLAB实现（牛顿差商插值误差龙格现象切比雪夫插值）插值是数值分析中的一种方法，通过已知数据点的函数值来估计函数在其他点的值。

MATLAB提供了多种方法来实现插值，包括牛顿差商插值、插值误差分析、龙格现象和切比雪夫插值。

下面将详细介绍这些方法的实现原理和MATLAB代码示例。

1.牛顿差商插值：牛顿差商插值是一种基于多项式插值的方法，其中差商是一个连续性的差分商。

该方法的优势在于可以快速计算多项式的系数。

以下是MATLAB代码示例：```matlabfunction [coeff] = newton_interpolation(x, y)n = length(x);F = zeros(n, n);F(:,1)=y';for j = 2:nfor i = j:nF(i,j)=(F(i,j-1)-F(i-1,j-1))/(x(i)-x(i-j+1));endendcoeff = F(n, :);end```该代码中，输入参数x和y分别表示已知数据点的x坐标和y坐标，返回值coeff表示插值多项式的系数。

2.插值误差分析：插值误差是指插值函数与原始函数之间的差异。

一般来说，通过增加插值节点的数量或使用更高次的插值多项式可以减小插值误差。

以下是MATLAB代码示例：```matlabfunction [error] = interpolation_error(x, y, x_eval)n = length(x);p = polyfit(x, y, n-1);y_eval = polyval(p, x_eval);f_eval = sin(pi*x_eval);error = abs(f_eval - y_eval);end```该代码中，输入参数x和y分别表示已知数据点的x坐标和y坐标，x_eval表示插值节点的x坐标，error表示插值误差。

3.龙格现象：龙格现象是插值多项式在等距插值节点上错误增长的现象。

数值分析中的插值误差控制技巧数值分析是解决实际问题中涉及数值计算的方法和技术的学科。

在数值计算中，插值是一种常用的数值分析技术，用于在给定的有限数据点集合上估计函数在其他点上的值。

然而，插值过程中会产生误差，为了保证插值结果的准确性，需要掌握一些插值误差控制技巧。

本文将介绍数值分析中常用的插值误差控制技巧。

一、余项估计法余项估计法是一种常用的插值误差控制技巧。

在数值分析中，我们通常使用多项式插值方法进行插值计算。

多项式插值的基本思想是通过已知数据点构造一个多项式，然后利用该多项式在其他点上的值来估计函数的值。

余项估计法通过对多项式插值的余项进行估计来控制插值误差。

二、龙格现象与插值节点的选择在实际问题中，插值节点的选择对插值结果的准确性有重要影响。

龙格现象是指在某些特定的插值节点选择下，插值多项式在边界上会出现振荡现象。

为了避免龙格现象，需要选择合适的插值节点。

常用的插值节点选择方法有均匀节点、切比雪夫节点等。

三、样条插值与光滑插值除了多项式插值，样条插值也是一种常用的插值方法。

样条插值通过在每个小区间上构造一个低次多项式来实现插值。

样条插值不仅能够满足插值条件，还能够保证插值函数在节点处的光滑性。

光滑插值是为了减小插值误差而采用的一种技巧。

四、自适应插值与网格剖分自适应插值是一种根据插值误差大小来调整插值节点的方法。

通过不断调整插值节点，自适应插值能够有效控制插值误差，并使插值结果更加精确。

网格剖分是自适应插值的一种实现方式，通过将插值区域划分成多个小区间进行插值计算，以提高插值的准确性。

五、边界条件的选取在插值过程中，边界条件的选取也对插值结果的准确性有重要影响。

常用的边界条件有自然边界条件、固定边界条件等。

合理选择边界条件能够有效控制插值误差，并提高插值结果的准确性。

综上所述，数值分析中的插值误差控制技巧是保证插值结果准确性的重要手段。

通过合理选择插值节点、掌握余项估计法、利用样条插值和自适应插值等方法，可以有效控制插值误差，提高插值结果的准确性。

龙格现象
在计算方法中，有利用多项式对某一函数的近似逼近，这样，利用多项式就可以 计算相应的函数值。例如，在事先不知道某一函数的具体形式的情况下，只能测 量得知某一些分散的函数值。例如我们不知道气温随日期变化的具体函数关系， 但是我们可以测量一些孤立的日期的气温值，并假定此气温随日期变化的函数满 足某一多项式。这样，利用已经测的数据，应用待定系数法便可以求得一个多项 式函数 f（x）。应用此函数就可以计算或者说预测其他日期的气温值。一般情 况下，多项式的次数越多，需要的数据就越多，而预测也就越准确。 例外发生了：龙格在研究多项式插值的时候，发现有的情况下，并非取节点（日 期数）越多多项式就越精确。著名的例子是 f（x）=1/(1+25x^2).它的插值函数 在两个端点处发生剧烈的波动，造成较大的误差。究其原因，是舍入误差造成的。 具体的情况可参考下列 Mathematica 程序： n = 10; x = Range[-1, 1, 2/n]; y = 1./(1 + 25 x^2); p = Transpose[{x, y}]; Clear[t]; f = LagrangeInterpolation[x, y, t]; Show[ Plot[{1./(1 + 25 t^2), f}, {t, -1, 1}], ListPlot[p, PlotStyle -> PointSize[0.02]] ] 程序演示 Matlab 程序演示 （一） 代码 >> f=inline('1/6-y/30','t','y'); [t,y]=ode45(f,[0,5],[0]); plot(t,y) >> hold on plot(t,5-5*exp(-t/30面是 MATLAB 中演示插值的 M 文件： %演示龙格函数的插值情况 for i=3:2:11

一、判断1、0.026900x *=-作为x 的近似值，它的有效数字位数为5位。

（ × ）2、迭代法的敛散性与迭代初值的选取无关。

（ × ）3、牛顿插值多项式的优点是：在计算时，高一级的插值多项式可利用前一次插值的结果。

（ √ ）4、已知观察值()(),0,1,i i x y i n =，用最小二乘法求得的拟合多项式其次数为n 次。

（ × ）5、改进欧拉公式是一种隐式的方法。

（ × ）6、一个近似数的有效数位愈多，其相对误差限愈小。

（ √ ） 6、求方程310x x --=在区间[1, 2]内根的迭代法总是收敛的。

（ × ）7、矩阵⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--521253113是主对角占优矩阵。

（ × ）8、在求插值多项式时，插值多项式的次数越高，误差越小。

（ × ） 9、具有n+1各节点的插值型求积公式至少具有n+1次代数精度。

( × ） 二、填空题1、误差来源： 舍入误差 ， 截断误差 ， 观测误差 ， 模型误差 。

2、古代数学家祖冲之曾以113355作为圆周率π的近似值，此近似值有 7 位有效数字。

3、用二分法求方程f(x)=x3+x-1=0在区间[0，1]内的根，进行一步二分后根所在区间为，进行二步二分后根所在区间为。

4、方程求根中牛顿迭代公式，收敛速度是。

5、求线性解方程组 5x1-3x2-0.1x3=1-2x1+6x2+0.7x3=0x1+2x2+3.5x3=0的高斯—赛德尔迭代格式为，取迭代初值x 1（0）=1，x 2（0）=-1，x 3（0）=1，则x 1（1）= -0.38 ，x2（1）= -0.24， x3（1）= 351。

6、Gauss 求积公式⎰baf(x )dx≈∑=Nn n)Anf(x 具有 2N+1 次代数精度。

7、n+1个插值节点构造的拉格朗日插值公式Ln(x)= 1 余项Rn(x)= 1 。

3． 多项式插值的龙格现象考虑在一个固定的区间上用插值逼近一个函数。

显然，拉格朗日插值中使用的节点越多，插值多项式的次数就越高，自然关心插值多项式的次数增加时，()n L x 是否也更加靠近被逼近的函数。

龙格给出的一个例子是极著名并富有启发性的。

设在区间[]1,1-上的函数为：()21125f x x =+，考虑区间[]1,1-的一个等距划分，分点为：21,0,1,2,,iix i nn=-+=则拉格朗日插值多项式为： ()()201125nn i i iL x l x x ==+∑ 其中(),0,1,2,i l x i n =是n 次拉格朗日插值基函数。

要求：（1）选择不断增大的分点数目2,3,n =画出原函数()f x 及插值多项式函数()n L x 在区间[]1,1-的图像，比较并分析实验结果。

解：算法为function lagrangeinterp% graphs of different 'n' clear all;clc x=-1:.01:1;y=1./(1+25.*x.^2); plot(x,y,'-') hold onn=input('n='); x=-1:2/n:1;y=1./(1+25.*x.^2); u=-1:.01:1;v=lagrange(x,y,u);function v = lagrange(x,y,u) % algorithm of lagrange n = length(x); v = zeros(size(u)); for k = 1:nw = ones(size(u)); for j = [1:k-1 k+1:n]w = (u-x(j))./(x(k)-x(j)).*w; endv = v + w*y(k); endplot(x,y,'o',u,v,'--') hold off当选定为2等分时：当选定为3等分时：当选定为5等分时：当选定为10等分时：当选定为15等分时：由上述五个图形可得：在一定范围内，拉格朗日插值中使用的节点越多，插值多项式的L x也更加靠近被逼近的函数，插值节点但并不是越多越好，当超过某一次数就越高，()n值后，就会在端点处出现龙格现象，而且节点越多，龙格现象越严重。

44
2013， 49 （3）
Computer Engineering and Applications 计算机工程与应用
龙格现象难题破解之系数与阶次双确定方法
张雨浓， 李名鸣， 陈锦浩， 劳稳超， 吴华荣
ZHANG Yunong, LI Mingming, CHEN Jinhao, LAO Wenchao, WU Huarong
1
引言
在数值方法领域中， 经常需要利用插值对某一函数进
出， 对于龙格函数， 在区间 [ - 1 1] 内， 选取等距插值点， 利 用插值多项式进行逼近时， 其逼近多项式在逼近区间两端 会产生振荡， 且插值多项式的阶次越高， 其振荡现象越严 重， 从而造成较大的逼近误差。因此， 一般认为， 龙格函数 不适宜利用基于等距节点的高阶多项式进行逼近。 为了良好地逼近龙格函数， 解决龙格现象， 通常使用 切比雪夫节点 [10] 代替等距插值点， 使逼近误差随插值多项 式的阶次的增大而减少。但由于统计与科学分析中采集 的数据点一般都是等间距的 （如等时间间距采样得到的数 据） ， 采集变间距的切比雪夫节点数据将会增加实际操作 的难度。另外， 也可以使用分段样条插值 [11] 代替多项式插 值， 利用分区间的低阶多项式对龙格函数进行良好的逼近。 区别于以上采用变间距的切比雪夫节点或分区间低 阶的分段样条插值的方法， 基于人工神经网络的最新研究
中山大学 信息科学与技术学院， 广州 510006 School of Information Science and Technology, Sun Yat-sen University, Guangzhou 510006, China ZHANG Yunong, LI Mingming, CHEN Jinhao, et al. Solving the problem of Runge phenomenon by coefficients-and-orderdetermination method. Computer Engineering and Applications, 2013, 49 （3） ： 44-49. Abstract：The Runge phenomenon demonstrates that it is not suitable to use high-order interpolation polynomials with equidistant nodes to approximate the Runge function, as oscillation occurs near the ends of the interpolation interval. Nevertheless, this paper presents an innovative method called Coefficients-And-Order-Determination （CAOD）method to solve the problem of the Runge phenomenon. This method can efficiently determine the coefficients and the order of the optimal polynomial that approximates the target function. By such a CAOD method, high-order optimal polynomials are constructed for different numbers of equidistant nodes, which all approximate the Runge function without causing oscillation. Thus, such constructed optimal polynomials can achieve high approximation accuracy （i.e., eliminate the Runge phenomenon） . Numerical experiment results further substantiate the efficacy and accuracy of the CAOD method. Key words：Runge phenomenon; function approximation; equidistant nodes; high-order polynomials; Coefficients-And-OrderDetermination （CAOD）method 摘 要： 龙格现象指出， 使用基于等距节点的高阶插值多项式逼近龙格函数时， 插值多项式在逼近区间两端会产生明显的

在 插 值 时 应 尽 可 能 使 内插 点 位 于 插 值 弧 段 的 中
ｆ （ ） ＝ 兀
３ 龙格 现象 处理策 略
， ≠
（ ２ ）
为了减弱 和 消除精 密 星历插 值 中龙 格现 象 的影 响， 提高插值 的精 度和可 靠性 ， 分 别采用 阶次 组合 、 增
加星历 和先外推后插值三种方法进行精密星历插值 。 （ １ ） 阶次 组合 法 ： 阶 次 组合 法 是 指 对 不 同位 置
１ 引 言
产 的精 密 星历 的事 后 星历 精 度则 优 于 ５ ｃ ｍ。Ｉ Ｇ Ｓ是
一
个 非军 方 的国 际协 作 组织 ， 其 开放 度 也 较 高 。因
在 高精 度 Ｇ Ｐ Ｓ数据 处 理 中 ， 为 了保证 结 果 的可 靠 性 和精确 性 ， 通 常使 用 Ｉ Ｇ Ｓ提 供 的精 密卫 星 星 历 进行计 算 。 由于实际 作业 时 Ｉ Ｇ Ｓ提供 的星历 时 间间 隔都 大于观 测数 据 的 采样 间隔 ， 使 用 时需 要 对 精 密 卫 星 星历进 行插 值 处 理来 满 足 计 算 的需 求 ， 以得 到 观测 历元 时刻所 需 要 的卫 星位 置 ， 提 高精 密 单 点 定
插值 是通 过构造 已知值 与未知值 之 间的多项 式 关 系来计 算未 知值 的数学 方法 。常用 的插 值方 法包 括 拉格 朗 日多项式插 值法 、 内维尔插 值法 、 牛顿 插值
法、 三次 样条 插值法 、 三 角多项 式插 值法 和切 比雪夫
ｎ ＋ １ 个点之间的任意位置的函数值 Ｊ 。
位 的精度 。
此， 精 密单 点定位 中通 常采用 Ｉ Ｇ Ｓ提供 的精 密星历 ， 给出 １ ５ ｍｉ ｎ等 时 间间隔 点上 的卫 星 坐标 数据 ， 坐 标 参考 基准 属于 Ｉ Ｔ Ｆ参 考框 架 。

差值里的龙格现象实验临床八年1004张馨予2204100412 一．实验任务：由书上例子2.2和2.3表明适当的提高多项式的次数，有可能提高插值的精度，但是绝对不可能由此认为插值多项的次数越高越好。

此次试验的任务便是验证差值多项式里的龙格现象。

二．算法设计：对函数f(x)=1/(1+25*x*x),(-1<=x<=1).先以xi=-1+2/5i(i=0,1,2,…,5)为节点做五次插值多项式P5(x)，再以xi=-1+1/5i(i=0,1,…,10)为节点做十次插值多项式P10(x)，并将曲线f(x)=1/(1+25*x*x),y=P5(x),y=P10(x)，在区间[-1,1]上，描绘在同一个坐标系。

程序设计，对于插值法，首先计算lagrange差值基本函数lk(x)。

再写出满足差值条件的n次插值多项式Ln(x)=yl(x)的总和。

三．计算机程序：1．求5个点对应y值的m文件function y=flongge2x=-1:0.4:1for i=1:length(x)y(i)=1/(1+25*x(i)*x(i));enddisp(y)2.求10个点对应y值的函数文件function y=flongge2x=-1:0.2:1for i=1:length(x)y(i)=1/(1+25*x(i)*x(i));enddisp(y)3. 差值里的龙格现象function f=Language(x,y,x0)syms t;if(length(x)==length(y))n=length(x);elsedisp('xand y are not of the same demision');return;endf=0.0;for(i=1:n)l=y(i);for(j=1:i-1)l=l*(t-x(j))/(x(i)-x(j));end;for(j=i+1:n)l=l*(t-x(j))/(x(i)-x(j));end;f=f+l;f=simplify(f);if(i==n)if(nargin==3)f=subs(f,'t',x0)elsef=collect(f);f=vpa(f,6);endendend并在命令编辑器里输入x y 矩阵，以及f=Language(x,y)4.龙格总图的m文件functiontu=longgezongtufplot('-220.940*t^10+494.907*t^8-381.433*t^6+123.360*t^4-16.8552*t^2+1.',[-1,1] ),holdon;fplot('1/(1+25*x*x)',[-1,1]), hold on;fplot('1.20199*t^4-1.73079*t^2+.567309',[-1,1],1e-4),grid四．调试以及运行结果1.在命令编辑器里输入flongge2，得到十个点的对应y值：（截的图）2.输入f，得到五个点对应的y值：3.在命令编辑器里输入x矩阵，和y矩阵，以及f=Language(x,y)，就会得到对应的两个差值公式:y=-220.940*t^10+494.907*t^8-381.433*t^6+123.360*t^4-16.8552*t^2+1.y=1.20199*t^4-1.73079*t^2+.567309根据这两个公式编出可以输出图的程序。

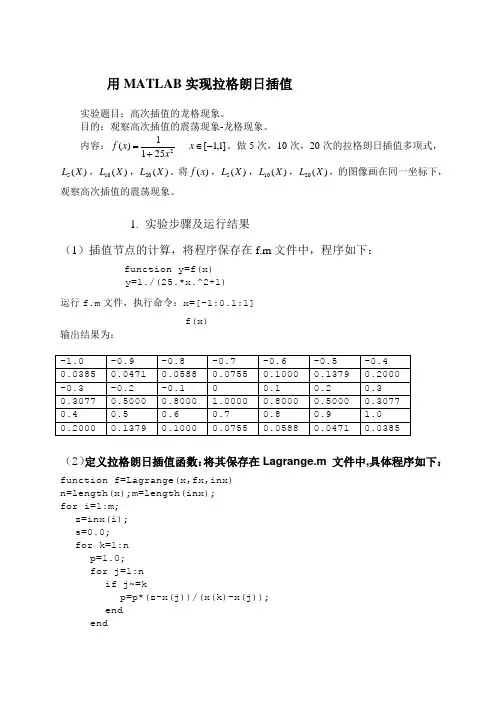
用MATLAB 实现拉格朗日插值实验题目：高次插值的龙格现象。

目的：观察高次插值的震荡现象-龙格现象。

内容：22511)(x x f += ]1,1[-∈x 。

做5次，10次，20次的拉格朗日插值多项式，)(5X L ，)(10X L ，)(20X L 。

将)(x f ，)(5X L ，)(10X L ，)(20X L ，的图像画在同一坐标下，观察高次插值的震荡现象。

1. 实验步骤及运行结果（1）插值节点的计算，将程序保存在f.m 文件中，程序如下：function y=f(x)y=1./(25.*x.^2+1)运行f.m 文件，执行命令：x=[-1:0.1:1] f(x) 输出结果为：（2）定义拉格朗日插值函数：将其保存在Lagrange.m 文件中,具体程序如下：function f=Lagrange(x,fx,inx) n=length(x);m=length(inx); for i=1:m; z=inx(i); s=0.0; for k=1:n p=1.0; for j=1:n if j~=kp=p*(z-x(j))/(x(k)-x(j)); end ends=p*fx(k)+s; endf(i)=s; endx0=-1:0.001:1;y0=(1+25.*x0.^2).^-1plot(x0,y0,'r',x,fx,'O',inx,f)1）运行程序执行命令： X=[-1：0.4：1]fx=[0.0385 0.1000 0.5000 0.5000 0.1000 0.0385] xi=[-1:0.001:1] Lagrange(x,fx,xi)得出)(x f ，)(5X L 在同一坐标系的图像：2）运行程序执行命令：X=[-1：0.2：1]fx=[0.0385 0.0588 0.1000 0.2000 0.5000 1 0.5000 0.2000 0.1000 0.0588 0.0385]xi=[-1:0.001:1] Lagrange(x,fx,xi)得出)(x f ，)(10X L 在同一坐标系的图像：3）运行程序执行命令：X=[-1：0.1：1]fx=[0.0385 0.0471 0.0588 0.0755 0.1000 0.1379 0.2000 0.3077 0.5000 0.8000 1 0.8000 0.5000 0.3077 0.2000 0.1379 0.1000 0.0755 0.0588 0.0471 0.0385] xi=[-1:0.001:1] Lagrange(x,fx,xi)得出)(x f ，)(20X L 在同一坐标系的图像：。

龙格现象结论龙格现象是指在数值计算中，由于数值误差的积累，计算结果与真实结果之间的误差会随着步长的增加而不断增大的现象。

这一现象在科学计算中具有重要的意义，需要我们认真对待和解决。

龙格现象的出现是由于数值计算过程中的截断误差和舍入误差的积累所致。

在数值计算中，我们往往需要将连续的数学问题转化为离散的数值计算问题，通过有限的计算步骤来近似求解。

然而，由于计算机的存储和计算能力是有限的，无法处理无穷小和无穷大的数值。

因此，在计算过程中，我们不得不进行截断和舍入操作，从而引入了误差。

在数值计算中，我们通常使用一些数值方法来近似求解数学问题，如数值积分、数值微分和常微分方程的数值解等。

这些数值方法本质上都是基于一些数值逼近和插值的原理。

而在这些数值方法中，步长的选择是非常重要的。

步长过大会导致精度降低，步长过小则会增加计算的复杂性。

而龙格现象则是指当步长过大时，数值误差的积累会导致计算结果的不准确性。

为了更好地理解龙格现象，我们可以通过一个简单的例子来说明。

假设我们要计算一个函数的积分，我们可以使用数值积分的方法来近似求解。

首先，我们将积分区间等分为若干小区间，然后通过插值方法来近似计算每个小区间的积分。

当步长较小时，插值近似的误差也较小，计算结果较为准确。

但当步长增大时，插值近似的误差也会随之增大，最终导致计算结果的不准确。

针对龙格现象，我们可以通过一些方法来减小误差和提高计算精度。

首先，我们可以选择合适的数值方法和步长，以平衡计算精度和计算复杂性。

其次，我们可以使用高精度的数值计算库或算法，以减小舍入误差。

此外，我们还可以结合数值计算和符号计算的方法，以提高计算精度和可靠性。

龙格现象是数值计算中不可忽视的问题，它提醒我们在进行数值计算时要谨慎选择步长和数值方法，以保证计算结果的准确性。

同时，我们也需要不断研究和改进数值计算的方法和算法，以提高计算精度和可靠性，为科学计算提供更加准确和可靠的结果。

龙格现象matlab程序龙格现象（Runge's Phenomenon）是数值分析中的一个现象，指的是在使用等距节点进行插值时，当节点数量增多时，插值多项式会出现振荡的现象。

这个现象最早由德国数学家卡尔·龙格（Carl Runge）于1901年发现，因此得名。

龙格现象的产生是由于等距节点在插值中的特殊性质导致的。

在等距节点插值中，节点的间距是相等的，例如在区间[-1,1]上选择n 个等距节点。

利用这些节点进行插值，我们可以得到一个n次多项式来拟合所给的函数。

然而，当n增大时，插值多项式在区间的两个端点附近会出现振荡现象，即多项式值在两个端点附近迅速增大然后迅速减小，最终达到函数值的波动。

为了更好地理解龙格现象，我们可以通过一个简单的例子来说明。

考虑函数f(x)=1/(1+25x^2)，我们在区间[-1,1]上选择不同数量的等距节点进行插值。

首先，选择5个等距节点进行插值，得到插值多项式P5(x)。

在图表中我们可以观察到，P5(x)在区间的两个端点附近出现了振荡现象。

随着节点数量的增加，振荡现象变得更加明显。

当节点数量增加到10时，插值多项式P10(x)的振荡现象更加明显。

这说明了龙格现象的存在。

为了解决龙格现象，我们可以采用非等距节点进行插值。

非等距节点插值可以通过使用更加合适的节点分布来减小振荡现象。

例如，在区间[-1,1]上使用Chebyshev节点进行插值可以有效地减小龙格现象的影响。

龙格现象在实际应用中具有重要的意义。

在数值计算中，我们经常需要使用插值来近似函数值。

如果不了解龙格现象，仅仅选择等距节点进行插值可能会导致误差的增大。

因此，了解龙格现象的存在和原因对于选择合适的插值方法具有重要的指导意义。

龙格现象是等距节点插值中的一个振荡现象，会导致插值多项式在区间的两个端点附近出现振荡。

为了解决龙格现象，可以采用非等距节点进行插值。

了解龙格现象的存在和原因对于数值计算具有重要的指导意义。

切比雪夫多项式解决龙格现象
近年来，由于信息技术的快速发展，许多技术人员倾向于
使用“切比雪夫多项式”解决龙格现象。

切比雪夫多项式是创
造于19世纪末期的数学工具，可以精确描述一维变化的数字
曲线。

特别地，它可以高度精确拟合一系列的数据，从而实现
高效的数据处理，降低龙格现象的出现几率。

龙格现象是指在计算机环境下，数据处理发生错误，导致
结果出现偏差，甚至令人十分诡异和无法解释的现象。

虽然由
技术人员精心设计，但其数学性质会使得计算机在处理数据时
存在一定误差，往往会仅有很小份量的数据出现有规律的错误。

切比雪夫多项式主要利用其弹性特性，可以对一系列的数
据进行精确拟合，从而实现高精度的数据处理，降低数据偏差
的出现几率。

例如，切比雪夫多项式可以在大量数据收集和分
析完毕后，准确地计算出偏差，进而使得程序表现正常，避免
数据出现偏差，减少龙格现象的出现几率。

其次，切比雪夫多项式不仅有利于减少数据偏差，而且还
可以提高计算效率。

在实际应用中，切比雪夫多项式可以提供
一组计算速度较快、精确度较高、处理结果可用性好的数学方法，以及更好地处理复杂数据并获得准确结果，这就有助于企
业加快项目进度，提升数据处理精度。

总而言之，切比雪夫多项式不仅有效地减少了龙格现象的
出现几率，而且可以显著地提升计算速度和精度，从而更有效
地管理数据，拓展业务，改善政务民生服务。

hermite多项式龙格现象
关于Hermite多项式和龙格现象，我可以从多个角度进行解释。

首先，让我们先来了解一下Hermite多项式。

Hermite多项式
是一类特殊的多项式，通常用来解决量子力学和概率论中的问题。

它们是Hermite微分方程的解，这些微分方程在量子力学中具有重
要的物理意义。

Hermite多项式在概率论中也有广泛的应用，特别
是在描述正态分布的概率密度函数时。

现在，让我们来谈谈龙格现象。

龙格现象是指在使用插值多项
式逼近某些函数时出现的现象。

当我们使用高次插值多项式来逼近
某些函数时，虽然在节点附近的逼近效果很好，但在远离节点的地
方却出现了振荡的现象，这就是龙格现象。

龙格现象对于数值计算
和插值问题具有重要的启示意义，需要我们谨慎选择插值多项式的
次数和节点的位置，以避免出现龙格现象导致的误差增大。

结合Hermite多项式和龙格现象，我们可以讨论在使用
Hermite插值多项式逼近某些函数时可能出现的龙格现象。

由于Hermite插值多项式是在给定节点处不仅给出函数值，还给出导数值，因此可以更好地逼近某些函数。

但是，当我们使用高次
Hermite插值多项式时，仍然可能会出现龙格现象，导致远离节点的地方逼近效果变差，甚至出现振荡现象。

总的来说，Hermite多项式和龙格现象都是数学和数值计算中重要的概念，它们在不同领域有着广泛的应用和深远的影响。

我们需要深入理解它们的性质和特点，以更好地应用于实际问题的求解和分析中。

埃尔米特龙格现象埃尔米特龙格现象一、前言在量子力学中，埃尔米特矩阵和波函数的展开系数被称为埃尔米特龙格函数。

埃尔米特龙格函数具有非常重要的物理意义，可以用于描述粒子在不能互相干扰的小箱子中运动的特性。

本文将从埃尔米特矩阵、埃尔米特龙格函数等方面来探究其相关的物理现象。

二、埃尔米特矩阵1. 定义埃尔米特矩阵是指具有对称性质的矩阵。

对于给定的矩阵A，若它的转置矩阵A^T与其共轭矩阵A†相等，即A=A†，则该矩阵就是埃尔米特矩阵。

2. 性质（1）埃尔米特矩阵的特征值都是实数；（2）埃尔米特矩阵的不同特征值所对应的特征向量是正交的；（3）任何一个矩阵都可以被分解成由普遍埃尔米特子矩阵和特殊埃尔米特子矩阵的直和。

其中，普遍埃尔米特子矩阵有不同的特征值，而特殊埃尔米特子矩阵只有一个特征值。

三、埃尔米特龙格函数1. 定义埃尔米特龙格函数Hn(x)可以通过下面的递归公式来定义：H0(x) = 1, H1(x) = 2x,Hn(x) = 2xHn-1(x) - 2(n-1)Hn-2(x) (n > 1)2. 物理意义在量子力学中，对于一维的粒子，其累积概率分布函数可以用埃尔米特龙格函数来表示。

即对于一个处于态n的粒子，其概率分布函数可以表示为：|Ψ(x)|2 = (1/2^n n! √π) exp(-x^2/2) Hn(x)^23. 应用除了上述描述粒子分布的应用外，埃尔米特龙格函数还常常用于描述粒子在各向同性非调和势场中的态。

特别地，当势场呈现出对称性时，例如球对称势场、径向势场等，埃尔米特龙格函数就成为了描述其状态的理想工具。

四、结论本文主要探究了埃尔米特矩阵和埃尔米特龙格函数在物理方面的应用。

通过对埃尔米特矩阵的定义和性质的分析，我们可以更好地理解埃尔米特龙格函数的含义和物理意义，并将其应用于描述粒子的分布和状态。

在实际问题中，埃尔米特龙格函数被广泛应用于各种领域，例如光学、量子力学等等。

随着技术和研究方法的不断进步，相信埃尔米特龙格函数的应用还将进一步得到发展和完善。